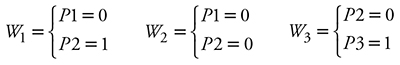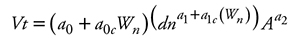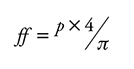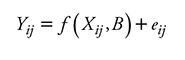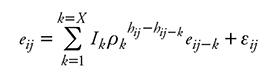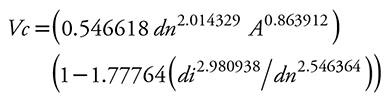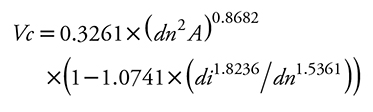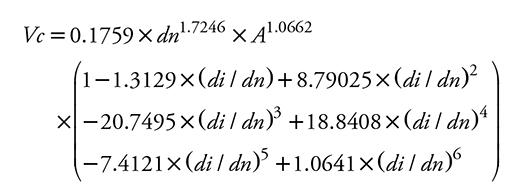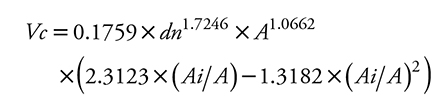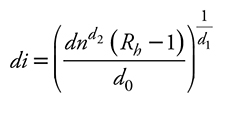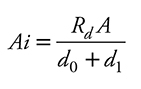Introducción
Las plantaciones forestales comerciales (PFC) son una opción para disminuir la presión sobre los bosques naturales de México (CONAFOR-COLPOS, 2012). Su establecimiento en la década reciente ha incrementado significativamente (CONAFOR, 2014) y han abastecido de productos maderables a la industria (Rodríguez-Juárez et al., 2014). El género Eucalyptus es uno de los más utilizados como fuente de germoplasma en PFC (Juárez-Palacios et al., 2013; CONAFOR, 2014) y ocupa el segundo lugar nacional en las especies establecidas entre 2000 y 2014 con una superficie de 32 452 ha (18.31 %) (CONAFOR, 2015).
Eucalyptus urophylla es la especie más usada en los climas tropicales (CONAFOR, 2012) y es plantada en el mundo por su rápido crecimiento (Rosa et al. 2011), su intervalo altitudinal amplio (0 a 1200 msnm) y sus requerimientos edáficos mínimos para su establecimiento (Nieto y Rodríguez, 2003). Además, se adapta a lugares con precipitaciones medias, entre 2000 y 3000 mm anuales y a temperaturas promedio de 24 a 28 °C (Vieira y Bucsan, 1980).
El volumen maderable de las plantaciones es un indicador del potencial productivo de un rodal (Moret et al., 1998) y puede ser dividido en volumen total (Vt) y volumen comercial (Vc) (Chauchard y Sbrancia, 2005). De acuerdo con Prodan et al. (1997), para estimar Vc de árboles individuales existen tres metodologías: 1) implementar funciones de Vt con la restricción de un diámetro o altura límite, en las cuales se omite en la predicción la porción del árbol restante (Gilabert y Paci, 2010), un ejemplo son las ecuaciones de volumen de fuste limpio (Vtfl); 2) ajustar funciones que describan el perfil del árbol y después estimar el Vc a un diámetro definido o una altura dada (Chauchard y Sbrancia, 2005), para lo cual se usa como base una función de ahusamiento; 3) implementar la razón proporcional entre un volumen predeterminado y el Vt para distintas clases de árboles (Pece, 1994), con funciones de razón volumétrica (frv).
El concepto de frv fue introducido por Honner (1967), desarrollado por Burkhart (1977) y complementado con algunas variantes por Alder (1980), Cao et al. (1980), Van Deusen et al. (1981) y Parresol et al. (1987). Su eficiencia fue discutida por Prodan et al. (1997), quienes señalan que el empleo de este tipo de funciones permite calcular de forma precisa el volumen a cualquier dimensión de diámetro o altura definida de una forma más simple, que el ajuste o el uso de un modelo de ahusamiento. Además, Gilabert y Paci (2010) compararon los resultados de este tipo de sistemas en dos especies, en Chile, con los de un ajuste de funciones de ahusamiento y señalaron la precisión de los resultados y sencillez al obtenerlos.
Estas funciones porcentuales son un sistema de ecuaciones integrado por una ecuación de Vt y una ecuación de razón de volumen (r), que operan en conjunto para estimar el volumen por tipos de productos por árbol (Vc) (Chauchard y Sbrancia, 2005; Gilabert and Paci, 2010); r corresponde al cociente del volumen hasta un porcentaje de utilización o un diámetro no comercial (Vi) y el Vt del fuste (Vi/Vt) (Trincado et al., 1997; Barrio et al., 2007; Barrios et al., 2014).
Los modelos que integran una frv son conceptual y matemáticamente simples, generan resultados consistentes, pueden ser utilizados en la estimación del Vc en diferentes rangos de diámetro y altura sin implementar métodos numéricos complejos de integración y permiten acoplarse a cualquier tipo de función de Vt (Chauchard y Sbrancia, 2005). Además, a partir de variables independientes, con una función de razón (r) se puede estimar el diámetro mínimo (di) o altura comercial (Ai) por tipo de producto (Chauchard y Sbrancia, 2005).
La demanda creciente de productos maderables de alta calidad y los cambiantes estándares de la industria del aserrío, ha causado el remplazo del concepto de volumen total (Vt) de madera, como indicador del rendimiento de las PFC, por el volumen de productos (Vp) o volumen comercial (Vc), conceptos importantes en la planificación, manejo y valoración de este tipo de masas forestales. Por ello, bajo la hipótesis de que mediante la representación matemática de las relaciones funcionales entre las variables de un árbol es posible realizar estimaciones precisas de Vt y Vc, el objetivo de este estudio fue proponer una herramienta conformada por un modelo de volumen total y un modelo de razón de volumen para cuantificar los volúmenes totales y comerciales en plantaciones comerciales provenientes de semilla y de dos fuentes clonales de E. urophylla en el sureste mexicano.
Materiales y Métodos
Área de estudio
Las PFC de E. urophylla evaluadas están en el municipio de Huimanguillo, Tabasco, México, el clima es cálido húmedo (Am), temperatura media anual de 26 °C y una precipitación promedio anual de 2500 mm. Los suelos son Phaeozem con un relieve de tipo lomerío (INEGI, 2005).
Descripción de la muestra y estimación del volumen total
La muestra provino de 727 árboles de E. urophylla, de estos, 175 pertenecen a los clones medidos en 2007 (P1), 93 a los clones medidos en 2014 (P2) y 459 a los árboles provenientes de semilla medidos en 2007 (P3). La edad de los clones (P1 y P2) fluctuó de uno a siete años, mientras que los provenientes de semilla (P3) variaron de dos a once años.
Los árboles muestra se eligieron según su condición morfológica, para cubrir la mayor variabilidad fenotípica posible dentro de las plantaciones, la variabilidad entre sus dimensiones de dn y A, y además de su distribución de edad. En cada árbol se midió el diámetro normal (dn) y altura total (A), y después fueron derribados y troceados para medir su diámetro y altura a diferentes secciones (di y Ai) sobre el fuste a 1 m de distancia entre mediciones, iniciando con el diámetro y altura del tocón (dt y ht, respectivamente). Para obtener el volumen de cada troza (Vtroza) se utilizó la fórmula de Newton y del cono para la punta (Vpunta). El volumen total (Vt), se calculó con el método de trozas traslapadas propuesto por Bailey (1995).
Comparación de árboles entre poblaciones
Para determinar diferencias entre las poblaciones de clones (P1 y P2) con respecto a los árboles provenientes de semilla (P3), se probaron las siguientes hipótesis sobre las variables dn y A. El análisis se realizó contrastando P1 vs. P2, P1 vs. P3 y P2 vs. P3.
Hipótesis nula (Ho). Las poblaciones son iguales entre sí.
Hipótesis alternativa (Ha). Las poblaciones son diferentes entre sí.
Para verificar si árboles de las tres poblaciones presentan diferencias en Vt y bajo el supuesto que dos árboles pueden tener el mismo volumen sin presentar forzosamente las mismas dimensiones de dn y A, se ajustó el Vt de los dos tipos de clones y las plantaciones de semilla. Además, para cuantificar el efecto de cada tipo de árbol ya sea clon o derivado de semilla, se insertó una variable indicadora en el modelo de volumen de Schumacher-Hall (Draper and Smith, 1966) (Cuadro 1). Los análisis se realizaron con SAS 9.2. (Institute Inc. Statistical Analysis System, 2008).
En el modelo de volumen de Schumacher-Hall (1) se programaron las variables indicadoras (Wn) de acuerdo con el contraste realizado para cada población.
La expresión del modelo es de la forma siguiente:
donde, a0, a1 y a2 son los parámetros de regresión, mientras que a 0c y a1c son los parámetros de adición para las distintas poblaciones.
Estimación del índice de esbeltez y factor de forma
El cálculo del índice de esbeltez (IE) se realizó para verificar el grado de estabilidad mecánica de los árboles contra la presencia de vientos o huracanes y se obtuvo al dividir el promedio de A entre el promedio de dn, como lo reportan Arias (2004 y 2005) y Nájera y Hernández (2008). Para verificar si estos son estadísticamente diferentes entre sí, se realizó un ANDEVA de un factor para el IE promedio entre las poblaciones a un nivel de p≤0.05.
El factor de forma (ff) se estimó mediante el cálculo de la pendiente (p) del volumen fustal con la variable combinada (dn 2 A), y después, la estimación del factor con respecto a un cilindro teórico se realizó con la fórmula siguiente:
Los modelos de volumen total ajustados son los de Da Cunha y Guimaraes (2009), Corral-Rivas y Návar-Cháidez (2009), Tschieder et al. (2011) y Casnati et al. (2014) y los de tipo estándar o de doble entrada (Prodan et al., 1997), solo presentan diferencia entre ellos en la forma y el número de parámetros a ser estimados (Cuadro 1).
La selección del modelo mejor se basó en el valor mayor del coeficiente de determinación ajustado por el número de parámetros (R2aj) y los valores menores en la suma de cuadrados del error (SCE) y la raíz del cuadrado medio del error (RCME), así como la mejor distribución gráfica de residuales. Con el modelo que cumpliera lo ya descrito y para evitar que aumentara la varianza a mayor diámetro (hererocedasticidad), se utilizó regresión ponderada (Cailliez, 1980; Tschieder et al., 2011) en la cual se usaron las variables de ponderación: 1/dn, 1/dn2, 1/dnA y 1/d2 A. Las estimaciones de volumen fustal para las tres poblaciones se hicieron con los modelos corregidos.
Modelos de razón volumétrica
La razón volumétrica (r) se calculó como el cociente del volumen a distintas alturas y diámetros y el volumen total (Vi/Vt). Para ello se utilizan modelos de razón de volumen que usan el dn, di, A y Ai como variables independientes y se utilizaron con éxito en otros estudios (Pece, 1994; Chauchard y Sbrancia, 2005; Barrio et al., 2007; Gilabert and Paci, 2010; Barrios et al., 2014) (Cuadro 2).
Cuadro 2 Modelos de razón de volumen utilizados en PFC de E. urophylla.
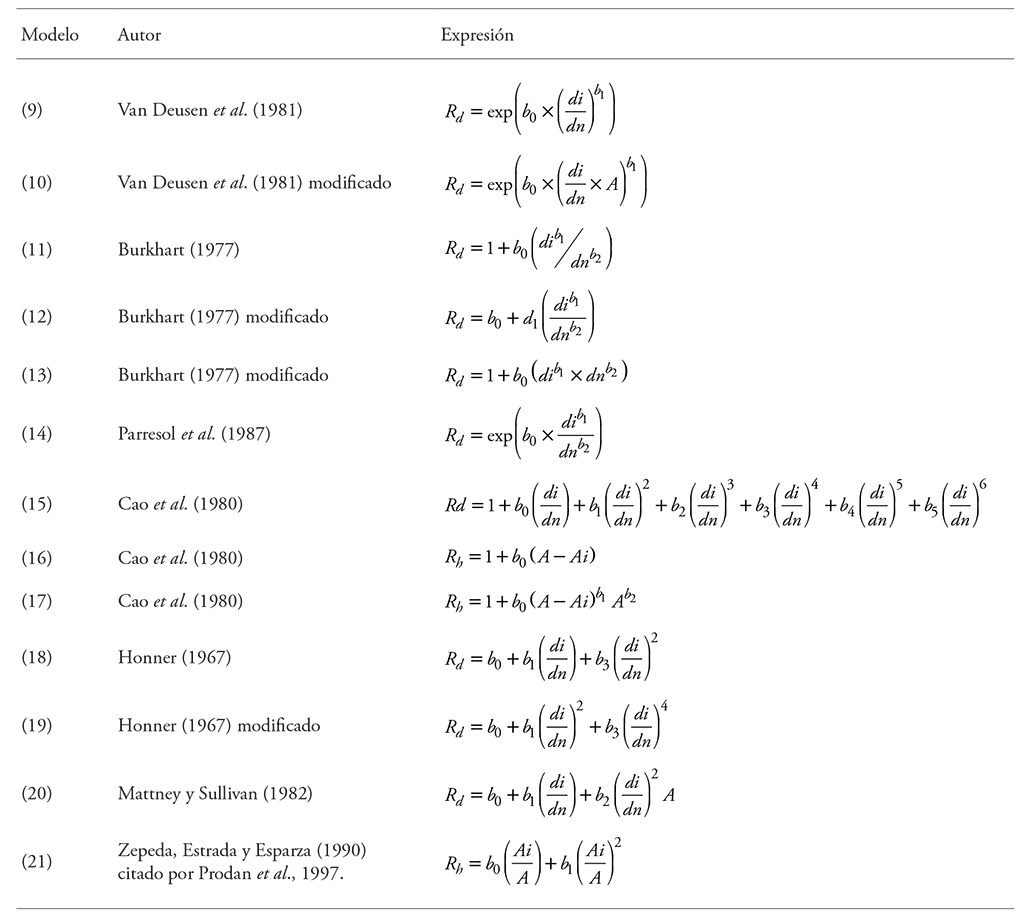
Rd es la razón de volumen que utiliza como variables independientes el diámetro normal (dn) y diámetro a distintas alturas (di); Rh, la que incluye en el modelo la altura total A) y la altura a diferentes secciones en el fuste (Ai); b0, b1, b2, b3, b5 y b6 son los parámetros a estimar.
En el ajuste de estos modelos se usaron 1958, 2113 y 6060 pares de datos di-Ai, de las poblaciones P1, P2 y P3, respectivamente. Como primera fase, los modelos de razón de volumen se ajustaron sin incluir el término del error con el propósito de verificar las tendencias de los residuales y el valor del estadístico de autocorrelación de Durbin-Watson (DW), como lo indican Barrios et al. (2014).
Para ajustar este tipo de modelos se calcula el volumen a diferentes alturas y diámetros, para así obtener una razón volumétrica, por lo cual es inevitable la estructura longitudinal de la información utilizada donde las diferentes medidas a lo largo del fuste tienen una correlación estrecha por ser del mismo individuo. Debido a ello se usó un modelo de tipo autoregresivo en tiempo continuo (CAR) para corregir la estructura de los errores (Zimmerman y Nuñez-Antón, 2001), y la expresión del modelo es:
donde Yij es el vector de la variable dependiente; Xij la matriz de las variables independientes; B es el vector de los parámetros a estimar; eij es el j-ésimo residuo del árbol i; Ik =1 para j>k y es 0 para j≤k; ρ k es el parámetro autoregresivo de orden k a estimar. hij -hij-k es la distancia que separa la altura de medición j-ésima de la altura de medición j-ésimo-k en cada árbol (hij >hij-k) y, εij es el error aleatorio (Barrios et al., 2014). El número de retrasos aplicados en el modelo CAR(X) se estableció al evaluar el estadístico DW, que deberá ser cercano a 2 como lo menciona Verbeek (2004).
Ajuste de modelos y criterios de evaluación
El ajuste estadístico de los modelos de Vt y de r se realizó con el procedimiento MODEL en SAS 9.2 y la técnica de máxima verosimilitud (FIML) (Institute Inc. Statistical Analysis System, 2008).
La evaluación y selección del mejor modelo se realizó con el valor mayor de R2aj y los valores menores en la SCE y RCME, además de las pruebas de independencia (DW) y normalidad de la frecuencia de los residuos (Da Cunha y Guimaraes, 2009). La homogeneidad de varianza se evaluó de forma gráfica (Tschieder et al., 2011), mientras que la capacidad predictiva de los mejores modelos se evaluó estimando el sesgo absoluto (Ē) y la desviación agregada (DA %) para cada población.
Determinación de volumen comercial (Vc)
Para estimar el volumen comercial en cualquier punto a lo largo del fuste, se conformó un sistema de cubicación compuesto por el mejor modelo de Vt y r, para cada una de las poblaciones. Con el Vt del árbol y aplicando el modelo de razón volumétrica, se tiene que el volumen comercial es el producto de la multiplicación de los resultados de las dos ecuaciones (Chauchard y Sbrancia, 2005). La evaluación de la precisión de las estimaciones se realizó con un gráfico de tendencia lineal de predichos contra los valores observados (Pece, 1994).
Resultados y Discusión
Comparación de Vt, dn y A de árboles entre poblaciones
El ajuste del modelo Schumacher-Hall fue aceptable (Cuadro 3) y los valores de los parámetros en la variable indicadora Wn fueron significativos (p≤0.05), por lo cual se ratifica que las tres poblaciones son diferentes en promedio de dn y A, además del promedio en el Vt, con tasas de crecimiento distintas. Esta diferencia entre los clones de 2007 y 2014 se debe a que la selección para reproducir estos últimos se realizó con base en las mayores dimensiones de dn o A, sin tomar en cuenta el Vt o el factor de forma.
Cuadro 3 Parámetros estimados y estadísticos de bondad de ajuste del modelo de Vt de Schumacher-Hall con variables indicadoras en las tres poblaciones de E. urophylla en Huimanguillo, Tabasco, México.

SCE: Suma de cuadrados del error; RCME: Raíz del cuadrado medio del error; R2aj: Coeficiente de determinación ajustado; Eea: Error estándar aproximado; an: Parámetros a estimar
Estimación del índice de esbeltez, factor de forma y volumen total
Una vez identificado que las tres poblaciones se debían analizar por separado, se calculó el IE. Los valores promedio por población fueron 114, 122 y 118 cm cm-1 para P1, P2 y P3, respectivamente. El valor promedio inferior de IE sugiere que los clones medidos en 2007 fueron seleccionados más por su crecimiento en diámetro que por su crecimiento en altura, porque es más práctico y sencillo tomar solo el diámetro normal como indicador de producción. En la prueba de ANDEVA la diferencia mínima significativa fue 4.77 para el IE; además, las medias del índice de esbeltez entre las poblaciones son estadísticamente diferentes (P1=122.571, P2=112.168 y P3=93.804), porque el valor de probabilidad de error es bajo (Pr>F=<0.0001).
Estos índices son semejantes a los de especies tropicales de rápido crecimiento como E. Nitens para el cual IE=124 (Díaz et al., 2012), Hieronyma alchorneoides (IE=111) y Terminalia amazonia (IE=106) (Arias, 2005). No obstante, debido a que el IE es superior a la relación de crecimiento 1:1 entre el dn y A, se asume que los árboles son delgados y se deberá tener cuidado al aplicar intensidades de aclareo fuertes (Arias, 2005; Díaz et al., 2012), por la susceptibilidad de daños mecánicos por efecto de los vientos en las PFC (Wilson y Oliver, 2000).
Respecto al ff, la forma de los árboles de las poblaciones P2 y P3 fue igual, de tipo cónico con un valor de 0.34, mientras la población P1 es diferente (ff=0.45), lo cual indica mayor semejanza a una forma paraboloide en los árboles.
Por los estadísticos de ajuste de los mejores modelos de Vt, determinados por los valores mayores en R2aj, los valores menores en la SCE, RCME y la significancia del valor de los parámetros (p<t), el modelo de mejor ajuste a los datos para P1 y P3 fue el de Schumacher-Hall, y para P2 el modelo de Spurr (Cuadro 4).
Cuadro 4 Parámetros estimados y estadísticos de ajuste de los modelos de Vt para las tres poblaciones de E. urophylla en Huimanguillo, Tabasco, México.
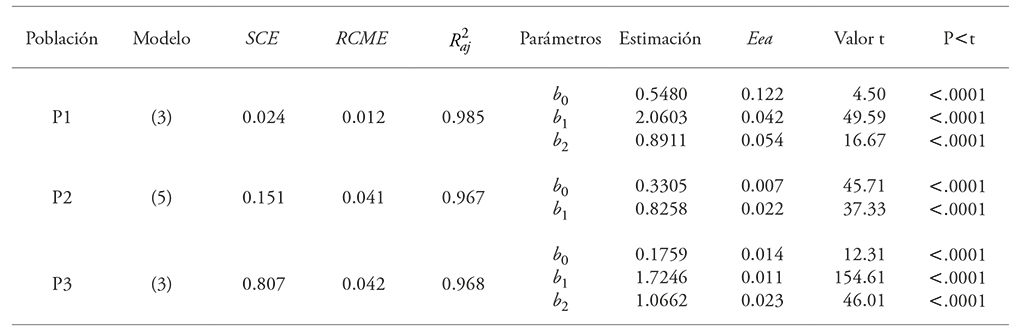
SCE: Suma de cuadrados del error; RCME: Raíz del cuadrado medio del error; R2aj: Coeficiente de determinación ajustado; Eea: Error estándar aproximado; bn: Parámetros estimados.
En los tres ajustes, todos los parámetros obtenidos fueron significativos con una confiabilidad de 95 %, la prueba de normalidad de Shapiro-Wilk presentó valores superiores a W=0.92 y un nivel de Pr<W=0.0001, mientras que las gráficas de residuales presentaron tendencia hacia una línea recta y con forma de campana de Gauss, lo cual indica normalidad de los datos. Sin embargo, en la prueba de homogeneidad de varianzas se observaron tendencias muy marcadas, por lo cual se asumen problemas de heterocedasticidad y, al corregirla, la variable de ponderación con mejores resultados fue 1/dn2A, con la cual se logró una distribución homogénea de los de residuales (Figura 1). La estimación de los parámetros y los indicadores de bondad de ajuste de las ecuaciones de volumen fustal para las poblaciones P1, P2 y P3 se muestran en el Cuadro 5.
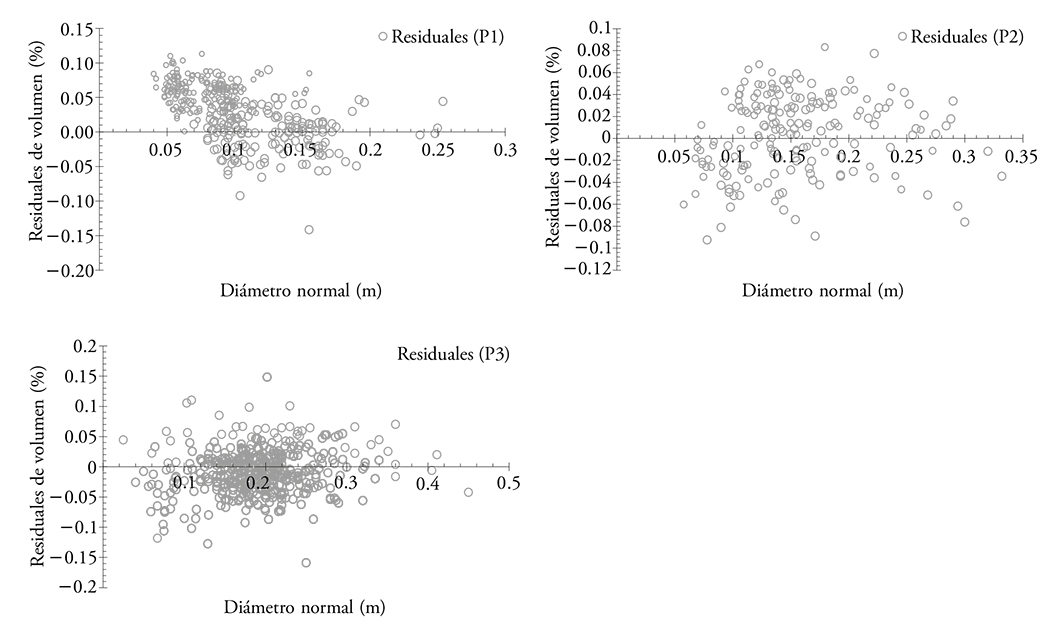
Figura 1 Distribución de residuales de Vt con respecto al diámetro normal (dn) de los modelos de mejor ajuste, corregidos por heterocedasticidad para las plantaciones P1, P2 y P3 de E. urophylla en Huimanguillo, Tabasco, México.
Cuadro 5 Parámetros estimados y estadísticos de bondad de ajuste de los modelos de Schumacher-Hall (P1 y P3) y Spurr (P2) corregidos por heterocedasticidad para las tres poblaciones de E. urophylla en Huimanguillo, Tabasco, México.
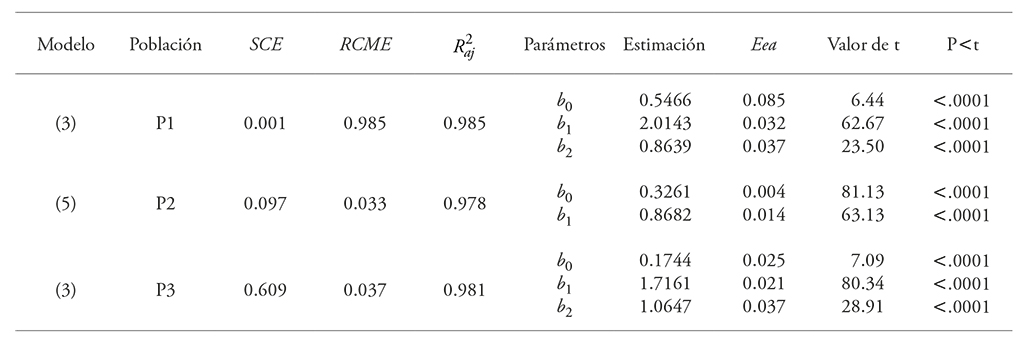
SCE: Suma de cuadrados del error; RCME: Raíz del cuadrado medio del error; R2aj: Coeficiente de determinación ajustado; Eea: Error estándar aproximado; bn: Parámetros estimados.
En las estimaciones realizadas con los modelos corregidos, así como sus proyecciones se consideró el IE promedio en el cálculo de la altura para cada una de las poblaciones. Y se observa que la selección del material vegetativo para producir los clones medidos en 2014, se realizó tomando las muestras de los mayores dn y A, sin considerar el Vt debido a que la línea correspondiente a esta población es la más baja de las tres y se refiere a que los árboles de esta población son más esbeltos (forma cónica) y tienen menor cantidad de volumen, comparados con los clones de 2007 y los árboles provenientes de semillas (Figura 2).
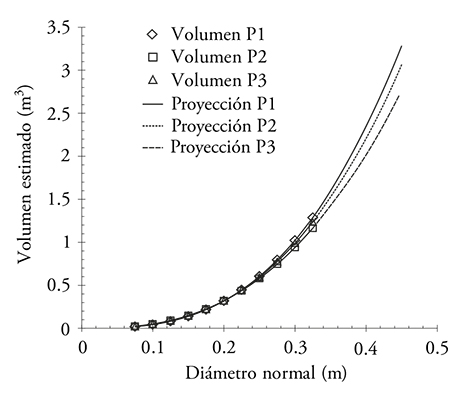
Figura 2 Estimación y proyección del Vt con el modelo de Schumacher-Hall para P1 y P3 y de Spurr para la población P2 de E. urophylla en Huimanguillo, Tabasco, México.
Al tomar como referencia las plantaciones de clones de 2007, las cuales tienen mayor cantidad de Vt que las demás, se observó que hasta la categoría diámetrica de 0.30, que en promedio es la máxima en las tres poblaciones, las plantaciones de 2014 tienen 3.60 % menos Vt respecto a las cultivadas en 2007, y 1.47 % menos que los árboles provenientes de semilla (Figura 2). Las proyecciones fuera de la muestra hasta 45 cm de diámetro indican que las diferencias de la población P2 aumentan a 11.35 % y de P3 a 4.72 %, con respecto al Vt proyectado de P1.
Modelos de razón volumétrica
Al realizar un primer ajuste los valores de los parámetros y los estadísticos obtenidos fueron adecuados, pero se observó que los residuales presentaron una tendencia heterocedástica y el valor de DW para P1 varió de 0.59 a 1.03, en P2 de 0.13 a 0.82, y en P3 de 0.44 a 1.09, lo cual muestra correlación entre los datos. Por lo anterior, y tras el análisis gráfico de la función de autocorrelación (ACF) en las tres poblaciones, se empleó una estructura auto regresiva de primero, segundo y tercer orden para corregir la autocorrelación de los errores (CAR(X)) y se seleccionó la que mejores resultados arrojara (Cuadro 5).
Para el modelo de Rd (11) de la P2 después de haber corregido la autocorrelación, se decidió que este fuera el mejor con base en lo propuesto por Fuentes et al. (2001a y 2001b) sobre la ausencia de correlación para valores en este estadístico superiores e iguales a 1 y a las estimaciones más precisas que generaba este modelo con respecto al resto. Esto se debe a que los valores de DW evidencian una correlación serial del tipo autoregresiva CAR(1) debida a la existencia de secciones con diámetros en el fuste a una altura dada, que se relacionan con el diámetro similar o igual a una distinta Ac (Pérez, 1996; 1998) y porque al aplicar un retraso más a los errores y mejorar el valor de DW, se perdía calidad en el ajuste al presentar parámetros no significativos, esto es, R2aj menores o estimaciones sesgadas con respecto a los datos observados.
En las tres poblaciones analizadas se eligió un modelo de razón de volumen de tipo Rd y uno de R h, con la finalidad de utilizar cualquiera de estas dos variantes en la estimación del Vc. Esta selección se hizo con base en los valores más altos de R2aj, y los valores más bajos de SCE y RCME, como lo reportan Trincado et al. (1997) y Barrio et al. (2007). El ajuste de los mejores modelos dio resultados satisfactorios y los valores de los parámetros fueron todos diferentes de cero (p≤0.05) (Cuadro 6).
Cuadro 6 Parámetros estimados y estadísticos de ajuste de los modelos de razón de volumen que mejor ajustaron a cada población en PFC de E. urophylla, en Huimanguillo, Tabasco, México.
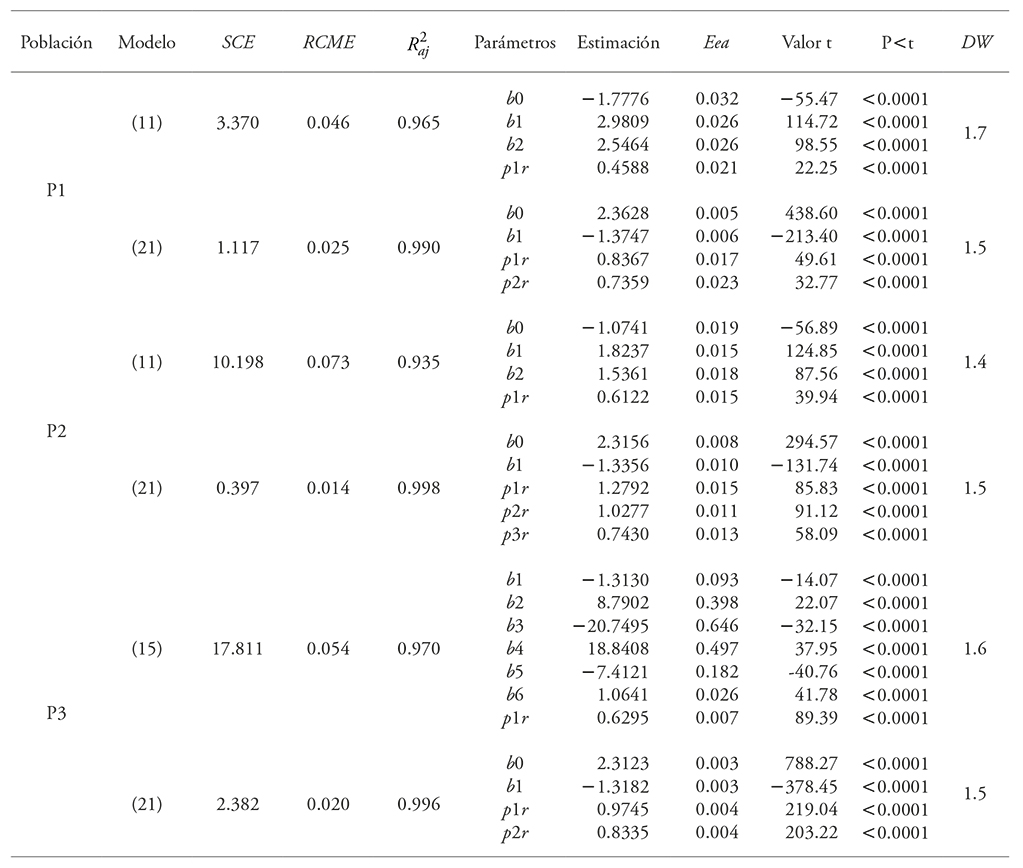
SCE: Suma de cuadrados del error; RCME: Raíz del cuadrado medio del error; R2aj: Coeficiente de determinación ajustado; Eea: Error estándar aproximado; bn: Parámetros estimados; p1r, p2r y p3r indican el orden y el número de retrasos aplicados en el modelo tipo CAR(X) aplicado.
Al verificar la distribución de los residuales (Figura 3) para los modelos Rd en las poblaciones P1 y P3, los resultados concuerdan con los mencionados por Barrios et al. (2014) en E. grandis, donde la distribución de éstos es homocedástica (a y c). No obstante, en P2 hay una ligera presencia de heterocedasticidad sin ser preocupante en las estimaciones realizadas con este modelo, ya que al calcular la razón de volumen con modelos de mejor distribución, el error absoluto fue menor en el modelo seleccionado (b). Los modelos Rh en ninguno de los casos muestran una tendencia (d, e y f), lo cual concuerda con lo expuesto por Pece (1994) al utilizar este tipo de modelos en E. pellita.
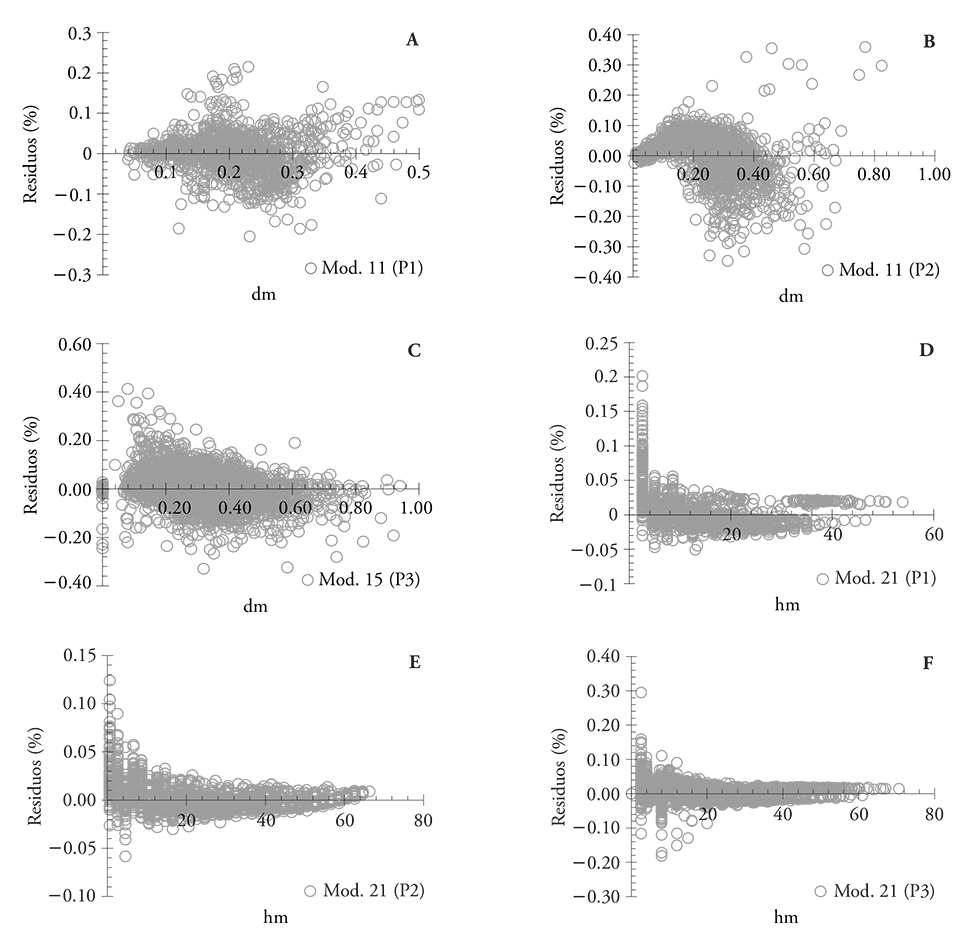
Figura 3 Residuales de los mejores modelos de razón volumétrica para árboles de las tres poblaciones de E. urophylla evaluadas en Huimanguillo, Tabasco, México
Al estimar el sesgo absoluto (Ē) y la desviación agregada (DA%) para cada población, y con la finalidad de verificar la precisión de las estimaciones con los modelos de tipo Rd y Rh, respectivamente, se observó que los valores de estos son bajos para las tres poblaciones, sin exceder 1.29 % para DA en ninguna situación (Cuadro 7).
Estimación de volumen comercial de árboles
Los modelos ajustados permiten encontrar la razón de como se acumula el volumen a medida que se llega a la altura total partiendo de la altura de tocón; además, la relación entre el volumen total y el volumen correspondiente a un diámetro o altura límite de utilización. Las expresiones para obtener el Vc de árboles individuales en cada una de las poblaciones están integradas por un modelo de Vt y r, que al multiplicarlos tendrán como resultado el Vc a cualquier diámetro o altura de aprovechamiento definido. Las ecuaciones resultantes se presentan a continuación.
Ecuaciones de Vc para la población P1.
Ecuaciones de Vc para la población P2.
Ecuaciones de Vc para la población P3.
Al comparar gráficamente de las predicciones de Vc obtenidas con el método de razón de volumen contra el volumen acumulado el resultado es cercano a una línea recta (Figura 4), y al aplicar una regresión lineal a estos datos muestra, por el valor de R2, que al utilizar los modelos de tipo Rd la estimación de la muestra es mayor a 94 % y al usar los modelos de tipo R h es 96 %. Al verificar la precisión y el sesgo absoluto tomando como referencia el valor de R2 y la diferencia en su aproximación a la unidad, para los modelos de Rd es 3.0, 5.4 y 5.5 % en las poblaciones P1, P2 y P3, respectivamente; mientras que en los modelos de tipo Rh es 1.1, 3.1 y 2.6 % (Figura 4). La tendencia observada y los valores de los ajustes entre los valores predichos y los observados concuerdan con lo indicado en estudios realizados por Pece (1994) en Eucalyptus pellita, Chauchard y Sbrancia, (2005) en P. radiata, y Barrios et al. (2014) en E. grandis.
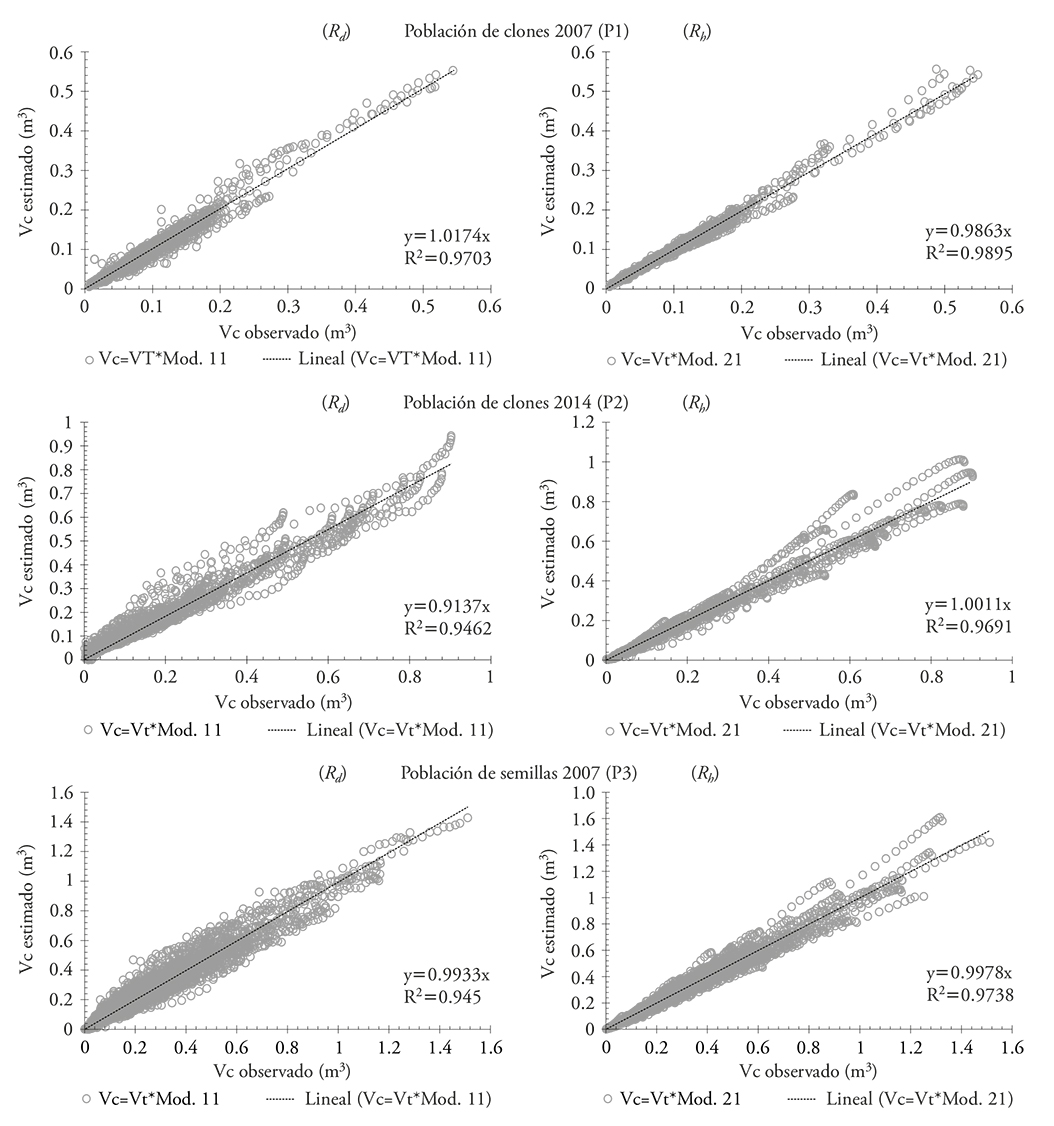
Figura 4 Volumen comercial (Vc) estimado vs. Vc predicho para las poblaciones P1, P2 y P3, utilizando los modelos seleccionados.
Para estimar algún diámetro comercial a una determinada altura comercial para las poblaciones P1 y P2, se despeja di de la ecuación (11) y se remplaza Rd por Rh (ecuación 30), de acuerdo con el procedimiento de Trincado et al. (1997), utilizando los parámetros estimados para cada modelo y sustituyéndolos en la ecuación resultante. En el caso de que se requiera realizar el cálculo inverso, es decir, estimar Ac para un diámetro específico en las tres poblaciones, se despeja Ai de la ecuación (21) y se sustituye Rh por Rd (ecuación 31).
Para la P3, en el modelo 15 de R d la estimación del di a cualquier altura se obtiene mediante una aproximación numérica con la herramienta SOLVER de Excel, debido a que al despejar esta variable de la ecuación existen raíces que matemáticamente pueden reducirse hasta desaparecer.
Los modelos seleccionados muestran consistencia en la determinación volumétrica total y comercial, no presentan entrecruzamiento de valores y permiten estimar de forma directa el diámetro del fuste a una altura establecida, o bien, la altura del fuste a un diámetro límite de utilización. Estos modelos en conjunto son altamente confiables y permiten realizar estimaciones de distribución de productos, elaborar tablas de volúmenes comerciales para cualquier diámetro o altura de aprovechamiento establecido por la industria del aserrío o cálculos de valoración económica de las plantaciones. Para la validación de los modelos generados son necesarios datos de inventarios y de cosecha operativa.
Conclusiones
Las relaciones funcionales entre las variables dn y A del árbol son confiables en la estimación del volumen total y comercial. Además, el ajuste de sus expresiones matemáticas sugiere que si la intención de los dueños o inversionistas es maximizar el volumen a obtener en las plantaciones de clones de Eucalyptus urophylla, la selección de árboles con fines de reproducción clonal deberá contemplar un análisis del volumen total del árbol, más que de las dimensiones de diámetro normal y altura total. De igual manera en este tipo de plantaciones de rápido crecimiento es necesario mantener la actualización de estos modelos al mismo ritmo del remplazo del material vegetativo usado y de las prácticas culturales aplicadas, pues se observó que en un lapso relativamente corto (7 años) hay cambios estadísticamente significativos en las poblaciones y, por lo tanto, en la confiabilidad de los modelos para estimar la cosecha maderable potencial y el valor de la inversión forestal.











 texto en
texto en