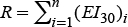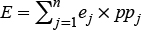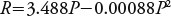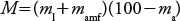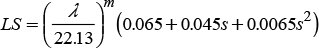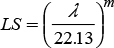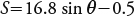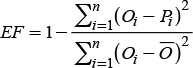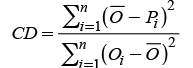Introducción
México tiene graves pérdidas de suelo ocasionadas por la erosión hídrica. La Secretaria de Medio Ambiente y Recursos Naturales (SEMARNAT, 2008), con base en un estudio realizado por la Universidad Autónoma Chapingo en 2003, informó una erosión hídrica potencial en 42 % de la superficie nacional; además informó erosión hídrica actual en 22.73 millones ha, de la cuales 56.4 % estaba en un nivel de erosión ligero (5 a 10 Mg ha-1 año-1), 39.7 % en situación moderada (10 a 50 Mg ha-1 año-1) y 3.9 % en categoría grave (más de 50 Mg ha-1 año-1). Estas degradaciones específicas potenciales implican que gran parte del territorio nacional rebasaría los límites máximos permisibles de pérdida de suelo establecidos en el manual de agricultura de EE.UU. (Wischmeier y Smith, 1978) y por la FAO (CP, 1991).
Los valores de erosión potencial deben tomarse solo como valores de referencia, puesto que el proceso de erosión es complejo y su representación adecuada depende de información y de la estimación precisa de las características del sitio de estudio (Sadeghi et al., 2014; Kinell, 2015). La cuantificación precisa de la erosión hídrica de los suelos en cuencas hidrográficas sirve para establecer las medidas de conservación para minimizar la pérdida del recurso suelo (Wischmeier y Smith, 1978). Con este propósito se realizaron estudios sobre la producción de sedimentos en cuencas en varias partes del mundo, empleando diferentes metodologías. Por ejemplo, en lotes experimentales desde unos cuantos metros cuadrados hasta enormes cuencas que cubren cientos de kilómetros cuadrados, se observó degradación específica mundial promedio de 1.9 Mg ha-1 año-1 con un máximo de 64 en China y mínimo de 0.00005 en Canadá (De Araújo y Knight, 2005).
Para estimar la producción de sedimentos a la salida de una cuenca se usan tres tipos de modelos: 1) empíricos, como USLE y MUSLE, con base en relaciones funcionales simples, resultado de observaciones experimentales (Williams, 1975; Wischmeier y Smith, 1978; Renard et al., 1997); 2) basados en procesos con soporte empírico fuerte como los desarrollados con redes neuronales (Heng y Suetsugi, 2013; Garg, 2015); 3) físicos con base en principios conservativos como EUROSEM y KINEROS (Morgan et al., 1998; Rosenmund et al., 2005).
Los modelos basados en principios físicos y en procesos demandan mucha información, cuya obtención es complicada. Por lo anterior, los modelos USLE (EUPS o Ecuación Universal de la Pérdida del Suelo, por sus siglas en inglés) y MUSLE (EUPS modificada) se usan de forma individual (Sadeghi et al., 2014) o integrados en modelos más complejos como el SWAT para cuantificar el transporte de sedimentos (Ayana et al., 2012; Prabhanjan et al., 2015). La estructura matemática de estos modelos es simple y su uso sería sencillo porque hay tablas, nomogramas y ecuaciones de referencia para calcular sus componentes (factores) en manuales y publicaciones, originadas en EE.UU. (Wischmeier y Smith, 1978; Renard et al., 1997; NEH, 2004), y en algunos casos adaptadas a las condiciones de otros países (Figueroa et al., 1991; Pongsai et al. 2010). Sin embargo, investigaciones realizadas en Asia (Sadeghi et al., 2007; Pongsai et al. 2010), África (Muche et al., 2013), Suramérica (Guevara-Pérez y Márquez, 2007; Besteiro y Gaspari, 2012) y Europa (Rosenmund et al., 2005) muestran que los modelos requieren ajustes.
En México también se usan como referencia los modelos USLE y MUSLE para cuantificar la erosión de los suelos pero, en su mayoría, los resultados son estimativos porque no se validaron con datos experimentales (Flores et al., 2003) o se compararon con poca información de campo, sin especificar ni argumentar los factores ajustados (Torres et al., 2005). Algunos experimentos se desarrollaron en el estado de Michoacán y destaca el de Ajuno (Tapia et al., 2002) sitio perteneciente a la cuenca del Lago de Pátzcuaro, y en la cuenca de la presa Cointzio (Bravo et al., 2009b). Sin embargo, por ser lotes experimentales con cultivos y tratamientos específicos, sus resultados no son válidos para representar el comportamiento de una cuenca como una sola unidad de respuesta hidrológica, pues solo una porción del suelo desprendido de la superficie llega a la salida de una cuenca y la producción de sedimentos es el resultado, además de la erosión laminar y en canalillos representada por los modelos USLE y MUSLE, de la erosión ocurrida en cárcavas, fondo y taludes de cauces, caminos, y del desprendimiento en masa (NEH, 1983). Al respecto, el modelo MUSLE puede representar de manera adecuada la producción de sedimentos a la salida de una cuenca, pues sus factores integran el proceso de erosión y el transporte del suelo (Sadeghi et al., 2007; Arekhi et al., 2012).
En este contexto es necesario estudiar la eficiencia predictiva de los modelos de estimación de producción de sedimentos en cuencas de México, para tener una herramienta de apoyo en la toma de acciones para un manejo sustentable. Por lo tanto, el objetivo de esta investigación fue calibrar los modelos USLE y MUSLE en la microcuenca forestal El Malacate, en la cuenca del Lago de Pátzcuaro, con base en un conjunto amplio de información experimental obtenida durante 2013 de: precipitación diaria, hidrogramas y cantidad de sólidos en suspensión en los eventos de escurrimiento, imágenes supervisadas de uso de suelo y vegetación, contenido de materia orgánica del suelo, y textura y estructura del suelo. En particular, los resultados servirían como referencia para estimar la producción de sedimentos en cuencas vecinas, con condiciones similares a las del estudio, para tomar medidas que detengan el deterioro del suelo en la cuenca de Pátzcuaro, porque las tasas de erosión superan los límites permisibles (Huerto y Vargas, 2014).
Materiales y Métodos
Descripción del lugar de estudio
Esta investigación se realizó en la microcuenca El Malacate con una extensión de 149.2 ha. La microcuenca forma parte de la cuenca cerrada del Lago de Pátzcuaro, municipio de Tzintzuntzan, estado de Michoacán de Ocampo, con una altitud media de 2,300 m, entre 19° 36’ 50’’ y 19° 38’ 30’’ N, y 101° 35’ 10’’ y 101° 36’ 20’’ O. De acuerdo con el sistema de clasificación climática de Köppen, modificado por García (2004), el clima del área es templado subhúmedo C (w2) con una temperatura media anual entre 12 °C y 18 °C, temperatura del mes más frío entre -3 °C y 18 °C y temperatura del mes más caliente de 20 °C a 30 °C, una precipitación anual de 200 a 1800 mm con un valor medio de 920.3 mm (IMTA, 2009).
Datos experimentales
La información cartográfica usada fue modelo digital de elevaciones (MED), mapa de usos del suelo y vegetación, y mapa del tipo de suelo del INEGI a escala 1:50 000. El mapa de usos del suelo y vegetación se verificó en campo y se identificó un predominio del uso forestal. Para verificar el tipo de suelo se hizo un recorrido por toda la cuenca encontrándose un tipo de suelo Luvisol nítico según la clasificación FAO-UNESCO, compuesto de cuatro capas, cuya capa superficial tiene un espesor de 25 cm de textura franco arcillo limosa (32.5 de arcilla, 51.3 de limo y 6.09 % de arena muy fina) y estructura granular fina con 4.98 % de materia orgánica.
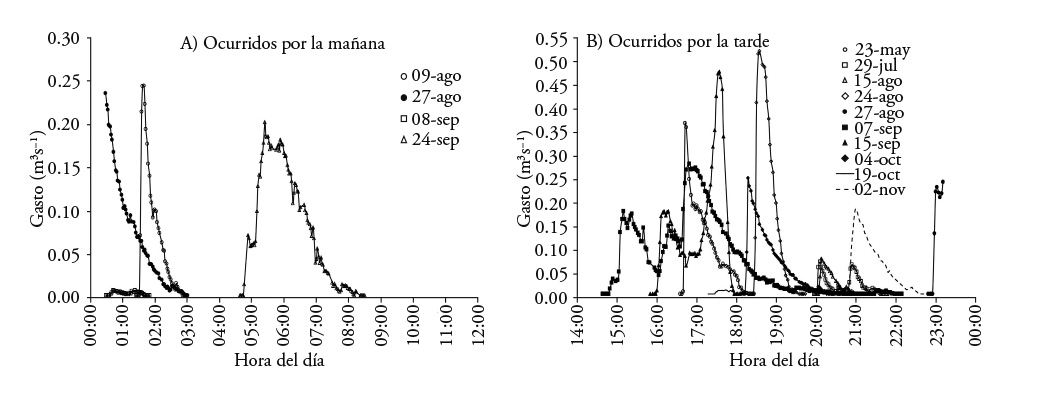
La precipitación diaria de 2013 se registró, aforada en intervalos de 0.2 mm con un pluviógrafo HOBO RG3-M, con un total anual de 769.6 mm. Además se usaron los hidrogramas (Figura 1) y la cantidad de sedimentos a la salida de la cuenca, obtenidos de 14 eventos de escurrimiento registrados en 2013. Los hidrogramas se obtuvieron mediante un aforador de garganta larga instrumentado con un sensor ultrasónico para la medición del tirante y un sistema automatizado para el registro de la información. La producción de sedimentos se obtuvo al cuantificar la cantidad de sólidos en suspensión de muestras tomadas a la salida de la cuenca durante los escurrimientos.
Modelos de estimación de la producción de sedimentos
Modelo USLE
La ecuación universal de pérdida de suelo (USLE) fue propuesta para calcular la erosión laminar y en canalillos (Wischmeier y Smith, 1978) y está definida como:
donde, y de acuerdo con el sistema métrico internacional de unidades (Foster et al. 1981), A es la tasa de erosión anual por unidad de área (Mg ha-1 año-1), R es el factor de erosividad de la lluvia (MJ mm ha-1 h-1 año-1), K es el factor de erosionabilidad del suelo (Mg ha-1 MJ-1 mm-1), L es un factor de longitud de la pendiente (adimensional), S es un factor del grado de la pendiente (adimensional), C es un factor de cultivo y manejo del cultivo (adimensional), y P es un factor de prácticas de manejo (adimensional).
Modelo MUSLE
El modelo MUSLE (Williams, 1975) es una modificación al modelo USLE, consiste en reemplazar el factor R de la erosividad de la lluvia por el escurrimiento superficial y el caudal pico de una tormenta, con la finalidad de calcular la producción de sedimentos por evento y se expresa como:
donde Y es la producción de sedimentos en un evento determinado (Mg evento-1), Qs es el volumen escurrido (m3) y qp es el gasto pico del evento (m3 s-1).
Cálculo de los factores de la USLE y MUSLE
Los volúmenes escurridos y los gastos pico se obtuvieron de los hidrogramas medidos. Se calcularon los valores promedio de los factores K, R, LS, C y P. El factor P de prácticas de manejo se consideró igual a la unidad porque no se realizan prácticas de conservación. El factor K se calculó usando un solo tipo de suelo con la información reportada en datos experimentales, el factor R se obtuvo con los datos de la lluvia, y los factores LS y C se obtuvieron de forma ponderada por el área (Sadeghi et al., 2007; Pongsai et al., 2010) mediante el procesamiento del MED y del mapa de uso de suelos y vegetación con ArcGis versión 10.1, cuyos procedimientos de cálculo se describen a continuación.
Factor R
Este factor representa la capacidad potencial que tienen las gotas de agua de lluvia para causar erosión y se calculó de dos formas: mediante el índice EI30 (Wischmeier y Smith, 1978), y con una ecuación adaptada por Figueroa et al. (1991) que considera una relación funcional de tipo cuadrática con la precipitación media anual registrada.
El método EI30 se usó porque hay información diaria de la precipitación, registrada a intervalos de minutos. Este método es el producto de la energía cinética total de un evento de lluvia por la intensidad máxima en 30 min, de manera que el valor total del factor de erosividad de la lluvia R es la suma de valores de erosividad de tormentas individuales, calculado así (Wischmeier y Smith, 1978):
donde E es la energía cinética de la lluvia de cada tormenta (MJ ha-1 mm-1), I30 es la intensidad máxima de la lluvia en cualesquiera 30 min de cada tormenta (mm h-1), y n es el número de tormentas en el año.
La energía cinética de cada tormenta es la suma de las energías cinéticas de los intervalos de lluvia, diferenciados por sus intensidades de lluvia, y se calculó con la ecuación propuesta por Wischmeier and Smith (1978):
donde ej es la energía cinética del intervalo de lluvia j de una tormenta (MJ ha-1 mm-1), y Ij es la intensidad de la lluvia del intervalo j (mm h-1), y ppj es la precipitación del intervalo j (mm). Para intensidades mayores de 76 mm h-1 se estableció un valor de e de 0.283.
De acuerdo con el criterio de cálculo del EI30 propuesto por Wischmeier y Smith (1978), no se consideraron las tormentas con precipitaciones menores de 12.5 mm con periodos de lluvia separados más de 6 h, a menos que la precipitación fuera 6.2 mm o más en 15 min (I15≥24.8 mm h-1). La existencia de los periodos de lluvia en las tormentas largas se definieron cuando en un lapso de 6 h lámina fue menor a 1.2 mm (Renard et al., 1997).
El factor R se calculó con la ecuación adaptada por Figueroa et al. (1991) como una alternativa metodológica a las cuencas donde no es posible calcular el EI30 por falta de información detallada de la precipitación a lo largo del año. La cuenca de estudio se localiza en la zona hidrológica V (Bravo et al., 2009a) y la ecuación:
donde P es la precipitación anual de 2013 en milímetros.
Factor K
El término erosionabilidad del suelo se utiliza para indicar la susceptibilidad de un suelo a la erosión. Se define como la tasa de pérdida de suelo por cada unidad adicional de EI30 cuando la pendiente y su longitud, la cobertura vegetal y las prácticas de conservación del suelo permanecen constantes y sus valores son iguales a uno (Wischmeier y Smith, 1978).
Como la suma de las partículas del limo más la de arena muy fina fue menos de 70 % del total de las partículas del suelo, el factor K se calculó con la ecuación propuesta por Wischmeier y Smith (1978):
donde M es un parámetro de tamaño de partícula, MO es el porcentaje de materia orgánica (%), Cestr es un código de estructura del suelo, Cperm es un código de permeabilidad del suelo, y 0.313 es un factor de conversión del sistema de unidades inglés al métrico internacional (Foster et al, 1981). El parámetro de tamaño de partícula se calculó como:
donde ml es el porcentaje de contenido de limo (diámetro de partículas de 0.002 a 0.05 mm), mamf porcentaje del contenido de arena muy fina (diámetro de 0.05 a 0.10 mm), y m a es el porcentaje del contenido de arcilla (diámetro de partículas menores de 0.002 mm).
El valor de la permeabilidad del suelo se determinó en función de su textura empleando las relaciones funcionales descritas por Saxton y Rawls (2006).
Otro método usado fue el de la FAO (1980) usado en México, ya que el factor K se determina solo en función de la unidad a la cual pertenece el suelo en la clasificación FAO-UNESCO y de la textura de la capa superficial.
Factor LS
Este factor representa el efecto de la topografía sobre la erosión del suelo. La erosión aumenta conforme se incrementa la longitud del terreno (L) en el sentido de la pendiente y la inclinación de la superficie (S) se hace mayor, calculados como (Wischmeier y Smith, 1978):
donde:
donde λ es la longitud de la pendiente (m), s es la pendiente del terreno (%), y el exponente m del factor de la longitud de pendiente considera la proporción de erosión causada por la erosión entre canalillos, debida al impacto de las gotas y la causada en canalillos por la fuerza de arrastre del flujo (Renard et al., 1997). El valor de m varía en función de la pendiente del terreno y se calculó con la ecuación propuesta por McCool (Renard et al., 1997):
donde θ es el ángulo de la pendiente.
La ecuación clásica para calcular el factor LS, propuesta por Wischmeier y Smith (1978), no representa bien el efecto de la topografía en la erosión del suelo para pendientes mayores de 16 % (Pongsai et al., 2010), por lo cual el factor S se calculó con la ecuación propuesta por McCool (Renard et al., 1997) para pendientes mayores a 9 %:
donde θ es el ángulo de la pendiente.
Factor C
El factor C de manejo de cultivo y cobertura del suelo es la relación de pérdidas de un terreno cultivado en condiciones específicas, con respecto a las pérdidas de un suelo desnudo y con barbecho continuo en las mismas condiciones de suelo, pendiente y lluvia (Wischmeier y Smith, 1978).
Para su cálculo se empleó la metodología y los valores propuestos por Wischmeier y Smith (1978). En la agricultura de temporal, donde se siembra maíz de manera preponderante, se cuantificó mediante los índices de erosividad EI30 en cada una de las etapas del cultivo y las pérdidas relativas de suelo en áreas de cultivo en relación a terrenos bajo barbecho continuo.
Evaluación del ajuste del modelo
La correspondencia entre las series de valores observados y los estimados se expresaron en términos de cuatro índices: Eficiencia del modelo (EF) propuesto por Nash y Sutcliffe (1971) y usado por Besteiro y Gaspari (2012) y Muche et al. (2013); error estándar (ES) (Pongsai et al. (2010); coeficiente de determinación (CD) (Rosenmund et al., 2005); y porcentaje de sesgo (PBIAS) (Moriasi et al., 2007). Las ecuaciones de los indicadores están dadas por:
donde Oi son los valores observados, Pi son los valores predichos, Ō es el promedio de los valores observados, y n es el número de datos evaluados.
El modelo aumenta la precisión de la predicción de los valores observados conforme los valores de los indicadores EF, ES, CD y PBIAS se aproximan a uno, cero, uno, y cero, respectivamente.
La correspondencia entre los pares de datos observados y estimados se hizo a través del error de estimación relativo, calculado como (Pongsai et al., 2010; Arekhi et al., 2012):
El valor óptimo de ER es cero; valores positivos indican el porcentaje de sobreestimación del modelo, mientras que valores negativos cuantifican el porcentaje de subestimación del modelo.
Resultados y Discusión
El valor del factor K fue 0.034 con la Ecuación (7) propuesta por Wischmeier y Smith (1978), y 0.013 con la metodología propuesta por la FAO. Los valores de los factores LS, C (Cuadro 1) y P fueron 10.1, 0.062 y 1.0, respectivamente.
Cuadro 1 Valores del factor C de acuerdo con el uso del suelo y vegetación en la cuenca El Malacate, Michoacán

El valor del factor R calculado con la Ecuación (6), propuesta por Figueroa et al. (1991) y calculado con una precipitación anual de 769.6 mm, fue 2163.2 MJ mm ha-1 h-1.
El valor del factor R calculado con los índices de erosividad, considerando solo las tormentas en las cuales hubo escurrimientos y que cumplieron con los criterios de Wischmeier y Smith (1978), fue 1154.9 MJ mm ha-1 h-1 año-1 (Cuadro 2). Este resultado correspondió a la suma de eventos de lluvia con láminas precipitadas mayores que 12.5 mm o con láminas inferiores a 12.5 mm, pero con intensidades de lluvia superiores que 24.8 mm h-1 en cualesquiera 15 min (I15). Las tormentas del 8 y 24 de septiembre produjeron arrastre de sedimentos pero no se consideraron por no cumplir con los criterios establecidos, ya que se presentaron precipitaciones inferiores a 12.5 mm y I15 inferiores a 24.8 mm h-1. En las tormentas del 23 de mayo y 27 de agosto se presentaron dos periodos de lluvia, y solo uno de ellos cumplió los requisitos para tomarse en cuenta en el EI30.
Cuadro 2 Índices de erosividad EI30 de las tormentas con eventos de escurrimiento del año 2013
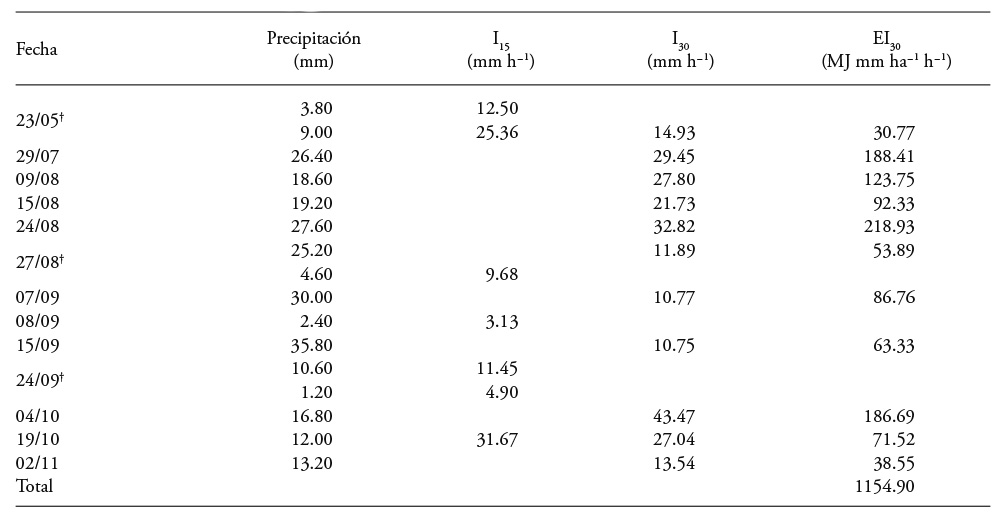
† Hubo dos periodos de lluvia en la tormenta.
Calibración del modelo MUSLE
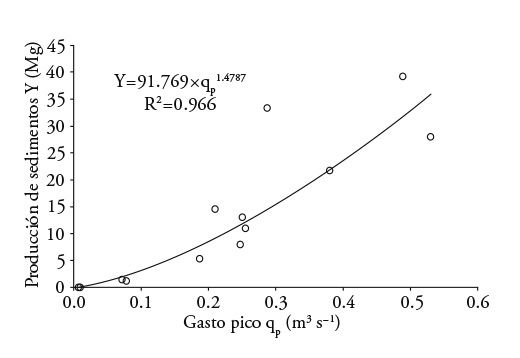
Las Figuras 2 y 3 muestran una relación potencial entre la producción de sedimentos y los volúmenes escurridos y caudales pico de cada tormenta de acuerdo con Williams (1975). El ajuste de estas relaciones fue R2>0.95, pero las desviaciones estándar fueron altas; al relacionar la producción de sedimentos con el volumen escurrido superficialmente, el error estándar fue 8.2, y 6.6 Mg cuando dependió del gasto pico, como lo reportan Sadeghi et al. (2007).
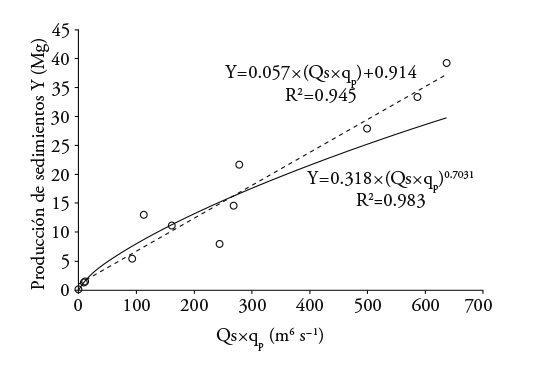
Al relacionar la producción de sedimentos con el producto del escurrimiento superficial por el gasto pico, término por el cual Williams (1975) sustituyó el factor de erosividad de la lluvia R de la USLE, hay un buen ajuste en un modelo de tipo potencial (R2=0.983; Figura 4). Sin embargo, el valor de la potencia (0.703) es superior al encontrado por Williams (1975) en EE. UU. (0.56) y el error estándar fue 4.4 Mg. Un modelo de tipo lineal también presentó ajuste R2=0.945 con un error estándar inferior al de tipo potencial (3.1 Mg), pero con la desventaja de no representar el fenómeno para productos Q sxqp cercanos a cero (Figura 4).
Los errores cometidos por la relación potencial entre la producción de sedimentos y el producto Qs xqp, sumados a los errores de estimación de los factores K, LS, y C, condujeron a errores fuertes entre los valores observados y predichos por el modelo MUSLE. En efecto, los resultados del Cuadro 3 y los indicadores estadísticos de las columnas 3 y 4 del Cuadro 4 muestran la necesidad de ajuste de los factores del modelo MUSLE.
Cuadro 3 Errores relativos en la estimación de la producción de sedimentos con el modelo MUSLE.
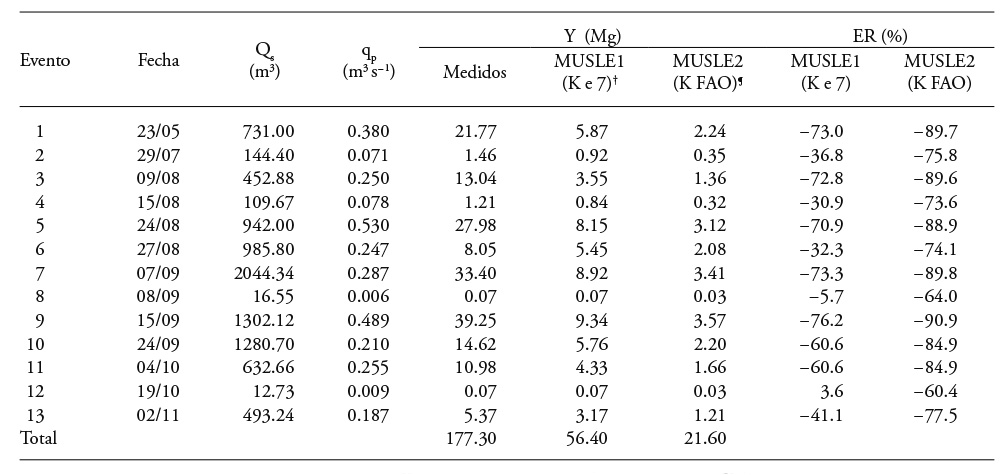
† El factor K se calculó con la Ecuación (7). ¶El factor K se calculó con la metodología FAO.
Cuadro 4 Indicadores estadísticos de las predicciones del modelo MUSLE antes y después de la calibración
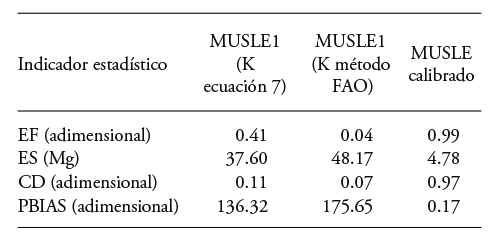
De acuerdo con los resultados totales de producción de sedimentos (Cuadro 3), se encontró que el modelo MUSLE1 (factor K calculado con la Ecuación 7) subestimó los resultados en 12 de los 13 eventos de lluvia y el modelo MUSLE2 (factor K calculado con la metodología de la FAO) subestimó los resultados en todos los eventos. Los resultados tienen las tendencias reportadas por Sadeghi et al. (2007) quienes encontraron subestimaciones del modelo MUSLE para tormentas pequeñas de corta duración. Esto se explica porque el modelo MUSLE fue desarrollado para cuencas de pastizales con tormentas más grandes y con pendientes inferiores a las de la cuenca de estudio (Williams, 1975).
Ambos modelos MUSLE subestimaron los resultados, pero es notable que el modelo FAO sea menos preciso y el error de estimación relativo calculado con la Ecuación (18) para los datos anuales reportados en el Cuadro 3 fue -68.2 %, mientras que con el otro modelo fue -87.8 %. Estos resultados implican que el modelo FAO no representó adecuadamente el factor K y es más recomendable usar la Ecuación (7) porque, además de considerar la textura del suelo, considera su estructura, permeabilidad y el contenido de materia orgánica.
Para la calibración del modelo solo se ajusta uno de los factores y suele ser aquel para el cual hay poca información, o en el cual las condiciones del sitio de estudio no están contempladas en las tablas, nomogramas y ecuaciones sugeridas en las publicaciones sobre el tema. Así lo indican Pongsai et al. (2010), Besteiro y Gaspari, (2012); Sadeghi et al., (2014).
Puesto que el factor P está bien definido con un valor de uno por no existir prácticas de manejo, la topografía cambia muy poco en el tiempo, las características del uso del suelo y la vegetación se mantienen similares a lo largo del año por ser una cuenca mayormente forestal y el crecimiento de las especies vegetales es lento. En nuestro estudio se planteó ajustar el factor K debido al comportamiento dinámico del suelo, que durante el año adquiere diferentes grados de humedad y vulnerabilidad a la erosión (Kinell, 2015). Una prueba de la dificultad para representar el valor del factor K es la gran diferencia en las estimaciones entre el modelo que incluyó el valor de K calculado con la Ecuación (7) y el obtenido con el método de la FAO.
El valor del factor K calibrado fue 0.107 y se obtuvo mediante la técnica de regresión por mínimos cuadrados. En México no hay valores experimentales de K de cuencas similares para su comparación. En microcuencas de la Cuenca del Lago de Pátzcuaro y en otras vecinas se han realizado estudios en lotes de escurrimiento de algunos cultivos con distintas formas de labranza, pero en la mayoría de los casos el factor calibrado corresponde al cultivo C (Tapia et al., 2002; Bravo et al., 2009b) y se asume que los demás factores del modelo USLE son los correctos y calculados con la metodología propuesta por Wischmeier y Smith (1978). En el Cuadro 4 se observa que los valores de tres (EF, CD y PBIAS) de los cuatro indicadores estadísticos de ajuste son muy próximos a sus óptimos. El valor próximo a la unidad del indicador de Nash y Sutcliffe (EF) establece que el modelo calibrado es eficiente. El valor de ES implica que existió un error estándar de 4.78 Mg en la producción de sedimentos y dadas las 149.2 ha de la cuenca, se traduce en un error estándar de 0.03 Mg ha-1. El valor de CD próximo a la unidad indica que los valores predichos siguieron la tendencia de los medidos, compensando los errores; así, en algunos eventos se sobrestimaron los resultados y en otros se subestimaron (Figura 5). El balance final resultó en una subestimación promedio de 0.17 Mg (PBIAS).
El modelo MUSLE calibrado se puede usar para estimar de forma aproximada la producción de sedimentos en otras cuencas de condiciones similares a la de nuestro estudio, y donde no se disponga de datos de aforo como lo observó Prabhanjan et al. (2015) con la aplicación del módulo SWAT, el cual está soportado por el modelo MUSLE (Ayana et al., 2012). Existen cuencas similares, como se constata en los resultados obtenidos en una cuenca de descarga al dren Tzurumútaro en el estado de Michoacán, también mayormente forestal, y la producción de sedimentos fue 0.8 Mg ha-1 año-1 desde 2007 a 2010 (Huerto y Vargas, 2014), la cual se asemeja a las 1.2 Mg ha-1 año-1 medidas en la microcuenca de nuestro estudio.
Calibración del modelo USLE
Para la revisión de los resultados del modelo USLE se retomaron los valores de los factores K, LS, C y P del modelo MUSLE calibrado y el valor medido del factor R, ya que el modelo MUSLE predice mejor la erosión del suelo (Muche et al., 2013). En la metodología establecida por Wischmeier y Smith (1978) y en la revisión del modelo USLE por Renard et al. (1997) no se especifica claramente si el criterio para calcular el índice de erosividad EI30 debe aplicarse solo para las tormentas donde hay escurrimientos o para todas las tormentas; tampoco se especifica si debe contemplarse la erosividad de tormentas que no satisfacen dicho criterio de cálculo del EI30 pero que si produjeron escurrimientos.
De considerar los EI30 de las tormentas con presencia de escurrimientos del Cuadro 2 (1154.9) y sin presencia de escurrimientos (992.1), resultado de sumar los valores fuera de los paréntesis del Cuadro 5, el valor total anual en el 2013 fue 2147.0 MJ mm ha-1 h-1, muy próximo al valor de 2163.2 obtenido con la Ecuación (6) propuesta por Figueroa et al. (1991). La buena representación del factor R del método estimativo es evidente para el año de estudio, con un error de 0.75 % respecto al total medido de eventos con y sin escurrimientos (2147.0 MJ mm ha-1 h-1). Sin embargo, si se emplea la precipitación media anual de 920.3 mm (IMTA, 2009) para calcular R, según Figueroa et al. (1991) en lugar de emplear la registrada en 2013, el valor de R es 2464.7 MJ mm ha-1 h-1 y superior en 14.8 % al medido (2147.0 MJ mm ha-1 h-1).
Cuadro 5 Valores mensuales de EI30 (MJ mm ha-1 h-1) de las tormentas sin escurrimientos.

† Los números entre paréntesis indican el día del mes cuando ocurrió en evento.
De acuerdo con la magnitud de la producción de sedimentos de algunas tormentas que no cumplieron los criterios para la inclusión del EI30 en el factor R, es necesario considerar las tormentas donde hubo escurrimientos y producción de sedimentos, aunque no cumplan con los requisitos fijados, como sucedió en el evento del 24 de septiembre que tuvo dos periodos de lluvia (Cuadro 2), y la producción de sedimentos de esa tormenta fue significativa (14.6 Mg) comparada con la producción de los otros eventos de escurrimiento (Cuadro 3). De forma similar, en el evento de escurrimiento del 23 de mayo, con una producción de sedimentos considerable (21.8 Mg) (Cuadro 3), no se consideró el índice de erosividad en uno de los dos periodos de lluvia (Cuadro 2). Además a este evento no le antecedieron tormentas inmediatas como posible influencia ya que la más próxima ocurrió el 14 de mayo con una precipitación de 1 mm en 2.7 h.
Con valores de 10.1, 0.062 y 1.0, respectivamente, para los factores LS, C y P, el valor calibrado de K (0.1067) para el modelo MUSLE y el valor de R medido (2147), empleando el modelo USLE resultó una tasa de erosión de 143.0 Mg ha-1 año-1. La producción de sedimentos a la salida de una cuenca va de 33 a 100 % de la erosión laminar y en pequeños canalillos representada por el modelo USLE, en EE.UU. (NEH, 1983; Calhoun y Fletcher III, 1999). Para el análisis del resultado, si se considera que la producción de sedimentos en la cuenca de estudio se debió solo a erosión laminar y en pequeños canalillos, y se supone que 37 % de su valor llegó al punto de descarga de la cuenca obtenido del manual nacional de ingeniería de EE.UU. (NEH, 1983) en función del área de la microcuenca, se esperaría una producción de sedimentos de 52.9 Mg ha-1 año-1, el cual es superior al medido en la cuenca de estudio (1.2 Mg ha-1 año-1) y aún a lo observado en cuencas con altas tasas de erosión como en Las Huertitas, que descarga 15 Mg ha-1 año-1 a la presa Cointzio en el estado de Michoacán (Duvert et al., 2010).
El modelo USLE estima la pérdida de suelo anual promedio de varios años en el terreno y para satisfacer la tasa de entrega de suelo a la salida de la cuenca de 37 % (1.2 Mg ha-1 año-1) tendría que ocurrir una erosión de 3.25 Mg ha-1 año-1. Pero esta cantidad representa una gran variabilidad respecto a los 143.0 Mg ha-1 año-1 estimados para el año 2013 e implica que para algunos años tendrían que ocurrir erosiones muy superiores a este valor. Estos resultados muestran que la tasa de entrega considerada no representa las características de la cuenca de estudio y que el factor de cultivo considerado no fue el adecuado.
Los resultados del modelo USLE sugieren la conveniencia de una adecuación de las metodologías empleadas para: 1) la obtención del factor R, y de la forma de su representación mediante el producto Qsxqp en el modelo MUSLE, ya que el valor de la potencia de este término (0.7031) fue mayor que el 0.56 propuesto por Williams (1975), como se observa en la relación funcional potencial de la Figura 4; 2) el cálculo del factor del cultivo C y de suelo K; y, 3) en el cálculo de la tasa de entrega a la salida de la cuenca en la que se tendría que considerar las aportaciones de sedimentos por erosión en cárcavas, cauces, caminos y de desprendimientos en masa (NEH, 1983; Calhoun y Fletcher III, 1999). La adecuación permitiría una compatibilidad de resultados entre los modelos USLE y MUSLE, cuando se apliquen a la cuenca de estudio.
Conclusiones
El modelo MUSLE se calibró para 2013 mediante el ajuste por mínimos cuadrados del factor K con valores de los indicadores de ajuste estadístico próximos a los óptimos. Previo a la calibración, se obtuvieron mejores resultados al usar el valor de K calculado con la Ecuación (7) propuesta por Wischmeier y Smith, en lugar del obtenido con la metodología de la FAO. El modelo puede emplearse para estimar la producción de sedimentos en cuencas de condiciones similares a la de El Malacate, Michoacán, en las cuales hay poca información hidrométrica detallada.
El modelo USLE no representó las pérdidas de erosión ocurridas en la cuenca de estudio y se sugiere revisar las metodologías para calcular las tasas de entrega a la salida de la cuenca, y los factores C, R y K.
Los valores del factor R calculados con las ecuaciones comparadas resultaron similares, si se consideran todos los eventos de lluvia en el año. Sin embargo, su significado y la metodología para calcularla con el modelo USLE y su equivalencia en el modelo MUSLE deben revisarse, ya que la pendiente del producto del escurrimiento por el gasto pico fue mayor respecto al sugerido por Williams (1975).











 texto en
texto en