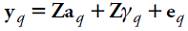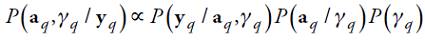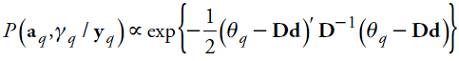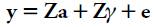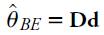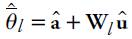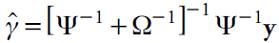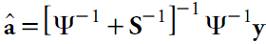Introducción
La predicción del mérito genético en plantas y animales por lo general se hace con el modelo lineal mixto (Robinson, 1991) o con alguna aproximación bayesiana (Blasco, 2001; Sorensen y Gianola, 2002) basados en los registros fenotípicos y de pedigrí de los candidatos a selección. Sin embargo, Meuwissen et al. (2001) mostraron que la selección genómica (SG) incrementa la precisión (correlación entre los valores observados y predichos) de la predicción del mérito genético de los candidatos a selección y reduce los intervalos entre ciclos de selección hasta en dos tercios cuando el número de genotipos y marcadores moleculares (MM) usado en la predicción es suficientemente grande. En la SG los valores predichos del mérito genético, llamados méritos genómicos estimados (genomic estimated breeding values, GEBV por sus siglas en inglés), se obtienen multiplicando los efectos estimados de los MM en la población base por los valores codificados de los MM obtenidos después del primer ciclo de selección. Los GEBV son el instrumento de la SG y permiten seleccionar caracteres cuantitativos en ausencia de información fenotípica (Gianola, 2013; Beyene et al., 2015).
Uno de los problemas más importantes en la SG es obtener GEBV suficientemente precisos para que la SG sea eficiente. Tal problema condujo a varias metodologías de predicción derivadas de los siguientes supuestos: 1) los efectos de los MM tienen distribución normal multivariada con media igual a cero y varianza constante, y 2) los efectos de los MM tienen distribución normal multivariada con media igual a cero pero la varianza de los MM tiene distribución a priori que puede ser uniforme, gamma, etc.. El punto 1) condujo al predictor lineal mejor insesgado genómico (genomic best linear unbiased predictor o GBLUP) (VanRaden, 2008) y al mejor predictor lineal insesgado bayesiano (Bayes-BLUP) (Verbyla et al., 2009, 2010). El punto 2) condujo a metodologías bayesianas como Bayes A, B, C, D, etc. (de los Campos et al., 2013; Gianola, 2013), que difieren sólo en el supuesto específico que hacen respecto a la distribución a priori de la varianza de los marcadores.
En la SG los métodos bayesianos se desarrollaron en el contexto de una variable fenotípica con el objetivo de mejorar la precisión de GBLUP; sin embargo, no se ha mostrado de manera irrefutable que la precisión de GBLUP sea significativamente menor que la de los métodos bayesianos (Massman et al., 2013). Los métodos bayesianos permiten un control mejor de la incertidumbre asociada a la predicción del mérito genético (Blasco, 2001) pero requieren métodos numéricos, como el el muestreador de Gibbs (Casella y George, 1992), para estimar los efectos de los MM y cualquier otro parámetro asociado al mérito genético. Verbyla et al. (2009) señalan que Bayes B requiere hasta 2440 h de cómputo para que el muestreador de Gibbs converja, mientras que Bayes A y BayesBLUP requieren al menos 6 h de cómputo para la convergencia de tal algoritmo. Según Verbyla et al. (2009), a pesar de grandes diferencias en el tiempo de cómputo en los métodos indicados, cuando el número de genotipos y MM es grande, la precisión alcanzada por todos ellos es prácticamente igual (promedio, 0.6).
Los procedimientos de predicción con modelos univariados no toman en cuenta las correlaciones genéticas entre caracteres, a pesar que en la práctica la evaluación de las variedades requiere varios caracteres de manera simultánea. Por ejemplo, los mejoradores de rendimiento y calidad de grano registran datos fenotípicos que incluyen componentes de rendimiento (e.g., peso de grano o biomasa), calidad del grano (e.g., sabor, forma, color, contenido de nutrientes), y resistencia a estrés biótico y abiótico (Jia y Jannink, 2012). La predicción del mérito genético multivariado tiene la ventaja de incorporar las correlaciones genéticas entre caracteres. Esta información debe aumentar la eficiencia de la predicción del mérito genético; por ello, Calus y Veerkamp (2011) propusieron un procedimiento similar a Bayes A, y Hayashi e Iwata (2013) adaptaron Bayes D al caso multivariado. Sin embargo, se requieren alternativas computacionalmente menos demandantes sin afectar la precisión de la predicción: Bayes empírico es un método alternativo de predicción con propiedades estadísticas deseables. En éste, bajo el supuesto de que las varianzas de los parámetros son conocidas, la esperanza de la distribución posterior del mérito genético se considera un estimador bayesiano empírico de tal mérito genético (Tempelman y Rosa, 2004). Éste es una variante del estimador bayesiano estándar y es muy eficiente; además, es robusto ante las especificaciones erróneas de la distribución a priori de los parámetros (Lehmann y Casella, 1998).
En los programas de SG el primer ciclo de selección incluye sólo información fenotípica, aunque la población base (donde se selecciona al primer grupo de progenitores) tiene datos fenotípicos y MM. Al hacer selección sólo con información fenotípica no se usa la información de los MM. Si se combina la información fenotípica y la información de los MM en la predicción, aumenta la precisión aun en el primer ciclo de selección debido al aumento de información en el modelo. Un problema similar ocurre cuando sólo algunos individuos de los candidatos a selección cuentan con MM y el resto no, como en el mejoramiento de plantas híbridas (Massman et al., 2013) o en la selección de animales (Legarra et al., 2009).
El objetivo del presente estudio fue proponer y evaluar, en el contexto Bayes empírico, un modelo lineal multivariado que usa información de pedigrí y genómica de manera conjunta para predecir el mérito genético de los candidatos a selección. En el modelo, la esperanza de la distribución posterior conjunta del mérito genético es el estimador bayesiano empírico. Los supuestos de este modelo son: 1) las varianzas y covarianzas genéticas son conocidas; 2) el efecto genómico y el efecto genético aditivo no explicado por los MM tienen distribución normal multivariada conjunta con media igual a cero y varianza común; 3) el mérito genético de los candidatos a selección es la suma del efecto genómico y del efecto genético aditivo no explicado por los MM. Además, se muestra que el modelo lineal multivariado genómico (que usa sólo información genómica en la predicción) y el modelo lineal multivariado estándar (que usa sólo información fenotípica y de pedigrí en la predicción) son casos particulares del modelo propuesto.
Materiales y Métodos
Poblaciones de maíz 1 y 2
En cada una de las dos Poblaciones de maíz (Zea mays) F2, se registraron tres variables: rendimiento de grano (RG, Mg ha‒1), altura de la mazorca en la planta (AM, cm), y altura de planta (AP, cm). La Población de maíz 1 tuvo 199 MM y 247 genotipos, mientras que en la Población de maíz 2 el número de MM fue 259 y el de genotipos 248. Las correlaciones genéticas estimadas entre RG y AM, RG y AP, y AM y AP en la Población de maíz 1 fueron, respectivamente, 0.53, 0.52 y 0.98, mientras que en la Población de maíz 2 las correlaciones fueron 0.58, 0.76 y 0.71.
Población 3 (población de trigo)
La Población de trigo (Triticum aestivum L.) doble haploide incluyó 1279 MM y 599 genotipos. En ella se registró el rendimiento de grano (RG, Mg ha‒1) en tres ambientes (RG1, RG2 y RG3). Para predecir el mérito genético de los candidatos a selección a RG1, RG2 y RG3 se le consideró una característica particular debido a que los genotipos se evaluaron en ambientes diferentes. Las correlaciones genéticas estimadas entre RG1 y RG2, RG1 y RG3, y RG2 y RG3 en la Población 3 fueron, respectivamente, ‒0.03, ‒0.21 y 0.73.
El modelo lineal propuesto con una variable
Sea
donde y
q
=
Distribución posterior conjunta de a q y 𝛾 q
La distribución posterior conjunta de a q y 𝛾 q puede escribirse como:
donde el símbolo “∝” indica que P(a
q
, 𝛾
q /
y
q
) puede escribirse como el producto de la función de verosimilitud de y
q
, P(y
q
/ a
q
/𝛾
q
) ∝
El lado derecho de la Ecuación 3 es el núcleo de una distribución normal con media Dd y varianza D, donde
Estimador de θ q
Por la Ecuación 3, el estimador bayesiano empírico de
Los componentes de varianza
El modelo lineal multivariado
Cuando se utilizan dos o más variables en la predicción del mérito genético, el modelo combinado de la Ecuación 1 puede escribirse como:
donde, ahora,
Estimación de a y 𝛾
Sea
donde, ahora, los componentes que conforman la matriz D
-1
son:
Predicción del mérito genético en el primer ciclo de selección
En el primer ciclo de selección el predictor del mérito genético de los candidatos a selección (
donde â y ŷ son subvectores de
Predicción del mérito genético después del primer ciclo de selección
Para obtener los valores predichos de los candidatos a selección a partir del segundo ciclo de selección, es necesario estimar los valores del vector
donde ŷ es el subvector de la Ecuación 6. Por la Ecuación 8, el predictor bayesiano empírico del mérito genético después del primer ciclo de selección es:
donde W l = I t ⊗ X l (l=2,3,…,N; N= número de ciclos de selección), I t ya se definió y X l es la matriz de valores codificados de los MM obtenida en el ciclo de selección l. Así, desde el segundo ciclo de selección, en la Ecuación 9 sólo cambiarán los valores codificados de la matriz X l .
Criterio para comparar la eficiencia de los modelos de predicción
Como la precisión es igual a la correlación entre los valores predichos y observados, su valor máximo es 1. Suponga que ρ c y ρ g denotan, respectivamente, la precisión del modelo combinado y del modelo genómico, entonces:
es la eficiencia (Bulmer, 1980) del modelo combinado respecto al modelo genómico. Así, cuando p=0 la eficiencia de ambos modelos es igual (ρ c = ρ g ); p>0 si ρ c > ρ g (la eficiencia del modelo combinado es mayor que la del modelo genómico) y p<0 si ρ c < ρ g (la eficiencia del modelo combinado es menor que la del modelo genómico). Así, la Ecuación 10 permite determinar el modelo más adecuado, o más eficiente, para predecir el mérito genético.
Resultados y Discusión
El modelo genómico está anidado en el modelo combinado
Uno de los resultados más importantes de la teoría de la SG es que la esperanza de la matriz de relaciones genómicas G es igual a la matriz de relaciones numéricas A
, i.e., E
(G) = A (Habier et al., 2007). Esto significa que G es una realización particular de A y que conforme el número de MM y genotipos se incrementa en la población base, el valor de G se concentra cada vez más alrededor de A, por lo que en el límite, puede asumirse que G=A. Lo mismo ocurre con la matriz de varianzas y covarianzas genómicas aditivas Γ en relación con la matriz de varianzas y covarianzas genéticas aditiva C. Es decir, conforme el número de MM y genotipos se incrementa, la matriz Γ se aproxima cada vez más a C, y en el límite Γ=C. Cuando G=A y Γ=C, S=Ω y las matrices que conforman la matriz
Esto indica que toda la información del mérito genético está concentrada en los efectos genómicos aditivos 𝛾 y que los valores del vector a son nulos. En tal caso, el estimador bayesiano empírico
Este resultado indica que el modelo genómico es un caso particular del modelo combinado.
El modelo con sólo información fenotípica está anidado en el modelo combinado
Cuando no se utiliza la información de los MM, la matriz Ω es nula y, en tal caso
Esto demuestra que el modelo con sólo información fenotípica es un caso particular del modelo combinado. A â se le llamará predictor estándar.
Precisión de los tres modelos de predicción
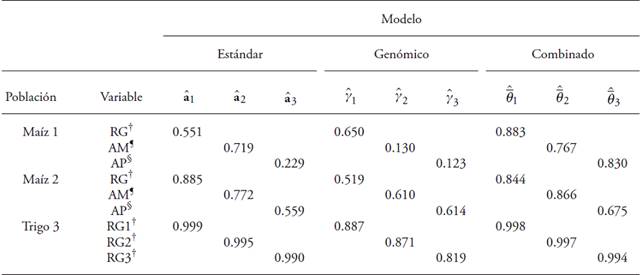
Los valores predichos del mérito genético de los candidatos a selección asociados a cada una de las tres variables de las dos poblaciones de maíz (Poblaciones 1 y 2) y de la población de trigo (Población 3) se denotaron como,
Evaluación numérica de los tres modelos de predicción
La eficiencia del modelo combinado respecto al modelo estándar y al modelo genómico; y la eficiencia del modelo estándar respecto al genómico, se evaluó por medio de la Ecuación 10 con los valores de las correlaciones presentadas en el Cuadro 1.
Población de maíz 1
Eficiencia del modelo combinado en comparación con el modelo estándar
El valor de p (Ecuación 10) asociado a las correlaciones entre el rendimiento de grano (RG) y sus valores predichos (
El valor de p obtenido a partir de la correlación entre altura de mazorca (AM) y
El promedio de los tres valores de p obtenidos con las correlaciones entre los valores predichos y observados de las tres variables es igual a 109.8 %.
Esto significa que el modelo combinado es más adecuado para predecir el mérito genético debido a que tiene una eficiencia 1.1 veces mayor que el modelo estándar.
Eficiencia del modelo combinado comparado con el modelo genómico
La eficiencia promedio del modelo combinado fue 366.9 % más alta que en el modelo genómico. Esto se debe a que los valores de las correlaciones entre AM y
Eficiencia del modelo estándar comparado con el modelo genómico
De nuevo, debido a los valores bajos de las correlaciones estimadas entre AM y
En resumen, el modelo combinado fue casi cuatro veces más eficiente que el modelo genómico y 1.1 más eficiente que el modelo estándar. Es evidente que el modelo combinado es más adecuado para predecir el mérito genético que los otros dos modelos en este conjunto de datos.
Población de maíz 2
Eficiencia del modelo combinado comparado con el modelo estándar y con el modelo genómico
Un procedimiento similar al de la Población de maíz 1 permite demostrar que la eficiencia promedio del modelo combinado fue 9.4 % más alta que en el modelo estándar, y 38.2 % más alta que en el modelo genómico, respectivamente. A pesar de que el número de marcadores aumentó relativamente poco en la Población de maíz 2 (sólo 60 MM más que en la Población de maíz 1), la eficiencia del modelo combinado respecto al genómico es sólo 38.2 % más alta, lo cual indica que el incremento del número de marcadores aumentó la eficiencia del modelo genómico. Sin embargo, el modelo combinado fue más eficiente que los otros dos modelos, por lo que también es recomendable utilizarlo para predecir el mérito genético en este conjunto de datos.
Población 3
Eficiencia del modelo combinado comparado con el modelo estándar y con el modelo genómico
La eficiencia promedio del modelo combinado respecto al modelo estándar y al genómico fue sólo 0.2 y 16.15 %, respectivamente. Debido al número de MM (1279) y de genotipos (599) en la Población 3, la eficiencia del modelo combinado respecto al modelo estándar y genómico fue mucho menor que en las Poblaciones de maíz 1 y 2. En este caso, tanto el modelo combinado como el modelo estándar podrían ser adecuados para predecir el mérito genético.
Los resultados de la Población 3 se deben a que la precisión del modelo estándar (Ecuación 12) es muy alta (Cuadro 1) porque el rendimiento de grano provino de una especie autógama. Por lo tanto, aunque el número de MM es grande, éstos contribuyeron muy poco a la precisión del modelo combinado.
Eficiencia del modelo estándar comparado con el modelo genómico
Aunque el número de MM fue relativamente alto, la eficiencia promedio del modelo estándar fue superior a la del modelo genómico en 15.9 %. Como ya se indicó, esto se debe a que la precisión del modelo estándar para esta población es muy alta (Cuadro 1). Sin embargo, las correlaciones obtenidas en el modelo genómico entre los valores predichos y los observados fueron más altas en la Población 3 que en las Poblaciones de maíz 1 y 2 (Cuadro 1). Esto sugiere que al aumentar el número de MM, la precisión del modelo genómico se incrementó.
De acuerdo con los resultados de las tres poblaciones anteriores, el modelo combinado fue más eficiente que los otros dos modelos, aunque, conforme el número de marcadores y genotipos aumentó, la eficiencia del modelo combinado respecto al modelo genómico se redujo. La eficiencia observada del modelo combinado en los resultados de las tres poblaciones debe atribuirse a que usa en la predicción dos fuentes de información: fenotípica y genómica. Entonces, si se usa en el primer ciclo de selección, la precisión de la selección en tal ciclo aumentará.
Ventaja del modelo genómico respecto al modelo estándar
La manera usual de predecir el mérito genético en plantas y animales en la SG es sustituir la matriz de relaciones numéricas (A) por la matriz de relaciones genómicas (G) en las ecuaciones de predicción. Por ello, la ecuación de predicción del modelo genómico (Ecuación 11) y del modelo estándar (Ecuación 12), son formalmente equivalentes. Cuando el número de MM y genotipos es grande, ambos modelos tienden a proporcionar predicciones que se asemejan cada vez más (Cuadro 1, Población 3). Sin embargo, la ventaja del modelo genómico respecto al estándar radica en la posibilidad de reducir los intervalos entre ciclos de selección en más de dos tercios. Así, el modelo genómico es más eficiente que el modelo estándar cuando la eficiencia se mide por año y no por ciclo de selección. Según Beyene et al. (2015), la selección genómica requiere 1.5 años para completar un ciclo de selección, mientras que la selección fenotípica requiere 4 años por cada ciclo de selección.
Importancia del modelo combinado
Existen varios métodos bayesianos (Gianola, 2013) y no bayesianos (VanRaden, 2008) para predecir el mérito genético en el contexto univariado bajo el supuesto de que el número de genotipos y MM es suficientemente grande en la población base. En la práctica, sin embargo, no todos los candidatos a selección (plantas o animales) cuentan con marcadores moleculares. Por ello, un modelo como el propuesto podría adaptarse fácilmente a este caso, aumentando así la precisión de la predicción.
Bayes empírico comparado con GBLUP
Debido a que los efectos de los MM tienen distribución normal multivariada, Bayes empírico y GBLUP debería proporcionar resultados muy similares (Robinson, 1991) cuando se usa el mismo modelo de predicción. Esto se debe a que los supuestos de GBLUP y Bayes empírico son básicamente los mismos y porque, cuando las varianzas de los parámetros son conocidas, GBLUP se considera un caso particular de los métodos bayesianos (Blasco, 2001).
Finalmente, ¿cómo predecir el mérito genético? ¿por medio del Bayes empírico propuesto, por GBLUP o con alguna de las aproximaciones bayesianas existentes? Los modelos bayesianos estándares proporcionan un mejor control de la incertidumbre asociada a la predicción del mérito genético (de los Campos et al., 2013, Gianola, 2013), lo cual se consigue con mucho trabajo de cómputo (Verbyla et al., 2009). GBLUP, por su parte, requiere el conocimiento de las varianzas de los parámetros para que sus predicciones sean insesgadas; cuando tales varianzas son desconocidas, las propiedades estadísticas de las predicciones de GBLUP son también desconocidas (Gianola, 2013). De acuerdo con Blasco (2001), la elección de un modelo de predicción sobre otro debería estar basada en que el modelo elegido ofrezca una solución que los otros no ofrecen, de la facilidad para resolver el problema, y de la confianza en sus resultados. Este último punto es el de mayor importancia, ya que si el investigador se siente cómodo con un determinado método, significa que conoce sus limitaciones y ventajas y sabe qué esperar del modelo al utilizarlo en un análisis estadístico específico.
Conclusiones
El modelo propuesto, con la información conjunta del pedigrí y genómica en el contexto Bayes empírico, proporcionó predicciones más precisas que los otros dos modelos porque en la predicción se incorporan la información fenotípica y genómica, y también las correlaciones genéticas entre caracteres.











 texto em
texto em