Agua–suelo–clima

 

Transferencia regional de información hidrológica mediante regresión lineal múltiple de tipo ridge

 

Regional transference of hydrologic information through multiple linear regression of ridge type

 

Daniel F. Campos–Aranda

 

Facultad de Ingeniería de la Universidad Autónoma de San Luis Potosí. Genaro Codina Número 240. 78280 San Luis Potosí, San Luis Potosí. Autor responsable.(campos_aranda@hotmail.com)

 

Recibido: April, 2012.
Aprobado: March, 2013.

 

Resumen

Cuando se emplean registros largos de escurrimiento, lluvia o crecientes anuales de una región con respuesta hidrológica similar, para ampliar una serie corta a través de la técnica estadística de regresión lineal múltiple (RLM), es probable que tales registros por su semejanza intrínseca den origen a un problema de multicolinealidad. Tal problema se debe detectar y cuantificar para saber si es aceptable, moderada, fuerte o grave y buscar soluciones alternativas al método de ajuste de la RLM por mínimos cuadrados de los residuos. En este estudio se diagnosticó la multicolinealidad mediante factores de inflación de la variancia e índices de condición, basados en los eigenvalores. Además se presenta como método alternativo el ajuste sesgado de la RLM, conocido como regresión Ridge. Una aplicación numérica en el sistema del río Tempoal, de la Región Hidrológica No. 26 (Pánuco, México), se describió para completar el registro corto de volúmenes escurridos anuales de la estación hidrométrica Platón Sánchez, con base en las otras cuatro estaciones de aforos que cuentan con registros amplios. Se concluye que las principales ventajas de la regresión Ridge son la facilidad de manejo de transferencia con seis o más regresores y la sencillez de su implementación y desarrollo a través de la traza Ridge.

Palabras clave: multicolinealidad, factores de inflación de la varianza, eigenvalores, eigenvectores, índices de condición, traza Ridge, homogeneidad regional, Río Tempoal.

 

Abstract

When annual long records are used of runoff, rainfall or flooding of a region with similar hydrological response, to amplify short series through the statistical technique of multiple linear regression (MLR), it is likely that those records by reason of their intrinsic similarity will lead to a problem of multicollinearity. This problem should be detected and quantified to know if it is acceptable, moderate, strong or serious and look for alternative solutions to the fitting method of the MLR by least squares of the residuals. In this study a diagnostic was made of multicollinearity through variance inflation factors and condition indices based on the eigenvalues. In addition, the biased fitting of the MLR is presented as an alternative method, known as Ridge regression. A numerical application in the system of the Tempoal river, of Hydrological Region No. 26 (Pánuco, México), was described to complete the short record of runoff volumes of the Platón Sánchez hydrometric station, based on the other four measuring stations that have long records. It is concluded that the principal advantages of Ridge regression are the ease of handling of transference with six or more regressions and the simplicity of its implementation and development by means of the Ridge trace.

Key words: multicollinearity, variance inflation factors, eigenvalues, eigenvectors, condition indices, Ridge trace, regional homogeneity, Tempoal River.

 

INTRODUCCIÓN

La transferencia regional de información hidrológica consiste en la utilización de registros largos de escurrimiento, lluvia o crecientes anuales, para ampliar series cortas disponibles en estaciones hidrométricas o pluviométricas, ubicadas dentro de la misma zona geográfica o de características climáticas y físicas similares. Esta ampliación es conveniente o necesaria porque entre más largo es un registro hidrológico, sus estimaciones estadísticas serán más confiables y exactas. Generalmente la cercanía geográfica no garantiza que los registros, amplio y corto, guarden una relación o correspondencia, sino el hecho de pertenecer a una región que se puede considerar homogénea en sus características de respuesta hidrológica.

Definida la región homogénea y seleccionados los registros amplios disponibles, la transferencia de información para ampliar una serie corta se puede realizar mediante la técnica estadística de regresión lineal múltiple. El hecho de que todos los registros por procesar sean parte de una región con respuesta hidrológica similar, implica que éstos guardarán cierta similitud, es decir, habrá alguna dependencia lineal entre las variables independientes o regresores, generando un problema de multicolinealidad en el análisis de regresión.

La regresión lineal múltiple de tipo Ridge o sesgada es una técnica estadística que permite evitar los problemas que genera la multicolinealidad, en relación con la inestabilidad de los coeficientes de la ecuación de regresión. Zhao et al. (1995) la emplearon para identificar hidrogramas unitarios bien formados. Yu y Liong (2007) la aplicaron para obtener pronósticos de series cronológicas hidrológicas y Weimin y Qian (2012) para obtener los parámetros de un modelo hidrológico en función de las características fisiográficas de las cuencas.

El objetivo de este estudio fue exponer como se diagnostica la multicolinealidad y como se desarrolla la regresión lineal múltiple de tipo Ridge para obtener estimaciones confiables de la variable dependiente. Se realiza una aplicación numérica, consistente en ampliar el registro corto de volúmenes escurridos anuales de la estación hidrométrica Platón Sánchez del río Tempoal, con base en las cuatro series amplias de las estaciones de aforos: Tempoal, Terrerillos, Los Hules y El Cardón; el sistema de río Tempoal está dentro de la Región Hidrológica No. 26 (Pánuco, México). Los resultados se contrastan con los obtenidos previamente mediante el método de selección de regresores.

 

MATERIALES Y MÉTODOS

La regresión lineal múltiple (RLM) y sus problemas

Frecuentemente se puede establecer una relación de tipo lineal entre la variable dependiente (Y ) y varias (p) independientes X1, X2, . . . . , Xp, que es la generalización o extensión natural de la regresión lineal simple y su expresión es (Ryan, 1998):

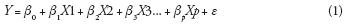
Por tanto, los principios que rigen a la regresión lineal simple y su expresión se aplican a la RLM. Por ejemplo, que tanto Y como las X estén normalmente distribuidas y que los errores e sean independientes con distribución normal de media cero y misma varianza (σ²) para cada X. La RLM implica una complejidad real en tres aspectos: 1) selección de cuántas y cuáles variables independientes utilizar; 2) interpretación de los resultados, especialmente de los coeficientes de la regresión (β_i); 3) determinación de cuándo usar un método de ajuste alternativo al de mínimos cuadrados de los residuos.

Para los dos primeros aspectos, un planteamiento correcto de tipo causa–efecto del problema por resolver con la RLM, ayudará a encontrar las mejores variables por utilizar y orientará sobre los valores por esperar en los coeficientes de la regresión. Para la transferencia regional de información hidrológica lo más probable es que se genere una situación de multicolinealidad, por la semejanza o correlación de los registros involucrados. Tal problema se debe diagnosticar y resolver, por ejemplo, a través de la regresión tipo Ridge.

Solución de mínimos cuadrados de los residuos

La solución matricial para la RLM, en el caso general de p variables independientes o regresores y n observaciones o datos de Y, X1, X2, . . . , Xp, es la siguiente (Ryan, 1998):

siendo:

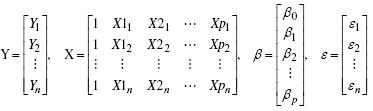
El planteamiento de esta solución implica que la sumatoria de uno a n de los residuos al cuadrado debe ser minimizada:

Entonces, diferenciando el lado derecho de la ecuación anterior con respecto a β₀, β₁, β₂ , . . . . , β_p, por separado, se originan las ecuaciones normales como función de los parámetros desconocidos. En notación matricial estas ecuaciones son:

cuya solución es:

en la cual, X^T es la matriz transpuesta de X, y (X^T∙X)^–1 indica la matriz inversa de X^T∙X.

Escalamiento de longitud unitaria de los datos

Sustraer a cada variable independiente o regresor su media aritmética, se conoce como centrado de los datos y su ventaja fundamental es que las matrices X involucradas de n renglones ahora tienen p columnas, ya que la ecuación de RLM es:

cuyo reacomodo para obtener la ecuación 1 implica que:

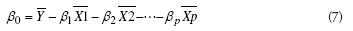
El escalamiento de longitud unitaria implica además del centrado, la división entre la raíz cuadrada de la varianza (Montgomery et al., 2002), por lo cual:

donde

El escalamiento de longitud unitaria produce, respecto a la ecuación 4, que la matriz W^T∙W sea la matriz de correlación simple entre los regresores Xj; además la matriz W^T∙Y es la matriz de correlación simple entre cada regresor Xj y la variable dependiente Y. Este escalamiento y el normal llevan a coeficientes estandarizados de regresión, cuya comparación entre ellos define la importancia de cada regresor. Otro escalamiento frecuentemente requerido está asociado con la estabilidad numérica de la matriz inversa de W^T∙W, pues es común obtenerla planteando esta igualdad A∙A^–1 = I; al transformar la matriz A en la matriz identidad I y realizar las mismas operaciones en I, ésta se convierte en la matriz A^–1 buscada. Cuando la matriz A tiene elementos muy grandes su inversa presentará elementos muy pequeños y entonces los errores por redondeo se vuelven importantes. En tales casos conviene dividir (escalar) todos los datos entre una cantidad fija o cociente reductor (COR), antes de aplicar la ecuación 5 y después los resultados de la ecuación 1 se multiplican por el COR.

Diagnóstico de multicolinealidad basada en W^T∙W o (W^T∙W)^–1

La manera más simple de descubrir la multicolinealidad es a través de la inspección de la matriz W^T∙W, cuyos elementos fuera de la diagonal principal corresponden a los coeficientes de correlación simple entre pares de regresores; si hay valores absolutos mayores de 0.80 hay dependencia entre tal pareja. Este método sólo detecta multicolinealidad pero no la cuantifica; en cambio, cuando los factores de inflación de la varianza VIF (variance inflation factor) son mayores de 10 implican que los coeficientes de regresión obtenidos con la ecuación 5, no son confiables debido a la multicolinealidad. La expresión de los VIF es (Montgomery et al., 1998; 2002):

donde R_j² es el coeficiente de determinación que resulta de la RLM entre el regresor Xj como variable dependiente y el resto p–1 como regresores. Los VIF corresponden a la diagonal de la matriz inversa de W^T∙W.

Diagnóstico de multicolinealidad con base en los eigenvalores de W^T∙W

Los eigenvalores de la matriz W^T∙W se designan por λ₁, λ₂, λ₃, . . . . , λ_p, se conocen como valores propios, corresponden a las raíces de la ecuación característica |A–λ^.I|=0 de la matriz A, y se obtienen con procedimientos de métodos numéricos, por ejemplo el método de potencias (Carnahan et al., 1969). Si existe una o más dependencias casi lineales en los datos, uno o más de los eigenvalores serán pequeños. El número de condiciónk_j de la matriz W^T∙W se define así (Montgomery et al., 1998; 2002):

y representa el espectro de variación de los eigenvalores de la matriz W^T∙W. En general, cuando k es menor de 100 prácticamente no existen problemas de multicolinealidad, cuando varía de 100 a 1000 hay multicolinealidad moderada a fuerte y cuando excede a 1000 habrá graves problemas asociados a ésta. Los índices de condición k_j de la matriz W^T∙W son:

Los valores de k_j definen el número y magnitud de las dependencias lineales que existen en los datos. Además, los eigenvectores asociados a cada eigenvalor permiten establecer numéricamente la dependencia lineal que existe entre los regresores. Esto último se mostrará en la aplicación numérica.

La regresión Ridge

En general, cuando el método de mínimos cuadrados de los residuos se aplica a datos que presentan multicolinealidad, la estimación de los coeficientes de regresión no es confiable, ya que su valor absoluto está exagerado y además es inestable. Las técnicas básicas para combatir la multicolinealidad son tres: 1) obtener más datos, lo cual puede no ser posible y además es probable que los datos nuevos reflejen el comportamiento de los anteriores; 2) reespecificar el modelo, redefiniendo los regresores, por ejemplo, si X1, X2 y X3 son linealmente dependientes, se puede adoptar una función de ellos del tipo X = (X1 + X2)/X3, o bien X = X1*X2*X3 que preserva el contenido de la información de los regresores originales, pero que reduzca el deterioramiento de los datos debido a la multicolinealidad; otro método de reespecificación efectivo consiste en la eliminación de una o más variables o regresores, que definitivamente reduce la multicolinealidad pero puede dañar notablemente la capacidad predictiva del modelo; 3) obtener estimaciones sesgadas, como la RLM de tipo Ridge.

El método de mínimos cuadrados de los residuos permite que la estimación (ecuación 5) tenga varianza mínima pero la multicolinealidad genera varianza muy grande, por lo cual sus estimaciones son inestables. Suponiendo que se obtiene un estimador sesgado con mucho menor varianza, se puede aceptar una cantidad pequeña de sesgo en , de manera que el error medio cuadrático de sea menor que la varianza del estimador insesgado . La menor varianza del estimador sesgado implica que es un estimador más estable de β que el insesgado .

Hay varios procedimientos para obtener estimadores sesgados de los coeficientes de regresión β. Uno de ellos es la regresión Ridge (Hoerl y Kennard, 1970) cuyo nombre se debe a la semejanza de sus operaciones matemáticas con el análisis Ridge usado para describir el comportamiento de superficies de respuesta de segundo orden. El estimador Ridge se obtiene resolviendo una versión ligeramente modificada de las ecuaciones normales, expuestas como ecuaciones 4 y 5 (Montgomery et al., 1998, 2002):

En esas expresiones la constante k>0, o parámetro de sesgo, se selecciona durante el proceso de aplicación de la regresión Ridge. El estimador Ridge es una transformación lineal del estimador de mínimos cuadrados de los residuos cuyo sesgo crece al aumentar k, pero al mismo tiempo disminuye su varianza. Con la regresión Ridge se obtiene una estimación estable de sus coeficientes, a cambio de no ser el mejor ajuste a los datos. Por tanto, aunque no hay demostración matemática concluyente, se considera que conduce a ecuaciones de regresión que funcionan mejor para predecir observaciones futuras, comparada con la de mínimos cuadrados de los residuos.

Hoerl y Kennard (1970) sugieren que un valor adecuado de k puede estimarse por inspección de la traza Ridge, que es una gráfica de las magnitudes de dibujados en las ordenadas, contra sus respectivos valores de k en las abscisas. Los valores de k suelen estar en el intervalo de 0 a 1. Si la multicolinealidad es grave, los coeficientes variarán mucho, pero en un cierto valor de k se estabilizan. Lo fundamental es seleccionar el valor de k más pequeño, donde los sean estables. Con ello es posible obtener una ecuación de regresión con menor error medio cuadrático que el correspondiente a mínimos cuadrados.

Aplicación numérica

El río Tempoal es uno de los afluentes importantes del río Moctezuma, que junto con el río Tampaón forman el río Pánuco, en la Región Hidrológica No. 26 de México. El río Tempoal tiene cinco estaciones hidrométricas: El Cardón (X4), Los Hules (X3), Terrerillos (X2), Tempoal (X1) y Platón Sánchez (Y). En la Figura 1 se muestra la ubicación y morfología del sistema del río Tempoal. Campos (2011) mostró las características generales de ellas y sus registros disponibles de volumen escurrido anual (en Mm³), en el periodo de 1961 a 2002, con seis años faltantes en el lapso de 1979 a 2002 (Cuadro 1). También verificó las características estadísticas de los datos y realizó la estimación del registro faltante en Platón Sánchez con base en los otros cuatro, siguiendo el método de selección de variables. Ahora se aplicará la regresión Ridge con el mismo propósito de ampliar el registro corto de esta estación de aforos y comparar resultados.

Verificación de la homogeneidad regional

El uso estadístico de la información del Cuadro 1 establece que se requieren dos verificaciones de la homogeneidad regional, la primera para el periodo común de los datos (1979–2002) pues éstos definirán los coeficientes de la ecuación de regresión, y la segunda para el lapso total de datos porque el periodo 1961–1978 permite ampliar del registro corto. La segunda verificación es más difícil de cumplir debido a la diferencia de amplitudes de registros y por ello, sólo de esta comprobación se presentan sus resultados. Antes de usar una prueba de homogeneidad, en este caso la versión corregida del Test de Langbein (Fill y Stedinger, 1995; Campos, 2012), se debe verificar la calidad estadística de la información, por ejemplo a través del Test de Discordancias aplicado en el periodo común, el cual permite detectar valores anómalos, tendencias determinísticas o cambios en la media, ya que mide lo discordante que es cada registro en sus cocientes L con respecto al promedio del grupo considerado como un todo (Hosking y Wallis, 1997; Campos, 2010). En el Cuadro 2 se exponen los resultados del Test de Discordancias, cuyo valor crítico de Discordancia es D_c=1.333, ya que sólo hay cinco estaciones en el grupo. Se observa que ningún registro es discordante con el grupo.

En el Cuadro 3 se muestran los resultados de la aplicación del nuevo Test de Langbein al sistema del río Tempoal, los cuales indican que sus cinco estaciones hidrométricas forman una región homogénea, pues ninguna de ellas queda fuera de sus curvas de control definidas por los periodos de retorno inferior (Tr_inf) y superior (Tr_sup), en años.

 

RESULTADOS Y DISCUSIÓN

Diagnóstico de multicolinealidad

Las matrices W^T∙W, W^T∙Y y (W^T∙W)^–1 obtenidas para los datos de Cuadro 1, procesados lógicamente con escalamiento unitario son:

La inspección de la matriz W^T∙W muestra que los cuatro registros están altamente correlacionados, mostrando la mayor relación Tempoal con El Cardón (r_xy=0.977) y la menor Terrerillos con Los Hules (r_xy=0.899). Lo anterior establece que existe un problema de multicolinealidad con tales datos. En la matriz W^T∙Y se observa que la mayor correlación entre los regresores y el registro de Platón Sánchez es con Tempoal y la menor con Los Hules, esto se reflejará en las variaciones de los coeficientes Ridge .

El primer renglón de resultados del Cuadro 4 procede de los elementos de la diagonal de la matriz inversa de W^T∙W, mostrando que existe multicolinealidad pues todos los VIF_j exceden de 10. Sin embargo no exceden de 100, de manera que tales problemas son moderados o aceptables. En el segundo renglón de resultados del Cuadro 4 se exponen los eigenvalores y en el tercero los índices de condición k_j de la matriz W^T∙W, los cuales ratifican los resultados anteriores en relación con la multicolinealidad, ya que sólo uno excede en valor absoluto a 100.

Con base en los elementos del cuarto eigenvector se establece la siguiente ecuación relativa a la multicolinealidad presente:

considerando que el coeficiente de X3 es cercano a cero se obtiene:

 

la ecuación anterior establece la relación entre X1 y aproximadamente las mitades de X2 y X4.

Cálculo y análisis de la traza Ridge

Aplicando la ecuación 16 con los valores de k indicados en el Cuadro 5 se obtuvieron los coeficientes de regresión tipo Ridge ahí mostrados, cuyos coeficientes de determinación (R²) respectivos, también se citan en este cuadro. El cálculo de R² se realizó haciendo el centrado de los datos y utilizando un COR=1000. Con base en los resultados del Cuadro 5 se ha construido la traza Ridge, mostrada en la Figura 2.

La inspección de la traza Ridge muestra que el coeficiente β₁ es el de mayor variación o cambio con k, siguiéndolo el β₄ y el β₂ que incluso cambian de signo; por el contrario, el coeficiente β₃ fue el más estable. Entonces, durante la regresión Ridge el coeficiente que más cambia es el correspondiente al registro de Tempoal y que menos lo hace el del registro de Los Hules. Teniendo en cuenta que el parámetro de sesgo (k) debe tener el menor valor posible, cuando ya los coeficientes de regresión Ridge se pueden considerar estabilizados, se seleccionaron dos valores para k: 0.050 y 0.100 (Figura 2).

Estimaciones Ridge y su contraste

En el Cuadro 6 se muestran las 18 estimaciones de la variable dependiente , es decir del registro histórico en Platón Sánchez Mm³ para el periodo 1979–2002, así como sus residuos respectivos, realizadas con las regresiones Ridge que emplean k=0.050 y 0.100. Los coeficientes de regresión respectivos se muestran en el Cuadro 7 y fueron obtenidos con datos centrados y usando un COR de mil.

En el Cuadro 7 están los resultados del contraste entre los residuos de los mejores modelos de regresión obtenidos a través de selección óptima de regresores (Campos, 2011) y las regresiones Ridge adoptadas. La regresión Ridge origina valores escasamente mayores de los residuos y de la suma de residuos al cuadrado, pero la suma algebraica de sus errores es menor.

Estimaciones Ridge adoptadas

En el Cuadro 8 se muestran los 18 volúmenes escurridos anuales estimados en la estación Platón Sánchez en el periodo de 1968 a 1978, mediante las regresiones Ridge adoptadas, así como sus respectivos parámetros estadísticos.

En la Figura 3 se muestra la comparación entre la segunda serie de volúmenes escurridos anuales estimados con regresión Ridge y los valores adoptados bajo el planteamiento de selección de regresores (Campos, 2011). Ambas series estimadas de volúmenes escurridos anuales presentan el mismo comportamiento, pero la procedente de la regresión Ridge es menor y con valores mínimos más acusados, lo cual origina una media y un coeficiente de variación más parecidos a los datos históricos de Platón Sánchez (Cuadro 1).

Comentarios en torno a la hidrología estadística

La regresión lineal múltiple de tipo Ridge permite realizar la ampliación de un registro hidrológico corto, empleando varios cercanos y aledaños que por lógica serán multicolineales. Esta técnica estadística y otras, basadas en el análisis multivariado de series cronológicas, permiten un mejor uso de la información hidrológica disponible. Sin embargo, ningún procedimiento de la Hidrología estadística genera nueva información o suple su escasez.

Por lo anterior, se debe requerir a la Comisión Nacional del Agua (CONAGUA) que restablezca la red de mediciones climatológicas y hidrométricas que había en los años ochenta. Lafragua et al. (2006) señalan que la situación respecto a la información hidrológica es verdaderamente crítica, a pesar de ser la base para la estimación de la disponibilidad superficial en las cuencas y en el país. Por ejemplo, en el 2004 había 50% de las estaciones climatológicas existentes en 1980 y las hidrométricas habían disminuido de casi 1,600 en 1980 a sólo 430 en el 2002.

 

CONCLUSIONES

Es mejor usar parte de la información estadística de todos los regresores, como lo hace la regresión Ridge, que emplear toda la información de algunos regresores y nada de otros, como actúa el método de selección de variables. Además, la regresión Ridge es un procedimiento directo, de fácil implementación dentro de la solución de mínimos cuadrados de los residuos y la interpretación de la traza Ridge no presenta dificultades.

Respecto a la aplicación numérica descrita, problema previamente abordado con eliminación de variables, los resultados de la regresión Ridge son bastante semejantes pero más apegados al coeficiente de variación de los datos disponibles en Platón Sánchez. En problemas con seis o siete registros amplios disponibles, la regresión Ridge será una mejor opción que la inspección de 64 o de 128 posibles modelos obtenidos por mínimos cuadrados de los residuos, como lo establece el esquema de eliminación de variables.

 

AGRADECIMIENTOS

Se agradecen las correcciones y sugerencias de los dos árbitros anónimos y del editor asignado, las cuales permitieron completar el trabajo en ciertos aspectos teóricos y cálculos no expuestos, entre los segundos el análisis de homogeneidad regional.

 

LITERATURA CITADA

Campos A., D. F. 2010. Verificación de la homogeneidad regional mediante tres pruebas estadísticas. Tecnología y Ciencias del Agua I(4): 157–165.         [ Links ]

Campos A., D. F. 2011. Transferencia de información hidrológica mediante regresión lineal múltiple, con selección óptima de regresores. Agrociencia 45(8): 863–880.         [ Links ]

Campos A., D. F. 2012. Descripción y aplicación de la versión corregida del Test de Langbein para verificar homogeneidad regional. Ingeniería, Investigación y Tecnología XIII(4): 411–416.         [ Links ]

Carnahan, B., H. A. Luther, and J. O. Wilkes. 1969. Matrices and related topics. In: Applied Numerical Methods. John Wiley & Sons. New York, U.S.A. pp: 210–268.         [ Links ]

Fill, H. D., and J. R. Stedinger. 1995. Homogeneity test based upon Gumbel distribution and a critical appraisal of Dalrymple's test. J. Hydrol. 166: 81–105.         [ Links ]

Hosking, J. R. M., and J. R. Wallis. 1997. Screening the data. In: Regional Frequency Analysis. An Approach Based on L–moments. Cambridge University Press. Cambridge, United Kingdom. pp: 44–53.         [ Links ]

Hoerl, A. E., and R. W. Kennard. 1970. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 12: 55–67.         [ Links ]

Lafragua C., J., D. González R., y Y. Solís A. 2006. Cantidad y calidad de la información climatológica e hidrométrica para el cálculo de la disponibilidad de agua superficial. In: Memoria del XIX Congreso Nacional de Hidráulica, Tema: Hidrología. Cuernavaca, Morelos, México. (En CD).         [ Links ]

Montgomery, D. C., E. A. Peck, y G. G. Vining. 2002. Multicolinealidad. In: Introducción al Análisis de Regresión Lineal. Compañía Editorial Continental. México, D. F. pp: 291–342.         [ Links ]

Montgomery, D. C., E. A. Peck, and J. R. Simpson. 1998. Multicollinearity and biased estimation in regression. In: Wadsworth, H. M. (ed). Handbook of Statistical Methods for Engineers and Scientists. McGraw–Hill, Inc. New York, U.S.A. 2nd ed. pp: 16.3–16.27.         [ Links ]

Ryan, T. P. 1998. Linear regression. In: Wadsworth, H. M. (ed). Handbook of Statistical Methods for Engineers and Scientists,. McGraw–Hill, Inc. New York, U.S.A. Second edition. pp: 14.1–14.43.         [ Links ]

Weimin, B., and L. Qian. 2012. Estimating selected parameters for the XAJ model under multicollinearity among watersheds characteristics. J. Hydrol. Eng. 17(1): 118–128.         [ Links ]

Yu, X., and S. Liong. 2007. Forecasting of hydrology time series with ridge regression in feature space. J. Hydrol. 332(3–4): 290–302.         [ Links ]

Zhao, B., Y. Tung, and J. Yang. 1995. Estimation of unit hydrograph by ridge least–squares method. J. Irrig. Drain. Eng. 121(3): 253–259.         [ Links ]