Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.47 no.2 Texcoco feb./mar. 2013
Agua–suelo–clima
Eficiencia de aplicación de agua en la superficie y en el perfil del suelo en un sistema de riego por aspersión
Efficient water application on soil surface and in the soil profile in a sprinkler irrigation system
Natalia Flórez–Tuta*, Ivo Zution–Gonçalves, Daniel Rodrigues–Calvacante Feitosa, E. Augusto Agnellos–Barbosa, Fabio Ponciano–de Deus, Maycon Diego–Ribeiro, Edson Eiji–Matsura
Universidad Estadual de Campinas, Facultad de Ingeniería Agrícola, Departamento de Agua y suelo, Av. Candido Rondón, 501, Barão Geraldo–Campinas /SP, Cidade Universitária Zeferino Vaz, CEP 13083–875. *Autor responsable: (natalia1_t@yahoo.es).
Recibido: agosto, 2012.
Aprobado: enero, 2013.
Resumen
Aplicaciones insuficientes o excesivas de agua se deben a dimensionamientos inadecuados de sistemas de riego, ocasionando pérdidas de agua y limitan su eficiencia. Así, la agricultura irrigada se debe realizar eficientemente adoptando prácticas pata racionalizar el uso del agua, haciéndola ambiental y económicamente sostenible. El objetivo del presente estudio fue evaluar la calidad de aplicación de agua en la superficie y en el perfil de un Oxisol, después del riego por aspersión convencional, utilizando la técnica de la TDR para monitorear el contenido de agua en el suelo. En campo se instalaron 196 colectores con espaciamiento de 2 m entre ellos y formando una malla con formato cuadrado. Con los datos recolectados se simularon sobreposiciones con diversos espaciamientos entre aspersores, determinando para cada espaciamiento la uniformidad y eficiencia de aplicación de agua; para esta última se usó un modelo matemático lineal. La uniformidad de distribución de agua fue mayor para los menores espaciamientos entre aspersores en la superficie y en el perfil del suelo. El coeficiente de uniformidad de distribución del agua en el perfil del suelo fue mayor que el obtenido para las láminas precipitadas en los colectores, en los espaciamientos 6×6 m y 6×12 m y menor en los demás espaciamientos. El análisis de los coeficientes de uniformidad y de las eficiencias de aplicación y almacenamiento de agua en el suelo, para diferentes simulaciones de espaciamientos entre aspersores, permite tomar decisiones en relación a la disposición de los aspersores en campo y en el uso del agua para riego de forma más confiable.
Palabras clave: uniformidad, modelo lineal, lámina infiltrada.
Abstract
Insufficient or excessive water applications are due to inadequate measurings of irrigation systems, causing water losses and limiting their efficiency. Thus, irrigated agriculture must be performed efficiently, adopting practices to rationalize the use of water, making it environmentally and economically sustainable. The objective of this study was to evaluate the quality of water application on the surface and profile of an Oxisol, after irrigation through conventional sprinkler, using the TDR technique to monitor the water content in the soil. In the field 196 collectors were installed with 2 m of space between them and forming a mesh with a square format. With the data collected, superpositions were simulated with various spacings between sprinklers, determining for each spacing the uniformity and efficiency of water application; for the latter, a linear mathematical model was used. The uniformity of water distribution was greater for the smaller spacing between sprinklers on the soil surface and profile. The coefficient of uniformity of water distribution in the soil profile was higher than that obtained for sheets precipitated in the collectors, in the 6×6 and 6×12 spacings and lower in the other spacings. The analysis of uniformity coeicients and eiciencies of water application and storage in the soil, for different simulations of spacings between sprinklers, allows making decisions with regards to the disposition of sprinklers in the field and for the more reliable use of water for irrigation.
Keywords: uniformity, linear model, infiltration sheet.
INTRODUCCIÓN
El sector agrícola realiza el mayor consumo de agua en el mundo y por tanto la agricultura irrigada debe ser eficiente para tener sostenibilidad ambiental y económica. Un parámetro principal para evaluar sistemas de riego es la uniformidad de aplicación de agua en la superficie del área irrigada, reflejándose directamente en el manejo y desempeño del cultivo, en la calidad y cantidad de los productos, en la eficiencia del uso del agua, en el costo del riego y por tanto de la producción (Bernardo et al., 2009).
Una baja uniformidad de aplicación de agua causa crecimiento desigual de las plantas y en algunos casos contaminación del suelo con sales, lo cual repercute en la degradación del suelo (Cunha et al., 2008). Esto se relaciona con el exceso de agua en el suelo que causa lixiviación de nutrientes, reducción en la concentración de oxígeno disponible para las raíces y aumento en la incidencia de plagas y enfermedades; además, la escasez de agua aumenta los riesgos de salinización del suelo e inhibe el potencial productivo de las plantas (Paulino et al., 2009). El movimiento del agua a través de los poros del suelo aumenta la humedad en profundidad, a expensas de las profundidades más superficiales humedecidas inicialmente y mejora la calidad del riego, lo que puede estar en disonancia con la evaluada en la superficie (Reichardt, 1996).
El primer coeficiente de uniformidad propuesto por Christiansen (1942) adoptó la desviación media como medida de dispersión (CUC), mientras que el coeficiente de uniformidad de distribución (CUD; Criddle et al., 1956) considera la razón entre la media del 25 % de los menores valores de las láminas de irrigación y la lámina media recolectada. Bajos valores de CUC y CUD pueden deberse a diseños incorrectos de los sistemas de riego que limitan su desempeño y funcionamiento óptimo (Buendía et al., 2004.)
La eficiencia de riego es un concepto usado en proyectos y en el manejo de sistemas de riego. La calidad del riego se evalúa con base en indicadores de desempeño como eficiencia y uniformidad y mediante índices de productividad de agua que relacionan el rendimiento de los cultivos y el valor económico de la producción por unidad de lámina de agua aplicada o consumida (Lorite et al., 2004; Bos et al., 2005). De esta forma, durante la operación del sistema de riego los valores de uniformidad de aplicación y de distribución deben ser altos y las pérdidas bajas para obtener altos valores de eficiencia.
La eficiencia de aplicación de agua irrigada es un parámetro que cuantifica cuanto del agua aplicada es realmente utilizada. Este parámetro es subdividido en eficiencia de aplicación (Ea), eficiencia de almacenamiento (Es), pérdida por percolación debajo de la zona radicular (Pp) y déficit de agua en el suelo (D). La Ea indica la cantidad de agua incorporada al suelo hasta la profundidad de estudio, en relación con la cantidad total de agua aplicada por el sistema de riego; así, la diferencia entre éstas indica el volumen de agua perdido por percolación o por evaporación. La Es muestra la relación entre el volumen de agua almacenado y el requerido para una determinada profundidad del suelo, y la diferencia de estos volúmenes es un indicador de déficit (Zocoler et al., 2004).
Para evaluar la calidad del riego a partir del análisis de distribución de agua en el suelo, se realizan ajustes de la relación entre la lámina de agua infiltrada y el área irrigada usando modelos matemáticos que permiten la simulación del desempeño de un sistema con otro tipo de manejo de irrigación (Fietz et al., 1999). El modelo lineal sugerido por Karmeli (1978) es usado en el estudio de padrones de precipitación de aspersores en función de la eficiencia, uniformidad de distribución, percolación profunda y otros parámetros de riego, relacionando la curva de frecuencia acumulada adimensional de la lámina de infiltración con la fracción del área irrigada, mediante regresión lineal.
La técnica de TDR (Time Domain Reflectometry) es adecuada para medir la humedad del suelo porque permite realizar mayor número de lecturas en menos tiempo, proporciona repeticiones de las lecturas, no es destructivo, es portátil y de fácil acoplamiento a dispositivos recolectores de datos, permite automatización y las mediciones se realizan en tiempo real, en condiciones de laboratorio o de campo en cualquier dirección o perfil del suelo (Topp et al., 1980; Coelho y Arruda, 2001; Souza et al., 2004).
De acuerdo con lo expuesto, el objetivo del presente estudio fue evaluar la calidad del riego para diferentes simulaciones de ubicaciones entre aspersores, por medio de la uniformidad y eficiencia de aplicación de agua, en la superficie y en el perfil de un Oxisol, después del riego por aspersión, utilizando la técnica de la TDR para monitorear la humedad.
MATERIALES Y MÉTODOS
El experimento se realizó en octubre del 2011 en el campo experimental de la Facultad de Ingeniería Agrícola de la Universidad Estadual de Campinas, en Campinas, SP, Brasil, 22° 53' S, 47° 05' O y altitud media de 620 m. Según la clasificación de Kóppen el clima de la región es Cwa/Cfa (subtropical/tropical de altitud), con temperatura media anual de 22.3 C, humedad relativa y precipitación media anual de 62 % y 1425 mm. El suelo del área experimental, de topografía homogénea y sin cobertura vegetal, fue clasificado como Oxisol (Soil Survey Staff, 2010) de acuerdo con las características físico–hídricas descritas en el Cuadro 1.
Antes de realizar el presente experimento se hicieron análisis para determinar el tiempo máximo de riego (sin percolación de agua abajo de 0.15 m, profundidad establecida para evaluar la humedad del suelo), área mojada (para el aspersor instalado a 0.6 m de altura), número de colectores necesarios para cubrir el área mojada y presión de servicio para las condiciones establecidas.
Para el experimento se usó un aspersor de ½ pulgada, boquilla azul de 3.5×2.5 mm, con las características de operación dadas por el fabricante: caudal 1115 a 1,430 m3 h–1, diámetro de mojado 23 a 26 m, presión de servicio 200 a 400 Kpa. La presión de operación del aspersor seleccionada fue 300 kPa.
La línea lateral tenía tubos PVC DN 50 con 6 m de largo. Al final de la línea de lateral se instaló un tubo de elevación de PVC (½ pulgada), con 0.6 m de altura, que conducía el agua hasta el emisor en el centro de la malla de colectores. Para controlar la presión y el caudal de entrada al emisor se instalaron un registro de cortina, un regulador de presión y un manómetro tipo Bourdon.
En campo se instalaron 196 colectores (0.08 m diámetro cada uno) para captar el agua rociada por el aspersor en la superficie del suelo, con espacio de 2 m entre ellos y formando una malla cuadrada (26×26 m). Los colectores fueron fijados en campo usando varillas metálicas instaladas a 0.40 m del suelo. Durante el experimento la velocidad del viento se midió cada 15 min con un anemómetro en el área experimental a 2 m de altura del suelo. A 1 m de distancia del área experimental se colocó un colector con 100 mL de agua para cuantificar las pérdidas por evaporación.
Con las láminas colectadas en cada punto de la malla y el tiempo del ensayo, se calculó la intensidad de aplicación de agua del aspersor (ecuación 1), en condiciones mínimas de viento (<2m s–1), obteniendo 6.6 mm h–1 como valor máximo de la intensidad (Imáx):

donde I es la intensidad de aplicación de agua (mm h–1), L es la lámina colectada (mm), t es el tiempo de duración del ensayo preliminar.
Para monitorear la humedad del suelo se usó la técnica TDR (Topp et al., 1980) con un equipo TDR 100 portátil con interface RS232 y recolector de datos (CR1000) para realizar automáticamente la lectura de la constante dieléctrica aparente (Ka). La sonda usada en el experimento tenía tres varillas de acero inoxidable (cada una 0.15 m de largo útil) según la profundidad de estudio (Figura 1). Bizari et al. (2011) describen los detalles del equipo.
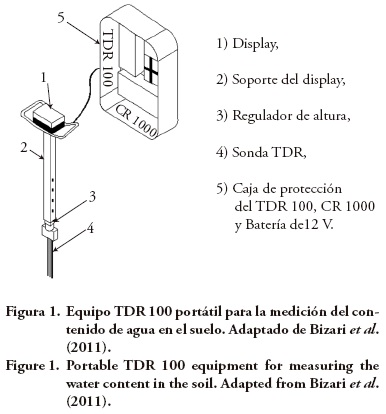
El dispositivo TDR y consecuentemente el valor de la constante dieléctrica fueron calibrados en función de los límites de humedad establecidos, que en el presente experimento está entre la humedad en capacidad de campo y punto de marchitez permanente (0.47 y 0.27 m3 m–3) para la profundidad de estudio que es 0.15 m, conforme a la ecuación (2):
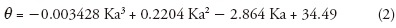
donde θ es la humedad volumétrica del suelo y Ka es la constante dieléctrica aparente.
La capacidad máxima de almacenamiento de agua en el suelo se calculó para la profundidad de evaluación establecida, de acuerdo con la ecuación (3) (Bernardo et al., 2009):

donde Amáx es la capacidad de almacenamiento máximo de agua en el suelo (mm), θcc es la humedad del suelo en capacidad de campo (m3 m–3), θi es la humedad inicial del suelo (m3 m–3), z es la profundidad de evaluación (mm).
La recolección de los datos con el TDR portátil se realizó antes y después del riego en 64 puntos distribuidos uniformemente (cada punto representaba 4 m2). Mediante geoestadística realizada a través da interpolación con la técnica de Kriging, usando el software SURFER® (Golden Software, Inc.), se calculó la humedad del suelo en otros puntos de la malla, donde no se midió con el TDR, a través de la construcción de un semivariograma experimental. Al calcular la semivarianza de cada punto en relación a los demás, se estimó el modelo de variograma que mejor se aproximó a la curva obtenida, y se se usó el modelo matemático esférico (Ecuación 4);

donde 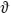 es la varianza, C0 es el nugget, a es el silo, C0 + C es la variancia asintótica y h es la distancia de separación.
es la varianza, C0 es el nugget, a es el silo, C0 + C es la variancia asintótica y h es la distancia de separación.
El tiempo de aplicación de agua por el aspersor fue calculado con la ecuación (5) (Bernardo et al., 2009):

donde Ti es el tiempo de aplicación de agua o riego (h), Amáx es la capacidad de almacenamiento máximo de agua en el suelo (mm), Imáx es la intensidad máxima de aplicación de agua (mm h–1).
Transcurrido el tiempo total de aplicación de agua se suspendió el riego, iniciando las lecturas del volumen de agua de los colectores (lámina precipitada) utilizando una probeta graduada en mL. El contenido de agua del suelo en la profundidad de 0.15 m se midió usando el TDR portátil descrito anteriormente. Esta profundidad se estableció considerando la longitud de la sonda TDR la cual no podía ser mayor debido a la dificultad para introducir la sonda en el suelo y recolectar datos.
Con una probeta se midió el volumen de agua del colector para medir el agua evaporada. La lámina infiltrada en cada cuadrante se calculó como la diferencia entre los valores de humedad obtenidos antes y después del riego.
Con las láminas precipitadas e infiltradas se simularon sobreposiciones en escenarios con diferentes espaciamientos entre aspersores (6×6 m, 6×12 m, 12×12 m, 12×18 m, 18×18 m, 18×24 m, 24×24 m, 24×30 m y 30×30 m) usando el software Catch 3D. Éste es un modelo matemático que analiza estadísticamente el desempeño de aspersores con base en los cálculos de uniformidad de distribución y eficiencia de aplicación de agua. Para cada espaciamiento se calculó CUC y CUD, expresados por las ecuaciones (6) y (7):

donde CUC es el coeficiente de uniformidad de Christiansen (%), n es el número de colectores, Xi es la lámina precipitada en el i–ésimo colector (mm), Xm es el valor medio de las láminas precipitadas (mm).

donde CUD es el coeficiente de uniformidad de distribución (%), X25 es la media de 25 % del total de colectores con las menores láminas (mm).
Para interpretar los valores obtenidos de CUC y CUD se usaron los parámetros de clasificación presentados en el Cuadro 2 (Bernardo et al., 2006).
La eficiencia de aplicación (Ea) y de almacenamiento (Es), pérdidas por percolación (Pp) y déficit (D), se calcularon usando el modelo matemático lineal descrito por Karmeli et al. (1978). La lámina requerida para cada sobreposición, la lámina bruta y el tiempo de riego se calcularon con las ecuaciones (8), (9) e (10):

donde Yr es lámina requerida (adimensional), LB es lámina bruta (mm) e, 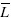 es lámina media infiltrada o precipitada para cada una de las sobreposiciones (mm).
es lámina media infiltrada o precipitada para cada una de las sobreposiciones (mm).

donde LB es lámina bruta (mm), LLR es lámina líquida de riego (mm), ε es eficiencia de aplicación adoptada correspondiente a 80 % para riego por aspersión (Bernardo et al., 2009).

donde TR es tiempo de riego (h), LB es lámina bruta (mm), Imáx es intensidad máxima de aplicación de agua (mm h–1).
RESULTADOS Y DISCUSIÓN
Los valores obtenidos de los parámetros de riego se presentan en el Cuadro 3. El volumen de agua evaporada, medida en el colector dispuesto cerca del experimento fue nula, lo cual puede estar en función de la hora en que se realizó el ensayo.
Los resultados obtenidos de Yr, CUC, CUD, Ea, Es, Pp y D, a partir de las láminas precipitadas e infiltradas, para los diferentes espaciamientos entre aspersores, se presentan en los Cuadro 4 y Cuadro 5. El comportamiento de los valores de CUC y CUD fue inversamente proporcional al espaciamiento entre aspersores, tanto para la lámina precipitada como para la infiltrada, es decir, a mayor espaciamiento los valores de los coeficientes son menores. Esto se debe a que con mayor espaciamiento entre aspersores el área irrigada aumenta, pero el radio de alcance del aspersor se mantiene constante dejando partes sin irrigar. Estos resultados son similares a los reportados por Rezende et al. (2002) al evaluar el CUC en la superficie y en el perfil del suelo hasta una profundidad de 0.40 m, usando tensiómetros para medir el contenido de agua en el suelo y simulando diferentes espaciamientos.
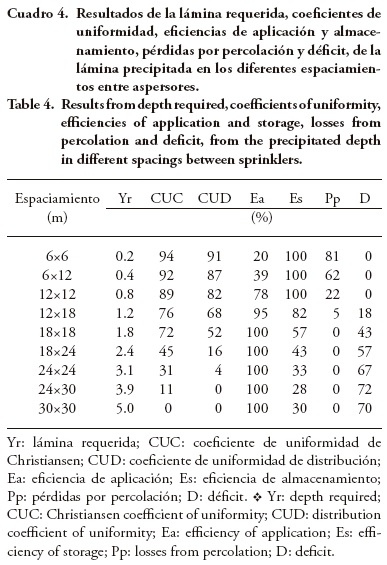
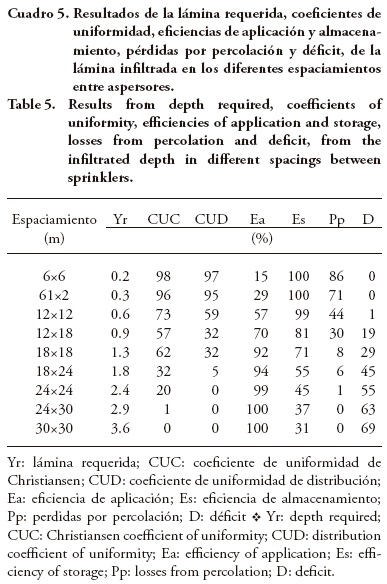
De acuerdo con los parámetros de clasificación presentados en el Cuadro 2 (Bernardo et al., 2006), las uniformidades de aplicación fueron: 1) excelentes en 6×6 y 6×12 m para la lámina precipitada y para la infiltrada; 2) en 12×12 m bueno para la lámina precipitada y regular para la infiltrada; 3) en 12×18 m, regular para la lámina precipitada e insuficiente para la infiltrada; 4) en 18×18 m, regular para la lámina precipitada y malo para la infiltrada; 5) en las demás sobreposiciones fue insuficiente para las dos láminas.
De la misma forma, los valores obtenidos del CUD fueron clasificados como: 1) excelentes para la lámina precipitada y para la infiltrada, en 6×6 y 6×12 m; 2) razonables para la lámina infiltrada, en 12×12; 3) insuficientes en las demás sobreposiciones. Para la lámina precipitada en las sobreposiciones 12×12 y 12×18 m el CUD fue clasificado como bueno, para 18×18 m como razonable y a partir de ésta los demás valores fueron insuficientes.
Al comparar los coeficientes calculados se verifica que el CUD es sensible a las variaciones en la distribución de agua de un sistema de riego por aspersión porque considera apenas la media del menor cuartil del total de datos. Paulino et al. (2009) muestran una observación similar al evaluar sistemas de riego por aspersión en cultivo de solanáceas irrigadas y usando varios coeficientes de uniformidad de agua en el suelo.
Para las condiciones del presente estudio y con el fin de obtener valores adecuados de CUC para sistema de riego por aspersión (> 80 %), los espaciamientos máximos que se podrían usar son 12×12 (lámina precipitada) y 6×12 m (lámina infiltrada). De acuerdo con lo anterior, la distribución de agua en el suelo es diferente de la observada en la superficie por lo cual se debe considerar los valores de la lámina infiltrada para el dimensionamiento y manejo del sistema de riego.
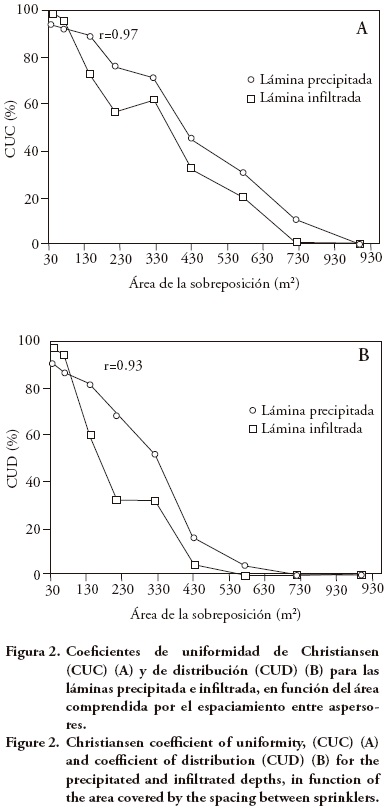
Los coeficientes de uniformidad Christiansen (CUC) y de distribución (CUD) para las láminas precipitadas e infiltradas se presentan en la Figura 2 (A y B). La correlación fue alta entre los valores CUC (Figura 2A) para las láminas precipitadas e infiltradas (r=0.97), así como la de CUD (Figura 2B) para las mismas láminas (r = 0.93). Pero con la lámina precipitada se sobrestiman los valores de los coeficientes, lo cual puede generar errores al evaluar un sistema de irrigación por aspersión. Según Bernardo et al. (2009), para una buena distribución de agua sobre el área irrigada, los aspersores se deben espaciar para obtener una superposición entre los perfiles de distribución de agua de los aspersores a lo largo de la línea lateral y entre líneas laterales a lo largo de la línea principal, lo cual dependerá del tipo de aspersor y de la intensidad del viento.
Los resultados obtenidos de la estimación de las eficiencias de aplicación (Ea) y almacenamiento (Es), perdidas por percolación (Pp) y déficit (D), en función de la diferenciación de las áreas entre aspersores para las láminas precipitada e infiltrada, se presentan en la Figura 3.
Para los menores espaciamientos, la Ea para lámina infiltrada es menor que la obtenida para la precipitada; y para mayores espaciamientos, la Es es mayor para la lámina infiltrada en relación a la precipitada. La Ea de agua es baja en los menores espaciamientos, considerando su relación con la pérdida por percolación; así, en condiciones de espaciamientos reducidos entre aspersores existe una alta sobreposición entre las láminas de agua y por tanto pérdidas por percolación altas. Adicionalmente, en algunos casos el acúmulo de agua en la superficie del suelo aumenta las posibilidades de pérdidas por evaporación directa del suelo, reduciendo la Ea. Según Zocoler et al. (2001), por medio de la Ea es posible verificar la cantidad de agua incorporada en el suelo hasta la profundidad efectiva del sistema radicular de cualquier cultivo, en relación a la cantidad de agua total aplicada por riego, y de esta forma verificar las pérdidas por percolación y evaporación directa del suelo.
Los valores obtenidos de D y Pp presentaron diferencia para los espaciamientos simulados en relación a la lámina precipitada e infiltrada en el suelo, mostrando que la respuesta de la aplicación de agua evaluada en la superficie del suelo difiere de la realizada en el perfil del suelo. Las Pp presentan un comportamiento inversamente proporcional al CUC; así, cuando la uniformidad disminuye, la cantidad de agua percolada es mayor. Este resultado es similar al obtenido por Ben–Asher y Ayars (1990) en un estudio realizado para pronosticar el impacto de la desunifomidad en las pérdidas de agua por percolación. Además, la evaluación en la superficie subestima los valores de eficiencia de riego comparado al sub–superficial en un sistema por aspersión, lo que se refleja en un manejo menos económico del riego (Rocha et al., 1999).
CONCLUSIONES
El coeficiente de uniformidad de distribución del agua en el perfil del suelo fue mayor que el obtenido para las láminas precipitadas en los colectores en los menores espaciamientos 6×6 m y 6×12 m, y fue menor en los demás espaciamientos.
Las altas sobreposiciones entre láminas de agua, generadas por los menores espaciamientos entre aspersores, tienen una influencia negativa en la calidad del riego por el aumento de las pérdidas por percolación y consecuentemente por la disminución de la eficiencia de riego.
El análisis de los coeficientes de uniformidad y de las eficiencias de aplicación y almacenamiento de agua en el suelo, para el diseño y manejo de sistemas de riego por aspersión, proporciona mayor confiabilidad cuando se utilizan las informaciones de humedad obtenidas en el perfil del suelo.
LITERATURA CITADA
Ben–Asher, J., and J. E. Ayars. 1990. Deep seepage under nonuniform sprinkler irrigation: I. Theory. J. Irrigation Drainage Eng. 116: 354–362. [ Links ]
Bizari, D. R., E. E. Matsura, C. Souza F., e M. W. Roque. 2011. Haste portátil para utilização de sonda de TDR em ensaios de Campo. Revista Irriga 16: 31–41. [ Links ]
Bernardo, S., A.A. Soares, e E. C. Mantovani. 2009. Manual de Irrigação. 8ª. ed. Impressora Universitária. Viçosa/MG, 355 p. [ Links ]
Bos, M. G., M. A. Burton, and D. J. Molden. 2005. Irrigation and Drainage Performance Assessment: Practical Guidelines. CABI International. Wallinford. 158 p. [ Links ]
Buendia, J. C. E., E. Palacios V., J. Chávez M., y B. Rojas M. 2004. Impacto del funcionamiento de los sistemas de riego presurizados en la productividad de ocho cultivos, en Guanajuato, México. Agrociencia 34(5): 477–486. [ Links ]
Christiansen, J. E. 1942. Irrigation by Sprinkling. Bullet 670. University of California. Agricultural Experimental Station. Berkeley, California. 124 p. [ Links ]
Coelho, E. F., e F. B. Arruda. 2001. Aplicações da técnica de TDR: Manejo da água no solo. In: Matsura, E. E., A. Tavares–Junior, E. Gomes P., e C. Souza F. (eds). Aplicações da Técnica da TDR na Agricultura. Feagri/Unicamp. Campinas. pp: 129–145. [ Links ]
Criddle, W. D., S. Davis, C., H. Pair, and D. G. Shuckely. 1956. Methods for evaluation irrigation systems. Agricultural Handbook 82. USDA. Washington. 24 p. [ Links ]
Cunha, F., P. R. Vieira, M. P. Borges, F. R. Silva, e L. X. Mesquita. 2008. Manejo de microirrigação baseado em avaliação do sistema na cultura do meloeiro. Rev. Caatinga 21: 147–155. [ Links ]
Fietz, C., M. Folegatti, S. Vieira, e J. Frizzone. 1999. Efeito da variabilidade do armazenamento de agua no solo na qualidade da irrigação por aspersão. Rev. Bras. Eng. Agríc. e Ambiental 3: 150–153. [ Links ]
Karmeli, D. 1978. Estimating sprinkler distribution patterns using linear regression. Trans. Am. Soc. Agric. Eng. Special Ed. 21(4): 682–686. [ Links ]
Lorite, I. J., L. Mateos, and E. Fereres. 2004. Evaluating irrigation performance in a Mediterranean environment: I. model and general assessment of an irrigation scheme. Irrigation Sci. 23: 77–84. [ Links ]
Paulino, M.de O., F. Figueiredo P., R. Fernandes C., J. T. Maia, D. Guilherme de O., e F. Barbosa S. 2009. Avaliação da uniformidade e eficiência de aplicação de água em sistemas de irrigação por aspersão convencional. Rev. Bras. Agric. Irrigada 3(2): 48–54. [ Links ]
Reichardt, K. 1996. Dinâmica da Matéria e da Energia em Ecossistemas. USP/ESALQ. São Paulo. 513 p. [ Links ]
Rezende, R., A. C. Gonçalves A., P. S. Freitas L., J. A. Frizzone, C. A. Tormena, e A. Bertonha, A. 2002. Influência da aplicação de água na uniformidade da umidade no perfil do solo. Acta Scientiarum 24:1553–1559. [ Links ]
Rocha, E. M. de M., R. N. Costa T., S. M. Mapurunga da S., e P. Castro T. de. 1999. Uniformidade de distribuição de água por aspersão convencional na superficie e no perfil do solo. Rev. Bras. Eng. Agríc. Ambiental 3: 154–160. [ Links ]
Soil Survey Staff. 2010. Keys to Soil Taxonomy. 11th ed. USDA–Natural Resources Conservation Service. Washington, DC. 338 p. [ Links ]
Souza, C. F., E. E. Matsura, e R. Testezlaf. 2001. Experiência de laboratório de hidráulica, irrigação e drenagem da Faculdade de Engenharia Agrícola/UNICAMP no uso da técnica da TDR. In: Matsura, E. E., A. Tavares–Junior, E. Gomes P., e C. Souza F. (eds). Aplicações da Técnica da TDR na Agricultura. Feagri/Unicamp. Campinas. pp: 147 – 176. [ Links ]
Topp, G., J. L. Davis, and A. P. Annan. 1980. Electromagnetic determination of soil water content: Measurement in coaxial transmission lines. Water Resources Res. 16: 574 – 582. [ Links ]
Zocoler, J. L., L. E. V. Cesar, e L. S. Vanzela. 2004. Efeito da posição relativa da linha lateral de um equipamento de irrigação do tipo pivô central na uniformidade de distribuição de água e eficiência de irrigação. Eng. Agric. 2 (4): 290–297. [ Links ]














