Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.46 no.4 Texcoco may./jun. 2012
Matemáticas aplicadas, estadística y computación
La colinealidad y la separación en los datos en el modelo de regresión logística
Collineartity and separated data in the logistic regression model
Flaviano Godínez-Jaimes1*, Gustavo Ramírez-Valverde2, Ramón Reyes-Carreto1, F. Julian Ariza-Hernandez1, Elia Barrera-Rodriguez1
1 Unidad Académica de Matemáticas, Universidad Autónoma de Guerrero. 39090. Chilpancingo, Guerrero. (fgodinezj@gmail.com), (rcarreto1@yahoo.com.mx), (arizahf@colpos.mx), (he-lya@hotmail.com). * Autor responsable.
2 Estadística. Campus Montecillo. Colegio de Postgraduados. 56230. Montecillo, Estado de México. (gramirez@colpos.mx).
Recibido: diciembre, 2011.
Aprobado: abril, 2012.
Resumen
La colinealidad y la falta de traslape en los datos son problemas que afectan la inferencia basada en el modelo de regresión logística. Mediante simulación se investigó como son afectados los estimadores que tratan la colinealidad (Ridge iterativo), la separación en los datos (de Firth, y de Rousseeuw y Christmann) o ambos problemas (de Shen y Gao). Estos estimadores se compararon considerando el número de condición escalado de la matriz de información estimada, el sesgo y el error cuadrático medio. En cada uno de los cuatro escenarios estudiados, formados al usar dos niveles de colinealidad y dos tamaños de muestra, se consideraron tres grados de traslape en los datos. Se encontró que los estimadores Ridge iterativo y de Shen y Gao tienen condicionamiento nulo, además el sesgo y el error cuadrático medio más pequeños. El grado de traslape y el nivel de colinealidad afectan fuertemente el sesgo y el error cuadrático medio de los estimadores de máxima verosimilitud, de Firth y de Rousseeuw y Christmann.
Palabras clave: estimador de Firth, estimador de máxima verosimilitud estimada, estimador doble penalizado, estimador Ridge iterativo, datos traslapados.
Abstract
Collinearity and the lack of overlap in the data are problems that afect inference based on the logistic regression model. Simulation was used to investigate how the estimators that deal with collinearity (iterative Ridge) are afected, along with separation in the data (Firth's, and Rousseeuw and Christmann's) or both problems (Shen and Gao's). These estimators were compared considering the scaled condition number of the estimated information matrix, the bias and the mean squared error. In each one of the four scenarios studied, formed by using two levels of collinearity and two sample sizes, three degrees of overlap were considered in the data. It was found that iterative Ridge and Shen and Gao's estimators have null conditioning, as well as smaller bias and mean square error. The degree of overlap and the level of collinearity strongly afect the bias and mean square error of the maximum likelihood, Firth's and Rousseeuw and Christmann's estimators.
Key words: Firth's estimator, estimated maximum likelihood estimator, penalized double estimator, iterative Ridge estimator, overlapped data.
INTRODUCCIÓN
Sean Yi, i=1,...n, variables aleatorias independientes con distribución Bernoulli con probabilidad de éxito  . Además, sea X la matriz diseño de orden n x (p+1) cuyos renglones son
. Además, sea X la matriz diseño de orden n x (p+1) cuyos renglones son  , que corresponden a la i-ésima observación de las variables independientes X1, ..., Xp. El modelo de regresión logística supone que las variables independientes y la variable respuesta están relacionadas por:
, que corresponden a la i-ésima observación de las variables independientes X1, ..., Xp. El modelo de regresión logística supone que las variables independientes y la variable respuesta están relacionadas por:

donde β=(β0, β1, ..., βp)T es el vector de parámetros desconocido.
El estimador de máxima verosimilitud (MV),  se obtiene al maximizar la función de logverosimilitud:
se obtiene al maximizar la función de logverosimilitud:

Bajo los supuestos de que X es de rango completo y β pertenece al interior del espacio de parámetros,  es la solución del sistema de p+1 ecuaciones formadas al igualar a cero las derivadas de l(β) respecto a β. El sistema de ecuaciones se resuelve usando métodos iterativos, como el método de Newton-Raphson, que está dado por:
es la solución del sistema de p+1 ecuaciones formadas al igualar a cero las derivadas de l(β) respecto a β. El sistema de ecuaciones se resuelve usando métodos iterativos, como el método de Newton-Raphson, que está dado por:

donde U(β) = XT (y—π(β)) es el vector de primeras derivadas parciales de l(β) e I(β) = XT  X la matriz de información estimada con
X la matriz de información estimada con  .
.
Si la matriz I(β(s)) no tiene inversa entonces no existe el estimador de MV. Lesafre y Marx (1993) demuestran que la matriz de información estimada del modelo de regresión logística es singular si: 1) X es de rango incompleto o 2)  se acerca a la frontera del espacio de parámetros.
se acerca a la frontera del espacio de parámetros.
Aun cuando X sea de rango completo pueden existir dependencias lineales cercanas entre sus columnas, esto es, c0 X 0 +...+cX ≈ 0 con c0,...,cp no todas cero. Entre más cerca a cero esté la combinación lineal, más cerca está X a la singularidad, fenómeno conocido como colinealidad entre las variables independientes.
La colinealidad en regresión logística causa los siguientes problemas: 1) es sensible a cambios pequeños en las variables independientes, 2) algunas componentes de
es sensible a cambios pequeños en las variables independientes, 2) algunas componentes de son grandes y 3) las varianzas estimadas de algunas componentes de
son grandes y 3) las varianzas estimadas de algunas componentes de son muy grandes. Como consecuencia de estos problemas resultan intervalos de confianza muy amplios y baja potencia de las pruebas de hipótesis relacionadas con la significancia de los parámetros (Schaefer et al., 1984; Lee y Silvapulle, 1988; Marx y Smith, 1990).
son muy grandes. Como consecuencia de estos problemas resultan intervalos de confianza muy amplios y baja potencia de las pruebas de hipótesis relacionadas con la significancia de los parámetros (Schaefer et al., 1984; Lee y Silvapulle, 1988; Marx y Smith, 1990).
Si se aproxima a uno o a cero, entonces el elemento i en la diagonal de
se aproxima a uno o a cero, entonces el elemento i en la diagonal de  es cero y no existe inversa de la matriz I(β). Para que
es cero y no existe inversa de la matriz I(β). Para que se aproxime a uno o a cero, con
se aproxime a uno o a cero, con  fijo, debe ocurrir que al menos una
fijo, debe ocurrir que al menos una  j→ ± ∞ , lo cual significa que βj está en la frontera del espacio de parámetros. Esto puede ocurrir cuando los datos tienen una configuración especial conocida como separación o casi separación. Albert y Anderson (1984) y Santner y Duffy (1986) demuestran que el estimador de MV del modelo de regresión logística no existe cuando hay separación o casi separación en los datos, y existe y es único cuando hay traslape en los datos.
j→ ± ∞ , lo cual significa que βj está en la frontera del espacio de parámetros. Esto puede ocurrir cuando los datos tienen una configuración especial conocida como separación o casi separación. Albert y Anderson (1984) y Santner y Duffy (1986) demuestran que el estimador de MV del modelo de regresión logística no existe cuando hay separación o casi separación en los datos, y existe y es único cuando hay traslape en los datos.
Hay separación en los datos si existe un θ∈Rp-1tal que,  θ>0 cuando Yi=1 y xTθ<0 cuando Yi=0, para i=1,...,n. La casi separación en los datos ocurre si existe un
θ>0 cuando Yi=1 y xTθ<0 cuando Yi=0, para i=1,...,n. La casi separación en los datos ocurre si existe un  tal que
tal que  θ>0 cuando Yi=1 y
θ>0 cuando Yi=1 y  θ≤0 cuando Yi=0, para todo i, y existe
θ≤0 cuando Yi=0, para todo i, y existe  tal que
tal que 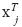 θ=0. Por último, existe traslape en los datos si no hay separación o casi separación en los datos. Si solamente hay una variable independiente continua X y existe separación en los datos, entonces X es una variable predictiva perfecta, pues para alguna constante k, cuando X<k todos son éxitos y cuando X>k todos son fracasos o viceversa. Lo contradictorio es que en esta situación no existe estimador de MV del modelo de regresión logística.
θ=0. Por último, existe traslape en los datos si no hay separación o casi separación en los datos. Si solamente hay una variable independiente continua X y existe separación en los datos, entonces X es una variable predictiva perfecta, pues para alguna constante k, cuando X<k todos son éxitos y cuando X>k todos son fracasos o viceversa. Lo contradictorio es que en esta situación no existe estimador de MV del modelo de regresión logística.
En resumen, la matriz de información estimada, XT X, se puede acercar a la singularidad por el efecto combinado de la colinealidad en las variables independientes, la cercanía a la separación en los datos o a que se presenten ambas condiciones.
X, se puede acercar a la singularidad por el efecto combinado de la colinealidad en las variables independientes, la cercanía a la separación en los datos o a que se presenten ambas condiciones.
Los estimadores Ridge en regresión logística son propuestos para reducir el tamaño de  ocasionado por la presencia de colinealidad. Schaefer et al. (1984) proponen un estimador Ridge logístico de un paso (RL) dado por:
ocasionado por la presencia de colinealidad. Schaefer et al. (1984) proponen un estimador Ridge logístico de un paso (RL) dado por:

le Cessie y van Houwenlingen (1992) proponen un estimador Ridge iterativo logístico que se obtiene al maximizar la logverosimilitud que es penalizada con el cuadrado de la norma de β y donde k se determina en función del desempeño del estimador.
Schaefer et al. (1984) muestran para el estimador Ridge de un paso que siempre es posible encontrar un valor de k que produce un estimador con menor error cuadrático medio que el del estimador de MV. Un problema con el estimador Ridge es que no existe una expresión única para determinar k; algunas propuestas son: 1/βTβ, (p+1)/βTβ2, traza (XTVX)/βTXTVXβ, donde
donde  es un vector propio de XT
es un vector propio de XT X (Schaefer et al., 194; Lee y Silvapulle, 1988; le Cessie y van Houwelingen, 1992). Para calcular k es necesario conocer β por lo que
X (Schaefer et al., 194; Lee y Silvapulle, 1988; le Cessie y van Houwelingen, 1992). Para calcular k es necesario conocer β por lo que  se usa en su lugar; como consecuencia, el estimador RL herede los problemas del estimador de MV. Una forma de determinar el parámetro de Ridge, independiente de
se usa en su lugar; como consecuencia, el estimador RL herede los problemas del estimador de MV. Una forma de determinar el parámetro de Ridge, independiente de  , es k=(λ1—100λp)/99, donde λ1 y λp son los valores propios mayor y menor de XTX (Liu, 2003).
, es k=(λ1—100λp)/99, donde λ1 y λp son los valores propios mayor y menor de XTX (Liu, 2003).
Firth (1993) propone un estimador para reducir el sesgo al usar muestras pequeñas en el modelo lineal generalizado. Heinze y Schemper (2002) muestran que ese estimador también existe cuando hay separación en los datos. Rousseeuw y Christmann (2003) proponen otro estimador cuando hay separación en los datos. Shen y Gao (2008) presentan un estimador para resolver los problemas de colinealidad y separación en los datos simultáneamente.
Aunque Shen y Gao (2008) proponen su estimador para tratar con la colinealidad en las variables independientes y separación en los datos, la simulación que realizan induce separación en los datos pero no induce colinealidad. Además, los estimadores Ridge se han propuesto para atenuar los efectos de la colinealidad, pero no han sido evaluados en presencia de separación de los datos, además de que en todos los casos tampoco se ha evaluado el condicionamiento del estimador. En esta investigación se utiliza simulación para estudiar el efecto del nivel de colinealidad y el grado de traslape en los estimadores propuestos para 1) tratar la colinealidad (Ridge iterativo), 2) la separación en los datos (de Firth, y de Rousseeuw y Christmann) o 3) ambos problemas (de Shen y Gao).
MATERIALES Y MÉTODOS
Estimadores estudiados
Estimador Ridge iterativo
Este estimador fue propuesto por le Cessie y van Houwenlingen (1992) penalizando la logverosimilitud con el cuadrado de la norma de β. La función de logverosimilitud es:
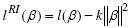
donde l(β) es la logverosimilitud del modelo de regresión logística y k es el parámetro de Ridge. El estimador Ridge iterativo logístico,  RI , se obtiene usando el método de Newton-Raphson:
RI , se obtiene usando el método de Newton-Raphson:

donde k se obtiene minimizando la media de una medida del error de predicción como el error de clasificación, el cuadrado del error o menos la logverosimilitud. En el presente estudio el parámetro Ridge se determina usando la propuesta de Liu (2003), k=(λ1-100λp)/99.
Estimador de Firth
Este estimador puede considerarse como un estimador penalizado donde la función de penalización es la a priori invariante de Jefreys. La función de logverosimilitud es:

donde I(β) es la matriz de información estimada del modelo de regresión logística. Las primeras derivadas parciales de lF(β) respecto a βr igualadas a cero son:

hi es el i-ésimo elemento en la diagonal de  , donde
, donde  . El estimador de Firth,
. El estimador de Firth,  F, se obtiene de manera iterativa usando el método de Newton-Raphson
F, se obtiene de manera iterativa usando el método de Newton-Raphson

Estimador de Rousseeuw y Christmann
Rousseeuw y Christmann (2003) proponen una modificación del modelo de regresión logística al que denominan modelo de regresión logística escondido. En este modelo se supone que el verdadero status T, con valores éxito (í) y falla (f), no se puede observar debido a un mecanismo estocástico adicional, pero existe una variable binaria observada Y fuertemente relacionada con T. Si el verdadero status es T=s, se observa Y=1 con P(Y=1| T=s)=δ1, por tanto, una clasificación incorrecta con P(Y=0| T=s)=1-δ1.
Análogamente, si el verdadero status es T=j se observa Y=0 con P(Y=0| T=f)=1-δ0 y una clasificación incorrecta con P(Y=1| T=f)=δ0. Si la probabilidad de observar el verdadero status es mayor a 0.5, entonces, 0< δ0<0.5< δ1<1. El estimador de Rousseeuw y Christmann,  RC, se obtiene después de estimar la verosimilitud pues depende de δ0 y δ1 por lo cual los autores lo llaman estimador de máxima verosimilitud estimada. Este estimador se obtiene con el siguiente algoritmo:
RC, se obtiene después de estimar la verosimilitud pues depende de δ0 y δ1 por lo cual los autores lo llaman estimador de máxima verosimilitud estimada. Este estimador se obtiene con el siguiente algoritmo:
1. Calcular  donde
donde  y δ=0.01.
y δ=0.01.
2. Calcular 
3. Calcular las pseudo-observaciones 
4. Ajustar el modelo de regresión logística en el cual se sustituyen las observaciones por las pseudo-observaciones.
Estimador de Shen y Gao
Para resolver simultáneamente los problemas de colinealidad y separación en los datos ellos usan una doble penalización de la logverosimilitud, una de tipo a priori no informativa de Jefreys y otra de tipo Ridge dada por el cuadrado de la norma de β, esto es:

El estimador de Shen y Gao,  SG, se obtiene usando el método de Newton-Raphson donde el parámetro λ se obtiene minimizando, mediante validación cruzada, la media del cuadrado del error,
SG, se obtiene usando el método de Newton-Raphson donde el parámetro λ se obtiene minimizando, mediante validación cruzada, la media del cuadrado del error, 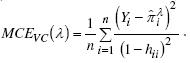
Diagnóstico
Belsley y Oldford (1986) estudiaron el comportamiento del sistema de ecuaciones ψ=f(w) ante pequeños cambios en w y lo llamaron análisis de condicionamiento. Si ψ tiene cambios grandes cuando w tiene cambios pequeños se dice que ψ está mal condicionado. Ellos identifican tres tipos de condicionamiento: de los datos, del estimador y del criterio.
Condicionamiento de los datos. En regresión logística el condicionamiento de los datos está relacionado con la colinealidad en las variables independientes y se diagnostica con el número de condición escalado de la matriz diseño propuesto por Belsley et al. (1980). El número de condición escalado de X se define por  donde
donde  y
y  son el máximo y el mínimo de los valores propios de XTX después de ser escalada. La colinealidad está presente en cualquier conjunto de variables independientes, pero no siempre afecta de manera importante la estimación o inferencia. Belsley et al. (1980) clasifican la colinealidad en tres niveles de acuerdo a su intensidad: 1) nula (ηx<10), 2) moderada (10≤ηx<30) y 3) severa (ηx<30).
son el máximo y el mínimo de los valores propios de XTX después de ser escalada. La colinealidad está presente en cualquier conjunto de variables independientes, pero no siempre afecta de manera importante la estimación o inferencia. Belsley et al. (1980) clasifican la colinealidad en tres niveles de acuerdo a su intensidad: 1) nula (ηx<10), 2) moderada (10≤ηx<30) y 3) severa (ηx<30).
Condicionamiento del estimador. El diagnóstico se realiza con el número de condición escalado de la matriz de información estimada, que se define por  , donde
, donde  y
y  son los valores propios máximo y mínimo de la matriz de información estimada escalada. El nivel de condicionamiento de esta matriz medido por ηMI se determina de forma similar a ηx.
son los valores propios máximo y mínimo de la matriz de información estimada escalada. El nivel de condicionamiento de esta matriz medido por ηMI se determina de forma similar a ηx.
Condicionamiento del criterio.  se obtiene maximizando la verosimilitud, Belsley y Oldford (1986) afirman que ηMI permite valorar este tipo de condicionamiento. Por esta razón no se considera en el presente estudio.
se obtiene maximizando la verosimilitud, Belsley y Oldford (1986) afirman que ηMI permite valorar este tipo de condicionamiento. Por esta razón no se considera en el presente estudio.
El condicionamiento de los estimadores de MV, de Firth, de Rousseeuw y Christmann, de Shen y Gao y Ridge iterativo se miden en las matrices de información estimadas: XT X, XT
X, XT FX, XT
FX, XT RCX, XT
RCX, XT SGX-2λI y XT
SGX-2λI y XT RIX +2kI. El estimador de Firth se obtiene usando el paquete logistf (Ploner et al., 2010) de R Development Core Team, 2011, y el estimador de Rousseeuw y Christmann con el paquete hlr de R (Rousseeuw y Christmann, 2008).
RIX +2kI. El estimador de Firth se obtiene usando el paquete logistf (Ploner et al., 2010) de R Development Core Team, 2011, y el estimador de Rousseeuw y Christmann con el paquete hlr de R (Rousseeuw y Christmann, 2008).
Separación de los datos
La detección de la separación en los datos fue analizada por Santner y Dufy (1986) usando un procedimiento basado en programación lineal, el cual no fue implementado en los paquetes estadísticos. En SAS se advierte al usuario cuando puede haber separación o casi separación en los datos pero el algoritmo usado no es preciso. Rousseeuw y Christmann (2004) proponen un procedimiento basado en regresión profunda e implementado en el paquete noverlap (Rousseeuw and Christmann, 2004) de R. Este procedimiento se usa en el presente estudio y determina el número de observaciones a eliminar para que haya separación en los datos. Konis (2009) propone un procedimiento basado en programación cuadrática implementado en el paquete safeBinaryRegresion de R; sin embargo, este procedimiento no se usa porque al identificar separación en los datos automáticamente declara la no existencia del estimador de MV.
Estudio de simulación
El estudio de simulación consistió en realizar 1500 repeticiones en cada uno de los escenarios generados por las combinaciones de los dos factores estudiados: colinealidad y tamaño de muestra.
Colinealidad entre las variables independientes (C). Se usaron dos grados de colinealidad: 1) moderada (ηx=16) y 2) severa (ηx=32).
Tamaño de muestra (TM). Se consideraron dos tamaños de muestra 20 y 40.
Grado de traslape (GT). Se consideraron cuatro grados de traslape que se construyeron después de generar los datos, clasificando cada caso en los grupos G0, G1, G2 y G3 de acuerdo a si las proporciones de observaciones traslapadas, detectadas con el paquete noverlap, están en los intervalos [0, 0.025], (0.025, 0.125], (0.125, 0.225] y (0.225, 0.325] respectivamente. El análisis considera solamente los primeros tres grupos porque no en todos los escenarios se obtuvieron los cuatro grupos.
Generación de los datos
Variables independientes
Se usaron dos variables independientes que se construyeron usando dos variables con distribución uniforme en [0,1], X1 y W; la variable X1 fue la primer variable independientes y la segunda se construyó con X2=X1+cW, donde c toma valores apropiados para obtener los números de condición escalados ηx=16 y ηx=32.
Variable respuesta
Se obtuvo con Yi=1 si πiUi y Yi=0 en otro caso; i=1,..., n; donde Ui tiene distribución uniforme en [0, 1] y  donde β es dos veces el vector propio asociado al valor propio mayor de XTX.
donde β es dos veces el vector propio asociado al valor propio mayor de XTX.
Comparación de estimadores
Se realizó en función de:
1. El número de condición escalado de la matriz de información estimada: ηMr.
2. El error cuadrático medio:  .
.
3. El sesgo: 
donde  es uno de los estimadores de βi en la r-ésima repetición.
es uno de los estimadores de βi en la r-ésima repetición.
RESULTADOS Y DISCUSIÓN
Se usan los términos estimadores originales para aludir a los estimadores de MV, de Firth (F), de Rousseeuw y Christmann (RC) y estimadores Ridge para referirse a los estimadores de Shen y Gao (SG) y Ridge iterativo (RI).
Efecto en el condicionamiento del estimador
Los estimadores originales fueron muy sensibles a la colinealidad y al grado de traslape estudiados, ya que presentaron un condicionamiento severo de la matriz de información para cualquier tamaño de muestra, niveles de colinealidad y grado de traslape estudiados (Cuadro 1).

También se observó, como se esperaba, que el número de condición escalado de los estimadores originales fue mayor cuando existe colinealidad severa, que en moderada o con TM 20, que con TM 40 y con grados de traslape bajos. Los estimadores RI y de SG presentaron condicionamiento nulo.
Efecto en el error cuadrático medio
Los estimadores originales tuvieron mayor ECM que los estimadores Ridge (Cuadro 2), lo cual es de esperarse ya que los estimadores Ridge surgieron con el fin de reducir el ECM (Schaefer et al., 1984).
Todos los estimadores estudiados tuvieron el mayor ECM en G0 donde hay separación o casi separación en los datos. Al aumentar el grado de traslape se observó una notable disminución en el ECM de los estimadores originales. El comportamiento del ECM es diferente en los estimadores Ridge pues en ellos el ECM es aproximadamente igual, como en SG, o incrementa, como en RI.
El efecto de la colinealidad fue muy fuerte en el ECM de los estimadores originales lo cual fue reportado por Schaefer et al. (1984), le Cessie y van Houwenlingen (1992), Lee y Silvapulle (1988), Weissfeld y Sereika (1991) y Månsson y Shukur (2011). En colinealidad severa el ECM fue 2 a 150 veces mayor que en colinealidad moderada, con excepción de los estimadores de MV y RC en el G0 y TM 20. En los estimadores Ridge el efecto observado fue al revés; en general; el ECM fue mayor en colinealidad moderada que en colinealidad severa.
En general, el ECM de los estimadores originales fue afectado de forma severa por el tamaño de muestra ya que su valor fue 2.64 a 130.58 veces más grande en TM 20 que en TM 40. Aunque también los estimadores Ridge tuvieron mayor ECM con TM 20 que en TM 40, esto fue menos frecuente y el incremento fue menor.
Entre los estimadores originales tuvo mejor desempeño el estimador F, aún en G0 donde hay separación y casi separación, y el estimador de peor desempeño fue el de MV. En los estimadores Ridge, el RI tuvo el menor ECM seguido del estimador de SG.
Efecto en el sesgo
Los estimadores originales tuvieron mayor sesgo que los estimadores Ridge en los tres grados de traslape al usar TM de 20, pero con TM 40 solamente ocurrió en G0 (Cuadro 3). Los estimadores originales tuvieron mayor sesgo en G0, donde hay separación o casi separación en los datos, y disminuyó en G1 y G2. Por el contrario, los estimadores Ridge generalmente tuvieron menor sesgo en G0 y al aumentar el porcentaje de traslape incrementó ligeramente el sesgo.
El efecto de la colinealidad fue fuerte en el sesgo de los estimadores originales. El mayor sesgo se obtuvo en colinealidad severa y disminuyó al incrementar el grado de traslape. En los estimadores Ridge se observó un comportamiento opuesto, pues en general fue mayor el sesgo en colinealidad moderada que en colinealidad severa. Es interesante notar que en los estimadores Ridge el sesgo, aunque pequeño, siempre fue negativo.
Schaefer (1983) y Ramírez-Valverde y Rice (1995) muestran que el sesgo de  es aproximadamente
es aproximadamente

por lo cual el sesgo del estimador de MV es afectado por ambos problemas, el de colinealidad en las variables independientes (matriz X) y el de la cercanía a la separación (matriz V).
Ramírez-Valverde y Rice (1995), aunque solamente estudiaron el efecto de la colinealidad, también muestran que el sesgo del estimador de MV es mayor que el sesgo del estimador Ridge de un paso. En la literatura revisada, no se encontraron investigaciones acerca del efecto del grado de traslape en el sesgo de los estimadores evaluados en el presente estudio.
El TM afectó fuertemente el sesgo de los estimadores originales. El sesgo en valor absoluto fue, generalmente, entre 1.05 y 130.77 veces mayor con TM 20 que con TM 40. Por el contrario, los estimadores Ridge tuvieron mayor sesgo con TM 40 que con TM 20. Entre los estimadores originales el estimador F tuvo el mejor desempeño, aun en el G0 donde hay menor traslape, mientras que el estimador de MV fue notoriamente malo. Los estimadores RI y SG tuvieron el menor sesgo entre los estimadores Ridge, especialmente el primero. Los estimadores Ridge en regresión logística, al contrario de los estimadores Ridge en regresión lineal, presentan menos sesgo que el estimador de MV.
Los resultados de este estudio coincidieron con los de Shen y Gao (2008) quienes también encontraron que el estimador F y SG son mejores que el de MV cuando se compararon en función del ECM. Además, el estimador SG fue mejor que F bajo el mismo criterio, pero en esta simulación se destaca que el estimador RI resultó mejor que F y que SG en términos del ECM.
Ejemplo
Para mostrar las diferencias entre los estimadores evaluados en el presente estudio, se analizó un ejemplo presentado por Riedwyl en 1997 y citado por Rousseeuw y Christmann (2004). Las 200 observaciones corresponden a siete variables medidas en billetes suizos. La variable respuesta Status (S) es 1 si el billete es falso y 0 si es genuino; las variables independientes son longitud del billete (L), ancho del borde izquierdo (LE), ancho del borde derecho (R), ancho del margen inferior (B), ancho del margen superior (T) y longitud diagonal de la imagen (D), medidas en milímetros.
Usando D y B para modelar la probabilidad de S=1 se presenta el problema de separación en los datos. Los estimadores estudiados fueron valorados con tamaños de muestra de 20 y 40, que fueron 10 y 5 veces menores que el tamaño de este conjunto de datos. Sin embargo, se consideró pertinente valorar su desempeño por la presencia de colinealidad severa (ηx=388) y separación en los datos. Los estimadores de MV, F y RC tienen condicionamiento severo y los estimadores RI y SG tienen condicionamiento nulo (Cuadro 4). Las estimaciones de MV son muy grandes lo que hace difícil su interpretación ya sea como incremento en el logaritmo de la razón de momios o como momios. Aunque no se conocen los parámetros, de acuerdo con los resultados obtenidos se espera que las estimaciones más cercanas a las verdaderas sean las de los estimadores SG y RI.

CONCLUSIONES
Es una ventaja que los estimadores de Firth y de Rousseeuw y Christmann existan cuando hay separación en los datos, pero son fuertemente afectados por el nivel de colinealidad entre las variables independientes y por bajos grados de traslape en los datos, efectos que son mayores cuando el tamaño de muestra es pequeño. Los estimadores Ridge iterativo y de Shen y Gao son mejores, en términos de error cuadrático medio y de sesgo, cuando se presentan simultáneamente los problemas de colinealidad, poco traslape en los datos y el tamaño de muestra sea pequeño. Aunque las diferencias fueron pequeñas, el estimador Ridge iterativo tuvo un mejor comportamiento que el estimador de Shen y Gao.
Respecto a los estimadores Ridge iterativo y de Shen y Gao hace falta investigación para proponer intervalos de confianza de los parámetros estimados; así como considerar un número mayor de variables en las que haya más de una relación de colinealidad. También merece atención proponer formas para determinar el parámetro de Ridge que tomen en cuenta el nivel de colinealidad, el número de relaciones de colinealidad y el grado de traslape en los datos.
LITERATURA CITADA
Albert, A., and J. A. Anderson. 1984. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 71:1-10. [ Links ]
Belsley, D. A., E. Kuh, and R. Welsh. 1980. Regression Diagnostics: Identifying Influential Data and Source of Collinearity. John Wiley & Sons. New York. 393 p. [ Links ]
Belsley, D. A., and R. W. Oldford. 1986. The general problem of ill-conditioning in statistical analysis. Comput. Stat. Data An. 4:103-120. [ Links ]
Firth, D. 1993. Bias reduction of maximum likelihood estimates. Biometrika 80: 27-38. [ Links ]
Heinze, G., and M. Schemper. 2002. A solution to the problem of separation in logistic regression. Stat. Med. 21: 2409-2419. [ Links ]
Konis, K. 2009. safebinaryRegression. R package version 0.1-2. http://www.r-project.org (Consulta: julio, 2010). [ Links ]
le Cessie, S. and J. C. van Houwelingen. 1992. Ridge estimators in logistic regression. Appl. Statistics 41(1): 191-201. [ Links ]
Lee, A. H., and M. J. Silvapulle. 1988. Ridge estimation in logistic regression. Comm. in Statistics-Theory and Methods 17(4): 1231-1257. [ Links ]
Lesaffre, E., and B. D. Marx. 1993. Collinearity in generalized linear regression. Comm. Statistics-Theory and Methods 22(7):1933-1952. [ Links ]
Liu, K. 2003. Using Liu-type estimator to combat collinearity. Comm. Statistics-Theory and Methods 32(5): 1009-1020. [ Links ]
Månsson K., and G. Shukur. 2011. On ridge parameters in logistic regression. Comm. Statistics - Theory and Methods 40(18): 3366-3381. [ Links ]
Marx, B. D., and E. P. Smith. 1990. Weighted multicollinearity in logistic regression: Diagnostics and biased estimation techniques with an example from lake acidification. Can. J. Fish. Aquat. Sci. 47: 1128-1135. [ Links ]
Ploner, M., D. Dunkler, H. Southworth, and G. Heinze. 2010. logistf: Firth's bias reduced logistic regression. R package version 1.10. http://CRAN.R-project.org/package=logistf (Consulta: agosto, 2010). [ Links ]
R Development Core Team. 2011. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/ (Consulta: octubre, 2010). [ Links ]
Ramírez-Valverde, G., and J. C. Rice. 1995. Bias and collinearity in logistic regression. ASA Proc. Epidemiology Section 97-101. [ Links ]
Rousseeuw, P. J., and A. Christmann. 2003. Robustness against separation and outliers in logistic regression. Comput. Stat. Data An. 43: 315-332. [ Links ]
Rousseeuw, P. J. and A. Christmann. 2004. noverlap: ncomplete. R package version 1.0-1. http://www.r-project.org (Consulta: agosto, 2010). [ Links ]
Rousseeuw, P. J., and A. Christmann. 2008. hlr: Hidden Logistic Regression. R package version 0.0-4. (Consulta: agosto, 2010). [ Links ]
Santner T. J., and D. E. Duffy. 1986. A note on A. Albert and J. A. Anderson's conditions for the existence of maximum likelihood estimates in logistic regression models. Biometrika 73: 755-758. [ Links ]
Schaefer R. L. 1983. Bias correction in maximum likelihood logistic regression. Stat. Med. 2: 71-78. [ Links ]
Schaefer, R. L., L. D. Roi, and R. A. Wolfe. 1984. A Ridge logistic estimator. Comm. Statistics-Theory and Methods 13(1): 99-113. [ Links ]
Shen, J., and S. Gao. 2008. A solution to separation and multicollinearity in multiple logistic regression. J. Data Sci. 6: 515-531. [ Links ]
Weissfeld L. A., and S. M. Sereika. 1991. A multicollinearity diagnostic for generalized linear models. Comm. Statistics-Theory and Methods 20(4) 1183:1198. [ Links ]














