Agua–suelo–clima

 

Transferencia de información hidrológica mendiante regresión lineal múltiple, con selección óptima de regresores

 

Transference of hydrologic information through multiple linear regression, with best predictor variables selection

 

Daniel F. Campos–Aranda¹

 

¹ Facultad de Ingeniería de la Universidad Autónoma de San Luis Potosí. Genaro Codina Núm. 240. 78280 San Luis Potosí, San Luis Potosí. (campos_aranda@hotmail.com). * Autor responsable.

 

Recibido: junio, 2011.
Aprobado: octubre, 2011.

 

Resumen

Es necesario contar con registros largos de información hidrológica anual para obtener una imagen más apegada a la realidad de su variabilidad, así como estimaciones confiables de sus propiedades estadísticas. Para obtener tales registros es común buscar fuentes adicionales de datos y técnicas de transferencia. Una técnica es la regresión lineal múltiple, cuya aplicación numérica lleva implícita la selección óptima de los registros largos cercanos (regresores) para buscar que la ampliación del registro corto sea una estimación confiable. Este proceso de selección implica tres análisis: 1) cómo definir las mejores estimaciones, 2) cuáles ecuaciones de regresión investigar, y 3) cuál modelo tiene mejor capacidad predictiva. Para el primer análisis se presentan cuatro criterios basados en las sumas de los cuadrados de los residuos; para el segundo se investigan todas las regresiones posibles porque en los problemas de transferencia de información hidrológica se dispondrá máximo de cinco regresores; para el tercero, seleccionar el mejor modelo predictivo se utiliza el análisis de residuales y la validación cruzada. La aplicación numérica descrita es una ampliación del registro de volúmenes escurridos anuales en la estación hidrométrica Platón Sánchez del sistema del río Tempoal, en la Región Hidrológica No. 26 (Pánuco, México). En este caso se utilizan cuatro regresores que son los registros del resto de las estaciones de aforos de tal sistema. Se concluye que incluso en problemas con multicolinealidad, los criterios de selección y los análisis expuestos conducen a resultados consistentes y permiten obtener las mejores ecuaciones de regresión. La similitud de los resultados alcanzados con los modelos de regresión seleccionados genera confianza en las estimaciones adoptadas.

Palabras clave: cuadrado medio de los residuos, multicolinealidad, análisis de residuales, prueba de Durbin–Watson, validación cruzada, Río Tempoal.

 

Abstract

It is necessary to have long records of annual hydrological data to get a truer picture of their variability, as well as reliable estimates of their statistical properties. To obtain these records it is common to use additional sources of data and transfer techniques. One technique is the multiple linear regression whose numerical application implies the optimum selection of close lengthy records (regressors) to have the extension of short registration be a reliable estimate. This selection process involves three analyses: 1) how to define the best estimates, 2) what regression equations should be investigated, and 3) which model has better predictive ability. For the first analysis four criteria based on the sums of the squares of the residuals are presented; for the second all possible regressions are investigated since in the problems of hydrological information transfer, we will have five regressors at the most; for the third, about selecting the best predictive model, we used the residual analysis and cross–validation. The numerical application described is an extension of the annual runoff volume record in the Platón Sánchez hydrometric station of the Tempoal river system in the 26 Hydrological Region (Pánuco, México). Here we used four regressors that are the records of other gauging stations in such system. We came to the conclusion that even in problems with multicollinearity, the selection criteria and analysis led to consistent results and allowed for the best regression equations. The similarity of the results obtained with the selected regression models generated confidence in the estimates adopted.

Keywords: residual mean square, multicollinearity, residual analysis, Durbin–Watson test, cross–validation, Rio Tempoal.

 

Introducción

En general, las estimaciones de las características estadísticas de un registro hidrológico de valores anuales son más confiables y consistentes si éste es más amplio, porque al ser más largo es más probable que incluya periodos de años secos y húmedos y no sólo de uno de ellos. Las principales variables en la práctica hidrológica son precipitación, escurrimiento y crecientes, donde el volumen escurrido anual tiene relevancia en todas las estimaciones asociadas con la disponibilidad y el diseño hidrológico de embalses para abastecimiento. La técnica básica para ampliar registros hidrológicos anuales es la regresión lineal, la cual permite la transferencia de información de un sitio a otro. Cuando esta técnica se aplica regionalmente, es decir, se transporta información de varios sitios o registros al de interés, se usa la regresión lineal múltiple y es necesario seleccionar las mejores variables predictivas o registros auxiliares, también llamados regresores.

El objetivo de este estudio fue exponer la técnica de transferencia de información hidrológica de variables anuales, mediante regresión lineal múltiple, para ampliar registros cortos de volúmenes escurridos con base en las series largas cercanas, seleccionando la mejor ecuación de regresión de entre todas las posibles. La formulación matemática se presenta de manera simple al utilizar la solución matricial, se exponen con detalle los criterios de selección y validación, y se desarrolla un ejemplo numérico en el sistema del río Tempoal, de la Región Hidrológica No. 26 (Pánuco, México), para ampliar el registro corto de la estación hidrométrica Platón Sánchez utilizando los cuatro registros largos disponibles en tal sistema.

 

Materiales y Métodos

Regresión lineal múltiple

Esta regresión es útil cuando la variable dependiente (y) no está relacionada sólo con otra (x), sino que depende de varias, las cuales no están correlacionadas entre si y tanto y como todas las otras variables x proceden de una población Normal multivariada (Gilroy, 1970; Salas et al., 2008). La expresión de este modelo de regresión es:

Las ecuaciones normales se obtienen igual que para la recta de regresión lineal, pero ahora la ecuación del error depende de xm variables y por tanto se establece igual número de ecuaciones; en forma matricial el sistema es el siguiente (Campos, 2003):

en notación matricial:

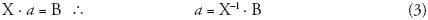
Cuando se utiliza este modelo de regresión para transportar información hidrológica desde varios sitios, el problema es seleccionar del grupo de regresores candidatos (registros disponibles), el subconjunto que conviene usar en el modelo. Tal selección implica dos objetivos contrapuestos (Montgomery et al., 2002): 1) que el modelo incluya tantos regresores como sea posible, para que el contenido de información en ellos pueda influir favorablemente en la estimación de y; y 2) que el modelo incorpore el menor número posible de regresores porque la varianza de la estimación de y aumenta con el número de éstos. El proceso de encontrar un modelo que cumpla ambos objetivos se llama selección óptima de regresores y, en general, los diferentes algoritmos para realizarlo conducen a resultados diferentes debido a la presencia de valores atípicos y correlación entre los registros candidatos (McCuen, 1998; Montgomery et al., 2002).

Dos aspectos fundamentales del problema de selección óptima de regresores son la generación de los modelos con subconjuntos y la decisión de si un subconjunto es mejor que otro. Aquí se exponen los cuatro criterios usados para evaluar y comparar ecuaciones de regresión con subconjuntos, y luego cuales modelos revisar.

Coeficiente de determinación múltiple

Es quizás la medida más utilizada para medir lo adecuado de un modelo de regresión. Se designa por R_p² cuando el modelo tiene un subconjunto de p términos, es decir, p–1 regresores y un término a₀ de ordenada al origen, y la ecuación es:

donde 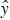p es la estimación de la variable y_i a través de la ecuación de regresión, por ello SC_Res(p) es la suma de cuadrados de los residuos y SC_y es la varianza total de la variable dependiente cuya media aritmética es 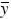. Siendo Kel número de regresores candidatos, el problema asociado al uso de R_p², es que aumenta conforme lo hace p y es máximo cuando p=K+1. Entonces, para aplicar este criterio de selección de modelos se agregan regresores hasta un número en que el siguiente ya no produce un aumento significativo en R_p².

Coeficiente de determinación múltiple ajustado

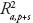Designado por , no necesariamente aumenta al introducir regresores, sino que al introducir s regresores, > si y sólo si, la estadística F parcial es mayor que 1. Por tanto, este criterio permite seleccionar el subconjunto óptimo a través de su valor máximo (Montgomery et al., 2002) y su fórmula es:

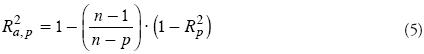
Cuadrado medio de los residuos

Este criterio tiene un comportamiento de decaimiento que se estabiliza y luego crece, pues en algún punto (p) la disminución del numerador no es suficiente para compensar la pérdida de un grado de libertad del denominador. Entonces el subconjunto óptimo será el que define el valor mínimo, cuya expresión es (Montgomery et al., 2002):

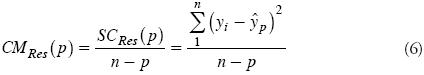
Estadística C de Mallows

El valor de C_p se puede dibujar en una gráfica de p en las abscisas que incluya la recta a 45° (C_p= p). Las ecuaciones de regresión con poco sesgo tendrán valores de C_p próximos a la recta y aquéllas con sesgo apreciable se apartarán de ésta. Se prefieren los valores menores de C_p, pues indican menor error total, y la ecuación de C es (Montgomery et al., 2002):

Al usar el cuadrado medio del modelo regresional completo como denominador se supone que tiene un sesgo despreciable. Si el modelo completo tiene varios regresores que no contribuyen significativamente, es decir que tienen coeficientes a_i cercanos a cero, el denominador de la ecuación 7 estará sobreestimado y los C_p serán pequeños. En tales casos se puede usar el mínimo cuadrado medio obtenido, sin importar que regresores lo originaron; ello conducirá a un C_p=p para tal modelo regresional.

Ecuaciones de regresión con subconjuntos

Hay dos procedimientos de análisis de los diferentes modelos de regresión que se pueden formar con los subconjuntos de variables regresoras candidatos; el primero consiste en procesar todas las regresiones posibles y el segundo en realizar una regresión por segmentos. Cuando se analizan todas las regresiones posibles se busca el mejor modelo según uno o varios criterios de selección, entre ecuaciones que tienen un regresor candidato, dos regresores, o más. Ya que el término de ordenada al origen (a₀) se incluye en todas las regresiones y como hay K regresores candidatos, entonces habrá 2^K ecuaciones por estimar y examinar; por ejemplo si K=4, hay 2⁴=16 ecuaciones posibles, en cambio si K=8, hay 2⁸=256 regresiones por analizar. Este procedimiento se vuelve impráctico para K> 5. En la regresión por segmentos se evalúa sólo una pequeña cantidad de ecuaciones, agregando o eliminando regresores uno por uno. Hay diversos algoritmos de este procedimiento, por ejemplo, selección hacia adelante, eliminación hacia atrás y sus combinaciones (McCuen, 1998).

Debido a que en la transferencia de información hidrológica difícilmente se dispone de cinco registros aledaños o regresores candidatos, el procedimiento sugerido para el análisis de las regresiones por subconjuntos, es el de procesar todas las ecuaciones posibles, las cuales se indican en el Cuadro 1.

Validación de los modelos seleccionados

Cuando los regresores usados son series cronológicas se debe verificar que sus residuos no estén autocorrelacionados, pues ello implica violar una de las hipótesis básicas de la regresión lineal: sus errores tienen media cero, varianza constante y no están correlacionados. Tal verificación se realiza mediante gráficas de residuales, cuyo comportamiento indica si se debe detectar autocorrelación positiva o negativa; en el primer caso los residuos se agrupan según su signo y en el segundo cambian demasiado de signo. Esto se verifica mediante la prueba de Durbin–Watson (Makrindakis et al., 1983; Montgomery et al., 2002), cuya hipótesis establece que los errores (e_t) los genera un proceso autorregresivo de primer orden. Cuando se busca autocorrelación positiva se usa el siguiente estadístico:

siendo

donde, n es el número de datos, y_t es la variable dependiente y 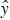t su estimación mediante el modelo de regresión lineal múltiple que se está probando. La hipótesis nula (H₀) establece que no existe autocorrelación y la alternativa (H₁) que sí. La tabulación de Durbin–Watson establece dos límites (d_L y d_U) según n, número de regresores (K) y nivel de significancia a de la prueba (α=5%, comúnmente). La regla de decisión es:

Cuando la prueba se emplea para detectar autocorrelación negativa se emplea el estadístico 4–d, usando como límites 4–d_L y 4–d_U y la misma regla de decisión.

Ya verificado que la autocorrelación de los residuos no existe o es aceptable, se busca el mejor modelo de acuerdo a la capacidad predictiva usando la técnica de validación cruzada, que se describe en la aplicación numérica expuesta.

Otro aspecto importante relacionado con el empleo de regresores que son series cronológicas, es su correlación entre sus elementos, lo cual conduce a la multicolinealidad y sus consecuencias. Ello se detecta a través de la matriz de coeficientes de correlación lineal entre regresores y se cuantifica con base en los factores de inflación de la varianza. Estos tópicos serán expuestos en la aplicación numérica.

Descripción del sistema de río Tempoal

Al río Tempoal lo forman los ríos Hules y Calabozo, aforados por las estaciones Los Hules y Terrerillos, cuyas cuencas de drenaje inician en la frontera del bajo río Pánuco (Región Hidrológica No. 26 parcial), en los estados de Hidalgo y Veracruz (20° 30' N). El río Tempoal tiene un recorrido de sur a norte y es uno de los colectores más importantes del Río Moctezuma, al cual se une por margen derecha en el poblado El Higo, Veracruz. Antes de la estación hidrométrica Tempoal, última del sistema, llega por margen izquierda el río San Pedro aforado en la estación El Cardón. Finalmente, cerca del poblado de Platón Sánchez, Veracruz, está la estación hidrométrica del mismo nombre sobre el río Tempoal. En la Figura 1 se muestra la ubicación y morfología del sistema del Río Tempoal, con base en la cual se adoptó el siguiente orden de regresores: x1=Tempoal, x2=Terrerillos, x3=Los Hules, y x4=El Cardón, para tomar en cuenta su posible relación física o de causa–efecto, con la estación Platón Sánchez.

Información hidrométrica procesada

En el Cuadro 2 se muestran los cinco registros disponibles de volúmenes escurridos anuales en millones de m³ (Mm³), en las estaciones hidrométricas del sistema del río Tempoal. Tales registros proceden del sistema BANDAS (IMTA, 2002) y están expuestos por orden creciente de tamaños de cuenca drenada, cuyo valores son: 609, 1269, 1493, 4700 y 5275 km², para las estaciones El Cardón, Los Hules, Terrerillos, Platón Sánchez y Tempoal. Las claves respectivas en tal sistema son: 26286, 26277, 26289, 26433 y 26248.

En el Cuadro 2 se observa que el periodo común lo define la estación Platón Sánchez, en el lapso de 1979 a 2002, con 24 años y la ampliación factible para tal registro será de 18 años en el periodo 1961 a 1978. Debido a datos faltantes en las estaciones El Cardón, Los Hules y Terrerillos, el periodo común se reduce a 18 años, pues no se consideró conveniente estimar los valores de los años faltantes, para evitar inducir errores por emplear datos no reales.

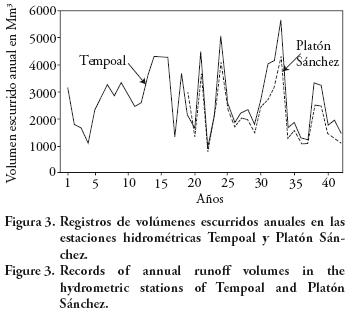
En la parte inferior de la Figura 2 se comparan los registros de volúmenes escurridos anuales de las estaciones hidrométricas El Cardón y Los Hules, y en la porción superior se muestra el relativo a la estación Terrerillos. En la Figura 3 se comparan los registros correspondientes de las estaciones Platón Sánchez y Tempoal. En las cuatro series cronológicas dibujadas no se observa tendencia ni saltos en la media y la variabilidad tampoco cambia, por lo cual tales series probablemente sean estacionarias.

Verificación de requerimientos estadísticos

Primeramente se verificó si es factible aceptar que los registros por procesar (Cuadro 2) proceden de poblaciones Normales, lo cual se realizó con la prueba W de Shapiro y Wilk (1965) y se encontró que sólo los registros de Los Hules y El Cardón no proceden de una población Normal. En la parte inferior del Cuadro 2 se muestran los siguientes parámetros estadísticos insesgados de los registros disponibles: media aritmética ( X ), desviación estándar (S) y coeficientes de variación (Cv), asimetría (Cs) y curtosis (Ck). Se observa que los registros procedentes de poblaciones Normales presentan coeficientes de asimetría y curtosis cercanos a cero y tres, correspondientes a la distribución Normal y que precisamente los registros de El Cardón y Los Hules tienen los valores del Ck más distantes de tres. Sin embargo, dada la similitud entre los valores de Cv y Cs de todos los registros, no se consideró necesario aplicar alguna transformación para trabajar con datos normalizados.

Además se aplicaron pruebas específicas para buscar componentes determinísticas como persistencia, tendencia y cambios en la media o la varianza; las pruebas fueron: coeficiente de correlación serial de orden uno, Kendall, Cramer y Bartlett (WMO, 1971; Ruiz, 1977). Únicamente se encontró que el registro de la estación Terrerillos muestra persistencia (r₁ = 0.290).

 

Resultados y Discusión

Detección de regresores colineales

Una consecuencia lógica del uso de registros hidrológicos ubicados dentro de una región homogénea, es que probablemente ellos serán semejantes, es decir, que sus periodos de años secos y húmedos son coincidentes y por tanto mostrarán correlación entre ellos (Figura 2 y 3). Entonces la detección de registros colineales se realiza buscando correlaciones altas (r_xy > 0.80) en la matriz de coeficientes de correlación lineal (Cuadro 3) y observando sus consecuencias en los coeficientes de los regresores, ya que cuando un regresor está correlacionado con otro, su coeficiente cambiará drásticamente al estar los dos en la ecuación de regresión.

En el Cuadro 3 se observa que todos los regresores usados son colineales, y la mayor correlación fue entre Tempoal (x1) y El Cardón (x4). Como consecuencia, en el Cuadro 4 se observa como los coeficientes de cada regresor (ec. 3) cambian debido a la presencia de otro(s) en la ecuación de regresión. Tales cambios ocurren en magnitud y también en signo; además, los coeficientes de los regresores x1 y x4 son los más estables o insensibles a la presencia de otro(s) en la ecuación.

Los factores de inflación de la varianza (VIF, de variance inflation factors) constituyen un diagnóstico cuantitativo importante, pues de acuerdo con los ejemplos numéricos de Montgomery et al. (2002), cuando exceden a 1000 implican gravísimos problemas de multicolinealidad, menores de 100 problemas aceptables y sin problemas cuando no exceden de 10. La expresión para su estimación práctica es: donde R_j² es el coeficiente de determinación múltiple obtenido haciendo la regresión de x_j con las demás variables regresoras. Los valores de los VIF para las variables regresoras x1 (Tempoal), x2 (Terrerillos), x3 (Los Hules) y x4 (El Cardón) fueron 49.53, 18.04, 11.33 y 28.15. Las magnitudes anteriores ratifican los resultados obtenidos con los valores del Cuadro 3 y establecen que es factible proseguir con la selección y validación de modelos.

Selección de ecuaciones de regresión

Con base en los resultados del Cuadro 5, se seleccionaron tres ecuaciones de regresión. La primera incluye sólo a x1 (Tempoal) como regresor y corresponde a los menores valores del cuadrado medio de los residuos (Ecuación 6) y de la estadística de Mallows (Ecuación 7). La segunda con regresores x1 y x4 (El Cardón) presenta el coeficiente de determinación múltiple ajustado más alto (Ecuación 5) y el segundo cuadrado medio de los residuos (Ecuación 6) más bajo, en los modelos de dos regresores. La tercera tiene por regresores x1, x2 (Terrerillos) y x4, con el coeficiente de determinación múltiple mayor (Ecuación 4) y el menor cuadrado medio de los residuos en los modelos de tres regresores.

Análisis de residuales

En el Cuadro 6 se muestran las estimaciones de la variable dependiente (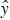_t) de cada uno de los tres modelos seleccionados y sus residuos en el periodo 1979–2002, así como sus respectivos valores del estadístico d (Ecuación 8). Para n=18, α=5.0 % y K=1, 2 y 3 se obtienen de la tabla de valores límite de Durbin–Watson (Makrindakis et al., 1983): d_L=1.16 y d_U=1.39, d_L=1.05 y d_U=1.53, d_L=0.93 y d_U=1.69, por lo cual la primera serie de residuos tiene autocorrelación positiva y para las otras dos la prueba no es concluyente. Lo anterior descarta al modelo del subconjunto x1.

Las tres gráficas de residuales (Figura 4) son similares, tienen magnitudes bastante reducidas, excepto el primer residuo, generado por un escurrimiento en Platón Sánchez que es incluso mayor que de Tempoal (Cuadro 2), lo cual es incorrecto. Por tanto, los tres modelos seleccionados tienen buena capacidad predictiva.

Análisis de validación cruzada

Cuando los datos de los regresores son series cronológicas, el tiempo es usado para la formación de los datos para estimación y para predicción. El lapso conocido de datos se dividió en dos sub–periodos con nueve valores cada uno. En el Cuadro 7 se muestran los coeficientes de regresión estimados con cada sub–periodo considerado como de estimación y en el Cuadro 8 están las estimaciones y sus correspondientes residuos, para cada subperiodo complementario o de predicción.

En el Cuadro 7 se observan cambios drásticos de un sub–periodo al otro en los coeficientes de los regresores de x2 y x4, además el coeficiente a₀ o constante también cambia bastante. Lo anterior se debe a la presencia de un ciclo húmedo y otro seco en el registro disponible en Platón Sánchez (Figuras 3 y 4).

El análisis de residuales por sub–periodos (Cuadro 8) muestra similitud con los mostrados en el Cuadro 6 y la Figura 4, ya que primero hay residuos positivos y después negativos. Los resultados de Cuadro 8 definen los modelos tercero y segundo como más convenientes por su mejor capacidad predictiva, medida por la menor suma de residuos en cada sub–periodo de predicción; es decir el modelo con subconjunto x1, x2 y x4 y el del subconjunto x1 y x4.

Validación con datos nuevos

A través de la Dirección Local San Luis Potosí de la CONAGUA se intentó conseguir las magnitudes del volumen escurrido anual después del año 2002, en las estaciones del sistema del río Tempoal pero no se obtuvo tal información en la estación Platón Sánchez, únicamente en el resto y sólo hasta 2006. Por tanto, no fue posible realizar una validación con datos nuevos.

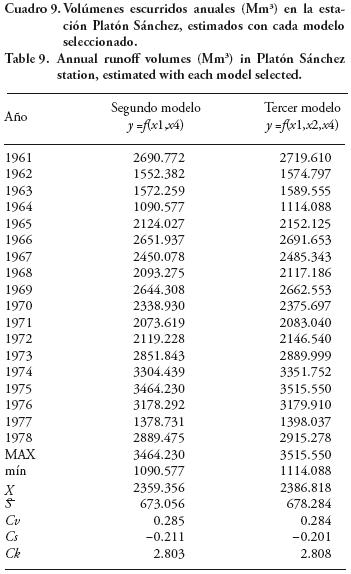
Estimaciones finales y su selección

En el Cuadro 9 se muestran los volúmenes escurridos anuales estimados en la estación Platón Sánchez, con cada uno de los dos modelos o ecuaciones de regresión seleccionados, y con sus respectivos parámetros estadísticos. Se observa que las dos estimaciones conducen a registros bastante similares, ya que sus parámetros estadísticos (Cv, Cs, Ck) y valores medios son casi idénticos. Lo anterior genera confianza en la predicción de los valores buscados y se puede adoptar cualquiera de las dos series. Si hay que seleccionar sólo una de ellas, se recomienda la primera por la magnitud menor en su media, lo cual implica cierta garantía en estimaciones asociadas con la disponibilidad.

 

Conclusiones

El ejemplo descrito para el sistema del río Tempoal, permitió exponer con detalle los análisis previos y de regresión lineal múltiple realizados con la información hidrológica disponible y sus consecuencias.

Aunque la aplicación numérica expuesta tiene un problema grave de multicolinealidad, lo cual es muy probable que ocurra en todas las aplicaciones prácticas de ampliación de registros de escurrimiento y de lluvia anuales, los criterios expuestos para selección de regresores conducen a resultados consistentes y son una ayuda efectiva en la búsqueda de la mejor ecuación de regresión lineal múltiple.

Cuando los criterios de selección sugieren ecuaciones de regresión diferentes, sus resultados se deben analizar a través del análisis de residuales y las validaciones cruzada y con datos nuevos, para adoptar el modelo candidato más conveniente. Pero la similitud en los resultados de tales modelos, como ocurrió con los datos del sistema del río Tempoal, origina confianza en las estimaciones y en aquéllas adoptadas.

 

Agradecimientos

Se agradecen los comentarios y sugerencias de los dos árbitros anónimos y del editor asignado, los cuales permitieron completar el trabajo en tópicos no tratados pero relevantes al tema, como: análisis de residuales, factores de inflación de la varianza y validación cruzada.

 

Literatura Citada

Campos A., D. F. 2003. Ajuste de curvas. In: Introducción a los Métodos Numéricos: Software en Basic y Aplicaciones en Hidrología Superficial. Librería Universitaria Potosina. San Luis Potosí, S.L.P. pp: 93–127.         [ Links ]

IMTA (Instituto Mexicano de Tecnología del Agua). 2002. Banco Nacional de Datos de Aguas Superficiales (BANDAS). Secretaría de Medio Ambiente y Recursos Naturales–Comisión Nacional del Agua–IMTA. Jiutepec, Morelos. 8 CD.         [ Links ]

Makrindakis, S., S. C. Wheelwright, and V. E. McGee. 1983. Multiple regression. In: Forecasting: Methods and Applications. John Wiley & Sons. New York, U.S.A. Second edition. pp: 246–317.         [ Links ]

McCuen, R. H. 1998. Stepwise regression. In: Hydrologic Analysis and Design. Prentice Hall. New Jersey, U.S.A. pp: 84–87.         [ Links ]

Montgomery, D. C., E. A. Peck, y G. G. Vining. 2002. Selección de variable y construcción del modelo. In: Introducción al Análisis de Regresión Lineal. Compañía Editorial Continental. México, D. F. pp. 261–290.         [ Links ]

Gilroy, E. J. 1970. Reliability of a variance estimate obtained from a sample augmented by multivariate regression. Water Resources Res. 6: 1595–1600.         [ Links ]

Ruiz M., L. 1977. Condiciones paramétricas del análisis de varianza. In: Métodos Estadísticos de Investigación. Instituto Nacional de Estadística. Madrid, España. pp. 233–249.         [ Links ]

Salas, J. D., J. A. Raynal, Z. S. Tarawneh, T. S. Lee, D. Frevert, and T. Fulp. 2008. Extending short record of hydrologic data. In: Singh, V. P. (ed). Hydrology and Hydraulics. Water Resources Publications. Highlands Ranch, Colorado, U.S.A. pp: 717–760.         [ Links ]

Shapiro, S. S., and M. B. Wilk. 1965. An analysis of variance test for normality (complete samples). Biometrika 52: 591–611.         [ Links ]

WMO (World Meteorological Organization). 1971. Standard test of significance to be recommended in routine analysis of climatic fluctuations. In: Climatic Chance. Technical Note No. 79. Secretariat of the WHO. Genova, Switzerland. pp:58-71.         [ Links ]