Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.44 no.4 Texcoco may./jun. 2010
Agua–suelo–clima
Algoritmos para estimar características físicas en cuencas rurales y su aplicación en el calibrado del método racional, en la región hidrológica No. 12 parcial (Río Santiago)
Algorithms used to estimate physical properties of rural watersheds and their application in the calibration of the rational methods, in hydrological region No. 12 partial (Santiago River)
Sergio I. Martínez–Martínez1 y Daniel F. Campos–Aranda2*
1 Centro de Ciencias del Diseño y de la Construcción, Universidad Autónoma de Aguascalientes. Dr. Jesús Díaz de León # 523. Barrio del Encino. 20240. Aguascalientes, Aguascalientes. E–mail: (simartin@correo.uaa.mx).
2 Facultad de Ingeniería, Universidad Autónoma de San Luis Potosí. Genaro Codina # 240. 78280. San Luis Potosí, San Luis Potosí. *Autor responsable: (campos_aranda@hotmail.com).
Recibido: Noviembre, 2008.
Aprobado: Mayo, 2010.
RESUMEN
Los procesos hidrológicos que generan las crecientes son bastante complejos, de manera que su modelación matemática requiere de información pluviográfica e hidrométrica que generalmente no está disponible en la mayoría de las cuencas. Los registros de gastos máximos anuales son los mejores datos para predecir estos eventos y para calibrar métodos de estimación que se puedan aplicar en cuencas similares, sobre todo en las que no están aforadas. Este trabajo comprende el procesamiento de dos tipos de datos. El primero se refiere al de información geográfica en su forma de modelos digitales de elevación (MDE) para obtener el parteaguas, el área de cuenca y las características físicas de su colector principal, incluyendo su selección. Este análisis concluye con la estimación del tiempo de concentración de cada una de las siete cuencas procesadas. El segundo procesamiento se basa en la información hidrométrica, pluviográfica y pluviométrica disponible en las siete cuencas, para identificar el coeficiente de escurrimiento del método Racional asociado con diferentes periodos de retorno. Con los resultados numéricos se desarrolla un método regional de estimación de crecientes en cuencas rurales sin aforos, con registros cortos o no confiables. Se muestra que las predicciones son bastante confiables, pues su error relativo por defecto es menor del 15 %. Este método aplica la fórmula Racional estimando el coeficiente de escurrimiento (CTr) con base en las relaciones (CTr/C10) regionales medianas calibradas.
Palabras clave: SIG, MDE, ArcHydro, método Racional, coeficientes de escurrimiento, estimación regional de crecientes.
ABSTRACT
The hydrological processes that cause floods are very complex, such that their mathematical modeling requires pluviographic and hydrometric information that is generally not available in most watersheds. The records of maximum annual flows are the best data for predicting these events and for calibrating estimation methods that can be applied to similar watersheds, in particular those that have not been gauged. This study comprises processing two types of data. The first type refers to geographic information in the form of digital elevation models (DEM) to determine the watershed divide, watershed area and physical characteristics of its main channel, including its selection. This analysis concludes with the estimation of the concentration time of each of the seven watersheds that were processed. The second type is based on hydrometric, pluviographic and pluviometric information available in the seven watersheds to identify the Rational method runoff coefficient associated with different return periods. With the numerical results the regional flood estimation method was developed for ungauged rural watersheds or those with unreliable records over short periods. The predictions are shown to be quite reliable since its relative error by defect is below 15 %. This method applies the Rational formula estimating the runoff coefficient (CTr) based on regional median calibrated ratios (CTr/C10).
Key words: GIS, DEM, ArcHydro, Rational method, runoff coefficients, regional flood estimation.
INTRODUCCIÓN
En México, los ciclones tropicales y las tormentas locales son fenómenos que originan crecientes o avenidas máximas, las cuales generan inundaciones y daños a la infraestructura de carreteras y de protección, como diques, rectificaciones, encauzamientos y todo tipo de presas de almacenamiento. Aunque se ha modelado matemáticamente y con éxito los procesos hidrológicos que generan las crecientes en cuencas rurales y urbanas, la información pluviográfica e hidrométrica conjunta requerida para tales análisis generalmente no está disponible en todas las cuencas aforadas. Por ello, los registros históricos de gastos máximos anuales son los mejores datos para predecir estos eventos, así como para calibrar métodos de estimación para aplicar en cuencas similares, incluso en aquellas que no están aforadas. Un procedimiento, quizás el más simple y difundido, es el método Racional.
Las técnicas de los análisis regionales conjuntan la información hidrométrica de una zona geográfica considerada homogénea hidrológicamente para obtener relaciones confiables válidas dentro de tal región. El desarrollo de las relaciones hidrológicas buscadas comienza con la evaluación de las características físicas de las cuencas con hidrometría y su aplicación en cuencas no aforadas se realiza con base en tales propiedades: área, longitud y pendiente promedio del cauce principal, desnivel total del mismo, etcétera.
Por tanto los objetivos básicos de este trabajo fueron: 1) la descripción detallada del procedimiento y del software desarrollado para esta investigación orientado a determinar las características físicas de las cuencas rurales, con los resultados obtenidos mediante el procesamiento de modelos digitales de elevación (MDE), usando el juego de herramientas ArcHydro, con base en las cuales se estimó su tiempo de concentración con fórmulas empíricas; 2) la calibración de los coeficientes de escurrimiento del método Racional, usando el análisis probabilístico de las respuestas de siete cuencas rurales de la Región Hidrológica No. 12 Parcial (Río Santiago) y de la estimación de sus predicciones según el método Racional. Los resultados numéricos se usaron para formular un método regional de predicción.
MATERIALES Y MÉTODOS
Método Racional e identificación de su coeficiente de escurrimiento
La fórmula del método Racional es:

donde, Q es el gasto máximo (m3 s–1); C es el coeficiente de escurrimiento que es adimensional y equivalente al cociente del escurrimiento entre la lluvia; i es la intensidad de la lluvia (mm h–1); A el área de cuenca (km2). La intensidad de lluvia i se estimó con base en las curvas Intensidad–Duración–Frecuencia (IDF) que caracterizan la cuenca; su duración es igual al tiempo de concentración (Tc) de la cuenca y un periodo de retorno (Tr) que corresponde al adoptado para el gasto máximo estimado. Por tanto, el coeficiente de escurrimiento será:

El procedimiento para usar la ecuación anterior en la identificación del CTr en cuencas rurales ha sido descrito y aplicado por Témez (1991) y Campos (2008). En el método Racional la acción de la lluvia y del área de cuenca son tomados explícitamente; en cambio, los efectos de sus condiciones físicas se consideran indirectamente mediante el Tc y el valor de C.
Selección de cuencas
Se acepta (Campos, 2008) que en cuencas de hasta 500 mi2 (≈1300 km2) es todavía muy probable que la lluvia originada por un fenómeno no ciclónico iguale la magnitud de las crecientes derivadas de las precipitaciones ciclónicas. Esto implica que en cuencas menores a dicha magnitud es probable que se cumplan las hipótesis básicas de método Racional: 1) intensidad de lluvia con duración igual al Tc, constante y uniforme a través de la cuenca; 2) la infiltración y otras pérdidas no se consideran de una manera física real, sino indirecta global en el coeficiente de escurrimiento; 3) efectos despreciables del almacenamiento del escurrimiento sobre el terreno y los cauces. En la columna 1 del Cuadro 1 se citan en orden progresivo de tamaños de cuenca (columna 4) de las siete estaciones hidrométricas usadas, cuyas cuencas varían de 97 a 857 km2.
Obtención y proyección de los modelos digitales de elevación (MDE)
La variación continua de alguna propiedad del medio geográfico se puede representar mediante un raster o malla. Por ejemplo, se pueden producir mallas de cobertura vegetal, precipitación, temperatura o elevación del terreno. Una malla de celdas cuadradas, más populares y fáciles de manipular que las rectangulares, que representa la distribución espacial de la elevación del terreno en una cierta región geográfica es conocida como MDE. En cada celda se asigna una elevación representativa del área cubierta por la celda y se designa por Z.
Los MDE con los cuales se definieron las cuencas que descargan a las siete estaciones hidrométricas (Cuadro 1) se obtuvieron en el sitio Web del Instituto Nacional de Estadística, Geografía e Informática (INEGI) http://www.inegi.gob.mx/geo/default.aspx. Estas mallas, que forman parte del Continuo de Elevaciones Mexicano (CEM), fueron obtenidas por el INEGI con sus propias cartas topográficas 1:50000 y tienen un tamaño de celda de 30×30 m. Una vez adquiridos los MDE deben ser alimentados a una aplicación informática para manipularlos y se usó la aplicación ArcGIS Desktop 9.2 (ESRI, 2006). Originalmente los MDE vienen en coordenadas geográficas y deben ser proyectados a un plano. En los MDE del CEM, las unidades de Z están en metros, el datum que usa el INEGI es el ITRF92 época 1988, elipsoide GRS80. Entre múltiples proyecciones disponibles se eligió la proyección Al–bers debido a que conserva las áreas. La lista de parámetros de la proyección Albers usada fue: Falso Este= 500 000 m; Falso Norte= 0 m; Meridiano Central= 105 grados; Paralelo Estándar 1 = 20 grados; Paralelo Estándar 2= 20 grados; Latitud de Origen= 0 grados.
Procesamiento de los MDE para obtener subcuencas y segmentos de corriente
Se usaron algunas herramientas ArcHydro (Maidment, 2002; ESRI, 2007), pero también pueden usarse las herramientas TauDEM (Tarboton, 2005). En el Cuadro 2 se presenta un resumen de las operaciones estándar realizadas con los MDE proyectados; después se explica brevemente cada una. Los detalles del uso de las herramientas ArcHydro, instaladas en el programa ArcMap del paquete ArcGIS Desktop de ESRI®, se pueden consultar en ESRI (2007).
Procesamiento para obtener el cauce principal
El procesamiento para obtener subcuencas y segmentos de corriente se hizo interactivamente usando una combinación de herramientas de ArcHydro y de ArcMap; pero el procesamiento posterior requirió desarrollar un algoritmo. Este algoritmo fue implementado en una macro escrita en Visual Basic para Aplicaciones (VBA) corriendo en el programa Microsoft® Excel® 2002 (MC, 2003). Requiere tres archivos: una tabla de atributos de subcuencas en formato dbf (dBASETM IV) (tabla Subcuencas); una tabla de atributos de segmentos de líneas de corriente definidas en tres dimensiones en formato dbf (tabla Lineas 3D); un archivo en formato texto con las coordenadas X, Y y Z de los puntos que forman cada segmento de corriente en tres dimensiones (texto CoorLin3D). Los dos archivos dbf son parte de los shapefile creados en ArcMap. El procesamiento inicial de los tres archivos lleva a crear la tabla Network, donde hay un registro para cada segmento. La tabla Network está basada en la tabla de atributos del shapefile de segmentos de corriente de las herramientas TauDEM (Tarboton, 2005) y sus campos se describen en el Cuadro 3.
El algoritmo para crear la tabla Network consiste esencialmente en identificar para cada segmento de corriente sus características físicas y topológicas. Esto es, el desnivel entre su punto inicial (aguas arriba) y su punto final (aguas abajo), su longitud, los segmentos que están aguas arriba del mismo, el área de drenaje acumulada hasta su punto final, su orden, su magnitud y el nodo final de aguas abajo. Para obtener las propiedades acumuladas se inicia por los segmentos que no tienen segmentos tributarios. Luego, secuencialmente se procesan los segmentos a cuyos tributarios se ha determinado todas sus propiedades hasta llegar al nodo final de aguas abajo.
Los renglones de la tabla Network se pueden procesar en un segundo paso para determinar, por ejemplo, los cocientes de bifurcación de las corrientes, de longitudes de las corrientes, de áreas o, como en este trabajo, el cauce principal. El cauce principal se identificó siguiendo las reglas usuales (Martínez, 2000); esto es, se inicia por el cauce en la salida; se avanza aguas arriba, hasta lleguar a confluencias que tengan un segmento de orden de corrientes menor al del cauce principal y otro igual al del cauce principal; y se sigue por este último. Sin embargo, cuando se llega a una confluencia de segmentos de orden de corriente menor en uno al del cauce principal, se sigue al segmento de mayor área. Si eventualmente se llega a una confluencia de segmentos de orden menor en uno al del cauce principal, y además éstos tienen la misma área drenada, entonces se escoge al segmento cuya red de drenaje esté más desarrollada: el que tenga una magnitud mayor. La macro ProcNetArcHydro desarrollada para implementar este algoritmo crea una hoja de cálculo llamada Profile, donde se da el número total de segmentos en la tabla Network. Luego, para cada red de drenaje o, equivalentemente, para cada cuenca presente en los datos, se crea una tabla con las columnas i, LinkNo, UpsLink1, UpsLink2, UpsLink3, DsNodeId, Order, Length, Magnitude, DS_Cont_Ar y Drop; y tantos renglones como segmentos de corriente formen parte de su cauce principal. La macro pide tres archivos de datos y uno de resultados. Para observar los resultados de la macro se puede abrir el archivo Excel que guarda el perfil. Este archivo tiene dos hojas, una llamada Network y la otra Profile; de la hoja Profile se puede extraer datos para hacer análisis geomorfológicos. La transformación de los datos para representar el perfil del cauce es directa. Finalmente, con los resultados obtenidos en Excel se puede volver a ArcMap para seleccionar los segmentos que forman el cauce principal de la cuenca estudiada.
RESULTADOS Y DISCUSIÓN
Resultados del procesamiento de todas las cuencas
Como muestra, se presentan en las Figuras 1 y 2 los resultados obtenidos al aplicar los procedimientos explicados a la cuenca de la estación Valle de Guadalupe.

En la Figura 3 se muestra un mapa con la localización de las siete cuencas estudiadas y se indican los cauces principales. En todos los casos se aplicó un umbral para comenzar corrientes igual al 1 % del área de la cuenca, excepto en la cuenca Cuixtla, cuyo tamaño es del orden del doble del de las otras cuencas; en ella se usó el 0.5 % de su área para definir una red de drenaje con densidad similar al de las otras cuencas.
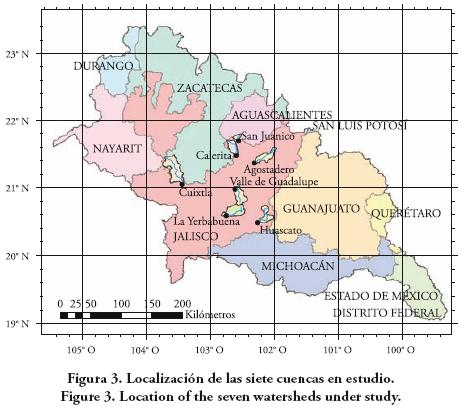
Los cauces principales se originan en la parte más alejada de la salida. Su desarrollo en planta es tortuoso con cambios de dirección más o menos bruscos, a excepción del cauce de la cuenca de la estación Agostadero. Las elevaciones se obtuvieron directamente, sobre los MDE rellenados, en los puntos de inicio y fin de los cauces principales. En el Cuadro 1 se muestra el resumen de los resultados, donde se pueden observar sus variaciones.
En las columnas cuarta y quinta del Cuadro 1 se observa semejanza entre las áreas reportadas por el BANDAS (IMTA, 2003) y las obtenidas en este trabajo usando MDEs, sin contar inicialmente con las correspondientes redes de drenaje vectoriales. Por tanto, si el error se cuantifica con las áreas, el valor absoluto máximo del error relativo cometido es 3.0 % que corresponde a la cuenca San Juanico, mientras que en el resto es menor del 1 %.
Estimación del tiempo de concentración
Se usó una recopilación de fórmulas empíricas las cuales requieren las siguientes tres características físicas del colector principal: longitud (Lc) en km, desnivel total (H) en m y pendiente promedio (Sc). Algunas ecuaciones usan el área de la cuenca (A) en km2. Entre las fórmulas empíricas usadas están las de Kirpich, Giandotti, Témez, etc., cuyos. resultados similares validan su aproximación. Los datos usados y los resultados adoptados se presentan en el Cuadro 1.
Información hidrométrica y su procesamiento
Las series de gastos máximos anuales correspondientes a las estaciones hidrométricas proceden del sistema BANDAS (IMTA, 2002) y se muestran en el Cuadro 4. Tomando en cuenta que las predicciones buscadas corresponden a periodos de retorno bajos (<100 años), se espera que resulten muy semejantes y por ello se adoptaron los valores medianos obtenidos con la aplicación de cinco criterios del análisis probabilístico: las transformaciones MIMEMA y Potencial, y el ajuste de las distribuciones de probabilidades Log–Normal, Log–Pearson tipo III y General de Valores Extremos (Campos, 2006). Para ilustrar, en el Cuadro 5 se muestran los resultados para la estación hidrométrica Agostadero.
Información pluviométrica y su procesamiento
Del plano general de la región se seleccionaron las estaciones pluviométricas base para cada cuenca procesada, las más cercanas, que se citan en el Cuadro 1. Se obtuvo del sistema ERIC II (IMTA, 2000) sus series de lluvias máximas diarias anuales (Cuadro 6) y se procesaron de manera idéntica a los gastos máximos.
Estimación de la intensidad de diseño
El procedimiento usado para estimar la intensidad  conjuga la información pluviográfica (SCT, 1990) con la pluviométrica disponibles (IMTA, 2000), mediante la fórmula de Chen:
conjuga la información pluviográfica (SCT, 1990) con la pluviométrica disponibles (IMTA, 2000), mediante la fórmula de Chen:
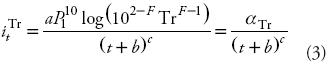
donde, a, b y c son parámetros función de R que es el cociente lluvia–duración; itTr es la intensidad buscada, en mm h–1; P110 es la precipitación en una hora y periodo de retorno (Tr) 10 años, en mm; t la duración, en minutos (5<t<1440); F es el cociente lluvia–frecuencia. Tanto R como F son adimensionales y con las expresiones siguientes:


El procedimiento detallado de aplicación de la fórmula de Chen para obtener las curvas IDF de la cuenca puede ser consultado en Campos (2008).
Resultados de la identificación del coeficiente de escurrimiento
Para la aplicación de la ecuación 2 las predicciones, como las mostradas en el Cuadro 5, son el numerador; su denominador se obtiene con base en las curvas IDF y el valor de A se obtiene del Cuadro 1. Los resultados se presentan en el Cuadro 7, en el cual además están las relaciones adimensionales CTr/C10 y los valores medianos adoptados para diseño, o magnitudes regionales.
En general, los resultados del Cuadro 7 son consistentes, lo cual se demuestra por su similitud, con excepción de los resultados encontrados en la estación hidrométrica La Yerbabuena, que resultaron extraordinariamente bajos en los periodos de retorno elevados.
Fórmulas empíricas para estimar el C10
Con base en los resultados del Cuadro 7, primero se calibró una fórmula propuesta para el coeficiente de escurrimiento del método Racional de periodo de retorno 10 años, según el procedimiento mostrado por Campos (2008):

donde, Pd10 es la precipitación diaria (mm) con periodo de retorno de 10 años y Po es la precipitación que no produce escurrimiento, con la expresión siguiente, al usar seis ternas de datos, ya que se eliminó la estación La Yerbabuena:
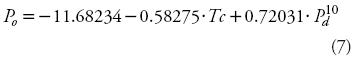
cuyo coeficiente de determinación fue 0.55, es decir bajo, pero con un error estándar de la estimación de sólo 2.5 mm, considerado bastante aproximado. Este tipo de resultados mejora con más datos (Campos, 2008).
Aplicación de los resultados regionales
Se puede llevar a cabo en cualquier cuenca no aforada de la Región Hidrológica No. 12 Parcial (Río Santiago) con el procedimiento siguiente: Paso 1): se localiza y cuantifica su área de cuenca (A) en km2 y su tiempo de concentración (Tc) en horas. Paso 2): se aplica el procedimiento propuesto por Campos (2008) para obtener las intensidades  necesarias con base en la fórmula de Chen. Paso 3): se estima el C10 con las ecuaciones 7 y 6; con ese valor y las relaciones regionales o finales del Cuadro 4 se estiman los coeficientes de escurrimiento correspondientes a los periodos de retorno de 2, 5, 25, 50 y 100 años. Paso 4): se aplica la ecuación 1 para obtener las predicciones buscadas.
necesarias con base en la fórmula de Chen. Paso 3): se estima el C10 con las ecuaciones 7 y 6; con ese valor y las relaciones regionales o finales del Cuadro 4 se estiman los coeficientes de escurrimiento correspondientes a los periodos de retorno de 2, 5, 25, 50 y 100 años. Paso 4): se aplica la ecuación 1 para obtener las predicciones buscadas.
La aplicación del procedimiento anterior en las siete estaciones hidrométricas distribuidas en el centro de la Región Hidrológica No. 12 Parcial (Río Santiago), condujo a las predicciones regionales citadas en el Cuadro 8, en contraste con las predicciones locales u observadas con el registro histórico. Además, en el Cuadro 8 se muestran los errores relativos (E.R.) en las estaciones procesadas, definido como:

donde, el error relativo se expresa en porcentaje y presenta un valor negativo cuando el gasto del método regional 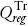 fue menor que la predicción local
fue menor que la predicción local 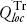 ; en cambio, cuando conduzca a un valor positivo, indica lo contrario.
; en cambio, cuando conduzca a un valor positivo, indica lo contrario.
CONCLUSIONES
Los procedimientos para obtener de las subcuencas y redes de drenaje de las cuencas procesadas son práctica estándar en diversas oficinas, especialmente los pasos realizados con las herramientas ArcHydro hasta antes de la obtención de la red de drenaje en 3D. La parte novedosa es obtener el cauce principal mediante un procedimiento computacional desarrollado ex profeso, usando como entrada algunos resultados proporcionados por dichas herramientas (ArcHydro y ArcMap). El proceso es más rápido y da resultados que dependen menos del criterio del analista que los obtenidos de un mapa de papel o de un dibujo en un sistema CAD. Para obtener resultados satisfactorios, la calidad del MDE original debe ser buena, aun cuando incluya hoyos que se deban rellenar. Se ha encontrado que los MDE del INEGI son buenos. Además, debe contar con una red de drenaje vectorial que pueda aplicarse al MDE antes de su procesamiento, lo cual redundará en una mejor modelación del terreno y por ende en una mejor determinación de la cuenca y del cauce principal. A la fecha, la macro ProcNetArcHydro no se ha implementado como herramienta dentro del programa ArcMap, o cualquier otro programa similar, de tal manera que permita la identificación del cauce principal sin tener que salir a otro programa para hacerla.
La uniformidad o consistencia numérica de los coeficientes de escurrimiento identificados del método Racional en la Región Hidrológica No. 12 Parcial (Río Santiago), concentrados en el Cuadro 7, muestran la aplicabilidad del procedimiento propuesto en cuencas rurales de hasta 900 km2 en dicha zona geográfica. Su exactitud se puede verificar con base en los resultados del Cuadro 8. Se recomienda la aplicación del procedimiento expuesto para obtener sus relaciones regionales en otras zonas geográficas del país.
AGRADECIMIENTOS
Se agradece al árbitro y editor anónimos, sus comentarios y observaciones, las cuales al ser atendidas mejoraron bastante la descripción de la parte operativa del trabajo.
LITERATURA CITADA
Campos A., D. F. 2006. Análisis Probabilístico Univariado de Datos Hidrológicos. Avances en Hidráulica 13. AMH–IMTA. México, D. F. 172 p. [ Links ]
Campos A., D. F. 2008. Calibración del método Racional en ocho cuencas rurales menores de 1650 km2 de la Región Hidrológica No. 10 (Sinaloa). Agrociencia 42: 615–627. [ Links ]
ESRI (Environmental Systems Research Institute). 2006. ArcGIS Desktop Help. Version 9.2. Redlands, California, U.S.A. [ Links ]
ESRI (Environmental Systems Research Institute). 2007. ArcHydro for ArcGIS 9 (version 1.2). Redlands, California, U.S.A. [ Links ]
IMTA (Instituto Mexicano de Tecnología del Agua). 2000. Eric II: Extractor Rápido de Información Climatológica 1920–1998. 1 CD. Comisión Nacional del Agua–Secretaría de Medio Ambiente y Recursos Naturales–IMTA. Jiutepec, Morelos. [ Links ]
IMTA (Instituto Mexicano de Tecnología del Agua). 2002. Banco Nacional de Datos de Aguas Superficiales (BANDAS). 8 CD. Comisión Nacional del Agua–Secretaría de Medio Ambiente y Recursos Naturales–IMTA. Jiutepec, Morelos. [ Links ]
Maidment, D. R. (ed). 2002. ArcHydro: GIS for Water Resources. Environmental Systems Research Institute Press. Redlands, California, U.S.A. 220 p. [ Links ]
Martínez M., S. I. 2000. Geomorfología de la cuenca. In: Introducción a la Hidrología Superficial. Universidad Autónoma de Aguascalientes. Aguascalientes, Ags. pp: 27–57. [ Links ]
MC (Microsoft Corporation). 2003. Ayuda en línea de Excel 2002. Seattle, Washington, U.S.A. [ Links ]
SCT (Secretaría de Comunicaciones y Transportes). 1990. ISOYETAS de Intensidad–Duración–Frecuencia. República Mexicana. Subsecretaría de Infraestructura. México, D. F. 495 p. [ Links ]
Strahler, A. N. 1964. Quantitative geomorphology of drainage basins and channel networks. In: Chow, V. T. (ed). Handbook of Applied Hydrology. McGraw–Hill, Inc. New York, U.S.A. pp: 4.39–4.76. [ Links ]
Tarboton, D. G. 2005. TauDEM Tools, Help online (version 3.1). Utah State University. Utah, U.S.A. [ Links ]
Témez P., J. R. 1991. Generalización y mejora del método racional. Versión de la Dirección General de Carreteras de España. Ingeniería Civil 82: 51–56. CEDEX. Madrid, España. [ Links ]














