Matemáticas aplicadas, estadística y computación

 

Efectos de especificar un modelo incorrecto para regresión logística, con dos variables independientes correlacionadas

 

Effects of specifying an incorrect model for logistic regression, with two independent correlated variables

 

Rigoberto Sifuentes–Amaya, Gustavo Ramirez–Valverde*

 

Estadística. Campus Montecillo. Colegio de Postgraduados. 56230. Montecillo, Estado de México, (rsifuentes@colpos.mx), *Autor responsable: (gramirez@colpos.mx)

 

Recibido: Enero, 2009.
Aprobado: Noviembre, 2009.

 

Resumen

El análisis de regresión logística se utiliza para estudiar la asociación entre una variable respuesta binaria con un conjunto de variables independientes. Cuando hay correlación alta entre dos variables independientes, se presentan varianzas grandes en los estimadores de los parámetros. Sin embargo, si el modelo lineal está mal especificado las varianzas pueden disminuir al aumentar la correlación entre las variables independientes. En este trabajo se evaluó mediante un estudio de simulación el efecto de la correlación entre las variables independientes en el modelo de regresión logística cuando el modelo tiene una especificación incorrecta. Al omitir una variable relevante el sesgo de 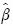aumentó y no desapareció al aumentar n. Se detectó un efecto de la correlación en la potencia de la prueba de hipótesis sobre el parámetro estimado y el tamaño de la prueba de hipótesis estuvo cerca del nominal. Al incluir una variable irrelevante no hubo efecto en el sesgo, el error cuadrado medio mostró evidencia de consistencia y la potencia de la prueba de hipótesis disminuyó cuando aumentó la correlación entre las variables independientes.

Palabras clave: correlación, especificación, omisión e inclusión de variables, regresión logística.

 

Abstract

Analysis of logistic regression is used to study the association between a binary response variable and a set of independent variables. When correlation is high between two independent variables, variances of the parameter estimators are large. However, if the linear model is poorly specified, the variances can decrease when the correlation between the independent variables increases. In this paper, using a simulation study, we evaluated the effect of the correlation between independent variables on the logistic regression model when the model has an incorrect specification. When a relevant variable was omitted, the 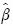bias increased and did not disappear even when n was augmented. An effect of the correlation was detected in the power of the hypothesis test on the estimated parameter, and the test size of the hypothesis was close to the nominal size. When an irrelevant variable was included, there was no effect on the bias, the mean square error showed evidence of consistency and power of the hypothesis test diminished when the correlation between the independent variables increased.

Key words: correlation, specification, variable omission and inclusion, logistic regression.

 

INTRODUCCIÓN

La regresión logística es un modelo lineal generalizado frecuentemente usado para medir la asociación entre una variable respuesta binaria y una o más variables independientes. El modelo supone que la probabilidad de que Y=1 (π_i) depende de p variables independientes X_x, X₂, ..., X_p. El modelo de regresión logístico está dado por:

El modelo está correctamente especificado cuando las p variables contribuyen a explicar la variabilidad de la variable respuesta, y cualquier otra variable independiente no incluida en el modelo no lo hace; esto es, las p variables son importantes y no hay otra que lo sea.

En regresión lineal Walls y Weeks (1969) advierten que agregar una variable al modelo nunca mejora la precisión de los estimadores de mínimos cuadrados, pero se remueve un posible sesgo y esto ocurre sin importar si la variable es importante o no. Rao (1971) muestra que omitir una variable relevante causa en los estimadores de mínimos cuadrados: 1) sesgo; 2) disminución de sus varianzas; 3) disminución del error cuadrado cuando el valor de su parámetro es menor que la desviación estándar de su estimador. Rosenberg y Levy (1972) determinaron las condiciones con las cuales el estimador de mínimos cuadrados en un modelo incorrectamente especificado por omitir una variable importante, es más eficiente en términos de error cuadrado medio. Según Hocking (1976), omitir una variable importante produce sesgo en los estimadores, excepto cuando las variables omitidas son ortogonales a las incluidas o cuando el coeficiente verdadero de las variables omitidas es cero (las variables omitidas no son relevantes). En relación a la inclusión de variables irrelevantes al modelo de regresión, Rao (1971) muestra que no generan sesgo en los estimadores, pero generan un incremento en sus varianzas y por consiguiente en sus errores cuadrados medios.

Para el modelo de regresión logística, Gail et al. (1984) mostraron que omitir variables independientes relevantes produce sesgo en los coeficientes de las variables independientes incluidas, aunque las variables excluidas eran independientes de las incluidas. Neuhaus y Jewell (1993) reportan resultados semejantes cuando hay una correlación de 0.5 entre la variable independiente omitida y la incluida.

En el modelo lineal generalizado Neuhaus (1998) encuentra que omitir una variable independiente relevante puede inducir pérdida en la eficiencia de los estimadores cuando la variable excluida es independiente de la variable incluida. Neuhaus (1998) reporta, en el modelo lineal generalizado, una pérdida de la potencia de las pruebas de hipótesis de las variables incluidas al modelo al omitir variables relevantes e independientes de las variables incluidas. Según Begg y Lagakos (1990), la prueba de Score de los modelos logísticos conserva el tamaño de prueba nominal, aunque se omitan variables aleatorias relevantes.

En regresión lineal un modelo correctamente especificado produce estimadores insesgados de los parámetros. Sin embargo, la correlación entre las variables independientes puede causar un aumento de la varianza de los estimadores de los parámetros (Wittink, 1988; Lehmann et al, 1997), aunque Mela y Praveen (2002) mencionan que en ciertas circunstancias la varianza de los estimadores de los parámetros puede disminuir.

Un modelo incorrectamente especificado es el caso donde el sesgo puede ser problemático y el problema puede aumentar si hay correlación alta entre las variables independientes (Mela y Praveen, 2002). Además, Clarke (2009) menciona que ante el riesgo de sesgo por omitir variables se podría suponer una mejora al incluir un número grande de variables de control pero en ambos casos, regresión lineal o modelo lineal generalizado, el aumento de variables de control puede aumentar o disminuir el sesgo y es difícil saber cual es el caso en una situación particular.

En el presente trabajo mediante un estudio de simulación, se analizó el efecto de una incorrecta especificación del modelo de regresión logística en presencia de diferentes grados de correlación en un modelo con dos variables independientes.

 

MATERIALES Y MÉTODOS

Estudio de simulación

El estudio de simulación se realizó con dos escenarios: uno para mostrar el desempeño del estimador de máxima verosimilitud y su prueba de hipótesis al omitir una variable relevante al modelo; otro para mostrar el desempeño del estimador de máxima verosimilitud y su prueba de hipótesis al incluir una variable irrelevante.

Primer escenario:

Omisión de una variable relevante

El modelo generador de los valores de la variable respuesta Y_i fue:

Hay dos variables independientes relevantes X₁ y X₂. Las propiedades en la inferencia asociada a la variable X₁ al omitir la variable relevante X₂; se estudiaron en tres situaciones:

1) El modelo fue correctamente especificado, la estimación y la prueba de hipótesis se hizo usando correctamente el modelo (1).

2) El modelo fue incorrectamente especificado; la estimación y la prueba de hipótesis se hizo usando incorrectamente el modelo:

Esto es, se omitió la variable X que es una variable importante para predecir Y_i.

3) Para estudiar el tamaño de la prueba de hipótesis H₀:/β₁= 0 vs H_s:/β₁≠0 en un modelo incorrectamente especificado donde la variable importante X₂ fue omitida y el valor de β₁ =0 (Ho es cierta). El modelo generador de los datos fue log[π_i / (1 – π_i)] = β₀ + β₂ X_2i y se probó H₀:β₁= 0 en el modelo log[π_i / (1 – π_i)] = β₀ + β₁ X_1i.

Segundo escenario:
Inclusión de una variable irrelevante

El modelo generador de los valores de la variable respuesta Y_i fue:

Sólo está la variable independiente relevante X₁. Las propiedades en la inferencia asociada a la variable X₁ al incluir la variable irrelevante X₂ se estudiaron en dos situaciones:

1) El modelo fue correctamente especificado, la estimación y la prueba de hipótesis se hizo usando correctamente el modelo (2):

2) El modelo fue incorrectamente especificado; la estimación y la prueba de hipótesis se hizo usando incorrectamente el modelo (1):

Esto es, se incluyó la variable X₂, que es irrelevante para predecir Y₁. En el Cuadro 1 se muestra un resumen de los dos escenarios estudiados.

La variable X₁ se simuló como una variable uniforme con media cero y varianza uno; la segunda variable independiente X₂ se generó usando una variable auxiliar X₃ y la variable X₁; la variable auxiliar X₃ se generó independiente de X₁ como una variable uniforme con media cero y varianza uno; finalmente, se obtuvo X₂ mediante la ecuación X₂= α₀+α₁X₁+α₂X₂, donde α₀=1, α₀=.5 y para el valor de α₂ se inició con α₂ =30 y se disminuyó en 0.1 hasta obtener un valor de α₂ que obtenga las correlaciones deseadas entre los valores X₁ y X₂.

Se estudiaron tres correlaciones en cada uno de los escenarios generados: a) la correlación nula (≈.05); b) correlación moderada (≈.5); c) correlación severa (≈.99). Una vez logradas las tres distintas correlaciones, las variables X₁ y X₂ se mantuvieron fijas para todas las situaciones estudiadas. Este proceso se repitió para cada tamaño de muestra estudiado.

Los tamaños de muestra usados en cada situación simulada fueron 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500 y 1000 observaciones.

La generación de la variable respuesta Y₁ se realizó utilizando el método de la transformada inversa (Ross, 1999), con los pasos siguientes:

1) Primero se generaron los valores de π_i (i=1, 2,..., n) para cada una de las n observaciones de la muestra. Para el primer escenario estos valores se obtuvieron con la ecuación:

Para el segundo escenario estos valores se obtuvieron con la ecuación:

El vector de parámetros β se seleccionó como el vector propio asociado al valor propio mayor de X^TX, que es el mejor de los escenarios teóricos para estimar β (Lee y Silvapulle, 1988; Duffy y Santner, 1989).

2) Se generó una variable auxiliar Z_i (i= 1,2,... ,n) donde Z. tiene distribución uniforme en (0,1).

3) Se generó el valor de Y_i (i=1,2,...,n) con la siguiente regla de decisión:

Los aspectos de la inferencia en el modelo de regresión logística evaluadas en la simulación siempre fueron sobre β₁ y consideraron:

1) Sesgo del estimador. El sesgo del estimador de β₁ dado por E (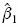) – β₁ se estimó como:

 

donde 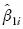, es el estimador de máxima verosimilitud de β₁ obtenido en la i–ésima simulación.

2) El error cuadrado medio (ECM). El ECM de β₁ dado por , se estimó como:

3) La potencia y tamaño de la prueba. Se estudió la función potencia de la prueba de hipótesis estadística H₀:β₁=0 vs H_a:β₁≠0 la función de potencia está dada por:

donde a(β₁)= Pr (Error tipo I) = Pr (Rechazar H₀ cuando H₀ es verdadero), y β (β₁) = Pr (Error tipo II) = Pr (No rechazar H₀ cuando H₀ es falso)

El valor a(β₁) para valores del β₁ bajo H₀ representa el tamaño de la prueba y el valor 1 – β (β₁) para valores de β₁ bajo H_a representa la potencia.

El valor de a(β₁) se estimó como la proporción de rechazos cuando en la simulación β₁=0.

El valor de 1 – β (β₁) se estimó como la proporción de rechazos cuando en la simulación β₁≠0.

El nivel de significancia en todas las pruebas de hipótesis fue a=0.05.

En los dos escenarios propuestos se realizaron 1000 simulaciones con el paquete R versión 2.7.1.

 

RESULTADOS Y DISCUSIÓN

Primer escenario

El modelo generador de los datos es:

Sesgo al omitir la variable relevante X₂

En el modelo correctamente especificado (Figura 1A) hay evidencia de que el sesgo tiende a cero al aumentar n; alrededor de n=300 el sesgo prácticamente desaparece.

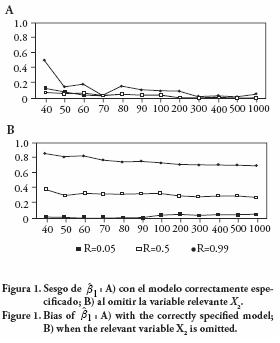
En el modelo incorrectamente especificado (Figura 1B) el sesgo de 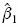al omitir X₂ se mantiene casi constante para cualquier tamaño de muestra, dando evidencias de que el sesgo no desaparece al aumentar n. Estos resultados coinciden con los de Gail et al. (1984) y Neuhaus y Jewell (1993).

Hay un efecto de la correlación en el sesgo, en general a mayor correlación mayor sesgo. El efecto es más marcado en el modelo incorrectamente especificado (Figura 1B).

Error cuadrado medio al omitir la variable relevante X₂

En la Figura 2 se observa un efecto fuerte de la correlación. El ECM es marcadamente más alto en los casos con correlación alta que cuando la correlación es nula o moderada.

El modelo incorrectamente especificado (Figura 2B) mostró ECM menor que el modelo correctamente especificado (Figura 2A) en tamaños de muestra pequeños. Sin embargo, al aumentar el tamaño de muestra disminuye la diferencia en ECM, hasta ocurrir lo contrario alrededor de n=300.

Potencia al omitir la variable relevante X₂

En la Figura 3 se observa que para correlación nula y media el modelo correctamente especificado (Figura 3A) presentó mayores potencias que en el modelo incorrectamente especificado (Figura 3B). Sin embargo, con una correlación alta, la potencia de la prueba tuvo una gran disminución en el modelo correctamente especificado (Figura 3A) pero en el modelo incorrectamente especificado (Figura 3B) la potencia tuvo un gran aumento.

Hay un efecto de correlación en la potencia de la prueba de Wald, en ambos casos. Así, cuando el modelo está correctamente especificado (Figura 3A) la potencia disminuye y el efecto es muy marcado para correlación alta; la potencia es menos de 0.3 cuando n=1000. Para el modelo mal especificado (Figura 3B) que omitió la variable X₂ el efecto de la correlación es positivo; al aumentar la correlación la potencia aumenta drásticamente y en n=50 la potencia es casi 1 en la correlación alta.

Tamaño de la prueba de hipótesis al omitir la variable relevante X₂

En la Figura 4 se muestra el comportamiento del tamaño de la prueba H₀β₁=0 vs β₁≠0 , al omitir una variable relevante; se nota que los valores fluctúan cerca del valor nominal de 0.05. Las fluctuaciones se pueden atribuir a que sólo se repitieron 1000 simulaciones en cada situación simulada. El resultado obtenido coincide con el reportado por Begg y Lagakos (1990) cuando la variable incluida y la no incluida son independientes.

Segundo escenario

Sesgo al incluir la variable irrelevante X₂

En la Figura 5 se muestra que para ambos casos: A) sesgo de 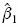con el modelo correctamente especificado y B) sesgo de 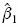al incluir la variable irrelevante X₂, los sesgos tienden a desaparecer al aumentar n (consistencia) y son mayores cuando el modelo está incorrectamente especificado por incluir la variable irrelevante X₂.

Error cuadrado medio al incluir la variable irrelevante X₂

En la Figura 6 se observa que con el modelo correctamente especificado (Figura 6A) el error cuadrado medio de 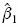no muestra efecto de la correlación.El ECM de 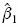al incluir la variable irrelevante X₂ (Figura 6b) es mayor sólo en las correlaciones severas (r_ij ≈ 0.99).

Potencia de la prueba de hipótesis al incluir la variable irrelevante X₂

En la Figura 7 se observa un gran efecto de la correlación en la potencia de la prueba sobre 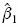al incluir la variable irrelevante X₂, principalmente en muestras pequeña. Este efecto de la correlación disminuye al aumentar n en las correlaciones nulas (r_ij ≈ 0.05) y moderadas (r_ij ≈ 0.05) principalmente.

 

CONCLUSIONES

Primer escenario

Al omitir una variable independiente relevante

El estimador de β₁ en el modelo correctamente especificado es consistente. Cuando el modelo estaba mal especificado el estimador fue sesgado y el sesgo no desapareció al aumentar el tamaño de muestra.

Existe efecto de la correlación en la potencia de la prueba de hipótesis. En el modelo correctamente especificado hay un efecto negativo de la correlación (la potencia disminuye al aumentar la correlación). En el modelo incorrectamente especificado hay un efecto positivo de la correlación (al aumentar la correlación la potencia aumentó).

El valor del tamaño de la prueba en todos los casos estuvo cercano al nominal de α=0.05.

Segundo escenario

Se incluye una variable independiente irrelevante

No hay efecto por incluir una variable irrelevante en el sesgo, excepto cuando la correlación es alta donde resultaron sesgos mayores que cuando el modelo estaba correctamente especificado.

Al aumentar una variable irrelevante hay efecto de la correlación en el error cuadrado medio y aumenta conforme incrementa la correlación. El efecto disminuye al aumentar el tamaño de muestra.

Al aumentar una variable irrelevante hay efecto de la correlación en la potencia de la prueba; al aumentar la correlación, disminuye la potencia.

 

LITERATURA CITADA

Begg, M. D., and S. W. Lagakos. 1990. On the consequences of model misspecification in logistic regression. Environ. Health Perspectives 87: 69–75.        [ Links ]

Clarke, K. A. 2009. Return of the phantom menace omitted variable bias in political research. Conflict Manage. Peace Sci. 26(1): 46–66.        [ Links ]

Duffy, D. E., and T. J. Santner. 1989. On the small sample properties of norm restricted maximum likelihood estimators for logistic regression models. Comm. Statistics–Theory and Methods 18(3): 959–980.        [ Links ]

Gail, M. H., S. Wieand, and S. Piantadosi. 1984. Biased estimates of treatment effect in randomized experiments with nonlinear regressions and omitted covariates. Biometrics 71: 431–444.        [ Links ]

Hocking, R. R. 1976. The analysis and selection of variables in linear regression. Biometrics 32(1):1–49.        [ Links ]

Lee, A. H., and M.J. Silvapulle. 1988. Ridge estimation in logistic regression. Comm. Statistics–Theory and Methods 17(4): 1231–1257.        [ Links ]

Lehmann, D. R., S. Gupta, and J. Steckel. 1997. Marketing Research, Addison–Wesley Educational Publishers, Inc. Reading. Massachussetts. 780 p.        [ Links ]

Mela, F. C, and K. K. Praveen. 2002. The impact of collinearity on regression analysis: the asymmetric effect of negative and positive correlations. Appl. Econ. 34: 667–677.        [ Links ]

Neuhaus, J. M. 1998. Estimation efficiency with omitted covariates in generalized linear models. J. Am. Stat. Assoc. 93(443): 1124–1129.        [ Links ]

Neuhaus, J. M., and N. P. Jewell. 1993. A geometric approach to assess bias due to omitted covariates in generalized linear models. Biometrika 80: 807–815.        [ Links ]

Rao, P. 1971. Some notes on misspecification in multiple regressions. The Am. Stat. 25(5):37–39.        [ Links ]

Rosenberg, S. H., and P.S. Levy. 1972. Note: a characterization on misspecification in the general linear regression. Biometrics 28(4):1129–1133.        [ Links ]

Ross, S. M. 1999. Simulation. Academic Press. Fourth edition. 312 p.        [ Links ]

Walls, R. C., and D.L. Weeks. 1969. A note on the variance of a predicted response in regression. The Am. Stat. 23(3): 24–26.        [ Links ]

Wittink, D. R. 1988. The Application of Regression Analysis. Simon & Schuster. Needham Heights. Massachusetts. 350 p.        [ Links ]