Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.43 no.3 Texcoco abr./may. 2009
Recursos naturales renovables
Diseño de un índice espectral de la vegetación desde una perspectiva conjunta de los patrones exponenciales y lineales del crecimiento
Design of a spectral vegetation index under the joint perspective of exponential and linear growth patterns
Enrique Romero–Sánchez, Fernando Paz–Pellat* , Enrique Palacios–Vélez, Martín Bolaños–González, René Valdez–Lazalde, Arnulfo Aldrete
Grupo de Gestión de Riesgos y Recursos Naturales Asistida por Sensores Remotos, Campus Córdoba y Montecillo, Colegio de Postgraduados, Km. 36.5 Carretera México–Texcoco, 56230. Montecillo, Estado de México. *Autor responsable: (pellat@colpos.mx).
Recibido: Abril, 2008.
Aprobado: Enero, 2009.
Resumen
En este trabajo se analizan diferentes experimentos con mediciones de reflectancia para revisar los patrones de las primeras dos constantes de los modelos de interacciones radiativas en el espacio del rojo (R) e infrarrojo cercano (IRC), concluyéndose de la evidencia experimental que el modelo de interacciones de orden uno es suficiente para este fin. En segundo lugar se desarrolla el algoritmo del índice espectral IV_CIMAS y se aplica a experimentos de cultivos, concluyéndose que este índice sólo tiene una relativa mejoría en relación con el índice NDVIcp, y que ambos describen bien la fase expo–lineal de la etapa vegetativa de la vegetación. La fase reproductiva no es modelada en forma adecuada por ninguno de los índices espectrales. Finalmente, se revisan los modelos de la geometría sol–sensor propuestos, y se concluye que éstos tienen buenos ajustes experimentales, permitiendo estandarizar esta geometría. La modelación de los patrones asociados a las constantes de las curvas espectrales de igual vegetación es muy difícil de realizar por las propiedades de los espacios usados. El problema del diseño de índices de vegetación es todavía un problema abierto.
Palabras clave: IV_CIMAS, índices de vegetación, reflectancias experimentales.
Abstract
This study analyzes different experiments with reflectance measurements to review the patterns of the first two constants of the models of radiative interaction in the red (R) and near infrared (NIR) space. From experimental evidence, it is concluded that the first order model of interactions is sufficient for this aim. Secondly, the algorithm of the spectral index IV_CIMAS is developed and applied to crop experiments, concluding that this index is only a relative improvement over the NDVIcp index and that the expo–linear phase of the vegetative growth stage of the vegetation are well–described by both. The reproductive phase is not adequately modeled by either of the spectral indexes. Finally, the models of sun–sensor geometry proposed are reviewed, and it is concluded that these have good experimental fit, allowing this geometry to be standardized. Modeling of the associated patterns to the spectral curve constants of equal vegetation is very difficult to do because of properties of the spaces used. The problem of designing vegetation indexes is still open.
Key words: IV_CIMAS, vegetation indexes, experimental reflectances.
INTRODUCCIÓN
El uso de índices de vegetación (IV) espectrales en las aplicaciones de la tecnología de los sensores remotos es muy común. Los IV intentan aproximar relaciones entre los datos espectrales capturados por sensores remotos y variables biofísicas, como el índice de área foliar (IAF), la biomasa o la cobertura aérea. El alto contraste entre las bandas del rojo (R) y del infrarrojo cercano (IRC) (Tucker, 1979) se usa para diseñar un gran número de IV, la mayoría basados en relaciones empíricas.
En este trabajo se analiza la evidencia experimental para entender las limitaciones intrínsecas de la mayoría de los IV publicados (Paz et al., 2009)[1]. La estructura matemática de la dinámica espectral de la vegetación se define mediante aproximaciones de interacciones de primer y segundo orden de la transferencia radiativa en el suelo–vegetación, para el caso homogéneo (medio turbio) y heterogéneo (medio tridimensional). Las consideraciones de efectos atmosféricos y de la geometría sol–sensor se analizaron y se concluyó que estos efectos no modifican los argumentos de los patrones estructurales esperados de la mezcla suelo–vegetación. Adicionalmente, se revisaron la mayoría de los índices de vegetación y se concluyó que ninguno de los IV analizados modela en forma correcta la dinámica del crecimiento de la vegetación en la etapa vegetativa Paz et al. (2008a)[2]. Sólo los IV NDVIcp (Paz et al., 2007) y MSAVI2 (Qi et al., 1994) aproximan correctamente la dinámica inicial de las constantes asociadas a los patrones lineales de curvas de vegetación similar (iso–IAF). Para la parte final de esta dinámica, se propuso el uso del índice β (Paz et al., 2005, 2006) para el desarrollo del índice IV_ CIMAS (KIMO_SAVI) o Índice de Vegetación CInemáticamente Modificado y Ajustado por Suelo, que considera las dos partes de la dinámica espectral del crecimiento de la vegetación en la etapa vegetativa o reproductiva).
En este trabajo se analizan los patrones espectrales y su estructura dinámica en dos experimentos de cultivos agrícolas contrastantes. La propuesta del índice IV_CIMAS y su desarrollo operativo es explorada con detalle. La modelación de la geometría sol–sensor es analizada para su estandarización, para que los efectos bidireccionales de la reflectancia permanezcan fijos y no incidan en los IV. Finalmente, se analizan los resultados de un experimento de sistemas arbolados, geometría sol–sensor variable, para caracterizar los efectos de la densidad del follaje de la vegetación en los IV.
Índices de vegetación y su estructura: evidencia experimental
Las argumentaciones teóricas para el establecimiento de un marco de referencia para el análisis de los IV parten de los patrones espectrales de vegetación similar (iso–IAF) en el espacio del R–IRC, Figura 1.

La Figura 1 fue generada usando simulaciones radiativas tipo medio turbio unidimensional, donde el cultivo de maíz fue modelado usando diferentes tipos de suelo (S2 a S12, del más oscuro al más claro). Paz et al. (2005) detallan estas simulaciones y su análisis para cambios en las propiedades ópticas y angulares de las hojas, así como el efecto de la geometría sol–sensor. Las simulaciones radiativas (Figura 1) se basan en los supuestos: 1) las propiedades ópticas y angulares del cultivo no cambian durante la etapa de crecimiento vegetativa; 2) el cambio de las propiedades ópticas del suelo (rugosidad y humedad) no cambia los patrones de crecimiento del cultivo y fertilidad del suelo; el medio físico es homogéneo (medio turbio en términos radiativos) y siempre cubre totalmente al suelo, independientemente del valor del IAF; la geometría sol–sensor y condiciones atmosféricas se mantienen constantes durante todo el ciclo de crecimiento del cultivo. Aunque se pueden objetar estos supuestos, los resultados de las simulaciones conservan los patrones espectrales asociados al caso tridimensional general (Gao et al., 2000).
Para interacciones de orden uno (los fotones que atraviesan la vegetación solo tocan al suelo una vez) en las bandas del R e IRC (sistemas suelo–vegetación) (modelo 11 – interacciones de orden uno en la banda del R y de orden uno en el IRC), la relación entre éstas estará definida por:
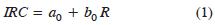
donde, a0 y b0 son constantes que dependen de las propiedades ópticas y geométricas del sistema analizado. Para el caso de interacciones de orden uno en la banda del R, e interacciones de orden dos (los fotones tocan el suelo dos veces) en la banda del IRC (modelo 12), la relación estará dada por:

Al igual que para el caso de interacciones de orden uno, las constantes a0, b0 y c0 son función de las propiedades y geometría del sistema.
Los casos más complejos que los dos modelos de interacciones (modelo 22) no se analizarán en este trabajo, porque no aportan información adicional y son complejos para su uso.
Los patrones entre las dos primeras constantes a0 y b0 de los dos modelos (11 y 12), de la Figura 1, se ilustran en la Figura 2. Las constantes de los modelos 11 y 12 fueron estimadas por regresión de los datos simulados de la Figura 1, incluyendo otros valores del IAF. Una forma alternativa de visualizar los patrones de la Figura 2 es usar el espacio transformado a0 – 1/b0 (Paz et al., 2007) (Figura 3).
Los patrones de los modelos 11 y 12 son similares en la fase inicial del crecimiento (IAF<2.5), algo curva (aproximada en forma lineal en el cambio de b0 por 1/b0), y después de la transición hay un cambio de pendiente (signo contrario); los patrones de 11 y 12 son diferentes en sus tendencias, pero no en sus patrones que pueden aproximarse en forma lineal. El modelo 12, asociado a un polinomio de segundo grado, (Figura 3b) muestra el problema de ajustar polinomios a patrones lineales (Figura 1), donde las constantes estimadas por regresión se comportan en forma inestable.
Para entender la problemática asociada a la modelación a través de índices de vegetación, es conveniente analizar dos IV: El NDVIcp (Paz et al., 2007) y el β (Paz et al., 2005 y 2006) (Figuras 2 y 3). El NDVIcp aproxima muy bien la primera fase de la Figura 2 (IAF<2.5, caso de la Figura 1) y el β lo aproxima muy bien la segunda fase (desde IAF grandes hasta un IAF cercano a 1.0, caso de la Figura 1). La fusión de los dos índices puede ser realizada para el desarrollo del índice IV_ CIMAS (KIMO_ SAVI).
El índice NDVIcp está definido por (Paz et al., 2007):

donde, c y d son dos constantes empíricas; a0 y b0 fueron definidas con anterioridad.
Para la determinación del índice β se requiere una transformación del espacio R–IRC al espacio dIRC–IRC, con dIRC= IRC – (aS + bSR); donde aS y bS son las constantes de la línea del suelo (Figura 1). Así, las relaciones de la transformación de espacios y la definición del índice β están dadas por (Paz et al., 2005 y 2006):

De estas relaciones, se establece (bS = 1):
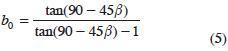
De la ecuación 5 y 3 se genera la relación entre el NDVIcp y β, usando c = 1 (Paz et al., 2007) lo que puede asociarse con aS = 0 y bS = 1. Para reducir la complejidad de esta relación, se usa un polinomio de cuarto grado para una aproximación (Figura 4).

Al igual que el caso entre a0 y 1/b0 de la relación (3), se ha propuesto una relación lineal ente a1 y β (Paz et al., 2005 y 2006):

donde, q y r son constantes empíricas.
Para el caso del NDVIcp, usando c = 1, de las relaciones (3) y (4) se establece:

Finalmente, para el caso de índice β se usan las relaciones (3) y (4) para establecer:

El índice IV_ CIMAS (KIMO_SAVI) está definido por:

donde, NDVIcp(β) es estimado de la relación (5) para b0 y su substitución en la relación (3) del NDVIcp. La constante fie es un valor umbral de β donde la relación (6) se hace inestable.
En los análisis para determinar cuales IV son mejores se utilizan formulaciones estadísticas asociadas a los errores de variación de la modelación (Baret y Guyot, 1991; Leprieur et al., 1994; Huete et al., 1994), donde una menor variación se considera óptimo. Este tipo de análisis parte del desconocimiento de la estructura de los patrones espectrales asociados al crecimiento de la vegetación, por lo que resulta muy difícil obtener conclusiones relevantes. En Paz et al. (2007) se usaron los patrones espectrales reales de las curvas iso–IAF para analizar varios IV, para visualizar las hipótesis intrínsecas. Este tipo de análisis será usado en lo siguiente, a partir de regresiones estadísticas aplicadas a las curvas iso–IAF.
Para analizar la estructura de los patrones de las curvas iso–IAF discutidos, en lo siguiente se analizan dos experimentos de campo con cultivos contrastantes: Maíz (Zea mays L.) (Bausch, 1993) y algodón (Gossypium spp.) (Huete et al., 1985). En estos experimentos se realizaron mediciones de reflectancia a nadir en cultivos sin estrés, se utilizaron charolas con diferentes suelos debajo de los cultivos. En el experimento de maíz el ángulo cenital solar durante todo el periodo de muestreo varió de 17.2° a 24.2°. En el experimento de algodón, las variaciones fueron de 22.0° a 31.7°. Considerando que las variaciones de la geometría sol–sensor fueron mínimas y la ventana de condiciones de iluminación fueron similares, no se intentó estandarizar la geometría sol–sensor de estos experimentos. Así, se integraron los datos de los dos experimentos, bajo el supuesto de condiciones similares de iluminación solar. Las reflectancias en las bandas del R e IRC están dadas en proporción 0 a 1.
En la Figura 5 se muestran las curvas iso–IAF, ajustadas a líneas rectas, de los dos experimentos mencionados; se observa que el ajuste del modelo 11 caracteriza en forma adecuada las interacciones radiativas del sistema suelo–vegetación (caso tridimensional) .
En la Figura 6 se muestran los patrones del modelo 11 para el espacio a0 – 1/b0 y a1 β. En el caso del primer espacio, se muestra un patrón similar al de la Figura 3a (c = 1 y d = 2.24). Para el patrón del espacio a1 – β (aS = 0 y bS = 1) la relación (6) se cumple bien usando un β = 0.25 (b0 = 1.25 y NDVIcp = 0.11), con q = 0.96 y r = 1.46.
Para el modelo 12 de interacciones de primer orden de la banda del R e interacciones de segundo orden para la del IRC, en la Figura 7 se muestra el espacio a0 – b0 para los experimentos del maíz y algodón. Los patrones asociados al espacio a1 – β permanecen inalterados si se usa una línea del suelo virtual (aS = 0 y bS = 1) o la real.
En la primera fase (etapa vegetativa) del crecimiento de los cultivos las constantes del modelo 12, tipo polinomio de segundo grado, tienen un patrón similar al modelo 11, pero con mayor dispersión (Figura 7), asociado al problema de inestabilidad del ajuste del polinomio a un patrón lineal. En la segunda fase del patrón entre a0 y b0, en la Figura 7 el comportamiento es tipo lineal y en sentido contrario al del modelo 12 (Figura 2b). En el caso del experimento con plantas de algodón, los ajustes del polinomio en esta fase fueron muy inestables, por lo que no fueron incluidos en la Figura 7.
De las Figuras 6 y 7, se puede concluir que el modelo 12 resulta en patrones incongruentes (segunda fase) con la evidencia experimental y éstos son resultado de ajustar un polinomio de segundo grado a una línea recta. Así, la complejidad del modelo 12 y modelo 22 no tienen soporte experimental (considerando un numero restringido de datos experimentales) pero sí problemas de inestabilidad numérica. La propuesta del IV_ CIMAS parece estar en el camino correcto, de acuerdo con la evidencia mostrada en la Figura 6.
Para analizar el ajuste del IV_ CIMAS a los datos experimentales, es necesario la estimación de la pendiente b0 directamente de las reflectancias asociadas a β, así como se realizo en NDVIcp (Paz et al., 2007). Así, si sustituimos la relación (8) en la (3) se obtiene:

Usando diferentes valores de R e IRC (en patrones de curvas iso–IAF), la relación (10) fue modelada en forma empírica para establecer una relación entre las reflectancias y b0 (R2 = 0.98):

En la Figura 8 se muestran el espacio a1 – β de las estimaciones del IV_CIMAS donde se uso βc = 0.5 (b0 = 1.70 y NDVIcp = 0.26), representando valores de IAF<1.0.
Las estimaciones del IV_ CIMAS (c = 1.0, d = 2.24, q = 0.96 y r = 1.46), mejoran ligeramente las del NDVIcp (Paz et al., 2007), lo cual es explicable si observamos que el uso del NDVIcp en el IV _CIMAS puede ser extendido para valores arriba de fie con buenos resultados (Figura 8).
Para poder ubicar en contexto las limitaciones del NDVIcp e IV_ CIMAS y entender los resultados mostrados en la Figura 9, es necesario revisar las diferencias entre modelos radiativos homogéneos (medios turbios) y heterogéneos (medios tridimensionales). En los medios turbios, el patrón entre a0 y b0 supone dos fases de crecimiento vegetativo: una exponencial y otra lineal (Figura 2a). En el tiempo, el crecimiento del IAF puede ser ajustado por un modelo expo–lineal (Goudriaan y Monteith, 1990). Esta modelación usa la hipótesis de un medio homogéneo para su desarrollo, por lo que para el caso de medios heterogéneos las fases del crecimiento deben ser reconsideradas. En la Figura 10 se muestran los patrones del crecimiento asociados al IAF de los experimentos de maíz y algodón analizados.
El término fase reproductiva es usado para denotar un cambio en las propiedades ópticas o angulares de las hojas o la emergencia de órganos reproductivos con propiedades ópticas diferentes a las hojas. En el caso de cultivos reales (caso tridimensional de la transferencia radiativa) es claro que la modelación de la etapa vegetativa completa (fase exponencial y lineal) puede ser realizada por el NDVIcp e IV _CIMAS (Figura 10). El crecimiento de la vegetación y el IAF máximo requiere de la extensión de los IV para la modelación de las dos fases de los patrones ente a0 y b0 (Figura 6).
La discusión previa pone en contexto el problema del desarrollo de los IV: aun cuando sea posible diseñar un IV que tome en cuenta, las dos fases de los patrones entre a0 y b0, su construcción deberá considerar cambios en las propiedades ópticas o angulares de los elementos de la vegetación. Esto implica que la relación entre el IAF, u otra variable biofísica, y el IV será al menos bi–lineal, por lo que ningún IV de enfoque clásico puede considerarse como óptimo en el sentido generalizado que se ha definido.
Estandarización de la geometría sol–sensor
Para evitar la consideración de los efectos bidireccionales de la reflectancia, es posible estandarizar la geometría sol–sensor para dejar éstos fuera de la discusión del análisis de los IV. El modelo de Bolaños y Paz (2007)[3], adaptado del de Bolaños et al. (2007), fue propuesto para tal fin y está definido por:

donde, θ es un ángulo cenital, v se refiere a visión y s a solar; Rn representa una reflectancia, R o IRC, normalizada [multiplicada por cos( )] y
)] y  es una variable angular de posición que reduce la complejidad de la geometría sol–sensor al usar simetrías angulares. La ventaja de la relación del modelo (12) es que solo requiere un dato, entonces la constante g puede ser estimada de la reflectancia medida.
es una variable angular de posición que reduce la complejidad de la geometría sol–sensor al usar simetrías angulares. La ventaja de la relación del modelo (12) es que solo requiere un dato, entonces la constante g puede ser estimada de la reflectancia medida.
En la Figura 11 se muestra el ajuste del modelo de la relación (12) a pastizales naturales medidos en campo en Arizona, EE.UU., Mongolia, China y Durango–Chihuahua en México (discutidas en Paz y Bolaños, 2008)[2,3].
Se deduce de la Figura 11 que el modelo propuesto se ajusta bien a las mediciones de campo, con algunos puntos problemáticos asociados a ángulos grandes de visión o solares que son difíciles de diferenciar cuando son debidos a errores de muestreo.
Las relaciones del modelo (12) permiten estandarizar a un ángulo de visión a nadir cualquier medición hecha a otro ángulo, por lo que la discusión de la sección anterior puede ser generalizada a cualquier ángulo de visión. En relación a la estandarización del ángulo cenital solar, para ángulos de visión a nadir, se puede utilizar el modelo de Paz (2006b)[4] para este fin:

donde, Ps es una constante; y n,n significa reflectancias normalizadas a nadir (R e IRC); θsx el ángulo cenital solar mínimo en el día de medición. La relación (13) asegura que R(θs – θsx)n,n = 0 cuando (θs – θsx) = 0. La relación (13) fue analizada usando una base de datos del cultivo soya (Glycine max) (Ranson et al., 1984a y b). Los ajustes experimentales al modelo son bastantes buenos en el caso de IAF=2.9 y suelo desnudo (Figuras 12 y 13).
Con la evidencia experimental se puede concluir que los efectos de la geometría sol–sensor en los IV se pueden estandarizar, de tal forma que los resultados obtenidos para un ángulo de visión a nadir y cualquier ángulo cenital de iluminación puedan ser generalizados a cualquier otra geometría sol–sensor.
Caso general de la aplicación de los índices de vegetación
Para usar los índices de vegetación para densidades del follaje (dejando fija la geometría y propiedades ópticas de las plantas), se diseñó un experimento tipo maqueta en las instalaciones del Colegio de Postgraduados, Campus Montecillo, Estado de México, en septiembre de 2006. Se usaron cinco especies forestales, descritas en el Cuadro 1.
De cada especie forestal se midió su función de distribución de reflectancias bidireccionales (BRDF, por sus siglas en inglés) usando tres configuraciones geométricas (Figura 14).
Para cada especie y configuración geométrica se usaron dos suelos (claro y oscuro) como fondo y se realizaron mediciones a tres o cuatro ángulos cenitales y acimutales de iluminación. Se usó un equipo de BRDF diseñado ex profeso para medir ángulos de visión de 0 a 50°, con incrementos de 10°, tanto en la dirección de iluminación solar como en la contraria, obteniéndose 12 mediciones. Los ángulos de nadir se midieron dos veces: iluminación y sombreado. El equipo de BRDF mantiene constante el área de observación, reduciendo la altura de medición, para el ángulo de visión del radiómetro, en función del ángulo de visión. Se usó un radiómetro hiperespectral con rango de 350 a 2500 nm (FR Jr de ASDMR). Para cada medición se tomó fotografías (Cybershot DSC–V1 de SonyMR) de la cobertura de la vegetación. Con estas fotografías se obtuvo la cobertura aérea de la vegetación COB (%) mediante un proceso de clasificación supervisada. Las reflectancias hiperespectrales se convirtieron a bandas espectrales del sensor TM (Landsat 5), usando las funciones de respuesta espectrales correspondientes, después de eliminar valores con problemas de vapor de agua atmosférico, aunque en el caso de la banda del IRC quedaron algunos ruidos residuales.
Efectos de la geometría sol–sensor y su modelación
En el experimento con sistemas arbolados en condiciones de iluminación natural, las mediciones en la dirección de iluminación solar resultaron muy problemáticas debido a cambios constantes en las condiciones de radiación (componentes directas y difusas). Por lo anterior sólo se presentan los análisis de las mediciones con ángulos de visión en el lado sombreado, donde el efecto de los cambios en la radiación son mínimos.
En la Figura 15a se muestran los resultados de ajustar el modelo de la geometría sol–sensor a todas las bandas (A o azul; V o verde; R o roja; IRC o infrarrojo cercano; IRM1 o infrarrojo medio 1; IRM2 o infrarrojo medio 2) del sensor TM del satélite LANDSAT. En la Figura 15b se muestran los resultados de las estimaciones de la reflectancias normalizadas a nadir (Rn,n) para las bandas del R e IRC.
Estructura de los patrones espectrales de igual vegetación
Con el supuesto de que las propiedades angulares y ópticas de los elementos de la vegetación son similares (todas las densidades de arbolado), a diferencia de los experimentos de maíz y algodón donde hubo cambios en la fase reproductiva, para un mismo sistema arbolado el cambio en la densidad es equivalente a un crecimiento en el tiempo. Así, se pueden generar curvas iso–vegetación en forma artificial y analizar sus patrones en los espacios espectrales.
Considerando que los análisis están orientados a la parte sombreada de la geometría sol–sensor, se puede suponer que los cambios en los ángulos cenitales de iluminación solo provocan cambios en el sombreado de los suelos (cambios mínimos en la vegetación), de tal manera que sus efectos se traducen en desplazamientos sobre la línea de igual vegetación, generando así puntos adicionales para caracterizar las constantes de estas líneas.
En la Figura 16a se muestran las curvas espectrales de igual vegetación (cobertura aérea) para el caso del sistema de Pinus gregii (dos suelos de fondo de la vegetación, cuatro ángulos cenitales solares y tres densidades del follaje). Los supuestos discutidos anteriormente se cumplen razonablemente para todos los casos de sistemas arbolados.
En la Figura 16b se muestran los sistemas arbolados donde había puntos en la parte negativa de a1 para tener una visión más completa de los patrones estructurales. Los resultados muestran que la relación a1 – β es diferente para cada especie (incluyendo las no mostradas en la Figura 16b); aunque hay cierta similitud entre las constantes de esta relación. Dejando fijas las constantes de la línea del suelo, las constantes de la relación entre a1 – β son fundamentalmente función de las propiedades ópticas y geométricas de las hojas.
La cobertura aérea de la vegetación en la etapa vegetativa del crecimiento es independiente de las propiedades ópticas de las hojas y sólo dependiente de la geometría de las plantas y de su arreglo (follaje) en una parcela, por lo que es esperada una relación lineal entre β y COB. En la Figura 17a se muestran estas relaciones para los sistemas arbolados de la Figura 16b, donde el patrón lineal está bien definido (las constantes son dependientes de las constantes de las líneas del suelo y cuando se usa aS = 0 y bS = 1 el origen es diferente de cero – caso actual). Como referencia, en la Figura 17b se muestra la relación entre β y COB para el experimento de algodón (Huete et al., 1985) analizado previamente (constantes medidas de la línea del suelo).
CONCLUSIONES
La modelación y estandarización de la geometría sol–sensor es confiable usando el modelo de Bolaños y Paz, lo que permite el uso robusto de información bidireccional de diferentes satélites en operación (SPOT, TERRA/AQUA, NOAA).
La evidencia experimental asociada a los patrones espectrales de las curvas de vegetación similar a la natural permite concluir que: a) ningún IV modela en forma adecuada las dos fases asociadas a los patrones entre a0 y b0, ya sea que representen una fase exponencial y lineal en la etapa vegetativa o una fase expo–lineal y una reproductiva; b) aun cuando se puede aproximar la estructura de los patrones entre a0 y b0, el parametrizar esta relación conlleva el uso de constantes empíricas que pueden ser diferentes para cada cultivo o tipo de vegetación, lo que hace problemático este enfoque.
El problema asociado a la dificultad del desarrollo de IV generales es la estructura del espacio a0 – b0, y sus transformaciones, aumentando la complejidad de modelación y difícil de realizar. Como consecuencia, es necesario el replanteamiento de los esquemas de generación de índices espectrales de la vegetación más generalizados y no dependiente de constantes empíricas y válidos para algunos cultivos o vegetación natural.
Se puede concluir que el uso de los sensores remotos aún no es confiable y robusto, y constituye, aún una problemática en discusión, independiente de la gran cantidad de enfoques empíricos utilizados en el campo de las aplicaciones.
LITERATURA CITADA
Baret F., and G. Guyot. 1991. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sensing of Environ. 35: 161–173. [ Links ]
Bausch, W.C. 1993. Soil background effects on reflectance–based crop coefficients for corn. Remote Sensing of Environ. 46: 213–222. [ Links ]
Bolaños, M., F. Paz, E. Palacios, E. Mejía, y A. Huete. 2007. Modelación de los efectos de la geometría sol–sensor en la reflectancia de la vegetación. Agrociencia 41: 527–537. [ Links ]
Gao, X., A. R. Huete, W. Ni, and T. Miura. 2000. Optical–biophysical relationships pf vegetation spectra without background contamination. Remote Sensing of Environ. 74: 609–620. [ Links ]
Goudriaan, J., and J. L. Monteith. 1990. A mathematical function for crop growth based on light interception and leaf area expansion. Ann. Bot. 66: 695–701. [ Links ]
Huete, A. R., R. D. Jackson, and D. F. Post. 1985. Spectral response of a plant canopy with different soil backgrounds. Remote Sensing of Environ. 17: 35–53. [ Links ]
Leprieur, D., M. M. Verstraete, and B. Pinty. 1994. Evaluation of the performance of various vegetation indices to retrieve cover from AVHRR data. Remote Sensing Rev. 10: 265–284. [ Links ]
Paz, F., E. Palacios, E. Mejía, M. Martínez, y L. A. Palacios. 2005. Análisis de los espacios espectrales de la reflectividad del follaje de los cultivos. Agrociencia 39: 293–301. [ Links ]
Paz, F., E. Palacios, E. Mejía, M. Martínez, y L. A. Palacios. 2006. Determinación del estado de crecimiento de cultivos usando la transformada de Hough de las reflectividades del follaje. Agrociencia 40: 99–108. [ Links ]
Paz, F., E. Palacios, M. Bolaños, L. A. Palacios, M. Martínez, E. Mejía, y A. Huete. 2007. Diseño de un índice espectral de la vegetación: NDVIcp. Agrociencia 41: 539–554. [ Links ]
Qi J., Chehbouni A., A. R. Huete, Y. H. Kerr, and S. Sorooshian. 1994. A modified soil adjusted vegetation index. Remote Sensing of Environ. 48: 119–126. [ Links ]
Ranson, K. J., L. L. Biehl, and M. E. Bauer. 1984a. Variation in spectral response of soybeans with respect to illumination, view and canopy geometry, LARS Technical Report 073184, Laboratory for Applications of Remote Sensing, Purdue University, West Lafayette, Indiana, USA. 24 p. [ Links ]
Ranson, K. J., L. L. Biehl, and M. E. Bauer. 1984b. Soybean canopy reflectance modeling data sets, LARS Technical Report 071584, Laboratory for Applications of Remote Sensing, Purdue University, West Lafayette, Indiana, USA. 46 p. [ Links ]
Tucker, C.J. 1979. Red and photographic infrared linear combination for monitoring vegetation. Remote Sensing of Environ. 8: 127–150. [ Links ]
1 Paz, F., E. Romero, E. Palacios, M. Bolaños, R. Valdez, y A. Aldrete. 2009. Mitos y falacias de los índices espectrales de la vegetación: marco teórico. Enviado a Ingeniería Hidráulica en México. [ Links ]
2 Paz, F., E. Romero, E. Palacios, M. Bolaños, R. Valdez, y A. Aldrete. 2008a. Mitos y falacias de los índices espectrales de la vegetación: análisis de índices actuales de banda ancha. Enviado a Ingeniería Hidráulica en México. [ Links ]
3 Bolaños, M., y F. Paz. 2007. Modelación general de los efectos de la geometría de iluminación–visión en la reflectancia de pastizales. Enviado a Técnica Pecuaria en México. [ Links ]
4 Paz. F. 2006b. Modelo generalizado de la BRDF: efecto del acimut relativo. Reporte Agosto para AGROASEMEX. 18 p. [ Links ]














