Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.43 no.2 Texcoco feb./mar. 2009
Matemáticas aplicadas, estadística y computación
Comparación de algunas pruebas estadísticas asintóticas de no–inferioridad para dos proporciones independientes
Comparison of some non–inferiority asymptotic statistical tests for two independent proportions
Félix Almendra–Arao1, David Sotres–Ramos2*
1 UPIITA del Instituto Politécnico Nacional. Avenida Instituto Politécnico Nacional 2580. 07340 México, D. F. (falmendra@ipn.mx).
2 Colegio de Postgraduados, Km. 36.5. Carretera México–Texcoco. 56230. Montecillo, México. *Autor responsable: (sotres.davida@kendle.com)
Recibido: Mayo, 2008.
Aprobado: Enero, 2009.
Resumen
En este trabajo se compararon las pruebas asintóticas de no–inferioridad de Blackwelder, Farrington–Manning, Böhning–Viwatwongkasen, Hauck–Anderson; la prueba de razón de verosimilitudes y dos variantes de estas pruebas con base en sus niveles de significancia reales y en sus potencias. La prueba de Farrington–Manning resultó con la mejor aproximación del nivel de significancia real al nivel nominal para tamaños de muestra 30<n<100 y para los tres límites de no–inferioridad más frecuentemente utilizados en la práctica. Además, la potencia de la prueba de Farrington–Manning fue muy similar a las potencias de aquellas pruebas con buena aproximación del nivel de significancia real al nominal.
Palabras clave: No–inferioridad, proporción, prueba asintótica.
Abstract
In this study, the asymptotic tests of non inferiority of Blackwelder, Farrington–Manning, Böhning–Viwatwongkasen and Hauck–Anderson, as well as the likelihood ratio test and two variants of these tests were compared based on their real significance levels and their powers. The Farrington–Manning test turned out to be the one with the best approximation to the real significance level to the nominal level for sample sizes 30<n<100 and for the three most frequently used non–inferiority margins. In addition, the power of the Farrington–Manning test was very similar to the power of those tests with good approximation to the real significance level of the nominal level.
Key words: Non–inferiority, proportion, asymptotic test.
INTRODUCCIÓN
Las pruebas estadísticas asintóticas de no–inferioridad se utilizan muy frecuentemente en ensayos clínicos. Estas pruebas sirven para demostrar que una terapia nueva (con menores efectos secundarios o menor costo) no es sustancialmente inferior en eficacia a la estándar (Chen et al., 2000).
El objetivo de este trabajo fue comparar las pruebas asintóticas para no–inferioridad de Blackwelder, Farrington–Manning, Böhning–Viwatwongkasen, Hauck–Anderson, la prueba de razón de verosimilitudes y dos variantes de estas pruebas con base en sus niveles de significancia reales y en sus potencias.
Se han reportado algunas comparaciones de pruebas para no–inferioridad, pero están basadas en simulaciones o en aproximaciones gruesas de los niveles de significancia exactos y de las potencias (Tu, 1997; Chen et al., 2000; Li y Chuang–Stein, 2006). En la literatura consultada no se encontró análisis comparativo de pruebas de no–inferioridad donde sean calculados los niveles de significancia y de las potencias.
Ésto probablemente se debe al muy extenso tiempo de cómputo requerido para calcular dichos valores. En el presente trabajo se usaron las condiciones de convexidad de Barnard y de simetría en la misma cola (Röhmel, 2005), para calcular los niveles de significancia y las potencias de las pruebas y compararlas para los tamaños de muestra 30<n<100, así como para los tres límites de no–inferioridad más frecuentemente utilizados.
MATERIALES Y MÉTODOS
Pruebas estadísticas consideradas
En este trabajo se utilizó el modelo estándar (Bernoulli) para comparar dos tratamientos con base en una variable dicotómica. Este modelo supone que las observaciones correspondientes al primer tratamiento (el estándar) provienen de una muestra aleatoria {X11X12 ,...X1,n1}de una distribución Bernoulli con probabilidad de éxito p1 y que las observaciones del segundo tratamiento (el nuevo o experimental) provienen de otra muestra aleatoria {X21X22 ,...X2n2} de una distribución Bernoulli con probabilidad de éxito p2; se supone además que estas dos muestras son independientes. La hipótesis de interés (hipótesis de no–inferioridad) que se desea probar es la alternativa (Ha) en el siguiente juego de hipótesis:

donde, d = p1 – p2 y d0 es el límite de no–inferioridad, que es una constante positiva y conocida. En el contexto de ensayos clínicos los valores usuales para d0 son 0.10, 0.15 y 0.20.
Seis de las estadísticas de prueba consideradas son del tipo:

donde,  es el estimador de máxima verosimilitud de pi para
es el estimador de máxima verosimilitud de pi para  es un estimador consistente de la desviación estándar de
es un estimador consistente de la desviación estándar de  ; la séptima estadística es aquélla para la prueba de razón de verosimilitudes:
; la séptima estadística es aquélla para la prueba de razón de verosimilitudes:

La diferencia entre las seis estadísticas del tipo (2) radica en la estimación elegida para la desviación estándar de  . Se consideran seis estimadores:
. Se consideran seis estimadores:

donde, 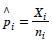 es el estimador de máxima verosimilitud de pi,
es el estimador de máxima verosimilitud de pi,  es el estimador de máxima verosimilitud restringida bajo la hipótesis nula de pi (Miettinen y Nurminen, 1985; Farrington y Manning, 1990); y
es el estimador de máxima verosimilitud restringida bajo la hipótesis nula de pi (Miettinen y Nurminen, 1985; Farrington y Manning, 1990); y 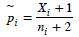 (Böhning y Viwatwongkasen, 2005).
(Böhning y Viwatwongkasen, 2005).
Cuando  la estadística T en (2) tiene distribución asintótica normal estándar para cualquier estimador consistente
la estadística T en (2) tiene distribución asintótica normal estándar para cualquier estimador consistente  de la desviación estándar de
de la desviación estándar de  ; para la estadística λ, la distribución asintótica de
; para la estadística λ, la distribución asintótica de  donde
donde  denota la función de distribución acumulada de una variable aleatoria ji–cuadrada con un grado de libertad.
denota la función de distribución acumulada de una variable aleatoria ji–cuadrada con un grado de libertad.
Las pruebas asintóticas para las estadísticas del tipo (2) para un nivel de significancia nominal a tienen región de rechazo de la forma 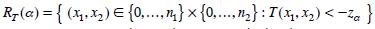 donde za es el percentil superior α de la distribución normal estándar, es decir, Φ(za) = 1 – α , donde Φ es la función de distribución acumulativa de una variable aleatoria normal estándar.
donde za es el percentil superior α de la distribución normal estándar, es decir, Φ(za) = 1 – α , donde Φ es la función de distribución acumulativa de una variable aleatoria normal estándar.
La región de rechazo para la prueba asintótica correspondiente a la estadística (3) es:

donde  es el percentil superior 1 – 2α de la distribución ji–cuadrada con un grado de libertad, i.e
es el percentil superior 1 – 2α de la distribución ji–cuadrada con un grado de libertad, i.e 
Las correcciones por continuidad analizadas son: 1


donde C0, C2 y C3 son consideradas por Hauck y Anderson (1986) para el caso de las estadísticas T1 y T4.
El análisis se realizó para diseños balanceados, es decir, para n1 =n2 = n. En esta situación es claro que Ci < Ci+1 para i = 0,1,2,3,4.
Así, las estadísticas de prueba consideradas son:

para i = 0,1,2,3,4,5,6 y j = 0,1,2,3,4,5 y
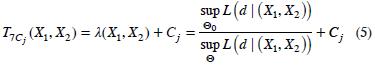
para j = 0,1,2,3,4,5.
Las pruebas TiCj fueron propuestas en los siguientes artículos: T1C0 en Blackwelder (1982), T2C0 en Farrington y Manning (1990), T3C0 en Böhning y Viwatwongkasen (2005), T4C0 en Hauck y Anderson (1986). T5C0 se obtiene de T2C0 al reemplazar n1 por n1 —1 y n2 por n2—1 en el denominador del estimador de la desviación estándar, mientras que T6C0 se obtiene de T3C0 al reemplazar n1 por n1 — 1 y n2 por n2—2 en el denominador del estimador de la desviación estándar. Finalmente, T7C0 es la conocida estadística de razón de verosimilitudes (Casella y Berger, 2002).
El nivel de significancia nominal usado en todo este trabajo fue p = 0.05. Las pruebas estadísticas serán simbolizadas de la misma forma que sus correspondientes estadísticas de prueba.
Estrategia para el cálculo del nivel de significancia
De acuerdo con el modelo Bernoulli usado en este trabajo, el espacio muestral es  , el
, el
espacio paramétrico es 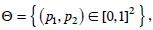 , y dado que Xi tiene distribución binomial con parámetros (ni,pi) para i = 1,2, la función de verosimilitud conjunta es:
, y dado que Xi tiene distribución binomial con parámetros (ni,pi) para i = 1,2, la función de verosimilitud conjunta es:
 y la función de potencia es
y la función de potencia es  además, el espacio nulo es
además, el espacio nulo es  y el nivel de significancia está dado por
y el nivel de significancia está dado por 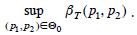
Chan (1998) calculó el nivel de significancia para la prueba de Farrington–Manning (T2C0) tomando el supremo no en todo el espacio nulo (Θ0), sino calculando el máximo únicamente en  , el cual es sólo una parte de la frontera del espacio nulo. Computacionalmente ésto representa una inmensa ventaja, pues el tiempo de cómputo se reduce aproximadamente a 0.22% del original. Sin embargo, el autor mencionado no justificó formalmente la validez de este argumento. Röhmel (2005) presentó una prueba formal que justifica el procedimiento usado por Chan (1998). En este trabajo se siguió la misma estrategia de Chan (1998). Por tanto, en lo que resta de esta sección, se verifica la validez de la llamada condición de convexidad de Barnard y de la condición de simetría en la misma cola (ver definiciones abajo) para todas las pruebas asintóticas consideradas.
, el cual es sólo una parte de la frontera del espacio nulo. Computacionalmente ésto representa una inmensa ventaja, pues el tiempo de cómputo se reduce aproximadamente a 0.22% del original. Sin embargo, el autor mencionado no justificó formalmente la validez de este argumento. Röhmel (2005) presentó una prueba formal que justifica el procedimiento usado por Chan (1998). En este trabajo se siguió la misma estrategia de Chan (1998). Por tanto, en lo que resta de esta sección, se verifica la validez de la llamada condición de convexidad de Barnard y de la condición de simetría en la misma cola (ver definiciones abajo) para todas las pruebas asintóticas consideradas.
Definición. Una prueba estadística para el problema en (1) con región de rechazo RT cumple la condición de convexidad de Barnard (C) si satisface las dos propiedades siguientes:

Röhmel y Mansmann (1999) demostraron el resultado ya mencionado para pruebas exactas. A continuación se demuestra el resultado correspondiente para pruebas asintóticas.
Proposición 1. Sea T una estadística con distribución asintótica AT para el problema de prueba de hipótesis:
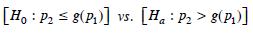
con región crítica dada por 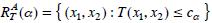 y sean
y sean  ,
,  cuando a>0 con g creciente y no intersecta p1 = p2 si la región crítica es no vacía y satisface la condición de convexidad de Barnard, entonces el supremo
cuando a>0 con g creciente y no intersecta p1 = p2 si la región crítica es no vacía y satisface la condición de convexidad de Barnard, entonces el supremo 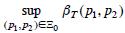 es un máximo y se alcanza en un punto frontera sobre la curva p2 = g(p1).
es un máximo y se alcanza en un punto frontera sobre la curva p2 = g(p1).
Demostración. Puesto que por hipótesis 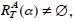 , entonces existe
, entonces existe  tal que max , es decir:
tal que max , es decir:

de donde, por el teorema demostrado para pruebas exactas por Röhmel y Mansmann (1999) se sigue el resultado.
En este trabajo se usa la función g(p1) = p1—d0.
Nótese que, por definición, si  y se cumple la condición (C), entonces necesariamente
y se cumple la condición (C), entonces necesariamente  además,
además,  y por tanto no T1 (0, n2) y T2 (0, n2) no están definidas, entonces
y por tanto no T1 (0, n2) y T2 (0, n2) no están definidas, entonces  y en consecuencia RT1 y RT4 no cumplen (C). Una forma de solventar esta dificultad es redefiniendo la estimación de la desviación estándar en los puntos donde se anula.
y en consecuencia RT1 y RT4 no cumplen (C). Una forma de solventar esta dificultad es redefiniendo la estimación de la desviación estándar en los puntos donde se anula.
Observación 1. Sea  entonces
entonces 
Como  para
para  se puede redefinir de la siguiente forma:
se puede redefinir de la siguiente forma:

de manera similar se redefine .
.
La demostración del siguiente resultado se establece en Almendra (2007).
Proposición 2. Sea T una estadística con distribución asintótica AT. Sean las regiones críticas para las pruebas exacta y asintótica RT y RTA . Si RT cumple la condición de convexidad de Barnard, entonces RTA también la cumple.
Como se mencionó, Röhmel (2005) demostró que la versión exacta de la región crítica para T2C0 cumple la condición de convexidad de Barnard. Entonces, por la proposición anterior, la versión asintótica también cumple la condición de convexidad de Barnard.
Definición. Si n1 = n2 = n, una región de rechazo R cumple la condición de simetría en la misma cola si 
Proposición 3. Si n1 = n2 = n entonces RTiCJ cumple la condición de simetría en la misma cola para i = 1,3,4,6 y j = 0,1,2,3,4,5.
Demostración. Almendra (2007).
Dado el problema de prueba de hipótesis (1) si se considera una estadística de prueba T(X1X2,) con región de rechazo
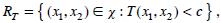 se define el espacio muestral lícito como
se define el espacio muestral lícito como  la región crítica restringida al espacio muestral lícito es
la región crítica restringida al espacio muestral lícito es 
La importancia del concepto anterior es reiterada por Martin y Herranz (2002, 2004a, 2004b) quienes enfatizan la necesidad de tal concepto, ya que de no restringirse el espacio muestral al espacio muestral lícito, podrían obtenerse inferencias inválidas en algunos casos. La razón de esta restricción es que de otra forma la prueba podría no tener significancia: por ejemplo, si  entonces es inferencialmente ilógico concluir que p1 – p2 < d0.
entonces es inferencialmente ilógico concluir que p1 – p2 < d0.
Proposición 4. Para estadísticas tipo (2), el espacio muestral coincide con el espacio muestral lícito, es decir, si T es una estadística de la forma  para una prueba con región de rechazo
para una prueba con región de rechazo  entonces RT = R'T .
entonces RT = R'T .
Para una demostración de la proposición anterior, ver Almendra (2007).
No obstante, para la estadística de razón de verosimilitudes los espacios muestral y muestral lícito no coinciden en general. Por esta razón el cálculo de los niveles de significancia y las potencias para T7 se realizó con base en el espacio muestral lícito.
Proposición 5. Sean n1 = n2 = n y R(α) una región crítica para el problema de prueba de hipótesis [H0 : d > d0] vs. [Ha : d < d0], si R(α) cumple la condición de convexidad de Barnard y la condición de simetría en la misma cola, entonces el nivel de significancia está dado por:

Demostración. Almendra (2007).
Observación 2. Todas las pruebas asintóticas  , i = 1,2,...,7: j = 0,1,.,5, con estadísticas de prueba definidas en (4) y (5) satisfacen la condición de convexidad de Barnard y la condición de simetría en la misma cola.
, i = 1,2,...,7: j = 0,1,.,5, con estadísticas de prueba definidas en (4) y (5) satisfacen la condición de convexidad de Barnard y la condición de simetría en la misma cola.
La condición de convexidad de Barnard para T2C0 se probó analíticamente en la proposición 2. La condición de simetría en la misma cola para TiCj para i = 1,3,4,6; j = 0,1,2,3,4,5; se probó analíticamente en la proposición 3. Para las demás pruebas, la verificación se efectuó numéricamente mediante programas de cómputo elaborados en S–PLUS®.
Con base en la proposición 5 y la observación 2, se usó la fórmula en (6) para calcular una aproximación del nivel de significancia exacto de todas las pruebas consideradas. La aproximación del nivel de significancia exacta α*, en la fórmula (6), se hizo reemplazando el intervalo continuo [d0(1 + d0)/ 2] por el conjunto discreto de puntos: {d0+ (.001)i = 0,1,2,..., 500(1 – d0)}, y al valor obtenido de esta aproximación de a* usando tal conjunto discreto se le ha llamado nivel de significancia real de la prueba, el cual será denotado por aR .
Es importante subrayar que la fórmula en (6), para el cálculo del nivel de significancia (α*) de cualquiera de las pruebas consideradas aquí, es una fórmula exacta. Así que la única aproximación que se hace para calcular el nivel de significancia real (aR) es al reemplazar al intervalo continuo [d0(1 + d0)/ 2] por el conjunto de puntos {d0+ (.001)i = 0,1,2,..., 500(1 – d0)}. El grado de error en que incurre esta aproximación se estimó de la siguiente manera: para todas las pruebas consideradas y para cada una de las doce combinaciones de parámetros (n1 = n2 = 30, 50 y 100), (a=0.05 y 0.10), (d0 = 0.10 y 0.15) se analizó el error incurrido al estimar a* por aR y en todos los casos se verificó que en los valores adyacentes al máximo estimado (aR) la variación en la función de potencia fue menor o igual a 0.00001, es decir, nuestra estimación del error  es que es menor o igual a 0.00001. Por ejemplo, para n1 = n2 = 50, a = 0.05 y d0 = 0.10 los valores adyacentes al máximo estimado (aR) de la función de potencia son:
es que es menor o igual a 0.00001. Por ejemplo, para n1 = n2 = 50, a = 0.05 y d0 = 0.10 los valores adyacentes al máximo estimado (aR) de la función de potencia son:

en este caso βT (0.550,.0450) – βT (0.549,.449) = 0.0000003, el cual es menor a 0.00001. Con base en este análisis es razonable concluir que el error incurrido al estimar α* por αR es aceptable desde el punto de vista práctico, ya que el nivel de significancia real (aR) difiere del nivel de sinificancia exacto (α*) cuando mucho en la quinta cifra decimal.
RESULTADOS Y DISCUSIÓN
Comparación de las pruebas con base en sus niveles de significancia reales
Para comparar las 42 pruebas estadísticas consideradas en este trabajo (TiC con 1 < i <7 y 0< j <5), parece razonable considerar que el nivel de significancia real (αR) de una prueba tiene un buen comportamiento cuando 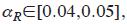 es decir cuando αR es menor o igual al nivel nominal (α=0.05), y cuando αR es una buena aproximación al nivel nominal
es decir cuando αR es menor o igual al nivel nominal (α=0.05), y cuando αR es una buena aproximación al nivel nominal  Con este propósito, para cada prueba
Con este propósito, para cada prueba  se calculó el porcentaje de αRs que pertenece al intervalo [0.04,0.05] con base en los 71 tamaños de muestra n en el rango 30< n <100, y para cada uno de los valores de d0 = 0.10, 0.15 y 0.20. En el Cuadro 1 se reportan estos resultados, pero únicamente para las pruebas que obtuvieron porcentajes mayores o iguales a 90%. T2C2 y T5C2 resultaron las pruebas con mejor comportamiento del nivel de significancia real (αR), para los tres valores considerados: d0 = 0.10, 0.15 y 0.20.
se calculó el porcentaje de αRs que pertenece al intervalo [0.04,0.05] con base en los 71 tamaños de muestra n en el rango 30< n <100, y para cada uno de los valores de d0 = 0.10, 0.15 y 0.20. En el Cuadro 1 se reportan estos resultados, pero únicamente para las pruebas que obtuvieron porcentajes mayores o iguales a 90%. T2C2 y T5C2 resultaron las pruebas con mejor comportamiento del nivel de significancia real (αR), para los tres valores considerados: d0 = 0.10, 0.15 y 0.20.

Comparación de las pruebas con base en sus potencias reales
Para cada valor de d0 (0.10,0.15,0.20) se compararon las potencias de las pruebas T2C2 y T5C2 para aquellos tamaños de muestra n, 30< n <100, donde la máxima diferencia entre los niveles de significancia reales resultó menor o igual que 0.0001 y donde al menos una de las potencias a comparar fue mayor o igual que 0.7. La comparación de las potencias se realizó en los puntos (p1, p2) con con p1 = 0(.5)1 y 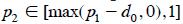 iniciando en max(p1– d0,0) y tomando incrementos de 0.05, es decir, con p2 = para aquellos i tales que
iniciando en max(p1– d0,0) y tomando incrementos de 0.05, es decir, con p2 = para aquellos i tales que 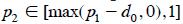 .
.
En resumen las potencias de T2C2 y T5C2 se compararon para un total de (40, 26, y 28) tamaños de muestra en los casos (d0 = 0.10, 0.15, y 0.20) respectivamente. Para todos estos tamaños de muestra en donde se realizó la comparación, las potencias de las pruebas T2C2 y T5C2 resultaron iguales en el 100% de los casos. Estos resultados dan como ganadoras a las pruebas T2C2 y T5C2 con ventaja de T2C2 para d0=0.15 y 0.20. Para el caso 2C25C2d0=0.10, T25C supera a T2C2 , aunque la diferencia es sólo 1.41%. Para una recomendación práctica se preferirá a la prueba T2C en todos los casos (d0 = 0.10, 0.15, y 0.20).
CONCLUSIONES
Para los tamaños de muestra 30< n <100, considerando un nivel de significancia nominal a=0.05 y para los tres límites de no–inferioridad analizados <100, considerando un nivel de significancia nominal α=0.05 y para los tres límites de no–inferioridad analizados (d0 = 0.10, 0.15, y 0.20), se recomienda usar T2C2; es decir, la prueba de Farrington–Manning con el factor de corrección C2.
AGRADECIMIENTOS
El primer autor desea agradecer a la UPIITA del Instituto Politécnico Nacional su apoyo al otorgarle licencia para la realización del presente trabajo.
LITERATURA CITADA
Almendra A., F. 2007. Comparación de algunas pruebas estadísticas asintóticas de no–inferioridad para contrastar dos proporciones independientes. Tesis Doctoral, Especialidad en Estadística, ISEI, Colegio de Postgraduados, México. 87 p. [ Links ]
Blackwelder, W. 1982. "Proving the null hypothesis" in clinical trials. Controlled Clinical Trials 3:345–353. [ Links ]
Böhning, D., and C. Viwatwongkasen. 2005. Revisiting proportion estimators. Statistical Methods in Medical Res. 14: 1–23. [ Links ]
Casella, G., and L. Berger. 2002. Statistical Inference. Second Edition. Duxbury, Thompson Learning. USA. 660 p. [ Links ]
Chan, I. S. F. 1998. Exact tests of equivalence and efficacy with a non zero lower bound for comparative studies. Statistics in Medicine 17: 1403–1413. [ Links ]
Chen, J., Y. Tsong, and S. Kang. 2000. Tests for equivalence or noninferiority between two proportions. Drug Information J. 34: 569–578. [ Links ]
Farrington, C., and G. Manning. 1990. Test statistics and sample size formulae for comparative binomial trials with null hypothesis of non–zero risk difference or non–unity relative risk. Statistics in Medicine 9: 1447–1454. [ Links ]
Hauck, W., and S. Anderson. 1986. A comparison of large–sample confidence interval methods for the difference of two binomial probabilities. The Am. Statistician 40: 318–322. [ Links ]
Li, Z., and C. Chuang–Stein. 2006. A note on comparing two binomial proportions in confirmatory noninferiority trials. Drug Information J. 40: 203–208. [ Links ]
Martin A., A., and I. Herranz T. 2002. Equivalence testing for binomial random variables: which test to use?. The Am. Statistician 56(3): 253–254, Letter to the editor. [ Links ]
Martin A., A., and I. Herranz T. 2004a. Asymptotical test on the equivalence, substantial difference and non–inferiority problems with two proportions. Biometrical J. 46: 305–319. [ Links ]
Martin A., A., and I. Herranz T. 2004b. Exact unconditional non–classics tests on the difference of two proportions. Computational Statistics & Data Analysis 45: 373–388. [ Links ]
Miettinen, O., and M. Nurminen. 1985. Comparative analysis of two rates. Statistics in Medicine 4: 213–226. [ Links ]
Röhmel, J. 2005. Problems with existing procedures to calculate exact unconditional p–values for noninferiority/superiority and confidence intervals for two binomials and how to resolve them. Biometrical J. 47: 37–47. [ Links ]
Röhmel, J., and U. Mansmann. 1999. Unconditional nonasymptotic one sided tests for independent binomial proportions when the interest lies in showing noninferiority and or superiority. Biometrical J. 2: 149–170. [ Links ]
Tu, D. 1997. A comparative study of some statistical procedures in establishing therapeutic equivalence of nonsystemic drugs with binary endpoints. Drug Information J. 31: 1291–1300. [ Links ]














