Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.42 no.5 Texcoco jul./ago. 2008
Matemáticas aplicadas, estadística y computación
Procedimiento para revisión (sin hidrometría) de la seguridad hidrológica de presas pequeñas para riego
Procedure for hydrological safety assessment of small irrigation dams (without hydrometry)
Daniel F. Campos–Aranda*
Universidad Autónoma de San Luis Potosí. Genaro Codina # 240. 78280. San Luis Potosí, San Luis Potosí *Autor responsable: (campos_aranda@hotmail.com)
Recibido: Abril, 2007.
Aprobado: Mayo, 2008.
Resumen
En este trabajo se define el concepto de seguridad hidrológica de las presas, se citan varias definiciones sobre cuencas y presas pequeñas como marco de referencia del objetivo del trabajo. Se describe cómo se procesó la información hidrométrica de gastos y volúmenes anuales disponible en 16 presas importantes de México. Con base en los resultados de tales análisis se formula un procedimiento de seis pasos para construir hidrogramas tipo Gamma esbeltos y aplanados en cuencas pequeñas sin datos hidrométricos, los cuales permiten la revisión de la seguridad hidrológica de una presa pequeña. Se expone una aplicación numérica de contraste y dos conclusiones indican que el procedimiento es simple, fácil de aplicar y sus resultados son de vital importancia, sobre todo en presas bajo riesgo hidrológico en las cuales hay que establecer soluciones cuantitativas para sobreelevar la cortina o ampliar la capacidad del vertedor de excedencias. Un procedimiento como el desarrollado es importante ya que existen miles de presas pequeñas para riego en México, que no disponen de la información hidrométrica citada y que, sin embargo, requieren de manera urgente ser revisadas hidrológicamente.
Palabras clave: Cuencas pequeñas, hidrogramas Gamma, presas pequeñas, seguridad hidrológica, tiempo al pico.
Abstract
In this paper is defined the concept of hydrologic dam safety, and several definitions of watersheds and small dams are cited as the framework for the objective of this study. A description is given of how the available hydrometric information on annual flows and volumes of 16 important Mexican dams was processed. Based on the results of these analyses, a six–step procedure was formulated to construct slender and flat Gamma–type hydrographs for small watersheds for which there is no hydrometric data. With these hydrographs, hydrologic safety of a small dam can be assessed. A numerical contrast application is presented and two conclusions indicate that the procedure is simple and easily applied, and that the results are of vital importance, especially for dams with hydrologic risk for which quantitative solutions are necessary when the dam is to be raised or the capacity of the spillways is to be enlarged. A procedure such as this is important since there are thousands of small irrigation dams in México for which this hydrometric information is not available and which urgently require hydrological evaluation.
Key words: Small watersheds, Gamma hydrographs, small dams, hydrological safety, peak time.
INTRODUCCIÓN
El diseño y la revisión por seguridad hidrológica de una presa o almacenamiento implican la determinación de la elevación máxima de la superficie libre del agua en el embalse, como resultado del paso de la llamada avenida de diseño, la cual es evacuada por el vertedor y además controlada por éste cuando tiene compuertas. Esta elevación, conocida como NAME (nivel de aguas máximas extraordinarias), permite definir el nivel mínimo de la corona de la cortina de la presa al sumarle el Bordo Libre, que es la altura de cortina que absorbe el oleaje que produce el viento, para que el agua no la desborde y cause daños originando un riesgo de falla. Una presa será segura hidrológicamente si durante su proceso de revisión la nueva avenida de diseño define un NAME inferior al del proyecto, o igual al que tiene actualmente; en caso contrario es insegura.
La cuenca topográfica es la totalidad del área drenada por una corriente o sistema interconectado de cauces, tales que todo el escurrimiento originado en el área es descargado a través de una salida única. Una división relativamente reciente de las cuencas topográficas las clasifica en rurales y urbanas; las segundas presentan áreas importantes o su totalidad con urbanización y por ello su respuesta hidrológica es más rápida y de mayor intensidad, pues la infiltración se reduce y la precipitación en exceso se incrementa.
Otra clasificación (Témez, 1978) distingue entre cuencas pequeñas y grandes según su comportamiento hidrológico, y aunque esta distinción está estrechamente relacionada al tamaño de la cuenca, también influyen las características de las tormentas y sus condiciones físicas. Una cuenca es pequeña cuando la cantidad y distribución del escurrimiento son influenciadas principalmente por las condiciones físicas del suelo y su cobertura vegetal; en una cuenca grande el efecto del almacenamiento que proporciona la red de cauces y los acuíferos es muy pronunciado. Para fines de este trabajo se entenderá por presa pequeña aquélla que tiene una cuenca rural pequeña.
La base de datos de la Comisión Nacional del Agua registra 4800 presas construidas en México, con alturas de cortina que varían de 3 a 260 metros y capacidades que van desde menos de 0.50 Mm3 (millón de m3) hasta más de 18 000 Mm3 (Oliva, 1999). La mayoría de estas presas aprovechan para riego los escurrimientos de cuencas rurales pequeñas las cuales no cuentan con datos de aforo, o bien en dichas presas no hay un registro de su operación. En ambos casos no será factible contar con registros de gastos máximos y mucho menos del correspondiente volumen de cada avenida anual. Sin embargo, muchas de esas presas pequeñas, por su ubicación, pueden ser consideradas peligrosas; otras quizás han sufrido modificaciones y requieren una revisión de su seguridad hidrológica
El objetivo de este trabajo es exponer en detalle el procesamiento seguido a la información disponible sobre gastos y volúmenes máximos anuales, para formular un procedimiento que permite revisar la seguridad hidrológica de una presa pequeña, a través del tránsito de hidrogramas de diseño tipo función de densidad de probabilidad Pearson tipo III, los cuales se pueden construir en cuencas sin aforos, con base exclusivamente en su estimación del tiempo al pico y conociendo el gasto máximo de diseño, o bien con una estimación del volumen máximo de la avenida.
MATERIALES Y MÉTODOS
Información hidrométrica utilizada
Corresponde a la disponible sobre gastos máximos anuales y sus volúmenes en 16 presas importantes en México (Aldama et al., 2006). Las características generales de esta información están en el Cuadro 1, cuyo orden de presentación corresponde a la de la referencia de que procede. El total de pares de datos de gasto–volumen procesados fue 625. En el Cuadro 2 se presentan los gastos pico (m3 s–1) y sus volúmenes bajo el hidrograma en millones de m3 (Mm3), para las presas Madín y La Angostura, las cuales definen extremos del tiempo al pico (Cuadro 3).
Cálculo del tiempo al pico representativo
Un hidrograma de tormenta aislada es una gráfica de la respuesta de una cuenca a un aguacero; en las ordenadas se representa al gasto y en las abscisas al tiempo. El hidrograma tiene una rama ascendente que termina en el gasto máximo o pico (Qp, m3 s–1), en una duración llamada tiempo al pico (Tp, s) y una rama descendente con una duración llamada recesión (Tr). El área bajo el hidrograma es el volumen (V, m3) de la avenida. Primero se determinó el Tp de cada par de datos de gasto–volumen, considerando el modelo de hidrograma triangular propuesto por el U. S. Soil Conservation Service (Snider, 1972), cuyo tiempo de recesión es 1.667 veces el Tp; por tanto:

A cada serie formada por los Tp calculados (ecuación 1), tantos como número de pares de gasto–volumen se tiene en cada presa (Cuadro 1), se les ajustó la distribución Pearson tipo III de dos parámetros, también conocida como modelo Gamma (Campos, 2005), para obtener el valor con probabilidad de excedencia de 75%, la mediana poblacional [P(X x) > = 50%] y la moda. Los resultados se presentan en el Cuadro 3, junto con otras estadísticas muestrales.
Hidrogramas Gamma y estimación de sus parámetros
Multiplicando por V la función de densidad de probabilidad de la distribución Pearson tipo III, se puede representar un hidrograma de tormenta aislada, cuya expresión es (Croley, 1980a, 1980b):
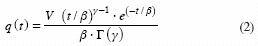
donde q(t) = gasto (m3 s–1) en cualquier tiempo t en segundos; V = volumen (m ), γ = parámetro de forma y β el de escala, ambos positivos, el primero adimensional y el segundo con unidades de tiempo (s); Γ(•) = función Gamma con las propiedades siguientes (Davis, 1972; Campos, 2005):

La derivada de la ecuación 2 respecto del tiempo, igualada a cero y despejando el valor de t, conduce a:
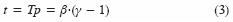
fórmula que corresponde a la moda según esta distribución. La adopción del hidrograma Gamma para representar a las crecientes de diseño es arbitraria y conveniente, pero igual lo es cualquier otra parametrización desarrollada y utilizada; por ejemplo, las propuestas por Aldama y Ramírez (1998). Combinando la ecuación 3 y la 2 evaluada en (Qp,Tp) se obtiene:
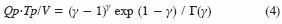
expresión que se utiliza como base de un proceso iterativo de solución para estimar γ y luego β con la ecuación 3 (Croley, 1980a, 1980b):
cuando Qp–Tp/V> 0.277
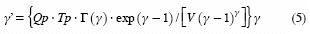
cuando Qp–Tp/V<0.277
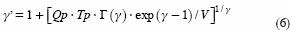
γ' es una estimación más aproximada del parámetro de forma, de manera que el proceso terminará cuando:
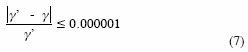
El valor 0.277 fue seleccionado por Croley (1980 a,b) por ensayo y error al utilizar la tolerancia indicada (10–6) y un valor inicial de 2 para y. En estos cálculos, la función gamma Γ(γ) se estima con la expresión:
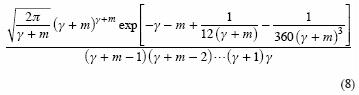
La aproximación a la ecuación 8 aumenta con el valor de m, un valor de m = 5 fue utilizado por Croley (1980b) y conduce a una exactitud de 6 a 7 dígitos significativos. En Davis (1972) se pueden consultar otros algoritmos de estimación más simples.
Relaciones γ—β
Para obtener las parejas anuales de parámetros de forma y escala (γ, β) que definen a los hidrogramas Gamma que representan a cada gasto pico anual y su correspondiente volumen máximo, se procesaron con el algoritmo de Croley (ecuaciones 4 a 8), las series de datos de gasto–volumen de cada presa, utilizando el valor redondeado de la moda del Tp obtenido con la ecuación 1 y mostrado en el Cuadro 3. Por ejemplo, para las series de datos expuestas en el Cuadro 2, los resultados obtenidos se muestran en este mismo, así como los valores adoptados para el Tp, (1.8 y 170 h). En el Cuadro 4 se presentan los valores mínimo y máximo de los parámetros de forma y escala encontrados en cada una de las 16 series de datos de gasto–volumen de cada presa.
Al dibujar en un papel logarítmico los resultados del Cuadro 2 llevando a las ordenadas los valores del parámetro de forma y a las abscisas las magnitudes del parámetro de escala, se definen las relaciones extremas que se presentan en la Figura 1. En ella también se han dibujado otras ocho series de resultados. El tramo de línea punteada corresponde a la presa Adolfo López Mateos (El Infiernillo), la cual se traslapa con los resultados de la presa La Boquilla, pues ambas tienen un tiempo al pico de 58 h.
La Figura 1 verifica la ecuación 3, pero además permite establecer dos regiones de comportamiento diferente de cada relación γ—β: la primera para valores grandes de 7 y menores de γ, se obtiene cuando los datos presentan gasto pico grande y volumen reducido, es el tramo recto de tal relación; la segunda ocurre en el tramo curvo y corresponde a valores pequeños del parámetro 7 y mayores de β, originados por hidrogramas de gasto pico reducido y gran volumen. Es decir que los hidrogramas esbeltos conducen a valores grandes del parámetro de forma (γ > 10.0) y los hidrogramas de base amplia a magnitudes reducidas (γ <1.6), según se muestra en el Cuadro 4.
El procedimiento que se propone se basa en estas dos propiedades observadas en los hidrogramas reales, por ello genera un hidrograma esbelto y uno aplanado. Los resultados del Cuadro 4 indican, para las presas con menor área de cuenca (Madín, Eustaquio Buelna y Abelardo L. Rodríguez), que los parámetros de forma (γ) mínimo–máximo fueron de 1.56–16.20, 1.20–20.94 y 1.53–13.79. Con base en tales magnitudes se consideró conveniente adoptar como valores de y para el diseño hidrológico inicial 1.40 y 14.0.
Procedimiento propuesto
Se acepta como límite arbitrario para las cuencas pequeñas 1300 km2 , es decir, las 500 mi2 en las que según Morris (1982), es muy probable que la lluvia originada por un fenómeno no ciclónico iguale la magnitud de las crecientes derivadas de las precipitaciones ciclónicas. Esto implica que en las cuencas pequeñas es aceptable esperar que sean abarcadas en su totalidad por los eventos extraordinarios que en ellas ocurran, lo cual conduce a hidrogramas que siempre alcanzan el tiempo al pico, y por ello el procedimiento propuesto construye este tipo de hidrogramas de diseño. El proceso tiene seis pasos:
1) Para la presa pequeña bajo análisis se define su cuenca topográfica y su colector principal, evaluando su área y la longitud y pendiente promedio. Con base en las magnitudes anteriores se calcula el tiempo de concentración (Tc) de la cuenca; por ejemplo, a través de fórmulas empíricas (Témez, 1978; Campos, 2007). El Tc se define como el tiempo que tarda el escurrimiento de la tormenta en viajar desde el punto hidráulicamente más distante hasta la salida de la cuenca. Se acepta que el Tc es una aproximación del tiempo al pico (Tp) de los hidrogramas de diseño.
2) A partir de las características físicas de la presa estudiada se establece el periodo de retorno de diseño, según la Norma Hidrológica de 1996 (GASIR; 1996), la cual se reproduce en el Cuadro 5.
3) Con base en métodos regionales de estimación de crecientes (Escalante y Reyes, 2002; Campos, 2006), se calcula el gasto máximo asociado al periodo de retorno de diseño. Únicamente en estudios de gran visión, o para cálculos provisionales, se pueden utilizar las envolventes regionales (Ramírez et al., 2005).
4) Se define un hidrograma esbelto, para un valor del parámetro de forma (γ) de 14, calculando el correspondiente valor del parámetro de escala (β) con la ecuación 3, al utilizar el Tp en segundos, calculado en el paso 1. Con base en los valores de Qp y Tp y la pareja de valores de γ y β se calcula el volumen máximo (V) respectivo del hidrograma usando de la ecuación 2 modificada, ésta es:
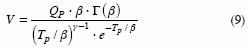
la función Gamma de β se estima con la fórmula 8. Por último, se calcula y dibuja el hidrograma respectivo con la ecuación 2.
5) Adoptando un valor del parámetro γ de 1.4 se obtiene, con la ecuación 3, la magnitud correspondiente del parámetro de escala β, utilizando el Tp en segundos. Con base en el volumen máximo (Vm) estimado según procedimiento siguiente, el tiempo al pico y la pareja de γ y β, se obtiene el gasto pico respectivo con la ecuación 9 modificada. Con la ecuación 2 se calcula y dibuja el hidrograma de duración amplia.
Estimación del Vm: para el periodo de retorno de diseño (paso 2), se calcula para la cuenca estudiada su precipitación máxima diaria, con base en las estaciones pluviométricas disponibles. El cálculo anterior se corrige por intervalo fijo y único de observación (Weiss, 1964), multiplicándola por 1.13 para transformarla a 24 h de duración. Con base en la ecuación de la envolvente mundial de lluvias máximas para diferentes duraciones (WMO, 1973; Smith, 1993), se distribuye en el tiempo el valor estimado para 24 h. Por ejemplo, si la precipitación máxima de diseño en 24 h se calculó en los 600 mm y el tiempo al pico es 2.5 h, la lluvia de diseño (Pd) asociada a tal duración de acuerdo a la ecuación de la envolvente mundial será:

con P en mm y D en horas, entonces:
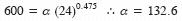
finalmente
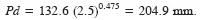
Al multiplicar Pd por el área de cuenca se obtiene el volumen máximo (Vm) buscado para el hidrograma de diseño aplanado. Cuando no sea posible calcular el valor Vm, por ausencia de estaciones pluviométricas dentro o en las cercanías de la cuenca de la presa pequeña analizada, se puede asignar un gasto pico del 10 a 20% del estimado en el paso 3, y entonces calcular el Vm con los valores de γ, β y Tp citados en el paso 5, usando la ecuación 9.
6) Se transitan en el embalse los dos hidrogramas calculados, para obtener el nivel máximo definido por alguno de ellos o NAME. Se calcula el bordo libre (Springall, 1970) y se suma al NAME, para establecer la altura mínima de la corona de la cortina.
RESULTADOS Y DISCUSIÓN
Extrapolaciones al procedimiento propuesto
En cuencas superiores a 1300 km2, que no tienen información hidrométrica de gasto y volúmenes máximos anuales, o bien para buscar condiciones más apegadas a la realidad según información de campo disponible sobre la ocurrencia de los hidrogramas de las crecientes, se puede emplear cualquiera o una combinación de las siguientes tres extrapolaciones:
1) utilizar valores del parámetro de forma (y) más extremos, por ejemplo, 16, 18, 20 y hasta 22 en la definición del hidrograma esbelto, paso 4 del procedimiento sugerido en cuencas pequeñas. Tales valores corresponden a los máximos calculados (Cuadro 4).
2) emplear magnitudes del parámetro de forma (γ) de 1.3 y 1.2 en la construcción del hidrograma aplanado, paso 5 del procedimiento establecido para cuencas pequeñas. Esos valores corresponden a los mínimos calculados (Cuadro 4).
3) si los valores del Cuadro 3, mínimo y máximo de los tiempos al pico evaluados en cada serie de datos pertenecientes a las 16 presas se dividen entre el valor de su moda se obtienen los cocientes indicados en las columnas 3 y última. Los valores medianos de estos cocientes, último renglón del Cuadro 3, se podrán utilizar como parámetros de diseño en cuencas grandes para estimar el tiempo al pico reducido, es decir el 44% del original en los hidrogramas esbeltos, así como el tiempo al pico ampliado, o sea 3.71 veces el original en los hidrogramas aplanados.
Aplicación numérica de contraste
Presa Eustaquio Buelna (Guamúchil)
Tiene un área de cuenca de 1630 km2 (Cuadro 1). Empezamos calculando el gasto pico correspondiente al periodo de retorno de diseño de 10 000 años; con base en los resultados regionales encontrados por Campos (1994) para la Región Hidrológica No. 10, se obtiene:
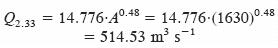
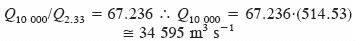
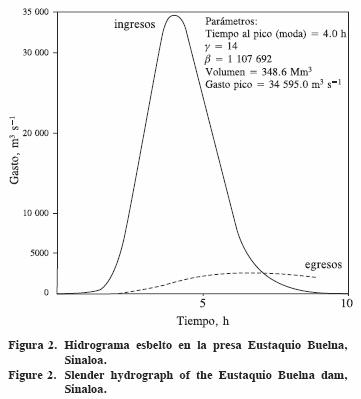
Para γ = 14 y Tp = 4 h se obtiene con la ecuación 3, β = 1 107 692 s. Los valores anteriores y el Qp = 34 595 m3 s–1 definen con la ecuación 9 un volumen máximo respectivo de 348.6 Mm3. El hidrograma correspondiente se muestra en la Figura 2. Los siguientes datos de elevaciones (H) y volúmenes (V) en la presa están disponibles (Aldama et al., 2006):
NAN (cresta) = 58.00 m
NAMO = 64.00 m Volumen = 112.74 Mm3
NAME = 68.65 m Volumen = 302.76 Mm3
Corona = 71.20 m Volumen = 433.95 Mm3
entonces, ubicando la cota cero en la elevación 50 se obtuvo, para la ecuación del embalse:

donde K = 19 777.44; N = 3.28123.
El tránsito de la creciente de diseño se realizó (NERC, 1975) al igual que en Aldama et al. (2006), considerando un vertedor de descarga libre a punto de derramar con longitud de cresta de 30.40 metros y coeficiente de descarga de 2.10, obteniéndose un gasto máximo de descarga de 2459.4 m3 s–1 ocurriendo a las 7 horas de iniciada la creciente y definiendo un NAME de 19.41 m, es decir, 69.41 m. Como tal elevación supera al NAME de la presa, ésta es considerada insegura desde un punto de vista hidrológico; resultado que coincide con el de Aldama et al. (2006).
Para la construcción del hidrograma aplanado se adoptó una extrapolación para el tiempo al pico; por ello se utilizó un valor de 15 h, resultando β = 135 000.0 s cuando γ = 1.4; con tales valores y Qp = 3500 m3 s–1, es decir 10% del gasto máximo regional, se obtiene un volumen máximo igual a 902.3 Mm3. Al transitar tal hidrograma en igualdad de condiciones que las establecidas para el hidrograma esbelto, se obtiene un gasto máximo de descarga de 2155 m3 s–1 que ocurre 52.5 h después de iniciada esta creciente, estableciendo un NAME de 68.45 m. Este hidrograma aplanado (Figura 3), genera unas condiciones menos críticas que el hidrograma esbelto.
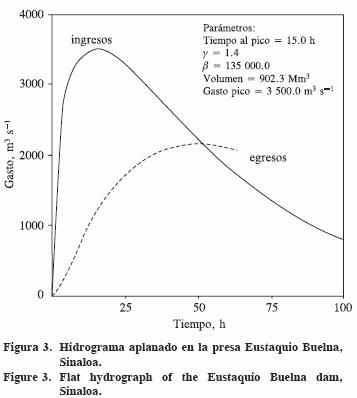
Ramírez y Aldama (2000) han demostrado teóricamente que tiene gran importancia el volumen del hidrograma en el comportamiento del embalse ante la creciente. Sin embargo, en las 16 presas analizadas por Aldama et al. (2006), ubicadas en climas muy diferentes y con tamaños de cuenca variando de 171.3 a 108 000 km2 (Cuadro 1), los hidrogramas de diseño que generaron las condiciones críticas fueron los de tipo esbelto.
CONCLUSIONES
Hay varios miles de presas pequeñas para riego en México, que no cuentan con información hidrométrica; sin embargo, es necesario y hasta urgente revisar su seguridad hidrológica. Para aprovechamientos ubicados en cuencas rurales pequeñas se ha formulado un procedimiento basado en información fácilmente obtenible que conduce a los hidrogramas de diseño, los cuales al ser transitados en el embalse definirán el nuevo NAME, con base en el cual se concluirá si la presa analizada es segura o está en riesgo hidrológico, según si el nuevo NAME es inferior o superior al actual.
Con base en los resultados de las aplicaciones numéricas realizadas, descrita solo una, se concluye que el procedimiento sugerido es muy fácil de aplicar y conduce a resultados sumamente importantes en relación con la seguridad hidrológica de la presa pequeña analizada. Cuando el almacenamiento resulte inseguro se deben formular y revisar estrategias para alterar su operación y mantenerla vacía antes de la época de ocurrencia de las avenidas, o bien, estudiar cuantitativamente las modificaciones que se deben realizar a su infraestructura, mediante la sobreelevación de su cortina o la ampliación de la capacidad de su vertedor de excedencias.
AGRADECIMIENTOS
Se agradecen las observaciones del editor asignado y de los dos árbitros anónimos, las cuales permitieron hacer más explícito el procedimiento sugerido.
LITERATURA CITADA
Aldama, A. A., y A. I. Ramírez. 1998. Parametrización de hidrogramas mediante interpolantes Hermitianos. Ingeniería Hidráulica en México. XIII: 19–28. [ Links ]
Aldama, A. A., A. I. Ramírez, J. Aparicio, R. Mejía, y G. E. Ortega. 2006. Seguridad Hidrológica de las Presas en México. Instituto Mexicano de Tecnología del Agua. Jiutepec, Morelos. 192 p. [ Links ]
Campos A., D. F. 1994. Aplicación del método del índice de crecientes en la Región Hidrológica No. 10, Sinaloa. Ingeniería Hidráulica en México. IX: 41–55. [ Links ]
Campos A., D. F. 2005. FDP Gamma Mixta. In: Agroclimatología Cuantitativa de Cultivos. Editorial Trillas. México, D. F. pp: 267–281. [ Links ]
Campos A., D. F. 2006. Análisis probabilístico con métodos regionales. In: Análisis Probabilístico Univariado de Datos Hidrológicos. Avances en Hidráulica 13. AMH–IMTA. México, D. F. pp: 133–161. [ Links ]
Campos A., D. F. 2007. Parámetros hidrológicos de la cuenca. In: Estimación y Aprovechamiento del Escurrimiento. Edición del autor. San Luis Potosí, S.L.P. pp: 41–50. [ Links ]
Croley, T. E. 1980a. Dimensionless hydrographs given peak discharge. In: Synthetic–Hydrograph Computations on Small Programmable Calculators. University of Iowa. Iowa, USA. pp: 98–118. [ Links ]
Croley, T. E. 1980b. Gamma synthetic hydrographs. In: Hydrologic and Hydraulic Calculation in Basic for Small Computers. University of Iowa. Iowa, USA. pp: 26–49. [ Links ]
Davis, P. J. 1972. Gamma Function and related functions. In: M. Abramowitz & I. A. Stegun (eds). Handbook of Mathematical Functions. Dover Publications, Inc. New York, USA. pp: 253–293. [ Links ]
Escalante, C., y L. Reyes. 2002. Análisis regional hidrológico. In: Técnicas Estadísticas en Hidrología. Facultad de Ingeniería de la UNAM. México, D. F. pp: 157–202. [ Links ]
GASIR (Gerencia de Aguas Superficiales e Ingeniería de Ríos). 1996. Norma Hidrológica que recomienda Períodos de Retorno para diseño de diversas obras hidráulicas. Subdirección General Técnica de la CNA. México, D. F. 6 p. [ Links ]
Morris, E. C. 1982. Mixed–Population Frequency Analysis. Training Document 17 of the Hydrologic Engineering Center, U.S.A.C.E. Davis, California, U.S.A. 43 p. [ Links ]
NERC (Natural Environment Research Council). 1975. Supplementary Studies (Flood routing). In: Flood Studies Report. London, England. pp. 486–539. [ Links ]
Oliva, C. 1999. Estado actual de las presas. Breve reseña histórica. In: El Desarrollo de las Presas en México. Avances en Hidráulica 5. AMH–IMTA. México, D. F. pp: 33–37. [ Links ]
Ramírez, A. I., y A. A. Aldama. 2000. Análisis de sensibilidad de los parámetros del hidrograma de ingresos a vasos. In: Análisis de frecuencias conjunto para la estimación de avenidas de diseño. Avances en Hidráulica 7. AMH–IMTA. México, D. F. pp: 163–169. [ Links ]
Ramírez, A. I., J. F. Gómez, y D. F. Campos. 2005. Actualización de las envolventes regionales de gastos máximos para la república mexicana. Ingeniería Hidráulica en México. XX: 99–108. [ Links ]
Smith, J. A. 1993. Precipitation. In: Maidment, D. R. (ed). Handbook of Hydrology. McGraw–Hill, Inc. New York, USA. pp: 3.1–3.47. [ Links ]
Snider, D. 1972. Hydrographs. In: National Engineering Handbook. Section 4: Hydrology. U. S. Soil Conservation Service. Washington, D. C., USA. pp: 16.1–16.26. [ Links ]
Springall, R. 1970. Libre Bordo en Presas. Publicación No. 264. Instituto de Ingeniería de la UNAM. México, D. F. 14 p. [ Links ]
Témez P., J. R. 1978. Tiempo de concentración. In: Cálculo Hidrometeorológico de Caudales Máximos en Pequeñas Cuencas Naturales. Dirección General de Carreteras. Ministerio de Obras Públicas y Urbanismo. Madrid, España. pp: 79–91. [ Links ]
Weiss, L. L. 1964. Ratio of true fixed–interval maximum rainfall. Journal of Hydraulics Division. 90: 77–82. [ Links ]
WMO (World Meteorological Organization). 1973. Greatest known rainfalls. In: Manual for Estimation of Probable Maximum Precipitation. Operational Hydrology Report No. 1. Geneva, Switzerland. pp: 175–179. [ Links ]














