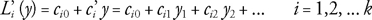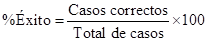Introducción
Las crisis económicas y financieras globales ocurridas recientemente, han puesto una vez más de manifiesto las crecientes dificultades que enfrentan muchos gobiernos en el cumplimiento de las pensiones, tanto en países de la Organización para la Cooperación y el Desarrollo Económicos (OCDE), como en los demás países (Collins et al., 2014; Coyle, 2012). Existen nuevas presiones para reformar los sistemas de pensiones, por los problemas de sostenibilidad debido a las tendencias demográficas recientes (Lewis y Cho, 2011). Entre varias otras razones, también se ha criticado la gestión de los fondos de pensiones por parte del sector público (Stalebrink, 2014, De León et al., 2010).
Los planes de pensiones de prestación definida (defined-benefit pension plans) pueden ser un camino de solución a esta problemática (DiNapoli, 2012). Otro camino surgió a partir del modelo de capitalización individual chileno (Superintendencia de Pensiones de Chile, 2010). Este sistema de políticas públicas de pensiones ha servido de base para reformas en otros sistemas de pensiones en Latinoamérica (Perú, Colombia y México a principios de la década de 1990), y hacia finales de la misma década en países de Europa del Este (Hungría, Polonia, Bulgaria o Croacia, entre otros). Estas reformas parecen modificar las fronteras entre lo público y lo privado en los mercados financieros, con gran efecto en el papel de los pensionados en la toma de decisiones que les afectan (Bilbao, 2012). Así, el concepto de “información de pensiones a nivel individual” parece adquirir cada vez mayor relevancia (Mitchell, 1988 y Regúlez-Castillo y Vidal-Meliá, 2012). Sin embargo, Orenstein (2013) señala que, a pesar de lo anterior, a partir de mediados de 2000 se aprecia una declinación del paradigma del nuevo sistema de pensiones, con explicaciones de tipo fiscal y conceptual.
Recientes estudios reflejan la búsqueda de nuevas herramientas para un aporte sostenible de las partes interesadas en los planes de pensiones, buscando incrementar el involucramiento de los stakeholders, y la privatización de los planes públicos de pensiones bajo ciertas circunstancias (De Kruijf y De Vries, 2014). En esta línea, el sistema privado chileno parece recoger gran parte de estas propuestas. En particular, hasta enero del año 2000, las Administradoras de Fondos de Pensiones (AFP) de Chile sólo ofrecían una alternativa de ahorro previsional a sus afiliados. No existía la posibilidad de elegir un fondo que se ajustara mejor al perfil de riesgo y edad de los cotizantes. A partir del año 2002 se crea el llamado “sistema de multifondos”, el que incluyó los fondos A, B, C, D y E, siendo el fondo A el más riesgoso, y el E el menos riesgoso. Estos ajustes parecen recoger algunos de los problemas específicos de los trabajadores individuales, en la línea propuesta por De Kruijf y De Vries (2014), al permitir ejercer las preferencias individuales de los afiliados respecto al horizonte de ahorro. En efecto, los afiliados jóvenes tienden a preferir fondos con mayor riesgo y mayor retorno esperado, mientras que afiliados de mayor edad generalmente tratan de minimizar las fluctuaciones.
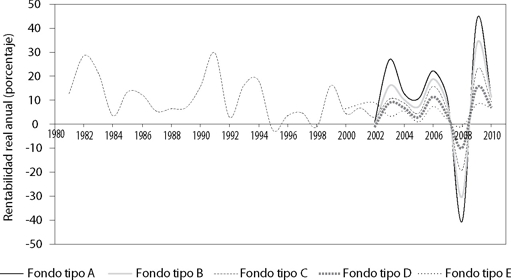
La crisis financiera internacional de fines del año 2008 generó una importante caída del valor y del rendimiento de los fondos de pensiones chilenos (gráfica 1). La caída fue cercana a 40 por ciento del valor previo, en el caso del Fondo A (gráfica 2). Parte de esta volatilidad es inherente a los mercados financieros. Sin embargo, esquemas de armonización de la regulación y de supervisión financiera, con regulación orientada a los bancos (Basilea II), pueden ayudar a prevenir crisis financieras y escándalos corporativos (Martínez, 2007). Aun así, importantes nuevos desafíos han surgido a partir de ella para las regulaciones financieras, la transparencia y una discusión del futuro desarrollo de la regulación (Liou, 2013 y 2013a).

Fuente: Superintendencia de Pensiones de Chile (2000-2011).
Gráfica 1 Total de activos de los fondos de pensiones de Chile por año (millones de dólares)
Fuente: Superintendencia de Pensiones de Chile (2000-2011) y Berstein et al. (2011).
Gráfica 2 Rentabilidad real anual de la cuota de los fondos de pensiones
La crisis de 2008 en Chile evidenció que muchos ahorrantes hicieron una selección inicial errada del multifondo. Pareció que las personas se dejaron llevar por las altas rentabilidades observadas por el fondo A, y no se dieron cuenta del riesgo implícito del mismo. En efecto, en el periodo 2002-2007 se había observado un incremento de la rentabilidad de los fondos A y B (los de mayor riesgo). Por esa razón, en el periodo precrisis muchos ahorrantes eligieron cambiarse desde los fondos C, D y E hacia dichos fondos. Pero cuando se produjo la crisis de 2008, en ese momento, al ver que el valor de los fondos caía, se provocó un retorno masivo de ahorrantes hacia fondos menos riesgosos (Berstein et al., 2011). Esta migración poscrisis llevó a asumir la pérdida neta significativa para los ahorrantes.
El origen del problema fue una selección inicial errada del multifondo por parte de muchos ahorrantes, quienes seleccionaron los fondos A y B, cuando en realidad el grado de aversión al riesgo era alto, y más bien debieron permanecer siempre en los fondos C, D o E. Los cuadros 1a y 1b muestran que efectivamente entre 2003 y 2007 hubo una tendencia decreciente en el porcentaje de ahorrantes previsionales chilenos que invertían en el fondo E (el fondo más seguro). Sin embargo, hacia fines de 2008 (en plena crisis) el número de ahorrantes de fondos de pensiones de ese fondo se triplicó, evidenciando la búsqueda de mayor seguridad. Una buena parte de este error individual pudo ser evitado por medio de educación financiera. Frijns et al. (2014) muestran que el conocimiento financiero a través de programas de educación, afecta significativamente a la toma de decisiones individuales. La experiencia financiera también parece conducir a un mayor conocimiento financiero y una mejor toma de decisiones, lo que finalmente se traduce en mayor desarrollo económico (Nam et al., 2013). Puede notarse que la implementación de técnicas cuantitativas de optimización y de transparencia en decisiones públicas ha sido de interés en revistas especializadas de gestión pública (Fernández et al., 2011; Chen, 2012, 2013).
Cuadro 1A Total de afiliados por fondo en cada año (en miles)

Fuente: Superintendencia de Pensiones de Chile (2000-2011).
Cuadro 1B Total de afiliados por fondo en cada año (porcentaje)
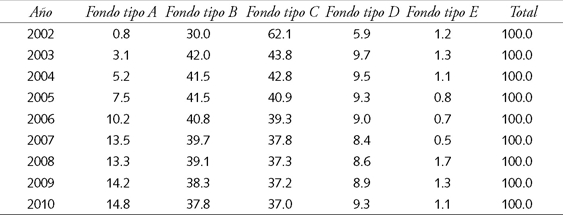
Fuente: Superintendencia de Pensiones de Chile (2000-2011).
Los efectos de esta crisis financiera internacional dejaron en evidencia la necesidad de que la autoridad reguladora del sistema de las AFP implemente políticas públicas que reduzcan los impactos negativos en las pensiones de las personas. Además, porque la crisis tuvo también implicancias económicas para el Estado de Chile, surgidas de la “garantía estatal”, un beneficio del Estado de Chile a los pensionados que, cumpliendo ciertos requisitos, registren en su cuenta individual un saldo reducido, entonces percibirán una pensión mínima financiada por el Estado. Una caída inesperada en el valor de los fondos de pensiones implica que un mayor número de trabajadores no alcanzará a financiar su pensión con los recursos ahorrados por él y, en consecuencia, el Estado deberá aportar los recursos faltantes.
El papel del Estado para prevenir este tipo de situaciones tiene por lo menos dos dimensiones relevantes. Por una parte, la Superintendencia de Pensiones es la que dicta la mayor parte de la normativa e indicadores que deben cumplir las AFP. Por otra, el Estado es el garante de jubilaciones mínimas en el caso de una crisis financiera de largo plazo. Desde el punto de vista de las políticas públicas, una forma de enfrentar este problema por parte de la autoridad es definiendo indicadores individuales que determinen la coherencia entre los perfiles de riesgo de los cotizantes del sistema de pensiones respecto del multifondo en que efectivamente se encuentran.
Un papel de las AFP en la solución es asegurarse de que los asesores profesionales (captadores) tengan las competencias necesarias para orientar apropiadamente a los ahorrantes, para que éstos seleccionen finalmente el multifondo apropiado. Esta orientación debe considerar el perfil de riesgo y horizonte de ahorro previsional de cada cotizante individualmente. La forma tradicional de estimar el perfil de riesgo de los ahorrantes es a través de cuestionarios, y prácticamente todos los portales WEB de las AFP en Chile los ofrecen a sus afiliados. Sin embargo, hemos verificado que respondiendo varios de estos cuestionarios con un mismo criterio, las recomendaciones en cuanto al fondo de ahorro a seleccionar resultan ser muy disímiles. Esto lleva a pensar que éstos en realidad no cuentan con un desarrollo metodológico y analítico que lleve a determinar qué preguntas son relevantes, y cuál debe ser el peso relativo de cada pregunta en la determinación de la recomendación final.
La literatura especializada proporciona formas de realizar mediciones empíricas de las actitudes hacia el riesgo. A partir del trabajo pionero de Pratt (1964) acerca de la hipótesis de aversión al riesgo absolutamente decreciente con la riqueza, muchos estudios han intentado conciliar las hipótesis con la evidencia empírica (Montmarquette y Blais, 1987; Binswanger, 1980; Yao et al., 2004, 2005; Hanna, 2005). Algunas variables con las que usualmente se mide el riesgo personal e individual se encuentran en Padgette y Paulin (2006), Sjöberg (2003, 2006).
Investigaciones de la forma en que el perfil de riesgo de los ahorrantes de fondos de pensiones individuales se refleja en la composición de su portafolio de ahorro previsional son escasas. El análisis discriminante (AD) es una técnica estadística multivariada que permite la clasificación de los ahorrantes en distintas categorías, de acuerdo con una serie de variables explicativas. Los estudios que han usado esta herramienta en esa dirección son pocos. Destaca (Cohn, 1975), quien utiliza AD para explicar la selección de ahorrantes de uno de cuatro grupos de activos, de acuerdo con la proporción de activos riesgosos mantenidos; Mc Crimmon y Wehrung (1990) usando AD para estudiar las decisiones de 500 ejecutivos; Grable (1998) usa AD para separar, discriminar y clasificar a los ahorrantes en categorías de tolerancia al riesgo; Grable (2000) usa también AD y encuentra que la menor tolerancia al riesgo estaba asociada con ser mujer, de edad avanzada, casado, empleado con altos ingresos, más educación, más conocimiento financiero y crecientes expectativas. El AD también ha sido usado con éxito en muchos otros campos de las ciencias humanas, abarcando desde las visiones políticas (Schuman et al., 1992), hasta la selección de viviendas (Cheng y Black, 1998). Estudios recientes acerca del perfil de riesgo de los ahorrantes de fondos de pensiones incluyen a Dohmen et al. (2005), Hallahana et al. (2003), Filbeck et al. (2005) y Van Rooij et al. (2007).
El objetivo de esta investigación es desarrollar una herramienta que permita recoger información básica de cotizantes de las AFP chilenas y, con base en esto, construir un modelo que permita sugerir el fondo de AFP más apropiado, aquel que con mayor probabilidad escogería el ahorrante. A par tir de esta herramienta es posible sugerir formas de regulación para que las agencias reguladoras del Estado monitoreen posibles divergencias. Para esto, a continuación, en el apartado metodológico del estudio, se describe la técnica aplicada, y en la siguiente sección se presentan y se discuten los resultados obtenidos, con énfasis en las implicaciones para las políticas públicas de pensiones en Chile.
Metodología
El análisis discriminante (AD) permite explicar y predecir la pertenencia de individuos o casos a uno de varios grupos, a partir de un conjunto de variables predictivas. Se trata de encontrar relaciones lineales entre las variables explicativas de modo que se discriminen de mejor forma los objetos en los grupos. Una vez hecho esto, se tiene una regla de decisión que permite asignar un nuevo objeto a uno de los grupos con el menor grado de incertidumbre posible. Los principales supuestos incluyen la existencia de una distribución normal para las variables, homogeneidad de varianzas y covarianzas a través de los grupos, y que la pertenencia a un grupo es exclusiva y exhaustiva. Esta técnica también puede ser considerada como un análisis de regresión multinomial, donde la variable dependiente es categórica (las categorías son las etiquetas de cada grupo), y las variables independientes determinan a qué grupos pertenecen los objetos. Rencher (2002) es uno de los buenos textos que desarrollan este tópico.
La aplicación clásica del AD en economía y gestión fue proporcionada por Altman (1968), quien estimó la probabilidad de que en un horizonte de dos años una empresa manufacturera pudiera quebrar, definiendo para esto tres grupos o zonas de discriminación: zona segura, zona gris y zona de quiebra, y usando como variables explicativas distintos ratios financieros.
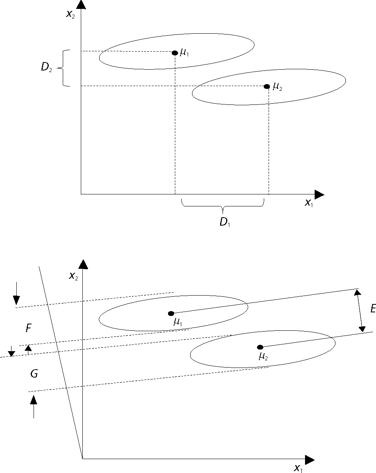
Para ilustrar la técnica en el caso de sólo dos grupos, considérese la gráfica 3 (arriba) donde se muestran dos grupos cuyos elementos-puntos aparecen en dos óvalos, respectivamente. El objetivo es encontrar la forma de visualizar ambos grupos de la forma más clara posible, evitando traslapamientos de los grupos, si es posible. Si los grupos son vistos desde abajo (es decir desde el eje X1), o lateralmente (es decir desde el eje X2) existe traslapamiento de los óvalos. Además, las distancias entre las medias ya no son máximas, las que corresponden a D1 y D2 respectivamente.
Fuente: Elaboración propia.
Gráfica 3 Análisis discriminante lineal simple: Ilustración gráfica de la operatoria
El procedimiento estándar de solución es el sugerido por Fisher (1936), consistente en encontrar las ecuaciones que maximizan la varianza entre los grupos y, simultáneamente, minimizar la varianza al interior de los grupos. Para esto, lo que se debe hacer es definir un nuevo eje (o plano), que permita visualizar ambos grupos de la forma más separada posible, maximizando la discriminación. Esto se logra rotando levemente el eje X2 a la izquierda, tal como muestra la gráfica 3 (abajo). Desde este nuevo eje se logra maximizar la distancia entre ambos grupos (distancia E, que es mayor a D2), y al mismo tiempo minimizar la distancia al interior de cada grupo (las distancias F y G).
Fisher (1936) demostró que la mejor forma de encontrar la función lineal discriminante es maximizar el ratio entre la varianza entre los grupos (B) y la varianza al interior de los grupos (W). En este caso los coeficientes de esa función deben ser los eigenvectores1 de λ1, donde λ1 es el eigenvalor dominante de la matriz W–1 B.
Para separar dos grupos es suficiente una función discriminante, sin embargo para el caso de más grupos se requieren más funciones discriminantes, y se siguen estimando los eigenvectores λ2, λ3, …, asociados a los siguientes eigenvalores (en orden decreciente). Como los eigenvectores son linealmente independientes entre sí, las funciones conforman nuevos espacios vectoriales.
Para visualizar la calidad de la discriminación es común graficar las observaciones en un plano de sólo dos dimensiones, para lo cual se usan sólo las dos primeras funciones, las que comparativamente logran la mayor proporción de la discriminación. Para evaluar la calidad de esta simplificación puede calcularse la proporción de la varianza total que es explicada, y que corresponde a la relación entre la suma de los dos primeros eigenvalores respecto a la suma del total de eigenvalores. En este plano se suele identificar la media de cada grupo, llamada centroide, y los círculos de confianza alrededor de cada centroide. Si los círculos de confianza de los distintos grupos se traslapan de modo importante entre sí, se puede concluir que el ajuste no ha sido satisfactorio. Nótese que si se usara solamente un eje para representar las observaciones, la proporción de la varianza explicada será el ratio entre el eigenvalor principal respecto a la suma del total de eigenvalores.
Para mejorar la interpretación comparativa de los coeficientes de las funciones de discriminación (funciones discriminantes canónicas), usualmente éstas también se presentan estandarizadas.
Asumiendo normalidad, igualdad de varianzas y de probabilidades previas (caso no-bayesiano), la clasificación óptima se logra minimizando la probabilidad de una mala clasificación. Para esto, la regla es asignar el nuevo vector de observaciones al grupo para el cual se maximiza la siguiente función de clasificación discriminante lineal (véase Rencher, 2002 ecuación 9.12):
donde los coeficientes de la función de clasificación son
Dos son las pruebas estadísticas usuales en el diagnóstico de este tipo de modelos. Primero, el estadístico multivariado M de Box (Rencher, 2002, ecuaciones 7.23 y 7.27) permite evaluar si se cumple el supuesto de igualdad de las matrices de covarianzas de cada grupo (homocedasticidad). La hipótesis nula es de igualdad de matrices de varianzas y covarianzas W para todos los grupos. Si se rechaza, puede ser necesario un modelo no lineal, como por ejemplo funciones discriminantes cuadráticas. Box (1949, 1950) entregan aproximaciones para las distribuciones Chi y F para esta prueba. Sin embargo, puede mostrarse que si hay muchas observaciones este test no es muy relevante. El test de Kullback (1967) hace un trabajo similar.
También se suele analizar si las variables logran separar apropiadamente los grupos, para esto existen pruebas de igualdad de medias de grupos, de significancia de las funciones discriminantes y pruebas estadísticas de Manova, tales como el test de lambda de Wilks con la aproximación de Rao, la traza de Pillai, la traza de Hotelling-Lawley y la raíz más grande de Roy. Actualmente existe una amplia discusión sobre los méritos de cada una de estas pruebas. El test lambda de Wilks (Rencher, 2002, ecuación 6.14) parece ser más útil aquí, ya que éste no requiere calcular todas las lambdas. En este caso, la hipótesis nula es que la diferencia entre los centroides o vectores de medias de los grupos no es significativa. Si se logra rechazar esta hipótesis, entonces las funciones discriminantes logran efectivamente generar grupos diferenciados estadísticamente.
Finalmente, la medida de éxito en la clasificación global más usada en este tipo de análisis es la llamada matriz de confusión. Ésta muestra el porcentaje de observaciones que resultan bien clasificadas ex post, en comparación con las observaciones mal clasificadas. En algunos programas computacionales a veces se le llama también cuadro de contingencia. Ésta es una matriz cuadrada de dimensión k, es decir el número de clases o grupos. En el cuadro 2 se ilustra un ejemplo de N observaciones a clasificar en solamente k=3 grupos.
Aquí, (1, 1) representa el número de casos que perteneciendo al grupo 1 resultaron ser asignados por el modelo de uno modo correcto al grupo 1. Por otro lado, (1, 2) representa el número de casos que perteneciendo al grupo 1, resultaron ser erróneamente asignados por el modelo al grupo 2. Y así sucesivamente. El éxito en la predicción para el grupo 1 es la proporción de predicciones correctas para el grupo 1, es decir la razón entre (1, 1) y el total de elementos del grupo 1, que equivale a la suma de los elementos de la fila correspondiente al grupo 1. Repitiendo este procedimiento para todos los grupos, el éxito global del modelo se mide por la suma de los elementos de la diagonal de la matriz, dividido entre el total de casos, es decir:
Es importante observar que si el modelo hiciera una predicción perfecta se obtendría una matriz donde todos los elementos se ubicarían en la diagonal, y en consecuencia el éxito sería de 100 por ciento. Si por el contrario no hay predicciones correctas, todos los elementos están fuera de la diagonal, y el éxito es cero. Un caso especialmente importante es cuando existe perfecta aleatoriedad en la asignación. Aquí el éxito no es 50 por ciento como se podría pensar, sino solamente 1/N, que en este caso ilustrativo es 1/3.
Las variables y el cuestionario
Metodológicamente el presente estudio define y utiliza una muestra de ahorrantes de los fondos de pensiones, a los cuales se les aplica una encuesta breve. En ésta se les consulta, entre otros, acerca de cuál es el fondo de AFP en el que actualmente mantienen sus ahorros para la jubilación (variable dependiente).
La literatura sugiere considerar variables como el género, la edad, estado marital, la ocupación, el tamaño de la familia, la educación y los ingresos (Cohn, 1975). Binswanger (1980) destaca la relevancia de las variables relacionadas con género, ingresos, edad y escolaridad para conocer las actitudes riesgosas. Con base en encuestas preliminares a una pequeña muestra de trabajadores, se verifica si la redacción de las preguntas es lo suficientemente clara, y se efectúan las correcciones necesarias. Con base en esto, se decidió incluir las diez preguntas que se muestran en el cuadro 3.
Se incluye la edad del cotizante, ya que ésta debe determinar en gran medida el horizonte de tiempo del ahorro (normalmente a mayor edad se tiende a ser más conservador). El sexo es una variable que también se considera importante, ya que pareciera que los hombres son más arriesgados que las mujeres (Mc Crimmon y Wehrung, 1990; Sjöberg, 2006). El nivel educacional que posee el cotizante también es una variable usualmente mencionada en los estudios de tolerancia al riesgo (Grable, 2000), ya que hay alguna evidencia de que quienes poseen un mejor nivel educacional toman posiciones más riesgosas, quizá por un mejor acceso a la información del sistema financiero.
También se busca capturar el perfil o actitud hacia el riesgo de los encuestados. A través de tres preguntas se somete al ahorrante a situaciones hipotéticas sobre las cuales debe decidir (véanse, por ejemplo, Morán y Troncoso, 2003; Sjöberg, 2003).
Por último, se incluye una pregunta referida a la experiencia personal en el sistema financiero, puesto que ésta debe tomar en cuenta una relación más cercana con conceptos tales como el riesgo y las expectativas financieras. Otros estudios incluyen la etnicidad como un factor relevante, por ejemplo Yao et al. (2005), sin embargo en el caso chileno esto no se considera relevante.
En el siguiente apartado se presentan los resultados de la investigación, fruto de la aplicación de las encuestas finales. Con base en esto se estima el modelo de selección, se realizan los análisis y se obtienen las conclusiones del estudio. Debe notarse que la estimación empírica que sigue obedece a la idea de ilustrar con una aplicación práctica la técnica del AD, la que es propuesta como una herramienta para una mejor política de jubilaciones.
Resultados
El modelo que plantea esta investigación establece que la pertenencia a uno de los cinco fondos del sistema de multifondos previsional es explicada razonablemente por un número reducido de variables. El universo estudiado fueron los trabajadores de una gran empresa de servicios con operaciones principales en el norte de Chile, con alrededor de 500 trabajadores. La población de trabajadores de esta empresa presenta gran heterogeneidad, tanto en nivel de remuneraciones, nivel de estudios, tipo de trabajo, características demográficas, y también respecto al tipo de fondo previsional al cual se encuentran afiliados individualmente.
La encuesta aplicada consta de solamente diez preguntas, que recogen la información a que se refiere el cuadro 3. Este cuestionario fue aplicado a una muestra de 192 funcionarios de forma aleatoria y personal durante el mes de diciembre de 2010. El objetivo fue recoger información de por lo menos 30 trabajadores de cada fondo previsional. La muestra obtenida representa aproximadamente 30 por ciento del total de trabajadores de la empresa. El cuadro 4 muestra un resumen del número de encuestas disponibles de acuerdo al fondo de pensión en que se encontraba cada trabajador, mostrando que el grupo 1 resultó ser claramente el más numeroso.
El cuadro 5 muestra estadísticas descriptivas para cada variable, incluyendo el número de observaciones, la media, la desviación estándar y el rango máximo-mínimo en el cual fluctúan los datos. Nótese que si bien la edad mínima de jubilación en Chile es de 65 años para los hombres, las personas pueden seguir trabajando, y simultáneamente cobrar una pensión. Esto explica que exista una edad máxima observada en la muestra de 70 años. Por otro lado, en la muestra existe una proporción bastante similar de hombres y mujeres, ya que la media observada de la variable sexo (1 para hombres y 2 para mujeres) es de 1.53.
Se evaluaron dos modelos alternativos. El primero (Modelo 1) incluye las diez variables explicativas anteriores conjuntamente y los cinco fondos de ahorro previsional posibles.
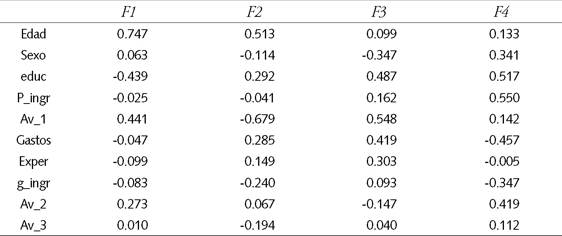
El cuadro 6 muestra los coeficientes estandarizados de las funciones discriminantes canónicas (el Modelo 1 requiere sólo cuatro funciones discriminantes). Por tratarse de coeficientes estandarizados, aquellas variables que reportan mayores coeficientes en valores absolutos tienen una mayor importancia o peso relativo en la clasificación. En este sentido, las variables edad, educ, Av_1 y Av_2 parecen permitir construir un modelo simplificado, excluyendo las demás variables. Esto se analiza más adelante, en el Modelo 2.
Cuadro 6 Modelo 1: Coeficientes estandarizados de las funciones discriminantes canónicas
Fuente: Elaboración propia.
La gráfica 4 muestra los centroides y círculos de confianza para el Modelo 1. Esta representación gráfica permite apreciar que después de la rotación descrita por la gráfica 3 (véase apartado metodológico), el eje F1 (horizontal) por sí solo captura prácticamente 76.77 por ciento de la dispersión/información total de las variables. Sin embargo, con dos funciones (F1 y F2) en conjunto se captura 90.46 por ciento. Luego, con solamente estas dos funciones los cinco grupos son claramente diferenciados a través del AD, sin que exista traslapamiento en los intervalos de confianza, aunque los grupos C y D aparecen bastante cercanos.
En la función F1 (la más importante) las variables más discriminatorias son la edad, la educación y las variables que miden aversión al riesgo Av_1 y Av_2. En efecto, a mayor edad, las personas tienden a preferir los fondos menos riesgosos D y E, las personas que tienen más años de formación tienden a ser menos conservadoras eligiendo los fondos A y B, y las personas que respondieron 1 o 2 en las preguntas de aversión Av_1 y Av_2 tienden a preferir los fondos de menor riesgo. Por otro lado, las variables muy poco explicativas fueron el sexo, la proporción de ingresos que en la etapa de jubilación provendrá de las AFP (P_Ingr), la proporción de los gastos futuros que serán financiados por las AFP (Gastos), la experiencia en inversiones financieras, la capacidad de generar ingresos actualmente (g_ingr) y el indicador de aversión al riesgo (Av_3).
Nótese también que los cinco grupos aparecen en la secuencia esperada si son vistos en el eje F1, es decir, el grupo 1 aparece a la extrema izquierda y los restantes grupos aparecen en una secuencia ordenada hacia la derecha. Además, el grupo 1 es estimado con una buena precisión relativa, debido a que su círculo de confianza es más pequeño.
El cuadro 7 muestra que el porcentaje de clasificación correcta en el Modelo 1 es de 50 por ciento, y entonces se tiene un modelo con una buena capacidad predictiva comparado con el caso aleatorio, que arrojaría un éxito de sólo 20 por ciento en este caso. Esto puede compararse con el estudio de Cohn (1975), quien en un análisis similar reportó sólo 32.5 por ciento de clasificaciones correctas. Los resultados en detalle muestran que del total de 66 encuestados que declararon estar en el fondo A, sólo 39 de ellos resultaron bien clasificados de acuerdo con el modelo 1. De los restantes, el modelo predijo que 14 debieran estar en el fondo B, 11 en el fondo C y dos en el fondo D. Los resultados para cada fondo se interpretan de igual forma.
Lo anterior apunta a que la calidad de ajuste y predicción in-the-sample del modelo es aceptable, y entonces no se hacen más pruebas estadísticas. Sin embargo, el Modelo 1, si bien es exitoso en la clasificación, plantea que es posible reducir la información requerida, puesto que algunas variables muestran bajo poder discriminatorio. Entonces, analizamos a continuación la posibilidad de que un modelo con menor número de variables explicativas (más parsimonioso) logre un éxito similar al del Modelo 1. El Modelo 2 que sigue, reduce el número de variables explicativas de diez a solamente cuatro, eligiendo aquellas que reportaron mayor valor absoluto en los coeficientes para las funciones F1 y F2 en el cuadro 6, es decir Edad, Educ, Av_1 y Av_2.
El cuadro 8 muestra en primer lugar el test de Box (aproximación asintótica) del Modelo 2, donde la hipótesis nula es que las matrices de covarianzas dentro de cada clase son iguales. Debido a que el p-value>0.05, no se rechaza la hipótesis, y entonces parece existir homogeneidad de matrices de covarianzas, y la prueba sugiere razonable aplicar el AD lineal.
Cuadro 8 Modelo 2: Test de Box (aproximación asintótica de chi-cuadrado)

Fuente: Elaboración propia. Nota: H0: Las matrices de covarianzas dentro de cada clase son iguales.
El test de Wilks para la igualdad de medias de las funciones tiene por hipótesis nula que la media de los cinco vectores (grupos) son iguales. Los datos del cuadro 9 muestran un p-value muy pequeño, y la hipótesis debe ser rechazada, implicando que los grupos están estadísticamente separados unos de otros. Resumiendo, ambas pruebas permiten concluir que el modelo discriminante puede ser aplicado exitosamente usando solamente cuatro variables explicativas.
Cuadro 9 Modelo 2: Test de lambda de Wilks (aproximación de Rao)

Fuente: Elaboración propia. Nota: H0: La media de los cinco vectores (grupos) son iguales.
El cuadro 10 muestra los coeficientes estandarizados de las cuatro funciones discriminantes canónicas para los cinco grupos. Para las primeras dos funciones, el valor absoluto de estos coeficientes muestra que tienen especialmente alto poder de clasificación las variables Edad y Av_1, y la variable Educación en tercer lugar. La edad y la educación son variables fáciles de recoger en una encuesta. Av_1 consulta cuál de varias reflexiones acerca de la posición al riesgo acomoda más al encuestado. Preguntas muy similares a ésta ya se encuentran en la mayoría de las encuestas existentes en los portales de internet de las AFP. En este sentido los resultados apoyan la pertinencia de esta pregunta.
Cuadro 10 Modelo 2: Coeficientes estandarizados de las funciones discriminantes canónicas

Fuente: Elaboración propia.
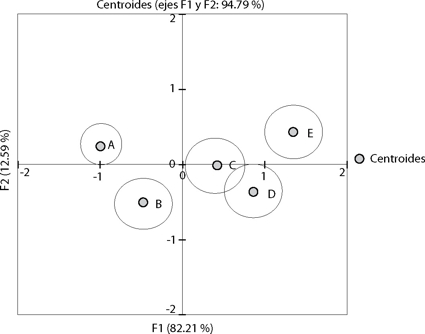
En la gráfica 5 se pueden observar los cinco grupos claramente separados, apareciendo solamente los grupos C y D levemente traslapados. Luego, el modelo logra separar especialmente bien a los ahorrantes de fondos de pensiones de los fondos A y E, es decir los fondos de mayor y menor riesgo, más el fondo B. Sin embargo, para el caso de los grupos C y D, éstos aparentemente son seleccionados con menor precisión, probablemente por una falta de elementos para diferenciar con claridad esos dos grupos. La gráfica 5 también permite apreciar su similitud con la gráfica 4, reflejando que si bien existe una pérdida de precisión al comparar el Modelo 2 respecto al Modelo 1, esta pérdida no es dramática. El eje horizontal muestra que F1 por si sólo logra explicar en 82.21 por ciento la separación de los grupos, y el eje F2 por su parte, permite explicar 12.59 por ciento.
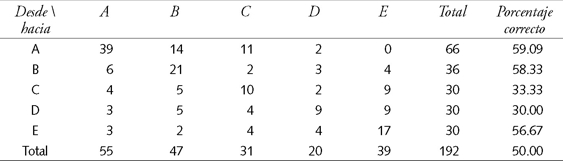
El cuadro 11 muestra la matriz de confusión para el Modelo 2, entregando un éxito en la clasificación (ajuste) razonable. Todos los grupos presentan un porcentaje de clasificación correcta superior a 33 por ciento, lo que es bastante superior a 20 por ciento del caso aleatorio. Luego, comparando con el Modelo 1 (cuadro 7) que contiene las diez variables y 50 por ciento de correcta clasificación, el resultado obtenido por el Modelo 2 es muy satisfactorio, considerando que solamente se usan cuatro variables, y obteniendo 49.48 por ciento de clasificaciones correctas.
Predicción
Uno de los principales objetivos de esta investigación ha sido proveer una herramienta útil para orientar a los ahorrantes de fondos de pensiones al momento de seleccionar el multifondo que mejor se ajusta a su perfil de riesgo. Entonces, para asignar nuevas personas a un fondo de ahorro previsional (A, B, C, D o E) con la mayor probabilidad de éxito, basta tener las funciones de clasificación previamente estimadas. Estas funciones son proporcionadas en el cuadro 12 para el Modelo 2. Entonces, con la información de las cuatro variables para un ahorrante de pensiones, un asesor previsional puede entregar una rápida recomendación del fondo de ahorro apropiado para ese ahorrante en particular. Para esto, de acuerdo con la ecuación 2 del apartado metodológico, se reemplazan los valores observados de las variables explicativas para cada caso u observación en cada función, eligiendo aquel grupo donde sea maximizada la evaluación numérica de cada función.
A modo de ilustración, se asume a continuación que un cotizante de AFP ha sido encuestado para obtener la información de las cuatro variables a que se refiere el Modelo 2, y que sus respuestas han sido: Edad = 45 años, Educ = ocho años, Av_1 = alternativa 1 y Av_2 = alternativa 2. Entonces, para evaluar la primera función de clasificación, la del grupo A, se tiene que:
x = –18.374 + 45 * 0.422 + 8 * 1.703 + 1 * 2.956 + 2 * 1.313
Repitiendo de igual forma para los demás fondos, se obtienen los siguientes resultados:
Fondo A = 19.8
Fondo B = 18.0
Fondo C = 17.9
Fondo D = 16.4
Fondo E = 16.6
De este modo, en el caso de esta ilustración, el ahorrante debería seleccionar el fondo A, es decir el más riesgoso.
Resumen y conclusiones
Los aspectos previsionales son uno de los aspectos centrales de las políticas públicas. A partir de principios de la década de 1980 se implementó en el mundo un nuevo paradigma en las pensiones, basado en sistemas de capitalización individual. A pesar de una rápida implementación de este sistema en varios países, el ritmo de su implementación parece haberse detenido, o al menos reducido (Orenstein, 2013). La crisis financiera mundial de 2008 y su impacto en los fondos de pensiones puso de manifiesto las crecientes dificultades que enfrentan muchos gobiernos en el cumplimiento de las pensiones. Esto, unido a los problemas de sostenibilidad debido a las tendencias demográficas, ha motivado la reforma de los sistemas de pensiones.
En el caso de Chile, una de las reformas relevantes fue la creación de los multifondos, que apuntó a que los ahorrantes pudieran elegir entre varias alternativas de ahorro previsional en función de su riesgo, mejorando aspectos relacionados con una mejor información de las pensiones individuales (De Kruijf y De Vries, 2014; Regúlez-Castillo y Vidal-Meliá, 2012). La crisis financiera del año 2008 puso en evidencia que muchos ahorrantes de estos fondos tomaron decisiones equivocadas. Un número de políticas públicas pueden ser implementadas para promover la educación financiera, como medida de mediano y largo plazo. La autoridad puede definir criterios que aseguren que los cotizantes elijan los fondos de ahorro previsional, tales que sean consistentes con su grado de aversión al riesgo individual y con otras características individuales relevantes.
Actualmente existen muy pocos elementos objetivos que permitan dar recomendaciones a los ahorrantes al momento de elegir un multifondo de entre las distintas alternativas que ofrecen las AFP. En efecto, luego de la crisis financiera mundial vivida en el año 2008, se hizo evidente que en muchos casos la selección realizada previamente por un ahorrante de un determinado multifondo no fue la adecuada. Al evidenciar pérdidas considerables en sus fondos, la respuesta de un gran número de ahorrantes chilenos en las AFP fue cambiarse rápidamente a un fondo menos riesgoso, lo que los llevó a asumir una pérdida irreparable, debido a que las opciones de menor riesgo conllevan menores rentabilidades en el largo plazo y, en consecuencia, conllevan menores posibilidades de recuperar lo perdido.
La selección apropiada de un multifondo por parte de los cotizantes de las AFP es un tema de la mayor importancia desde el punto de las políticas públicas, esto debido al gran número de usuarios del sistema y a la gran magnitud de recursos monetarios. Hacia fines del año 2013 existen alrededor de 4 900 000 personas que mantienen cuentas de ahorro en las AFP en Chile, y todos ellos son potenciales usuarios de la herramienta que sugiere el presente estudio. Los dineros mantenidos en los fondos de pensiones en Chile representan cerca 70 por ciento del PIB del país. Esto permite apreciar la trascendencia evidente que tiene disponer de mejoras en las técnicas de selección de fondos por parte de los ahorrantes de los fondos de pensiones.
Al menos dos son las dimensiones relevantes de la selección apropiada de portafolios de pensiones respecto de las políticas públicas. Por una parte, al Estado chileno, a través de las Superintendencias de Pensiones, le cabe responsabilidad en el éxito de la gestión de las pensiones. Por eso debe desarrollar instrumentos de planificación y de control efectivos, que reduzcan las brechas entre los portafolios de ahorro previsional ideal y los efectivamente observados. La técnica desarrollada en el presente estudio propone una forma eficiente de avanzar en esa línea.
Por otra parte, al Estado de Chile le corresponde por ley garantizar que todo cotizante en el sistema de AFP con un número mínimo de cotizaciones reciba por lo menos una jubilación mínima mensual. En este sentido, si una errada selección lleva a deterioros de algunos patrimonios individuales, tal que se hagan insuficientes para alcanzar una jubilación mínima, se activa entonces la garantía estatal. En ese caso es el Estado el que debe aportar los recursos faltantes. En este sentido, en la gestión eficiente de los fondos privados de pensiones hay implicancias para los recursos fiscales. Luego, la gestión eficiente de los recursos públicos obliga a monitorear la forma en que los ahorrantes de los fondos de pensiones están invirtiendo sus recursos.
La originalidad de este estudio se encuentra en la implementación de una variante del análisis discriminante (una de las herramientas del análisis multivariado), para ayudar a resolver un problema financiero real, y de gran importancia, y sobre lo cual se ha avanzado muy poco en los años recientes. Es importante clarificar que en este estudio no se analiza si las técnicas de conformación de los fondos por parte de las AFP son las apropiadas. Por el contrario, se propone una nueva herramienta para ser usada por las AFP y por los asesores de ahorro como ayuda a los ahorrantes en la selección de un fondo en particular. El objetivo es facilitar a estos últimos el proceso de selección entre las alternativas de multifondos que las AFP les hacen disponibles. Hasta la fecha, en Chile no se ha hecho uso de técnicas formales para orientar a los cotizantes hacia una correcta clasificación de sus decisiones, con el fin de disminuir los errores de selección, facilitar los procedimientos de orientación por parte de las AFP y lograr un mayor grado de satisfacción en los ahorrantes de fondos de pensiones.
Para ilustrar numéricamente la operación de la técnica de selección que este estudio sugiere, se elabora una aplicación real. El objetivo es solamente ilustrar la forma en que se implementa la técnica, y no se trata de una forma de validación de la técnica a partir de dichos resultados. En este sentido, el verdadero aporte de esta investigación es proponer de un modo innovador y práctico el uso de una técnica multivariada basada en el análisis discriminante para la selección de fondos de ahorro, y mostrar que esto no sólo es factible, sino que también es relativamente sencillo y económico de implementar. En la ilustración de la técnica se realizaron estimaciones empíricas para una muestra de trabajadores de una gran empresa chilena. Se efectuaron estimaciones de un modelo base con diez variables explicativas, y de un modelo simplificado con solamente cuatro variables explicativas. En este último caso el modelo utiliza únicamente estimaciones de la edad y del nivel educacional del trabajador, más dos preguntas que recogen su grado de aversión personal al riesgo. A partir de los resultados, el modelo base entregó prácticamente 50 por ciento de asignaciones correctas al momento de clasificar a los ahorrantes de fondos de pensiones en uno de los cinco fondos disponibles en el sistema de pensiones chileno, muy por encima de 20 por ciento de éxito que es lo que arrojaría una asignación al azar. El modelo simplificado obtiene resultados muy parecidos, con una muy baja pérdi da de capacidad predictiva. Es decir, el modelo así estimado logra superar claramente a una estrategia de toma de decisiones realizada sin información o al azar. Se debe insistir en que el caso de estudio busca solamente ser una ilustración de la técnica, y no una forma de validación estadística de la misma, algo que va más allá del alcance de este estudio.
El trabajo finaliza con una ilustración numérica de cómo aplicar el modelo en un nuevo ahorrante, para el cual se tiene información de algunas variables críticas, y a partir de ello el modelo entrega una sugerencia de fondo de ahorro. Naturalmente, el modelo proporciona una guía útil en una situación de total incertidumbre respecto a qué fondo elegir, lo que es representado con una selección completamente aleatoria. Los modelos calibrados con base en la técnica que aquí se siguiere deben ser periódicamente reestimados para ser calibrados. Esto puede hacerse basándose en encuestas aplicadas a un mayor tamaño muestral, y también por la vía de su aplicación a subgrupos más específicos de ahorrantes, con el objeto de lograr una mejora significativa en cuanto a su precisión. La popularización de este tipo de modelos por parte de las administradoras de fondos de ahorrantes facilitaría y fortalecería la asesoría profesional financiera, no sólo en el ámbito de las inversiones previsionales, sino también en las asesorías de inversiones financieras personales en general. En este sentido puede visualizarse un gran número de nuevas aplicaciones de la técnica, así como nuevas perspectivas de desarrollo futuro.
Finalmente, desde el punto de vista de la gestión pública, la historia reciente en Chile ha mostrado un comportamiento de ahorro errado en un gran número de cotizantes de las AFP. Esto revela grados de desconocimiento de la relación riesgo-rentabilidad de largo plazo, creándose un importante espacio para políticas públicas de educación financiera (Frijns et al., 2014 y Nam et al., 2013). También ha surgido la necesidad de que las decisiones de las personas en relación con los multifondos deben ser monitoreados permanentemente por la autoridad regulatoria, con el fin de mantener alineados los portafolios seleccionados por los ahorrantes respecto de los portafolios que se ajustan a sus verdaderos perfiles de riesgo. Esta investigación proporciona entonces una herramienta que permite diseñar instrumentos de monitoreo permanente a la autoridad, ayudando a definir los benchmarks o portafolios de referencia para cada grupo de ahorrantes.











 nova página do texto(beta)
nova página do texto(beta)