Gestión regional y local

 

Aplicación de metaheurísticas multiobjetivo a la solución de problemas de cartera de proyectos públicos con una valoración multidimensional de su impacto

 

Application of Multi–Objective Metaheuristics to Public Portfolio Selection Through Multidimensional Modelling of Social Return

 

Eduardo Fernández González*, Edy López Cervantes**, Jorge Navarro Castillo*** e Inés Vega López***

 

* Profesor–investigador de la Facultad de Ingeniería, Universidad Autónoma de Sinaloa. Blvd. Las Americas s/n, Ciudad Universitaria, Culiacán, Sinaloa. Tel: 667 71340 53. Correo–e: eddyf@uas.uasnet.mx.

** Adscrito a la Facultad de Informática, Universidad Autónoma de Sinaloa. Josefa Ortiz de Domínguez s/n, Ciudad Universitaria, Culiacán, Sinaloa. Tel. 66 77 16 13 61. Correo–e: edy@uas.uasnet.mx.

*** Adscritos a la Facultad de Informática de la Universidad Autónoma de Sinaloa. Josefa Ortiz de Domínguez s/n, Ciudad Universitaria, Culiacán, Sinaloa; Tel: 667716 13 61. Correos—e: jnavarro@uas.uasnet.mx, ifvega@uas.uasnet.mx.

 

Artículo recibido el 8 de junio de 2009
y aceptado para su publicación el 6 de diciembre de 2010.

 

Resumen

Se discuten las ventajas de la modelación multicriterio y del enfoque subjetivo asociado para resolver problemas de cartera de proyectos/programas/políticas del sector público. Sobre esa base, se presenta una definición de mejor solución de un problema de distribución de recursos públicos y su representación como problema de optimización multiobjetivo. Se describe también un método de solución mediante algoritmos evolutivos multiobjetivo, en el cual se incorporan las preferencias del decision–maker utilizando el enfoque de los métodos ELECTRE. La propuesta se ejemplifica con buenos resultados en casos de tamaño real, que ilustran métodos de selección de programas de asistencia social y de proyectos de investigación básica.

Palabras clave: carteras de proyectos públicos, optimización multiobjetivo, algoritmos evolutivos, relaciones de no inferioridad borrosas.

 

Abstract

This paper is devoted to the problem of allocating public funds to competing programs, projects or policies. Under a subjective approach, we apply multi–criteria analysis to define the concept of highest social portfolio return. This concept is modeled as the best compromise solution of a 0–1 multi–objective optimization problem. Often powerful metaheuristics are required for solving real size problems, but with many objectives evolutionary algorithms are also inefficient. Such difficulty is overcome using a new method which incorporates decision–maker's preferences to the evolutionary search. We used a model based on a binary fuzzy outranking relation provided by ELECTREE methods for multi–criteria decision making. The proposal is examined through real size problems, in which good solutions are reached; examples illustrating the case of basic research project portfolios and social action program portfolios are shown here.

Keywords: public portfolio selection, multi–objective optimization, evolutionary algorithm, fuzzy outranking relations.

 

INTRODUCCIÓN

Una de las principales tareas de dirección en los distintos niveles de gobierno, organizaciones del sector público descentralizadas, fundaciones y centros de investigación es evaluar un conjunto de proyectos o políticas que compiten por apoyo financiero y con ellos formar una cartera. Con una cantidad disponible para distribuir inferior a la demanda no se puede otorgar el beneficio a todos los proyectos en competencia, aun cuando fueran aceptables individualmente. La decisión sobre la distribución de los recursos es política (Peterson, 2005) y de contenido ideológico. En el marco de ciertas restricciones determinadas por la orientación de las políticas públicas, es preciso formar carteras de calidad donde se maximice la repercusión (con connotaciones ideológicas) de la solución escogida. Se trata de un problema de enorme importancia social en que el costo de pobres soluciones es sencillamente inmenso, aunque su complejidad ha impedido hasta ahora avances verdaderos para resolverlo.

Algunas características comunes que distinguen a los proyectos sociales son las siguientes (Cohen y Franco, 1992; Fernández y Navarro, 2001):

• Muchas veces tienen repercusión económica indudable, pero que se manifiesta de modo indirecto, a largo plazo, y en forma muy difícil de cuantificar.

• Generalmente, además de su potencial impacto económico sobre el bienestar de toda o parte de la sociedad, el proyecto se caracteriza por otros atributos intangibles, que también son relevantes y que tomados integralmente determinan el beneficio esperado.

• Son importantes las consideraciones de equidad (grado de repercusión y grupo social beneficiado).

Aunque puedan diferir en el significado del impacto social de un proyecto, y por supuesto en la valoración del mismo, las diferentes corrientes ideológicas de la modernidad y la posmodernidad pueden coincidir en la siguiente proposición, de valor casi axiomático: Dados dos proyectos sociales A y B con similar costo, el consenso social debe preferir A si y sólo si su impacto social es mayor. Pasando por alto la dificultad de definir el impacto de una cartera de proyectos, dadas dos carteras C y D sujetas al mismo presupuesto, C debería ser preferida por el consenso social si y sólo si supera a D en la valoración de su impacto.

Luego, una dificultad principal para el análisis y la búsqueda de la mejor cartera es la necesidad de disponer de una medida de impacto de los proyectos sociales o al menos de una forma de estimarlo y comparar alternativas. La segunda dificultad importante es la complejidad exponencial del problema matemático asociado a la exploración del conjunto de alternativas; si se tienen TV proyectos o políticas candidatos a recibir apoyo, la cantidad de carteras posibles es 2^N, cantidad inmanejable por métodos de exploración rudimentarios aun para pequeños valores de N.

Las políticas públicas se evalúan por su contribución a la equidad y a la eficiencia de la producción social (Cohen y Franco, 1992). La repercusión social de un proyecto debería ser una medida integrada de esos criterios. No faltan métodos que, aunque con serias dificultades para manejar atributos intangibles, pueden estimar la contribución al aumento de la riqueza social. Pero es muy cuestionable la objetividad de una medición de la contribución de proyectos o políticas a la equidad social. La diversidad de intereses y de ideologías que coexisten, en general no permiten un consenso social al respecto, consenso necesario para asegurar una objetividad de la medida. Esa falta de objetividad está relacionada estrechamente con la no existencia de una función de preferencia social y con la ambigüedad de las preferencias colectivas manifiesta desde Condorcet hasta Arrow y más recientemente Sen. El impacto social es objetivo, pero su valoración es parcialmente subjetiva porque depende de la cosmovisión de los que evalúan, de su particular sistema de preferencias, creencias y valores. Esta concesión a la subjetividad no debe ser vista en forma peyorativa, como sinónimo de lo arbitrario. La toma de decisiones siempre tiene elementos de subjetividad; la medición de los criterios en que se basa la decisión debe tratar de ser objetiva, pero la valoración, que implica siempre una integración de información a veces contradictoria, es un producto de la mente que resulta de hacer pasar la información objetiva disponible por el tamiz de la propia subjetividad. La objetividad de la ciencia de la decisión no radica en descartar los elementos subjetivos, sino en lograr un modelo que refleje plenamente el sistema de valores de quien decide.

El objetivo central de este trabajo es desarrollar un método general que permita explorar el espacio de carteras y buscar su optimización, sin necesidad de disponer de una medida numérica del impacto social de las soluciones. Para esto se deberá, además, i) justificar la equivalencia entre la optimización del impacto y la solución de un problema de optimización multiobjetivo; ii) precisar el rol de lo objetivo y lo subjetivo en la valoración del impacto de la cartera; iii) proponer un procedimiento efectivo de exploración de un espacio que tiene complejidad exponencial con el número de proyectos.

 

PERSPECTIVA CRÍTICA DE LOS ENFOQUES PREDOMINANTES

En la selección de proyectos públicos hay tres problemas estrechamente vinculados:

1. La evaluación de proyectos individuales.

2. La comparación de proyectos alternativos y la selección de los mejores.

3. La distribución de recursos y la formación de una cartera.

Son tres problemas de decisión con características propias. La evaluación (1) supone esencialmente una decisión de clasificación (aceptable o inaceptable, excelente, bueno, malo, etc.), y descripción con la mayor precisión posible de los costos y las diferentes dimensiones de repercusión del proyecto o política pública. La comparación (2) es un problema de selección de la mejor alternativa de un conjunto, o quizás el problema de ordenar (hacer un ranking) de un conjunto de opciones que por sí mismas son aceptables, pero que apoyar más de una carece de sentido. La distribución de recursos (3) significa seleccionar un subconjunto de las propuestas que en sí mismas son aceptables; se trata de seleccionar el mejor de los subconjuntos de proyectos que se puede apoyar con los recursos disponibles; es también un problema de selección pero sobre el conjunto potencia (conjunto de todos los subconjuntos) de proyectos aceptables. Tanto en (2) como en (3) se supone que el apoyo se le brinda solamente a proyectos aceptables, por lo tanto el proceso de evaluación siempre está presente. Pero (2) y (3) de ninguna manera se reducen a problemas de simple evaluación.

En todo problema de decisión existe un actor central encargado de tomar la decisión. Llamaremos decision–maker (DM) a esta persona o grupo, cuyo sistema de preferencias, valores, prioridades, es determinante en la solución del conflicto entre atributos que se contradicen. El DM es el factor subjetivo del problema de decisión, es el encargado de valorar lo objetivo (los atributos del proyecto) a través de su particular visión. Los métodos existentes para resolver los problemas anteriores se diferencian por el rol que se le asigna al DM y su subjetividad. Algunos, como el análisis costo–beneficio o el análisis costo–efectividad, aspiran a la objetividad total, procesando argumentos positivos y negativos que permitan asignar al proyecto una evaluación (1), o un lugar en el orden (2), que sea prácticamente independiente del DM. La alternativa es reconocer que el manejo de múltiples criterios y de varios intangibles requiere poner en primer plano la subjetividad del DM.

El intento más aceptado para estimar el impacto de proyectos sociales en una escala común es el enfoque costo–beneficio (e.g. Boardman, 1996).

Toda consecuencia positiva de un proyecto es equivalente a cierto beneficio económico; consecuencias negativas equivalen a costos. La distribución en el tiempo de los costos y los beneficios tomados como flujos de caja netos, y descontados con un cierto valor de la tasa de descuento social, permite calcular el valor presente del proyecto. La repercusión del proyecto corresponde al valor actual neto social, medido en términos de incremento de la riqueza nacional (cf. Cohen y Franco, 1992). Su magnitud puede utilizarse para decidir la aceptabilidad del proyecto en caso de que sea positivo, para ordenar las propuestas alternativas (2) o para seleccionar carteras. El impacto de una cartera de proyectos es la suma de sus valores netos sociales. Se puede encontrar la mejor cartera resolviendo un problema de programación matemática en que se maximiza el valor actual neto de la cartera.

El enfoque costo–beneficio tiene serias dificultades para manejar la complejidad multidimensional de las consecuencias de un proyecto, sobre todo cuando es necesario valorar intangibles que carecen de referencia en el mercado. Aunque muy popular entre los economistas, el enfoque costo–beneficio ha sido severamente cuestionado por la literatura de análisis multicriterio (French, 1993; Dorfman, 1996; Bouyssou et al, 2000). Algunas de las deficiencias que se señalan son:

• La virtual imposibilidad de evaluar válidamente algunos efectos en unidades monetarias. Se intenta resumir los efectos de un proyecto en un simple número, el cual aparentemente refleja el resultado de un proceso bastante discutible de monetarización de su impacto; en dicho proceso se llega a extremos como ponerle precio a la vida humana y a daños ecológicos irreversibles. Al margen de las valoraciones éticas, cabe preguntarse qué sentido tiene intentar valorar monetariamente intangibles para los que nunca ha existido un mercado, muchas veces prohibido por razones morales.

• Debido a la gran cantidad de parámetros estimados con distinto nivel de precisión que se utilizan en el cálculo del valor actual neto social, el análisis de sensibilidad se reduce a estudiar el impacto en la variación de unos pocos de ellos, modificando uno cada vez; un análisis de sensibilidad robusto debería combinar simultáneamente variaciones de todos los parámetros.

• La dificultad de evaluar la razón social de descuento (e.g. French, 1993; Chapman et al, 2006).

• Las limitaciones del valor actual neto social como criterio de decisión.

• Quedan sin considerar criterios de equidad y de redistribución de la riqueza.

• La linealidad implícita en el enfoque es únicamente válida para cambios marginales.

• La excesiva atención que se brinda a la valoración monetaria hace que dejen de considerarse otras consecuencias importantes.

El análisis costo–efectividad es otro popular enfoque que pretende la objetividad en la evaluación de proyectos sociales, estableciendo un juicio comparativo entre diferentes proyectos que se estiman previamente aceptables (cf. Cohen y Franco, 1992). El juicio se basa en el cálculo del costo por unidad de beneficio que aporta cada proyecto. Se prefieren naturalmente las propuestas que logran mayor beneficio por el mismo costo, o un costo menor por unidad de beneficio. El método funciona satisfactoriamente para ordenar un conjunto de proyectos alternativos que ofrecen beneficios cuantificables. Confronta serias dificultades para manejar intangibles y no ofrece medidas que se puedan integrar a nivel de carteras.

El análisis multicriterio ofrece un camino alternativo. Comprende un conjunto de técnicas para modelar las preferencias del DM y analizar responsablemente la complejidad inherente a los problemas reales de decisión. Algunos de los métodos más conocidos son MAUT (cf. Keeney y Raiffa, 1976), AHP (cf. Saaty, 2005), y los métodos de sobreclasificación (Roy, 1990; Figueira et al., 2005; Brans y Mareschal, 2005). Constituyen una buena opción para tratar ventajosamente varias limitaciones del análisis costo–beneficio, pues pueden manejar criterios cualitativos e intangibles, preferencias mal definidas, conocimiento ambiguo e impreciso, y condiciones de veto. Diferentes enfoques del análisis multicriterio se han aplicado recientemente para evaluar y seleccionar proyectos públicos (e.g. Gabriel et al, 2006; Duartey Reis, 2006; Bertolini et al., 2006; Mavrotas et al., 2006; Sugrue et al., 2006; Mavrotas et al., 2008; Fernandez et al., 2009a). Las ventajas del enfoque multicriterio han sido reconocidas por varias fuentes (e.g. Kaplan y Ranjithan, 2007; Liesio et al., 2007).

Los métodos multicriterio permiten obtener un ranking de calidad (o de impacto) del conjunto de proyectos. A partir del ranking la forma natural de llegar a la decisión final sobre la cartera es asignar los recursos de acuerdo con el orden de los proyectos en el ranking hasta su agotamiento (e.g. Martino, 1995); pero esto supone que:

i) se confía plenamente en las prioridades que se derivan del ranking,

ii) diferencias en costo no pueden alterar esa prioridad;

iii) pueden olvidarse las medidas de cartera;

iv) se considera despreciable la interacción entre proyectos.

Esta forma de distribución de recursos es simple pero muy rígida y ha sido criticada por otros autores (e.g. Gabriel et al, 2006); nunca sería razonable sustituir un proyecto muy costoso por dos o más proyectos baratos que se encuentren en posición algo inferior en el ranking, obtener la mejor cartera es lograr un compromiso entre impacto y costo, y repartir los recursos siguiendo estrictamente la información del ranking deja, de lado el último atributo. No considera las medidas de cartera. La decisión del conflicto entre costo y calidad de un proyecto sólo puede resolverse en el marco de la interrelación del conjunto de proyectos que satisfacen un nivel mínimo de aceptabilidad. Para aclarar, consideremos la siguiente situación: los proyectos son evaluados con una función de valor de la que emana el ranking, supongamos que el modelo asigna 82 puntos al proyecto 1, y 80 puntos a los proyectos 2 y 3; supongamos también que el costo de 1 alcanza para financiar 2 y 3. Puede que la mejor solución fuera apoyar 2 y 3, pasando por alto la información del ranking. La decisión deseada de encontrar la cartera de más impacto no se garantiza siguiendo el orden del ranking. La verdadera elección es entre carteras, no entre proyectos. No se puede encontrar la mejor decisión si no se comparan carteras. Para medir el impacto de una cartera es necesario balancear la calidad y la cantidad de proyectos que se apoyan, integradas en una medida de valor de la cartera, que refleje su impacto. Posteriormente se requiere la optimización de esa medida (e.g. Gabriel et al, 2006).

Una propuesta para optimizar una medida directa de impacto fue presentada por Fernández y Navarro (2001,2002). Se desarrolla un modelo subjetivo de la calidad de la cartera de proyectos públicos desde una perspectiva normativa multicriterio. Se crea una escala de proporción para reflejar el valor subjetivo (valor para el DM) del proyecto en dependencia de su evaluación y de su naturaleza. El valor subjetivo es de hecho una medida de impacto. La suma de los valores subjetivos de los proyectos que se apoyan es una medida del impacto de la cartera. Se llega a un modelo numérico del impacto susceptible de ser optimizado con notable eficiencia (cf. Fernández et al, 2009a; Litvinchev et al., 2010) para una aplicación de gestión de i & d en grandes organizaciones públicas). Desde un punto de vista normativo la idea de este modelo posee sustento, pero en la práctica exige mucho esfuerzo del decision–maker. En la creación del modelo se supone que los proyectos de la misma naturaleza que comparten un grado de evaluación tienen el mismo impacto. Es dudoso que se pueda, en general, obtener información precisa sobre el impacto social a partir simplemente de la evaluación del proyecto.

Si no se dispone de una medida de valor de la cartera, un enfoque posible consiste en abordar la búsqueda de la mejor cartera a través de la optimización multiobjetivo. En la literatura se reportan numerosas aplicaciones para la distribución de recursos públicos (cf. Zanakis et al., 1995; Steuer y Na, 2003 para revisiones documentadas de esas propuestas). Dentro del espacio de carteras se busca una solución de Pareto aceptable de un problema de optimización vectorial. Los objetivos representan ciertos beneficios o costos sociales de cada proyecto apoyado, de manera que se puedan cuantificar en alguna escala y agregar a nivel de cartera. La forma matemática es de un problema de mochila multiobjetivo. Apreciablemente, el método más utilizado es la programación por metas 0–1 (Chan et al, 2005; Steuer y Na, 2003; Lee y Kim, 2001; Badri et al, 2001; Fandel y Gal, 2001; Santhanam y Kyparisis, 1995; Zanakis et al, 1995). La solución de Pareto se obtiene por la asignación de ciertas metas para cada objetivo (modelación a priori de las preferencias del DM).

La modelación como problema de mochila multiobjetivo parece adecuada para considerar varios criterios en conflicto y sus medidas de cartera. Sin embargo, los métodos que se han aplicado parecen válidos en situaciones específicas y carecen de una sustentación suficientemente general. En su mayoría, los métodos parecen diseñados ad hoc para el problema al que se aplican y difícilmente pueden abordar situaciones más complejas que las descritas en la literatura. Cuando se hace necesario manejar muchos atributos y numerosos proyectos, se necesitan formas más potentes de modelar preferencias y de obtener soluciones óptimas. Importan la complejidad exponencial de los problemas de mochila y las limitaciones cognitivas del DM para evaluar soluciones con numerosos atributos en conflicto, que se manifiestan ya con cinco criterios en contradicción (Marakas, 2002). La modelación a priori de las preferencias difícilmente puede encontrar una buena solución de compromiso. La incorporación de preferencias durante la búsqueda (interactivamente) o a posteriori se hace muy difícil cuando aumenta la dimensión del problema, porque a) la generación de soluciones es un proceso lento y, más importante, b) las limitaciones cognitivas del DM no le permiten evaluar soluciones en conflicto de manera cómoda y consistente.

 

EL SENTIDO DE OPTIMIZAR EL IMPACTO DE UNA CARTERA DE PROYECTOS PÚBLICOS

Asignar un contenido completamente objetivo al impacto social supone la existencia de preferencias sociales bien definidas. En la base de la teoría que sustenta el enfoque costo–beneficio se halla la existencia de una función de "bienestar social" o función de "utilidad social"

donde W es un valor real y U_j representa la utilidad del individuo j–ésimo, que es a su vez una función de los bienes (en sentido general) que la sociedad produce (Bouyssou et al, 2000). Declarar que Wcs una función de preferencia social significa que si la sociedad comparara dos estados diferentes, debería preferir el que arroja un valor mayor de W. La relación de preferencia–indiferencia sería entonces transitiva y completa sobre todos los estados posibles de la sociedad (French, 1993). Debido a las limitaciones para dar un contenido racional a las preferencias colectivas —paradoja de Condorcet, Teorema de Imposibilidad de Arrow, preferencias dependientes del contexto, etc.— (Bouyssou et al., 2000; Tversky y Simonson, 1993; French, 1993), la existencia de W es fuertemente cuestionada por Sen y otros (e.g. Sen, 2000, 2008). La amalgama de intereses contradictorios y sistemas de valores contrapuestos en un organismo tan complejo como la sociedad hace imposible definir una medida de valor W desde el punto de vista de la sociedad. Sin negar el contenido objetivo del interés social, es indudable que la dificultad para aprehenderlo abre espacio a métodos que pretenden modelar las preferencias de individuos concretos, capaces de expresar sus preferencias de modo más o menos consistente. Si no existe o no se dispone de una medida objetiva de impacto social, se puede trabajar con medidas subjetivas que se aproximen aceptablemente. La subjetividad es una categoría esencial en la decisión. En presencia de múltiples criterios, no se puede resolver ningún problema de decisión sin apelar a cierto componente subjetivo que determine la solución del conflicto de atributos. Cuando existe contradicción de atributos, la solución del conflicto depende del sistema de preferencias de quien decide. En este sentido la valoración del impacto social no puede separarse de quien la realiza.

Si se renuncia a la objetividad de W, los métodos del análisis multicriterio centran su atención en la modelación de las preferencias del DM. Si exigimos normativamente su apego a los axiomas de la racionalidad postulados por la teoría de la decisión (véase por ejemplo, French, 1993), entonces existe una función Wque refleja sus preferencias sobre "estados" de la sociedad, en el sentido de que

a) W'(A) > W'B) si y sólo si el DM considera que el "estado social" A es mejor que B

b) W'(A) = W' (B) si y sólo si manifiesta indiferencia entre A y B.

Postular la existencia de W' no significa acogerse necesariamente al modelo normativo de diseño de políticas públicas (e.g. Tresch, 2002). W'es una función de preferencias del DM, que responde a su sistema de valores, cualquiera que éste sea. El apego estricto a la ética de la democracia (no sólo al factor electoral, sino a la democracia como gobierno del pueblo y para el pueblo) debería hacer que W' fuera una apropiación subjetiva, una cierta interpretación de las preferencias sociales. Así, se asume que el DM se comporta como un planificador benevolente. Si Wresponde al modo en que el DM interpreta el bienestar social, desde su visión particular y en correspondencia con su posición ideológica, su comportamiento semeja el de un dictador benevolente (e.g. Brennan y Buchanan, 1980). Según los modelos de competencia electoral Wpodría coincidir también con los intereses electorales del DM, del grupo o partido que él representa; así, la valoración que el DM realiza de un estado potencial del objeto social está determinada por el comportamiento que espera del votante medio (Ponce, 2010). El DM, que desde la perspectiva normativa ideal de Samuelson (1954) debería distribuir los recursos públicos según W, en la práctica sólo puede hacerlo según W' debido a varias razones: 1) porque aun adoptando el rol del planificador benevolente desconoce la real preferencia social de la mítica W; 2) porque en un sistema democrático el DM se siente éticamente cómodo cuando actúa según su interpretación del deseo del votante que promete el éxito electoral; 3) porque W' incluye, además del sistema de valores del DM, sus aspiraciones, sus creencias y las presiones a las que está sometido; en cualquier caso, como entidad racional, el DM actuará en el sentido de lo que cree que aumenta su satisfacción o disminuye su desagrado.

Centrar la atención en las preferencias del DM es un acto eminentemente pragmático, pero que en condiciones de legitimidad democrática, no carece de sentido ético. Se supone que el DM es actor y resultado de un proceso democrático, y depositario de la confianza popular. En condiciones de democracia participativa, la sociedad dispone de mecanismos para de alguna manera castigar (encuestas, procesos electorales nítidos, rendición de cuentas, revocación de mandato) si W' se aleja mucho de W', o al menos de las preferencias de los votantes. Por lo tanto, resolver un problema de cartera de proyectos públicos es encontrar la mejor solución desde el punto de vista del DM, persona o grupo que representa, al menos parcialmente, el interés social.

Los métodos del análisis y la ayuda para la decisión son herramientas para que el DM pueda realizar un buen proceso de decisión, de modo que sea posible lograr la integración de los elementos objetivos y subjetivos bajo un paradigma que elimine probables inconsistencias. En este sentido:

• El DM debe tener acceso a la información relevante sobre las alternativas que valora. La información objetiva que recibe debe ser asimilada por su subjetividad para crear un nuevo estado de lo subjetivo (Buchanan y Henig, 1997).

• El proceso de decisión debe conducir a un esclarecimiento de las preferencias del DM, y a lograr que realice una elección acorde con sus preferencias y creencias consistentes (French, 1993; Howard y Matheson, 1984).

• El DM ha de tener la posibilidad de explorar el conjunto de alternativas, someter sus opciones a comparación, y enriquecer su juicio analizando otras variantes que quizá no fueron consideradas al principio (French, 1993; Buchanan y Henig, 1997).

El objetivo de la ayuda para la decisión en los problemas de cartera de proyectos públicos debe ser suministrar al DM un marco de trabajo que, ajustándose a los enunciados anteriores, lo ayude a encontrar la mejor solución. Luego, se requiere definir ese concepto, el modelo matemático que lo describe, las premisas que apoyan su existencia, el modo de identificarlo en la práctica, los procedimientos algorítmicos que se pueden emplear para abordar los casos más complejos y los aspectos de ingeniería de software que sean relevantes.

 

Definición de la mejor cartera

Denotemos por E₀ el estado actual de la sociedad o del objeto social respecto al que se va a resolver un problema de cartera, desde la percepción del DM. Sea P el presupuesto disponible. Consideremos un conjunto de proyectos candidatos individualmente aceptables y sea C= {C₁, C₂ ... C_L} el conjunto de las diferentes combinaciones (carteras) de proyectos que cumplen con las restricciones presupuéstales. Estas restricciones pueden estar influidas por consideraciones del DM relativas a equidad, eficiencia, distribución geográfica, prioridades sobre distintos tipos de proyectos, etc. Sea E= {E₁, E₂,... E_M} {M≤L) el conjunto de los distintos estados del objeto social al que se puede arribar, desde el punto de vista del DM, al ejercer el presupuesto P según todas las combinaciones factibles.

Nótese que existe una correspondencia funcional entre C y E.

A partir de la premisa de que el problema lo resuelve el DM y según su sistema de preferencias, se puede dar un significado directo al concepto de optimizar una cartera de proyectos sociales: Supongamos que la cartera C₁ provoca que el estado social cambie de E₀ a E_k si no existe un estado E_j del conjunto E tal que el DM pueda establecer una relación de preferencia asimétrica a favor de E_jsobre E_K, entonces C₁ es la mejor cartera.

Si se acepta que las preferencias del DM se rigen por W', es posible dar una interpretación cuantitativa del impacto social que para el DM produce una cartera C_j que hace cambiar el estado social al nivel E_j . La medida de impacto I (C_j ) puede definirse como la diferencia W'E_j) — W'(E₀). Y la cartera de mayor impacto (la mejor cartera factible) es la que maximiza esa diferencia en el conjunto C, que está determinado por las restricciones al presupuesto y a las formas en que puede ser empleado. Luego, optimizar la cartera de proyectos públicos puede definirse como:

donde R_F denota la región factible determinada por todas las restricciones presupuéstales que el DM considere conveniente o necesario incluir.

Entonces, la formulación (2) presupone dos problemas: a) la modelación de W'(en realidad basta con modelar W'(E_K)—W'(E_J), y b) la solución de un problema de optimización combinatoria en el conjunto de carteras factibles. Naturalmente b) está sujeto a la forma del modelo que resulte de a).

 

MODELO MATEMÁTICO MULTICRITERIO

Consideraremos un problema de cartera de proyectos públicos P bajo las siguientes premisas:

A) El estado del objeto social se puede caracterizar por un conjunto finito F= {f₁,f₂,.. .f_n } de atributos.

B) F'F está compuesto por atributos que poseen una escala cuantitativa natural. F" = F– F' está formado por atributos intangibles que se pueden representar por variables indirectas que los reflejan en cierta escala. Puede haber varias medidas indirectas para representar un único atributo. De manera que el estado del objeto social se puede caracterizar por un conjunto V={v₁,v₂,...v_N} de variables que directa o indirectamente reflejan a F(generalmente N≥ n).

C) El encargado de la decisión (el decision–maker) es una persona única o un grupo suficientemente homogéneo de modo que sea admisible suponer preferencias comunes. De acuerdo con la teoría normativa de la decisión (e.g. French, 1993), existe una función de valor W' (f_x, f₂,... f_n) = = U{v_x, v₂,...v_N) que expresa las preferencias del DM sobre los estados del objeto social.

D) La función Ucs creciente con cada v_i

E) Existe un conjunto de proyectos P_r={p₁, ... p_α} candidatos a recibir apoyo, sin que la distribución temporal de sus comienzos o términos sea relevante.

F) Sea p_j un elemento cualquiera de P_r . Se asume que: i) p_r cumple las restricciones presupuéstales de P ; ii) p_j es considerado aceptable por el DM.

G) Si C_j ,es una cartera de proyectos compuesta por un subconjunto de elementos de P_r, C_j produce una variación estimada (Δv) en las variables que describen el estado del objeto social. (Δv)_j se calcula a partir del conocimiento de los (Δv)_j de los proyectos que forman parte de Cj mediante un número finito de pasos. Es decir, (Δv)_j = g ((Δv)_J), j toma todos los valores de los proyectos que están en C_j, y g es una función elemental.

A y B son perfectamente sustentables. Ya que no se impone una condición al tamaño de F o V, un proceso creativo que involucre a un analista de la decisión trabajando con el DM debe permitir determinar atributos y variables de medición que ofrezcan un reflejo razonable del objeto social prácticamente en cualquier caso (cf. Keeney y Raiffa, 1976; French, 1993). Siguiendo a Keeney y Raiffa (1976) se buscará un conjunto de atributos completo, operacional y de tamaño mínimo. Ces una consecuencia de la teoría normativa de la decisión; ésta no implica que W"o U sean conocidas por el DM; menos aún que exista una forma analítica para esas funciones, pero sí implica la posibilidad de un proceso de aprendizaje en que el DM paulatinamente precise información sobre ellas, y la posibilidad de llegar a tener un sistema de preferencias consistente y reconocer la mejor solución de cartera en un proceso de búsqueda del máximo de U. La premisa D es trivial pero necesaria para poder pasar a una formulación multiobjetivo en el sentido de maximizar. La premisa E restringe el análisis a decisiones de cartera en que el tiempo interviene débilmente y no existen efectos de secuenciación. Por su parte, F implica que se ha realizado un proceso previo de evaluación de los proyectos, después de que cada uno queda caracterizado por su impacto sobre las variables indicadoras del estado del objeto social, pero sin tomar en cuenta su potencial sinergia. La condición de aceptabilidad a que se refiere la premisa significa que el proyecto satisface de manera razonable los objetivos del DM, de forma que merecería ser apoyado si no existieran restricciones presupuéstales que obligan a priorizar proyectos en la cartera. De este modo se asegura que la cartera solución no contendrá proyectos que, tomados individualmente, sean inaceptables. G implica que se conoce el modo de agregar los efectos de los proyectos que integran la cartera y que se puede realizar utilizando una función elemental; en el caso más simple la función ¡–es una suma de los efectos individuales (con interacción despreciable entre proyectos y consecuencias sumables a nivel de cartera). En otros casos ¡puede incluir efectos de interacción o probabilistas.

Bajo las premisas anteriores, el impacto de la cartera C_J puede definirse

donde v₀ representa el estado inicial del objeto social. Y de forma equivalente a (2), el problema de encontrar la mejor cartera es

 

El desconocimiento de U hace imposible resolver (4) mediante ningún proceso que implique evaluaciones de esa función. La solución debe ser entonces indirecta, en la que interviene solamente la capacidad del DM para comparar soluciones (o sea, estados del objeto social caracterizados por el vector v₀ + (Δv)_j . Consideremos el problema de optimización multiobjetivo

donde v₁. es la i–ésima componente de v₀ + (Δv)_j . Introduzcamos además la siguiente definición para caracterizar las soluciones de un problema multiobjetivo como (5).

Definición 1: Se dice que x R_F es solución de Pareto del problema (5) si para todo y R_F tal que v_i(y) > v_j(x) para cierto i, se tiene necesariamente que v_j(x) > v_j(y) para algún valor del subíndice j.

Definición 2: Se dice que x R_F domina a y R_F si v_j(x)≥ v_j (y) para todo j, y existe i tal que v_i (x) > v_i(y).

Las soluciones de Pareto también se llaman no dominadas.

Resolver un problema de optimización multiobjetivo es encontrar el mejor compromiso, una solución de Pareto suficientemente satisfactoria que el DM acepte como solución final (Hwang y Masud, 1979). Resolver (5) es identificar una solución tal que no se encuentre otra en R_F que sea preferible a ella. Bajo la premisa Cel máximo global de U al resolver (4) daría una solución que cumple con el enunciado que define ese mejor compromiso de (5). Simultáneamente, si existe U, el mejor compromiso en (5) es el máximo global buscado en (4). Luego, los problemas (4) y (5) son equivalentes bajo la premisa C.

La existencia de una función de valor es más restrictiva que la del mejor compromiso de (5). La primera implica que para toda pareja de soluciones el DM puede establecer un enunciado de preferencia o indiferencia, que tiene además la propiedad de transitividad. Contrariamente, al resolver (5) no se exige la transitividad de la preferencia–indiferencia, y se tolera la incomparabilidad (el deseo de no establecer un enunciado de preferencia–indiferencia entre una pareja de soluciones) (cf. Roy, 1996). La mayor generalidad de (5) permite remover la premisa C, considerando entonces que encontrar la mejor cartera es identificar el mejor compromiso de (5). Entonces, C puede sustituirse por una premisa más laxa si existe un método para determinar el mejor compromiso de (5). Desechar C puede ser importante, pues permite que el rol de DM sea desempeñado por actores de la decisión que actúan como delegados, por grupos de cierta heterogeneidad, en general por entes con preferencias mal definidas. Esto supone renunciar a (3) como definición de impacto de la cartera; pero no es una desventaja significativa, pues lo importante es optimizar, no evaluar el impacto.

 

BÚSQUEDA DE LA MEJOR CARTERA EMPLEANDO ALGORITMOS EVOLUTIVOS

Resolver el problema (5) es prácticamente imposible con las técnicas convencionales de la investigación operativa en instancias de gran tamaño y con numerosos atributos. Proponemos emplear algoritmos evolutivos multiobjetivo (AEMO) para resolverlo. Las ventajas de la computación evolutiva para la optimización multicriterio radican en i) su capacidad para generar una aproximación a la frontera de Pareto ya desde las primeras generaciones; ii) su independencia de las propiedades matemáticas de las funciones objetivo y de las restricciones, y Hi) su dependencia polinómica del tamaño de la instancia (cf. Coello et al., 2002).

La tendencia que ha predominado en los últimos años es hacia el desarrollo de AEMO basados en ranking de Pareto y con elitismo (Coello et al., 2002), que son capaces de generar la frontera de Pareto en muchos problemas. Sin embargo, los AEMO basados en Pareto tienen serias limitaciones para tratar problemas con numerosos objetivos. Cuando se incrementa el número de objetivos, ya en las primeras generaciones aumenta considerablemente la cantidad de soluciones no dominadas en cada población, que no son miembros de la verdadera frontera de Pareto. Entonces es muy débil, casi inexistente, la presión selectiva hacia esa frontera y el AEMO pierde la capacidad de converger en ella. Según Coello et al. (2007), cinco objetivos es ya una cifra crítica para los mejores AEMO basados en Pareto. En particular, la efectividad del que es quizás el benchmark más importante en computación evolutiva, el algoritmo NSGA–II (Deb, 2001), se degrada muy rápidamente con la dimensión del espacio de los objetivos (Coello et al., 2002).

Pero generar la frontera de Pareto es sólo un primer paso hacia la solución final. No se puede resolver un problema multicriterio sin modelar las preferencias del DM en la búsqueda del "mejor compromiso". Con mucho, la mayoría de las propuestas y aplicaciones de los AEMO pretenden realizar una modelación aposteriori de esas preferencias; esto es perfectamente posible en problemas con dos o tres objetivos y algunas decenas de soluciones de Pareto. Pero tratando con cinco o más objetivos o con centenares de soluciones de Pareto, las limitaciones cognitivas del DM imposibilitan que pueda manejar situaciones tan complejas. Lo más probable es que el DM, sin herramientas matemáticas ni heurísticas para manejar tal complejidad, se conforme con una solución quizás aceptable pero distante del mejor compromiso. Coello et al. (2005) reconocen que el manejo de las preferencias es uno de los pendientes principales del estado del arte de los AEMO.

Para incorporar las preferencias del DM en forma más eficiente, Fernández et al. (2010a) propusieron una idea muy promisoria. De una relación de sobreclasificación borrosa construida siguiendo las ideas de los métodos ELECTRE (cf. Roy, 1990; Figueira et al., 2005), definida en el espacio de soluciones, se deriva una relación de sobreclasificación no borrosa S con un valor de credibilidad suficientemente alto. A partir de S se define el concepto de solución no superada que generaliza el concepto de no–dominancia. La solución a es no superada si con la información generada hasta la iteración t, no existe otra solución conocida b tal que b Say no dSb. A diferencia del concepto de no dominancia, la relación de no superación contiene las preferencias del DM, y su cardinal no depende significativamente del número de objetivos. Si S refleja adecuadamente las preferencias del DM, se puede demostrar que el mejor compromiso de un problema de optimización multiobjetivo debe ser una solución no superada (cf. Fernández et al., 2010a). De acuerdo con Fernández et al., (2010a) el concepto de no superación reemplaza a la no dominancia en el algoritmo NSGA–II, que es el benchmark de la optimización evolutiva multicriterio. El algoritmo propuesto (NOSGA, proveniente de non–outranked sorting genetic algorithm) es casi idéntico a NSGA–II, pero con ese reemplazo conceptual. A continuación presentamos cómo se adecua la propuesta de Fernández et al. (2010a) a la determinación de la mejor cartera de proyectos públicos. Conviene añadir la siguiente premisa:

H) Sean x, y dos soluciones diferentes del problema (5) en el espacio de los objetivos, que representan dos carteras denotadas por C_x y C_y respectivamente. Suponemos que el DM en colaboración con un analista de la decisión puede construir un modelo funcional σ(x,y) que dé como imagen una buena aproximación al grado de credibilidad del enunciado "la solución x es al menos tan buena como la solución y"'.

La experiencia de los métodos de la tendencia europea de decisión multicriterio sustenta aceptablemente esta premisa a través de la creación de relaciones borrosas de sobreclasificación como las que se derivan de los métodos ELECTRE (cf. Roy, 1990) y PROMETHEE (Brans y Mareschal, 2005). Hes bastante menos restrictiva que C. Las relaciones borrosas son una buena alternativa de compromiso al enfoque funcional (premisa C), pues al generalizarlo tienen mayor capacidad de expresión y son un buen modelo para fenómenos de intransitividad e incomparabilidad (Fodor y Roubens, 1994) que se manifiestan al resolver (5). El modelo de preferencias borrosas es más fácil de construir, necesita menos información e impone requisitos mucho menos severos al actor del proceso de decisión (Fernández y Olmedo, 2005). Puede reflejar preferencias mal definidas y preferencias colectivas (e.g. Fernández y Olmedo, 2005). Algunos trabajos recientes avanzan en la modelación de efectos de intensidad de preferencia en modelos derivados de la filosofía ELECTRE (cf. Roy y Slowinski, 2008; Fernández et al, 2010b).

Una crítica frecuente a los métodos ELECTRE es la cantidad de parámetros diversos que contiene y la dificultad del DM para asignar sus valores. No obstante, en los últimos años han aparecido varios procedimientos que logran identificar los parámetros del modelo a partir de cierta información preferencial que el DM emite cuando evalúa objetos aislados o compara pares de ellos (e.g. Doumpos et al., 2009; Fernández et al., 2009b; DiasyMousseau, 2006).

A partir de la premisa H, pasaremos a explicar el modo de resolver (5).

 

Modelo borroso de preferencias

Siguiendo a Fernández et al. (2010a), sea V el conjunto de objetivos del problema (5) y O su espacio imagen. Un elemento x O es un vector (x₁ ...x_N), x_i es el valor del i–ésimo objetivo. Suponemos que para cada criterio j hay un sistema relacional de preferencias (P_j, I_j) (preferencia, indiferencia) completo sobre el criterio j; o sea, para todo par de valores (x_j, y_j) del objetivo j y una y solamente una de las siguientes proposiciones es verdadera:

(6) permite utilizar umbrales de indiferencia para modelar imprecisiones. Es más general que la formulación usual x_j P_j 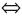x_j > y_j.

Según la metodología ELECTRE, la proposición xSy ("x sobreclasifica a y") ("el actor del proceso de decisión considera que x es al menos tan buena como y") se cumple si y sólo si la coalición de criterios que concuerda con ese enunciado es suficientemente fuerte y, al mismo tiempo, la coalición en discordancia no lo es. Formalmente, ese enunciado se puede expresar mediante la siguiente equivalencia lógica (cf. Perny, 1998):

donde:

C (x, y) es el predicado que modela la fuerza de la coalición de concordancia; D(x, y) es el predicado sobre la fuerza de la coalición en discordancia; Λ y ~ son conectivas lógicas para conjunción y negación, respectivamente.

Hay que observar que en el problema de cartera, el enunciado de sobreclasificación "el actor del proceso de decisión considera que x es al menos tan buena como y" es análogo a "el actor del proceso de decisión considera tener argumentos de peso para afirmar que la cartera x tiene al menos tanto impacto como y".

Denotemos por C_x,j = {v_j, V tales que x_j P_jy_j V x_j I_j y_j,} la coalición de concordancia con xSy. Sea D_x,y = { v_jV tales que y_j, P_j x_j} la coalición de discordancia.

Se denotan por c(x, y) y d(x, y) los valores de verdad de los predicados C(x, y) y D(x, y). De (7) y utilizando el operador "producto" para la conjunción, el valor veritativo de xSy se puede calcular como:

expresión en la que N(d(x, y)) representa el valor de verdad del predicado sobre la debilidad de la coalición discordante.

La forma más simple de modelar el predicado de concordancia es como en las primeras versiones de ELECTRE:

expresión en la que w' s denotan "pesos" (w₁ + w₂ + ... + w_n = 1)

La fuerza de la discordancia se mide en comparación con un umbral de veto vt_j–, que es la máxima diferencia y_j – x compatible con σ(x, y) >0. Siguiendo a Mousseau y Dias (2004), utilizaremos

donde _j=y_j — x_j y u_j es un umbral de discordancia (figura 1).

Si λ > 0.5 la condición σ (x, y) ≥ λ puede emplearse para definir una relación no borrosa de sobreclasificación xSy. λ= 0.67 puede considerarse un nivel aceptable de credibilidad (cf. Ostanello, 1983). σ{x,y) > ≈ 0.5 se asocia con una relación de sobreclasificación dudosa; σ(x, y) < 0.5 niega la sobreclasificación.

Siguiendo a Fernández et al. (2010a), con la información de a puede definirse una relación de preferencia asimétrica entre carteras.

Definición 3: Diremos que la cartera C_x supera a C_y si se cumple al menos una de las siguientes condiciones:

donde δ es un parámetro de sobreclasificación estricta propuesto por Fernández et al. (2010a). La relación de superación se denota por C_x P C_y , o equivalentemente xPy.

En el sentido de Roy (1996) pueden definirse relaciones de indiferencia, de preferencia débil y de incomparabilidad como sigue:

Defiinición 4: C_x y C_y son indiferentes si σ(x,y) ≥ 0.67, σ{y, x) ≥ 0.67 y además |σ(x,y) — σ(y, x)| <δ. Se denota por: C_xIC_y o por xIy.

Defiinición 5: Diremos que la cartera Cx supera en forma débil a C_y si se cumplen simultáneamente las siguientes condiciones:

1. σ(x,y) > 0.5 Λ σ(x,y) > σ(y, x)

2.   not xPy

3.  not xly

La superación débil se denota por C_x Q C_yo por xQy. Es también una relación asimétrica.

Definición 6: Si σ(x,y) <0.5 y σ(y, x) < 0.5 diremos que C_x y C_y son incomparables (C_xRC_y o xRy).

Definición 7: Sea A un subconjunto de R_F. Si no existe C_y A tal que C_y PC_X, diremos que C_x es no superada en A (x es no superada en la imagen de A).

Se plantea el siguiente teorema:

Teorema 1: Sea O la imagen de la región factible del problema (5). Entonces, el conjunto de soluciones no superadas en O es subconjunto de la frontera de Pareto de (5).

Demostración

Si el conjunto de soluciones no superadas en O está vacío, entonces es un subconjunto propio de la frontera de Pareto de (5). Si no está vacío debemos probar que α es no superada en O α es una solución de Pareto.

La demostración es trivial. Supongamos que la tesis es falsa. Entonces α es dominada por b O. Entonces, por la definición 3 se tiene que bPα. Es una contradicción con la hipótesis.

El recíproco es falso. A puede ser solución de Pareto y ser, sin embargo, superada por b. Basta encontrar b tal que bPα por satisfacer ii o iii.

Observaciones

1) Para cada elemento x O hay un conjunto que lo supera (S₀)_x= {y O tal que yPx}. card (S₀)_x denota su cardinal, que es una función entera dependiente de x. Obviamente, si x es no superada card (S_o )_x = 0.

2) Si no toda x de O está en un ciclo de P, entonces existe al menos una solución no superada en O.

Definición 8: Llamaremos frontera no superada de (5) al conjunto N_s = = {x O tal que card(S_o)_x = 0}.

N_s está vacío sólo en el caso de que todo elemento de O pertenezca a un ciclo de P. En los experimentos de López (2008) siempre se encontraron soluciones no superadas.

En lo que sigue intentaremos caracterizar el mejor compromiso de (5). Empleando un enfoque operacional, supongamos que el DM está comparando soluciones de (5). x*de O es el mejor compromiso si el DM no logra identificar y O tal que pueda establecer una preferencia asimétrica de y sobre x*. Si no hay argumentos de algún peso para que el DM reemplace a x* como la solución más aceptable del problema de optimización multiobjetivo bajo consideración, entonces se puede justificar que x*es el mejor compromiso.

Es obvia la siguiente proposición:

Proposición 1: Si N_s no está vacío, entonces el mejor compromiso de (5) es una solución x* N_S.

Si x* L N_s existe y de O tal que yPx*. Luego, el DM tendría argumentos de fuerza para reemplazar x*y colocar zy en su lugar. Por lo tanto, x*no puede ser el mejor compromiso de (5). La contradicción indica que el mejor compromiso es necesariamente una solución no superada.

Se requiere un modo de distinguir x*dentro de N_s. La relación de preferencia P está vacía en N_s, pero no así Q, que también es asimétrica. Para cada x N_S hay un conjunto D_x = {y N_S tal que y Qx}. card (D_x) denota su cardinal, un conteo de "debilidad" en N_s que es una función entera dependiente de x. El conjunto de soluciones débilmente no superadas en N_s es N_SD ={y N_S tal que card (D) = 0}.

Proposición 2: Si N_SD no está vacío el mejor compromiso es un elemento de N_SD.

La demostración es casi idéntica a la anterior. Si x* N_SD existe y de N_s tal que yQx*. Luego, el DM tendría alguna razón para reemplazar x*y colocar a.y en su lugar, puesto que la segunda es al menos tan aceptable como la primera. Por lo tanto, x*no puede ser el mejor compromiso de (5).

Si N_SD contiene varios elementos, no hay razones basadas en P y Q para determinar el mejor compromiso. Sin embargo, la relación borrosa de preferencia contiene más información, y el DM puede identificar argumentos a favor de algún elemento de N_SD si emplea medidas de calidad calculadas sobre todo el conjunto objeto de decisión. El score del flujo neto de sobre–clasificación es un método muy aceptado para realizar un ordenamiento de un conjunto sobre el que está definida una relación borrosa de preferencia (cf. FodoryRoubens, 1994). Si σ(x,y) es una relación borrosa de preferencia sobre un conjunto A, el flujo neto se define como . Su valor calculado sobre N_SD puede servir para justificar la elección de uno de sus elementos como solución final.

Si N_SD está vacío, todo elemento de N_s está en un ciclo de Q. Eso cuestiona la existencia de mejor compromiso del problema (5) en el sentido de la definición de la sección cuarta. No obstante, el DM puede llegar a una solución final si encuentra argumentos para identificarla utilizando otras medidas de calidad tomadas sobre el conjunto objeto de decisión, que ahora es N_s. Sugerimos que el DM compare los elementos de N_s utilizando como criterios de evaluación card (D_x) yF_n(x).

 

Conclusiones parciales

1. Un procedimiento de búsqueda debe comenzar por identificar N_s, pues admitiendo que no está vacío, el mejor compromiso es miembro de ese conjunto.

2. Si N_s contiene varios elementos, se debe identificar N_SD. Entonces: a) Si N_SD tiene un solo elemento, ese es el mejor compromiso para la proposición 2; b) si hay varios elementos en N_SD, determinar el mejor compromiso aplicando una medida de flujo neto de sobreclasificación en N_SD; o) Si Agesta vacío, determinar una mejor solución en N_svalorando dos criterios: card(D) yF_n(x) calculados ambos sobre N_s.

 

El algoritmo evolutivo

Siguiendo a Fernández et al. (2010a) y a López (2008), para determinar una aproximación a la frontera no superada se utiliza una variante de NSGA–II pero reemplazando no dominancia por no superación.

NSGA–II utiliza dos procesos principales: 1) la división en clases de no dominancia y su ranking, y 2) el cálculo de la distancia crowding. La nueva propuesta es crear y ordenar clases de no superación (de acuerdo con el card (S_o)) y sustituir la distancia crowding por una medida de debilidad como card (D_x), pero tomada sobre la población. La distancia crowding se omite para guiar la búsqueda hacia una zona preferida de la frontera de Pareto y de N_s. Se realiza un proceso de filtrado similar al de NSGA–II, en que se extraen frentes formados por individuos no superados. Si no hay individuos no superados, se pueden separar los individuos en frentes en que lo común sea el valor del cardinal del conjunto S_o. Entonces los individuos de la primera clase serán aquellos con el menor cardinal de S_o; la segunda clase estará conformada por el segundo menor cardinal de S_o y así sucesivamente.

La adaptación de este algoritmo se denominó non–outranked–sortinggenetic algorithm (NOSGA) . A continuación su pseudocódigo:

Las restricciones se imponen a través del proceso de selección. En el torneo binario, un individuo factible predomina sobre uno infactible. Si ambos son infactibles, predomina el que este tenga menor card (S_o); si los individuos pertenecen a la misma clase de no superación se elige el que tenga menor medida de infactibiliddd, dada por el número de violaciones a las restricciones. Si los dos individuos son factibles de nuevo predomina el de menor card (S_o); si ese criterio no decide se elige el que tenga menor conteo de debilidad en la población.

Para seleccionar los K individuos que pasan a la próxima generación se utiliza como en NSGA–II el criterio de pertenencia a los mejores frentes; en caso de empates se decide por el conteo de debilidad en la población.

 

CASO DE ESTUDIO: EXAMEN DEL PROBLEMA DE CARTERA DE PROYECTOS O POLÍTICAS DE ASISTENCIA SOCIAL

En este tipo de problemas el objetivo principal del gasto público es la búsqueda de la equidad; incidir directamente sobre determinados sectores de la población suministrándoles ciertos satisfactores que de otro modo estarían en un nivel inferior al que se juzga necesario. En correspondencia con la premisa Cy la expresión (1) aceptamos como hipótesis de trabajo que el DM, de manera implícita, considera una función de preferencias del tipo

que incluye la dependencia con el bienestar de los individuos (recogido en U_i que denota la función de preferencia de cada individuo que recibe impacto de la solución), y también respecto al bienestar general de la sociedad como lo percibe el DM (recogido en E). La dependencia explícita de W' respecto a E (denotada como W_e' E)) intenta modelar los beneficios intangibles que son generales para la sociedad aunque no repercuten directamente en el nivel de consumo de bienes y servicios de los individuos; entre ellos se incluyen los que tienen que ver con el desarrollo, el medio ambiente, la seguridad y otros.

Sea q un "satisfactor" y asumamos que un proyecto social produce una variación δq en el nivel de consumo de n individuos. Si se prescinde del efecto sobre W' _e (E) tenemos:

Ahora es conveniente introducir tres suposiciones:

a) Como media, las funciones de utilidad dependen del nivel social. Por lo tanto, suponemos que la derivada (∂U₁ / ∂q) es igual para todos los individuos del mismo estrato social.

b) La razón de cambio en la preferencia del DM respecto al beneficio del individuo j–ésimo depende del estrato social del mismo. Luego, la derivada ∂W' / ∂U_j se considera igual para todos los individuos que se puedan clasificar en el mismo estrato social.

c) El nivel social de un individuo no cambia al recibir el beneficio δq de uno o varios proyectos.

El punto (a) se justifica porque las preferencias individuales dependen del nivel y posibilidades de consumo, y siguen por ende un patrón social, que no es determinista pero refleja en promedio las características del grupo social. El punto (b) recoge el principio ético de la indistinguibilidad del individuo dentro de su estrato social, es una expresión de la ideología del DM y refleja su compromiso con diferentes sectores sociales. Por su parte, el punto (c) enfatiza en la marginalidad de los cambios que el proyecto produce.

Tomando en cuenta (a) y (b), la expresión 13 se puede escribir como:

donde n_i es la cantidad de personas del estrato i beneficiadas por el proyecto, y el índice i corre por el total de estratos en los que el DM divide el universo social bajo consideración en cada problema particular.

δU_i ≈ (∂U_i / ∂q) δq puede interpretarse como una medida del impacto del proyecto sobre un individuo del j–ésimo estrato. δW' de (14) es la repercusión social del proyecto desde la perspectiva del DM, que puede verse como una suma de los impactos sobre los grupos sociales (el número de beneficiarios del grupo social multiplicado por el impacto sobre cada individuo de ese grupo), pero modulado por el factor ∂W' l ∂U_i, que expresa la intensidad en que la preferencia del DM depende del aumento de bienestar del j–ésimo estrato social.

Consideremos ahora una cartera de proyectos o políticas independientes, o que así se puedan aceptar aproximadamente (son independientes si sus impactos pueden superponerse para estimar el impacto conjunto). La suma de los impactos de los proyectos aislados arroja entonces W'(E_k) –W'(E₀) del problema (2).

Por consiguiente, si no consideramos la variación de W'_e (E), se tiene

En realidad la expresión (15) solamente da la variación de preferencia relativa a los beneficios directos que obtienen los individuos, pero no contempla los beneficios intangibles generales.

La búsqueda de la mejor cartera a través de la optimización de la función expresada por (15) es un complejo problema combinatorio. Más aún, el desconocimiento de las derivadas ∂W'I∂U_i obliga a considerar una formulación multiobjetivo en que los distintos objetivos tienen la forma Σ_j n_ij (∂U_i / ∂q_j) δq_j, mientras que las derivadas ∂W' / ∂U_i contienen información preferencial del DM. Hay que notar que la expresión (15) tiene la forma de una función suma ponderada clásica de la modelación multicriterio, en la que los objetivos son del tipo Σ_j n_ij(∂U_i / ∂q_j) δq_j, y las derivadas ∂W' / ∂U_i asumen el rol de factores de ponderación. Debido a que las preferencias son generalmente dependientes del contexto (Tverskyy Simonson, 1993), esta información preferencial es muy probablemente desconocida incluso para el propio DM, que sólo podrá precisarla en un proceso de aprendizaje y reflexión sobre sus propias preferencias. El desconocimiento de las funciones de utilidad individuales no permite evaluar ∂U_i/ ∂q_j , pero el producto (∂U_i/ ∂q_j ) δq_j es un nivel de impacto sobre los individuos del i–ésimo grupo social. Ese nivel no se puede evaluar cuantitativamente, pero es posible asignarle un estado cualitativo con cierta escala, quizá {muy alto, alto, medio, bajo}. Cada término de la expresión (15) se puede caracterizar por un número de individuos que reciben beneficios del proyecto (n_ij), su pertenencia a un estrato social que influye en la preferencia del DM (información relativa a ∂W' / ∂U_i), y que reciben un grado de impacto dado por (∂U_i / ∂q_j ) δq_j. Los individuos beneficiados del mismo estrato social que reciben el mismo grado de impacto se suman a nivel de cartera, y su número puede verse como un objetivo de decisión para el DM. El número de objetivos depende de cómo se realice la partición de estratos sociales y de niveles de impacto.

donde N_j = n_ik, es el número de individuos del i–ésimo estrato social que reciben el k–ésimo nivel de impacto de la cartera; m es el total de pares (estrato social, nivel de impacto) que el DM decide considerar en un problema específico. El efecto de W_e'{E) se puede incluir de manera sencilla en (16) al añadir un objetivo (el m+l) que simplemente cuente el número de políticas o proyectos en la cartera que sean estratégicos para la sociedad más allá de su repercusión sobre individuos específicos.

(16) se derivó a partir de aceptar la premisa Cen (12), pero puede aceptarse como una forma de (5) y prescindir así de la necesidad de (12).

 

Optimización de cartera de proyectos de asistencia social: un ejemplo numérico

Un hipotético DM está resolviendo un problema de cartera con cien proyectos candidatos, cada uno de ellos con un beneficio directo sobre ciertos estratos de la población. El DM considera tres niveles de impacto (alto, medio, moderado) y tres segmentos de la población (extrema pobreza, pobreza, clase media baja). Dispone de recursos por 25 000 millones de pesos. Los proyectos se dividen en tres tipos por su naturaleza y en dos regiones geográficas. El DM desea mantener cierto balance en la cartera, por eso se imponen las siguientes restricciones por tipo y por región:

En este problema las consideraciones de equidad son fundamentales, pues es el sentido de la política asistencial del Estado. Hay que considerar las grandes dificultades para aplicar convincentemente el análisis costo–beneficio a un problema así. El DM tendría que estimar el valor de mercado o la contribución al aumento de la riqueza social, de que un individuo de cada segmento de la población obtuviera beneficios de cada uno de los niveles de impacto; debería ser diferente por segmento social para incluir las consideraciones de equidad.

Para el algoritmo genético de nuestra propuesta empleamos codificación binaria; un '1' en la posición y' de un individuo (cromosoma) significa que el proyecto y pertenece a la cartera que ese individuo representa; un '0' significa que el proyecto y no recibe apoyo. Otros parámetros del procedimiento son: probabilidad de cruzamiento = 1; probabilidad de mutación = 0.02; tamaño de la población = 100. Se emplean los operadores clásicos de cruzamiento y mutación (cf. Goldberg, 1989).

Los parámetros asignados al modelo de preferencias de la sección "Modelo borroso de preferencias" son los siguientes:

A) Pesos, que expresan la importancia de los criterios. Aquí se asignaron según la interpretación de pesos como "votos", que es típica de los métodos ELECTRE (Ostanello, 1983). Los valores asignados fueron (23,14, 11,14,11,7,9,7,4).

B) Umbrales de indiferencia; usualmente se emplean para modelar imprecisión e incertidumbre; aquí representan una medida del error que se comete al evaluar cada objetivo, que estimamos en 10 por ciento de su valor nominal.

C) Umbrales de veto; se asignaron como 0.5*(Max N_i — Min N_i ) como en algunas aplicaciones de ELECTRE (cf. Ostanello, 1983; Opricovic y Tzeng, 2007); los operadores Max and Min actúan sobre la población.

D) El parámetro de sobreclasificación estricta δ recibió el valor de 0.10.

El algoritmo se programó en turbo C++ 3.0, y se ejecutó en una computadora Laptop con procesador de 1.67 Ghz , 2 Gb RAM y disco duro de 120Gb. Se generaron cinco instancias de manera aleatoria. El tiempo promedio de una corrida con 500 generaciones fue de 1.25 minutos.

En una de las instancias generadas, después de ejecutar 50 veces el algoritmo evolutivo con 500 generaciones en cada corrida se obtuvo la aproximación a N_s que se muestra en el cuadro 1.

De las seis soluciones que componen N_s, solamente las dos primeras pertenecen a N_SD (su conteo de debilidad es nulo). La solución 1 es mejor que la 2 debido a que la supera en el segundo atributo, que es más importante que el séptimo. Otro argumento es el mayor conteo de flujo neto. Parece que 1 es el mejor compromiso.

La descripción de los proyectos de esta instancia se muestra en el apéndice. El experimento se replicó en otras cuatro instancias sin diferencias apreciables.

 

EJEMPLO DE CARTERA DE PROYECTOS DE INVESTIGACIÓN BÁSICA

Este ejemplo simula la financiación de proyectos básicos de investigación. Además de varios criterios clásicos de las investigaciones (avances importantes, publicaciones, formación de recursos humanos), el DM está interesado en apoyar a miembros del Sistema Nacional de Investigadores (SNI), universidades públicas, universidades regionales, estudiantes de posgrado e incluso estudiantes universitarios sobresalientes. Los atributos relevantes—las variables v_i del problema (5)— y sus niveles de prioridad se muestran en el cuadro 2.

Hay que notar la virtual imposibilidad de aplicar convincentemente el análisis costo–beneficio a este problema. Sería necesario evaluar, a precios de mercado, valores tan poco tangibles como resultados de investigación básica relevantes, publicaciones en revistas indexadas y arbitradas, en editoriales prestigiosas, apoyo a universidades públicas, a universidades regionales, a miembros del SNI, etc.

Se generaron instancias de 150 proyectos. Cada proyecto se describe con 16 valores de atributos (varios pueden ser cero), y por su costo. Los valores fueron generados aleatoriamente, pero manteniendo relaciones entre aquellos que son interdependientes (e.g. N₄ y N₁₂; N₇ y N₁₄). Los requisitos monetarios también están correlacionados con algunos valores (e.g. N₈, N₁₃,N₁₂,N₁₄yN₁₆).

N^m_i denota el valor de N_i asociado al m–ésimo proyecto. Sea C una cartera; el valor de N_t para toda la cartera se calcula de la siguiente forma: N_i (C) = = z₁₅₀ N_i¹⁵⁰ + .... + z N_i¹⁵⁰ donde z_j = 1 si el j–ésimo proyecto es apoyado, y z_j= 0, de otra forma. El problema es:

La región factible se define por restricciones al presupuesto general. σ(x, y) fue calculada por el método ELECTRE (cf. Roy, 1990), como en la sección "Modelo borroso de preferencias". Los parámetros del modelo son pesos, umbrales de indiferencia, preferencia y veto. La información sobre los "pesos" se proporciona en el cuadro 3.

Otros parámetros del modelo

Los umbrales de indiferencia se tomaron como q_j = 0.01 {max (v_j(x), v_j {y))). Se concedió capacidad de veto a los criterios del primer y segundo nivel de prioridad. El umbral de veto vt se asignó igual a 0.3 (max (v_j(x), v_j(y))); el umbral de discordancia se asignó como u_j = (q_j + vt_j)/2. También se concedió capacidad de veto a coaliciones de criterios del tercer nivel de prioridad. El parámetro de sobreclasificación 8 se tomó como 0.1. La codificación de los individuos y los parámetros del algoritmo genético son similares al ejemplo de la sección "Optimización de cartera de proyectos de asistencia social". La frontera no superada (conocida) de una instancia aleatoria de este problema se muestra en el cuadro 4.

Las soluciones 3,11 y 17 cumplen las condiciones necesarias para ser las mejores carteras. La cartera 3 parece ser la mejor opción. Si el DM no tuviera suficiente confianza en la relación Q, también podría considerar la cartera 1.

El experimento se replicó en otras cuatro instancias aleatorias. El tiempo promedio de ejecución fue aproximadamente de ocho minutos. En todos los casos el algoritmo fue capaz de determinar uno o dos mejores compromisos en la frontera no superada, utilizando la información de los conteos de debilidad y flujo neto.

 

CONCLUSIONES

Cumplimentando los objetivos enunciados en la introducción, hemos propuesto un método general que permite explorar el espacio de carteras y acercarnos a la solución óptima. El enfoque subjetivo y la modelación de preferencias de la decisión multicriterio permite definir sin ambigüedad el concepto de cuál es la mejor cartera de proyectos públicos. Bajo premisas muy generales la mejor cartera es el mejor compromiso de un problema de optimización multiobjetivo, cuyos criterios son ciertas medidas directas o indirectas de la repercusión de los proyectos sobre el objeto social. La condición suficiente de existencia de solución es que la relación de preferencia asimétrica del DM no sea cíclica. Bajo premisas más restrictivas, si se admite que el DM es un solo individuo o un grupo suficientemente homogéneo, se puede definir una medida de impacto social.

Quizás un mérito de este trabajo es justificar la generalidad de la formulación multiobjetivo para abordar cualquier problema de cartera pública que se someta a las premisas bastante laxas aquí discutidas; y proponer un algoritmo capaz de obtener buenas soluciones en casos de elevada complejidad. Semejante generalidad no la tiene ningún otro enfoque.

Una ventaja de esta propuesta es que el estado del objeto social se representa por atributos medibles, en las escalas que el DM determine. Algunos atributos pueden representar medidas de eficiencia; otros, consideraciones de equidad; se hace posible la búsqueda de compromisos aceptables entre eficiencia y equidad. La solución se dirige hacia satisfacer los objetivos en un sentido multidimensional, compatible con los enfoques de planeación estratégica y dirección por objetivos. Su generalidad permite aplicarlo a una vasta gama de problemas, pues su condición necesaria es solamente que los atributos sean calculables a partir de conocer qué proyectos o políticas componen una cartera. La cantidad de variables que se introduzca para reflejar el estado del objeto social no es un problema si se dispone de una buena medida del grado de credibilidad de una afirmación del tipo "la cartera C_x es al menos tan preferible como la cartera C_y. El enfoque de los métodos de sobreclasificación, y de ELECTRE en particular, conduce a un modelo aceptable, pero que debe ser mejorado y adaptado a la especificidad de los problemas de cartera con muchos objetivos.

En algunos ejemplos de tamaño real el algoritmo evolutivo aquí descrito para hallar la mejor cartera mostró buenas propiedades. Converge hacia una zona privilegiada de la frontera de Pareto donde se encuentran las mejores soluciones de compromiso del problema multiobjetivo equivalente a la búsqueda de la cartera óptima. Sin embargo, cuánto se acerque la solución que se obtenga a la verdadera mejor cartera depende de cuan precisamente el modelo del grado de credibilidad refleje las verdaderas preferencias del DM.

De este trabajo se derivan varias líneas de investigación:

i) Mejorar el modelo de la relación borrosa de preferencia a través de 1) procedimientos para identificar sus parámetros; 2) incorporación de la intensidad de la preferencia como en (Roy y Slowinski, 2008; Fernández et al, 2009b); 3) consideración más flexible de la discordancia y los efectos de veto (Fernández et al., 2009b).

ii) Explorar cómo un proceso de optimización interactiva puede potenciar el proceso de aprendizaje del DM y favorecer la obtención del mejor compromiso.

iii) Modelar las situaciones en que el DM es un grupo bastante heterogéneo, con intereses conflictivos. Esto ocasiona una duda seria sobre la validez de la premisa H y sobre otros elementos importantes de la presente propuesta.

 

REFERENCIAS BIBLIOGRÁFICAS

Badri, M. A., D. Davis, D. Davis (2001): "A Comprehensive 0–1 Goal Programming Model for Project Selection", International Journal of Project Management, 19 (4), pp. 243–252.         [ Links ]

Bertolini, M., M. Bragliay G. Carmignani (2006), "Application of the AHP Methodology in Making a Proposal for a Public Work Contract", International Journal of Project Management, 24 (5), pp. 422–430.         [ Links ]

Boardman, A. (1996), Cost–benefit Analysis: Concepts and Practices, Upper Saddle River, Prentice Hall.         [ Links ]

Bouyssou, D., Th. Marchant, P. Perny, A. Tsoukias y Ph. Vincke (2000), Evaluations and Decision Models: A Critical Perspective, Dordrecht, Kluwer Academic Publishers.         [ Links ]

Brans, J. P. y B. Mareschal (2005), "PROMETHEE Methods", en Figueira, Greco y Erghott (eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Nueva York, Springer Science and Bussiness Media, pp. 163–190.         [ Links ]

Brennan, G. y J. M. Buchanan (1980), The Power to Tax: Analytical Foundations of a Fiscal Constitution, Cambridge, Cambridge University Press.         [ Links ]

Buchanan, J. T. y M. Henig (1997), "Objectivity and Subjectivity in the Decisión Making Process", Department of Management Systems, Research Report Series 1997–1, disponible en: http://www.mngt.waikato.ac.nz/depts/mnss/john/subobj1.htm.         [ Links ]

Chapman, C. B., S. C. Ward y J. H. Klein (2006), "An Optimised Multiple Test Framework for Project Selection in the Public Sector, with a Nuclear Waste Disposal Case–based Example", International Journal of Project Management, 24 (7), pp. 373–384.         [ Links ]

Chan, Y. J. Di Salvo y M. Garrambone (2005), "A Goal–seeking Approach to Capital Budgeting", Socio–Economic Planning Sciences, 39 (2), pp. 165–182.         [ Links ]

Coello, C, D. Van Veldhuizen y G. Lamont (2002), Evolutionary Algorithms for Solving Multi–Objective Problems, Nueva York–Boston–Dordrecht–Londres–Moscú, Kluwer Academic Publishers.         [ Links ]

Coello, C, G. Toscano y E. Mezura (2005), "Current and Future Research Trends in Evolutionary Multi–Objective Optimization", en M. Grana, R. Dura, A. d'Anjou y P. Wang (eds.), Information Processing with Evolutionary Algorithms: From Industrial Applications to Academic Speculations, Nueva York Springer Verlag, pp. 213–231.         [ Links ]

–––––––––– (2007), Evolutionary Algorithms for Solving Multi–Objective Problems, Nueva York, Springer.         [ Links ]

Cohen, E. y R. Franco (1992), Evaluación de proyectos sociales, México, Siglo XXI.         [ Links ]

Deb, K. (2001), Multi–Objective Optimization Using Evolutionary Algorithms, Chichester–Nueva York–Weinheim–Brisbane–Singapur–Toronto, John Wiley and Sons.         [ Links ]

Dias, L. C. y V. Mousseau (2006), "Inferring ELECTRE's Veto –related Parameters from Outranking Examples", European Journal of Operational Research, 170(1), pp. 172–191.         [ Links ]

Doumpos, M., Y Marinakis, M. Marimaki y C. Zopounidis (2009), "An Evolutionary Approach to Construction of Outranking Models for Multicriteria Classification: The Case of ELECTRE tri Method", European Journal of Operational Research, 199 (2), pp. 496–505.         [ Links ]

Dorfman, R. (1996), "Why Cost–benefit Analysis is Widely Disregarded and What to Do about it?", Interface 26 (1), pp. 1–6.         [ Links ]

Duarte, B., A. Reis (2006), "Developing a Projects Evaluation System Based on Multiple Attribute Value Theory", Computers and Operations Research, 33 (5), pp. 1488–1504.         [ Links ]

Fandel, G. y T Gal (2001), "Redistribution of Funds for Teaching and Research among Universities: The Case of North Rhine Westphalia", European Journal of Operational Research, 130 (1),pp. 111–120.         [ Links ]

Fernández, E. y J. Navarro (2001), "Modelo y sistema de apoyo a la decisión para problemas de cartera de proyectos con relevancia social", Gestión y Política Pública, 10 (1), pp. 31–52.         [ Links ]

–––––––––– (2002), "A Genetic Search for Exploiting a Fuzzy Preference Model of Portfolio Problems with Public Projects", Annals of Operations Research, 117 (1–4), pp. 191–213.         [ Links ]

Fernández, E. y R. Olmedo (2005), "An Agent Model Based on Ideas of Concordance and Discordance for Group Ranking Problems", Decision Support Systems, 39 (3), pp. 429–443.         [ Links ]

Fernández, E., F. López, J. Navarro, I. Litvinchev e I. Vega (2009a), "An Integrated Mathematical–computer Approach for R & D Project Selection in Large Public Organizations", International Journal of Mathematics in Operational Research, 1 (3), pp. 372–396.         [ Links ]

Fernandez, E., J. Navarro y S. Bernal (2009b), "Multicriteria Sorting Using a Valued Indifference Relation under a Preference–disaggregation Paradigm", European Journal of Operational Research, 198 (2), 602–609.         [ Links ]

Fernández, E., E. López, S. Bernal, C. Coello y J. Navarro (2010a), "Evolutionary Multiobjective Optimization Using an Outranking–based Dominance Generalization", Computers & Operations Research, 37 (2), pp. 390–395.         [ Links ]

Fernández, E., S. Bernal, J. Navarro y R. Olmedo (2010b), "An Outranking–based Fuzzy Logic Model for Collaborative Group Decision", TOP 18 (2), pp. 444–464.         [ Links ]

Figueira, J., V Mousseau y B. Roy (2005), "ELECTRE Methods", en J. Figueira, S. Greco y L. Erghott (eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Nueva York, Springer Science and Bussiness Media.         [ Links ]

Fodor, J. y N. Roubens (1994), Fuzzy Preference Modeling and Multicriteria Decision Support, Dordrecht, Kluwer.         [ Links ]

French, S. (1993), Decision Theory: An Introduction to the Mathematics of Rationality, Londres, Ellis Horwood.         [ Links ]

Gabriel, S., S. Kumar, J. Ordonez y A. Nasserian (2006), "A Multiobjective Optimization Model for Project Selection with Probabilistic Consideration", Socio–Economic Planning Sciences, 40 (4), pp. 297–313.         [ Links ]

Goldberg, D. (1989), Genetic Algorithms in Search, Optimization and Machine Learning, Reading, Addison–Wesley.         [ Links ]

Howard, R. A. y J. E. Matheson (1984), The Principles and Applications of Decision Analysis, Menlo Park, California, Strategic Decision Group.         [ Links ]

Hwang, C. L. y A. S. Masud (1979), "Multiple Objective Decision Making: Methods and Applications", Lecture Notes in Economic and Mathematical Systems, 164, Berlin, Springer Verlag.         [ Links ]

Kaplan, P. y S. R. Ranjithan (2007), "A New MCDM Approach to Solve Public Sector Planning Problems", Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi Criteria Decision Making, pp. 153–159.         [ Links ]

Keeney, R. L. y H. Raiffa (1976), Decisions with Multiple Objectives: Preferences and Value Trade–off, Nueva York, Wiley and Sons.         [ Links ]

Lee, J. y S. Kim (2001), "An Integrated Approach for Interdependent Information System Project Selection", International Journal of Project Management, 19 (2), pp. 111–118.         [ Links ]

Liesio, J., P. Mild y A. Salo (2007), "Preference Programming for Robust Portfolio Modeling and Project Selection", European Journal of Operational Research, 181 (3), pp. 1488–1505.         [ Links ]

Litvinchev, I., R López, A. Alvarez y E. Fernández (2010), "Large Scale Public R & D Portfolio Selection by Maximizing a Biobjective Impact Measure", IEEE Transactions on Systems, Man and Cybernetics, 40 (3), pp. 572–582.         [ Links ]

López, E. (2008), "Incorporación de preferencias en algoritmos evolutivos multiobjetivo utilizando la información de una relación borrosa de sobreclasificación", tesis de maestría en informática aplicada, Universidad Autónoma de Sinaloa.         [ Links ]

Marakas, G. (2002), Decision Support Systems and Megaputer, 2a ed., Upper Saddle River, Prentice Hall.         [ Links ]

Martino, J. (1995), Research and Development Project Selection, Nueva York–Chichester–Brisbane–Toronto–Singapur, Wiley.         [ Links ]

Mavrotas, G., D. Diakoulaki e Y Caloghirou (2006), "Project Prioritization under Policy Restrictions. A Combination of MCDA with 0–1 Programming", European Journal of Operational Research, 171 (1),pp. 296–308.         [ Links ]

Mavrotas, G., D. Diakoulaki y A. Koutentsis (2008), "Selection Among Ranked Projects under Segmentation, Policy and Logical Constraints", European Journal of Operational Research, 187(1), pp. 177–192.         [ Links ]

Mousseau, V. y L. C. Dias (2004), "Valued Outranking relations in ELECTRE Providing Manageable Disaggregation Procedures", European Journal of Operational Research, 156 (2), pp. 467–482.         [ Links ]

Opricovic, S. y G. Tzeng (2007), "Extended VIKOR Method in Comparison with Outranking Methods", European Journal of Operational Research, 178 (2), pp. 514–529.         [ Links ]

Ostanello, A. (1983), "Outranking Methods", proveniente del First Summer School on MCDA, Sicilia, pp. 41–60.         [ Links ]

Peterson, S. (2005), "Interview on Financial Reforms in Developing Countries", Kennedy School Insight, John Kennedy School of Government, Harvard University, disponible en: www.ksg.harvard.edu/ksgnews/KS–Glnsight/speterson.htm.         [ Links ]

Perny, P. (1998), "Multicriteria Filtering Methods Based on Concordance and Non–Discordance Principles", Annals of Operations Research, 156 (2), pp. 37–165.         [ Links ]

Ponce, R. A. (2010), "Externalidades regionales y la provision de bienes públicos en un sistema descentralizado de gobiernos subnacionales", Frontera Norte, 22 (43), pp. 159–186.         [ Links ]

Roy, B. (1990), "The Outranking Approach and the Foundations of ELECTRE methods", en C. A. Baña e Costa (ed.), Reading in Multiple Criteria Decision Aid, Berlin, Springer–Verlag, pp. 155–183.         [ Links ]

–––––––––– (1996), Multicriteria Methodology for Decision Aiding, Boston, Kluwer.         [ Links ]

Roy, B. y R. Slowinski (2008), "Handling Effects of Reinforced Preference and Counterveto in Credibility of Outranking", European Journal of Operational Research, 188 (1), pp. 185–190.         [ Links ]

Saaty, T. L. (2005), "The Analytic Hierarchy and Analytic Network Processes for the Measurement of Intangible Criteria and for Decision–making", en Figueira, Greco y Erghott (eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Nueva York, Springer Science and Business Media, pp. 345–407.         [ Links ]

Samuelson, PA. (1954), "The Pure Theory of Pub lie Expenditure", The Review of Economics and Statistics, 36 (4), pp. 387–389.         [ Links ]

Santhanam, R. y J. Kyparisis (1995), "A Multiple Criteria Decision Model for Information System Project Selection", Computers and Operations Research, 22 (8), pp. 807–818.         [ Links ]

Sen, A. (2000), Development as Freedom, Nueva York, Anchor Books.         [ Links ]

–––––––––– (2008), On Ethics and Economics, 18a ed., Malden–Oxford–Carlton, Blackwell Publishing.         [ Links ]

Steuer, R. E. y P. Na (2003), "Multiple Criteria Decision Making Combined with Finance: A Categorized Bibliographic Study", European Journal of Operational Research, 150 (3), pp. 496–515.         [ Links ]

Sugrue, P., A. Mehrotra y P. M. Orehovec (2006), "Financial Aid Management: An Optimisation Approach", International Journal of Operational Research, 1 (3), pp. 267–282.         [ Links ]

Tresch, R. (2002), Public Finance: A Normative Theory, San Diego, Academic Press.         [ Links ]

Tversky A. e I. Simonson (1993), "Context Dependent Preferences", Management Science, 39 (10), pp. 1179–1189.         [ Links ]

Zanakis, S. H., T. Mandakovic, S. Gupta, S. Sahay y S. Hong (1995), "A Review of Program Evaluation and Fund Allocation Methods within the Service and Government Sectors", Socio–Economic Planning Sciences, 29 (1),pp. 59–79.         [ Links ]

 

NOTA

Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (Conacyt), que ha financiado esta investigación a través del proyecto "Aplicación de metaheurísticas multiobjetivo a la solución de problemas de cartera de proyectos públicos" (57255) (CB–2006–01).