Introducción
El transporte del agua en las plantas ocurre principalmente sin gasto de energía en dirección axial y radial, generalmente a través de la red de conductos formados por las células especializadas en la conducción del agua, conocidos como elementos traqueales que se clasifican en elementos de vaso y traqueidas, los primeros se comunican entre sí en sus extremos y porciones laterales, las segundas son células alargadas conectadas entre ellas en sus costados; a través de estas conexiones fluye el agua desde la raíz hasta las hojas en un gradiente de presiones negativas (Fig. 1). Estas células forman parte del xilema, tejido especializado en la conducción de agua, el soporte y almacenamiento de sustancias. La solución acuosa que es transportada por este sistema también contiene hormonas, proteínas, minerales y otros nutrimentos en pequeñas cantidades (Buhtz, Kolasa, Arlt, Walz y Kehr, 2004).
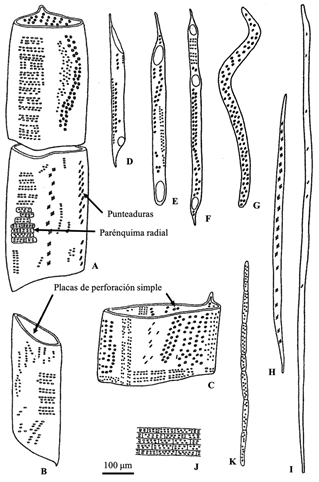
Figura 1 Tipos de células del xilema secundario de Quercus sp. A-C) Elementos de vaso anchos. D-F) Elementos de vaso estrechos. G) Traqueida. H) Fibrotraqueida. I) Fibra libriforme. J) Parénquima radial. K) Parénquima axial (Modificada de Evert, 2006).
La capacidad que tienen las plantas para transportar el agua determina las tasas de fotosíntesis, crecimiento y acumulación de materia viva; esta actividad metabólica depende de su contenido de agua: si disminuye, ocasiona pérdida de turgencia, cese del crecimiento, cierre de los estomas, reducción de la tasa fotosintética, marchitamiento y muerte (Taiz y Zeiger, 2012). El estudio de la arquitectura hidráulica contribuye al conocimiento de la fisiología de las comunidades vegetales, en relación con el ambiente en el cual se desarrollan. Por tanto, en esta revisión se analizan los conceptos básicos y algunas técnicas para comprender el fenómeno del ascenso del agua en las plantas vasculares.
Relaciones hídricas y arquitectura hidráulica, un poco de historia
La primera publicación donde se indica que las plantas absorben agua del suelo se remonta al siglo XVI. En De Plantis Libri XVI (1583), Andrea Cesalpino afirmó que los materiales nutritivos para el desarrollo de las plantas eran absorbidos del suelo por las raíces, y que, transportados por las venas, ascendían por el tallo para producir los frutos. Propuso que la fuerza responsable de este movimiento se encontraba en la médula y la llamó “calor vital”. En el siglo XVII, Marcello Malpighi describió e ilustró los vasos del xilema, señaló que aireaban los tejidos, de manera análoga a los “elementos traqueales” del sistema respiratorio de los artrópodos (Jansen y Schenk, 2015). Grew (1682) sugirió que los vasos transportaban la savia y que las células de la médula impulsaban el transporte del agua.
En Vegetable staticks: or, an account of some statical experiments on the sap in vegetables (1727), Stephen Hales describió los mecanismos de absorción y flujo radial del agua, la interconexión lateral de los vasos y la entrada de aire. Además, estableció que la transpiración de las hojas determina el movimiento del agua a través de los vasos (Fig. 2). Durante el siglo XIX, algunos autores consideraban que el agua no se movía a través del lumen de los vasos, sino por sus paredes celulares o por los espacios intercelulares (Jansen y Schenk, 2015).

Figura 2 Experimentos realizados por Stephen Hales. Registro de la transpiración. A) En una planta de menta. B) En girasol (Modificada de Hales, 1727).
A finales del siglo XIX y principios del XX, surgieron varias interpretaciones acerca de la presencia de burbujas de aire en el xilema. Por ejemplo, que el transporte del agua en las células conductoras del xilema ocurría como cadenas de burbujas alternadas con columnas de agua (denominadas “cadenas de Jamin”; Ewart, 1908), o que las burbujas adheridas a las paredes de los vasos participaban en el transporte de agua (Laschimke, Burger y Vallen, 2006), y que la vulnerabilidad del xilema a la formación de burbujas era mayor de lo que se ha registrado actualmente (Maherali, Pockman y Jackson, 2004; Wheeler, Huggett, Tofte, Rockwell y Holbrook, 2013).
Existen dos publicaciones que constituyeron avances fundamentales en el estudio de las relaciones hídricas de las plantas, una de ellas es Transpiration and the ascent of sap in plants (1914), de Henry H. Dixon, en ella argumenta que cuando la presión positiva de las raíces no actúa y las hojas transpiran, la cohesión del agua explica la transmisión de la tensión hacia las raíces y por tanto, el ascenso del agua a través del xilema; la otra publicación es Xylem structure and the ascent of sap, de Martin H. Zimmermann (1983), en la que presenta una descripción anatómico-funcional del fenómeno de ascenso del agua en las plantas, revisa los modelos y teorías biológicas y físicas que determinan el transporte de este líquido desde las raíces hasta las hojas, y explica los mecanismos que hacen disfuncional al xilema.
El desarrollo de este campo del conocimiento en países de habla hispana es más reciente. Martínez-Vilalta y Piñol (2003) explican el fenómeno del transporte de agua a través del xilema y la disfunción de este tejido debido al estrés hídrico en términos de las hipótesis más aceptadas. Ángeles-Álvarez (2013), discute algunas generalidades del fenómeno de ascenso del agua en las plantas vasculares y ofrece una reseña histórica de esta temática.
¿Qué es la arquitectura hidráulica?
Se define como la estructura del sistema conductor de agua usado por las plantas para distribuirla a través del sistema raíz-tallo-hoja (Tyree y Ewers, 1991; López-Portillo, Ewers, Ángeles y Fisher, 2000). De acuerdo con Cruiziat, Cochard y Améglio (2002), la arquitectura hidráulica integra la teoría de la cohesión-tensión del ascenso del agua y la ley de Ohm, considerando esta última como una analogía eléctrica que trata del flujo de electrones a través de circuitos eléctricos para modelar la transferencia del agua en el continuo suelo-planta-atmósfera (CSPA).
La arquitectura hidráulica también incluye características del sistema conductor, como la longitud y el diámetro de sus células y vasos (Domec et al., 2008; Chave et al., 2009). El triple compromiso (tradeoff) de la anatomía del xilema, basado en la división de las funciones de este tejido, transporte de agua, soporte mecánico y almacenamiento de sustancias, explica la evolución del sistema conductor en términos de diferentes soluciones adaptativas a problemas de estructura y función. Por tanto, hay un compromiso entre la eficiencia y seguridad del transporte del agua, el cual considera que la eficiencia en la conducción de agua es inversamente proporcional a la resistencia mecánica y a la disfunción por bloqueo del lumen celular o embolismo (Baas, 2004). Sin embargo, dada la variabilidad de los caracteres anatómicos del tejido conductor del agua en las plantas, es posible que no siempre exista una relación negativa entre la eficiencia y la seguridad en el transporte del agua a través de los elementos traqueales. Gleason et al. (2016) analizaron este compromiso del xilema en 335 especies de angiospermas y no registraron especies donde este tejido fuera eficiente y seguro contra el embolismo, como lo propuso Baas (2004), sin embargo, sí registraron especies con xilema poco eficiente y vulnerable al embolismo; de acuerdo con Gleason et al. (2016), el compromiso entre seguridad y eficiencia del xilema no siempre se cumple, y su relación puede deberse a la especialización del sistema conductor del agua, en función del hábitat y el hábito de las plantas.
La arquitectura hidráulica se puede estudiar mediante el análisis de la estructura del tejido vascular o considerando a la planta como un sistema hidráulico. En el primer caso se analiza la anatomía del xilema, su estructura tridimensional y las características morfométricas de sus células (Tyree y Zimmermann, 2002); en el segundo se estudian los elementos básicos de los sistemas hidráulicos, como la fuerza motriz, los conductos, reservorios y sistemas de regulación (Cruiziat, Cochard y Améglio, 2002).
¿Cómo asciende el agua en las plantas? Teoría de la cohesión-tensión
Esta teoría establece que el ascenso del agua a través de los elementos traqueales ocurre bajo tensión, esto permite explicar el ascenso del agua en el interior de las plantas a grandes alturas (Dixon y Joly, 1895). La cohesión intermolecular del agua líquida y su adhesión a las paredes de los elementos traqueales, permiten esta tensión. La teoría de la cohesión-tensión es la más aceptada para explicar el ascenso del agua en el sistema raíz-tallo-hoja (Ángeles et al., 2004). Poco después de su publicación se realizaron estudios que confirmaron la presencia de la tensión en el agua dentro de los elementos traqueales (Renner, 1925; Scholander, Hammel, Bradstreet y Hemmingsen, 1965).
La evaporación es la fuerza motriz que ocasiona el ascenso del agua, esta provoca la transpiración en el mesófilo, tejido que se localiza entre la epidermis del haz y el envés de las hojas, excluyendo los haces vasculares, en la región de interfase del agua líquida a vapor. La tensión en las columnas de agua hace que esta ascienda desde las raíces hasta las hojas, al mismo tiempo que se reduce la energía potencial del agua en los elementos traqueales de las raíces y esta entra por difusión; dentro de ellas el agua se mueve a través del apoplasto, espacios extracelulares y paredes, y el simplasto, que incluye a las membranas celulares, sus interconexiones y al citoplasma (Fig. 3, Fig. 4). Para el ascenso continuo del agua es necesario que se cumplan las siguientes condiciones: la cohesión de las moléculas de agua debe soportar la tensión, las columnas de agua dentro de las células conductoras deben ser continuas, y la diferencia de presión entre las raíces y hojas tiene que ser suficiente para elevar el líquido a través de toda la altura de la columna (Niklas, 1992; Sane y Singh, 2011).
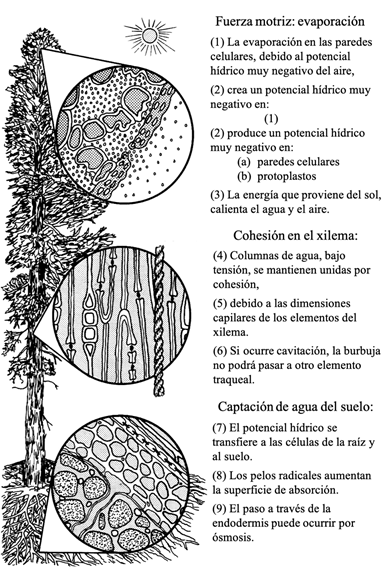
Figura 3 Ascenso del agua de acuerdo con la teoría de cohesión-tensión (Modificada de Salisbury y Ross, 1992).
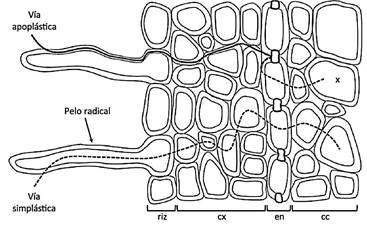
Figura 4 Vías de transporte del agua desde el suelo hasta el xilema (cc=cilindro central, cx=córtex, en=endodermis, riz=rizodermis, x=xilema) (Modificada de Trakal, Martínez-Fernández, Vitková y Komárek, 2015).
Schenk et al. (2017) introdujeron a la teoría de cohesión-tensión el efecto de sustancias que alteran la tensión superficial del agua (surfactantes), que fluye por los elementos traqueales y hacen posible su ascenso bajo tensión aunque haya burbujas en el sistema. Las burbujas cubiertas de sustancias surfactantes en el xilema, son más estables que las contenidas en agua pura, por tanto, estas evitan que las burbujas se expandan y ocupen todo el lumen celular de los elementos traqueales. Los surfactantes como proteínas y fosfolípidos en el agua del xilema, permiten explicar el ascenso de la misma de acuerdo con la teoría de la cohesión-tensión (Schenk, Steppe y Jansen, 2015; Schenk et al., 2017).
Algunos autores argumentan que esta teoría tiene limitaciones (Salisbury y Ross, 1992; Kirkham, 2005), y otros han propuesto teorías alternativas (Canny, 1995; Zimmermann, Schneider, Wegner y Haase, 2004). Sin embargo, los argumentos en contra de la cohesión-tensión son inválidos y las teorías alternativas no se han aceptado (Comstock, 1999; Stiller y Sperry, 1999; Ángeles et al., 2004).
Analogía de la ley de Ohm con el flujo hídrico
La ley de Ohm establece que la diferencia de potenciales entre los extremos de un material conductor, es proporcional a la intensidad de la corrienteque circula por el mismo. Van den Honert (1948) propuso que el flujo de agua que ocurre a través del CSPA, es semejante al flujo de electrones a través de un circuito eléctrico. En esta analogía, el flujo del agua también está determinado por la transpiración de las hojas que produce una diferencia de potenciales hídricos entre el suelo y la superficie foliar.
Al considerar la analogía de la ley de Ohm, la arquitectura hidráulica del tallo
y la hoja se pueden analizar como un diagrama de resistencias (Tyree, Nardini y Salleo, 2000). De este
modo, la resistencia al flujo del agua que ofrece cada elemento hidráulico está
en función de la diferencia de presiones que induce dicho flujo a través del
elemento traqueal y del flujo resultante; la relación que guardan estas
variables se expresa con la ecuación,
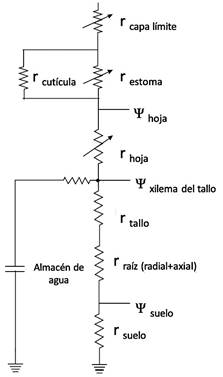
Figura 5 Flujo del agua en el continuo suelo-planta-atmósfera, analogía con la ley de Ohm. Las flechas representan resistencias variables (Ψ=potencial hídrico, r=resistencia hidráulica) (Modificada de Blum, 2011).
Características cualitativas de la arquitectura hidráulica
Estas características se relacionan con el individuo y son: integración, compartimentación y redundancia (Cruiziat et al., 2002). La primera implica que el sistema vascular de las plantas forma una red que conecta una raíz determinada con una o varias ramas, sin embargo, en algunas monocotiledóneas se distribuye helicoidalmente a lo largo del tallo y su integración ocurre cuando los haces vasculares ascienden desde las raíces, se aproximan al centro del tallo, y después se alejan hacia la periferia ramificándose para vascularizar las hojas (Tyree y Zimmermann, 2002). La segunda indica que el sistema conductor del agua está formado por muchas unidades de conducción que se conectan entre sí a través de las punteaduras y las placas de perforación. La redundancia significa que en cualquier eje (axial o radial) y órgano de la planta están presentes e interconectados varios elementos conductores del xilema; también incluye la porción de la pared celular donde se unen y comunican los elementos traqueales que permiten un flujo de agua continuo. En las monocotiledóneas la redundancia es menor que en las dicotiledóneas debido a que sus elementos traqueales generalmente son solitarios y la comunicación entre el tejido conductor de las hojas es mayor que en el tallo, pues ocurre principalmente por medio del protoxilema que conecta las nervaduras primarias.
La compartimentación se relaciona con la hipótesis de la segmentación hidráulica (Zimmermann, 1983), esta señala que las plantas “sacrifican” segmentos hidráulicamente vulnerables para mantener las partes restantes activas. Tyree y Ewers (1991) modificaron esta hipótesis y la llamaron de segmentación de vulnerabilidad hidráulica, la cual establece que las porciones más distales de las plantas deben ser más vulnerables al embolismo que las zonas basales. Según Ewers, Ewers, Jacobsen y López-Portillo (2007), es posible que la redundancia de los elementos traqueales proporcione mayor seguridad en el transporte del agua, ya que existirían rutas alternativas cuando algunos elementos conductores embolizan.
Características cuantitativas de la arquitectura hidráulica
El agua en el interior de las plantas fluye a favor de un gradiente de presiones
negativas o potenciales hídricos. El potencial hídrico (Ψ)
expresa la energía libre del agua por unidad de volumen (Slatyer y Taylor, 1960; Kirkham, 2005; Taiz y Zeiger,
2012). El Ψ se calcula con la ecuación,
Entre otras técnicas el Ψ se puede determinar con una cámara de presión o con un psicrómetro de termopar (Kirkham, 2005). El primer método fue introducido por Scholander, Hammel, Bradstreet y Hemmingsen (1965) y es el más utilizado para expresar el estado de hidratación de una planta. Los psicrómetros de termopar determinan el Ψ al registrar la humedad relativa a través de la presión de vapor en una cámara pequeña usando técnicas psicrométricas, donde se compara la humedad relativa entre un bulbo húmedo y otro seco (Kirkham, 2005).
El flujo de agua en las plantas es proporcional a la diferencia de potenciales
hídricos a través de las estructuras que presentan resistencia a dicho flujo,
como las membranas de las punteaduras y los rebordes de las punteaduras
areoladas o de las placas de perforación (Nobel,
2009). Tyree y Zimmermann
(2002) consideran que el flujo del agua a través de un elemento
traqueal es similar al de un tubo capilar. La tasa de flujo de agua a través de
este tubo es proporcional al gradiente de presión aplicada y a la conductividad
hidráulica, esta última es la capacidad de un conducto para permitir el flujo de
agua por unidad de área, transversal a la dirección del mismo. La conductividad
se obtiene con la ecuación de Hagen-Poiseuille, que establece que el volumen de
un fluido que se mueve a través de un conducto cilíndrico por unidad de tiempo,
es proporcional a la cuarta potencia de su radio, y se define por la ecuación,
Al modificar la ecuación de Hagen-Poiseuille se puede calcular la conductividad
hidráulica relativa, al estimar el volumen de agua que fluye a través de los
elementos traqueales en función de su radio elevado a la cuarta potencia y del
número de elementos traqueales por milímetro cuadrado de tejido en sección
transversal (Fahn, Werker y Baas, 1986;
Carlquist, 1988), de acuerdo con la
ecuación,
Sperry, Donnelly y Tyree (1988)
desarrollaron un método experimental para determinar la conductividad hidráulica
y el embolismo por presencia de aire en el xilema de un segmento de tallo, al
registrar la tasa del flujo de agua a través de este por unidad de tiempo. La
conductividad hidráulica es el cociente entre la tasa de flujo del agua y el
gradiente de presión, calculada como,
El cálculo de la K
h
sobreestima la conductividad hidráulica, pues se supone que el agua fluye
por todo el diámetro del segmento de tallo y no solamente por los elementos
traqueales. Para obtener un valor de conductividad hidráulica más preciso, es
necesario considerar el área del xilema en el cálculo. La conductividad
específica se calcula con la ecuación,
Sperry et al. (1988) desarrollaron un sistema de tubos en el que se acoplan segmentos de tallo y se registra el flujo hidráulico en una balanza analítica. Melcher et al. (2012) proponen que es posible simplificar el sistema de Sperry, sustituyendo esta balanza por una pipeta o un tubo calibrado que se conecta a un transductor de presión. También existe un modelo comercial del aparato de Sperry denominado “Xyl’em” (Cochard, 2002), que registra el flujo de agua con flujómetros de alta precisión y la ΔP con transductores de presión electrónicos.
La conductividad específica de la hoja es igual a la K
h
, dividida entre el área foliar de la porción distal del segmento de
tallo (A
l
, m2), y estima la suficiencia hidráulica de una porción de
tallo para suministrar agua a las hojas distales del mismo (Tyree y Ewers, 1991). Si se conoce la tasa
de transpiración promedio de las hojas y se asume que el contenido de agua es
constante, el gradiente de presión a través del segmento de tallo se calcula con
la ecuación,
Cuando aumenta la tensión del agua en las células conductoras del xilema ocurre cavitación, fenómeno físico que implica la formación de burbujas por cambios en la presión o en la temperatura de los líquidos (Streeter, Wylie y Bedford, 2000), en este caso, se trata del cambio súbito de agua líquida a vapor dentro de los elementos traqueales. Conforme se retira el agua del conducto que ha cavitado, el vapor se expande hasta ocupar todo el interior de la célula, se interrumpe el flujo del agua y se produce embolismo.
Zimmermann (1983) propuso cuatro posibles mecanismos que inducen la cavitación: siembra de burbujas (air-seeding) (Fig. 6A), siembra de burbujas por medio de una fisura hidrofóbica (Fig. 6B), nucleación homogénea (Fig. 6C) y falla de adherencia hidrofóbica (Fig. 6D). El primero sucede cuando la diferencia de presiones entre las punteaduras de dos elementos traqueales contiguos es suficiente para que una o más burbujas pasen a través de ellas. El segundo se presenta cuando una burbuja estable se localiza en la base de una fisura de la pared de un elemento traqueal, al disminuir la presión, la burbuja es succionada y sale de la fisura. La nucleación homogénea genera espontáneamente vacío en un fluido, es un proceso aleatorio que requiere el movimiento térmico de las moléculas de agua; conforme aumenta la tensión, los enlaces de hidrógeno de estas moléculas se estiran y se debilitan, así, la energía necesaria para romperlos disminuye y aumenta la probabilidad de que se forme una burbuja. En la falla de adherencia hidrofóbica, los enlaces de hidrógeno del agua se rompen en la porción hidrofóbica de las paredes de los elementos conductores, reduciéndose la energía que une la pared celular con las moléculas de agua.

Figura 6 Cavitación en los elementos traqueales. A) Siembra de burbujas (air-seeding). B) Siembra de burbujas por medio de una fisura hidrofóbica. C) Nucleación homogénea y D) Falla de adherencia hidrofóbica (Modificada de Tyree y Zimmermann, 2002).
Con base en las características anatómicas del xilema y de los elementos
traqueales, Carlquist (1977) propuso los
índices de vulnerabilidad (IV) y mesomorfia
(IM), expresados como,
Hacke, Sperry, Pockman, Davis y McCulloh
(2001) desarrollaron el índice de colapso (IC), que
permite evaluar la resistencia de los elementos traqueales a la implosión por la
tensión asociada con el ascenso del agua; proponen que la resistencia al
embolismo por cavitación, el refuerzo de las paredes de los elementos traqueales
y la densidad de la madera están relacionadas; argumentan que al aumentar la
densidad es mayor la resistencia a la cavitación y se mantiene un intervalo de
presiones negativas donde no ocurre el colapso de las células conductoras. Según
estos autores la resistencia de los elementos traqueales al colapso está en
función del grosor de sus paredes y su diámetro promedio. El IC
se calcula con la fórmula,
La resistencia a la cavitación indica la respuesta de las plantas al estrés hídrico y determina el límite de la presión negativa que se desarrolla en el xilema; también expresa la tensión que tolera una columna de agua antes de cavitar. Se determina mediante la elaboración de una curva de vulnerabilidad, que indica la relación entre la disminución de la conductividad hidráulica del xilema y su Ψ correspondiente (Tyree y Sperry, 1989).
Existen diferentes métodos para obtener los datos del Ψ y PLC necesarios para la construcción de las curvas de vulnerabilidad, uno de ellos es el de deshidratación (Sperry, 1986), donde se deshidratan ramas de una planta para producir presiones progresivamente más negativas en los elementos traqueales, con la correspondiente pérdida de conductividad hidráulica. La curva se construye con los valores de la conductividad y la presión en múltiples segmentos de las ramas, conforme estas se van deshidratando.
Otro método para generar curvas de vulnerabilidad es el de inyección de aire (Cochard, Cruiziat y Tyree, 1992; Salleo et al., 1992; Sperry y Saliendra, 1994), donde se utilizan cámaras de cavitación para forzar la dispersión de las burbujas formadas por este fenómeno, a través de las punteaduras de los elementos traqueales. En esta técnica se considera que la presión necesaria para introducir aire dentro de las células conductoras funcionales es equivalente y opuesta a la presión necesaria para causar cavitación (Hacke, Sperry, Wheeler y Castro, 2006). En este caso, se asume que la cavitación ocurre por siembra de burbujas (Zimmermann, 1983; Sperry et al., 1996).
Otros dos métodos para construir las curvas de vulnerabilidad son el gravitacional y el spin method, en ambos se aplica una fuerza centrífuga a segmentos de tallo donde se induce tensión en el agua que provoca cavitación por medio de máquinas centrífugas especiales (Pockman, Sperry y O’Leary, 1995; Alder, Pockman, Sperry y Nuismer, 1997; Cochard et al., 2005). La tensión generada en el interior de los elementos traqueales por medio de la centrifugación de las muestras es similar al Ψ que se registra con la cámara de presión, en este contexto, las técnicas de centrifugación validan el uso de la cámara de presión y apoyan la teoría de la cohesión-tensión.
Se han empleado diferentes modelos para describir las curvas de vulnerabilidad.
Los más utilizados son el exponencial-sigmoidal y el de Weibull (Neufeld et al., 1992;
Pammenter y Van der-Willigen, 1998).
El primero se describe con la ecuación,
El modelo de Weibull se ajusta a diferentes tipos de curvas y se basa en la
función de distribución de probabilidades de Weibull (Rawlings y Cure, 1985; Neufeld et al., 1992; Li et al., 2015). Está definido por la
ecuación,
De las curvas de vulnerabilidad se obtiene el P50 y la presión media
de cavitación (PMC) (Hacke et
al., 2006), esta última se calcula con la ecuación,
Los valores de P50 y PMC son buenos indicadores de la tolerancia de las plantas al estrés hídrico. En plantas leñosas se han registrado valores de P50 de -0.5 hasta -19.0 MPa (Maherali et al., 2004; Scoffoni, Rawls, McKown, Cochard y Sack, 2011; Choat et al., 2012). Sin embargo, los estudios en plantas herbáceas se limitan aproximadamente a 14 especies, con registros de P50 de 0 a -2 MPa (Stiller y Sperry, 2002; Kocacinar y Sage, 2003), básicamente por la baja conductividad de sus tallos y la fragilidad de sus tejidos.
Es común inferir que las plantas herbáceas son menos resistentes a la cavitación que las leñosas, debido a que los valores de P50 son menos negativos, además, las raíces de las hierbas como Poaceae ejercen presiones positivas (Lens et al., 2016). De acuerdo con Lens et al. (2016), se presentan ciclos diarios de embolismo y recarga de las células conductoras, esto implica que el potencial hídrico de las plantas herbáceas al medio día, es más negativo que su P50, y significa que estas plantas tienen células conductoras vulnerables a la cavitación, caracterizadas por un margen de seguridad hidráulica negativo, que se expresa como la diferencia entre el potenciál hídrico más negativo y el P50. Mientras que el margen de seguridad hidráulica de la mayoría de los árboles es ligeramente positivo (Choat et al., 2012b).
Lens et al. (2016) estudiaron 44 especies de angiospermas herbáceas, observaron que 94% de los valores de P50 se traslapan con los obtenidos en otros estudios, correspondientes a 301 especies de angiospermas leñosas. El intervalo amplio de estos valores (-0.5 a -7.5 MPa) en las plantas herbáceas, indica que no son tan vulnerables a la cavitación y que tienen una capacidad similar a los árboles para resistir potenciales hídricos muy negativos. También indicaron que el P50 de cinco especies de monocotiledóneas, es más negativo que el potencial hídrico registrado al medio día, por tanto, los ciclos de cavitación y recarga, debido a la presión positiva de las raíces, no ocurre habitualmente en este tipo de plantas.
Los parámetros fisiológicos como la conductividad del xilema y la resistencia de este a la cavitación dependen de las características de sus células conductoras, la estructura de las punteaduras y de la composición química de la solución acuosa que fluye a través de ellas (Cochard, Herbette, Hernández, Hölta y Mencuccini, 2010; Lens et al., 2010). El diámetro y el número de elementos conductores por unidad de área están relacionados con la eficiencia de la conductividad hidráulica, el soporte mecánico y con la resistencia del xilema a la cavitación (Baas, 2004).
Las plantas que son más resistentes a la cavitación generalmente tienen elementos conductores de menor longitud, índices de vulnerabilidad y mesomorfia más bajos, paredes de los elementos traqueales más gruesas y mayor resistencia al colapso (Lens, Endress, Bass, Jansen y Smets, 2009). En cambio, las de ambientes xéricos tienen más vasos, agrupados en mayor número, y rodeados por fibras comparadas con aquellas más vulnerables a la cavitación (Carlquist, 2009).
Lens et al. (2010) evaluaron la importancia de la estructura de las punteaduras, como el grosor de su membrana, porosidad y la profundidad de su cámara en relación con la resistencia a la cavitación. Mostraron que en cinco especies de Acer (Aceraceae), más que el número, la estructura de las punteaduras tiene mayor influencia en la PMC. Las especies estudiadas más resistentes a la cavitación tienen cámaras de las punteaduras menos profundas, punteaduras con membranas más gruesas y poros más pequeños que las especies más vulnerables. Registraron que las especies con una PMC más negativa tienen un área mayor de pared celular ocupada por punteaduras, y en general en estas especies el diámetro de los vasos no se relaciona con la PMC. Las especies de Acer menos resistentes a la cavitación tienen una conductividad específica inicial mayor que aquellas con una PMC más negativa, por tanto, la resistencia a la cavitación es mayor y el xilema presenta menor conductividad específica.
Las membranas de las punteaduras son paredes celulares primarias modificadas, están constituidas de microfibrillas de celulosa embebidas en una matriz gelatinosa, conformada por hemicelulosa, enzimas y pectinas hidratadas (Salazar y Gamboa, 2013). Las pectinas son heteropolisacáridos con cinco dominios, uno de ellos es el homogalacturonano (Willats, McCartney, Mackie y Knox, 2001), que es susceptible de enlazarse con cationes de calcio como consecuencia de la acción de la enzima pectin metil esterasa (PME) (Pelloux, Rusterucci y Mellerowicz, 2007). Estas pectinas se encuentran en las membranas de las punteaduras intervasculares y son particularmente comunes en las punteaduras areoladas (Hafren, Daniel y Westermark, 2000); el calcio que se les une afecta la elasticidad de la pared celular (Derbyshire, McCann y Roberts, 2007), por tanto, es posible que se relacione con el proceso de cavitación por siembra de burbujas y con la resistencia a la misma. El flujo del agua a través de las membranas de las punteaduras ocurre debido a una pequeña diferencia de presiones a través de ellas, durante este flujo las membranas están relajadas. Durante el proceso de cavitación por siembra de burbujas, aumenta el gradiente de presiones entre las membranas de dos vasos contiguos, estas se deforman, se estiran, sus poros aumentan de diámetro y ocurre la cavitación (Herbette y Cochard, 2010).
Herbette y Cochard (2010) registraron que en Fagus sylvatica (Fagacaeae), con el aumento de la alcalinidad del agua que fluye a través de sus vasos, disminuye la resistencia a la cavitación; de acuerdo con sus resultados, remover el calcio de la pared celular modifica la elasticidad de las membranas de las punteaduras, disminuye la resistencia a la cavitación y no se altera la conductividad hidráulica.
Cochard et al. (2010) señalaron que la composición iónica del agua que fluye a través de los elementos traqueales induce cambios en la conductividad, pero no necesariamente afecta la resistencia a la cavitación. Si se altera la concentración de iones de la solución acuosa que fluye a través de las células conductoras, las pectinas de las membranas de las punteaduras se pueden dilatar o contraer y ocasionan un cambio reversible en la resistencia al flujo del agua (Zwieniecki, Melcher y Holbrook, 2001). La dilatación de las pectinas determina las dimensiones de los microcanales de las membranas de las punteaduras a través de las cuales fluye el agua y también se relaciona con la resistencia al flujo de esta. Sin embargo, las alteraciones estructurales de los poros de las membranas no afectan la resistencia a la cavitación, pues aún dilatados, no son suficientemente grandes para permitir el paso de burbujas (Shane, McCully y Canny, 2000; Choat, Ball, Luly y Holtum, 2003).
La variación en la conductividad hidráulica como consecuencia de la composición iónica del agua se conoce como “efecto iónico” (Nardini, Dimasi, Klepsch y Jansen, 2012), y sirve para regular el flujo hídrico a través de los elementos traqueales (Cochard et al., 2010). La hipótesis original establece que los cambios en el volumen de la matriz de pectinas en las membranas de las punteaduras son responsables de las modificaciones del tamaño de los poros de estas (Van Doorn, Hiemstra y Fanurakis, 2011). El efecto iónico se relaciona con diversas funciones de las plantas, entre ellas, la evasión al estrés hídrico por medio de la regulación de la conductividad y la compensación de la pérdida de la misma por cavitación (Trifilò, Nardini, Raimondo, Lo Gullo y Salleo, 2011).
Arquitectura hidráulica de la hoja
La conductancia de las hojas (k
l
) es una medida de la eficiencia del transporte del agua a través de
estas y es inversa a la resistencia (r
l
). La k
l
es la relación entre la diferencia de potenciales hídricos con la tasa de
flujo del agua a través del peciolo, las nervaduras y el parénquima, hacia los
sitios donde ocurre evaporación (Sack y
Holbrook, 2006). La conductancia de las hojas se calcula con la
ecuación,
En las dicotiledóneas el agua se mueve desde los elementos traqueales del tallo hacia el peciolo o hacia la vaina foliar en las monocotiledóneas y de aquí a las nervaduras primarias (Evert, 2006), el flujo continúa al tejido circundante o a las nervaduras secundarias (Altus, Canny y Blackman, 1985). La mayor parte del volumen de agua que se transpira proviene de las nervaduras secundarias, por tanto, los dos tipos de venas funcionan en serie para el transporte del agua (Sack, Cowan y Holbrook, 2003). Los patrones de venación son muy diversos entre especies y entre grandes grupos de plantas, por tanto, varían en su disposición y número de órdenes de venación, así como en el tamaño y la forma de los elementos traqueales de las nervaduras. Estas características determinan la distribución del agua a través de la hoja, y en consecuencia, se considera que la conductividad máxima en la misma se correlaciona con las dimensiones de las células conductoras en las nervaduras primarias (Sack y Frole, 2006).
Una vez que el agua sale del xilema se mueve hacia las células de la vaina del haz vascular, con la participación de las acuaporinas fluye a través del protoplasto de estas células y se transfiere al mesófilo. Las células del parénquima esponjoso tienen mayor área de contacto y son más eficientes en la conducción. Después, el agua se transporta hacia la epidermis por medio de las extensiones de la vaina de los haces; si no están presentes, el agua se desplaza a través del mesófilo, por medio del apoplasto o el simplasto (Martre, Morillon, Barrieu, North y Nobel, 2002; Evert, 2006) (Fig. 7). En las hojas, la evaporación del agua ocurre principalmente en el mesófilo que se encuentra debajo de los estomas, en la epidermis adyacente a estos y también en sus células guarda (Tyree y Yianoulis, 1980).
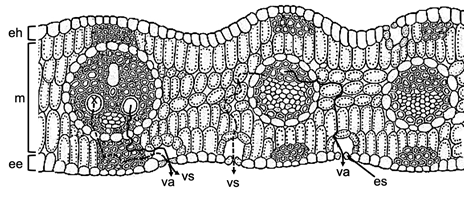
Figura 7 Sección transversal de una hoja de monocotiledónea mostrando las vías de transporte del agua, desde el xilema hasta la atmósfera (ee=epidermis del envés, eh=epidermis del haz, es=estoma, m=mesófilo, va=vía apoplástica, vs=vía simplástica, x=xilema) (Modificada de Gupta, 2017).
Conclusiones
El estudio de la arquitectura hidráulica se ha enfocado en las plantas leñosas; en este contexto, hacen falta más investigaciones de este tipo en plantas herbáceas, principalmente en las monocotiledóneas. Esta temática es importante en el ámbito global, pues el cambio climático está afectando la estabilidad de los ecosistemas, donde las comunidades vegetales están sometidas a regímenes hídricos cambiantes que afectan su productividad y supervivencia.











 nueva página del texto (beta)
nueva página del texto (beta)


