Introducción

La medición de la diversidad biológica de una comunidad vegetal es fundamental para conocer su funcionamiento, manejo y conservación. La diversidad biológica se entiende como la variedad y abundancia de especies en un área determinada de estudio, la cual se puede medir en cuanto a su riqueza de especies y homogeneidad en su distribución a través de los múltiples índices desarrollados (^{Magurran, 2004}).

La caracterización de los atributos estructurales de las comunidades arbóreas, así como de la mayoría de las comunidades vegetales, se han realizado mediante el uso de los índices de diversidad clásicos tales como ^{Shannon-Wiener (1949)}, ^{Simpson (1949)}, ^{Margalef (1958)} y ^{Menhinick (1964)}, entre otros, los cuales están basados en la riqueza de especies, su abundancia y distribución (^{Magurran, 2004}). De esta manera, la selva alta perennifolia (SAP) (sensu^{Miranda y Hernández-X., 1963}) se ha caracterizado por ser una comunidad arbórea más diversa que la selva mediana subperennifolila (SMS) como lo refieren múltiples estudios (^{Cascante y Estrada, 2001}; ^{Godínez-Ibarra y López-Mata, 2002}; ^{Basáñez, Alanís y Badillo, 2008}; ^{Maldonado-Sánchez y Maldonado-Mares, 2010}; ^{Sánchez-Pérez, Castillo-Acosta y Cámara-Cabrales, 2011}; ^{Martínez-Sánchez y Cámara, 2012}; ^{Dzib-Castillo, Chanatásig-Vaca y González-Valdivia, 2014}). Así también, los mismos estudios muestran que la SAPgeneralmente presenta mayores densidades y tamaño de árboles que la SMS, sin embargo, los valores de estos atributos varían dentro de ciertos intervalos para ambas comunidades, haciendo la comparación en algunos casos fácil, pero en otros no.

Sin embargo, alrededor del año 2000 surgió el concepto de diversidad estructural de las comunidades arbóreas, el cual considera al tamaño de los árboles como otro atributo estructural de la comunidad. La diversidad estructural de una comunidad arbórea es la combinación de la diversidad de especies y el tamaño en diámetro y altura de los árboles, con la finalidad de ser un mejor indicador de la diversidad de los ecosistemas forestales (^{Staudhammer y LeMay, 2001}; ^{Pommerening, 2002}; ^{Bohl y Lanz, 2005}; ^{McElhinny, Gibbons, Brack y Bauhus, 2005}). Debido a la variación en el tamaño de los árboles, los índices de diversidad clásicos son limitados en la estimación de una diversidad más completa (^{Lähde, Laiho, Norokorpi y Saksa, 1999}). Dos comunidades arbóreas o plantaciones (una juvenil y una madura, por ejemplo) con el mismo número de especies y abundancia de árboles por especie tendrán diferente diversidad estructural al considerarse la dimensión de los árboles.

La aportación de los índices estructurales es la de incorporar las dimensiones de los árboles a los índices de diversidad clásicos. Diversos autores han propuesto índices estructurales basados principalmente en la diversidad de especies y tamaño de los árboles (^{von Gadow, 1999}; ^{Lahde et al., 1999}; ^{Staudhammer y LeMay, 2001}; ^{Kant, 2002}; ^{Bohl y Lanz, 2005}; ^{LeMay y Staudhammer, 2005}; ^{Másisi, Nelwamondo y Marwala, 2008}; ^{McRoberts et al., 2008}; ^{Lei, Wang y Peng, 2009}; ^{Wang, Lei, Ma, Kneeshaw y Peng, 2011}), mientras otros han propuesto una combinación de índices (^{Pommerening, 2002}; ^{del Rio, Montes, Cañellas y Montero, 2003}). El índice de diversidad de Shannon-Wiener (Hs) comúnmente utilizado, se determina considerando el área basal de todos los árboles de las especies de la comunidad en conjunto. En contraste, los índices estructurales consideran el área basal del arbolado por clases diamétricas (Hd) y de altura (Hh) de las especies de la comunidad, y más aún, por clases diamétricas y de altura de cada especie (Hsd y Hsp respectivamente) donde el valor máximo ocurre cuando el área basal esta uniformemente distribuida en todas las especies o clases de tamaño de árboles (^{Lei et al., 2009}).

La importancia de la estructura de una comunidad arbolada radica en que es un elemento importante de la biodiversidad (^{MacArthur y MacArthur, 1961}; ^{Willson, 1974}; ^{Ambuel y Temple, 1983}), funcionalidad (^{Buongiorno, Dahir, Lu y Lin, 1994}; ^{Önal, 1997}), manejo (^{Pretzsch, 1997}; ^{Lei et al., 2009}; ^{Wang et al., 2011}), productividad (^{Long y Shaw, 2010}) y ecología de las especies animales (^{Goreaud y Pélissier, 1999}). La vida silvestre y diversidad animal (incluyendo aves e insectos) de un área se encuentra asociada a la presencia de un gran número de especies vegetales y tamaños de árboles (^{Whittaker, 1972}; ^{Buongiorno et al., 1994}; ^{Recher, Majer, Ganesh,1996}; ^{Kimmins, 1997}; ^{McCleary y Mowat, 2002}). La diversidad de fisonomía de las comunidades arbóreas está relacionada a la complejidad estructural (^{Oliver y Larson, 1996}). Finalmente, en las comunidades arbóreas en particular, la estructura del arbolado mantiene una estrecha relación con los factores abióticos básicos como radiación lumínica, humedad y temperatura (^{Hubbell et al., 1999}) y flujos biogeoquímicos (^{Wang et al., 2011}).

Si bien, los índices clásicos han sido útiles para estimar la diversidad de especies de una comunidad arbórea, integrar la estructura del arbolado puede proporcionar una estimación más completa de la comunidad. Por lo anterior, en el presente trabajo se pretende comparar la estructura de dos selvas (una alta y una mediana, sensu^{Miranda y Hernández-X., 1963}) de una forma más completa mediante el uso de índices de diversidad estructural.

Objetivos

El objetivo del presente trabajo fue comparar la diversidad estructural de una selva alta perennifolia y una selva mediana subperennifolia, esperando encontrar una mayor diversidad estructural de la primera que de la segunda, debido a una mayor riqueza de especies, tamaño y abundancia del arbolado.

Materiales y métodos

El presente trabajo se desarrolló en una selva mediana subperennifolia (SMS) y una selva alta perennifolia (SAP) ubicadas en el estado de Tabasco, México (Fig. 1, Tabla 1). Ambos tipos de selva son importantes por su diversidad y productividad tanto para la conservación de especies como para la provisión de servicios ambientales. Los cuadros para el muestreo se ubicaron en áreas de vegetación madura a una distancia mínima entre sí de 300 m en la SMS, y de 100 m en la SAP. Cada cuadro se dividió en 9 (SMS) y 25 (SAP) subcuadros contiguos de 10 m x 10 m donde se midió el diámetro y la altura total de cada árbol mayor de 10 cm de DAP.

Figura 1 Ubicación de las áreas de estudio de la selva mediana subperennifolia (SMS) y la selva alta perennifolia (SAP) en el estado de Tabasco, México. 

Tabla 1 Caracterización de las áreas de estudio de selva mediana subperennifolia (SMS) y selva alta perennifolia en el estado de Tabasco, México. 

Debido a que el número y tamaño de unidades de muestreo, así como el área total de estudio en cada selva fueron diferentes, se usó el programa de EstimateS para Windows Ver. 9 (^{Colwell, 2013}) para despejar cualquier duda sobre la efectividad del esfuerzo de muestreo realizado para la caracterización de la riqueza de especies de cada comunidad. Para ello, y con el fin de reducir al máximo la dependencia entre unidades de muestreo y con esto la posible autocorrelación espacial de los individuos y especies, se usaron los subcuadros evitando que fueran contiguos. Debido a esto, la estimación de la riqueza de especies se hizo a partir de 15 subcuadros para la SMS(las cuatro esquinas del cuadro y el subcuadro del centro) y 52 subcuadros para la SAP (las cuatro esquinas del cuadro). Se calcularon los estimadores de riqueza Chao 1 y Cole debido a que se encuentran diseñados para datos de abundancia de individuos como en este caso (^{Villarreal et al., 2004}). Para las dos comunidades arboladas, el muestreo realizado fue suficiente, ya que en ambos casos se observa la tendencia horizontal de la curva de acumulación de especies (Fig. 2). Para el caso de la SAP se presentó una subestimación de siete especies que representa 11.5% del estimado por Chao 1, mientras que para la SMS hubo una subestimación de dos especies que representa 14% del estimado por Chao 1. Sin embargo, debido a que el área real muestreada fue mayor que la analizada mediante este software, es muy probable que esta subestimación en los dos casos se haya reducido.

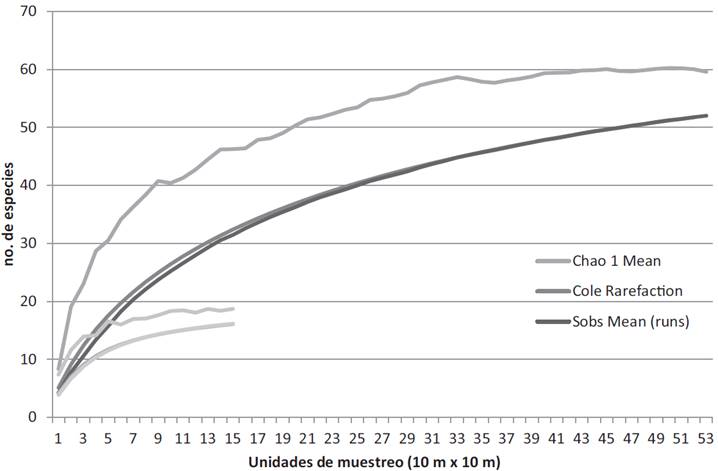
Figura 2 Riqueza de especies observada (S obs) y estimada mediante los estimadores Chao1 y Cole, para la selva mediana subperennifolia (SMS) y la selva alta perennifolia (SAP). 

Se obtuvo el índice de valor de importancia para cada especie con la fórmula: (IVI) = densidad relativa + frecuencia relativa + dominancia relativa de cada especie (^{Krebs, 1986}), donde densidad relativa = % de individuos para cada especie/total de individuos de la comunidad, frecuencia relativa = % de ocurrencia de cada especie en las unidades de muestreo/la suma de las frecuencias relativas de todas las especies de la comunidad, y dominancia relativa = % del área basal para cada especie/total del área basal de la comunidad.

Para medir la diversidad estructural vertical y horizontal de la comunidad se utilizaron únicamente las variables DAP, altura total del árbol y especie (^{Staudhammer y LeMay, 2001}), ya que según ^{Magurran (2004)} los índices de diversidad basados en el área basal de la comunidad como ^{Shannon-Wiener (1949)} resultan más precisos que muchos otros. Con estas variables se calcularon seis índices de diversidad estructural basados en el índice ^{Shannon-Wiener (1949)} y dos coeficientes Gini como otra medida de diversidad estructural (Anexo 1): Índice de diversidad de especies (Hs, ^{Magurran, 2004}), índice de diversidad del tamaño de los árboles (Hd, ^{Buongiorno et al., 1994}), índice de diversidad de la altura de los árboles (Hh, ^{Staudhammer y LeMay, 2001}), índice integrado de la diversidad de especies y diámetro de los árboles (Hsd, ^{Buongiorno et al., 1994}), índice del perfil de las especies (Hsp, ^{Pretzsch, 1996}), índice promedio de la diversidad estructural (Hsdh, ^{Staudhammer y LeMay, 2001}), el coeficiente Gini para el diámetro (Gcd, ^{Lexerød y Eid, 2006}) y el coeficiente Gini para la altura (Gch, ^{Lexerød y Eid, 2006}). Los índices Hd, Hh, Hsd y Hsp requieren que la altura y diámetro de los arboles sean agrupadas en clases discretas (^{Lei et al., 2009}). Para la elaboración de las clases del diámetro y altura de los árboles se utilizó la fórmula de ^{Sturges (1926)}: K = 1 + 3.333*log (n); donde K = número de clases, y n = número de árboles. Para la SMS resultaron ocho clases diamétricas y nueve clases de altura, mientras que para la SAP resultaron diez clases diamétricas y diez de altura.

Debido a que los índices Hd, Hh, Hsd, Hsp y Hsdh se encuentran basados en el índice Shannon-Wiener (Hs), presentan cierta correlación con este índice. Hd y Hh tienen un baja correlación (r = 0.426-0.527, P < 0.001), representando, consecuentemente, diferentes estimaciones de la diversidad estructural de la comunidad (^{Lei et al., 2009}). Hsd, Hsp y Hsdh presentan una correlación mayor (r = 0.814-0.871, P < 0.001), por lo que se deben considerar con cierta reserva. Los coeficientes Gini (Gcd y Gch) particularmente son una medida de heterogeneidad entre 0 y 1, donde el 0 significa que todos los árboles son iguales en su diámetro o altura, y el 1 que todos son diferentes en diámetro o altura, y según ^{Lexerød y Eid (2006)} se recomiendan debido a la sensibilidad e incertidumbre que posee el índice de Shannon-Wiener a los cambios de las amplitud de las clases de diámetros y alturas de los árboles.

Los índices de diversidad Hs, Hd, Hh, Hsd y Hsp se compararon estadísticamente entre las dos comunidades arbóreas mediante la prueba de t de Hutchenson (^{Magurran 1988}) (Anexo 2). Para el índice Hs la prueba se aplicó sin ninguna variación. Sin embargo, debido a que en los índices Hd, Hh, Hsd y Hsp la agrupación del área basal no es por especies como en el caso de Hs, sino por categorías diamétricas y de altura, el valor del número de especies (S) para el cálculo de la varianza del índice H' (VarH') de la prueba de t (ver Anexo 2) se sustituyó por el número de categorías de DAP y de altura que resultaron en cada índice. De esta manera para el caso de Hd el valor de S correspondió al número de clases de diámetros, para Hh correspondió al número de clases de altura, para Hsd correspondió al número de clases de diámetro para cada especie, y para Hsp al número de clases de altura para cada especie. El índice Hsdh y los índices Gini no se compararon estadísticamente debido a que carecen de la abundancia relativa de las especies (Pi) que requiere la prueba. Finalmente se realizaron histogramas de distribución de frecuencias de árboles por clases diamétricas y de altura.

Resultados

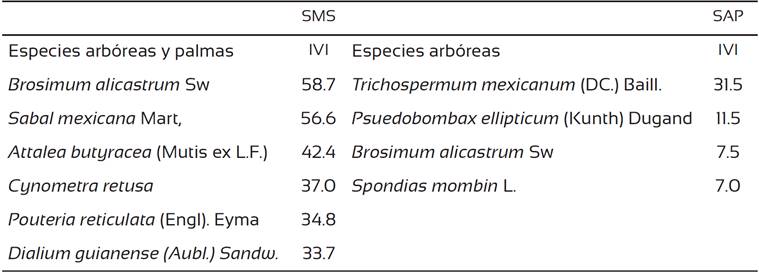
La SAP presentó una mayor riqueza de especies y densidad de individuos que la SMS. Así también el árbol más alto alcanzó una altura mayor en la SAP que en la SMS, sin embargo, el árbol más grueso se presentó en la SMS (Tabla 2). La SMS presentó más especies con valores de IVI altos (33.7 al 58.7), mientras que en la SAP las especies presentaron un valor de IVI por debajo de 31.5 siendo muchas las especies con valores de IVI bajos (< 7. 0) (Tabla 3).

Tabla 2 Principales características dasométricas de la selva mediana subperennifolila (SMS) y selva alta perennifolia (SAP). 

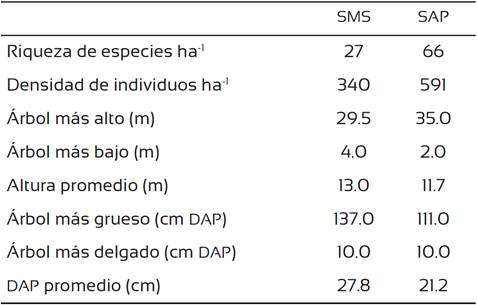
Tabla 3 Índice de valor de importancia (IVI) de las especies dominantes de la selva mediana subperennifolia (SMS) y selva alta perennifolia (SAP). 

La distribución de árboles por clases diamétricas para los dos tipos de selvas presentó una distribución típica en forma de J invertida con una baja proporción de arbolado de diámetro grueso y una alta proporción de árboles de diámetros pequeños (Fig. 3). Por el contrario, la distribución por clases de altura presentó una distribución donde la mayoría de los árboles se ubicó en la tercera clase de altura (11.6 m - 16.2 m) para la selva mediana sub-perennifolia y en la segunda (6.8 m - 11.5 m) para la selva alta perennifolia (Fig. 4).

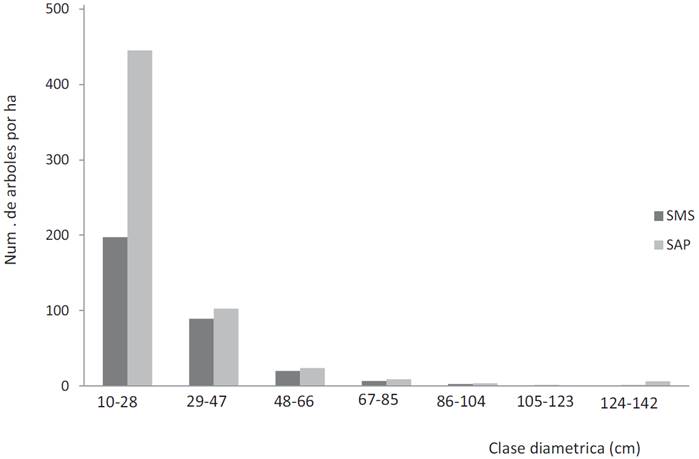
Figura 3 Distribución de árboles por clases diamétricas para la selva mediana subperennifolia (SMS) y la selva alta perennifolia (SAP). 

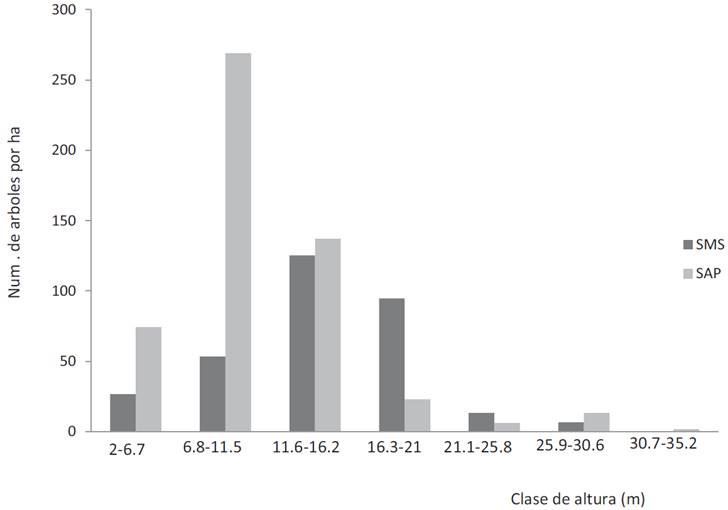
Figura 4: Distribución de árboles por clases de altura para la selva mediana subperennifolia (SMS) y la selva alta perennifolia (SAP). 

La diversidad de especies a partir de su área basal (Hs) fue mayor en la SAP que en la SMS (P = 0.0001, t de Hutchenson = 24.3, gl = 2,973.7) (Tabla 4). Considerando la estructura a partir de los diámetros y alturas de los árboles, la diversidad de especies también fue mayor en la SAP (Hd, P = 0.001, t de Hutchenson = 4.82, gl = 45.14; Hh, P = 0.001, t de Hutchenson = 5.187, gl = 273.1). Considerando los diámetros dentro de cada especie (Hsd), la diversidad también fue mayor en la SAP (P = 0.0001, t de Hutchenson = 17.25, gl = 578.3), y considerando la altura también dentro de cada especie (Hsp), la diversidad fue aún mayor en la SAP (6.6 vs. 3.75, P = 0.0001, t de Hutchenson = 27.17, gl = 646.9). La diversidad estructural en promedio (Hsdh) fue también mayor en la SAP, aunque esta no fue evaluada estadísticamente debido a que constituye un promedio aritmético de tres índices (Anexo 1) y no existen varianzas que permitan calcular la prueba de t de Hutchinson (Anexo 2). La heterogeneidad de los árboles de la selva también fue mayor en la SAP que en la SMS, considerando su tamaño tanto por DAP como por su altura (Gcd y Gch) (Tabla 4).

Tabla 4 Índices de diversidad estructural para una selva mediana subperennifolia (SMS) y una selva alta perennifolia (SAP) en Tabasco, México. 

Valor de P calculado mediante la prueba t de Hutchenson (^{Magurran, 1988}). Hs está calculado con el área basal para todos los individuos en conjunto, mientras que los demás índices están calculados con el área basal para individuos por clase de DAP y altura (ver ^Anexo).

Discusión

En cuanto a la hipótesis planteada, claramente la SAP tuvo mayor número de especies e individuos que la SMS, sin embargo, en cuanto a la altura y diámetro de los árboles la comparación no es tan sencilla (Tabla 2). Con base en los datos dasométricos, no es fácil caracterizarlas estructuralmente como selva alta y selva mediana, ya que en la selva mediana el árbol más bajo y la altura promedio de todos los árboles tienen valores mayores que en la selva alta. Así también, la figura 4 tampoco indica una mayor altura de la selva alta, ya que la mayor abundancia de árboles en la SMS se presentó en la clase de 11.6 m a 16.2 m, la cual fue más alta que la clase de 6.8 m a 11.5 m de la SAP. Lo mismo sucede para el DAP donde el árbol más grueso y el DAP promedio son mayores en la SMS que en la SAP, pero con base en el análisis de frecuencia de árboles por clases diamétricas, la SAP tiene más árboles delgados (Fig. 3).

Lo anterior constituye un problema cuando se consideran estas variables o atributos estructurales de las comunidades en forma aislada. Por el contrario, los índices estructurales incluyen estos atributos en el índice de diversidad haciendo una estimación más completa. De esta manera, la SAP resultó estructuralmente más diversa que la SMS al tener valores mayores en cuatro índices (Hd, Hh, Hsd y Hsp) (Tabla 4). Al tratar de resumir la diversidad estructural de las dos comunidades arbóreas mediante el índice integrado de la diversidad de las especies arbóreas (Hsd) y el índice promedio (Hsdh), estos fueron mayores para la SAP. La selva alta presentó más clases diamétricas y de altura que la selva mediana (ver método), lo cual se refleja en esta mayor diversidad estructural a través de los índices. El índice del perfil de las especies (Hsp) constituye una estimación más completa del perfil vertical de la comunidad que las descripciones a partir de los resultados dasométricos aislados de altura de los árboles o distribución del arbolado por clases de altura. Lo mismo sucede para el índice Hd con respecto a las mediciones aisladas del DAP. Otra ventaja de los índices estructurales es que permiten la comparación estadística a diferencia de las estimaciones dasométricas individuales donde para realizar una comparación estadística se requieren al menos tres comunidades arbóreas del mismo tipo. El índice promedio de la diversidad estructural (Hsdh), por su parte, intenta englobar los diámetros, alturas y especies de la comunidad, mientras que el coeficiente Gini (Gcd, Gch) constituye una medida de la heterogeneidad del área basal de la comunidad en relación con los diámetros y alturas de los árboles, y cuantifica la desviación de la igualdad perfecta de cero (^{Lei et al., 2009}). En este sentido, la SAP fue más heterogénea que la SMS en cuanto al tamaño de los árboles al ser mayores los valores de Hsdh y del coeficiente Gini. Esto indica que la SAP presenta más árboles de diferentes tamaños tanto en diámetro como en altura que la SMS, haciéndola estructuralmente más diversa que una comunidad con menos árboles o tamaños similares como podría ser el caso de una plantación. Sin embargo, en relación con el crecimiento del arbolado, los índices estructurales Hd y Hh resultaron mejores predictores que los índices de Gini (^{Lei et al., 2009}).

En relación con la mayor diversidad estructural de la SAP habría que considerar que la SMS es un área protegida donde la estructura y el dosel arbolado han tomado su curso natural, mientras que en la SAP no se puede descartar la extracción maderable selectiva a lo largo del tiempo, lo cual pudo haber influido en la mayor heterogeneidad estructural de la vegetación. En este sentido, obviamente lo ideal sería comparar áreas de estudio similares con relación al uso de suelo, sin embargo en la actualidad aun las áreas protegidas sufren de algún grado de perturbación humana.

La diversidad estructural de una comunidad tiene como ventajas que puede estar mejor relacionada con la diversidad biológica de la fauna y entomofauna, que los índices clásicos de diversidad de especies de la vegetación. Lo anterior es evidente al considerar la altura de los árboles, variable que resulta altamente importante para los hábitos de las aves, insectos y reptiles. Los diferentes tamaños de los árboles proveen una variedad de hábitats para diversas especies de flora y fauna (^{Lei et al., 2009}). Según ^{MacArthur y MacArthur (1961)}; ^{Buongiorno et al. (1994)} y ^{Franklin et al. (2002)} la biodiversidad de las comunidades arbóreas se puede mantener con el manejo de su diversidad estructural, de tal forma que este concepto se ha incorporado a las practicas del manejo forestal actual (^{Kant, 2002}). Así también, se ha encontrado una relación positiva entre la diversidad estructural y los almacenes de carbono en un bosque de coníferas en Norteamérica (^{Wang et al., 2011}). La diversidad estructural de una comunidad es importante para su diversidad biológica y afecta a otros componentes como los valores ecológicos, económicos y sociales del ecosistema (^{Lexerød y Eid, 2006}), por ejemplo, al influir el tamaño y número de árboles de la comunidad en la captura de carbono, creación de mantos acuíferos, producción maderable y ecoturismo; por mencionar los principales.

Comparando la diversidad estructural de las selvas húmedas (Tabla 4) con los bosques templados de Norteamérica donde originalmente se aplicaron estos índices, se puede ver que los valores máximos de las selvas (6.737) son mucho más altos que los máximos documentados por ^{Lei et al. (2009)}: 2.347, y ^{Wang et al. (2011)}: 2.355, lo que refleja una mayor diversidad estructural de las selvas tropicales.

Los índices de diversidad estructural describen en forma más completa la diversidad de las comunidades arbóreas, lo que permite establecer una mejor relación con el hábitat de la comunidad que los índices de diversidad clásicos. Ciertamente su procedimiento de análisis es un poco más laborioso que el de los índices clásicos de diversidad, pero permiten tener resultados de mayor utilidad.

Conclusiones

Los índices de diversidad estructural fueron efectivos para comparar la estructura de dos selvas tropicales siendo más diversa la selva alta perennifolia que la selva mediana subperennifolia. Por lo anterior, se recomienda el uso de estos índices con la intensión de realizar una medición más completa de estas comunidades arbóreas estructuralmente complejas, así como para poder establecer comparaciones más precisas de diversidad de especies entre diferentes comunidades arbóreas en el trópico.