Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Madera y bosques
versão On-line ISSN 2448-7597versão impressa ISSN 1405-0471
Madera bosques vol.16 no.4 Xalapa Jan. 2010
Artículos de investigación
Modelos de crecimiento de árbol individual: Aplicación del Simulador BWINPro7
Individual tree growth models: Application of the BWINPro7 Simulator
Benedicto Vargas–Larreta1, Javier Corral–Rivas2, Óscar Aguirre–Calderón3 y Jürgen Nagel4
1 Instituto Tecnológico de El Salto, Mesa del Tecnológico s/n. El Salto, P.N., Dgo. México. bvargas@correo.itelsalto.edu.mx.
2 Facultad de Ciencias Forestales, Universidad Juárez del Estado de Durango.
3 Facultad de Ciencias Forestales, Universidad Autónoma de Nuevo León. Carr. Nacional km 145. Linares, Nuevo León, México.
4 Nordwestdeutsche Forstliche Versuchsanstalt, Grätzelstr. 2, 37075 Göttingen, Alemania.
Manuscrito recibido el 23 de octubre de 2008
Aceptado el 29 de junio de 2010
RESUMEN
Se describe el simulador de crecimiento y producción de rodales forestales BWINPro7 versión El Salto, Durango. Es una herramienta de sencillo manejo para ser utilizada por gestores y propietarios forestales como apoyo a la toma de decisiones en el manejo forestal. El programa incorpora modelos de crecimiento de árbol individual, desarrollados en los últimos años para las principales especies de pino y encino de los bosques mixtos e irregulares del noroeste de México. Específicamente, fueron incorporados al simulador de crecimiento BWINPro7: 1) modelos para estimar el diámetro de copa y la altura de fuste limpio, 2) modelos para la estimación del crecimiento en altura y área basal de árboles individuales y, 3) un modelo para la cuantificación de la mortalidad natural. Adicionalmente, el simulador puede ser usado con parcelas permanentes de inventario para describir la estructura espacial y prescribir cortas de aclareo y aprovechamientos forestales a escala industrial.
Palabras clave: Manejo forestal, modelo de crecimiento, simulador de crecimiento forestal.
ABSTRACT
This paper describes a user–friendly computer application developed for forest management planning in El Salto, Durango (Mexico). The computer program BWINPro7 version El Salto allows for forest growth and predicts future stand development. It represents an easy tool that can be used by forest managers and owners of forest lands in the decision–making process. The program incorporates individual tree growth models developed for most pine and oak species during recent years in mixed and uneven–aged forests in the north–eastern region of Mexico. Specifically, the models that were incorporated into the program BWINPro7 are: (1) models to estimate crown width and the height to the live crown base, (2) individual tree basal area and height growth models, and (3) a model to predict individual tree mortality. In addition, the simulator can be used in permanent sample plots to describe stand spatial structure, and to prescribe thinning and timber harvest at industrial scale.
Keywords: Forest management, Growth Model, Forest Growth Simulator.
INTRODUCCIÓN
Los modelos de crecimiento forestal predicen el desarrollo de un bosque, empleando características del sitio y opciones de manejo como variables de entrada, y constituyen una herramienta importante para la toma de decisiones en el manejo forestal sostenible (Newnham, 1964). La mayoría de estos modelos son empíricos y pueden ser organizados en tres tipos: modelos de rodal, modelos de clases de tamaños y modelos de árbol individual. El tipo de modelo a desarrollar depende tanto de los propósitos de su aplicación como de los recursos disponibles (Vanclay, 1995). Estos factores determinan también los datos necesarios y la exactitud de las estimaciones.
La mayoría de los estudios de crecimiento y producción realizados en Durango, México, utilizan modelos a nivel de rodal para predecir la evolución en el tiempo de las principales variables dasométricas del rodal (Valles, 2007). Dichos modelos son de naturaleza estática, en el sentido de que no predicen, directamente, tasas de cambio de ninguna de dichas variables. Por el contrario, los modelos de carácter dinámico predicen fundamentalmente tasas de cambio, es decir, el crecimiento de alguna variable dasométrica que, normalmente, es el diámetro medio cuadrático, el área basal o el volumen. A partir de estas ecuaciones se obtiene, bien por integración o por aplicación sucesiva de incrementos, la evolución del rodal en el tiempo (Alder, 1980).
En el marco de la planificación forestal se ha fortalecido la aplicación de los simuladores de crecimiento a través de su implementación en los programas de manejo de recursos forestales (Hasenauer, 2006). Estos tienen claras ventajas sobre las tablas de producción tradicionales, especialmente en el aprovechamiento de bosques mixtos, ya que, teóricamente, con ellos se puede representar cualquier situación del rodal y predecir su desarrollo futuro. Además, algunos de ellos ofrecen una amplia gama de información adicional, por ejemplo, distribución de productos y parámetros estructurales del rodal (Vargas–Larreta, 2006).
Debido a que las decisiones para un manejo forestal sostenible se basan en información sobre las condiciones presentes y futuras de los recursos (von Gadow et al., 2004), los datos de periodos largos son indispensables. Cuando se carece de este tipo de información, los simuladores de crecimiento forestal que describen la dinámica de bosques (i.e., crecimiento, sucesión, mortalidad, regeneración y otros cambios de los rodales) pueden ser utilizados para predecir el rendimiento futuro, la composición de especies, la estructura y la función de los ecosistemas bajo condiciones ambientales cambiantes. Estos simuladores permiten también el análisis de opciones de manejo y alternativas silvícolas (Vanclay, 1995).
La aplicación del simulador forestal BWINPro (Nagel et al., 2002) en la práctica forestal en Alemania ha alcanzado una amplia distribución. El simulador fue desarrollado para las regiones forestales del noreste de ese país y actualmente es usado por el Servicio Forestal de Baja Sajonia. El programa ha sido desarrollado en el lenguaje de programación Java (Sun 2 Plattform, Standard Edition 1.5.0) bajo el ambiente NetBeans 4.0 y publicado a través del proyecto TreeGrOSS (Tree Growth Open Source Software) y se encuentra disponible bajo el concepto de Licencia Pública General (GPL, por sus siglas en inglés), lo cual permite al usuario modificar casi todos los parámetros de las ecuaciones del modelo de crecimiento, observando el efecto de dichas modificaciones de manera visual. El simulador se encuentra disponible en la dirección http:/www.nw–fva.de (Nagel y Sprauer, 2009). Los resultados de las simulaciones pueden ser exportados en forma gráfica o tabular a otros programas del ambiente Windows©; además, el programa puede trabajar en otras plataformas como Linux y MacOS. El simulador ha sido adaptado para tres regiones: Noroeste y Noreste de Alemania y El Salto, Durango, México (Vargas–Larreta, 2006).
Dado que los responsables de la gestión de los recursos de las regiones forestales del estado de Durango requieren herramientas de fácil aplicación que sirvan de apoyo a la toma de decisiones, el presente trabajo pone a disposición un instrumento de predicción que puede ser integrado como alternativa a los modelos de crecimiento utilizados hasta ahora en la práctica forestal en la región de El Salto, Durango, México.
OBJETIVO
Presentar el desarrollo de un modelo de crecimiento de árbol individual para rodales mixtos e irregulares, evaluando su aplicabilidad en los bosques de la región de El Salto, Durango, a través del simulador de crecimiento forestal BWINPro7.
MATERIALES Y MÉTODOS
Área de estudio
La región forestal El Salto abarca aproximadamente 580 000 ha (Corral–Rivas et al., 2004). Se localiza en el estado de Durango, entre los 23°30'–24°15' de Latitud y los 105°15' –105°45' de Longitud (Figura 1). El área se ubica a una altitud entre 1400 msnm y 2600 msnm. La temperatura media anual oscila entre los 20°C y los 22°C, mientras que la precipitación promedio varía de los 800 mm a los 1200 mm.
Datos de campo
Los datos proceden de 58 sitios que la Unidad de Conservación y Desarrollo Forestal de El Salto estableció en 1997 para desarrollar el sistema biométrico de los programas de manejo forestal en la región. Dicha red de sitios está distribuida de tal manera que cubre las diferentes densidades y calidades de estación existentes. El tamaño del sitio fue de 1000 m2 y la medición de las variables de los árboles muestra fue realizada por personal de las diferentes unidades de manejo de la región a través de protocolos y aparatos de medición convencionales.
En la segunda medición realizada en el año 2003, en cada parcela se identificaron con una chapa numerada todos los árboles y en ellos se realizó la medición del diámetro normal en cruz (a 1,3 m sobre el nivel del suelo), utilizando una forcípula con graduación milimétrica. Asimismo, se midió con hipsómetro digital la altura total de todos los árboles presentes en la parcela con precisión de centímetros. Además se midió el diámetro de copa (m), la altura de fuste limpio (m) y la ubicación de cada árbol dentro del sitio mediante coordenadas X, Y. Debido a que la mayoría de los rodales son heterogéneos, no se colectó información sobre la edad de los árboles. La segunda medición fue dirigida por los autores, por lo que se asume una mayor confiabilidad tanto en el procedimiento de medición como en el manejo de los aparatos utilizados.
Desarrollo del modelo
El modelo global de crecimiento se compone de "submodelos" (nombrados posteriormente modelos por facilidad): un modelo generalizado altura–diámetro, de diámetro de copa, de altura de fuste limpio, de incremento en área basal, de incremento en altura y de mortalidad.
Todos ellos fueron desarrollados para cada una de las siguientes especies del género Pinus: Pinus cooperi, P durangensis, P teocote, P. ayacahuite, P. leiophylla y P. herrerae, así como para el grupo de especies del género Quercus y el grupo de otras hojosas (Alnus, Arbutus y Cupressus). Las especies del género Quercus fueron identificadas de acuerdo con la clasificación utilizada por la Unidad de Conservación y Desarrollo Forestal No. 6, esto es, encino de hoja chica, mediana y ancha.
Modelo altura–diámetro
El modelo ajustado para describir la relación altura–diámetro para rodales mezclados e irregulares fue el de Schröder y Álvarez (2001):
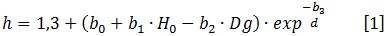
Los parámetros de la ecuación (b0, b1, b2 y b3) fueron estimados en función del diámetro medio cuadrático (Dg), el diámetro normal (d) y la altura dominante H0 (definida por Assmann (1970) como la altura media de los 100 árboles más grandes por hectárea).
Modelo de diámetro de copa
La cuantificación de las relaciones de competencia entre los árboles de un rodal es un factor importante, para lo cual frecuentemente son utilizadas las dimensiones de las copas como variables explicativas del proceso. En el presente trabajo se utilizó la siguiente ecuación para estimar el diámetro de copa de las especies consideradas en el estudio.
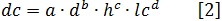
Donde dc = Diámetro de copa (m), d = Diámetro normal (cm), h = Altura total (m), lc = Longitud de copa (m), a, b, c, d = Coeficientes de regresión.
Modelo de altura de fuste limpio
La altura de fuste limpio o la longitud de copa, han sido utilizadas exitosamente durante décadas para evaluar el incremento de árboles (Wykoff, 1990; Hasenauer, 1994; Monserud y Sterba, 1996; Pretzsch y Kahn, 1998; Nagel, 1999).
Se ajustó el modelo de altura de fuste limpio de Schmidt (2001), el cual ha sido implementado en el simulador BWINPro7 para otras regiones.
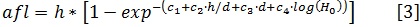
donde afl = Altura de fuste limpio (m), h = Altura total (m), d = Diámetro normal (cm), H0 = Altura dominante, c1 ... c4 = Coeficientes de regresión, exp = exponencial.
Modelo para estimar el área superficial de copa
El área superficial de copa es el área del paraboloide conformado por la periferia de la copa de los árboles (Van Laar y Akça, 2007) y representa uno de los valores de entrada más importantes en el simulador para la cuantificación de los incrementos en área basal y en altura. La base para su cálculo es un paraboloide que considera la altura total, la longitud y el radio de copa como variables.

Donde asc = Área superficial de copa (m2), lc = Longitud de copa (m), medida desde la base de ésta hasta la punta del árbol, rc = Radio de copa (m).
El radio de copa en una altura determinada (rchc) es calculado con la ecuación propuesta por Nagel (1999):

Donde: hc = Radio de copa a la altura de corte (m), h=Altura total (m), hc = Altura de corte (m).
Modelo de competencia
La competencia es cuantificada en el simulador BWINPro7 a través de índice C66 (Nagel, 1999). El modelo calcula primero el valor de este índice independiente de la distancia para después compararlo con un parámetro denominado "grado máximo de cierre de copas" para el rodal completo. El fundamento para el cálculo del índice C66 es la "altura de corte" (hc) del árbol de referencia. Esta altura se localiza en el 66% de la longitud de la copa, de la punta del árbol hacia abajo (Figura 2).
El valor del índice C66 de un árbol es la suma de las áreas de copa de todos los árboles del rodal, cuya copa es cortada por la línea hipotética (altura de corte) que se proyectaría a partir del 66% de la longitud de la copa del árbol de referencia. Si la base de la copa de un competidor se ubica por encima de la altura de corte del árbol de referencia (árbol 2), la totalidad del área de copa del competidor (árbol 4) es considerada en el cálculo del índice. Por el contrario, si un árbol es más pequeño que la altura de corte (árboles 3 y 5), éste no es seleccionado como competidor y el área de su copa no es incluida en el cálculo del índice de competencia. El índice C66 para el árbol de referencia i estará dado entonces por:
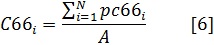
donde: A = Superficie del sitio o rodal [m2], pc66 = Proyección del área de copa (m2) y que es igual a la suma de los cuadrados de los radios de copa a la altura o sobre la altura de corte del árbol de referencia i, multiplicado por Ï (pi) y dividido entre la superficie del sitio o rodal (A).
El índice C66 puede interpretarse como el grado de cierre de copas a una determinada altura. La altura de corte fue fijada en los 2/3 de la altura de copa asumiendo que en esta zona se localiza el cambio entre la copa de luz y la copa de sombra (Biging y Dobbertin, 1992).
El efecto de una corta sobre el valor de la competencia también es evaluado. El cambio en el valor del índice es denominado C66c y es calculado como la diferencia de los valores de competencia antes y después de la corta, cuyo punto de comparación es fijado al inicio del periodo de crecimiento. El valor de C66c es cero si no se aplicó ningún tratamiento, o positivo, cuando el rodal fue aclarado durante el periodo de crecimiento.
Modelo de incremento en área basal
Para calcular el incremento en área basal, se utilizó un modelo que estima el logaritmo del incremento en área basal como una función del área superficial de copa (asc), la competencia antes y después de la corta (C66 y C66c), la altura dominante (H0) y la proporción de especies en el rodal (ME).
La proporción que ocupa cada especie (ME) fue considerada como un factor que podría describir la competencia interespecífica y, por tanto, influir en el incremento en área basal. La proporción que ocupa cada especie en el rodal fue incluida entonces como variable independiente en el análisis de regresión y fue definida como:

Donde MEi = Proporción del área basal del rodal que ocupa la especie i, gi = Área basal de la especie i en el rodal (m2), G = Área basal total del rodal (m2).
En los análisis exploratorios se utilizaron diferentes valores de árbol individual y de rodal como variables independientes. La selección de las variables se realizó utilizando el procedimiento Stepwise del módulo REG del paquete estadístico SAS/STAT® (SAS, 2004). La forma general del modelo de incremento en área basal para cada especie o grupo de especies tras dichos análisis fue:

donde In(Δgi) = Logaritmo natural del incremento en área basal para un periodo de crecimiento de 5 años del árbol i, asci = Área superficial de copa del árbol i (m2), H0 = Altura dominante (m), MEi = Proporción del área basal de la especie i en el rodal, C66–C66c = Índice de competencia antes y después de una corta, bo...b5 = Coeficientes.
Modelo de crecimiento en altura
Para la predicción del crecimiento en altura se ajustaron los modelos de Lundqvist–Korf (Korf, 1939; Lundqvist, 1957) y de McDill–Amateis (McDill y Amateis, 1992) en su forma de diferencias algebraicas.
Dado que no se tuvo información disponible sobre la edad y que la forma en diferencias algebraicas de los modelos probados exige el uso de las edades al inicio y al final del periodo de crecimiento, se utilizó una forma alternativa de los modelos originales. Ésta consistió en utilizar el diámetro normal al inicio y al final del periodo de crecimiento. El diámetro del árbol al final del periodo de crecimiento es obtenido mediante el modelo de incremento en diámetro. La forma en diferencias algebraicas de los modelos de crecimiento en altura se presenta en la tabla 1.
Modelo de mortalidad
La mortalidad natural fue evaluada utilizando el valor máximo de cierre de copas y los valores máximos del índice de competencia C66. De acuerdo con este principio, aquel árbol que tiene un valor de índice de competencia C66 que sobrepasa el valor máximo de cierre de copas se considera que no sobrevive el periodo de crecimiento. El grado de cierre de copas máximo posible (CCmax) para una densidad máxima (IDRmax) es estimado con la ecuación [11].
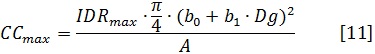
Donde IDRmax es el índice de densidad máxima del rodal, el cual es obtenido a partir de la ecuación [12], Dg es el diámetro medio cuadrático del rodal (cm), A es la superficie del sitio (m2), y b0 y b1 son los coeficientes de regresión.
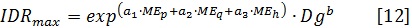
Donde MEp, MEq, MEh = Proporción del área basal del rodal que ocupan las especies de los géneros Pinus y Quercus y el grupo de otras hojosas, respectivamente; a1, a2, a3 y b = Parámetros de regresión.
El valor CCmaxobtenido con la ecuación [11] es fijado como límite en el modelo de mortalidad, es decir, si el valor del índice C66 de un árbol es mayor al CCmax calculado para esa especie, entonces el árbol es eliminado. Los parámetros b0 y b1 en la ecuación [11] fueron tomados del modelo de diámetro de copa para árboles solitarios desarrollado para las especies maderables más importantes de la región de Pueblo Nuevo, Dgo. (UCODEFO 6, 2006).
Análisis estadístico
Para el ajuste de los modelos se utilizaron los paquetes estadísticos R y SAS/STAT®(SAS, 2004). El análisis de la bondad de ajuste de los modelos se basó en comparaciones numéricas y gráficas. Se calcularon, a partir de los residuos obtenidos en la fase de ajuste, los siguientes estadísticos: el sesgo, la raíz del error medio cuadrático (REMC), el coeficiente de determinación ajustado (R2adj) y el criterio de información de Akaike en diferencias (AICd), que es un índice que se emplea para seleccionar el mejor modelo y se basa en minimizar la distancia de Kullback–Lieber (Burnham y Anderson, 2002). Las expresiones de estos estadísticos son las siguientes:
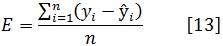
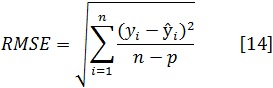
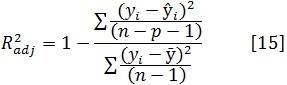
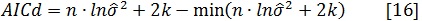
donde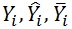
son, respectivamente, los valores observado, predicho y promedio de la variable dependiente; n es el número total de observaciones utilizado para ajustar el modelo; p es el número de parámetros a estimar; k = p+1; σ2 y es el estimador de la varianza del error del modelo.
El simulador de crecimiento forestal BWINPro7
BWINPro7 es un programa de cómputo para la simulación y el análisis del crecimiento de árboles y de rodales que fue desarrollado en los años 90's como un modelo de árbol individual independiente de la distancia en el Centro de Experimentación Forestal de Baja Sajonia, Alemania (Nagel, 1999). Fue concebido originalmente como un modelo de manejo para realizar proyecciones del crecimiento forestal en periodos de 20 a 30 años para los bosques del noroeste de Alemania. Con BWINPro7 es posible visualizar rodales puros o mezclados, regulares o irregulares y pronosticar su desarrollo a través del tiempo. Para lograr esto, BWINPro7 cuenta con rutinas dendrométricas, modelos de forma y de volumen, modelos para estimar el diámetro de copa y la altura de fuste limpio, modelos por especie para la estimación del crecimiento de árboles individuales y un modelo para la cuantificación de la mortalidad natural. También incluye rutinas para la aplicación de tratamientos silvícolas a nivel rodal así como un visualizador de rodales en tres dimensiones (3–D), además de un módulo manejador de especies. El efecto de distintos regímenes de aclareo y tratamientos silvícolas puede ser observado, analizado y visualizado con ayuda de un módulo gráfico. La figura 3 muestra la estructura general del simulador BWINPro7.
Los árboles del sitio o rodal son posicionados por el simulador utilizando las coordenadas X, Y, obtenidas en el levantamiento de la información, de tal forma que cada árbol es ubicado en el lugar que ocupa dentro el sitio; sin embargo, el simulador permite crear rodales hipotéticos en los cuales la ubicación del árbol es aleatoria. Además, permite cambiar el ángulo de visión a través de la rotación del rodal y la posición del usuario (Figura 4). También, permite visualizar el estado actual de cada uno de los rodales que se desean analizar, pero además, una vez realizada la simulación de la aplicación de un tratamiento, se puede observar de manera gráfica, el desarrollo de cada unidad de manejo, con base en el régimen de tratamientos que se haya seleccionado. El tamaño de la unidad de manejo en este caso corresponde al tamaño del sitio de inventario (1000 m2), sin embargo, tanto la forma como el tamaño del sitio puede ser definido por el usuario, mientras que los resultados son presentados en valores por hectárea. El simulador genera en cada ciclo de simulación de cinco años un listado de valores para cada árbol, tanto de los residuales como de los extraídos. La tabla de rodal muestra, además de información individual para cada árbol, parámetros estructurales e índices de diversidad.
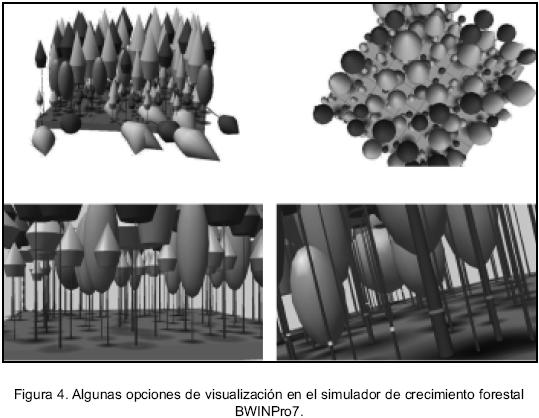
De esta manera el manejador puede entender fácilmente las consecuencias económicas y ecológicas de aceptar el plan de cortas propuesto, siendo más fácil analizar aspectos como diversidad o la continuidad horizontal y vertical del estrato arbóreo.
Adaptación del simulador BWINPro7 a la región de El Salto
Los modelos ajustados para la región de El Salto se incorporaron a la plataforma estándar de BWINPro7, misma que permite incluir nuevos modelos de crecimiento para distintas regiones (Nagel, 1999). Tanto la estructura del programa como la programación abierta Tree–GrOSS (Nagel, 2005) permiten al usuario verificar los modelos de crecimiento, adaptarlos y optimizarlos a sus necesidades de información e integrarlos en otro software o agregar partes de modelos de crecimiento locales o regionales.
RESULTADOS Y DISCUSIÓN
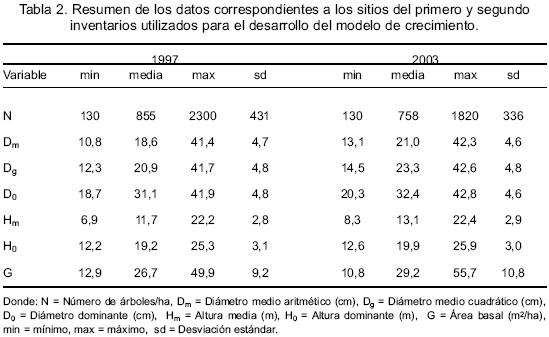
La tabla 2 muestra los valores medios y extremos de las principales variables de rodal medidas en cada uno de los inventarios. Los valores obtenidos se usaron para el ajuste de los modelos mencionados en el apartado de metodología.
Relación altura–diámetro
Los coeficientes de regresión, así como los estadísticos de ajuste, coeficiente de determinación ajustado (R2adj), sesgo ( ) y raíz del error medio cuadrático (REMC) para el modelo de Schröder y Álvarez (2001) se presentan en la tabla 3.

El porcentaje de la variabilidad observada en las alturas de los árboles explicada por el modelo de Schröder y Álvarez (2001) oscila entre 63% y 83% para las especies de pino, lo cual puede ser considerado como un valor adecuado considerando la gran variabilidad en los pares de datos altura–diámetro en las masas irregulares. Para el grupo de especies del género Quercus y el de otras hojosas los valores del coeficiente de determinación ajustado fueron de 0,66 y 0,60, respectivamente. Aunque estos valores son relativamente bajos comparados con los resultados de trabajos similares, cuyos coeficientes de determinación ajustados siempre son superiores de 0,9 (Peng y Liu, 2001; Castedo et al., 2005; Diéguez–Aranda et al., 2005; Schröder y Álvarez, 2001; López et al., 2003), otros autores reportan valores similares a los encontrados en el presente estudio cuando describen la relación altura–diámetro (López et al., 2003; Barrio–Anta et al., 2006; Sharma y Parton, 2007), incluso algunos autores han obtenido valores por debajo de 0,64 (Colbert et al. , 2002; Yuancai y Parresol, 2001). Además, de acuerdo con Zhang (1997), más importante que los valores de este estadístico es la evaluación de las relaciones altura–diámetro en función de su capacidad predictiva (exactitud, precisión y flexibilidad) dentro del rango de datos utilizados. Cabe mencionar que para el área de estudio, no existe una modelización previa de la relación altura–diámetro para las masas mixtas e irregulares, por tanto, el modelo propuesto representa la primera contribución formal al respecto.
Modelo de diámetro de copa
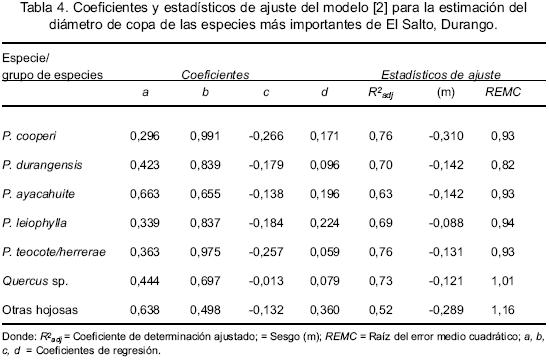
El diámetro de copa para las especies se predice a partir del diámetro normal, la altura total y la longitud de copa. En comparación con la ecuación de Romero (UCODEFO 6, 1997) utilizado hasta la fecha en la región de El Salto, Durango, el nuevo modelo presenta para todas las especies menor sesgo y mayor exactitud en las estimaciones (Tabla 4).
Modelo de altura de fuste limpio
En la tabla 5 se observan los estadísticos de ajuste para el modelo que predice la altura de fuste limpio de cada especie y grupo de especies.

El modelo que estima la altura de fuste limpio es idéntico al utilizado en la versión original de BWINPro y utiliza, en consecuencia, las variables h/d, d y H0. La precisión de las estimaciones de la altura de fuste limpio para todas las especies de pino, excepto para Pinus ayacahuite, pudo ser constatada con un nivel de confiabilidad altamente significativo.
Modelo de incremento en área basal
Un modelo lineal resultó ser adecuado para la estimación del incremento en área basal. Las variables área superficial de copa (asc), altura dominante (H0), competencia antes y después de la corta (C66 y C66c) y proporción de especies (MEi) pudieron explicar las tendencias de crecimiento en área basal. La proporción de la variación explicada por la competencia resultó ser pequeña.
El ajuste del modelo de incremento en área basal aporta resultados poco satisfactorios (Tabla 6). El motivo de esto puede ser la amplia dispersión de los valores de incremento para un determinado diámetro normal.
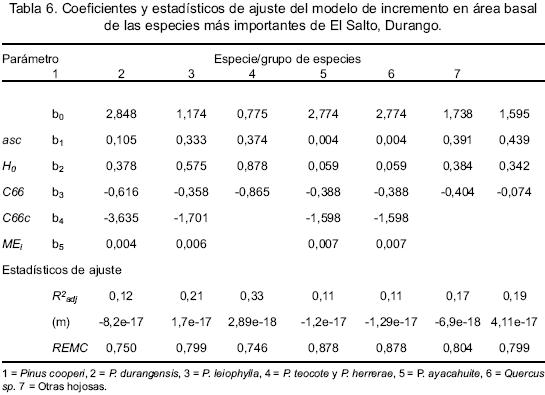
Los valores del coeficiente de determinación ajustado son bajos, sin embargo, el modelo logra explicar hasta un 33% de la variabilidad del incremento en área basal en el caso de Pinus leiophylla. El valor de R2adj para Pinus oscila entre 0,11 (Pinus teocote, P. ayacahuite) y 0,33 (Pinus leiophylla) (Tabla 6). Para los encinos y el grupo de otras hojosas el valor de R2adjes cercano a 0,2.
La raíz del error medio cuadrático (REMC) alcanza valores de 0,75 hasta 0,88, mientras que el sesgo es muy cercano a cero en todos los casos. Cabe mencionar que se observó una variación alta en relación con los valores individuales de incremento predichos. Gran parte de estas desviaciones puede ser asumida como efecto de la probable falta de precisión en la medición de los diámetros en el primer inventario. Lo anterior plantea la necesidad de realizar más investigación en la modelización del incremento de los bosques del estado de Durango, a través del uso de parcelas permanentes establecidas a través de una metodología estandarizada, como la desarrollada recientemente por Corral–Rivas et al. (2009).
La mezcla de especies (MEi) tuvo un efecto significativo en el incremento en área basal para las especies de pino. Los resultados permiten asumir que la mezcla de especies en un rodal afecta frecuentemente el crecimiento de un árbol. Sin embargo, este efecto no es siempre positivo. La hipótesis acerca de un mejor crecimiento en rodales dominados por pino en comparación con rodales dominados por encino no pudo ser confirmada debido a la carencia de datos.
Modelo de incremento en altura
Los modelos de McDill–Amateis (McDill y Amateis, 1992) y Lundkvist–Korf (Korf, 1939; Lundqvist, 1957) (Korf_ken la tabla 7) fueron seleccionados para describir el crecimiento en altura.

Estos modelos fueron ajustados en forma de ecuaciones en diferencias algebraicas. Se pudo demostrar que esta alternativa de ajuste para la estimación del incremento en altura, a pesar de las limitaciones de los datos utilizados, proporciona resultados altamente satisfactorios.
El modelo Korf_k fue seleccionado para Pinus ayacahuite y el grupo de otras hojosas. Para el resto de especies y grupos de especies se utilizó el modelo de McDill–Amateis. El sesgo máximo obtenido es de 0,33 m, lo que permite asumir que los modelos presentan errores promedio bajos en las estimaciones de altura. El modelo de crecimiento en altura desarrollado es adecuado para describir el desarrollo de esta variable para todas las especies investigadas. La comparación de los incrementos en altura entre especies mostró solo pequeñas diferencias.
Evaluación de la mortalidad natural
De manera concreta se evaluó el uso de un valor crítico de cierre de copas (CCmax) y valores máximos del índice de competencia C66 para diferentes proporciones de mezcla de especies. Se pudo constatar que el modelo no muestra ninguna diferencia significativa en el número de árboles muertos estimado, comparado con los valores reales de mortalidad observados. La tabla 8 contiene los parámetros de la ecuación [14] que permite estimar la densidad máxima de los rodales evaluados.

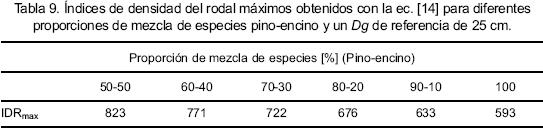
Debido a que las especies del grupo de otras hojosas juegan un papel económico poco importante en el manejo forestal en la región de El Salto, se presentan valores de densidad máxima solo para mezclas de pino y encino. Sin embargo, los parámetros presentados en la tabla 8 fueron obtenidos para la totalidad de los datos, por lo que son válidos para el cálculo de la densidad máxima para cualquier combinación de especies. Así se tiene por ejemplo, que para un Dg de referencia de 25 cm se obtiene una densidad máxima de 593 árboles por hectárea cuando el rodal es ocupado completamente por pino. Este valor crece paulatinamente conforme la presencia de especies de encino aumenta en el rodal, hasta llegar a 823 árboles cuando la mezcla es 50–50 (Tabla 9).
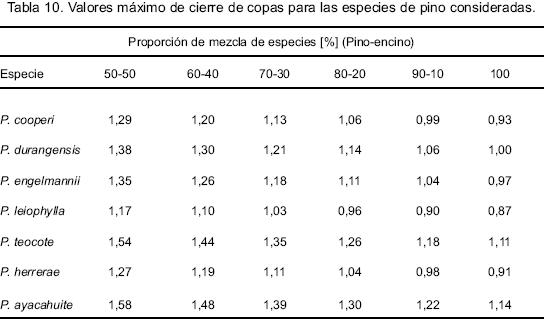
Los valores máximos de cierre crítico de copas para las especies de pino para una determinada proporción de mezcla de especies se presentan en la tabla 10. De acuerdo con este principio, aquel árbol que sobrepasa un determinado valor de índice de competencia C66 comparado con un valor máximo de cierre de copas se elimina durante la simulación.
Simulación de escenarios silvícolas
El primer paso para llevar a cabo la planificación forestal es la simulación de regímenes silvícolas alternativos para cada rodal. Para ello se deben definir en el simulador las características de cada alternativa silvícola que se desea analizar, lo cual se hace a través de la pantalla "especificaciones de simulación" (Figura 5).
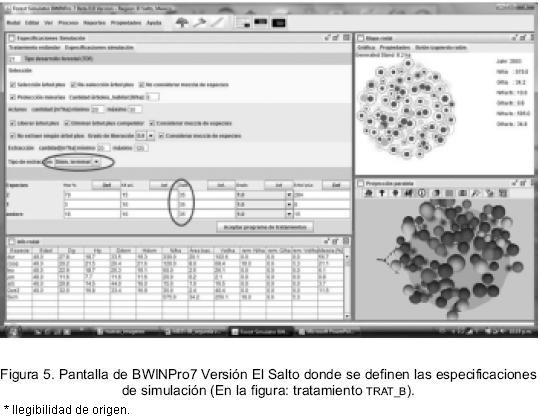
Con el objeto de generar regímenes silvícolas alternativos, las densidades, áreas basales y volúmenes a extraer durante las cortas son modificados mediante la especificación de estos parámetros. De esta manera cada usuario puede simular diferentes programas de cortas, sean éstas sucesivas hasta la cosecha final o selectivas (árbol por árbol), proyectando el crecimiento del rodal hasta por 30 años, variando el régimen de cada programa de cortas (intensidad, periodicidad, etc.) y visualizar los efectos de dichos cambios.
A manera de ejemplo y utilizando datos reales y los modelos desarrollados en el presente trabajo, se analizó el efecto de dos esquemas de cortas sobre el desarrollo de un rodal natural en El Salto, Dgo. En el tratamiento A (TRAT_A) se promovió el desarrollo de la especie económicamente más importante (Pinus durangensis), para lo cual el programa de cortas consistió en extraer el resto de las especies cosechando árboles con un diámetro mínimo de 30 cm. El régimen de manejo TRAT_A representa una alternativa de aprovechamiento intensivo con aclareos y cortas de cosecha fuertes. En el tratamiento B (TRAT_B) se buscó mantener la estructura original del rodal en relación con el número de especies, así como con la proporción de éstas dentro del rodal, a través de un aclareo y una corta de cosecha de intensidad moderada, extrayendo árboles con un diámetro mínimo de corta de 35 cm (Figura 5).
La figura 6 muestra el rodal en su condición original y después de aplicados los dos esquemas de aprovechamiento, después de 20 años de crecimiento. Las simulaciones se llevaron a cabo considerando la misma condición inicial del rodal para ambas variantes.

Las imágenes generadas por el simulador permiten ver el efecto del tratamiento A (TRAT_A) sobre la especie de interés (P. durangensis), ya que al final del periodo de simulación se observa un rodal dominado por dicha especie. Se observa por el contrario, que a aplicación del tratamiento B (TRAT_B) se mantiene la estructura de especies original, logrando una mayor proporción de algunas especies que al inicio del periodo de simulación estaban poco representadas (Pinus cooperi, P. teocote, etc.).
BWINPro7 versión El Salto, permite valorar el desarrollo de distintos rodales considerando aspectos de crecimiento, estabilidad y estructura utilizando distintos indicadores. En este sentido, los criterios de valoración del crecimiento para las dos variantes silvícolas simuladas fueron cubiertos satisfactoriamente por el modelo. Igualmente, el simulador permite que las características ecológicas y estructurales sean caracterizadas a través de los distintos índices de estructura del rodal calculados. Como se observa en las figuras 7 y 8, los escenarios de manejo teóricos planteados muestran claramente que los resultados del modelo pueden ser considerados biológicamente razonables.
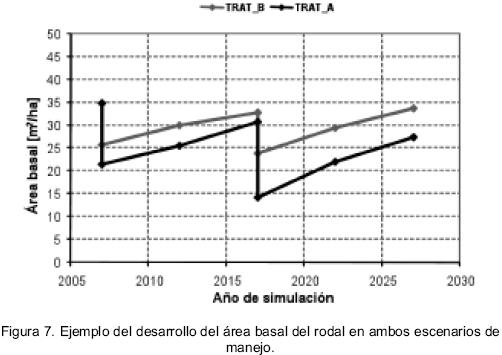

En la figura 7, por ejemplo, el valor del área basal al inicio del periodo de simulación fue de 35,0 m2/ha. Después de aplicadas las dos cortas y con el respectivo periodo de crecimiento de 10 años después de cada una, el área basal final fue de 27,4 m2/ha y 33,9 m2/ha para TRAT_A y TRAT_B, respectivamente. Estos valores permiten observar que, para el ejemplo, un régimen de cortas con aclareos y cosecha de intensidad fuerte, no garantiza la recuperación del rodal. Por otra parte, la figura 8 muestra el volumen extraído y el volumen residual para ambos tratamientos. Se observa que en el TRAT_B predominan las clases diamé–tricas mayores de 30 cm después de los 20 años de simulación, mientras que el volumen distribuido en las clases diamé–tricas menores a es relativamente bajo en los dos tratamientos. La distribución del volumen por categoría diamétrica muestra que el volumen extraído se concentra en las clases diamétricas que exceden los 35 cm, valores que fueron fijados como diámetro mínimo de corta. Se observa además, la incorporación de una cantidad importante de árboles a las categorías diamétricas comerciales mayores de 30 cm al final del periodo de simulación. Este análisis puede ser realizado para evaluar el patrón de desarrollo de otras variables y parámetros del rodal, por ejemplo, el diámetro medio cuadrático (Dg), la altura media o la altura dominante (H0), o el número de árboles por hectárea.
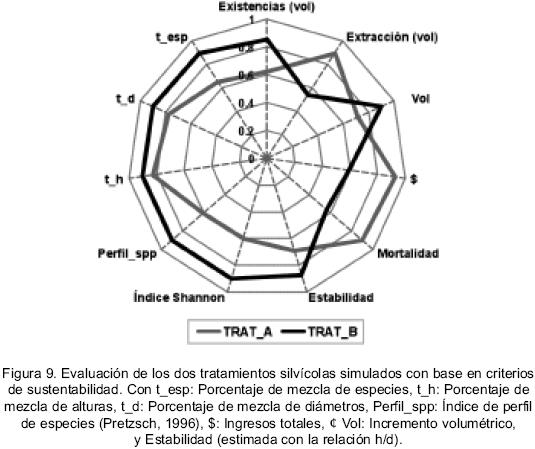
En BWINPro7 Versión El Salto, la comparación de las distintas alternativas de decisión se basa en la aplicación del criterio del manejador forestal, que puede ser definido por los objetivos de manejo predefinidos. La utilidad total de los resultados dependerá de los beneficios que el manejador o el propietario experimente si se llevan a la práctica. Los objetivos pueden representar aspectos productivos y económicos (por ejemplo, producción total de madera, volumen residual al final del turno o ingresos netos), pero también es posible seleccionar objetivos relacionados con criterios ecológicos (especies para conservación, árboles hábitat, árboles de cosecha futuros, diversidad de especies y estructura dimensional y espacial). En este sentido, los criterios de valoración del crecimiento para las dos alternativas silvícolas simuladas fueron cubiertos satisfactoriamente por el modelo. De igual manera, las características ecológicas y estructurales fueron caracterizadas adecuadamente a través de los distintos índices estructurales del rodal calculados (Figura 9).
Mediante esta herramienta el gestor tiene el control directo del proceso, pudiendo ver de inmediato los efectos de cada una de las opciones de manejo. Los resultados muestran que el modelo de crecimiento desarrollado, en combinación con parcelas permanentes de muestreo, puede ser aplicado con propósitos de control o monitoreo de la sustentabilidad.
Cabe mencionar que la precisión de las simulaciones se corresponde con la bondad de ajuste de los submodelos que integran el simulador. Por ejemplo, el error de las simulaciones del crecimiento en altura de los árboles es mínimo, variando de 0,14 m a 1,0 m, dependiendo de la especie, mientras que para el área basal el error es relativamente más alto, presentando un rango de 0,74 cm2 a 0,87 cm2. En términos generales, al utilizar el simulador de crecimiento para proyectar el crecimiento de variables de rodal, como el volumen por hectárea, el error es menor a 10%.
CONCLUSIONES
Los resultados de las simulaciones utilizando el modelo global de crecimiento desarrollado, muestran buena precisión para periodos cortos. El modelo predice el crecimiento de árboles individuales y se distingue como un prototipo versátil de un modelo de manejo forestal, con el cual se puede realizar no solamente la comparación de distintos escenarios silvícolas, sino también la valoración ecológica con base en criterios de sustentabilidad. Bajo la consideración de un determinado plan de manejo forestal pueden compararse escenarios silvícolas y económicos concretos para un área forestal específica y seleccionar la mejor alternativa en función de valores de árbol individual o criterios de sustentabilidad.
El nuevo modelo de crecimiento fue desarrollado principalmente para especies de pino y encino de la región de El Salto. Por ello se recomienda su utilización específicamente en aquellos rodales donde existan estas especies. Sin embargo, es necesario validar los parámetros de estimación a través de una reparametrización del modelo y la ampliación de la base de datos. En este sentido, la utilización e implementación del modelo está limitada por la amplitud de los valores reales utilizados para su elaboración. La modelización del incremento en área basal requiere especialmente de mayor investigación.
AGRADECIMIENTOS
Al Consejo Nacional de Ciencia y Tecnología, por el apoyo otorgado a través de los proyectos: FOMIX–DGO 94895 y FONCICYT 92739. Los comentarios del editor y los revisores anónimos contribuyeron de manera importante a mejorar la primera versión de este trabajo.
REFERENCIAS
Alder, D. 1980. Estimación del volumen forestal y predicción del rendimiento. Estudios FAO. Montes 22/2. Roma. 198 p. [ Links ]
Assmann, E. 1970. The principles of forest yield study. Pergamon Press, Oxford, Nueva York. 506 p. [ Links ]
Barrio–Anta. M., U. Diéguez–Aranda, F. Castedo–Dorado, J.G. Álvarez and A. Rojo. 2006. Mimicking natural variability in tree height using a stochastic height–diameter relationship. New Zealand Journal of Forestry Science 36(1):21–34. [ Links ]
Biging, G.S. and M. Dobbertin, 1992. A comparison of distance–dependent competition measures for height and basal area growth of individual conifer trees. Forest Science 38:695–720. [ Links ]
Burnham, K.P. and D.R. Anderson. 2002. Model selection and multi–model inference: A practical information–theoretic approach. 2ª ed. Springer Verlag, Nueva York. 488 p. [ Links ]
Castedo–Dorado F., M. Barrio, B.R. Parresol and J.G. Álvarez. 2005. A stochastic height–diameter model for maritime pine ecoregions in Galicia (northwestern Spain). Annals of Forest Science 62:455–465. [ Links ]
Colbert, K.C., D.R. Larsen and J.R. Lootens. 2002. Height–diameter equations for thirteen midwestern bottomland harwood species. Northern Journal of Applied Forestry 19(4): 171–176. [ Links ]
Corral–Rivas J.J., B. Vargas L., Wehenkel C., O. Aguirre C., J. Álvarez G. y A. Rojo A. 2009. Guía para el establecimiento de sitios de investigación forestal y de suelos en bosques del estado de Durango. Editorial UJED. Durango. 81 p. [ Links ]
Corral–Rivas, J.J, J.G. Álvarez, A.D. Ruíz and K. v. Gadow. 2004. Compatible height and site index models for five pine species in El Salto, Durango (Mexico). Forest Ecology and Management 201:145–160. [ Links ]
Diéguez–Áranda, U., F. Castedo, J.G. Álvarez and A. Rojo. 2006. Dynamic growth model for Scots pine (Pinus sylvestris L.) plantations in Galicia (north–western Spain). Ecological Modelling 191:225–242. [ Links ]
Diéguez–Aranda, U., M. Barrio, F. Castedo y J.G. Álvarez, 2005. Relación altura–diámetro generalizada para masas de Pinus sylvestris L. procedentes de repoblación en el noroeste de España. Invest. Agrar: Sist. Recur. For. 14(2):229–241. [ Links ]
Gadow, K. v., S. Sánchez O. y O.A. Aguirre. 2004. Manejo forestal con bases científicas. Madera y Bosques 10(2):3–16. [ Links ]
Hasenauer, H. 1994. Ein Einzelbaumwachstumssimulator für ungleichaltrige Fichten–Kiefern–und Buchen–Fichtenmischbestände. Forstliche Schriftenreihe der Univ. für Bodenkultur Wien, Band 8, Wien, Austria. 152 p. [ Links ]
Hasenauer, H. 2006. Sustainable forest management: Growth models for Europe. Springer, Berlin. 398 p. [ Links ]
Korf, V. 1939. A mathematical definition of stand volume growth law. Lesnicka Prace 18:337–339. [ Links ]
López, C.A., J.J. Gorgoso, F. Castedo, A. Rojo, R. Rodríguez, J.G. Álvarez–González and F. Sánchez. 2003. A height–diameter model for Pinus radiata D. Don in Galicia (Northwest Spain). Annals of Forest Science 60:237–245. [ Links ]
Lundqvist, B. 1957. On the height growth in cultivated stands of pine and spruce in Northern Sweden. Medd. Fran Statens Skogforsk. Band 47(2):1–64. [ Links ]
McDill, M.E. and R.L. Amateis. 1992. Measuring forest site quality using the parameters of a dimensionally compatible height growth function. Forest Science 38(2):409–429. [ Links ]
Monserud, R.A. and H. Sterba. 1996. A basal area increment model for individual trees growing in even– and uneven–aged forest stands in Austria. Forest Ecology and Management 80:57–80. [ Links ]
Nagel, J. 1999. Konzeptionelle Überlegungen zum schrittweisen Aufbau eines waldwachstumskundlichen Simulationssystems für Nordwestdeutschland. Schriften aus d. Forstl. Fak. D. Univ. Göttingen u. d. Nieders. Forstl. Vers., Band 128, 122 p. [ Links ]
Nagel, J. and S. Sprauer. 2009. Langfristige Simulation der Zielstärkennutzung in Buchenbestünden. In: Nagel, J. ed. Tagungsband der Jahrestagung der Sektion Ertragskunde im DVFFA. Ascona, Schweiz. p: 159–164. [ Links ]
Nagel, J., M. Albert and M. Schmidt. 2002. Das waldbaulich Prognose– und Entscheidungsmodell BWINPro 6.1. Neuparametrisierung und Modellerweiterungen. Forst und Holz 57:486–492. [ Links ]
Nagel, J. 2005. TreeGrOSS eine Java basierte Softwarekomponente zur Waldwachstumsmodellierung für Forschung, Lehre und Praxis. Deutscher Verband Forstlicher Forschungsanstalten – Sektion Forstliche Biometrie und Informatik 15:33–37. [ Links ]
Newnham, R.M. 1964. The development of a stand model for Douglas–fir. PhD Thesis. Faculty of Forestry, University de British Columbia, Vancouver. 201 p. [ Links ]
Peng, C., L. Zhang and J. Liu. 2001. Developing and validating nonlinear height–diameter models for major tree species of Ontario's boreal forest. Northern Journal of Applied Forestry 18:87–94. [ Links ]
Pretzsch, H. and M. Kahn. 1998. Forschungsvorghaben Konzeption und Konstruktion von Wuchs– und Prognosemodellen für Mischbeständen in Bayern. Abschlußbericht Projekt W 28, Teil 2–Methodische Grundlagen. 279 p. [ Links ]
SAS Institute Inc. 2004. SAS/STAT® 9.1.2. User's Guide. Cary, NC: SAS Institute Inc. [ Links ]
Schmidt, M. 2001. Prognosemodelle fur ausgewahlte Holzqualitätamerkmale wightiger Baumarten. Dissertation, Fakultat fur Forstwissenschaften und Waldökologie, Universitat Gottingen, 296 pp. [ Links ]
Schröder, J. and J.G. Álvarez. 2001. Developing a generalized diameter–height equations for Maritime pine in Northwestern Spain. Fw. Cbl. 120(1):18–23. [ Links ]
Sharma M. and J. Parton. 2007. Height–diameter equations for boreal tree species in Ontario using a mixed–effects modeling approach. Forest Ecology and Management 249: 187–198. [ Links ]
UCODEFO 6, 2006. Programa de Manejo Forestal 2006–2016. El Salto, P.N., Dgo. [ Links ]
Valles, G.A. 2007. Modelos biométricos que conforman a SICREMARS 2.0. Libro científico No. 1. Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Centro Regional Norte–Centro. Durango, México. 166 p. [ Links ]
Vanclay, J.K. 1995. Modelling forest growth and yield: Applications to mixed tropical forests. CAB International, Reino Unido. 312 p. [ Links ]
Vargas–Larreta, B. 2006. Analyse und Prognose des Einzelbaumwachstums in Strukturreichen Mischbeständen in Durango, Mexiko. Diss. Univ. Göttingen, Alemania. 173 p. [ Links ]
Van Laar, A. and A. Akça. 2007. Forest mensuration. Managing forest ecosystems, Vol. 13. Springer, Dordrecht, Holanda. 383 p. [ Links ]
Wykoff, W.R. 1990. A basal area increment model for individual conifers in the Northern Rocky Mountains. Forest Science 36(4): 1077–1104. [ Links ]
Yuancai, L. and B.R. Parresol. 2001. Remarks on height–diameter modelling, USDA Forest Service, Research Note SRS–10, Southern Research Station, Asheville, NC. 5 p. [ Links ]
Zhang, L. 1997. Cross–validation of nonlinear growth functions for modeling tree height–diameter relationships, Ann. Bot. 79:251–257. [ Links ]
Nota
Este documento se debe citar como: Vargas–Larreta, B., J. Corral–Rivas, O. Aguirre–Calderón y J. Nagel. 2010. Modelos de crecimiento de árbol individual: Aplicación del simulador BWINPro7. Madera y Bosques 16(3):81–104.














