Coeficiente de endogamia de una población autoestéril con muestreo de familias

 

Inbreeding coefficient of a self sterile population with sampling of families

 

J. Sahagún–Castellanos

 

Departamento de Fitotecnia. Universidad Autónoma Chapingo. Km. 38.5 Carretera México–Texcoco, Chapingo, Estado de México. C. P. 56230. México. Correo–e: jsahagun@correo.chapingo.mx

 

Recibido: 26 de marzo, 2007
Aceptado: 12 de mayo, 2008

 

Resumen

Para medir la intensidad de la endogamia que se produce en poblaciones finitas de especies alógamas en que el apareamiento aleatorio no incluye la autofecundación [como en el caso de algunas especies de ornato del género Primula y del tomate de cáscara (Physalis ixocarpa Brot.)] ya existe una fórmula. Ésta se derivó en términos probabilísticos, bajo el supuesto de que desde el ciclo 1 el paso de una generación a la siguiente se basa en que de cada ciclo o generación se toma una muestra al azar de n individuos cuya semilla dará lugar a n familias de m medios hermanos cada una que constituirán el ciclo siguiente, como suele suceder en la selección masal. Dado que para m = 1 dicha fórmula no se reduce a ninguna de las fórmulas conocidas para este caso, se hizo una investigación teórica en términos probabilísticos para explicar la causa de esta discrepancia y dar satisfacción a la necesidad de disponer de un coeficiente de endogamia (CE) exacto para la población objeto de estudio. Se encontró que cuando el ciclo cero se forma por mn individuos no endogámicos ni emparentados, para los ciclos o generaciones 0, 1 y 2 los CEs fueron F₀ = 0, F₁ = 0 y F₂ = 1/(2mn), respectivamente, y para t = 3,4,5,... el CE exacto fue F_t = (1 + F_t–2) /(2mn) + (m–1)(1 + F_t–3 + 6F_t–2) /(8mn) + (n–1) F_t–2 /n, que sí se reduce a la fórmula exacta cuando se hace m = 1. Además, para el caso en que el ciclo cero está formado por n familias de m medios hermanos no endogámicos se derivó una fórmula que a partir del ciclo uno produce CEs mayores que los correspondientes del caso anterior.

Palabras clave: Coeficiente de coancestría, población ideal, identidad por descendencia, familia de medios hermanos, respuesta a la selección.

 

Abstract

To measure the inbreeding intensity produced in finite populations of alogamous species that undergo random mating without selfing [as in the case of some ornamental species of the Primula genus and husk tomato (Physalis ixocarpa Brot.)], a formula for the inbreeding coefficient (IC) has been derived in probabilistic terms under the assumption that in the studied population each cycle was formed by n families of m half sibs each. Each family is formed by the seed of a set of n random individuals from the previous generation, as occurs in mass selection. Since for m = 1 this formula is not reduced to any known formula for this case, theoretical research in probabilistic terms was undertaken to explain the cause of this discrepancy and to identify or derive an exact IC for the case under study. It was found that when cycle zero is formed by mn noninbred and unrelated individuals, for cycles 0, 1, and 2 the exact ICs were F₀ = 0, F₁ = 0, and F₂ = 1/(2mn), respectively, and for t = 3,4,5, ... the exact IC was F_t = (1+F_t–2) /(2mn) + (m–1)(1+F_t–3 + 6F_t–2) /(8mn) + (n–1)F_t–2 /n. For the case where cycle zero is formed by n families of m noninbred half sibs each, the IC formula, as of cycle one produces higher IC values than those produced by the previous case.

Key words: coancestry coefficient, ideal population, identity by descent, half–sib family, response to selection.

 

INTRODUCCIÓN

Es bien sabido que los tamaños finitos de las poblaciones que se manejan para efectos de mejoramiento genético son fuentes de endogamia que en el caso de los cultivos de especies alógamas pueden estar relacionados inversamente con la respuesta a la selección (e.g., Robertson, 1960; Márquez–Sánchez, 1998). Entre las especies cuyo estudio teórico se hace mediante el modelo de una población finita que se reproduce por apareamiento aleatorio hay unas que incluyen la autofecundación [como el maíz (Zea mays L.)], y otras que son autoestériles [como el tomate de cáscara (Physalis ixocarpa Brot.) y algunas especies de ornato del género Primula]. Cuando sí ocurre la autofecundación, los estudios teóricos relativos a la endogamia y otros temas relacionados con ella se han realizado con base en el modelo de población ideal (v.g., Wright, 1922; Crow y Kimura, 1970; Falconer, 1987) que a su vez se sustenta en principios probabilísticos.

Para las poblaciones cuyos individuos se reproducen por apareamiento aleatorio sin autofecundación se han hecho estudios teóricos para derivar sus coeficientes de endogamia. Crow y Kimura (1970) muestran una fórmula general para el coeficiente de endogamia de la generación t en términos de los coeficientes de endogamia de las dos generaciones anteriores. Sahagún (2006) derivó directamente los coeficientes de endogamia de los dos primeros ciclos. Estos dos estudios tienen en común al menos dos características: a) fueron hechos en términos probabilísticos aplicados al modelo de población ideal sin autofecundación, y b) no consideran que en la realidad la muestra de individuos de cuyo apareamiento al azar se generará el ciclo siguiente, en casos como el tomate de cáscara y el maíz, está formada por varias familias de medios hermanos. Ignorar este parentesco intrafamiliar puede producir coeficientes de endogamia que subestiman el verdadero valor endogámico de estas poblaciones.

Márquez–Sánchez (1998) derivó una fórmula para el coeficiente de endogamia de una población que se reproduce por apareamiento aleatorio sin autofecundación y el paso de un ciclo al siguiente se hace mediante este tipo de apareamiento entre los individuos de n familias de m medios hermanos maternos cada una. Sin embargo, la fórmula que derivó este autor cuando se hace m = 1 no se reduce a la fórmula de Crow y Kimura (1970) para la población ideal en que se suprime la autofecundación, fórmula a la que, de haber congruencia entre ambas, se debe reducir la fórmula del CE de la población estudiada por Márquez–Sánchez (1998) cuando m = 1. Ante este escenario se emprendió esta investigación teórica con el fin de esclarecer esta inconsistencia y de identificar o derivar la fórmula exacta del coeficiente de endogamia esperado cuando cada ciclo está formado por n familias de m medios hermanos cada una y el apareamiento aleatorio no incluye la autofecundación.

 

MÉTODOS Y MARCO TEÓRICO

El estudio de la endogamia se ha hecho con varios enfoques. Wright (1922) se refirió a ella como la correlación de los gametos que se unen para formar el cigote; este enfoque, sin embargo, parece estar confinado al modelo de dos alelos por locus. Por su parte, Barret et al. (2004) han hecho estudios de la endogamia de poblaciones naturales de una especie silvestre con potencial de ornato (Narcissus longispathus) con base en técnicas de electroforesis, lo que demanda equipo y personal especializados. El enfoque probabilístico, en cambio, no tiene los problemas anteriores y permite alcanzar los objetivos de este trabajo; por ello fue el que se adoptó, particularmente en el contexto de los coeficientes de endogamia, coancestría y población ideal.

El modelo de población en que se basó este estudio fue similar al de la población ideal descrito por Falconer (1989). La ideal es una población conceptual formada por un conjunto de tamaño infinito de individuos no endogámicos ni emparentados; el ciclo 1 lo forma el apareamiento aleatorio, que incluye la autofecundación, de los N individuos obtenidos al azar de la población base. Similarmente, del ciclo 1 se toma una muestra aleatoria de N individuos de cuyo apareamiento aleatorio surge el ciclo 2, y así sucesivamente. El modelo que se utilizó en este estudio difiere del modelo de población ideal en que en el apareamiento aleatorio no incluye la autofecundación, que sí es incluida en la población ideal; y el paso de una generación a la siguiente se hace mediante el apareamiento aleatorio (sin autofecundación) de los mn individuos que resultan de m semillas de cada uno de los individuos de una muestra al azar de tamaño n obtenida en la generación antecedente. El punto de partida o ciclo cero fue visualizado de dos maneras: a) una muestra de la población base formada por mn individuos no endogámicos ni emparentados [como lo hizo Márquez–Sánchez (1998)] que, para efectos de consistencia con la notación de ciclos más avanzados, se clasificaron en n grupos de m individuos cada uno, y b) como la muestra del caso anterior excepto que está formada por n familias no emparentadas de m medios hermanos no endogámicos cada una. En ambos casos, el ciclo uno se consideró como la población que resulta de m semillas de cada uno de n individuos tomados al azar de entre los mn individuos del ciclo cero que previamente fueron sometidos a apareamiento aleatorio (sin autofecundación). Similarmente, después del apareamiento aleatorio sin autofecundación de los mn individuos, se toma una muestra de tamaño n que en el ciclo dos será una población formada por n familias de m medios hermanos cada una. Los ciclos siguientes se forman de la misma manera.

El genotipo pésimo (p = 1,2,..., m) del grupo o familia i (i = 1,2,..., n) del ciclo cero (C₀) fue representado como A_pi1 A_pi2. El arreglo genotípico (Kempthorne, 1969) del C₀, por lo tanto, fue representado en la forma . El arreglo gamético que produce el C₀ debe ser (tanto el de machos como el de hembras). La ausencia de autofecundación en la reproducción por apareamiento aleatorio del C₀ producirá el ciclo uno (C1) cuyo arreglo genotípico esperado es . No obstante la restricción de que el genotipo de ningún individuo del C₁ puede estar formado por dos genes que provienen de un mismo individuo del C₀ (expresada como pi≠qj) el arreglo gamético esperado del C₁ es . Este arreglo gamético esperado es así debido a que como se han considerado ausentes la migración, mutación y selección, no debe esperarse pérdida de genes ni cambio de sus frecuencias. El ciclo dos (C₂) y demás ciclos se generan de una manera similar a la que se describió para el C₁.

 

RESULTADOS Y DISCUSIÓN

El C₀ es un conjunto de individuos no endogámicos ni emparentados

De acuerdo con los conceptos y métodos descritos en el apartado anterior, los ciclos 0 y 1 deben tener coeficientes de endogamia iguales a cero; es decir, F₀ = 0 y F₁ = 0. Con respecto al ciclo dos (C₂), es de esperarse que contenga individuos producidos por el apareamiento de medios hermanos del C₁ que así contribuirán al coeficiente de endogamia del C₂ (F₂). Éste es equivalente al coeficiente de coancestría del C₁ debido a que la reproducción se hace mediante apareamiento aleatorio. Si en el C₁ se hace un muestreo al azar de dos individuos y de un locus cualquiera de cada uno de éstos se elige un gen al azar, la única posibilidad de que ambos genes sean idénticos por descendencia es que ambos sean copia de genes de un mismo progenitor del C₀. Para un individuo del C₀ cuyo genotipo es A_pi1 A_pi2, el muestreo con reemplazo de dos genes puede producir con una probabilidad de ¼ en cada caso, los genotipos A_pi1A_pi1, A_pi1 A_pi2, A_pi2 A_pi1 y A_pi2 A_pi2 de manera que la contribución al coeficiente de endogamia del C₂ de este progenitor particular es y hay mn progenitores con igual capacidad de participación en el F₂, resulta que

El ciclo 3 (C₃) se forma a partir del apareamiento aleatorio, sin autofecundación, del ciclo 2 y el subsecuente muestreo al azar de n individuos cuya semilla producirá las n familias de m medios hermanos cada una. El coeficiente de coancestría del C₂ [coeficiente de endogamia del ciclo 3 (F₃)] es la probabilidad de identidad por descendencia de los dos genes tomados al azar de sendos individuos del C₂, también elegidos al azar. Con respecto al origen de estos dos genes, las tres únicas posibilidades es que provengan de: 1) un mismo individuo del C₁; 2) sendos medios hermanos de una familia del C₁, y 3) sendos individuos del C₁ que pertenecen a familias diferentes de medios hermanos. Las frecuencias de ocurrencia de estos tres eventos mutuamente excluyentes son: (mn)^–1, (m–1)(mn)^–1 y (n–1)n^–1, respectivamente. Además, respecto a la probabilidad de que los dos genes en cuestión sean idénticos por descendencia: 1) para el caso en que ambos genes provienen de un mismo individuo del C₁, por analogía con lo que al respecto se encontró en la derivación de F₂, esta probabilidad es (1+F₁)/ 2 = ½; 2) si los dos genes provienen de sendos medios hermanos del ciclo 1 (C₁), con respecto al ciclo cero (C₀) pueden provenir, con probabilidad de ¼, del progenitor común, y con una probabilidad de identidad por descendencia de (1+F₀)/2; y con probabilidad de ¾ de dos progenitores diferentes del C₀ que concurrieron aleatoriamente a su apareamiento, de manera que la probabilidad total de identidad por descendencia en este caso es (¼)(1+F₀)/2 + (¾)F₁ = (1+F₀+6F₁)/8, y 3) si los dos genes muestreados provienen de sendos individuos aleatorios de dos familias de medios hermanos del C₁ la probabilidad de que los genes sean idénticos por descendencia debe ser F₂. De acuerdo con las frecuencias de ocurrencia de los eventos en 1), 2) y 3) y las probabilidades de identidad por descendencia en estos tres casos, el coeficiente de endogamia del ciclo 3 (F₃) debe expresarse como:

De acuerdo con los resultados también ya derivados, F₀ = 0, F₁ = 0 y F₂ = 1/(2mn) (Ec. 1), la Ec. 2 puede escribirse más concisamente como:

Para el ciclo 4 (C₄), por extensión del razonamiento utilizado para derivar F₃ (Ec. 2) debe resultar que:

Con la consideración de que F₁ = 0, de la Ec. 4 se encuentra que:

Generalizando, para la generación t = 3,4,5,6,... el coeficiente de endogamia del C_t (F_t) debe ser expresable como

La Ec. 7 es la que muestran Crow y Kimura (1970) para una población que difiere de la población ideal que describe Falconer (1989) sólo porque en la primera la autofecundación no ocurre. Sin embargo, la fórmula que derivó Márquez–Sánchez (1998) para la población a la que corresponde la Ec. 6 aquí derivada, difiere de ésta y para el caso en que m = 1 se reduce a la expresión

La Ec. 8, sin embargo, difiere de la que aquí se derivó para el mismo caso (Ec. 7). Por ejemplo, una diferencia entre estas dos ecuaciones es que sólo una, la Ec. 7, incluye F_t–2, no obstante que la inclusión de este término es correcta pues corresponde a la coancestría, no nula, entre individuos del ciclo t–1 que tienen un progenitor en común en el ciclo t–2. También es notable que para m = 1 la Ec. 8 implica que para n = 1, F_t = [1 + 2F_t–1 + F_t–3] / 4; sin embargo, en este caso, (n = 1 y m = 1), no existirían C₁, C₂, C₃,..., puesto que con sólo un individuo la única vía reproductiva sería la autofecundación, que en este caso no es posible. Estas dos consideraciones son evidencias de la falta de exactitud de la ecuación que derivó Márquez–Sánchez (1998) para el coeficiente de endogamia de la población que es objeto de estudio en este trabajo.

La derivación que se hizo de la Ec. 7 permite determinar que, como F₀ = F₁ = 0, con m = 1, F₂ = 1/(2n), resultado que también se deriva directamente de lo hecho en este estudio (Ec. 1) y que deja otra lección: la fórmula que derivó Sahagún (2006) para este caso específico tampoco es exacta ya que ahí se consigna que F₂ = [4n – 5] /{2 [4n (n–1) –1]}.

El ciclo cero es un conjunto de familias de individuos no endogámicos

Al parecer, resulta muy realista considerar que el punto de partida en un programa de selección masal sea la semilla de cada uno de varios individuos. Si el C₀ está formado por n familias no emparentadas de medios hermanos no endogámicos, el C₀ tendrá un coeficiente de endogamia (F_0,F) igual a cero; i.e., F_0,F = 0. Sin embargo, el ciclo 1, originado por el apareamiento aleatorio del C₀ y la subsecuente toma de una muestra al azar de n individuos, cada uno con m semillas, debe tener un coeficiente de endogamia (F_1,F) mayor que cero debido a que ocurre apareamiento entre medios hermanos con una frecuencia de (m–1) /(mn). La probabilidad de que un apareamiento de este tipo produzca un individuo cuyo genotipo esté formado por dos genes idénticos por descendencia, por analogía y adecuación de la derivación de la Ec. 2, debe ser (1/8) (1 + F_–1,F + 6F_0,F). Como en este caso F_–1,F = F_0,F = 0, la probabilidad en cuestión es igual a (1/8). De acuerdo con estos resultados, F_1,F = (m–1) /(8mn).

Con respecto al ciclo 2 (C₂), formado por los mn elementos que produce la muestra aleatoria de n individuos del C₁, con m semillas cada uno, su coeficiente de endogamia (F_2,F) se determinará como el coeficiente de coancestría del C₁. A éste sólo contribuyen la identidad por descendencia de dos genes muestreados de sendos individuos del C₁ debida a que: a) los genes provienen de un mismo progenitor del C₀, y b) los genes provienen de dos medios hermanos del C₀. Las probabilidades de identidad por descendencia de genes en estos dos eventos son (1+F_0,F) /2 = 1/2 y (1+F_–1,F) /8=1/8, respectivamente. Como las frecuencias de estos dos eventos son 1/(mn) y (m–1) /mn, respectivamente, el coeficiente de endogamia del ciclo 2 (F_2,F) es:

Si el punto de partida (C₀) es un conjunto de n familias de m medios hermanos, cuando m = 1 este caso se reduce al caso anterior, en el que el punto de partida (C₀) es un conjunto de mn individuos no endogámicos ni emparentados. Con m = 1, como era de esperarse, la Ecuación 9 se reduce a la fórmula F_2,F = 1 /(2n), igual a la previamente discutida que, con este resultado, refrenda su autenticidad. El coeficiente de endogamia del C₃ (F_3,F), se determinará con el procedimiento utilizado en el ciclo anterior; es decir, F_3,F se derivará vía el coeficiente de coancestría del C₂.

El muestreo al azar de dos individuos del C₂ (sin reemplazo por no haber autofecundación) y el muestreo aleatorio subsecuente de sendos genes de los genotipos de estos dos individuos puede formar genotipos con dos genes idénticos por descendencia debido a que, como en la derivación de F₃ (Ec. 2), los genes muestreados provienen: a) de un mismo individuo del C₁; b) de dos medios hermanos del C₁, y c) de dos individuos de familias diferentes del C₁. Las probabilidades de identidad por descendencia de estos tres casos, por analogía con lo derivado para el F₃, del caso en que el C₀ está formado por mn individuos no endogámicos ni emparentados (Ec. 2), son: (1+F_1,F)/2, (1/8)(1+F_0,F+6F_1,F) y F_2,F, respectivamente. Con base en éstas y en las respectivas frecuencias de ocurrencia de los tres eventos descritos en a), b) y c), el coeficiente de endogamia del C₃ (F_3,F), debe expresarse como:

Nótese que las Ecuaciones 6 y 12 tienen la misma estructura, no obstante deben diferir porque los dos puntos de partida (los dos ciclos cero) son diferentes. Las diferencias se aprecian directamente en las magnitudes de los coeficientes de endogamia derivados para los ciclos C₁ [F₁ = 0 y F_1F = (m–1) /(8mn)] y C₂ [F₂ = 1 /(2mn) y F_2F = 1 / (2mn) + (m–1) /(8/mn)] y lo que estas diferencias implican en los coeficientes de endogamia de los ciclos más avanzados. Evidentemente, para t = 1,2,3, ... y m > 1 F_tF siempre será mayor que F_t, aunque en el límite () ambos convergen en la unidad.

El efecto de la presión de selección en el coeficiente de endogamia

El efecto de la presión de selección en el coeficiente de endogamia se puede apreciar mediante los conceptos de número (o tamaño) efectivo en términos de varianza [N_e(v)] o en términos de endogamia [N_e(f)] (Márquez–Sánchez, 1998). Con respecto al primero, Crossa y Vencovsky (1997) encontraron que, aproximadamente (cuando nm es grande), N_e(v) = 4mns /(1+2s) en donde s es la presión de selección que para el caso del ejemplo referido al maíz por Márquez–Sánchez (1998), con n = 200 y m = 20, es igual a n/mn = 1/n = 0.05 (5%). Al substituir mn, m y n por N_e(v), [N_e(v)m/n]^0.5 y [N_e(v)n/m]^0.5, respectivamente, en el coeficiente de endogamia que se derivó para el caso en que el C₀ es un conjunto de mn individuos no endogámicos ni emparentados y en que el apareamiento aleatorio no incluye la autofecundación, este autor generó una fórmula para el coeficiente de endogamia que refleja el efecto de la presión de selección. Al proceder de esa manera para el mismo caso (Ecuación 6) la fórmula para el coeficiente de endogamia en la generación t (F_t^') que se derivó en este trabajo para t = 4,5,6,..., adquiere la forma:

Evidentemente, para el caso en que el C₀ es un conjunto de n familias no emparentadas de medios hermanos no endogámicos la expresión del coeficiente de endogamia es igual que la de la Ecuación 13 excepto que los coeficientes de endogamia serían F_t^'_,F , F_t^'_–1,F , F_t^'_–2,F y F_t^'_–3,F (Ecuación 12) en lugar de F_t^' , F_t^'_–1 , F_t^'_{– 2} y F_t^'_–3 (Ecuación 13), respectivamente.

Con respecto a los coeficientes de endogamia que reflejan el efecto de la presión de selección en los primeros ciclos, de acuerdo con lo derivado para el caso en que el C₀ es un conjunto de mn individuos no endogámicos ni emparentados, son: 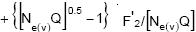en donde Q = n/m. Con respecto al caso en que el C₀ es un conjunto de n familias de m medios hermanos cuyo coeficiente de endogamia es cero, los coeficientes de endogamia en cuestión son

 

CONCLUSIONES

En este estudio se derivó el coeficiente de endogamia exacto de una población ideal en que no se incluye la autofecundación; el ciclo cero es un conjunto de mn individuos, no endogámicos ni emparentados, y cada ciclo posterior se establece con n familias de m medios hermanos cada una. Para las generaciones cero, uno y dos los coeficientes de endogamia son F₀ = 0, F₁ = 0 y F₂ = 1 / (2mn), respectivamente; y para la generación t = 3,4,5,... F_t = (1 + F_t–2)/(2mn)+(m–1)(1+F_t–2+ 6F_t–1)/(8mn)+(n–1) F_t–1/n. Para el caso que difiere de la población anterior sólo en que el ciclo cero es un conjunto de n familias no emparentadas de m medios hermanos cuyo coeficiente de endogamia es cero, los coeficientes de endogamia exactos de las generaciones cero, uno, dos y tres son F_0,F=0, F_1,F=0, F_2,F=1/(2mn)+(m–1)/(8mn) y F_3,F=1/(2mn)+(m–1)/(8mn)+(n–1)/(2mn), respectivamente, y para t = 4,5,6,...F_t,F = (1+F_t–2,F)1/(2mn)+(m–1)(1+F_t–3,F+6F_t–2,F)/(8mn) + (n–1)F_t–1,F /n.

 

LITERATURA CITADA

BARRET, S. C. H.; COLE, W. W.; HERRERA, C. M. 2004. Mating patterns and genetic diversity in the wild Daffodil Narcissus longispathus (Amaryllidaceae). Heredity 92:459–465.         [ Links ]

CROSSA, J.; VENCOVSKY, R. 1997. Variance effective population size. Crop Science. 37: 14–26.         [ Links ]

CROW, J. F.; KIMURA, M. 1970. An Introduction to Population Genetics Theory. Burgess Ed. Minneapolis. 591 p.         [ Links ]

FALCONER, D. S. 1989. Introduction to Quantitative Genetics 3^rd. edition. Longman, New York. 438 p.         [ Links ]

KEMPTHORNE, O. 1969. An Introduction to Genetic Statistics. Wiley, New York. 545 p.         [ Links ]

ROBERTSON, A. 1960. A theory of limits in artificial selection. Proc. Royal Soc. London 153:234–239.         [ Links ]

MÁRQUEZ–SÁNCHEZ, F. 1998. Expected inbreeding with recurrent selection in maize: I. Mass selection and modified ear–to–row selection. Crop Sci. 38:1432–1436.         [ Links ]

SAHAGÚN C., J. 2006. El coeficiente de endogamia de una población finita autoestéril. Revista Chapingo serie Horticultura XII(1): 65–68.         [ Links ]

WRIGHT, S. 1922. The effects of inbreeding and cross–breeding on guinea pigs. Tech. Bull. U.S. Dep. Agric. 1112. Washington D. C.         [ Links ]