Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias geológicas
versión On-line ISSN 2007-2902versión impresa ISSN 1026-8774
Rev. mex. cienc. geol vol.27 no.2 Ciudad de México ago. 2010
Sección especial
Planet formation in a disk around a star: The two dense–ring model
Formación de planetas en un disco alrededor de una estrella: el modelo de dos anillos densos
Erick Nagel–Vega
Centro de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México, Antigua Carretera a Pátzcuaro 8701, Ex–Hda. San José de la Huerta, Apartado Postal 3–72 (Xangari), 58089 Morelia, Michoacán, Mexico. Present address: Departamento de Astronomía, Universidad de Guanajuato, Callejón de Jalisco s/n, Apartado Postal 144, Valenciana, 36000 Guanajuato, Mexico. erick@astro.ugto.mx
Manuscript received: August 8, 2007.
Corrected manuscript received: June 25, 2008.
Manuscript accepted: March 20, 2010.
ABSTRACT
A disk around a star is the initial configuration commonly accepted for the material that forms a planetary system such as our own. In this work, the first stage in the evolution from a disk to a set of planetesimals is studied. This stage consists in the formation ofdense regions, which are able to collapse into objects that are the seedsfor planetformation. This process is examinedfor a stationary configuration containing two dense rings, fixed in Keplerian radii and with mass continually increasing with time, which was reported in a previous study as the final outcome of a hydrodynamic simulation of a cloud collapse toward a star (Nagel, E., 2007, Rev. Mex. Astron. Astrof., 43, 257–270). Results indicate that in such a configuration the rings will eventually acquire enough mass to be prone to gravitational instabilities, which will cause fragmentation. The existence of unstable modes allows estimating typical sizes of the collapsed objects, given by the unstable wavelengths. Ring masses may be found via the mass surface density of the analysed model. The conclusion is that the unstable rings contain enough mass to result in the fragmentation and formation ofplanetesimals, which eventually accumulate in objects with masses typical of planets in the Solar System.
Key words: accretion disks, gravitational instabilities, hydrodynamics, rings.
RESUMEN
Un disco alrededor de una estrella es la configuración inicial comúnmente aceptada para el material de donde provienen los sistemas planetarios como el nuestro. En este trabajo se estudia la primera etapa de la evolución de un disco a un conjunto de planetesimales, la cual consiste en la formación de regiones suficientemente densas para colapsar y formar objetos que sean la semilla para la formación de planetas. Este proceso se examina para una configuración estacionaria que contiene dos anillos densos, fijos en radios keplerianos y cuya masa aumenta continuamente en el tiempo, la cual se obtuvo en un estudio previo como resultado de la simulación hidrodinámica del colapso de una nube hacia una estrella (Nagel, E., 2007, Rev. Mex. Astron. Astrof., 43, 257–270). Los resultados indican que una configuración de este tipo permite asegurar que eventualmente los anillos adquieran masas suficientemente grandes para ser propensos a inestabilidades gravitacionales que los puedan fragmentar. La existencia de modos inestables permite estimar tamaños típicos de los objetos colapsados, dadas las longitudes de onda inestables. Con la densidad superficial de masa del modelo analizado es posible encontrar las masas de estos objetos. La conclusión a la que se llega es que los anillos inestables contienen suficiente masa para que el resultado de la fragmentación forme planetesimales que eventualmente puedan acumularse en objetos con masas típicas de los planetas del Sistema Solar.
Palabras clave: discos de acreción, inestabilidades gravitacionales, hidrodinámica, anillos.
INTRODUCTION
It has been well known for many decades that gravitational instabilities (GI) are an important mechanism for the collapse of clumps in protoplanetary disks, the seeds of planets. Studies of systems such as our own are important to understand the origin of other planets; of course, Earth's origin is also a very interesting subject. Based on this idea, Cameron (1978) studied several disk models, characterized by parameters such as the angular momentum and mass accretion rate of a cloud that collapses to form a star–disk system. His conclusion was that at many times of its life, the disk was unstable against axisymmetric GIs. Thus, rings that are prone to collapse would form, with a planetesimal as a likely outcome. However, the dynamics of the collapse was not taken into account by Cameron (1978); he assumed that the gas falls onto the disk at the position where the specific angular momentum of the infalling particles equals that of the material already contained in the disk. This assumption is not true if the correct solution for the trajectories of the collapsing material (Cassen and Moosman, 1981; Ulrich, 1976) is used. Thus, in this paper I follow the work by Nagel (2007), in which a dynamically correct initial configuration is given.
The importance of the work by Nagel (2007) is that, from the cloud collapse, a configuration with dense zones can naturally be produced. The disk is characterized by two dense rings located at Keplerian radii, positions where the gravitational force of the star is compensated by the centrifugal force. The rings are in equilibrium because their central parts correspond to a density maximum; hence, there are no pressure forces. This pattern is stationary in the sense that increasing disk size (due to material with ever–increasing angular momentum, continuously falling from the cloud toward the disk) is followed by motion of the rings to new equilibrium positions. During this process, the mass of the disk increases, such that the rings accumulate material at a constant rate. All the details of this configuration can be found in Nagel (2007); the salient feature is that a disk configuration physically consistent with the collapse of the cloud that forms it, has dense zones that at some time are able to activate GI.
Gravitational instabilities were studied by Nakamoto and Nakagawa (1994) in a disk evolving due to viscosity and accounting for the cloud material that continuously falls into it. The model includes self–gravity, viscous heating, and accretion shock heating. The arrival to instability was studied using the Toomre parameter (Toomre, 1964), which gives a mass threshold for axisymmetric gravitational instabilities. The disk is formed by the accretion of material from the cloud; however, the evolution is followed on a longer time scale than the one analysed in Nagel (2007). Thus, the disk structure found in the latter is not present in the former. For the purposes of this paper, the use of Nagel (2007) model is more appropriate.
Another attempt to characterize the disk at the stage of disk formation was developed by Tomley et al. (1991). They used the falling solution of Cassen and Moosman (1981) as initial condition, giving a surface density that increases linearly in time —the same dependence found by Nagel (2007) for the stationary state. Simulations were given with a parameterized cooling and the instabilities were monitored with the parameter given by Toomre (1964). In this way, they demonstrated that the evolution of unstable states is strongly dependent on the cooling efficiency. There is a difference in the stationary state between Tomley et al. (1991) and Nagel (2007), however. In Nagel (2007), the full dynamical evolution in the disk plane is followed, thus, I consider that the disk pattern found in the latter is more reliable.
Instability due to self–gravity is not the only mechanism that generates regions with increasing density that eventually could collapse to form a planetesimal. Youdin and Goodman (2005) found that interpenetrating streams of solids and gas in a Keplerian disk produce a local, linear instability, without requiring self–gravity of the clump. Numerical simulations were developed by Youdin and Johansen (2007) and Johansen and Youdin (2007). The first paper confirms the analytical values for the instability growth rate and the second one studies the nonlinear behaviour, characterizing the density enhancements. The fate of these regions inside a realistic picture of planetary formation must include self–gravity and collisions of the solid particles.
The evolution of solids and gas in a disk with viscosity parameterized with a (Shakura and Sunyaev, 1973) is presented in Stepinski and Valageas (1996a, 1996b). The most important physical result given by these authors is that small particles are strongly coupled to the gas, in the sense that the particles follows the gas motion. For larger particles, which have coagulated from smaller ones, the evolution differs appreciably. They are decoupled from the gas, so the velocities of both components are not the same. In this case, interactions like gas drag become relevant. Afterwards, the system evolves until the gas density is reduced to levels where the only relevant force that acts on a solid body is the gravitational interaction with the rest of the solid. Stepinski and Valageas (1996a) also followed the coagulation, sedimentation and evaporation/condensation of the particles. They found particles with sizes up to 105 cm at times t= 105 yr from the beginning of the evolution. The solids are initially given by 1 mm particles uniformly distributed and with a density of one percent of the gas density. These large particles are completely decoupled from the gas; thus, their position is not dependent on gas drag and they will continue to grow in mass at the expense of solid and gaseous material in the disk. The time scale for the evolution depends on the viscosity parameter a; the disk evolves more slowly for a lower value. Unfortunately, this value is difficult to restrict by observations, and thus, the times scales for the evolution are not well–known. An important thing to point out, which is clearly stressed by Stepinski and Valageas (1996b), is that the final outcome in a disk composed of solids and gas strongly depends on the initial conditions. In other words, the final density profile differs for each initial density configuration. For example, one such initial density profile is given by the "Minimum Solar Nebula'' model, a gas disk with the mass of the planets increased to solar abundances; the mass of this disk is between 0.01 and 0.02 Msolar.
This work analyses the chances for a dense ring in the disk described by Nagel (2007) to reach instability within the framework of planet formation. Extensive details of other mechanisms can be found in Wetherill (1980).
The instabilities described in the main body of this paper result in a set of solid objects immersed in a gaseous disk, but their final fate is beyond the scope of this paper. For a recent paper on the evolution of such objects, including the accretion of other bodies, gas accretion onto the cores thus formed, their secular migration, and the characterization of the resulting planetary systems in terms of the distribution of masses and semimajor axes of the planets, I recommend the work by Ida and Lin (2004). The growth of a core by the accretion of planetesimals and its migration toward the star was studied by Chambers (2006).
STATIONARY TWO DENSE–RING–PATTERNED DISK INSIDE A COLLAPSING CLOUD
Almost all theories for the formation of planets begin with a disk around a star. Two main points sustain this assertion. The first is that the planets and the disk contain angular momentum. The second is the fact that the planets in the Solar System are rotating in the same plane, reminiscent of a flat disk. Thus, in this paper, I also begin with this assumption. An additional assumption is that processes in the disk, during its formation by material falling from the progenitor cloud, are able to create a configuration prone to form dense objects that could be the seeds of planets. The physical mechanism on which this work is based is the activation of gravitational instabilities (GI) by the presence of dense zones in the disk. By definition, a GI requires a dense zone to begin with, and an instability means that an increase in density will lead to an even higher density. This process works as a chain reaction, until some other mechanism is able to halt the collapse.
For instance, Boss and Bodenheimer (1979) were able to produce such dense zones in numerical simulations of cloud collapse by explicitly putting in small density perturbations. Instead of such initial perturbations, I use a massive ring to obtain the same result.
The main premise in this work is that a disk with a physical mechanism to form dense zones is a natural system for the study of GI processes; these dense zones then collapse to form planetesimals. A disk with dense zones is the outcome of a hydrodynamical simulation for cloud collapse developed in Nagel (2007). The initial condition in density and velocity was taken from Ulrich (1976). These works use the fact that typical velocities of the material falling to the star–disk system are supersonic, so that a ballistic description is ad hoc for the purpose of the paper. The cloud is axisymmetric and rotates uniformly. In this solution, the material falls towards the star, however, because of rotation, the trajectories never touch the star. This set of particles will arrive from above and below the plane perpendicular to the angular velocity axis that contains the star. Any particle coming from above (below) has a twin coming from below (above) as in a mirror image. The interaction of this huge set of pairs results in a shock parallel to the plane. Thus, the shocked material is restricted to move in the plane, and will form the disk.
The material deposited in the disk has a negative radial velocity. Due to this, the particles will move within the plane, initially moving towards the star, until they arrive to their pericenter, the closest approach of the orbit with respect to the star. At this position, which is different for each ring (the system is axisymmetric), the material will begin to move in the opposite direction. The collective behaviour of these particles is represented by a dense ring, which becomes denser and more massive as its outward evolution proceeds. This ring eventually will arrive to an equilibrium location at the Keplerian radius (which depends on the specific angular momentum) associated with it. The calculation of this radius is straightforward, because the material that is continuously incorporated into the ring mixes perfectly with the material that is already there. Thus, the outcome is a ring with constant specific angular momentum (γ).
The formation and evolution of the dense ring can be explained by analysing the dynamical evolution of the material that arrives at the disk plane. Moreover, a continuous flux of material from the cloud does not change the key elements of the explanation given in the last paragraph. A well–defined structure, moving with positive radial velocity, i.e., the ring, will clear the material on the inner side of the disk, where fresh material from the cloud can be incorporated. This matter will evolve as does the material forming the ring, thus, an inner dense ring is also produced. This two–dense–ring pattern is maintained during the infall stage of the cloud, hence, this configuration is stationary, see Figure 1.
A physical way to explain this (for a more complete description see Nagel, 2007), is as follows: a rigidly rotating cloud is feeding the star–disk system; in such a cloud, γ increases from zero at the rotation axis to a maximum value in the disk plane. Taking any two particles, the one with the larger value for y will arrive further out in the disk, due to γ conservation. A particle with γ=0 will fall to the star. The picture that emerges from these ideas, based on the simulation presented in Nagel (2007), is that the cloud can be divided into three parts: the part with smaller values for γ will feed the star, the part with larger values for γ will eventually end in the outer dense ring, and finally, the intermediate y region will be associated with the inner dense ring.
From the point of view of spectral modeling of stars with disks (Adams et al., 1990; D'Alessio et al., 1997; Lay et al., 1997; Kikuchi et al., 2002), it is practical to have a model for the disk that can be fitted to any total mass. In the model described in Nagel (2007), the ratio between the masses of the two rings is constant. The mass surface density S, in terms of radius, for a disk with mass Md = 0.02 Msolar is shown in Figure 2, where Rd is the maximum Keplerian radius. This paper will focus on the study of GIs that also require a disk (or rings) with any specified mass. In the two–ring disk model (Nagel, 2007), it is easy to calculate the time when either ring becomes unstable, establishing in this way a powerful tool to model these disks. The study of GIs for some disk states will be described in the next section.
GRAVITATIONAL INSTABILITIES THAT BREAK THE RINGS
In an equilibrium state of all the external forces, a region denser than the surroundings can become unstable if the density is larger than a threshold value. In this case, the self–gravity of the unstable clump will dominate, resulting in collapse. In this section, various configurations prone to instability will be reviewed and applied to the stationary disk with two dense–rings described in the previous section.
Instabilities in a gaseous disk
The first gravitational stability criterion well–known to astronomers is the Jeans criterion (Jeans, 1928). This criterion is applied to a non–moving fluid of density ρ. The material is stable if

where cs is the sound velocity, G is the gravitational constant and kT is the total wave number of the (un)stable mode.
In the case of a fluid that is uniformly rotating and has infinite thickness, some modes with wave vectors perpendicular to the rotation axis are unstable (Chandrasekhar,1961). The stability criterion then becomes
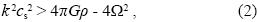
where k is a wave vector restricted to the plane perpendicular to the rotation axis, and Ω is the magnitude of the angular velocity. Thus, rotation has an influence in defining the unstable wavelengths.
Using the definition k =2π/λ, I conclude that the minimum unstable wavelength is
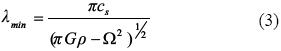
for a rotating gaseous disk. This result means that the outcome of an unstable structure would be a set of objects with characteristic sizes larger than λmin. From the disk with Md= 0.02 Msolar described in Nagel (2007), I take the value for the typical density in any of the dense rings (ρ= 2×10–13g cm–3), the angular velocity at the center of the rings (Ωi and Ωe, for the inner and outer rings, respectively) and sound velocity (Cs = 3.57×104 cm–1) of a cloud at T= 15 K composed of atomic hydrogen. This set of values, substituted in Equation 3, allows finding an imaginary λmin, which means that the stability criterion given in Equation 2 is fulfilled. Hence, the system is stable and there are no unstable wavelengths.
For specified values of the stellar mass, Mstar, and disk radius, Rd, the value of Ω at the center of each ring will be fixed. Thus, πGp > Ω2 can eventually be fulfilled, because p increases monotonically with time. The minimum density for unstable modes to appear is ρunst,i= Ωi2/πG = 0.272×10–10 g cm–2 for the inner ring and ρunst,e = Ωe2/πG = 0.881×1012 g cm–2 for the outer ring.
It is noteworthy that the previous values allow concluding that the outer ring is the first to become unstable and prone to form cores that could be the seeds for the outer planets. The instability criteria for a dust layer around the disk midplane discussed in the following section also show that the outer ring becomes unstable before the inner one. The mass of the gas objects thus formed is not the final mass, because additional gas and solid objects can be accreted by them. A study of this process for a solid body slowly increasing its mass with material that comes close enough to be trapped in its gravitational well can be found in Hayashi et al. (1977). As previously mentioned, the fate of the collapsed objects is beyond the scope of this paper; the qualitative approach given here estimates typical sizes of the bodies but does not give a detailed account of the size distribution. The answer to this problem is addressed with full hydrodynamical simulations in protoplanetary disks (Boss, 2001; Mejía et al., 2005; Boley et al., 2006). For the stationary configuration described in the previous section, an appropriate simulation will be developed in the future.
Goldreich and Lynden–Bell (1965) solve the problem for a disk with finite thickness that is uniformly rotating. The typical size of the unstable wavelength is found, with a value around the thickness of the disk, H. The results from that paper can be applied to the disk described in the previous section, where the angular velocity (Ω) depends on radius, by noting the following: First, the disk is geometrically thin, H << R. In this case, a typical unstable wave will not cover a large radial zone, so that the angular velocity (Ω) is approximately constant, thus fulfilling the Goldreich and Lynden–Bell (1965) assumption. For the two–ring disk model, the disk is considered isothermal (Nagel, 2007), thus I concentrate on a fluid with an equation of state given by P α ρ, where P is the gas pressure. Goldreich and Lynden–Bell (1965) also give stability criteria for gases described by P α ρ2 and P αρ∞; the latter corresponds to an incompressible fluid. For an isothermal disk, the stability criterion can be written as:

Application to a two–ring disk
Equation 4 can be used for the two–ring pattern disk described in the previous section, for characteristic values of ρ and Ω. These values can be taken from Nagel (2007), estimating ρ using the relation ρ=S/H with S and H given as typical values, and Ω as the Keplerian angular velocity of the center of either of the rings. From here on, variables with a subscript i refer to the inner ring while those with the subscript e refer to the external ring. The instability criterion is applied to a disk with mass Md= 0.02 Msolar, where Si= 10 g cm–2, Se= 30 g cm–2, Hi= 3 AU, He=10 AU, Ωi= 2.39×10–9 s–1 and Ωe= 4.3×10–10 s–1 Both H values for the rings are taken from Figure 1. The typical S values for the rings are shown in Figure 2. From these data, ρi and ρe are almost the same, thus, the typical value for both rings in a disk with this mass is ρ= 2×10–13 g cm–3. Substitution of these values in Equation 4 gives Ii= 0.00184 and Ie= 0.0567. Thus, for a disk with Md= 0.02 Msolar, both rings are stable to this kind of instability. This result is expected for a disk much less massive than a solar mass. A more massive disk can be easily produced, allowing the accretion from the cloud to last longer. In the model by Nagel (2007), Md and Ω increase and decrease as a function of time, respectively, in the same proportion for both rings. On the other hand, assuming that the thickness of the disk is time independent during the time it takes to reach a gravitational instability state, then Ie/Ii does not depend on time either. At this particular moment, Ie and I have the ratio Ie/Ii= 30.89. At the time when the outer ring reaches an instability state (Ie= 0.73), Ii=0.024, so it is far away from an unstable configuration. A strong and valuable conclusion is that the outer ring becomes unstable before the inner one. The relevance of this result is that with a large mass reservoir there is a chance to form large solid objects, which are first produced on the outer side of the disk. Hence, if this instability is responsible for the formation of the planets, the outer planets are formed before the terrestrial planets. This attractive suggestion is based on the assumption that the outer and inner planets are formed from the outer and inner dense rings. However, in order to prove this idea, a complete treatment of the problem is required, including all the elements that characterize the physical processes relevant to it, elements able to describe, for instance, the growth and evolution of the planetesimals toward their final (gas free) configuration.
Goldreich and Lynden–Bell (1965) provided a critical wavelength (λcrit), and showed that some modes with wavelengths around this value are unstable. For the isothermal case λcritt= 4.49 H; using this length, the mass of a collapsed object is given by M = λcrit2Hρ. For the stable case given by the disk with mass Md = 0.02, Mi= 0.18×10–3 Msolar and Me= 6.7×10–3 Msolar. The first (second) is almost an order of magnitude smaller (larger) than the mass of Jupiter, thus I conclude with this simplified analysis that the outer dense ring is able to produce objects of the mass of Jupiter. In any case, the planetesimals that form by this mechanism are gaseous, like the ones found by Boss (2001), which performs a full three dimensional simulation of a self–gravitating disk, with heating and cooling, including radiative transfer in the diffusion approximation.
The Goldreich and Lynden–Bell instability is associated to a disk, but the important feature in the pattern found by Nagel (2007) is the clearly defined rings. Yabushita (1966, 1969) studied the stability for a (Saturn–like) ring with inner radius a and outer radius b, where the density smoothly decays to zero. The non–perturbed configuration is given by the equilibrium between the centrifugal force, the gravitational force of the planet (or star) and the self–gravity of the ring. The density distribution of the ring that was studied is axisymmetric and is given by
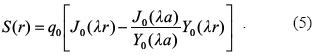
In this equation, the value for λ can be calculated using the fact that the density is zero at r = a, and also at r= b. J0 and Y0 are Bessel functions of the first and second type, respectively.
Yabushita (1966, 1969) found the critical mass (Mcrit) for instability in terms of the ratio alb. For two values for this ratio, his result were
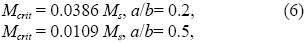
where Ms is the Saturn mass. For the two–ring disk, the material is moving around the star, thus, Ms corresponds to the mass of the star.
This result can be applied to the inner and outer dense rings described previously. For the outer ring, a= 0.4 Rd and b= 0.8 Rd, so, a/b=0.5; and for the inner ring, a= 0.1 Rd and b= 0.3 Rd, so, a/b=0.33. These values and the ones given at the beginning of this section, in Mring=ρπ(b2–a2)H, can be used to find the mass associated with each ring. As before, subscripts i and e refer to the inner and outer rings, respectively. From this relation, Mring,i= 0.0025 Msolar and Mring,e= 0.05 Msolar. Compared to Equation 6, this means that the outer ring is gravitationally unstable and the inner one is stable. Note that from the analysis of Goldreich and Lynden Bell (1965), the material in the ring is stable; however, the analysis presented here should be more precise because the ring is better characterized. Probably, the objects formed by this instability require coagulation between them to form an object massive enough to resemble an outer planet of the Solar System. As a general conclusion, the study of both stability criteria mentioned in this section give an argument in favour of the formation of clumps of the size required to form the seeds of objects as large as the planets of the solar system.
Instabilities in a dust layer around the disk midplane
The instabilities described up to now only consider a gaseous disk, an thus a solid core cannot be produced. The next step was taken by Goldreich and Ward (1973); they considered a thin disk of particulate matter that forms from material that sinks towards the disk midplane. This process begins with the condensation of metals and silicates during the cooling of the disk, which results in a distribution of small grains.
These particles move towards the midplane through the gas; the forces that determine their dynamical evolution are the vertical component of the star gravity and the gas drag force. The amount of material accumulation in the mid–plane disk is characterized by a dust density, S. This density can be used in the dispersion relation for local axisymmetric perturbations (Goldreich and Ward 1973), given by
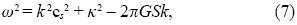
where κ2=2Ω[Ω + d(rΩ)/dr], and ω is the rate of exponential increase of the perturbation. The original derivation of this relation was constructed for a system made of gas; for its application to a dust disk it is necessary to consistently define an appropriate cs. Goldreich and Ward (1973) argue that cs= 0 is a reasonable assumption, thus, from Equation 7, the critical wavelength can be written as

where a Keplerian disk (Ω ∞ R–3/2) is assumed.
Axisymmetric perturbations with λ<λc are unstable. In such cases, the larger fragments obtained with this mechanism are of size λc. Goldreich and Ward (1973) calculated λc at the actual position of the Earth's orbit, using the Keplerian angular velocity Ω = 2×10–7 s–1 and an estimated S~7.5 g cm–2 implied by the mass of the terrestrial planets. Using these values, a critical wavelength of λc~5×108 cm is obtained; the typical mass of an object of this size can be found from m~S λ2c, which gives m~2×1018 g.
A more detailed study of this instability was given by Sekiya (1983), who found a threshold in the density of particles and gas in terms of the distance r from the star of mass Mstar. However, a drawback for the application of this mechanism to a real disk is that the settling of material towards the midplane should be accomplished in a non turbulent medium. Unfortunately, the difference in velocity between the particulate–dominated subdisk and the surrounding gas disk is able to produce turbulent eddies, which invalidate the previous assumption. Some years later, the same author (Sekiya, 1998) confirmed the impossibility of the gravitational instability occuring in a turbulent dust layer unless the ratio of dust to gas surface density is enhanced over cosmic values.
Finally, Youdin and Shu (2002) surmounted this problem by describing possible mechanisms to increase the solids to gas ratio, with respect to the "Minimum Solar Nebula'', to the values required for the GI to appear. The solids include metals, silicates and even ice; the latter is taken into account if the location is outside the "ice line'', a boundary that divides a region far away (close to) the star, where the ice can(not) survive. Another element that is important to consider is that some materials are volatile at sufficiently high temperatures (Gómez and D'Alessio, 2000). Thus, the dust concentration will strongly depend on the temperature profile of the disk.
The advantage of this planetesimal formation mechanism is that the relatively small amount of gas with respect to solids represents a gas depleted configuration, which reduces the influence of gas (by drag, for example) in the nascent planets. In other words, the reduction of tidal interaction between a core and the gaseous disk should reduce the rate of migration towards the star, improving the chances for survival.
Application to a two–ring disk
The main assumption in the Goldreich and Ward (1973) analysis is that the medium is non turbulent in the sense that solids floating in the gas will continuously settle towards the midplane (Kusaka et al., 1970), forming a high density dust layer. For the case of a dense, two–ring disk, the particles fall from the cloud and then move within the disk until they arrive to one of the dense rings. Because the velocity is well defined at each point and, more importantly, because the velocity at each position varies slightly in time, I can safely assume that the system is non–turbulent. Another argument in support of this is that from the outskirts to the center of the ring, the magnitude of the radial velocity continuosly decreases. Exactly at the center, this velocity is zero, thus, the motion towards this point is smooth. As a result, two particles in collision trajectory avoid the interaction, because they will halt at the last moment. This kinematic configuration is not consistent with the one required to "create'' turbulence; thus, I assume that the material will eventually arrive to the center of the ring. The matter that arrives to the center should be composed of dust and gas. As in Kusaka et al. (1970), the dust will settle in the midplane disk. The resulting increase in dust density will enhance the collision rate, hence, the solid particles will grow in size. This is the essential fact required for the aim of this paper. In other words, there is a real mechanism able to increase the solid density up to levels where the Goldreich and Ward gravitational instability can operate
Given the justification in the last paragraph, the method presented in this section can be applied to the pattern with two rings of Nagel (2007), with the following procedure: Equation 8 is applied to the inner and outer dense rings, getting for the former λc,i= 4.617×1012 cm and for the latter λc,e= 4.279×1014 cm. Note that there is a huge difference for the sizes between the unstable fragments in a ring located at the actual position of the Earth, and those values estimated for the dense rings in the model of Nagel (2007). This is due to the fact that the surface densities are of the same order but the angular velocities are two to three orders of magnitude lower for the rings in the latter case. Rotation has a stabilizing effect (see Equation 7), thus, slower rotation can naturally produce larger objects. Note that λc,i is an order of magnitude less than the thickness of the disk at the position of the dense inner ring, however, λc,e is of the same order as the disk thickness at the outer dense ring position. In the last case a wavelength can just fit in the height of the disk, thus, this result is marginally correct.
The mass associated to an inner fragment is mi~ Siλ2c,i= 1.13×10–4 MJ and for an outer one me~Seλ2c,e= 2.906 MJ, where MJ is the Jupiter mass. An interesting conclusion is that fragments as massive as Jupiter can be produced with this mechanism, however, this result should be taken with caution because of all the assumptions made. Also, it is required that excitation of this specific mode be possible, in the frame of a consistent and complete picture based on an appropriate simulation.
From this qualitative picture only typical sizes and masses for the fragments can be extracted. For a quantitative picture, a detailed analysis of the dynamical evolution of the solids that eventually will arrive to the center of the ring and coalesce there is needed. The material will move from the edges of the ring towards the center. This behaviour is given by the dynamics of the collapsing cloud in a way that promotes the accumulation of material at the center of the ring. Following this process, the most likely outcome for particle agglomeration by collisions will be the formation of larger particles. On the other hand, if the dust–gas density ratio increases, then the Goldreich and Ward instability can appear. The next question is: how will the solid material already in the ring evolve? Haghighipour and Boss (2003a, 2003b) developed a simulation of the interaction of the solids immersed in a gaseous disk –in the size range of microns to 100 m objects– with the disk itself, around a local density enhancement. They take into account the hydrodynamical forces due to the density profile and the drag force of the gas. Their main conclusion is that the particles rapidly migrate towards the location of maximum density. This result moves in the right direction, promoting the accumulation of material at the center of any of the rings when the cloud is exhausted, i.e., the time when planetary formation is expected to take place. A following paper (Haghighipour, 2005) studied the same system but took into account the growth of micron–sized particles up to a few centimeters in several tens of thousands of years.
In conclusion, there are mechanisms acting in the presence of a density enhancement that promote the growth of the particles and sedimentation around the center of the dense ring. These mechanisms will eventually create a configuration prone to gravitational instabilities in the Goldreich and Ward sense.
DISCUSSION
The fate of density enhancements in the form of clumps or rings is not easily addressed because many ingredients work in favour of or against their fragmentation andlor collapse to objects that resemble planetesimals. The self gravity of a ring promotes its fragmentation because this force is directed towards its center. On the other hand, the cooling (heating) of the material, reduces (increases) the pressure support against collapse. In the hydrodynamical simulations of Mejía et al. (2005), these processes are taken into account, and the result is disk fragmentation; however, the fragments have a brief life. In a following paper (Boley et al., 2006), more realistic cooling (D'Alessio et al., 2001) was considered, in which the dust opacities are carefully calculated. This influences the cooling in such a way that the cooling times are longer, and fragmentation does not occur.
For the instability of a dust layer (Goldreich and Ward, 1973) the dust particles must settle onto the midplane of the disk, something that can occur in a non turbulent medium. However, Supulver and Lin (2000) simulate a disk with global turbulence in which a single particle is followed; they found that condensation and sublimation of water are the processes that dominate the particle growth. These mechanisms are able to form icy planetesimals in the outer part of the disk. Thus, turbulence in the disk is not enough to prohibit particle growth to planetesimal sizes.
A simulation of the dust settling in a laminar flow disk is presented in Garaud and Lin (2004), and is followed until the onset of GI. This process was analyzed for various ratios between the dust and gas surface density. They characterized the rate of growth of the perturbation, but not the spectra of the size distribution of the fragments. This will be one of our goals in the near future, applied to the two–dense–rings disk.
The application of the stability criteria discussed in the previous sections to a dense ring gives only characteristic sizes for resultant fragments, whereas either the final outcome or the evolution towards larger objects resembling a realistic planetary system is not considered.
Besides all the difficulties reviewed in this paper for a complete characterization of the final system, there is at least one more issue that should be taken into account. When two particles collide, there is a chance for the particles to coalesce or, alternatively, they could fragment into smaller pieces, and thus, the growth of particles is not monotonic, due to destructive collision events. Agglomeration and fragmentation mainly depend on the relative velocity between the colliding particles. It is important to recognize that the problem at hand has many facets; here only a small piece of the puzzle is addressed.
CONCLUSIONS
This work gives typical unstable wavelengths for gravitational instabilities in a disk with a two dense rings pattern. Using the density of an unstable location for the disk, typical masses for the collapsed objects can be obtained. However, these results were obtained with an oversimplified scheme; a detailed analysis for the contribution of the interaction between the gas and solids, heating and cooling mechanisms of the gas, etc., is required to conclude that the fragmentation can actually take place.
For a disk with finite thickness and uniform rotation, Goldreich and Lynden–Bell (1965) found stable and unstable modes. In the two dense–ring model, for a disk with mass Md= 0.02 Msolar, both rings are stable. By increasing the mass of the disk, the outer ring is the first that turns unstable. The typical mass of a collapsed object is of the order of the Jupiter mass.
The stability of a gas ring was studied by Yabushita (1966, 1969). The mass of an unstable ring is much less than the mass of a typical fragment for the uniformly rotating disk. In the case of a disk with two dense rings, the gas ring instability criteria is probably better suited for a reasonable analysis. Thus, consistent with Yabushita (1966, 1969), the outer ring is unstable and the inner one is stable in a disk with mass Md= 0.02 Msolar.
For an instability in a Keplerian disk (Ω ∞ R–3/12) with a dust layer in the midplane, as that described by Goldreich and Ward (1973), the dense rings produce larger collapsed objects than the material at the same position for a disk with a decreasing density profile. Besides, λc ∞ Ω2 α R3, thus, the typical size of a fragment given by the break of the outer ring is larger than an object associated to the inner ring. This is an important result, because I speculate that the formation of the outer planets in the Solar System takes place in the outer dense ring while the inner planets form in the internal ring. A relevant fact supporting this conclusion is that the mass of an inner fragment is much less than one Jupiter mass, while the mass of a collapsed piece of the outer ring is of the order of one Jupiter mass.
ACKNOWLEDGEMENTS
I thank Daniel Flores for inviting me to the Meeting "Origen y Estructura del Sistema Solar" held at Instituto de Astronomia, UNAM, 7–9 August 2007, which was the inspiration for this paper. Also, I acknowledge the comments of two referees, that helped to improve the clarity of this paper.
REFERENCES
Adams, F.C., Emerson, J.P., Fuller, G.A., 1990, Submillimeter photometry and disk masses of T Tauri disk systems: Astrophysical Journal, 357, 606–620. [ Links ]
Boley, A.C., Mejía, A.C., Durisen, R.H., Cai, K., Pickett, M.K., D'Alessio, P., 2006, The thermal regulation of gravitational instabilities in protoplanetary disks. III. Simulations with radiative cooling and realistic opacities: Astrophysical Journal, 651, 517–534. [ Links ]
Boss, A.P., 2001, Gas giant protoplanet formation: disk instability models with thermodynamics and radiative transfer: Astrophysical Journal, 563, 367–373. [ Links ]
Boss, A.P., Bodenheimer P., 1979, Fragmentation in a rotating proto–star –A comparison of two three–dimensional computer codes: Astrophysical Journal, 234, 289–295. [ Links ]
Cameron, A.G.W., 1978, Physics of the primitive solar accretion disk: Moon and Planets, 18, 5–40. [ Links ]
Cassen, P., Moosman, A., 1981, On the formation of protostellar disks: Icarus, 48, 353–376. [ Links ]
Chambers, J.E., 2006, Planet formation with migration: Astrophysical Journal, 652, 133–L136. [ Links ]
Chandrasekhar, S., 1961, Hydrodynamic and Hydromagnetic Stability: Clarendon, Oxford University Press, 589 pp. [ Links ]
D'Alessio, P., Calvet, N., Hartmann, L., 1997, The structure and emission of accretion disks irradiated by infalling envelopes: Astrophysical Journal, 474, 397–406. [ Links ]
D'Alessio, P., Calvet, N., Hartmann, L., 2001, Accretion disks around young objects.III. Grain growth: Astrophysical Journal, 553, 321–334. [ Links ]
Garaud, P., Lin, D.N.C., 2004, On the evolution and stability of a protoplanetary disk dust layer: Astrophysical Journal, 608, 1050–1075. [ Links ]
Goldreich, P., Lynden–Bell, D., 1965, I.Gravitational stability of uniformly rotating disks: Monthly Notices of the Royal Astronomical Society, 130, 97–124. [ Links ]
Goldreich, P., Ward, W.R., 1973, The formation of planetesimals: Astrophysical Journal, 183, 1051–1062. [ Links ]
Gómez, J.F., D'Alessio, P., 2000, Resolving molecular line emission from protoplanetary disks: observational prospects for disks irradiated by infalling envelopes: Astrophysical Journal, 535, 943–958. [ Links ]
Haghighipour, N., 2005, Growth and sedimentation of dust particles in the vicinity of local pressure enhancements in a solar nebula: Monthly Notices of the Royal Astronomical Society, 362, 1015–1024. [ Links ]
Haghighipour, N., Boss, A.P., 2003a, On pressure gradients and rapid migration of solids in a nonuniform solar nebula: Astrophysical Journal, 583, 996–1003. [ Links ]
Haghighipour, N., Boss, A.P., 2003b, On gas drag–induced rapid migration of solids in a nonuniform solar nebula: Astrophysical Journal, 598, 1301–1311. [ Links ]
Hayashi, C., Nakazawa, K., Adachi, I., 1977, Long–term behavior of planetesimals and the formation of the planets: Publications of the Astronomical Society of Japan, 29, 163–196. [ Links ]
Ida, S, Lin, D.N.C., 2004, Towards a deterministic model of planetary formation.I.A desert in the mass and semimajor axis distribution of extrasolar planets: Astrophysical Journal, 604, 388–413. [ Links ]
Jeans, J.H., 1928, Astronomy and Cosmogony: Cambridge, Cambridge University Press, 337 pp. [ Links ]
Johansen, A., Youdin, A.N., 2007, Protoplanetary disk turbulence driven by the streaming instability: nonlinear saturation and particle concentration: Astrophysical Journal, 662, 627–641. [ Links ]
Kikuchi, N., Nakamoto, T., Ogochi, K., 2002, Disk–halo model for flat–spectrum T Tauri stars: Publications of the Astronomical Society of Japan, 54, 589–597. [ Links ]
Kusaka, T., Nakano, T., Hayashi, C., 1970, Growth of solid particles in the primordial solar nebula: Progress of Theoretical Physics, 44, 1580–1595. [ Links ]
Lay, O.P., Carlstrom, J.E., Hills, R.E., 1997, Constraints on the HL Tauri protostellar disk from millimeter– and submillimeter–wave interferometry: Astrophysical Journal, 489, 917–927. [ Links ]
Mejía, A.C., Durisen, R.H., Pickett, M.K., Cai, K., 2005, The thermal regulation of gravitational instabilities in protoplanetary disks. II. Extended simulations with varied cooling rates: Astrophysical Journal, 619, 1098–1113. [ Links ]
Nagel, E., 2007, Formation of a two–dense–rings–pattern disk from the collapse of a cloud: Revista Mexicana de Astronomía y Astrofísica, 43, 257–270. [ Links ]
Nakamoto, T., Nakagawa, Y., 1994, Formation, early evolution, and gravitational stability of protoplanetary disks: Astrophysical Journal, 421, 640–650. [ Links ]
Sekiya, M., 1983, Gravitational instabilities in a dust–gas layer and formation of planetesimals in the solar nebula: Progress of Theoretical Physics, 69, 1116–1130. [ Links ]
Sekiya, M., 1998, Quasi–equilibrium density distributions of small dust aggregations in the solar nebula: Icarus, 133, 298–309. [ Links ]
Shakura, N.J., Sunyaev, R.A., 1973, Black holes in binary systems. Observational appearance: Astronomy and Astrophysics, 24, 337–355. [ Links ]
Stepinski, T.F., Valageas, P., 1996a, From dust to planetesimals: global evolution of ice in the solar nebula: Lunar and Planetary Science, 27, 1269–1270. [ Links ]
Stepinski, T.F., Valageas, P., 1996b, Global evolution of solid matter in turbulent protoplanetary disks. I. Aerodynamics of solid particles: Astronomy and Astrophysics, 309, 301–312. [ Links ]
Supulver, K.D., Lin, D.N.C., 2000, Formation of icy planetesimals in a turbulent solar nebula: Icarus, 146, 525–540. [ Links ]
Tomley, L., Cassen, P., Steiman–Cameron, T., 1991, On the evolution of gravitationally unstable protostellar disks: Astrophysical Journal, 382, 530–543. [ Links ]
Toomre, A. , 1964, On the gravitational stability of a disk of stars: Astrophysical Journal, 139, 1217–1238. [ Links ]
Ulrich, R. K. , 1976, An infall model for the T Tauri phenomenon: Astrophysical Journal, 210, 377–391. [ Links ]
Wetherill, G.W., 1980, Formation of the terrestrial planets: Annual Review of Astronomy and Astrophysics, 18, 77–113. [ Links ]
Yabushita, S., 1966, Stability analysis of Saturn's rings with differential rotation: Monthly Notices of the Royal Astronomical Society, 133, 247–263. [ Links ]
Yabushita, S., 1969, Stability analysis of Saturn's rings with differential rotation–II: Monthly Notices of the Royal Astronomical Society, 142, 201–212. [ Links ]
Youdin, A.N., Goodman, J., 2005, Streaming instabilities in protoplanetary disks: Astrophysical Journal, 620, 459–469. [ Links ]
Youdin, A.N., Johansen, A., 2007, Protoplanetary disk turbulence driven by the streaming instabiblity: linear evolution and numerical methods: Astrophysical Journal, 662, 613–626. [ Links ]
Youdin, A.N., Shu, F.H., 2002, Planetesimal formation by gravitational instability: Astrophysical Journal, 580, 494–505. [ Links ]














