Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias geológicas
versión On-line ISSN 2007-2902versión impresa ISSN 1026-8774
Rev. mex. cienc. geol vol.26 no.2 Ciudad de México ago. 2009
Eficiencia relativa de 15 pruebas de discordancia con 33 variantes aplicadas al procesamiento de datos geoquímicos
Relative efficiency of 15 discordancy tests with 33 variants for processing geochemical data
Rosalinda González–Ramírez1, Lorena Díaz–González1 y Surendra P. Verma2,*
1 Posgrado en Ingeniería (Energía), Universidad Nacional Autónoma de México, Privada Xochicalco s/n, Centro, 62580 Temixco, Morelos, México.
2 Centro de Investigación en Energía, Universidad Nacional Autónoma de México, Privada Xochicalco s/n, Centro, 62580 Temixco, Morelos, México. * spv@cie.unam.mx
Manuscrito recibido: Enero 27, 2009
Manuscrito corregido recibido: Marzo 31, 2009
Manuscrito aceptado: Marzo 31, 2009
RESUMEN
Las pruebas de discordancia son una herramienta estadística útil en los diferentes campos de las ciencias e ingenierías, incluyendo Ciencias de la Tierra. El procedimiento consiste en una metodología rigurosa para la detección de datos desviados en una muestra estadística "contaminada" y posteriormente su depuración, logrando que los datos restantes tengan una distribución normal sin contaminación estadística, con los cuales puedan ser determinadas correctamente las medidas de tendencia central (media) y de dispersión (desviación estándar). En la evaluación empírica de las 15 pruebas de discordancia con 33 variantes, se utilizó una base de datos geoquímicos grande con información sobre 35 materiales de referencia geoquímica (MRG) procedentes de cuatros países (Canadá, E.U.A., Japón y Sudáfrica) que representa 2220 casos con 41,821 datos individuales geoquímicos. Fueron evaluadas nueve pruebas sencillas con 13 variantes y siete pruebas múltiples con 20 variantes (la prueba N4 pertenece a ambos tipos) utilizando valores críticos nuevos de gran precisión y exactitud en la obtención de los resultados. Para la eficiencia de las pruebas de discordancia se emplearon dos términos estadísticos: (1) Criterio de eficiencia relativa ("relative efficiency criterion", REC) previamente conocido; y (2) criterio de valores desviados relativo ("relative outlier criterion" ROC) propuesto en el presente trabajo. Adicionalmente, se utilizó una metodología combinada de regresión lineal y pruebas de significancia de F de Fisher y t de Student. En pruebas de discordancia sencillas, la eficiencia mayor fue para el coeficiente de exceso o curtosis (N15) seguida por las pruebas tipo Grubbs (N1 y N4) y de coeficiente de asimetría (N14), mientras que en pruebas de discordancia múltiples, la prueba N4 en sus tres variantes se caracterizó por eficiencias mayores. Las pruebas tipo Dixon, mucho más populares que las de Grubbs, por lo general presentaron valores menores de la eficiencia. Una implicación importante de estos resultados sería otorgar preferencias a las pruebas N15, N1, N4 y N14 para la aplicación de la metodología de valores desviados en el manejo de datos geoquímicos. Las interpretaciones cuantitativas de regresiones lineales combinadas con pruebas de significancia confirman los resultados de los parámetros REC y ROC. Finalmente, se afirma que independientemente del método analítico usado para determinar la composición geoquímica de materiales de referencia, los valores desviados altos son mucho más comunes que los bajos y las muestras con contaminación estadística simétrica, a ambos lados de la muestra, son relativamente escasas. Los parámetros robustos, como la mediana o la media de Gastwirth, serán muy probablemente sesgadas para este tipo de datos geoquímicos. Así mismo, la aplicación rigurosa de las pruebas de discordancia antes de estimar los valores de la media y desviación estándar parece ser un requerimiento básico.
Palabras clave: materiales de referencia geoquímica, métodos de valores desviados, pruebas de discordancia, pruebas de Dixon, pruebas de Grubbs, sesgo, coeficiente de asimetría, curtosis, valores críticos, pruebas de significancia.
ABSTRACT
Discordancy tests provide us with a statistical tool that is useful in different areas of science and engineering, including Earth Sciences. Their application represents a rigorous methodology for the detection and elimination of discordant outliers in statistically contaminated normal samples and provides us remaining data without any statistical contamination, which can then be used to estimate the central tendency (mean) and dispersion (standard deviation) parameters. For the empirical evaluation of 15 discordancy tests with 33 variants, an extensive database of 35 reference materials (RM) from four countries (Canada, U.S.A., Japan, and South Africa) having 2220 applicable cases with 41,821 individual geochemical data, was established. Nine single–outlier tests with 13 variants and seven multiple–outlier tests with 20 variants (test N4 belongs to both types) along with the new, most precise and accurate critical values, were employed for this evaluation. Two statistical parameters quantified the efficiency of discordancy tests: (1) Relative efficiency criterion (REC) known from previous work; and (2) relative outlier criterion (ROC) proposed in this work. Additionally, a methodology was used that combines linear regression analysis with Fisher F and Student t significance tests. Among the single–outlier discordancy tests, the greatest efficiency was shown by kurtosis test (N15), followed by Grubbs type tests (N1 and N4) and skewness test (N14), whereas, among multiple–outlier tests, the Grubbs test N4 in its three variants seemed to be characterized by the greatest efficiency values. The Dixon tests, being much more popular than the Grubbs tests, in general presented the smallest efficiencies. One important implication of these results would be to prefer N15, N1, N4, and N14 tests for the application of this outlier–based methodology for geochemical data handling. The quantitative interpretation using the combined methodology of linear regressions and significance tests confirms the results of REC and ROC parameters. Finally, it is inferred that independently of the analytical methods used for the determination of geochemical composition of reference materials, upper discordant outliers are much more common than the lower ones, and samples with a symmetrical statistical contamination on both sides of the sample are relatively scarce. Robust estimates, such as the median or Gastwirth mean, are likely to be biased for such geochemical data. The application of discordancy tests before estimating the mean and standard deviation values is a basic requirement.
Key words: reference material, outlier–based methods, discordancy tests, Dixon tests, Grubbs test, skewness, kurtosis, critical values, significance tests.
INTRODUCCIÓN
Existe una amplia literatura relacionada con los métodos aplicados a la estimación de los parámetros de la tendencia central y la dispersión de datos univariados (Barnett y Lewis, 1994). Estos se distribuyen en dos tipos de metodologías generales (Verma, 2005): (a) métodos robustos, que utilizan criterios de estimación que se ven poco afectados por la presencia de valores desviados; y (b) métodos de valores desviados, que consisten en la aplicación de pruebas de discordancia para la detección y eliminación de valores desviados en muestras estadísticas previo a los cálculos de parámetros de la tendencia central y la dispersión.
Los métodos robustos no serán abordados en el presente trabajo, ni los métodos de valores desviados basados en la desviación estándar (σ) de las poblaciones, siendo éstos de tipo "múltiples de σ" como 2σ o 3σ. En la práctica, para la aplicación de estos métodos a datos experimentales no se conoce σ y se le reemplaza, en forma aproximada, por la desviación estándar (s) de las muestras estadísticas (Verma, 2005). Una discusión sobre las limitaciones estadísticas de los métodos robustos y aquéllos de valores desviados basados en el criterio de dos desviaciones estándar (±2s) puede ser consultada en Verma (1997, 1998, 2005), Verma et al. (1998) y Verma y Quiroz–Ruiz (2008).
Las pruebas de discordancia, aplicadas en la detección de valores desviados, se distribuyen en cuatro tipos básicos (Barnett y Lewis, 1994; Verma, 2005): (a) estadísticos de desviación o dispersión (tipo Grubbs N1–N3; Grubbs, 1950); (b) estadísticos de suma de cuadrados (tipo Grubbs N4 y N5); (c) estadísticos de intervalo total o de dispersión (N6 y tipo Dixon N7–N13; Dixon, 1951); y (d) estadísticos de momento de alto orden ("skewness", sesgo o coeficiente de asimetría N14 y curtosis N15).
Estas pruebas de discordancia para la detección de valores desviados o discordantes también pueden ser clasificadas en dos tipos o clases: (a) pruebas sencillas, las cuales evalúan un valor a la vez como discordante, tipo k=1; y (b) pruebas múltiples, las cuales evalúan dos o más valores a la vez como discordantes, tipo k=2–4. Esta distinción será usada en el presente trabajo.
Las pruebas de discordancia han sido aplicadas o apreciadas de forma extensiva en diferentes campos de las ciencias geológicas y de otras áreas del conocimiento, incluyendo el control de calidad mediante materiales de referencia. Aunque en la literatura moderna existen miles de estudios sobre el tema de aplicación de pruebas de discordancia, se pueden citar como ejemplos los siguientes trabajos: Dybczynsky (1980); Linkosalo et al. (1996); Freeman et al. (1997); Verma (1997, 1998); Zaric y Niketic (1997); Velasco y Verma (1998); Verma et al. (1998, 2008); Taylor (2000); Guevara et al. (2001); Velasco–Tapia et al. (2001); Schaber y Badeck (2002); Li et al. (2003); Serbest et al. (2003); Graybeal et al. (2004); Farre et al. (2006); Gabrovská et al. (2006); Sang et al. (2006); Colombo et al. (2007); Gutiérrez–Ruiz et al. (2007); Hayes et al. (2007); Kasper–Zubillaga y Zolezzi–Ruiz (2007); Méndez–Ortiz et al. (2007); Nagarajan et al. (2007, 2008); Ram et al. (2007); Salleh et al. (2007); Shekhawat et al. (2007); Castrellon–Uribe et al. (2008); Díaz–González et al. (2008); Jafarzadeh y Hosseini–Barzi (2008); Obeidat et al. (2008); Palabiyik y Serpen (2008); Vargas–Rodríguez et al. (2008); Vattuone et al. (2008); Gómez–Arias et al. (2009); Madhavaraju y Lee (2009); Marroquín–Guerra et al. (2009); Pandarinath (2009); Torres–Alvarado et al. (en prensa); y Verma (2009a).
Dada la gran diversidad de pruebas de discordancia, es pertinente conocer sus potencias o eficiencias relativas para detectar valores discordantes. Las eficiencias dependerán seguramente del tipo de estadísticos (las fórmulas o expresiones matemáticas), en los cuales estas pruebas han sido basadas (Barnett y Lewis, 1994; Verma, 2005). Sin embargo, el funcionamiento de los estadísticos y, por consecuencia, la eficiencia de las pruebas pueden estar afectados por el así denominado efecto de enmascaramiento (masking effect; Barnett y Lewis, 1994), el cual se define como la inhabilidad del procedimiento para identificar un valor desviado debido a la presencia de un valor sospechoso cercano (Tietjen y Moore, 1972). Este efecto se conoce desde hace mucho tiempo (Pearson y Chandra Sekar, 1936) y constituye una posible limitación, especialmente de las pruebas de discordancia de tipo sencillo, aunque puede estar presente también en las de tipo múltiple. Un efecto contrario llamado swamping effect (Barnett y Lewis, 1994) puede alterar –en realidad aumentar– la potencia de pruebas de discordancia de tipo múltiple, ya que uno o más datos verdaderamente discordantes pueden llevar otro(s) dato(s) aparentemente concordante(s), resultando ambos tipos como discordantes. Este efecto no influye a las pruebas sencillas que evalúan un valor a la vez.
Es importante, por lo tanto, establecer la eficiencia (definida en la siguiente sección) de las pruebas, ya que a partir de este conocimiento es posible decidir la aplicación de un esquema basado en un número pequeño de ellas o, si es necesario, aplicar todas las disponibles como inicialmente fue propuesto por Verma (1997). Hasta el momento, no existe una evaluación completa de estas pruebas.
En este contexto, Velasco et al. (2000) compararon la eficiencia de 14 pruebas estadísticas, utilizando datos de composición de lantánidos (rare–earth elements, REE) en 26 materiales de referencia geoquímica (MRG). Estos autores reportaron: (a) que en la detección individual de valores desviados (k=1), las pruebas más eficientes son los estadísticos de momento de alto orden (N14 y N15); y (b) que existe una mayor eficiencia de los procedimientos en bloque (k=2–4), en comparación con la aplicación consecutiva de pruebas de discordancia de detección individual (k=1). Sin embargo, la evaluación de Velasco et al. (2000) debió de haber sido limitada, ya que no fue posible hacer una comparación completa entre pruebas. Esto fue porque en ese tiempo no existían valores críticos disponibles para determinados tamaños de muestra (n), por ejemplo, para las pruebas Dixon N7–N13 para n >30 (Dixon, 1951), o para la prueba de desviación N2 para n >20 (Barnett y Lewis, 1994; Verma, 2005). Este problema fue solucionado por Verma y Quiroz–Ruiz (2006a, 2006b, 2008) y Verma et al. (2008), quienes a partir de simulaciones tipo Monte Carlo, generaron nuevos valores críticos, de mayor precisión y exactitud que los disponibles en la literatura, y con tamaño de muestra de n=3–30,000. Con estos nuevos trabajos se hizo evidente que los valores críticos de la literatura anteriores a los nuevos no sólo se caracterizaban por poca precisión sino también por poca exactitud, por lo cual la evaluación empírica de todas las pruebas de discordancia debe ser realizada nuevamente.
Por lo tanto, recientemente Verma et al. (2009) llevaron a cabo una evaluación de la eficiencia relativa de las pruebas de discordancia, específicamente las variantes que detectan un valor desviado (k=1) y considerando valores críticos nuevos de hasta n=30,000. Esta evaluación se basó en la información de composición de elementos mayores y traza en 35 MRG. Los resultados de esta evaluación indican que la prueba N15 (coeficiente de curtosis) presenta la mayor eficiencia entre los estadísticos estudiados, mientras que la prueba N7 (tipo Dixon) fue la menos eficaz en esta detección.
Con el fin de profundizar en el conocimiento sobre la capacidad de detección de valores desviados por las pruebas de discordancia, se presentan los resultados de la evaluación de 15 estadísticos de aplicación sencilla (k=1) y múltiple (k=2–4), que incluyen 33 variantes. El presente análisis también fue realizado considerando una base de datos geoquímicos (elementos mayores y traza) de los 35 MRG, empleando para ello otros indicadores de eficiencia nuevos y adicionales al usado por Velasco et al. (2000) y Verma et al. (2009). Los resultados de este análisis de eficiencia han permitido: (a) la comparación entre variantes de tipo sencillo (k=1) y múltiple (k=2–4), siendo k el número de datos a probar "a la vez"; (b) contar con principios y lineamientos estadísticos para elegir el número y tipo de estadísticos necesarios para la detección de valores desviados en muestras geoquímicas univariadas y decidir si la aplicación de un número menor de pruebas de discordancia es suficiente, o si deben ser aplicadas todas las pruebas disponibles; y (c) demostrar la potencia de las pruebas de discordancia, al evaluar la eficiencia relativa de datos desviados en forma de un parámetro estadístico existente y otro propuesto en el presente trabajo (ambos serán definidas en este trabajo) así como una combinación de regresión lineal y pruebas de significancia.
Cabe aclarar que la importancia del presente trabajo radica en apreciar que los parámetros de la media aritmética y la desviación estándar pertenecen al método estadístico de valores desviados y, por lo tanto, es necesario aplicar las pruebas de discordancia a los datos univariados, antes de emplear estos parámetros para la estimación de la tendencia central y la dispersión, respectivamente (Verma, 2005). Además, estos parámetros son fundamentales en las calibraciones de instrumentos analíticos que nos proporcionan datos geoquímicos que sirven para inferir procesos geológicos dominantes. Por consecuencia, es pertinente contar con mayor conocimiento sobre estas pruebas de discordancia, por ejemplo, sus potencias o eficiencias relativas globales (Verma et al., 2009), siendo el objetivo primordial del presente trabajo.
METODOLOGÍA
Base de datos
Se llevó a cabo la recopilación exhaustiva de la composición química (11 elementos mayores y 71 elementos traza, incluyendo REE) para 35 MRG provenientes de cuatro países: (a) Canadá (Energy, Mines and Resources) – gabro MRG–1 y sienitas SY–2 y SY–3 (Abbey, 1979; Gladney y Roelandts, 1990); (b) E.U.A. (U. S. Geological Survey, USGS) – basalto BIR–1 y diabasa W–2 (Gladney, 1988), gabro GSM–1 (Flanagan, 1986), basalto BHVO–1, cuarzo QLO–1 y riolita RGM–1 (Gladney y Roelandts, 1988), dunita DTS–1, diabasa W–1 (Gladney et al., 1991) y granito G–2 (Gladney et al., 1992); (c) Japón (Geological Survey of Japan, GSJ) –http://riodb02.ibase.aist.go.jp/earthsci/welcome.html– para andesitas JA–1, JA–2 y JA–3, basaltos JB–1, JB–1a, JB–2 y JB–3, feldespatos JF–1 y JF–2, granodioritas JG–1 y JG–1a, granitos JG–2 y JG–3, horblendita JH–1, peridotita JP–1, y riolitas JR–1 y JR–2; y (d) Sudáfrica (National Institute of Metallurgy, NIM) – dunita NIM–D, granito NIM–G, lujavarita NIM–L, norita (gabro) NIM–N, pyroxenita NIM–P y sienita NIM–S (Steele et al., 1972, 1978). Los datos fueron capturados en el software comercial Statistica® que es una herramienta estadística para el manejo de gran cantidad de datos y permite exportar o importar datos en otros formatos como Excel®.
Aplicación estadística
La detección de datos desviados en muestras univariadas se realizó aplicando el programa DODESYS (Discordant Outlier Detection and Elimination SYStem; Verma y Díaz–González, en preparación), el cual incluye 15 pruebas de discordancia y sus 33 variantes (nueve pruebas sencillas y siete pruebas múltiples), considerando que la prueba N4 pertenece a ambas clasificaciones (sencilla una variante N4(k=1) y múltiple tres variantes N4(k=2,3,4)). Además, DODESYS utiliza, en su versión actual, los nuevos valores críticos, precisos y exactos, para un nivel de confianza estricto de 99%, simulados recientemente por Verma et al. (2008). Una versión anterior fue programada con valores de Verma y Quiroz–Ruiz (2006a, 2006b) mientras que una posterior (UDASYS; Univariate Data Analysis SYStem; Verma y Díaz–González, en preparación), más actualizada, se basaría en ecuaciones para diferentes niveles de confianza en vez de tablas (Verma y Quiroz–Ruiz, 2008), e involucraría adicionalmente pruebas de significancia (Verma, 2009b) y cálculos de parámetros robustos para el manejo de datos experimentales.
Para un arreglo de n datos univariados x1, x2, x3,..., xn–2, xn–1, xn, suponemos que el arreglo ordenado de estos datos es dado por x(1), x(2), x(3),..., x(n–2), x(n–1), x(n). En el presente trabajo, los datos analíticos para un elemento químico generados por un grupo de métodos en diferentes laboratorios para un MRG, representan un arreglo estadístico o una muestra estadística. Todos los métodos analíticos fueron agrupados de acuerdo con los criterios físicos en los cuales se basaron Velasco–Tapia et al. (2001), formándose un total de ocho grupos de métodos: (1) clásicos (químicos, gravimétricos y volumétricos); (2) absorción atómica; (3) fluorescencia de rayos–X; (4) espectrometría de emisión; (5) nucleares; (6) espectrometría de masas; (7) cromatográficos; y (8) misceláneos (que no pertenecen a ninguno de los grupos anteriores).
Para la evaluación de las pruebas de discordancia se emplea el arreglo ordenado x(1), x(2), x(3),..., x(n–2), x(n–1), x(n), el cual nos permite identificar valores extremos (outliers) susceptibles a probar como valores discordantes. Siguiendo a Verma y Quiroz–Ruiz (2006a, 2006b, 2008), se utilizó, para pruebas sencillas (k=1), la terminología "Upper" (U), cuando se evalúa al valor más alto en una serie de datos, es decir, x(n), p. ej., para N1, se dice N1U. De igual manera, el término "Lower" (L), fue usado cuando se trataba del valor más bajo x(1), p. ej., para N1, sería N1L. Para un valor extremo cuando la prueba está evaluando el valor más alejado de los dos extremos, es decir, x(n) o x(1), p. ej., para N2, sería N2E, pero, por simplicidad, se conservó el nombre original N2. Al contrario de las pruebas tipo "Upper" o "Lower", también llamadas de una cola, las de un valor "extremo" fueron denominadas como de dos colas por Barnett y Lewis (1994). Cabe aclarar también que para más de un dato a probar (k=2–4), la terminología fue similar, aunque algo más compleja. Por ejemplo, una prueba múltiple, como la N3, cuando evalúa dos datos a la vez, fue expresada como N3U2 (U para "Upper" y 2 para k) y como N3L2 (L para "Lower" y 2 para k). De igual manera, la prueba múltiple N4 se denominaría como N4U4 cuando se evalúan 4 datos a la vez en el lado más alto de la muestra estadística. No se utilizó la terminación de k cuando se trató de una prueba sencilla; en otras palabras, por simplicidad a N1, p. ej., se le denominó N1U y no N1U1. Finalmente, cuando se necesitó referir al resultado de la combinación de estas dos pruebas (tipo U y L) para un determinado k, se utilizó el signo de +, por ejemplo, para la prueba N3 con k=2 se diría, N3U2+N3L2.
Las pruebas de discordancia, para ser aplicadas, requieren el "número mínimo de datos" que varía del 3 (p. ej., N1U) hasta el 9 (p. ej., N3U4 o N3L4). Se decidió que, para evaluar y comparar las pruebas de discordancia de la forma más objetiva, era necesario realizar la aplicación en exactamente los mismos tamaños de muestras. Por lo tanto, de la base de datos de MRG se separaron todos los casos con n > 9, siendo un total de 2220 casos con estas características. De esta manera, un "caso" (una muestra estadística) se define como un conjunto de datos de un MRG para un elemento químico que ha sido analizado por un determinado grupo de métodos analíticos.
Con el fin de comparar las eficiencias o potencias de las pruebas, se definieron dos parámetros estadísticos (REC y ROC), los cuales se describen en la sección de "Criterios cuantitativos de comparación". Para comparar las eficiencias relativas mediante el primer parámetro REC, las pruebas de discordancia fueron clasificadas en 14 categorías, mostradas en la Tabla 1. Las primeras cinco categorías (1–5) constan de pruebas de discordancia sencillas (k=1). De esta manera, la categoría 5 se formó de todas las pruebas sencillas (N1, N2, N4, N7, N8, N9, N10, N14 y N15). Las pruebas múltiples (k=2–4), por su parte, fueron agrupadas en ocho categorías (6–13). Por ejemplo, en la categoría 6 existen todas las pruebas múltiples que evalúan los dos datos (k=2) más altos (N3U2, N4U2, N11U2, N12U2 y N13U2). La categoría 13 consta de todas las pruebas múltiples. Finalmente, todas las 15 pruebas de discordancia con sus 33 variantes fueron comparadas en la categoría 14. De igual manera, se establecieron cuatro categorías (A–D) para el parámetro ROC (Tabla 1), el cual nos permitió una comparación más justa que el parámetro REC para las categorías 13 y 14.
Por otra parte, para calcular los parámetros de eficiencia en una iteración se estableció, de forma arbitraria, que el número mínimo de casos aplicables sea, al menos, 30 para ser considerado como representativo para estos cálculos, aunque esto no es tan arbitrario ya que el número 30 es estadísticamente significativo. Cuando los casos "aplicables" para la evaluación de una prueba no cumplían con la condición de >30, no se calculó ningún parámetro de eficiencia. De esta manera, llegaron a finalizar las iteraciones para una determinada prueba de discordancia.
Una evaluación estadística adicional consistió en usar regresiones lineales empleando el programa OYNYL (Verma et al., 2006) y posteriormente en aplicar las pruebas F de Fisher y t de Student (Jensen et al., 2000; Verma, 2005, 2009b) para la comparación estadística de las pendientes de las regresiones obtenidas por OYNYL.
CRITERIOS CUANTITATIVOS DE COMPARACIÓN
En este trabajo se utilizaron parámetros estadísticos, tanto el existente "criterio de eficiencia relativa" (REC; Velasco et al., 2000; Verma et al., 2009) como el nuevo "criterio de datos desviados relativo" (ROC). Además, se aplicó una manera distinta de evaluar la eficiencia de las pruebas mediante regresiones lineales y pruebas de significancia de F y t. El suplemento electrónico del presente trabajo proporciona detalles sobre estos parámetros y, a continuación, se presenta una síntesis.
El criterio de eficiencia relativa (relative efficiency criterion, REC), definido con anterioridad por Velasco et al. (2000) y Verma et al. (2009), es un parámetro estadístico que expresa la potencia que tiene una prueba de discordancia para detectar y eliminar datos desviados en una muestra estadística. La fórmula para el REC global (REC)g en una prueba de discordancia se define de la siguiente manera:
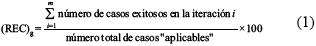
donde un "caso" (una muestra estadística) es un conjunto de datos de un MRG para un elemento químico que ha sido determinado por un grupo de métodos analíticos; el "éxito" indica el número de casos en los cuales, en una determinada iteración, se detectaron 1 ó 2–4 datos desviados, para pruebas tipo k=1 o k=2–4, respectivamente; y m es el total de iteraciones. Para mayores detalles sobre la definición de REC para cada iteración (REC)1, (REC)2, etc., ver el suplemento electrónico. En realidad, la expresión matemática reporta el porcentaje de eficiencia que tiene la prueba para detectar datos desviados. Un ejemplo detallado del cálculo del parámetro REC se presenta en el suplemento electrónico (ver Tabla A1 y la explicación correspondiente).
El criterio de datos desviados relativo (relative outlier criterion, ROC) se define, por primera vez, en el presente trabajo e indica el porcentaje de datos desviados que se ha depurado en una muestra, después de haberse aplicado una prueba de discordancia. El ROC global (ROC)g se puede calcular por:

La utilidad de esta expresión radica en que se tiene la posibilidad de conocer el número de datos desviados que fueron depurados en la totalidad de las muestras estadísticas iniciales. Además, (ROC)g proporciona una comparación más justa para algunas categorías en comparación con el parámetro (REC)g como se verá en la siguiente sección.
RESULTADOS
Organizamos nuestra presentación de acuerdo con los parámetros (REC)g y (ROC)g y las distintas categorías formadas para las pruebas, seguido por la combinación de regresiones lineales y las pruebas de significancia de F de Fisher y t de Student.
Criterio de eficiencia relativa (REC)
Para esta evaluación las pruebas de discordancia fueron clasificadas en 14 categorías (Tabla 1), definidas con la finalidad de comparar los parámetros de eficiencia relativa. El parámetro REC fue calculado para todas las categorías. Se presentan los resultados de estos cálculos en las Figuras A1–A11 (en el suplemento electrónico) y Figuras 1–(2)–3 (en este trabajo); en todas ellas (excepto Figuras 1 y 3) se emplea la misma escala en el eje "y" del REC, a fin de facilitar su comparación visual. Cabe aclarar que todas las Figuras y Tablas con numeración iniciada en "A" se ubican en el suplemento electrónico.



Categoría 1: N1U, N4U, N7U, N9U y N10U (Figura A1): Pruebas sencillas que evalúan el dato más alto x(n)
En la primera iteración (iteración 1, Figura A1a) aplicada a 2220 casos, las pruebas tipo Grubbs (N1U y N4U) presentaron valores de (REC)1 de 25.59% y 25.63%, respectivamente, mayores que las pruebas tipo Dixon (N7U, N9U y N10U; 19.81%, 21.04% y 20.90%, respectivamente). Adicionalmente, los valores de los parámetros (REC)2 y (REC)3 (iteraciones 2 y 3, Figura A1b–c) para las pruebas tipo Grubbs fueron significativamente mayores (20.21%–27.83%) que los valores obtenidos para las pruebas tipo Dixon (8.62%–12.20%). En la cuarta iteración (iteración 4, Figura A1d), únicamente las dos pruebas tipo Grubbs presentaron un número significativo de casos "aplicables" (> 30), por lo cual el parámetro (REC)4 se calculó sólo para estas pruebas de discordancia, resultándose un valor de 34.4% para ambas. Para las pruebas tipo Dixon (N7U, N9U y N10U), los casos "aplicables" para la iteración 4 fueron solamente 4–5, por lo cual no se calculó (REC)4. Estas consideraciones fueron aplicadas de manera similar en la descripción de las categorías subsecuentes (categorías 2–14).
Categoría 2: N1L, N4L, N9L y N10L (Figura A2): Pruebas sencillas que evalúan el dato más bajo x(1)
En la primera iteración (iteración 1, Figura A2a) las pruebas tipo Grubbs (N1L y N4L) presentaron valores de (REC)1 de 11.22% para ambas, ligeramente menores que la prueba tipo Dixon N10L (11.31%) y mayores que la prueba tipo Dixon N9L (10.45%). Para fines prácticos, se puede considerar que, de acuerdo con este parámetro, las pruebas N1L, N4L y N10L son parecidas y sólo ligeramente mejores que N9L. No obstante, en la iteración 2 (Figura A2b) las pruebas tipo Grubbs presentaron valores de (REC)2 significativamente mayores (14.9% para ambas N1L y N4L) que las pruebas tipo Dixon N9L y N10L (6.5% y 6.4%). En la tercera iteración (Figura A1c), únicamente las pruebas tipo Grubbs tuvieron valores de (REC)3 que fueron 16.2% para ambas.
Categoría 3: N2, N8, N14 y N15 (Figura A3): Pruebas sencillas que evalúan un dato extremo x(1) o x(n)
En la Figura A3a (iteración 1) se puede apreciar que la prueba del coeficiente de exceso o curtosis N15 presentó el valor del (REC)1 mayor (34.10%), seguido por la prueba tipo Grubbs N2 (31.94%) y por la prueba del coeficiente de asimetría o sesgo N14 (27.48%). Mientras tanto, la prueba tipo Dixon N8 dió el valor (25.50%) de (REC)1 menor que N14. En las iteraciones 2 y 3 (Figura A3b–c), las pruebas N14 y N15 mostraron valores de (REC)2 y (REC)3 (29.67%–40.33%) mayores que las pruebas tipo Grubbs N2 (22.43% y 27.04%) y tipo Dixon N8 (12.19% y 8.70%). En la iteración 4 (Figura A3d), la prueba tipo Dixon N8 únicamente fue aplicable a seis casos (que corresponden al número de casos "exitosos" en la iteración 3) mientras que las pruebas N2, N14 y N15 fueron aplicadas a un número significativo de casos (43, 73 y 86, respectivamente) y presentaron valores significativamente grandes del (REC)4 (34.9%, 39.7% y 46.5%, respectivamente). Finalmente, en la iteración 5 (Figura A3e) se puede observar que las pruebas N14 y N15 presentaron valores del (REC)5 significativamente grandes (44.8% y 42.5%).
Categoría 4: N1, N4, N9 y N10 (Figura A4): Todas las pruebas sencillas con dos versiones (más alto y más bajo) x(1), x(n)
En esta evaluación se sumaron los casos "exitosos" obtenidos en una iteración, de ambas versiones (más alto y más bajo) de las pruebas de discordancia que integran esta categoría. En la iteración 1 (Figura A4a), las pruebas tipo Grubbs (N1 y N4) presentaron valores del (REC)1 muy parecidos (18.40% y 18.42%) mientras que las pruebas tipo Dixon (N9 y N10) dieron valores menores (15.74% y 16.10%). En la iteración 2 (Figura A4b), los valores de (REC)2 para las pruebas tipo Grubbs fueron significativamente mayores (18.60% para N1 y 18.58% para N4) que los de las pruebas tipo Dixon (8.15% para N9 y 7.83% para N10). En la iteración 3 (Figura A4c), los valores de (REC)3 para las pruebas tipo Grubbs N1 y N4 fueron aún mayores (ambos 25%) que los de las de Dixon N9 y N10 (12.2% y 10.0%, respectivamente). Finalmente, en la cuarta iteración (Figura A4d) el parámetro (REC)3 para las pruebas tipo Grubbs (N1 y N4) proporcionó valores altos de 34%.
Categoría 5 (Figura 1): Todas las pruebas sencillas (N1, N2, N4, N7, N8, N9, N10, N14 y N15)
Esta categoría incluye todas las pruebas sencillas, es decir, aquellas que evalúan un sólo dato discordante: N1 (con ambas versiones: dato más alto y más bajo), N2 (extremo), N4 (con ambas versiones: más alto y más bajo), N7 (más alto), N8 (extremo), N9 (con ambas versiones: más alto y más bajo), N10 (con ambas versiones: más alto y más bajo), N14 (extremo, coeficiente de asimetría "skewness") y N15 (extremo, coeficiente de exceso "kurtosis"). Con la finalidad de realizar una comparación "justa" de todas las pruebas de discordancia de esta categoría, se contaron todos los casos "exitosos" en todas las iteraciones de una prueba determinada (incluyendo ambas versiones, más alto y más bajo). Se consideró como casos "aplicables" el número de casos inicial (2220 casos con n > 9 datos cada uno). Los resultados del parámetro REC global (REC)g (ver ecuación 1) de las pruebas de discordancia de esta categoría (Figura 1) mostraron la siguiente secuencia (en orden descendente): (i) la prueba de dos colas basada en el coeficiente de exceso o curtosis N15 (51.58%); (ii) la prueba de una cola tipo Grubbs N4 (46.13%); (iii) la prueba de una cola tipo Grubbs N1 (46.08%); (iv) la prueba de dos colas tipo Grubbs N2 (41.85%); (v) la prueba de dos colas basada en el coeficiente de asimetría o sesgo N14 (41.08%); (vi) la prueba de una cola tipo Dixon N10 (34.91%); (vii) la prueba de una cola tipo Dixon N9 (34.28%); (viii) la prueba de dos colas tipo Dixon N8 (28.87%); y (ix) la prueba de una cola tipo Dixon N7 (21.94%). En otras palabras, la eficiencia o la potencia de las pruebas de discordancia sencillas tiene el orden siguiente: N15 > N4 ≈ N1> N2 ≈ N14 > N10 ≈ N9 > N8 > N7.
Categoría 6: N3U2, N4U2, N11U2, N12U2 y N13U2 (Figura A5): Pruebas que evalúan los dos datos más altos x(n), x(n–1)
En la primera iteración (Figura A5a), los valores de (REC)1 presentaron la siguiente secuencia (el valor del (REC)1 del mayor al menor): la prueba tipo Grubbs N4U2 (28.60%), la prueba tipo Dixon N13U2 (26.17%), la prueba tipo Dixon N12U2 (26.13%), la prueba tipo Dixon N11U2 (24.82%) y finalmente, la prueba tipo Grubbs N3U2 (18.47%). Mientras tanto, en la segunda iteración (Figura A5b) los valores de (REC)2 para las pruebas tipo Grubbs (N3U2; 16.10% y N4U2; 11.65%) fueron mayores que los valores obtenidos para las pruebas tipo Dixon N11U2, N12U2 y N13U2 (6.17%, 6.21% y 4.99%, respectivamente). En la iteración 3 (Figura A5c), nuevamente las pruebas tipo Grubbs (N3U2 y N4U2) presentaron valores significativamente mayores (19.7% y 17.6%) que la prueba tipo Dixon N12 (2.8%). El resto de las pruebas tipo Dixon (N11U2 y N13U2) no presentaron un número de casos "aplicables" significativo para esta iteración.
Categoría 7: N3L2, N4L2, N11L2, N12L2 y N13L2 (Figura A6): Pruebas que evalúan los dos datos más bajos x(1), x(2)
En la primera iteración (Figura A6a) las pruebas tipo Dixon N12L2 y N13L2 presentaron los valores de (REC)1 ligeramente mayores (12.16% y 13.24%) que el resto de las pruebas N3L2, N4L2 y N11L2 (con 8.51%, 12.07% y 10.68%, respectivamente). Sin embargo, en la segunda iteración (Figura A6b) los valores de (REC)2 fueron mayores para las pruebas tipo Grubbs N3L2 (7.94%) y N4L2 (5.22%) que las de tipo Dixon N11L2 (2.11%), N12L2 (1.48%) y N13L2 (2.38%). El número de casos "aplicables" en la tercera iteración no fueron significativos.
Categoría 8: N5UL y N6UL (Figura A7): Pruebas que evalúan el dato más alto y el más bajo x(1), x(n)
Las pruebas de discordancia que integran esta categoría son solamente las dos pruebas tipo Grubbs. En la primera iteración (Figura A7a) la prueba N5UL presentó un valor mayor (29.86%) que la prueba N6UL (16.67%). En la iteración 2 (Figura A7b) el valor de (REC)2 de ambas pruebas fueron similares (N5UL; 15.84% y N6UL; 15.14%). Mientras tanto, en la iteración 3 (Figura A8c) se puede apreciar que la prueba N6UL (21.4%) presentó un valor ligeramente mayor de (REC)3 que la prueba N5UL (20.0%).
Categoría 9: N3U3 y N4U3 (Figura A8): Pruebas que evalúan los tres datos más altos x(n) , x(n–1), x(n–2)
Estas pruebas múltiples tipo Grubbs pudieron lograr una sola iteración. Por lo tanto, únicamente se calculó el (REC)1. La prueba N3U3 presentó un valor de (REC)1 significativamente menor (10.95%) que la prueba N4U3 (27.03%).
Categoría 10: N3L3 y N4L3 (Figura A9): Pruebas que evalúan los tres datos más bajos x(1), x(2), x(3)
Al igual que la categoría 9, las pruebas lograron sólo una iteración. La prueba N3L3 presentó un valor de (REC)1 significativamente menor (4.77%) que la prueba N4L3 (11.49%). El resultado en esta categoría coincidió con el de la categoría 9 ya que la prueba N4 presentó mayor eficiencia que la N3.
Categoría 11: N3U4 y N4U4 (Figura A10): Pruebas que evalúan los cuatro datos más altos x(n) , x(n–1), x(n–2), x(n–3)
La eficiencia de la primera iteración (REC)1 para la prueba N3U4 presentó un valor significativamente menor (6.76%) que para la prueba N4U4 (25.01%), consistente al resultado de las variantes de k=2 y 3 (categorías 9 y 10).
Categoría 12: N3L4 y N4L4 (Figura A11): Pruebas que evalúan los cuatro datos más bajos x(1), x(2), x(3), x(4)
El valor del (REC)1 para la prueba N3L4 (2.61%) fue significantemente menor al de la prueba N4L4 (10%). Esto nuevamente sugiere que la prueba N4 es más eficiente que la prueba N3.
Categoría 13 (Figura 2): Todas las pruebas de discor–dancia múltiples (N3, N4, N5, N6, N11, N12 y N13) con sus variantes
La presente categoría se encuentra integrada por todas las pruebas de discordancia múltiples (estas pruebas evalúan de dos hasta cuatro datos a la vez, k=2–4). Con el fin de realizar una justa comparación de las pruebas en esta categoría, se sumaron los casos "exitosos" de todas las iteraciones realizadas por una determinada prueba (incluyendo ambas versiones que evalúan tanto los datos más altos como los más bajos). La comparación de las pruebas de esta categoría requirió el cálculo del parámetro de eficiencia relativa global (REC)g (ecuación 1). Los valores de (REC)g de las pruebas múltiples (Figura 2) mostraron la siguiente carácterísticas: (i) la prueba tipo Grubbs de una cola N3 (con tres combinaciones de seis variantes N3U2+N3L2, N3U3+N3L3 y N3U4+N3L4; 31.58, 15.72 y 9.37%, respectivamente); (ii) la prueba tipo Grubbs de una cola N4 (con tres combinaciones de seis variantes N4U2+N4L2, N4U3+N4L3 y N4U4+N4L4; 45.36, 38.51 y 35.09%, respectivamente); (iii) la prueba tipo Grubbs de dos colas N5 (N5UL; 35.86%); (iv) la prueba tipo Grubbs de dos colas N6 (N6UL; 19.82%); (v) la prueba tipo Dixon de una cola N11U2+N11L2 (37.25%); (vi) la prueba tipo Dixon de una cola N12U2+N12L2 (40.14%); y (vii) la prueba tipo Dixon de una cola N13U2+N13L2 (41.04%).
Si comparamos las pruebas de discordancia múltiples para un determinado valor de k, se puede inferir el siguiente orden en la eficiencia relativa (REC)g de las pruebas: (i) pruebas que evalúan dos datos a la vez (k =2)): N4U2+N4L2 > N13U2+N13L2 > N12U2+N12L2 > N11U2+N11L2 > N5UL > N3U2+N3L2 > N6UL; (ii) pruebas que evalúan tres valores (k=3): N4U3+N4L3 > N3U3+N3L3; y (iii) pruebas que evalúan cuatro valores (k=4)): N4U4+N4L4 > N3U4+N3L4.
Categoría 14 (Figura 3): Todas las pruebas de discordancia sencillas y múltiples
Los resultados finales de la presente evaluación empírica de 15 pruebas de discordancia con 33 variantes mediante el parámetro (REC)g fueron calculados de manera similar que en las categorías 5 y 13. Se obtuvo el número total de casos "exitosos" (numerador de la ecuación 1) sumando todos los casos "exitosos" en todas las iteraciones de una prueba determinada que incluyó ambas versiones de datos desviados (tipo más alto y más bajo). Por ejemplo, para la prueba N1 se sumaron los casos "exitosos" de N1U y N1L, por lo cual aquí N1 (Tabla 1) representa N1U+N1L; N3UL2 equivale a N3U2+N3L2; etc. De esta manera, se obtuvieron 20 pruebas con variantes de prueba combinadas (Figura 3). La secuencia de las eficiencias (REC)g para estas variantes combinadas fueron: N15 > N4U+N4L ≈ N1U+N1L ≈ N4U2+N4L2 > N2 ≈ N14 ≈ N13U2+N13L2 ≈ N12U2+N12L2 > N4U3+N4L3 ≈ N11U2+N11L2 > N5UL ≈ N4U4+N4L4 ≈ N10U+N10L ≈ N9U+N9L > N3U2+N3L2 > N8 > N7 > N6UL > N3U3+N3L3 > N3U4+N3L4.
Necesidad de un nuevo criterio estadístico: Criterio relativo de datos desviados (relative outlier criterion, ROC)
Es importante señalar que el parámetro REC es útil para comparar justamente las pruebas en la mayoría de las 14 categorías, excepto en las categorías 13 y 14. En estas dos categorías, debido a la comparación de pruebas con distintos valores de k (1–4), el número de datos probados a la vez no se toma en cuenta correctamente. El parámetro REC es simplemente la relación de casos "exitosos" con casos "aplicables" (ecuación 1). Es deseable, por lo tanto, que el parámetro estadístico tome en cuenta tanto el número de datos desviados en casos "exitosos" como el total de los datos en los casos "aplicables". Se formuló un nuevo criterio llamado criterio relativo de datos desviados (ROC)g (el subíndice g representa "global") para la evaluación de las 15 pruebas de discordancia con 33 variantes. La evaluación basada en este nuevo parámetro estadístico (ROC)g se presenta a continuación.
La determinación de este parámetro (ROC)g (ecuación 2) para una prueba se obtiene al dividir el número de datos desviados detectados por la prueba entre el número total de datos que contienen los 2220 casos "aplicables", siendo un total de 41,821 datos individuales geoquímicos. Debido a la definición en términos de la relación de datos desviados entre el total de datos, este parámetro es totalmente libre de la unidad, por lo cual cuando en una categoría se comparan pruebas con distintos k (1–4), (ROC)g pudiera ser más objetiva y justa para realizar una comparación que el parámetro (REC)g, que aunque se basa también en la relación de número de casos y es libre de unidad, no toma en cuenta el valor de k (1–4). Por todo esto, se puede afirmar que el valor de (ROC)g permite conocer el número de datos totales que una prueba de discordancia detecta y elimina en las muestras estadísticas en función de todos los datos presentes. Para la aplicación de (ROC)g, se formaron cuatro categorías de pruebas (Tabla 1).
Categoría A (Figura A12a): (ROC)g para pruebas que detectan desde uno hasta cuatro valores discordantes altos x(n) , x(n–1), x(n–2), x(n–3)
En la categoría A fueron incluidas todas las pruebas de discordancia que evaluaron a los valores más altos. Esta categoría cuenta con cinco variantes de cuatro pruebas sencillas (N1U, N4U, N7U, N9U y N10U) y nueve variantes de cinco pruebas múltiples (de tipo k=2: N3U2, N4U2, N11U2, N12U2 y N13U2; de k=3: N3U3 y N4U3; y de k=4: N3U4 y N4U4). En la Figura A12a se observa que la prueba múltiple N4, en sus tres versiones (k=2–4), presenta valores de (ROC)g de 3.46%–5.33%, significativamente mayores que todas las otras pruebas en esta categoría (1.16%–2.95%). El valor mayor del (ROC)g corresponde a la prueba tipo Grubbs N4U4, en su versión de k=4, debido a que esta prueba detectó un total de 2228 datos discordantes en un total de 41,821 datos individuales geoquímicos. Por otra parte, la prueba N7U tipo Dixon, con el menor valor del (ROC)g, detectó un total de solamente 487 datos discordantes en el mismo total de 41,821 datos individuales geoquímicos.
Esto aclara también que, aunque el parámetro (REC)g referente a casos o muestras estadísticas, presentó valores de entre 21.94% y 32.84% para pruebas sencillas tipo "Upper" y entre 6.76% y 27.79% para pruebas múltiples tipo "Upper", el (ROC)g concerniente a los datos desviados se encuentra entre valores significativamente menores (1.16%–5.33%). Esto significa que, en los datos geoquímicos interlaboratorios de MRG, relativamente pocos datos se identificaron como valores discordantes y que la gran mayoría de los datos restantes (94.68%–98.84%) representan fielmente muestras estadísticas normales sin "contaminación" estadística.
Finalmente, se infiere que el orden de (ROC)g para pruebas de discordancia que evaluaron a los valores más altos fue el siguiente: N4U4 > N4U3 > N4U2 > N12U2 ≈ N13U2 > N11U2 > N3U2 > N3U3 = N1U ≈ N4U > N3U4 > N9U ≈ N10U > N7U.
Categoría B (Figura A12b): (ROC)g para pruebas que detectan desde uno hasta cuatro valores discordantes bajos x(1), x(2), x(3), x(4)
Al igual que la categoría A, aquí se consideraron todas las pruebas de discordancia de tipo sencillo y múltiple que evalúan al valor más bajo. La prueba N4 en su versión de k=4 representó el valor del (ROC)g más alto aunque solamente de 2.12%, equivalente a sólo 886 datos discordantes en un total de 41,821 datos individuales geoquímicos. Por su parte, en esta categoría la prueba N3L4 presentó el menor valor de (ROC)g, de 0.55%, equivalente a 232 datos en toda la base de 41,821 datos individuales geoquímicos analizada en este trabajo. En comparación, el parámetro anterior (REC)g referente a casos o muestras estadísticas, por su parte, presentó valores de entre 11.17% y 13.24% para pruebas sencillas tipo "Lower" y entre 2.61% y 13.56% para pruebas múltiples tipo "Lower".
El orden de (ROC)g para pruebas de discordancia con valores bajos fue el siguiente: N4L4 > N4L3 > N13L2 > N4L2 > N12L2 > N11L2 > N3L2 > N3L3 > N4L ≈ N1L > N10L2 > N9L > N3L4.
Categoría C (Figura A12c): (ROC)g para pruebas que detectan desde uno o dos valores discordantes extremos x(1) o x(n) o ambos
En esta categoría se evalúa las eficiencias de las pruebas de tipo "valor(es) extremo(s)", viz., N2, N5, N6, N8, N14 y N15. El mayor valor de (ROC)g fue de 3.81% para la prueba múltiple tipo Grubbs N5, seguido por la prueba sencilla N15 (curtosis) con 2.74% y la prueba sencilla tipo Dixon N8 fue la menos eficiente (1.53%). En términos de datos desviados, el mayor número de discordantes fue 1592 (prueba tipo Grubbs N5) y el menor solamente 631 (prueba tipo Dixon N8). En comparación, el parámetro anterior (REC)g referente a casos o muestras estadísticas presentó valores significantemente mayores de entre 19.82% y 51.58% para pruebas tipo "extremo".
El orden del criterio de eficiencia relativa de valores desviados (ROC)g en pruebas que evaluaron datos extremos, fue el siguiente: N5 > N15 > N2 ≈ N14 > N6 > N8.
Categoría D (Figura 4): (ROC)g para todas las pruebas sencillas y múltiples
Finalmente, se presenta una comparación de todas las 15 pruebas de discordancia con las 33 variantes presentados en 20 combinaciones (Figura 4). En el histograma se observa que los valores mayores de (ROC)g corresponden a las variantes de la prueba múltiple tipo Grubbs N4. Para pruebas sencillas, el mayor valor (2.74%) de (ROC)g correspondió a la prueba de curtosis N15 mientras que el menor (1.17%) a la prueba tipo Dixon N7. Para pruebas múltiples, por su parte, el mayor valor (7.45%) de (ROC)g fue para la combinación de la prueba tipo Grubbs N4 (N4U4+N4L4) y el menor (1.99%) también para la prueba tipo Grubbs N3 (N3U4+N3L4). Estos porcentajes son significativamente menores a los representados por el parámetro anterior (REC)g referente a casos o muestras estadísticas de 21.95%–51.58% para combinaciones iguales de pruebas sencillas y de 9.37%–45.36% para pruebas múltiples.

El orden de (ROC)g para pruebas de discordancia que evaluaron a los valores más altos y más bajos fue el siguiente: N4U4+N4L4 > N4U3+N4L3 > N4U2+N4L2 > N13U2+N13L2 > N11U2+N11L2 > N5UL > N3U2+N3L2 > N12U2+N12L2 > N15 > N3U3+N3L3 ≈ N4U+N4L ≈ N1U+N1L > N2 ≈ N14 > N6UL > N3U4+N3L4 > N10U2+N10L2 > N9 > N8 > N7.
DISCUSIÓN
Regresión lineal y pruebas de significancia
Con el fin de evaluar la eficiencia relativa de las pruebas de discordancia mediante este nuevo procedimiento estadístico –la combinación de regresión lineal y pruebas de significancia–, se investigó la posible dependencia del criterio de eficiencia relativa de la primera iteración (REC)1 sobre el tamaño de la muestra estadística (n, el número de datos en casos "aplicables" o el tamaño del grupo). Para ello, los casos "aplicables" fueron separados por sus tamaños y el parámetro (REC)1 fue calculado para cada una de las pruebas de discordancia. Los resultados de las correlaciones lineales entre el tamaño n y (REC)1 se presentan gráficamente en las Figuras A13 y A14, mientras que una síntesis de los parámetros estadísticos de la regresión (intercepto y pendiente así como sus errores) se muestra en la Tabla 2. Debido a los valores altos del coeficiente de correlación lineal (r) con la probabilidad de no–correlación baja (Miller y Miller, 2000; Bevington y Robinson, 2003; Verma, 2005), se infiere la validez de una correlación lineal entre estos dos parámetros –n y (REC)1– a nivel de confianza de 99%. Esto fue válido para 33 relaciones de las pruebas de discordancia agrupadas en 11 categorías (de las 14 en la Tabla 1), con la excepción de cuatro relaciones que también fueron válidas a nivel de confianza de 95% (ver las relaciones identificadas por un asterisco en la Tabla 2).
En el presente análisis no se tomará en cuenta el intercepto de las regresiones debido a que no tiene significado para la pruebas de discordancia, las cuales son inaplicables para n < 3 (Verma, 2005). El intercepto de una regresión lineal se define por el valor en el eje–y para el eje–x=0, en nuestro caso para n=0; este valor cero de tamaño de muestra (n) carece de sentido alguno, por lo cual es difícil interpretar el significado del intercepto en el presente estudio. De cualquier manera, los valores negativos grandes de un intercepto en una categoría de pruebas donde otros valores de interceptos son positivos, como es el caso de la categoría 6 (ver el intercepto de –11.48 para N3U2 en comparación con +11.31 a +15.54 para las otras pruebas; Tabla 2), pueden causar problemas en la interpretación de las pendientes que sí son importantes para evaluar las eficiencias relativas de las pruebas.
Todas las pendientes son positivas (Tabla 2), lo cual confirma que a mayor tamaño de muestra (n) corresponde una mayor eficiencia de las pruebas de discordancia (REC)1 y viceversa. Esto también permite interpretar que las muestras con un tamaño menor tendrían menor número de valores desviados que las muestras grandes. Aunque una correlación más compleja (tipo polinomial) pudiera ser mejor (Figuras A13 y A14), es útil comparar estadísticamente las pendientes de las regresiones lineales para evaluar las eficiencias de las pruebas. Esto se llevó acabo mediante las pruebas de significancia de F de Fisher y t de Student (Jensen et al., 2000; Verma, 2005), aplicadas a nivel de confianza de 99%. Para la mayoría de los pares de pruebas no se encontró diferencias significativas entre las dos varianzas.
Para cada par de pruebas en una determinada categoría (Tabla 2) se probó la hipótesis nula si una de las dos pruebas demostraba una mayor eficiencia (REC)1, utilizando para ello valores críticos de t de Student para una cola a nivel de confianza de 99% (Verma, 2005, 2009b).
En la categoría 1 de las pruebas sencillas con su versión "Upper" del dato más alto (Tabla 2), las pendientes (b) para N1U y N4U fueron significativamente mayores que para N7U, N9U y N10U. Se infiere que las pruebas tipo Grubbs N1 y N4 en su versión "Upper" presentaron eficiencias significativamente mayores que las pruebas tipo Dixon N7, N9 y N10. Para las pruebas sencillas tipo "Lower" (categoría 2 en la Tabla 2), N1L y N4L tuvieron pendientes significativamente mayores que N9L, pero no con respecto a N10L. Se concluye que las pruebas tipo Grubbs N1 y N4 ("Lower") demostraron eficiencias mayores que la prueba N9 tipo Dixon. De igual manera, la prueba curtosis N15 presentó eficiencia significativamente mayor que la prueba N8 tipo Dixon y la prueba de sesgo N14 (categoría 3 en la Tabla 2). Las pruebas combinadas ("Upper+Lower"; categoría 4 en la Tabla 2) tipo Grubbs N1 y N4 demostraron significativamente mayor eficiencia que las pruebas N9 y N10, ambas tipo Dixon.
Para las pruebas múltiples tipo k=2 para dos datos más altos ("Upper") y sin tomar en cuenta la prueba N3U2 con un valor negativo grande en su intercepto (–11.48; categoría 6 en la Tabla 2), se encontró que la prueba tipo Grubbs N4U2 fue significativamente más eficiente que las pruebas N11U2 y N12U2 tipo Dixon. Para las versiones tipo "Lower", la prueba N4L2 presentó mayor eficiencia que la prueba N11L2 (categoría 7 en la Tabla 2). Solamente dos pruebas tipo Grubbs N3 y N4 tienen versiones con k=3 y k=4. La prueba N4 presentó mayor eficiencia en relación con la prueba N3, consistente con la relación de las pendientes de regresiones lineales (ver categorías 9–12 en la Tabla 2).
Estas consideraciones son abordadas para (REC)g con el fin de confirmar las inferencias de (REC)1 . Las gráficas (Figuras A15 y A16) en el suplemento electrónico demuestran que los valores de (REC)g para las pruebas de curtosis N15, coeficiente de asimetría N14 y tipo Grubbs N1 y N4, son más altos que para las pruebas tipo Dixon N7–N13. Esta conclusión es totalmente consistente con el análisis de los parámetros REC y ROC (Figuras 1–(2–3)–4). De igual manera, se confirma que los valores de (REC)g para las pruebas tipo "Upper" son significativamente mayores a los de tipo "Lower".
Consideraciones finales
El parámetro REC, usado anteriormente por Velasco–Tapia et al. (2001) y Verma et al. (2009), así como el parámetro ROC demostraron su utilidad en la evaluación de las pruebas de discordancia. La combinación de regresiones lineales y aplicación de pruebas de significancia de F y t también fueron útiles para documentar las eficiencias relativas.
De mucha relevancia para datos geoquímicos interlaboratorios es que los resultados de (ROC)g en MRG demuestran claramente que la mayor parte de los datos desviados se localizan en el extremo de los valores altos, en comparación con los del extremo de los valores bajos. Las distribuciones, por lo tanto, de estos datos geoquímicos, debido a la "contaminación" estadística, estarían sesgadas positivamente en mayor número de los casos y negativamente en menor número de los casos. En la categoría D con todas las pruebas, las pruebas N5 y N6 que evalúan el par de datos formado por un dato a cada lado de las muestras, ocuparon lugares desde intermedios hasta los últimos en la secuencia de eficiencias y no los primeros, lo cual equivale a que la contaminación simétrica (a ambos lados de las muestras) no es particularmente frecuente. Además, dentro de la categoría 13 de las pruebas tipo k=2, estas pruebas N5 y N6 demostraron relativamente eficiencias (REC)g bajas.
Todo esto tiene implicaciones importantes para los métodos robustos, como la mediana o media de Gastwirth, los cuales, a pesar de su supuesta robustez, presentarían la estimación de tendencia central afectada por la contaminación dominada por valores altos. Trabajos de simulación para evaluar el comportamiento de métodos robustos y de valores desviados se encuentran actualmente en proceso por Verma y colaboradores, mismos que proporcionarán mayores criterios acerca de los métodos más apropiados para el procesamiento de datos experimentales.
Un mayor éxito de las pruebas múltiples puede deberse en parte al "swamping effect" que afecta favorablemente a este tipo de pruebas, estando ausente en las pruebas sencillas. Las pruebas sencillas, por su parte, pueden verse disminuidas en su eficiencia por el "masking effect" que influye mayormente a esta clase de pruebas y no tanto a las múltiples. Trabajos de simulaciones computacionales para abundar más sobre este tipo de comparaciones son sumamente necesarios y se encuentran actualmente en preparación por Verma y colaboradores.
En resumen, los parámetros robustos, como la mediana o la media de Gastwirth, a pesar de su robustez, serán muy probablemente sesgados para este tipo de datos. Así mismo, la aplicación rigurosa de pruebas de discordancia antes de estimar los valores de la media y desviación estándar parece ser un requerimiento básico. Adicionalmente, se recomienda considerar el tamaño de la muestra para la selección de las pruebas de discordancia. En muestras estadísticas pequeñas, lo recomendable es aplicar pruebas de discordancia sencillas, mientras que para las muestras grandes, todas las pruebas con mayores eficiencias, tanto sencillas como múltiples, pueden ser aplicadas.
CONCLUSIONES
Se encontraron los patrones siguientes para las eficiencias de las pruebas de discordancia.
(1) La eficiencia o potencia (REC)g de las pruebas de discordancia sencillas (categoría 5) tiene el orden: N15 > N4 ≈ N1> N2 ≈ N14 > N10 ≈ N9 > N8 > N7. En pruebas sencillas, la que reportó el mayor valor en la eficiencia fue la de curtosis N15 y la de menor eficiencia fue la N7 de tipo Dixon.
(2) El siguiente orden en la eficiencia relativa (REC)g de las pruebas múltiples (categoría 13) fue: (i) pruebas que evalúan dos datos a la vez (k=2): N4U2+N4L2 > N13U2+N13L2 > N12U2+N12L2 > N11U2+N11L2 > N5UL > N3U2+N3L2 > N6UL; (ii) pruebas que evalúan tres valores (k=3): N4U3+N4L3 > N3U3+N3L3; y (iii) pruebas que evalúan cuatro valores (k=4): N4U4+N4L4 > N3U4+N3L4. En pruebas múltiples, la prueba tipo Grubbs N4 es la más recomendable.
(3) El orden de (ROC)g para pruebas de discordancia que evaluaron a los valores más altos (categoría A) fue el siguiente: N4U4 > N4U3 > N4U2 > N12U2 ≈ N13U2 > N11U2 > N3U2 > N3U3 = N1U ≈ N4U > N3U4 > N9U ≈ N10U > N7U. Se afirma la importancia de la prueba N4 tipo Grubbs para su uso con datos geoquímicos.
(4) El orden de (ROC)g para pruebas de discordancia con valores bajos (categoría B) fue: N4L4 > N4L3 > N13L2 > N4L2 > N12L2 > N11L2 > N3L2 > N3L3 > N4L ≈ N1L > N10L2 > N9L > N3L4.
(5) El orden del criterio de eficiencia relativa de valores desviados (ROC)g en pruebas que evaluaron datos extremos (categoría C) fue: N5 > N15 > N2 ≈ N14 > N6 > N8.
(6) El orden de (ROC)g para pruebas de discordancia que evaluaron a los valores más altos y más bajos (categoría D) fue: N4U4+N4L4 > N4U3+N4L3 > N4U2+N4L2 > N13U2+N13L2 > N11U2+N11L2 > N5UL > N3U2+N3L2 > N12U2+N12L2 > N15 > N3U3+N3L3 ≈ N4U+N4L ≈ N1U+N1L > N2 ≈ N14 > N6UL > N3U4+N3L4 > N10U2+N10L2 > N9. En esta categoría más completa, se afirma nuevamente la importancia de la prueba N4 tipo Grubbs como la de mayor eficiencia en todas sus versiones de k=2–4.
Finalmente, si el objetivo es contar con muestras estadísticas con distribución normal sin contaminación estadística y determinar parámetros estadísticos confiables, como debe ser para cualquier experimento en ciencias o ingenierías, es indispensable aplicar pruebas de discordancia previamente a los cálculos de la media y la desviación estándar.
AGRADECIMIENTOS
La primera autora (RGR) agradece a la Secretaría de Educación Pública por el permiso otorgado para llevar acabo los estudios de doctorado en la Universidad Nacional Autónoma de México mientras que la segunda (LDG) lo hace al CONACYT por la beca otorgada para realizar y concluir sus estudios doctorales. Expresamos nuestro agradecimiento a Alfredo Quiroz–Ruiz por la constante ayuda computacional durante el desarrollo de esta investigación. De manera similar, agradecemos a los tres árbitros –Alfredo Aparicio, John S. Armstrong–Altrin y uno anónimo– por habernos proporcionado valiosos comentarios para mejorar nuestra presentación.
APÉNDICE. SUPLEMENTO ELECTRÓNICO
Información adicional a este artículo se encuentra disponible en el sitio web de la revista <http://rmcg.unam.mx/>, en la tabla de contenido de este número (suplemento electrónico 26–2–02).
REFERENCIAS
Abbey, S., 1979, Reference materials – rock samples SY–2, SY–3, MRG–1: Energy, Mines and Resources Canada, Report 79–35, 66 pp. [ Links ]
Barnett, V., Lewis, T., 1994, Outliers in Statistical Data: New York, John Wiley & Sons, Third edition, 584 pp. [ Links ]
Bevington, P.R., Robinson, D.K., 2003, Data Reduction and Error Analysis for the Physical Sciences: Boston, MA, USA, McGraw–Hill, 320 pp. [ Links ]
Castrellon–Uribe, J., Cuevas–Arteaga, C., Trujillo–Estrada, A., 2008, Corrosion monitoring of stainless steel 304L in lithium bromide aqueous solution using transmittance optical detection technique: Optics and Lasers in Engineering, 46(6), 469–476. [ Links ]
Colombo, F., Pannunzio–Miner, E.V., Gay, H.D., Lira, R., Dorais, M.J., 2007, Barbosalita y lipscombita en Cerro Blanco, Córdoba (Argentina): descripción y génesis de fosfatos secundarios en pegmatitas con triplita y apatita: Revista Mexicana de Ciencias Geológicas, 24(1), 120–130. [ Links ]
Díaz–González, L., Santoyo, E., Reyes–Reyes, J., 2008, Tres nuevos geotermómetros mejorados de Na/K usando herramientas computacionales y geoquimiométricas: aplicación a la predicción de temperaturas de sistemas geotérmicos: Revista Mexicana de Ciencias Geológicas, 25(3), 465–482. [ Links ]
Dixon, W.J., 1951, Ratios involving extreme values: Annals of Mathematical Statistics, 22(1), 68–78. [ Links ]
Dybczynsky, R., 1980, Comparison of the effectiveness of various procedures for the rejection of outlying results and assigning consensus values in interlaboratory programs involving determination of trace elements or radionuclides: Analytica Chimica Acta, 117(1), 53–70. [ Links ]
Farre, M., Martinez, E., Hernando, M.D., Fernandez–Alba, A., Fritz, J., Unruh, E., Mihail, O., Sakkas, V., Morbey, A., Albanis, T., Brito, F., Hansen, P.D., Barcelo, D., 2006, European ring exercise on water toxicity using different bioluminescence inhibition tests based on Vibrio fischeri, in support to the implementation of the water framework directive: Talanta, 69(2), 323–333. [ Links ]
Flanagan, F.J., 1986, Rock reference samples, San Marcos Gabbro, GSM–1 and Lakeview Mountain Tonalite, TLM–1: Geostandards Newsletter, 10(1), 111–119. [ Links ]
Freeman, B.D., Quezado, Z., Zeni, F., Natanson, C., Danner, R.L., Banks, S., Quezado, M., Fitz, Y., Bacher, J., Eichacker, P.Q., 1997, rG–CSF reduces endotoxemia and improves survival during E. coli pneumonia: Journal of Applied Physiology, 83(5), 1467–1475. [ Links ]
Gabrovská, D., Rysová, J., Filová, V., Plicka, J., Cuhra, P., Kubík, M., Barsová, S., 2006, Gluten determination by gliadin enzyme–linked immunosorbent assay kit: Interlaboratory study: Journal of AOAC International, 89(1), 154–160. [ Links ]
Gladney, E.S., 1988, 1987 compilation of elemental concentration data for USGS BIR–1, DNC–1 and W–2: Geostandards Newsletter, 12(1), 63–118. [ Links ]
Gladney, E.S., Roelandts, I., 1988, 1987 compilation of elemental concentration data for USGS BHVO–1, MAG–1, QLO–1, RGM–1, SCo–1, SDC–1, SGR–1, and STM–1: Geostandards Newsletter, 12(2), 253–262. [ Links ]
Gladney, E.S., Roelandts, I., 1990, 1988 compilation of elemental concentration data for CCRMP reference rock samples SY–2, SY–3 and MRG–1: Geostandards Newsletter: 14(3), 373–458. [ Links ]
Gladney, E.S., Jones, E.A., Nickell, E.J., Roelandts, I., 1991, 1988 compilation of elemental concentration data for USGS DTS–1, G–1, PCC–1, and W–1: Geostandards Newsletter, 15(2), 199–396 [ Links ]
Gladney, E.S., Jones, E.A., Nickell, E.J., 1992, 1988 compilation of elemental concentration data for USGS AGV–1, GSP–1 and G–2: Geostandards Newsletter, 16(2), 111–300. [ Links ]
Gómez–Arias, E., Andaverde, J., Santoyo, E., Urquiza, G., 2009, Determinación de la viscosidad y su incertidumbre en fluidos de perforación usados en la construcción de pozos geotérmicos y su aplicación en el campo de Los Humeros, Puebla, México: Revista Mexicana de Ciencias Geológicas, 26(2), 516–529. [ Links ]
Graybeal, D.Y., DeGaetano, A.T., Eggleston, K.L., 2004, Improved quality assurance for historical hourly temperature and humidity: development and application to environmental analysis: Journal of Applied Meteorology, 43(11), 1722–1735. [ Links ]
Grubbs, F.E., 1950, Sample criteria for testing outlying observations: Annals of Mathematical Statistics, 21, 27–58. [ Links ]
Guevara, M., Verma, S.P., Velasco–Tapia, F., 2001, Evaluation of GSJ intrusive rocks JG1, JG2, JG3, JG1a, and JGb1: Revista Mexicana de Ciencias Geológicas, 18(1), 74–88. [ Links ]
Gutiérrez–Ruiz, M., Romero, F.M., González–Hernández, G., 2007, Suelos y sedimentos afectados por la dispersión de jales inactivos de sulfuros metálicos en la zona minera de Santa Bárbara, Chihuahua, México: Revista Mexicana de Ciencias Geológicas, 24(2), 170–184. [ Links ]
Hayes, K., Kinsella, A., Coffey, N., 2007, A note on the use of outlier criteria in Ontario laboratory quality control schemes: Clinical Biochemistry, 40 (3–4), 147–152. [ Links ]
Jensen, J.L., Lake, L.W., Corbett, P.W.N., Goggin, D.J., 2000, Statistics for Petroleum Engineers and Geoscientists: Amsterdam, The Netherlands, Elsevier, 338 pp. [ Links ]
Kasper–Zubillaga, J.J., Zolezzi–Ruiz, H., 2007, Grain size, mineralogical and geochemical studies of coastal and inland dune sands from El Vizcaíno Desert, Baja California peninsula, México: Revista Mexicana de Ciencias Geológicas 24(3), 423–438. [ Links ]
Jafarzadeh, M., Hosseini–Barzi, M., 2008, Petrography and geochemistry of Ahwaz sandstone member of Asmari Formation, Zagros, Iran: implications on provenance and tectonic setting: Revista Mexicana de Ciencias Geológicas, 25(2), 247–260. [ Links ]
Li, X.J., Zhang, H., Ranish, J.A., Aebersold, R., 2003, Automated statistical analysis of protein abundance ratios from data generated by stable–isotope dilution and tandem mass spectrometry: Analytical Chemistry, 75, 6648–6657. [ Links ]
Linkosalo, T., Hakkinen, R., Hari, P., 1996, Improving the reliability of a combined phenological time series by analyzing observation quality: Tree Physiology, 16(7), 661–664. [ Links ]
Madhavaraju, J., Lee, Y.I., 2009, Geochemistry of the Dalmiapuram Formation of the Uttatur Group (Early Cretaceous), Cauvery Basin, Southeastern India: Implications on Provenance and Paleo–redox conditions: Revista Mexicana de Ciencias Geológicas, 26(2), 380–394. [ Links ]
Marroquín–Guerra, S.G., Velasco–Tapia, F., Díaz–González, L., 2009, Evaluación estadística de Materiales de Referencia Geoquímica del Centre de Recherches Pétrographiques et Géochimiques (Francia) aplicando un esquema de detección y eliminación de valores desviados y su posible aplicación en el control de calidad de datos geoquímicos: Revista Mexicana de Ciencias Geológicas, 26(2), 530–542. [ Links ]
Méndez–Ortiz, B.A., Carrillo–Chávez, A., Monroy–Fernández, M.G., 2007, Acid rock drainage and metal leaching on mine waste material (tailings) from a Pb–Zn–Ag skarn deposit: Environmental assessment through static and kinetic laboratory tests: Revista Mexicana de Ciencias Geológicas, 24(2), 161–169. [ Links ]
Miller, J.N., Miller, J.C., 2000, Statistics and Chemometrics for Analytical Chemistry: Essex, England, Prentice Hall, 288 pp. [ Links ]
Nagarajan, R., Madhavaraju, J., Nagendra, R., Armstrong–Altrin, J.S., Moutte, J., 2007, Geochemistry of Neoproterozoic shales of the Rabanpalli Formation, Bhima Basin, Northern Karnataka, southern India: implications for provenance and paleoredox conditions: Revista Mexicana de Ciencias Geológicas, 24(2), 150–160. [ Links ]
Nagarajan, R., Sial, A.N., Armstrong–Altrin, J.S., Madhavaraju, J., Nagendra, R., 2008, Carbon and oxygen isotope geochemistry of Neoproterozoic limestones of the Shahabad Formation, Bhima Basin, Karnataka, southern India: Revista Mexicana de Ciencias Geológicas, 25(2), 225–235. [ Links ]
Obeidat, M.M., Ahmad, F.Y., Hamouri, N.A., Massadeh, A.M., Athamneh, F.S., 2008, Assessment of nitrate contamination of karst springs, Bani Kanana, northern Jordan: Revista Mexicana de Ciencias Geológicas, 25(3), 426–437. [ Links ]
Palabiyik, Y, Serpen, U, 2008, Geochemical assessment of Simav geothermal field, Turkey: Revista Mexicana de Ciencias Geológicas, 25(3), 408–425. [ Links ]
Pandarinath, K., 2009, Clay minerals in SW Indian continental shelf sediments cores as indicators of provenance and paleomonsoonal conditions: a statistical approach: International Geology Review 51(2), 145–165. [ Links ]
Pearson, E.S., Chandra Sekar, C., 1936, The efficiency of statistical tools and a criterion for the rejection of outlying observations: Biometrika, 28, 308–320. [ Links ]
Ram, J.L., Thompson, B., Turner, C, Nechuatal, J.M., Sheehan, H., Bobrin, J., 2007, Identification of pets and raccoons as sources of bacterial contamination of urban storm sewers using a sequence–based bacterial source tracking method: Water Research, 41(16), 3605–3614. [ Links ]
Salleh, S.H., Rosales, E., Flores de la Mota, I., 2007, Influence of different probability based models on oil prospect exploration decision making: A case from Southern Mexico: Revista Mexicana de Ciencias Geológicas, 24(3), 306–317. [ Links ]
Sang, H.Q., Wang, F., He, H.Y., Wang, Y.L., Yang, L.K., Zhu, R.X., 2006, Intercalibration of ZBH–25 biotite reference material utilized for K–Ar and 40Ar–39Ar age determination: Acta Petrologica Sinica, 22(12), 3059–3078. [ Links ]
Schaber, J., Badeck, F.W., 2002, Evaluation of methods for the combination of phenological time series and outlier detection: Tree Physiology, 22(14), 973–982. [ Links ]
Serbest, J.R., Burgess, R.M., Kuhn, A., Edwards, P.A., Cantwell, M.G., Pelletier, M.C., Berry, W.J., 2003, Precision of dialysis (peeper) sampling of cadmium in marine sediment interstitial water: Archives of Environmental Contamination and Toxicology, 45(3), 297–305. [ Links ]
Shekhawat, L.S., Pandit, M.K., Joshi D.W., 2007, Geology and geochemistry of low grade metabasic volcanic rocks from Salumber area in the Palaeoproterozoic Aravalli Supergroup, NW India: Journal of Earth System Science, 116(6), 511–524. [ Links ]
Steele, T.W., Russell, B.G., Goudvis, R.G., Domel, G., Levin, J., 1972, Preliminary report on the analysis of the six NIMROC geochemical standard samples, Randsburg, South Africa: National Institute for Metallurgy Report, 1351, 74. [ Links ]
Steele, T.W., Wilson, A., Goudvis, R., Ellis, P.J., Radford, A.J., 1978, Analyses of the NIMROC reference samples for minor and trace elements, Randsburg, South Africa: National Institute for Metallurgy Report, 1945, 218. [ Links ]
Taylor, B.J., 2000, A statistical analysis of the metallicities of nine old superclusters and moving groups: Astronomy and Astrophysics, 362, 563–579. [ Links ]
Tietjen, G.L., Moore, R.H., 1972, Some Grubbs–type statistics for the detection of several outliers: Technometrics, 14(3), 583–597. [ Links ]
Torres–Alvarado, I.S., Smith, A.D., Castillo–Román, J., en prensa, Sr, Nd, and Pb isotopic and geochemical constraints for the origin of magmas in Popocatépetl volcano (Central Mexico) and their relationship with adjacent volcanic fields: International Geology Review. [ Links ]
Vargas–Rodríguez, Y.M., Gómez Vidales, V., Vázquez–Labastida, E., García–Bórquez, A., Aguilar–Sahagún, G., Murrieta–Sánchez, H., Salmón, M., 2008, Caracterización espectroscópica, química y morfológica y propiedades superficiales de una montmorillonita mexicana: Revista Mexicana de Ciencias Geológicas, 25(1), 135–144. [ Links ]
Vattuone, M.E., Leal, P.R., Crosta, S., Berbeglia, Y., Gallegos, E., Martinez–Dopico, C., 2008, Paragénesis de zeolitas alcalinas en un afloramiento de basaltos olivínicos amigdaloides de Junín de Los Andes, Neuquén, Patagonia, Argentina: Revista Mexicana de Ciencias Geológicas, 25(3), 483–493. [ Links ]
Velasco, F., Verma, S.P., 1998, Importance of skewness and kurtosis statistical tests for outlier detection and elimination in evaluation of Geochemical Reference Materials: Mathematical Geology, 30(1), 109–128. [ Links ]
Velasco, F., Verma, S.P., Guevara, M., 2000, Comparison of the performance of fourteen statistical tests for detection of outlying values in geochemical reference material databases: Mathematical Geology, 32(4), 439–464. [ Links ]
Velasco–Tapia, F., Guevara, M., Verma, S.P., 2001, Evaluation of concentration data in geochemical reference materials: Chemie der Erde–Geochemistry, 61(1), 69–91. [ Links ]
Verma, S.P., 1997, Sixteen statistical tests for outlier detection and rejection in evaluation of international geochemical reference materials: example of microgabbro PM–S: Geostandards Newsletter: Journal of Geostandards and Geoanalysis, 21(1), 59–75. [ Links ]
Verma, S.P., 1998, Improved concentration data in two international geochemical reference materials, (USGS basalt BIR–1 and GSJ peridotite JP–1) by outlier rejection: Geofísica Internacional, 37(3), 215–250. [ Links ]
Verma, S.P., 2005, Estadística Básica para el Manejo de Datos Experimentales: Aplicación en la Geoquímica (Geoquimiometría): México, D. F., Universidad Nacional Autónoma de México, 186 pp. [ Links ]
Verma, S.P., 2009a, Continental rift setting for the central part of the Mexican Volcanic Belt: A statistical approach: The Open Geology Journal, 3, 8–29. [ Links ]
Verma, S.P., 2009b, Evaluation of polynomial regression models for the Student t and Fisher F critical values, the best interpolation equations from double and triple natural logarithm transformation of degrees of freedom up to 1000, and their applications to quality control in science and engineering: Revista Mexicana de Ciencias Geológicas, 26(1), 79–92. [ Links ]
Verma, S.P., Quiroz–Ruiz, A., 2006a, Critical values for six Dixon tests for outliers in normal samples up to sizes 100, and applications in science and engineering: Revista Mexicana de Ciencias Geológicas, 23(2), 133–161. [ Links ]
Verma, S.P., Quiroz–Ruiz, A., 2006b, Critical values for 22 discordancy test variants for outliers in normal samples up to sizes 100, and applications in science and engineering: Revista Mexicana de Ciencias Geológicas, 23(3), 302–319. [ Links ]
Verma S.P., Quiroz–Ruiz, A., 2008, Critical values for 33 discordancy test variants for outliers in normal samples for very large sizes of 1000 to 30,000: Revista Mexicana de Ciencias Geológicas, 25(3), 369–381. [ Links ]
Verma, S.P., Orduña–Galván, L.J., Guevara, M., 1998, SIPVADE: A new computer programme with seventeen statistical tests for outlier detection in evaluation of international geochemical reference materials and its application to Whin Sill dolerite WS–E from England and Soil–5 from Peru: Geostandards Newsletter: Journal of Geostandards and Geoanalysis, 22(2), 209–234. [ Links ]
Verma, S.P., Díaz–González, L., Sánchez–Upton, P., Santoyo, E., 2006, OYNYL: A new Computer Program for Ordinary, York, and New York least–squares linear regressions: WSEAS Transactions on Environment and Development, 2(8), 997–1002. [ Links ]
Verma, S.P., Quiroz–Ruiz A., Díaz–González L., 2008, Critical values for 33 discordancy test variants for outliers in normal samples up to sizes 1000, and applications in quality control in Earth Sciences: Revista Mexicana de Ciencias Geológicas, 25(1), 82–96. [ Links ]
Verma, S.P., Díaz–González, L., Gónzalez–Ramírez, R., 2009, Relative efficiency of single–outlier discordancy tests for processing geochemical data on reference materials and application to instrumental calibrations by a weighted least–squares linear regression model: Geostandards and Geoanalytical Research, 33(1), 29–49. [ Links ]
Zaric, S., Niketic, S.R., 1997, The anisotropic p–effect of the nitro group in ammine–nitro cobalt(III) complexes: Polyhedron, 16(20), 3565–3569. [ Links ]














