Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias geológicas
versión On-line ISSN 2007-2902versión impresa ISSN 1026-8774
Rev. mex. cienc. geol vol.24 no.3 Ciudad de México dic. 2007
Extracción automática de trazas de deslizamientos utilizando un modelo digital de terreno e imágenes de satélite de alta resolución IKONOS. Ejemplo en la Sierra Norte de Puebla, México
Automated extraction of landslide traces using a digital terrain model and IKONOS high–resolution satellite images. An example from Sierra Norte de Puebla, Mexico
Verónica Ochoa–Tejeda1* y Jean–François Parrot2,**
1 Posgrado en Ciencias de la Tierra, Universidad Nacional Autónoma de México, Cd. Universitaria, Delegación Coyoacán, 04510 México D.F., México. * veronikot@yahoo.com.mx
2 Instituto de Geografía, Universidad Nacional Autónoma de México, Cd. Universitaria, Delegación Coyoacán, 04510 México D.F., México. ** parrot@igiris.igeograf.unam.mx
Manuscrito recibido: Diciembre 12, 2006
Manuscrito corregido recibido: Junio 19, 2007
Manuscrito aceptado: Junio 22, 2007
RESUMEN
Los procesos de remoción en masa ocurridos en octubre de 1999 en la Sierra Norte de Puebla, se estudiaron en la región de La Soledad, utilizando imágenes IKONOS de alta resolución y Modelos Digitales de Terreno (MDT). Se desarrolló un algoritmo específico que permitió establecer un modelo de extracción automática de las trazas de los movimientos de terreno. Un estudio estadístico mostró que tres parámetros fueron suficientes para extraer dichas trazas: dos índices de reflectancia extraídos de las imágenes de satélite [índice de vegetación normalizado (Normalized Difference Vegetation Index, NDVI), e índice de brillantez del suelo (Soil Brightness Index, SBI)] y el valor de la pendiente calculada del MDT. Así se redujo a un modelo M (SBI, NDVI, Pendiente). Para caracterizar las formas extraídas que representaron el 75% de los deslizamientos censados en el terreno, se definieron parámetros morfológicos y para calcular su dirección de movimiento se desarrolló un algoritmo. Se observó que existe una relación estrecha entre la dirección E de la mayoría de los procesos de ladera y una de las dos direcciones privilegiadas de las pendientes del MDT de la región en estudio; se supone que esta relación no fue aleatoria y que pudo depender de la exposición de las laderas frente a la llegada de las lluvias torrenciales de 1999. La metodología propuesta en este artículo es una herramienta poderosa para extraer y caracterizar los procesos de remoción en masa a partir de las imágenes de satélite de alta resolución y de los MDT.
Palabras clave: procesos de remoción en masa, extracción automática, IKONOS, modelos digitales de terreno, morfometría, orientación, dirección, Sierra Norte de Puebla, México.
ABSTRACT
Landslides triggered by torrential rainfalls of October 1999 in the Sierra Norte de Puebla region have been studied in La Soledad sector. The present study is based on IKONOS images and a Digital Terrain Model (DTM). A new algorithm has been developed to define a model M that extracts automatically the landslide traces. A statistical analysis of all the parameters extracted from the images and all the primary attributes derived from the DTM, shows that three indicators are enough to extract these traces, in such a way that the model only corresponds to M(SBI, NDVI, Slope). The extracted items represent more than 75% of the landslides observed in the field. A new algorithm is present for estimating the landslide movement directions. Most landslides present an eastern trend that corresponds to one of the two main directions of the DTM slopes, suggesting that it may respond to the direction of rainfall in relation to the slopes exposition when the phenomenon occurred. The proposed method represents a powerful tool to extract, characterize and define the direction of landslide traces.
Key words: landslides, automated extraction, shape characteristics, direction, IKONOS, Digital Terrain Model, Sierra Norte de Puebla, Mexico.
INTRODUCCIÓN
El 4 y 5 de octubre de 1999 se desencadenaron numerosos procesos de ladera en una amplia superficie de la zona montañosa de Puebla, principalmente en la Sierra Norte, debido a las lluvias torrenciales que causo la Depresión Tropical Número 11, la cual se creó en el Golfo de México (Lugo, 2001).
El fenómeno que afectó esta región se estudió desde varios puntos de vista: geomorfológico (Lugo et al., 2005), identificación de los movimientos y de la naturaleza de los materiales involucrados (Capra et al., 2003a y 2003b), tomando en cuenta la inestabilidad de las laderas (Borja–Baeza et al., 2006), la degradación de la cobertura vegetal (Alcántara–Ayala et al., 2006), etc.
Los tipos de procesos de remoción en masa que se generaron fueron principalmente: procesos de caída libre, deslizamientos y flujos que formaron cicatrices o huellas. En general tuvieron forma alargada y estrecha a lo largo de la ladera, excepto algunos cuantos deslizamientos que fueron más anchos que largos. En longitud varían de unos 10 metros a centenas de metros (Lugo et al., 2005).
De manera general, las investigaciones relacionadas con el estudio de los movimientos de remoción en masa requieren del apoyo de varias técnicas y herramientas como son la percepción remota, la extracción de diferentes parámetros del modelo digital de terreno (MDT), el estudio in situ, el acceso a datos preexistentes (mapas geológicos, geomorfológicos, etc.), así como el uso de un sistema de información geográfica (SIG). De hecho, muchas investigaciones recientes se centran principalmente en la percepción remota y los SIG para definir el papel y el peso de cada uno de los parámetros involucrados en la inestabilidad de laderas (Gupta y Joshi, 1990; Rengers et al., 1992; Terlien et al., 1995, Temesgen et al., 2001; De la Ville et al., 2002, Ochoa–Tejeda, 2004).
La resolución actual de los modelos digitales de terreno relacionada con el avance en el campo de la informática, permiten extraer de la superficie del MDT atributos primarios y secundarios (Wilson y Gallant, 2000). Los atributos primarios como la pendiente, el aspecto, la curvatura, la dimensión fractal local (Taud y Parrot, 2005), etc., se extraen directamente de la superficie y también provienen del ajuste de una función de interpolación z =f (x, y) a la superficie del MDT, con la finalidad de calcular las derivadas de dicha función (Moore et al., 1993; Mitasova et al., 1996; Florinsky, 1998). Estos atributos corresponden a diferentes indicadores que describen la morfometría (Jenson y Domingue, 1988; Dikau, 1989; Dymond et al., 1995; Giles, 1998; Borrough et al., 2000). Los parámetros secundarios provienen de la interacción de los atributos primarios, la red fluvial y/o los datos externos (insolación, espesor del suelo, datos climáticos, etc.) y dan como resultado información sobre la humedad y la degradación de los suelos, las tazas de erosión, la densidad de disección, entre otros.
Por otro lado, las imágenes de satélite de alta resolución IKONOS dan información detallada de la superficie terrestre. Sus propiedades espectrales son: una banda pancromática (0.45–0.90 µ) con resolución espacial de 1 m, cuatro bandas multiespectrales, de las cuales tres bandas son del visible (azul 0.45–0.52 µ, verde 0.52–0.60 µ y rojo 0.63–0.69 µ) y una banda del infrarrojo (0.76–0.90 µ); dichas bandas tiene una resolución espacial de 4 m.
La zona en estudio queda comprendida entre las provincias geológico–geomorfológicas Sierra Madre Oriental y el límite norte de la porción oriental de la Faja Volcánica Transmexicana. Geográficamente se localiza entre las coordenadas 19°53' y 20°00' de latitud N y las coordenadas 97°25' y 97°32' de longitud W (Figura 1).
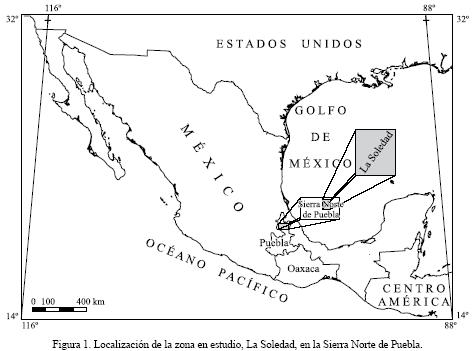
Las principales unidades geológicas van del Paleozoico al Cuaternario (Ángeles–Moreno y Sánchez–Martínez, 2002). En las unidades del Paleozoico se distinguen dos complejos miloníticos: La Soledad y Xucayucan que se divide en tres subunidades litológicas (Chicuaco, Cozolexco y El Mirador). Se presenta un contacto discordante entre el complejo y las unidades sobreyacentes que consisten en: Formación Huayacocotla (Jurásico Inferior), Formación Tenexcate (Jurásico Medio), formaciones Tamán y Pimienta (Jurásico Superior) y Formación Tamaulipas [Cretácico Inferior (Neocomiano)]. El Plioceno (Formación Teziutlán) corresponde a derrames andesíticos discordantes sobre las formaciones anteriores y, por último, las unidades del Cuaternario se constituyen de tobas andesíticas y de las ignimbritas de la Formación Xaltipan (productos de la caldera de los Humeros). Además, existen afloramientos probablemente terciarios de diques o sills riolíticos (Figura 2).
En la presente investigación se utilizaron los datos de las imágenes de satélite IKONOS, así como un MDT para extraer de manera automática las trazas dejadas por los procesos de remoción en masa de 1999, para definir sus características morfológicas y sus orientaciones.
METODOLOGÍA
En primer lugar se tomó en cuenta la ubicación de todos los deslizamientos censados por el servicio de protección civil del estado de Puebla poco después del evento; también se estudiaron en el terreno los rasgos de dichos deslizamientos (forma, extensión, tipo, pendiente, material involucrado, uso del suelo, etc.). Se utilizaron imágenes de alta resolución IKONOS adquiridas en diciembre de 2000. El área que tienen las imágenes IKONOS por cada escena de toma es de 13×13 km; la altitud del sensor es de 681 km y la escala de representación para las imágenes del visible e infrarroja es de 1:20,000 y para la imagen pancromática es de 1:10,000.
En el presente trabajo se eligió una zona de 2270 columnas y 2374 líneas (11.350 km × 11.870 km) que se redimensionó para sobreponerse al Modelo Digital de Terreno (MDT) que tiene una resolución de 5 metros, máximo de resolución que se puede obtener utilizando curvas de nivel cada 20 metros sin generar artefactos. Este MDT se generó digitalizando las curvas de nivel de la hoja Teziutlán E14B15 de INEGI (1999), escala 1:50,000 aplicando la metodología descrita en el manual de Parrot y Ochoa–Tejeda (2004), así como los algoritmos correspondientes. Estos programas y todos los que se utilizaron en este trabajo se desarrollaron en C++ con el software Borland C++ en una plataforma PC Windows XP.
La extracción de las zonas donde ocurrieron los procesos de ladera a partir de dichas imágenes IKONOS y de los atributos primarios provenientes del MDT, consistió en la definición de un modelo de extracción capaz de tomar en cuenta las características de la forma estudiada y sus relaciones espaciales. El modelo M(α, β, γ,...., ω) se basó en definir los parámetros α, β, γ,...., ω que jugaban un papel eficaz para extraer las trazas de los deslizamientos en función de sus rasgos morfológicos. Entre ellos, se utilizaron dos índices de reflectancia: el índice de vegetación normalizado (Normalized Difference Vegetation Index, NDVI), el índice de brillantez del suelo (Soil Brightness Index, SBI), y también diversos atributos primarios extraídos de la superficie del MDT.
Parámetros utilizados
Índices de reflectancia
Antes de calcular los índices de reflectancia, se hizo un pretratamiento para normalizar entre 0 y 255 los valores de las bandas, para evitar los agrupamientos de valores que se originan al hacer una elongación clásica (streching). Para ello, se desarrolló un algoritmo que elonga la escala de valores de tonos de gris sin crear espacios libres en el histograma resultante.
El algoritmo es el siguiente:
V(i, j) = [(P (i, j) – Min)/(Max – Min)] × 255
donde
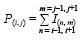
cuando se utiliza una conectividad 8 o
P(i, j) = Ii, j) + I(i–1, j) + I(i, j+1)+ I(i+1, j)+I(i, j–1)
en el caso de la conectividad 4.
I corresponde al valor inicial de los píxeles involucrados; P es el resultado de la suma del píxel central y de sus vecinos (4 u 8); V el valor del píxel normalizado resultante; Min el mínimo de los valores de P y Max el máximo de los valores de P.
Después de normalizar las imágenes IKONOS se realizó un estudio de correlación de varios índices de reflectancia [Normalized Difference Vegetation Index (NDVI), Soil Adjust Vegetation Index (SAVI), Green Vegetation Index (GVI), Difference Vegetation Index (DVI), Soil Brigthness Index (SBI), Brigthness (B)] para elegir los que mostraban mayor información en la localización e identificación de las trazas de los procesos de ladera.
La mayoría de los índices de reflectancia se definieron a partir de las bandas espectrales de los satélites Landsat; en el caso de TM y ETM+, los valores espectrales de las bandas son los siguientes: 0.45–1.515 µm para la banda 1 (azul), 0.525–0.605 µm para la banda 2 (verde), 0.63–0.69 µm para la banda 3(rojo), 0.76–0.90 µm para la banda 4 (infrarrojo cercano), 1.55–1.75 µm para la banda 5 (infrarrojo medio), 2.08–2.35 µm para la banda 7 (infrarrojo lejano). Existe una correspondencia estrecha entre los valores espectrales de las cuatro bandas del satélite IKONOS (0.45–0.52 µm para el azul, 0.52–0.60µm para el verde, 0.63–0.69 µm para el rojo y 0.76–0.90 µm para el infrarrojo cercano), y las bandas 1, 2, 3 y 4 del satélite ETM+, lo que permite utilizar las mismas formulas para calcular diversos índices.
Se determinó (ver párrafo Extracción de los procesos de remoción en masa) que los dos más relevantes fueron el índice normalizado de vegetación (NDVI) y el índice de brillantez del suelo (SBI).
Índice de vegetación normalizado (NDVI)
El índice de vegetación normalizado corresponde a una transformación no lineal de las bandas del visible rojo (R) e infrarrojo cercano (NIR) (Rouse et al., 1973; Jackson et al., 1983; Tucker et al., 1991). El NDVI es el resultado de la diferencia entre los valores de estas bandas (R, 0.63–0.69 µm; NIR, 0.76–0.90 µm) y corresponde a una medida del vigor de la vegetación en cuanto a contenido de humedad (Figura 3a). Los valores del NDVI están comprendidos entre –1 y +1 (sobre las imágenes de 8 bits se normalizó entre 0 y 255) y se calcula como:

donde: (i, j) son los coordenadas del píxel en estudio.
De hecho, como lo demostraron Guyot y Gu (1994), para evitar la subestimación de los valores de reflectancia de la banda roja, se necesita ponderar estos valores de la manera siguiente:

en el caso de las imágenes Landsat TM y ETM+ y también para las imágenes IKONOS.
Índice de brillantez del suelo (SBI)
El índice de brillantez del suelo proporciona información sobre las áreas potencialmente erosionadas y corrobora la información proveniente del NDVI. Existen varios índices de brillantes del suelo como el Tasseled Cap Transformation Brightness Index (BI) de Crist y Cicone (1984a y 1984b) que adaptaron a seis bandas el concepto inicial de Kauth y Thomas (1976) desarrollado a partir de los datos MSS (Landsat Multispectral Scanner), el Brightness (B) y el Soil Brightness Index (SBI), entre otros. Estos índices se calculan a partir de las imágenes Landsat TM con las siguientes ecuaciones:

donde TM1 a TM7 son las bandas 1, 2 , 3, 4, 5 y 7 respectivamente. Este índice no se puede utilizar en el caso de las imágenes IKONOS que no tienen bandas correspondientes al infrarrojo medio y lejano.

es decir la banda roja y la banda infrarroja cercana en el caso de Landsat TM lo que corresponde a las bandas 3 y 4 de IKONOS.
y

donde B2 es la banda verde, B3 la banda roja y B4 la banda del infrarrojo cercano, tanto para Landsat ETM+ como para IKONOS.
El SBI (Figura 3b) se utiliza generalmente para mostrar las variaciones cromáticas de los suelos y por esta razón es muy útil para identificar los rasgos de los suelos.
Atributos primarios y secundarios extraídos del modelo digital de terreno (MDT)
Se calcularon a partir del MDT (Figura 4) diferentes atributos primarios provenientes directamente de su superficie (pendiente, aspecto, concavidad, convexidad, curvatura, rugosidad y dimensión fractal local).

La evaluación del papel que juegan respectivamente todos estos atributos (ver Extracción de los procesos de remoción en masa) mostró que el uso de la pendiente es suficiente para extraer las trazas de los movimientos de ladera. Por otro lado, aunque no directamente relacionado con el proceso de extracción, el aspecto (es decir la dirección de las pendientes entre 0° y 359°) se calculó porque sirve para definir las relaciones existentes entre las orientaciones de las pendientes y la orientación de las trazas. Por esta razón se presenta aquí solamente el cálculo de estos dos parámetros.
Existen diferentes algoritmos que deducen la pendiente y la orientación a través del cálculo de las normales a la superficie estudiada; la pendiente corresponde al ángulo entre la normal a la superficie y la normal al plano horizontal y la orientación a la proyección de la normal a la superficie sobre el plano horizontal. Algunos autores (Peet y Sahota, 1985; Philipp y Smadja, 1994; Cocquerez y Philipp, 1995) propusieron crear una aproximación local en un punto P, por medio de superficies bicuadráticas. Schweizer (1987) propone una expresión simplificada de la normal que corresponde a la suma de las cuatro normales (n1, n2, n3, n4) de las cuatro superficies que encierran un nudo P. En este caso, la expresión de la superficie local centrada en un punto P de coordenadas (0,0) se hace tomando una forma cuadrática
z = αx2 + by2 + dxy + gx + hy + j
El gradiente de la superficie está definido por:

También como se hizo en el presente trabajo, el cálculo de la pendiente y de su orientación (en el sentido de las manecillas del reloj con el origen 0° al norte), puede utilizar el detector de bordes de Sobel (González y Wintz, 1977; Rosenfeld y Kak, 1981) utilizando las dos matrices de filtraje siguientes:

donde A es la altitud de los píxeles de las matrices y p es el tamaño del píxel.
Así, el valor de la pendiente se calcula de la siguiente manera:
pendiente = (arctan 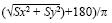 �
�
Por otro lado, la dirección de la pendiente es igual a:
dirección = arctan(–Sx, Sy) × (180/π)
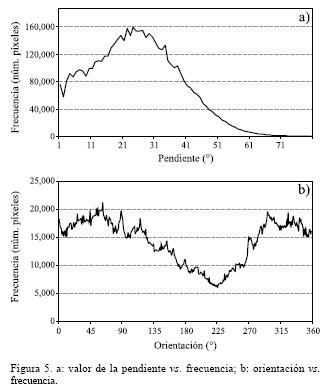
y, con origen 0 en dirección del norte y sentido inverso al sentido trigonométrico: dirección = 180 – dirección. Los histogramas de la pendiente y de la dirección se presentan en la Figura 5.
Extracción de los procesos de remoción en masa
En primer lugar se definieron zonas de entrenamientos cartografiando en el terreno los principales tipos de movimiento de ladera, tomando en cuenta el mecanismo y el material involucrado. Asimismo, se pudo determinar cuales fueron los parámetros provenientes de las imágenes de satélite o del MDT que caracterizan las trazas de los deslizamientos presentes en las zonas de entrenamiento.
Las diferentes pruebas realizadas de esta manera mostraron que el SBI, el NDVI y la pendiente son suficientes para extraer de manera automática las trazas de los procesos de remoción en masa, de tal manera que el modelo de extracción M utilizado se redujo a tres parámetros esenciales (SBI, NDVI y pendiente). En el caso de los índices, el NDVI no permite caracterizar por sí solo los rasgos investigados que no corresponden solamente a una ausencia de vegetación activa, sobre todo debido a que la imagen IKONOS fue tomada trece meses después del evento y a que se observó localmente una reactivación de la vegetación. Por lo cual, se necesita tomar en cuenta los valores del SBI.
Por otro lado, también se obtiene una primera estimación de los rangos de valores de cada parámetro dentro de las zonas de entrenamiento. Una variación regular del abanico de estos valores permite establecer con precisión el umbral de cada parámetro en función de la respuesta al nivel de toda la imagen.
Finalmente se obtuvo la siguiente segmentación. Para el SBI (histograma de la Figura 6a), se definió un único corte dando dos segmentos: segmento 1 de 0 a 133 y segmento 2 de 134 a 255, lo que corresponde a los suelos desnudos. En el caso del NDVI (histograma de la Figura 6b), se definieron cuatro segmentos: segmento 1 de 0 a 29 correspondiente a los cuerpos de agua, segmento 2 de 30 a 140 donde se ubican las trazas de los procesos de ladera, segmento 3 de 141 a 165 que corresponde a la vegetación poco densa y segmento 4 de 166 a 255 correspondiente a la vegetación activa. Se definieron tres segmentos en el caso de la pendiente (histograma de la Figura 6c): segmento 1 de 0° para las zonas horizontales y planas, segmento 2 de 1° a 14°, zonas de pendiente ligera y finalmente segmento 3 de 15° a 80°, valores relacionados con la presencia de los procesos de ladera, tomando en cuenta las observaciones hechas en el terreno.

La extracción se basa sobre estos valores. Como se muestra en la Tabla 1, se hizo una clasificación utilizando un programa que calcula todos los cruces posibles que generan la segmentación de los diversos parámetros definidos anteriormente. El algoritmo atribuye un código a cada combinación de los segmentos de cada parámetro e indica el número total de píxeles. En el presente caso se obtuvieron 24 códigos que corresponden a todas las combinaciones que generan los segmentos siguiendo el orden SBI, NDVI, Pendiente (por ejemplo, el código 1 corresponde a la combinación SBI 1 – NDVI 1 – Pendiente 1, el código 2 a la combinación 1–1–2, el código 3 a la combinación 1–1–3, el código 4 a la combinación 1–2–1, etc.)
El tema etiquetado con el código 18 pertenece al segmento 2 del SBI (134–255), al segmento 2 del NDVI (30–140) y al segmento 3 de la pendiente (>14°). La combinación que presenta el código 18 corresponde a las características definidas para los procesos de ladera en la zona en estudio.
Definición y extracción de algunos parámetros morfológicos
La forma de las trazas de los procesos de ladera extraídas como se presentó anteriormente se analizó definiendo los siguientes parámetros morfológicos. Existen parámetros que se relacionan directamente con la forma en estudio, es decir, el componente de píxeles conectados que describe una traza: por ejemplo, la superficie S, el perímetro P, las relaciones entre ambos, así como la presencia de huecos, lo que permite definir un índice de porosidad.
La manera más simple para calcular la superficie consiste en medir el número total de píxeles Nbp que se encuentran en el componente de píxeles; pero también se puede considerar que la superficie
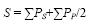
donde PS son los píxeles que pertenecen a la superficie y PP los píxeles que describen el perímetro (Pratt, 1978). La superficie en m2 o km2 se obtiene multiplicando S por la superficie del píxel. Existen también medidas más precisas de la superficie que toman en cuenta la configuración que describe PP y los píxeles vecinos para definir la porción del píxel que se debe realmente tomar en cuenta para calcular la superficie (Parrot, 2007).
El perímetro P se expresa de dos maneras: a) el número total de píxeles (Np) que bordean la forma, o b) la longitud real (Lp) calculada en función de la configuración que presentan los píxeles que pertenecen a este perímetro. Se pueden establecer relaciones entre estos dos parámetros: por ejemplo, el radio perímetro/superficie
ρ = (Np/Nbp)×100
y el índice de circularidad
Ï–
También, la noción de porosidad representa un rasgo importante para caracterizar conjuntos de píxeles como se presentan a veces en los procesos de ladera. Por eso, se calcula el número de píxeles Ph correspondientes a los huecos que se encuentran en la forma y este parámetro es igual a:
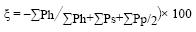
donde Ps y Pp corresponden a todos los píxeles que describen la forma.
Otra manera de describir las formas consiste en comparar la forma estudiada y formas simples tales como el rectángulo, el círculo, el cuadrado o la región convexa más pequeña que circunscribe la forma. En la mayoría de los casos, estos cálculos requieren definir el Centro de Gravedad (CG) de la forma y también definir el eje principal (EP) del objeto.
El eje principal de una forma es una línea que pasa por el Centro de Gravedad (CG). Con esta información, se puede calcular el ancho y el largo de la forma, la relación existente entre estos valores, así como el rectángulo donde se inscribe la forma.
La definición de la zona convexa se basa en la noción de la marcha de Jarvis (Akl y Toussaint, 1978), un algoritmo sencillo pero eficaz que dibuja el perímetro de esta zona (Figura 7). Al inicio, se busca el píxel de la forma que se ubica en la esquina inferior izquierda. Este punto, p1, representa el punto de origen de la zona convexa. Se calculan las distancias y las direcciones (sentido trigonométrico) entre el punto de origen y todos los píxeles del perímetro de la forma en estudio. Se buscan entonces las direcciones que tiene el ángulo mínimo y dentro de ellas se toma en cuenta la distancia máxima. Así se define el punto p2 que describe la zona convexa y este punto a su vez corresponde al punto inicial del siguiente tratamiento. Así se van calculando las distancias y los ángulos entre este nuevo punto inicial y todos los píxeles del perímetro. El siguiente punto de la zona convexa corresponde al ángulo mínimo pero superior al anterior y a la distancia máxima. Se repite la operación hasta encontrar el punto de origen. Todas las 98 formas convexas así obtenidas se presentan en la Figura 8 y cada una tiene su propia etiqueta.
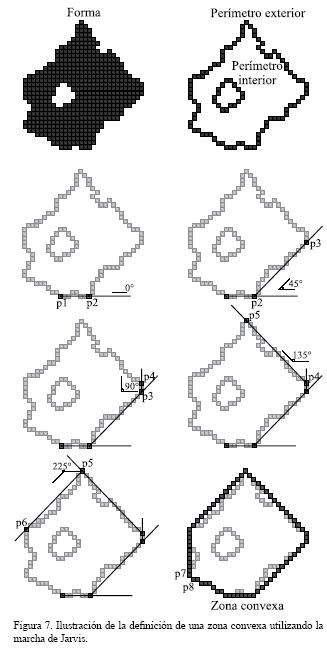

La superficie de la zona convexa Sc (o el número total de píxeles Ntc de esta zona) y su perímetro Pc permiten calcular diferentes parámetros, tales como por ejemplo las relaciones S/Sc, Nbp/Ntc (dos índices de convexidad), Pp/Pc (convexidad del perímetro o coeficiente de rugosidad de la forma) o Ph/Ntc (porosidad de la zona convexa).
Estos valores se encuentran en la Tabla 2 para las 30 primeras formas etiquetadas.
Cálculo de la dirección de los deslizamientos
La dirección de los procesos de ladera corresponde a la dirección del máximo de la pendiente dentro de la superficie de arrastre generada por el proceso de ladera. Para ello se requiere en primer lugar definir el centro de gravedad de la forma en estudio.
El centro de gravedad (CG) de coordenadas Xc, Yc y los momentos de segundo orden μxx , μyy y μxy se definen como sigue:

Nbp es el número de píxeles del objeto y Xi Yi las coordenadas del píxel i.
El eje principal EP que pasa por el centro de gravedad CG es igual a:
tg(2α) = 2μxy/(μyy – μxx) si (μyy – μxx) ≠ 0.
Cuando la diferencia entre μxx y μyy es igual a cero, el objeto presenta una simetría de revolución sin orientación privilegiada. La orientación de EP se expresa en grados (desde 0° hasta 180°, correspondiendo 0° al norte) en el sentido de las manecillas del reloj.
También se pueden calcular todas las distancias entre CG y los píxeles del contorno; en este caso, EP corresponde a la perpendicular a la línea recta que une CG de coordenadas ic, jc y el píxel (ip, jp) más cercano que pertenece al contorno. La orientación geográfica (O) del EP se calcula como sigue:
OT = arctan (dj, di) (180/π)
donde, dj = jc–jp y di = ic–ip. El valor trigonométrico OT se normaliza entre 0° y 360°, y su correspondencia geográfica (sentido de las manecillas del reloj con origen en el Norte) O es igual a: O = 90 – OT (con una normalización entre 0° y 360°). Por otro lado, cuando O > 180, O = O – 180 y cuando O = 180, O = 0.
El EP se interseca con el perímetro de la forma en dos puntos. En el espacio trigonométrico las dos direcciones D1 y D2 que permiten calcular las intersecciones del EP con el contorno son respectivamente iguales a: D1 = OT y D2 = D1 + 180 (con una normalización 0°, 360°). D1 genera una línea recta que va de ic, jc hasta id1, jd1, donde
id1 = ic + (–sin(D1×(π/180)) × dist),
jd1 = jc + (cos(D1×(π/180)) × dist)
y dist es una distancia generalmente igual a Max(nb_lin, nb_col); nb_lin y nb_col corresponden respectivamente al número de líneas y al número de columnas de la imagen en estudio. El punto (ia, ja) es el punto donde la línea recta sale de la forma en estudio.
A su vez, siguiendo el mismo procedimiento, D2 genera la segunda línea recta que permite buscar la segunda intersección entre EP y el contorno. La altitud relativa de estos dos puntos (D1 y D2) permite definir un mínimo (Amin) y un máximo (Amax). La dirección D del deslizamiento corresponde a la línea recta que une CG y Amin.
Estos valores se reportan en la Tabla 3 para las 30 primeras formas etiquetadas. También se indica en esta tabla el valor del ancho y el valor del largo, así como la relación ancho/largo.

RESULTADOS Y DISCUSIÓN
Extracción automática de las trazas de los procesos de ladera
Dentro de los 24 códigos que genera el cruzamiento de los segmentos definidos para hacer el umbral de las imágenes SBI, NDVI, y Pendiente, los píxeles que tienen el código 18 correspondiente a la combinación 2–2–3, es decir el segmento 2 de la banda 1 (SBI), el segmento 2 de la banda 2 (NDVI) y el segmento 3 de la banda 3 (pendiente), corresponden a los rangos radiométricos que caracterizan las trazas de los movimientos de ladera en la zona en estudio.
Se observa que el 75% de las trazas extraídas automáticamente corresponden a la ubicación de los movimientos de ladera censados poco después del evento. El 25% restante se debe por un lado a que se extrajeron solamente trazas que tienen más de 15 metros de ancho por 35 metros de largo y, por otro lado, a la reactivación de la vegetación durante el año que transcurrió antes de tomar la imagen, especialmente en el caso de los deslizamientos que removilizaron materiales de coluvión.
Parámetros morfológicos
Los parámetros morfológicos, así como sus relaciones entre sí permiten definir con precisión los rasgos de las diferentes trazas extraídas de movimiento de ladera. Se presentan en este apartado solamente dos diagramas que ilustran algunas de las características de estas trazas. El diagrama ancho/largo (Figura 9a) revela que, excepto dos individuos, los pequeños deslizamientos forman un grupo denso esencialmente de tipo lineal; la relación ancho/largo va de 0.2 a 0.8 con un promedio de 0.55; 40% de las trazas presentan una relación ancho/largo inferior o igual a 0.5 y 24% de ellas tienen una relación inferior o igual a 0.4. Existen dos deslizamientos importantes: el primero (símbolo A en la Figura 8), que corresponde a un proceso de ladera de tipo rotacional que se desencadenó en la región de San José Chachaltzin, tiene una forma casi circular (relación ancho/largo de 0.82) con un tamaño de 238 m de ancho y 289 de longitud, y el segundo (símbolo B en la Figura 8), localizado al norte del poblado El Dos, es un deslizamiento lineal con una dimensión de 90 m de ancho y 480 de longitud; su relación ancho /largo es de 0.18.

El segundo diagrama (Figura 9b) establece la relación existente entre la convexidad RCI (es decir la relación entre el perímetro P de la forma y el perímetro Pc de la zona convexa) y la superficie S. Entre menos es el valor de RCI, más irregular será la forma. La mayoría de los procesos de remoción en masa se agrupan en la zona en donde hay pequeñas formas casi regulares; el centro de gravedad de la nube de puntos de dicho grupo tiene un valor de RCI igual a 75, es decir que estas formas no son totalmente convexas. Los dos deslizamientos grandes se caracterizan, en el caso del individuo B por un RCI de 75 como los deslizamientos del grupo anterior, pero en el caso del individuo A se nota una gran irregularidad de sus contornos en relación con el carácter heterogéneo de los materiales arrastrados durante el deslizamiento de tipo rotacional.
Dirección de los deslizamientos
Se calculó la orientación y la dirección de las trazas de los procesos de ladera extraídas a partir de la zona convexa que las encierra. El diagrama de la Figura 10a ilustra la relación que existe entre la dirección y la orientación. Globalmente, la mayoría de los puntos analizados se encuentran en la línea de tendencia inferior, con una nube de puntos ubicada entre 75° y 110° de orientación.

La visualización de este comportamiento en el diagrama de la Figura 10b muestra que la mayoría de las direcciones de las trazas de los procesos de remoción en masa se encuentran en el rango 70°–110°, es decir en dirección al Este. Se debe observar que esta dirección de procesos de ladera corresponde a una de las dos direcciones privilegiadas de la totalidad de las pendientes del MDT (ver la curva bimodal de la Figura 5b), sin que el promedio de la pendiente de estas dos direcciones sea diferente.
CONCLUSIONES
La definición de un modelo de extracción basado en tres parámetros determinantes, los dos primeros provenientes de las imágenes de satélite IKONOS (índices de vegetación normalizada y de brillantez del suelo) y la pendiente calculada a partir del MDT, permite extraer de manera automática las trazas de la mayoría de los procesos de ladera que ocurrieron en la Sierra Norte de Puebla en 1999. Este modelo se obtuvo a partir de un estudio estadístico de todos los parámetros susceptibles que juegan un papel en la extracción de las trazas que dejaron en el paisaje los procesos de remoción en masa. Se demuestra que solamente tres parámetros son necesarios y suficientes para conseguir esta extracción. Por otro lado, la definición de parámetros morfológicos permite clasificar y caracterizar los deslizamientos en estudio, comprobando los resultados obtenidos en el terreno.
Finalmente, el estudio de la dirección que presentan las trazas de los procesos de ladera extraídas a partir del modelo de extracción, mostró que la mayoría de éstas tienen una dirección este–noreste (70°–110°), que corresponde a unas de las direcciones privilegiadas de la zona en estudio donde la orientación principal de la red fluvial es norte–sur. Asumimos que este fenómeno no es aleatorio y que puede resultar de la acción y de la orientación de las lluvias como factor desencadenante de los movimientos de ladera, por lo que se necesitaría tomar en cuenta los factores meteorológicos.
La metodología propuesta en este artículo se revela como una herramienta poderosa para extraer y caracterizar las trazas de los procesos de remoción en masa en las imágenes de satélite de alta resolución y con la ayuda de los modelos digitales de terreno.
AGRADECIMIENTOS
Los autores agradecemos a Luca Ferrari, Lucia Capra y un arbitro anónimo por su colaboración en la revisión del manuscrito y sus atinadas observaciones.
REFERENCIAS
Akl, S.G., Toussaint, G., 1978, Efficient convex hull algorithms for pattern recognition applications, en Proceedings of the 4th International Joint Conference on Pattern Recognition, Kyoto, Japan, 483–487. [ Links ]
Alcántara–Ayala, I., Esteban–Chávez, O., Parrot, J.–F., 2006, Landsliding related to land–cover change: A diachronic analysis of hillslope instability distribution in the Sierra Norte, Puebla, Mexico: CATENA, 65, 152–165. [ Links ]
Ángeles–Moreno, E., Sánchez–Martinez, S., 2002, Geología, Geoquímica y Geología Estructural de las Rocas del Basamento del macizo de Teziutlan, Estado de Puebla: México, Universidad Nacional Autónoma de México, Facultad de Ingeniería, Tesis de licenciatura, 105 p. [ Links ]
Borja–Baeza, R.C., Esteban–Chávez, O., Marcos–López, J., Garnica–Peña, R.J., Alcántara–Ayala, I., 2006, Slope instability on pyroclastic deposits: landslide distribution and risk mapping in Zacapoaxtla, Sierra Norte de Puebla, México: Journal of Mountain Science, 3(1), 1–19. [ Links ]
Borrough, P.A., Van Gaans, P.F.M., MacMillan, R.A., 2000, High–resolution landform classification using fuzzy k–means: Journal to Fuzzy Sets and Systems, 113, 37–52. [ Links ]
Capra, L., Lugo–Hubp, J., Borseli, L., 2003a, Mass movements in tropical volcanic terrains: the case of Teziutlan, Mexico: Engineering Geology, 69, 359–379. [ Links ]
Capra, L., Lugo–Hubp, J., Dávila–Hernandez, N., 2003b, Fenómenos de remoción en masa en el poblado de Zapotitlán de Méndez, Puebla: relación entre litología y tipo de movimiento: Revista Mexicana de Ciencias Geológicas, 20(2), 95–106. [ Links ]
Cocquerez, J–P., Philipp, S., 1995, Analyse d'images: filtrage et segmentation: Paris, Ed. Masson, 460 p. [ Links ]
Crist, E.P., Cicone, R.C., 1984a, A physically–based transformation of thematic mapper data–The TM Tasseled Cap: IEEE Transactions on Geoscience and Remote Sensing, 22(3), 256–263. [ Links ]
Crist, E.P., Cicone, R.C., 1984b, Application of the tasseled Cap concept to simulated thematic mapper data: Photogrammetric Engineering and Remote Sensing, 343–352. [ Links ]
De La Ville, N., Chumaceiro–Diaz, A., Ramirez, D., 2002, Remote sensing and GIS technologies as tools to suppot sustainable magagement of areas devastated by landslides: Evironment, Development and Sustaintainability, 4(2), 221–229. [ Links ]
Dikau, R., 1989, The application of a digital terrain model to landform analysis in geomorphology, in Raper, J. (ed.), Three–Dimensional applications in Geographic Information Systems: London, Taylor & Francis, 51–78. [ Links ]
Dymond, J.R., Derose, R.C., Harmsworth, G.R., 1995, Automated mapping of land components from digital elevation data: Earth Surface Processes and Landforms, 20, 131–137. [ Links ]
Florinsky, I.V., 1998, Accuracy of local topographic variables derived from digital elevation models: International Journal of Geographical Information Science, 12, 47–62. [ Links ]
Giles, P.T., 1998, Geomorphological signatures: classification of aggregated slope unit objects from digital elevation and remote sensing data: Earth Surface Processes and Landforms, 20, 581–594. [ Links ]
González, R.C., Wintz, P., 1977, Digital Image Processing: Adisson–Wesley, 503 p. [ Links ]
Gupta, R.P., Joshi, B.C., 1990, Landslide hazard zoning using the GIS approach –A case study from th Ramganga catchment, Himalayas: Engineering Geology, 28, 119–131. [ Links ]
Guyot, G., Gu, X.F., 1994, Effect of radiometric corrections on NDVI determined from SPOT–HRV and Landsat–TM data: Remote Sensing of Environment, 49, 169–180. [ Links ]
Instituto Nacional de Estadistica Geográfica e Informática (INEGI), 1999, Carta topográfica Teziutlán E14B15, esc. 1:50,000: Aguascalientes, Ags., Instituto Nacional de Estadistica Geográfica e Informática, 1 mapa. [ Links ]
Jackson, R.D., Slater, P.N., Pinter, P.J., 1983, Discrimination of growth and water stress in wheat by various vegetation indices through clear and turbid atmospheres: Remote Sensing of the Environment, 15, 187–208. [ Links ]
Jenson, S.K., Domingue, J.O., 1988, Extracting topographic structure from digital elevation data for geographic information system analysis: Photogrammetric Engineering and Remote Sensing, 54(11), 1593–1600. [ Links ]
Kauth, R.J., Thomas, G.S., 1976, The tasseled Cap –A graphic description of the spectral –Temporal Development of Agricultural Crops as Seen by LANDSAT, en Proceedings of the Symposium on Machine Processing of Remotely Sensed Data: Indiana, Purdue University of West Lafayette, 4B–41–4B–51. [ Links ]
Lugo, H.J., 2001, Los conceptos geomorfológicos en la obra de Ezequiel Ordóñez (1867–1950): Revista Mexicana de Ciencias Geológicas, 18(1), 89–102. [ Links ]
Lugo, J., Zamorano, J.J., Capra, L., Inbar, M., Alcántara–Ayala, I., 2005, Los procesos de remoción en masa en la Sierra Norte de Puebla, octubre de 1999, causas y efectos: Revista Mexicana de Ciencias Geológicas, Instituto de Geología, 22(2), 212–228. [ Links ]
Mitasova, H., Hofierka, J., Zlocha, M., Iverson, L.R., 1996, Modeling topographic potential for erosion and deposition using GIS: International of Geographical Information Systems, 10, 611–618. [ Links ]
Moore, I.D., Lewiss, A., Gallant, J.C., 1993, Terrain attributes: estimation methods and scale effects, en Jakeman, A.J., Beck, M.B., McAleer, M.J. (eds.), Modeling Change in Environmental Systems: New York, Willey, 189–214. [ Links ]
Ochoa–Tejeda, V., 2004, Propuesta metodológica para el estudio de la inestabilidad de laderas a partir de los MDT y la Percepción Remota. Sierra Norte de Puebla: México, Universidad Nacional Autónoma de México, Facultad de Filosofía y Letras, Tesis de Maestría, 209 p. [ Links ]
Parrot, J.–F., 2007, Tri–dimensional parameterisation: an automated treatment to study the evolution of volcanic cones: Géomorphologie, 3, 37–47. [ Links ]
Parrot, J.–F., Ochoa–Tejeda, V., 2004, Generación de Modelos Digitales de Terreno raster. Método de digitalización: México, D.F., Universidad Nacional Autónoma de México, Instituto de Geografía, Geografía para el Siglo XXI, Serie Textos universitarios, 31 p. [ Links ]
Peet, F.G., Sahota, T.S., 1985, Surface curvature as a measure of image texture: IEEE Transactions on Pattern Analysis and Machine Intelligence, 7(6), 734–738. [ Links ]
Philipp, S., Smadja, M., 1994, Approximation of granular textures by quadric surfaces: Pattern Recognition, 27(8), 1051–1063. [ Links ]
Pratt, W.K., 1978, Digital Image Processing: New York, Ed. Wiley, 750 p. [ Links ]
Rengers, N., Soeters, R., Westen, C.J.V., 1992, Remote sensing and GIS applied to mountain hazard mapping: Episodes, 15(1), 36–45. [ Links ]
Rosenfeld, A., Kak, A.C., 1981, Digital Picture Processing, v. 1 y 2.: London, Academic Press, 349 p. [ Links ]
Rouse, J.W. Jr., Haas, R.H., Schell, J.A., Deering, D.W., 1973, Monitoring vegetation systems in the Great Plains with ERTS, en Proceedings of the Third Earth Resources Technology Satellite–1 Symposium, v. 1 Techical Presentations: Washington, D.C., NASA, Goddard Space Fligt Cent, Special Paper 351, 309–317. [ Links ]
Schweizer, P., 1987, Infographie v. 1 and 2: Lausanne, Presses polytechniques et universitaires romandes, 418 p. [ Links ]
Taud, H., Parrot, J.–F., 2005, DEM roughness measurement by local fractal dimension: Géomorphologie, 4, 327–338. [ Links ]
Terlien, M.T.J., Van Westen, J., Van Asch, T.W.J., 1995, Deterministic modeling in GIS based landslide hazard assessment, en Carrara, A., Guzzetti, F. (eds.), Geographic Information Systems in Assessing Natural Hazards: Dordrecht, Holanda, Kluwer Academic Publisher, Advances in Natural and Technological Hazards Research, 5, 57–77. [ Links ]
Temesgen, B., Mohammed, M.U., Korme, T., 2001, Natural hazard assessment using GIS and remote sensing methods, with particular reference to the landslides in the Wondogenet area, Ethiopia: Physics and Chemistry of the Earth, 26(9), 665–675. [ Links ]
Tucker, C.J., Newcomb, W.W., Los, S.O., Prince, S.D., 1991, Mean and inter–year variation of growing–season normalizet difference vegetation index for the Sahel 1981–1989: International Journal of Remote Sensing, 12, 1113–1115. [ Links ]
Wilson, J.P., Gallant, J.C., 2000, Terrain Analysis. Principles and Applications: New York, John Willey & Sons, 479 p. [ Links ]














