Porosidad de los yacimientos naturalmente fracturados: una clasificación fractal

 

Porosity in naturally fractured media: A fractal classification

 

Ma. Eugenia Miranda–Martínez¹*, Klaudia Oleschko², Jean–Francois Parrot³, Fernando Castrejón–Vacio⁴, Hind Taud⁴ y Fernando Brambila–Paz⁵

 

¹ Posgrado en Ciencias de la Tierra, Instituto de Geología, Universidad Nacional Autónoma de México, Circuito de la Investigación Científica s/n, Ciudad Universitaria, Del. Coyoacán, Apartado Postal 70296, 04510 México D.F.
* mmirandamartinez@yahoo.com

² Centro de Geociencias, Universidad Nacional Autónoma de México, Campus Juriquilla, Apdo. Postal 1–742, 76001, Querétaro, Qro., México.

³ Instituto de Geografía, Universidad Nacional Autónoma de México, Circuito de la Investigación Científica s/n, Ciudad Universitaria, Del. Coyoacán, 04510 México D.F.

⁴ Instituto Mexicano del Petróleo, Eje Central Lázaro Cárdenas Norte No. 152, 07730 México D.F.

⁵ Departamento de Matemáticas, Facultad de Ciencias, Universidad Nacional Autónoma de México, Ciudad Universitaria, Del. Coyoacán, 04510, México D.F.

 

Manuscrito recibido: Marzo 2, 2005
Manuscrito corregido recibido: Agosto 24, 2005
Manuscrito aceptado: Febrero 16, 2006

 

RESUMEN

El movimiento y la distribución de fluidos a través de los medios porosos están determinados por su geometría. La naturaleza autosimilar de la estructura de estos medios ha sido el objeto de numerosos estudios que han documentado las relaciones de potencia ('power law') entre las principales medidas de poros y sólidos, y la resolución del método utilizado para su análisis. En la presente investigación se introduce un esquema fractal para clasificar los yacimientos naturalmente fracturados (YNF) a partir de imágenes de tomografía computarizada de rayos X. Esta clasificación tiene como propósito extraer y medir algunos rasgos geométricos de los poros tanto a nivel global (firmagrama), como local (líneas de referencia) vía los clasificadores fractales. Los clasificadores fractales, extraídos de las imágenes digitales, fueron útiles para hacer un diagnóstico simple y rápido del tipo de porosidad de un núcleo a partir de su imagen. La dimensión fractal de masa (D_m y 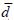), la dimensión espectral ofractón (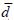),el exponente de Hurst (H) y la lagunaridad (Λ) de los YNF del sureste de México, son estadísticamente diferentes para los tres patrones de porosidad representativos de estos materiales: fracturas, cavidades y porosidad mixta. Para estimar los primeros dos (D_m y 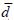), es necesario presegmentar la imagen en conjuntos de poros y sólidos, creando una imagen binaria, previo a la cuantificación fractal. En los últimos (H y Λ), la extracción de los parámetros se realiza directamente a partir de las imágenes originales evitando el proceso de segmentación, lo que permite proponer a los clasificadores H y Λ como estimadores más confiables de la porosidad de los YNF. Todos los clasificadores fractales, y en especial la dimensión fractal de masa y la lagunaridad de los tres patrones de porosidad arriba especificados, mostraron una correlación estadísticamente significativa con la porosidad (medida con técnicas tradicionales) de las capas geológicas con distinta capacidad productora de hidrocarburos. Este hecho abre un nuevo panorama para la modelación y pronóstico de la geometría de los YNF.

Palabras clave: dimensión fractal, tomografía computarizada de rayos X, imágenes digitales, estructura, yacimientos fracturados, porosidad.

 

ABSTRACT

The flow and distribution of fluids through pores in porous media are governed by their geometry. The self–similar behavior of the structure of these sets has been the subject of numerous studies that have documented the power laws relationship, among the principal measures of pores and solids, and the resolution of the method used for their analysis. A fractal scheme is introduced in order to extract and measure some geometric features of pores, using the mean values of their fractal classifiers, dividing these in global (ftrmagram) and local (reference line) classifiers. The mass fractal dimension (D_m), the spectral dimension orfracton (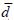), the Hurst exponent (H) and the lacunarity (Λ) of naturally fractured reservoirs (YNF) of southeastern Mexico, have shown to be statistically different for the three most representative porosity sets: fractures, cavities and mixed porosity. The fractal classifiers, extracted from digital images obtained using X–ray computerized tomography, were useful for porosity classification in different patterns, starting from the core images. D_m and 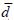must be determined on presegmented images, which distinguish the pore and solid sets, prior to the fractal quantification, while H and Λ can be extracted from the original image, which drastically diminishes the bias in the porosity estimation. All fractal classifiers, including mass dimensions and lacunarity of the porosity patterns specified above for YNF, showed a statistically significant correlation with the porosity of the geological strata as determined by traditional techniques. All our results offer new perspectives for the modeling and forecasting of porosity in the naturally fractured deposits.

Key words: fractal dimension, X–ray tomography, digital images, structure, porosity, fractured media.

 

INTRODUCCIÓN

Más de 80% de la producción de hidrocarburos en México proviene de los yacimientos naturalmente fracturados (YNF). Estas formaciones geológicas presentan una amplia gama de propiedades estructurales (Martínez–Ángeles et al, 2002), cuya descripción cuantitativa es una tarea fundamental para lograr una explotación sustentable y eficiente en la industria petrolera (Blunt, 1998). En los últimos años, el Instituto Mexicano del Petróleo (IMP) ha puesto en marcha numerosos programas de investigación, dirigidos al estudio y modelación de los principales rasgos estructurales de estas formaciones, generando una importante base de datos multiespectrales, multitemporales y multiescalares (Martínez–Ángeles et al., 2002), cuya naturaleza específica requiere del uso de nuevas técnicas analíticas capaces de integrar la información polifacética. Entre las técnicas más prometedoras, por su alta precisión, destaca la Geometría Fractal (Hirata, 1989; Norte et al., 1989).

Para representar los medios fracturados se utilizan diversos modelos geométricos (Blunt, 1998; Mendoza, 1998; Santos et al, 2002; Farber et al, 2003; Cunningham et al, 2004). El más simple de ellos considera la separación de los bloques rocosos por planos de anchura variable que representan a las fracturas (Nolte et al, 1989). En este modelo se reconoce que las fracturas tienen una influencia poco importante sobre la porosidad de almacenamiento de las formaciones, siendo decisivo su papel en la permeabilidad del sistema. Por esto último, el desplazamiento de fluidos se modela como un proceso controlado por la geometría de las fracturas, mientras que la capacidad de almacenamiento de la capa productora se relaciona con la porosidad interna de los bloques (Farber et al, 2003). El patrón de distribución de los planos de fracturamiento entre los bloques rocosos, así como la geometría de los espacios al interior de estos últimos se derivan del arreglo geométrico entre los conjuntos de sólidos y poros, cuya naturaleza es diferente y particular para cada uno de los YNF. El conjunto de los rasgos mencionados se denomina "estructura del yacimiento" (Santos et al, 2002).

La importancia de la porosidad en el comportamiento físico y mecánico de las rocas sedimentarias es ampliamente reconocida (IMP, 2000; Cunningham et al., 2004), en especial cuando se trata de formaciones productoras de hidrocarburos (Santos et al, 2002). Desde un enfoque tradicional, la porosidad se define como la relación entre el volumen de los espacios vacíos, llamado el volumen de poros (V_v), y el volumen total del sistema (V,_t) (Martínez–Ángeles et al, 2002). Su magnitud, así como la distribución de poros y sólidos por tamaño, caracterizan la estructura del medio. La porosidad es un parámetro adimensional, generalmente reportado en porcentaje, y los límites de sus valores para cualquier medio poroso van de 0 a 1 (Martínez–Ángeles et al, 2002). La porosidad total (_tot) se calcula mediante la siguiente expresión:

 

La porosidad de las rocas en los YNF se agrupa en tres patrones geométricos: fracturas, cavidades y la combinación de ambos, denominado el patrón mixto (Martínez, 2002). La morfología de estos patrones, así como las dimensiones de fracturas y cavidades, no siempre son fácilmente cuantificables, en parte debido a la extensión y compleja distribución de la porosidad en el espacio Euclidiano (Antonellini, 1992; Nieto–Samaniego et al, 2005).

Como ya se mencionó, la geometría de los patrones de porosidad determina, por un lado, la intensidad de los flujos sub–superficiales de las substancias a través de los YNF y, por el otro, su capacidad de almacenamiento de hidrocarburos. La apertura, distribución y conectividad de los patrones de fracturas y cavidades, conjuntamente con la permeabilidad de las rocas, son de importancia primordial para la primera (intensidad del flujo), mientras que la morfología, el diámetro efectivo y la continuidad de los poros, son rasgos decisivos para la segunda (capacidad de almacenamiento, IMP, 2000).

Del análisis de los registros de pozos se deriva que el flujo interno se concentra en un pequeño porcentaje de fracturas que intersectan las paredes de núcleos (Santos et al., 2002; Cunningham et al., 2004). Es común observar que estas fracturas son completamente transversales al ancho del pozo y contienen una porosidad visible (cavidades) a lo largo del plano de fractura. La interfase de producción y las pruebas de presión sugieren que estas formaciones son parte de una red interconectada (Berfield, 1994).

La distribución en el espacio de los complejos patrones de fracturas se ha modelado tradicionalmente a través de técnicas geoestadísticas (Long y Billaux, 1987). Sin embargo, al observarse una invarianza de las medidas básicas de poros con el cambio de escala, es decir, el comportamiento autosimilar del patrón espacial de la porosidad, ahora ya documentado dentro de un intervalo amplio de escalas por Nieto–Samaniego et al. (2005), se han introducido los principios de la Geometría Fractal a su caracterización cuantitativa (Barton y Larsen, 1985).

En los últimos 20 años, la Geometría Fractal ha sido aplicada al análisis de medios geológicos fracturados con resultados variables (La Pointe y Hudson, 1985; Aviles et al, 1987; Chiles, 1988; Hirata, 1989; Velde et al, 1990; Berfield, 1994; Marrett y Allmendinger, 1991; Walsh et al, 1991; Gauthier y Lake, 1993; Balankin, 1997; Diego y Giampiero, 2000; Babadagli y Develi, 2003; Oleschko et al, 2004). Sin embargo, la principal dificultad en el uso de las técnicas fractales sigue siendo la necesidad de manejar los datos espaciales multiescalares, cuya adquisición se realiza con métodos de distinta base física. Estos últimos abarcan desde el mapeo directo de las superficies rocosas fracturadas, hasta el análisis de los registros geofísicos de pozos, de las imágenes de afloramientos adquiridas por diversos sensores del satélite o de las fotografías tomadas in situ, y/o con un microscopio óptico o electrónico (Van Dijk et al, 2000; Oleschko et al, 2004). El análisis de las fracturas, realizado a diferentes escalas y empleando diversas medidas de su densidad, conductividad hidráulica y resistividad del medio, ha confirmado la invarianza de la porosidad al cambio de escala (Berfield, 1994; Paredes y Elorza, 1999). Esta invarianza define el rasgo principal de un conjunto fractal: su auto similitud.

La autosimilitud es una propiedad intrínseca y genérica del conjunto fractal y se refiere a que cada parte de una forma es geométricamente similar al todo (autosimilitud física), o a que sus momentos estadísticos son similares e independientes del submuestreo (autosimilitud estadística, Mandelbrot, 1983; Turner et al, 1998). Bajo este enfoque, un caso particular de los conjuntos autosimilares es el conjunto autoafín, cuyo escalamiento (la preservación de la forma o de los momentos estadísticos) se efectúa de diferente manera a lo largo de distintas direcciones geométricas (Carr, 1997). En la presente investigación los fractales autoafines juegan un papel central.

La naturaleza fractal de los conjuntos de fracturas se ha comprobado dentro de un amplio intervalo de escalas en diferentes sistemas naturales, (Marrett y Allmendinger, 1991; Walsh et al, 1991; Gauthier y Lake, 1993; Balankin, 1997; Piggott, 1997; Diego y Giampiero, 2000; Babadagliy Develi, 2003; Nieto–Samaniego etal, 2005). Hewett (1994) realizó un estudio sobre la potencialidad de los métodos fractales para la caracterización de fracturas, llegando a las siguientes conclusiones, mismas que hemos tomado como base para la presente investigación: 1) El marco teórico–metodológico de la Geometría Fractal es adecuado para caracterizar la distribución y organización de las redes de fracturas dentro de un amplio intervalo de escalas; 2) los modelos jerárquicos de la fragmentación de rocas, que relacionan entre sí el tamaño de bloques, su número y la longitud de fracturas, generan dos tipos de distribuciones comunes: la potencial y la exponencial, siendo la primera (ley de potencia) estadísticamente más representativa; y 3) los modelos fractales incrementan la precisión y exactitud de la representación geométrica de los sistemas fracturados.

En un trabajo reciente, Nieto–Samaniego etal. (2005) reportan resultados del análisis fractal detallado de las fracturas, cuyos resultados abarcan un intervalo de longitud de escalas del orden de 10⁴. Todas las mediciones realizadas por estos autores se efectuaron sobre el mismo afloramiento rocoso, obteniendo cada vez imágenes con mayor acercamiento, y así con una resolución progresivamente mayor. Este estudio, a pesar de reportar una alta dispersión de los exponentes en la relación longitudes acumuladas de fracturas versus resolución de la imagen, además de una importante variabilidad entre las dimensiones y densidades de fracturas obtenidas, confirmó de manera firme, la naturaleza fractal, autosimilar de los conjuntos de fracturas analizadas.

Los fractales son construcciones geométricas complejas con propiedades específicas (Mandelbrot, 1983), cuya textura heterogénea o la rugosidad superficial pronunciada sigue un patrón autosimilar (Smith et al, 1996). La dimensión fractal de masa (D_m) y la lagunaridad Λ(r) son medidas de la heterogeneidad de la distribución de la masa en el espacio común Euclidiano (Mandelbrot, 1983; Allain y Cloitre, 1991), mientras que la dimensión espectral o fractón, (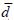) y el exponente de Hurst (H), son medidas de la continuidad y rugosidad del objeto fractal, respectivamente (Orbach, 1986; Balankin, 1997). La lagunaridad, además de la heterogeneidad arriba mencionada, mide la invarianza de un fractal al traslado (Allain y Cloitre, 1991). Las medidas básicas de un fractal (su longitud, área, volumen, masa, densidad, etc.) se relacionan matemáticamente con la escala de observación vía las leyes de potencia, cuyos exponentes son valores fraccionarios (la dimensión fractal, Mandelbrot, 1983).

Para extraer y cuantificar los principales rasgos de la porosidad de las imágenes multiescalares del conjunto fractal, Oleschko et al. (2004) propusieron un esquema cuya calibración se realizó en minerales de cuarzo con diversos grados de intemperismo. Los cuatro clasificadores fractales arriba especificados fueron medidos en granos, desde frescos (Clase A), hasta los extremadamente intemperizados (Clase E). Los resultados numéricos del análisis fractal mostraron buena correlación con la clasificación tradicional, aceptada a nivel internacional (Marcelino y Stoops, 1996), y diseñada para describir el avance del intemperismo de un modo semi–cuantitativo.

En el presente estudio fue utilizado el esquema de cuatro clasificadores fractales, propuesto para cuantificar la dinámica de la geometría del patrón de poros en función del intemperismo, para realizar el análisis comparativo de los tres patrones de porosidad representativos de las imágenes de los núcleos de YNF. Se emplean estos clasificadores como base para diseñar un procedimiento de referencia que permita el análisis cuantitativo de la estructura en los yacimientos naturalmente fracturados, siendo este esquema de gran utilidad como base para un diagnóstico automatizado de la capacidad productora de hidrocarburos de las capas geológicas, a partir de sus imágenes multiescalares originales.

 

MATERIALES Y MÉTODOS

Aspectos generales

El Programa de Investigación de Yacimientos Naturalmente Fracturados (YNF) del Instituto Mexicano del Petróleo (IMP) clasifica la porosidad de las rocas productoras en tres patrones característicos: fracturas, cavidades y porosidad mixta (combinación de las dos primeras). Los cuatro núcleos (N–I, N–II, N–III y N–IV) analizados en la presente investigación son representativos de los patrones señalados y corresponden a: fracturas (N–I), cavidades (N–II) y porosidad mixta (N–III y N–IV). Las muestras provienen de una zona productora de hidrocarburos del sureste de México y están constituidas principalmente por carbonates (calizas y dolomías), con una porosidad matricial primaria baja (entre 1 y 5%), y con porosidad secundaria, asociada a las fracturas, cavidades y cavernas, alta (entre 5 y 40%). La permeabilidad del sistema matriz–fracturas–cavidades en estos materiales es intermedia (de 10 a 500 mDarcies) y su saturación inicial con aceite es alta, llegando a ocupar hasta 80% del espacio poroso (Martínez–Ángeles, 2002).

Las imágenes digitales de los núcleos estudiados fueron obtenidas a partir de la tomografía computarizada de rayos X, que es una técnica no destructiva diseñada para analizar la estructura de muestras inalteradas de distinta naturaleza, dado que permite visualizar y caracterizar detalladamente el interior de un objeto por medio de la distribución de densidades de los elementos presentes dentro de dicho objeto (Babout et al., 2001). Los equipos de tomografía computarizada de rayos X generan una imagen digital de la sección transversal a partir de las proyecciones en diferentes ángulos de visión. La resolución de los equipos de tomografía de rayos X permite detectar cambios en las características másicas de los materiales hasta de un 0.1% en áreas de 2 mm² o menores, según el equipo empleado (Martínez–Ángeles, 2002).

La principal ventaja que ofrece la técnica de tomografía computarizada de rayos X a la ingeniería de yacimientos es la posibilidad de obtener, en forma oportuna, precisa y no destructiva, una imagen digital del interior de una roca porosa, fracturada y con cavidades, lo que permite el análisis del comportamiento del desplazamiento de fluidos en medios porosos, así como la caracterización de núcleos de campo en estudios de laboratorio (Martínez–Ángeles, 2002). La imagen final permite visualizar los rasgos geométricos de los conjuntos de sólidos y poros. Para caracterizar la porosidad de los patrones evaluados se analizó la rugosidad de las firmas de los rayos X dispersados por la distribución de sus principales componentes (sólidos y poros), en el espacio Euclidiano 2–dimensional (2–D).

El tomógrafo empleado en la presente investigación es propiedad del IMP, marca PICKER IQ PREMIER, acondicionado para el análisis de los fluidos en los núcleos de pozos petroleros (Hernández y Martínez, 2001).

La imagen final del tomógrafo se construye empleando un algoritmo diseñado en el IMP (Martínez–Ángeles y Pérez –Rosales, 2000; Martínez–Ángeles et al, 2002). Posteriormente, esta imagen se analiza mediante las diversas técnicas de procesamiento de imágenes digitales (paquetes de computo Paint Shop, Adobe, Corel, etc.).

En el presente estudio, para cuantificar la textura de las imágenes en tonos de gris se utilizó el esquema fractal diseñado y calibrado previamente por Oleschko et al. (2004). La textura de la imagen se definió como una variación espacial de los tonos de gris (Turner et al., 1998). La heterogeneidad (Cl) de distribución de estos últimos, su continuidad (C2), la rugosidad (C3) y lagunaridad (C4) fueron medidas en las imágenes tomográficas de los núcleos con porosidad contrastante. A cada uno de los rasgos arriba enumerados (C) se le refiere con el término "clasificador" del patrón de porosidad. A continuación se presentan los detalles básicos de los procedimientos diseñados para su estimación. Sin embargo, primeramente es necesario hacer referencia a dos aspectos cuyo análisis previo a la cuantificación fractal de las imágenes digitales es de suma importancia. El primero se refiere a la necesidad de segmentar o binarizar una imagen en conjuntos de poros y de sólidos, mientras que el segundo hace hincapié en la comprobación empírica, obligatoria y anterior a cualquier medición fractal: la comprobación del comportamiento fractal del patrón del conjunto estudiado.

Naturaleza de las imágenes de tomografía

La clasificación fractal de la porosidad de los YNF se realizó empleando dos tipos de datos obtenidos a partir de las imágenes digitales del tomógrafo de rayos X:

a)  Las imágenes presegmentadas en el IMP por el grupo del Ing. Hernández Escobedo (Hernández y Martínez, 2001). El propósito del análisis fractal en esta etapa fue correlacionar las magnitudes de los clasificadores fractales extraídos a partir de las imágenes digitales de los núcleos con diversa porosidad, con los valores de esta última, obtenidos a través de las técnicas diseñadas por el Proyecto D.01116 "Caracterización de núcleos mediante tomografía de rayos X". Por esta razón, los tonos de gris seleccionados por el grupo del IMP fueron utilizados sin ningún cambio para segmentar cada una de las imágenes de interés, con objeto de cuantificar los primeros dos clasificadores fractales: la heterogeneidad (C1) y la continuidad (C2) de la distribución de los tonos de gris sobre las imágenes. Para definir los tonos de gris que corresponden a cada uno de los tres patrones de porosidad contrastante, en el IMP fue diseñado un procedimiento de segmentación de las imágenes en el "Sistema de tratamiento de Imágenes PROTOM 1.0" (Hernández y Martínez, 2001).

Las imágenes de tomografía fueron segmentadas en tres temas o rasgos etiquetados con tres tonos de gris constantes e independientes de la naturaleza del material analizado: la matriz, las fracturas y las cavidades. En la presente investigación, la heterogeneidad y la continuidad de estos tres rasgos en el espacio común Euclidiano se estimó mediante la dimensión fractal de masa (D_m) y la dimensión espectral ().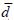

b)  Las imágenes originales del tomógrafo, sin una presegmentación previa al análisis, se transformaron a una distribución de tonos de gris (de 0 a 255), siguiendo su orden espacial original, codificándoseles en un archivo ASCII (.raw). Sobre estas imágenes no binarizadas fueron medidos los otros dos clasificadores fractales (C3 y C4) de la porosidad: la rugosidad (vía el exponente de Hurst) y la lagunaridad (A).

Finalmente, se correlacionaron todos los clasificadores con la porosidad de las capas geológicas estudiadas, medida esta última con las técnicas comunes empleadas en el IMP.

Naturaleza autosimilar de las imágenes

Al inicio, la naturaleza autosimilar de los tres patrones de porosidad estudiados (fracturas, cavidades y el mixto), se confirmó al aplicar el procedimiento tradicional del conteo de caja (box counting) a las imágenes presegmentadas de los núcleos. Al obtener una relación lineal (con R²=0.99) de las gráficas doble–logarítmicas que relacionan el número (TV) de cajas ocupadas por cada tipo de porosidad de interés vs. el tamaño (a) de la caja (Figura 1), se comprobó empíricamente la naturaleza fractal de la porosidad a la escala de observación correspondiente a la resolución del tomógrafo de rayos X. Posteriormente se analizó la rugosidad de la distribución global (el firmagrama) y local (las líneas de referencia) de los tonos de gris en cada una de las imágenes normalizadas. Este análisis, que se detalla más adelante, esta enfocado a describir la variabilidad espacial de las distribuciones mencionadas. El análisis fractal de la rugosidad de los firmagramas y de las líneas de referencia extraídos de las imágenes originales, se realizó vía el exponente de Hurst, y confirmó una vez más la naturaleza autoafín y por ende la autosimilitud de las imágenes analizadas.

 

Clasificadores fractales de la estructura de los yacimientos naturalmente fracturados

Los clasificadores fractales de la porosidad se calcularon utilizando cuatro algoritmos, diseñados en el Laboratorio de Análisis Fractal de los Sistemas Naturales (LAFSINA) de la UNAM por Parrot (1997) y Parrot y Taud (1998). La calibración de estos algoritmos se realizó comparando los valores de C1 y C3 con los extraídos de las mismas imágenes aplicando las técnicas disponibles en el paquete de computo comercial Benoit, recomendado como el de referencia para el análisis fractal de las imágenes y de las series de tiempo (Seffens, 1999).

Dimensión fractal de masa (C1)

El primer clasificador (C1) se extrajo de las imágenes digitales del tomógrafo y corresponde a la dimensión fractal de masa (D_m), que se calcula aplicando el programa de computo Fractals, diseñado en LAFSINA por Parrot (1997), y que es una versión ajustada del procedimiento tradicional del conteo de caja (box counting; Feder, 1988; Falconer, 1990; Korvin, 1992; Anderson et al, 1996). La dimensión fractal de masa o dimensión de capacidad se calcula para cada conjunto de interés (poros o sólidos) sobre una imagen de 8 bits, llenando el intervalo de tonos de gris, previamente seleccionado por el usuario para dicho conjunto (umbral), con las cajas de tamaño progresivamente mayor. El intervalo de tamaños de caja utilizado, depende de las dimensiones originales de la imagen de interés y está en función de los divisores comunes que éstas tienen. El tamaño mínimo de la caja siempre es de un pixel, mientras que el tamaño máximo coincide con el mayor divisor de la imagen. Por ejemplo, una imagen regular del tamaño 216 por 216 pixeles, tiene 16 divisores comunes, por lo que Fractals utiliza 16 tamaños de caja a lo largo del conteo. Si la forma de la imagen es rectangular, el número de divisores es diferente para el largo (eje x) y el ancho (eje y) de la imagen, por ende, Fractals busca los divisores comunes para ambas direcciones y ajusta a ellos el intervalo de tamaños de caja utilizado para el llenado del conjunto de interés. Este método es descrito en mayor detalle por Anderson et al. (1996). En el presente estudio se trabajó con imágenes regulares de dos tamaños: 256x256 (N–I y N–II), y 444x444 (N–III y N–IV), cortadas a partir de las imágenes circulares de los núcleos originales. La diferencias en el tamaño de las imágenes se debe a los distintos formatos proporcionados por el IMP.

El algoritmo Fractals calcula la dimensión fractal del conjunto de interés a partir de un archivo de salida con datos XY, con los cuales se construye la gráfica log–log que relaciona el número de cajas (N) con su tamaño (a) correspondiente y cuya pendiente es la dimensión fractal de masa del conjunto seleccionado (Figura 1).

El fractón (C2)

La dimensión espectral o fractón (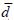) es el segundo clasificador utilizado en el presente estudio para cuantificar la continuidad del espacio poroso. El cálculo de la dimensión espectral se realizó con el algoritmo denominado Bromov, diseñado en LAFSINA por Parrot (Oleschko et al, 1998), que se basa en el análisis de la facilidad para efectuar un movimiento Browniano o describir caminos aleatorios (random–walk) al interior de una imagen. El procedimiento consiste en trazar n caminos aleatorios (para este análisis en particular n=1,000), que puede recorrer una partícula a lo largo del flujo de tipo difusivo al interior del espacio, determinado por el intervalo de tonos de gris que corresponde al conjunto de interés (poros en el presente estudio). Cada camino se inicia en un punto (pixel) seleccionado al azar dentro del conjunto analizado. A partir de este pixel se traza una primer trayectoria, que se define como un vector por la relación b–cosα, donde α es el ángulo entre 0º y 360° y b una distancia cuya longitud va de un pixel hasta un máximo definido por el usuario. La dirección, ángulo y longitud de esta trayectoria son aleatorias, coincidiendo esta última con el tamaño de la imagen.

La trayectoria diseñada es válida únicamente si todo el vector queda ubicado dentro del conjunto estudiado, en el intervalo de tonos de gris seleccionado durante la pre–segmentación de la imagen. Si esta condición se cumple, el punto alcanzado se vuelve el punto de inicio para trazar una nueva trayectoria (segmento), si por el contrario sale del conjunto analizado, el programa regresa al punto inicial, repitiéndose el procedimiento de un modo aleatorio hasta satisfacer la condición arriba especificada y continuar con la siguiente trayectoria. El número de veces que se realiza esta iteración queda definido por el usuario. Cuando una trayectoria alcanza el límite del conjunto estudiado, el pixel ubicado en el borde se considera el punto final del recorrido y, a partir de este punto, se inicia un nuevo camino.

En cada trayectoria diseñada se cuenta el número total de pixeles visitados (S_t), el número de "pasos nulos" (S_o) y el número de pasos que se ubicaron dentro del conjunto (S_n). Los pasos nulos se definen como los puntos de las trayectorias que intersectan algún punto de otro camino, trazado anteriormente. Si el paso coincide con el sitio ya visitado (un paso nulo) se añade 1 al número total de los pasos realizados (S_t) y 0 al S_n. Este método es dicutido en detalle por Orbach (1986). Un camino concluye cuando las distancias acumuladas por las trayectorias llegan a una longitud máxima, o bien, cuando se alcanza un máximo de pasos nulos previamente establecido, ambos criterios definidos por el usuario al entrar al menú del programa Bromov. En ese momento, se inicia un nuevo camino aleatorio.

El usuario decide el número de caminos que habrá de trazarse sobre la imagen. Entre mayor sea el número de caminos, mayor será el recubrimiento del rasgo seleccionado por las trayectorias del movimiento Browniano. El fractón se calcula como la pendiente de la recta que relaciona entre sí: log (S_n) vs. log (S_t). Sus límites topológicos mencionados por Oleschko et al. (1998) están entre 0 (no hay rasgo de interés sobre la imagen o la probabilidad de alcanzarlo por una trayectoria es baja) y 2 (el conjunto de sólidos o poros ocupa todo el espacio Euclidiano).

Rugosidad global (firmagrama) y local (líneas de referencia) de la distribución de tonos de gris (C3)

El siguiente procedimiento propuesto por Oleschko et al. (2004) permite cuantificar la rugosidad de una imagen vía dos parámetros fractales: el exponente de Hurst y la lagunaridad generalizada, los cuales se extraen a partir de la variabilidad en el espacio de los tonos de gris sobre la imagen. La distribución completa de estos últimos se representa gráficamente en coordenadas XY. A la densidad global de los tonos de gris sobre la gráfica se le denomina firmagrama (Figura 2), y a nivel local (cualquier segmento de la imagen seleccionado por el usuario por algún interés especial) se llama línea de referencia (Figura 3). Una vez obtenida esta distribución autoafin se calcula la dimensión fractal del intervalo de reescalado (D_R/s), el coeficiente de Hurst (H) y la lagunaridad generalizada (Λ) tanto de los firmagramas como de las líneas de referencia.

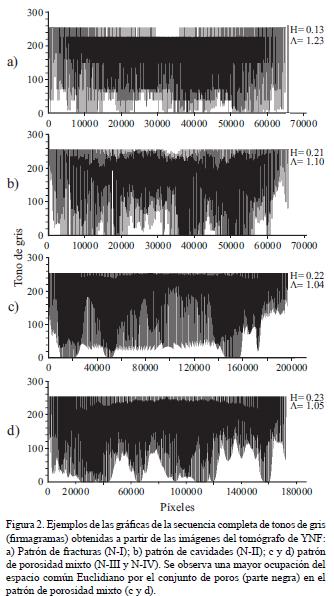
El procedimiento para obtener la distribución XY de los tonos de gris a partir de una imagen de tamaño N x N (en extensión .raw de 8 bits), consiste en transformarla a un arreglo lineal de los tonos de gris que la conforman, utilizando el algoritmo Histo–Gene (diseñado por J. F. Parrot en el Laboratorio de Análisis Fractal de los Sistemas Naturales de la UNAM). El arreglo mencionado abarca desde el primer pixel de la primera línea hasta el último pixel de la última línea, de tal manera que, por ejemplo, las imágenes de N–I y N–II cuyo tamaño es de 256 x 256 generan archivos con 65,536 datos, mientras que las de los núcleos N–III y N–IV, con tamaños de 444 x 444 se conforman por 197,136 pixeles. En el caso de las líneas de referencia, las posiciones del primer y del último pixel son definidas por el usuario en función de los objetivos del análisis.

Una vez obtenido el archivo que corresponde al arreglo lineal de los tonos de gris en formato .ts, éste entra a una de las rutinas del paquete Benoit 1.2, que calcula la dimensión fractal D_R/S o el exponente de Hurst que mide la rugosidad de los datos antes especificados.

Lagunaridad generalizada (C4)

El cuarto clasificador introducido por Oleschko et al. (2004) corresponde a una función Λ(r) que mide la invarianza al traslado de una imagen. Para un cuadrado completamente negro o blanco Λ(r)=1, lo cual significa su invarianza u homogeneidad total. El clasificador C4 se calcula a partir de la relación entre el cuadrado medio de las fluctuaciones de los tonos de gris a lo largo de la imagen y la media de los grises elevada al cuadrado:

En las imágenes empleadas en esta investigación se utilizó sólo un tamaño de r=l, que corresponde al tamaño del pixel, por lo que el procedimiento común del Allain and Cloitre (1991) recibió el nombre de "lagunaridad generalizada", la cual permite cuantificar cierto aspecto de la rugosidad de imágenes de medios porosos.

En este nuevo procedimiento, Oleschko et al. (2004) proponen calcular C4 a partir del histograma de frecuencias de los tonos de gris extraídos de su arreglo lineal, obteniendo así un archivo en formato .xls del cual se calcula la lagunaridad generalizada. El procedimiento mencionado requiere emplear otros dos algoritmos (Histo–Gene y Freq–hist), ambos diseñados por J. F. Parrot en el Laboratorio de Análisis Fractal de los Sistemas Naturales de la UNAM. En la presente investigación fueron obtenidos dos tipos de lagunaridad: la global, extraída a partir del firmagrama y la local, correspondiente a las líneas de referencia. En este estudio, con un propósito comparativo, se utilizaron solamente las líneas de referencia ubicadas en la posición central de las imágenes analizadas.

Comparación estadística de los clasificadores

Los datos de la porosidad medida por las técnicas tradicionales en el IMP, así como los clasificadores fractales (D_m, 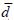, H y Λ) extraídos a partir de las 96 imágenes analizadas fueron sometidos a tres tipos de análisis estadístico, empleando el paquete especializado Statgraphics 5.0. Al principio se calcularon los parámetros estadísticos convencionales, tales como: media, valores máximo, mínimo y desviación estándar. Después, se aplicó una prueba de intervalo múltiple con el propósito de evaluar la variabilidad de los clasificadores a través del error estándar y la significancia de diferencias entre las medias extraídas a partir de los núcleos estudiados. La última prueba consistió en un análisis de regresión lineal entre los valores de porosidad (θ) y cada uno de los clasificadores fractales propuestos. Al inicio, los 96 datos de cada una de las variables de interés se correlacionaron, todos juntos, con los datos de porosidad de los núcleos y después, el análisis se realizó de manera individual para cada patrón de porosidad considerados de referencia para los yacimientos naturalmente fracturados (cavidades, fracturas y mixta).

 

RESULTADOS Y DISCUSIÓN

La discusión para caracterizar cuantitativamente la porosidad interna de los YNF se presenta de manera individual para cada clasificador propuesto, para discutir las tendencias de la dinámica de cada uno en función del patrón de porosidad, se emplearon las medias obtenidas para cada dimensión.

 

Dimensión fractal de masa (C1)

El primer clasificador, denominado C1, se refiere a la dimensión fractal de masa del espacio poroso (D_m), y caracteriza las propiedades estáticas de la estructura de los conjuntos fractales. Por un lado, D_m mide el grado de ocupación del espacio común Euclidiano y, por otro, la heterogeneidad de la distribución de un conjunto dado a lo largo de este último (Orbach, 1986; Crawford et al, 1993; Anderson et al., 1998; Oleschko et al., 1998). En el presente estudio, D_m se utilizó para distinguir de manera cuantitativa tres patrones de porosidad en imágenes de tomografía de YNF. El análisis de D_m se basó en la suposición de que los poros forman conjuntos autosimilares. En la Figura 1 se muestra un ejemplo de las imágenes representativas de los cuatro núcleos estudiados (en el formato que se requiere para el algoritmo Fractals), a la derecha de cada imagen se encuentra su gráfica log–log y la ecuación a partir de la cual se obtiene la dimensión correspondiente. El comportamiento lineal (R²=0.99) de la relación log–log entre el número (TV) y tamaño (a) de las cajas utilizadas para cubrir los conjuntos de poros y fracturas de tamaño variable, confirma la naturaleza autosimilar de la porosidad en los cuatro núcleos estudiados. La pendiente de cada gráfica corresponde a la dimensión fractal de masa D_m de los poros presentes en cada imagen.

El clasificador C1 mostró ser una medida precisa del grado de ocupación del espacio Euclidiano por la porosidad, además de ser también un indicador estadísticamente significativo de la heterogeneidad del patrón de poros en los YNF. El valor máximo de D_m se observó en los núcleos con porosidad mixta (N–III y N–IV), cuyos promedios fueron similares entre sí: D_m=1.84±0.02 en N–III y D_m=1.85±0.02 en N–IV. El patrón de fracturas (N–I) tuvo una dimensión fractal intermedia (D_m=1.71±0.06), mientras que las cavidades (N–II) se han caracterizado por una D_m mínima (D_m=l.59 ± 0.06). La variabilidad de C1, estimada mediante el error estándar de los datos, fue significativamente menor en el patrón de porosidad mixta y se incrementó casi tres veces en fracturas y cavidades (Figura 4a).

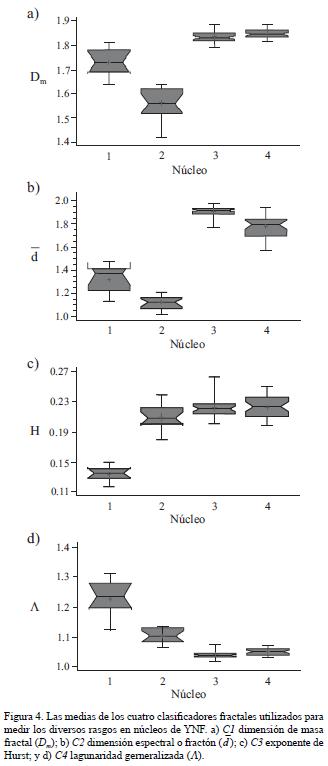
Estas diferencias indican la variación que existe en la forma de ocupar el espacio común Euclidiano por los tres patrones de poros comparados. Para confirmar la tendencia señalada, se compararon los valores del exponente de Hurst, calculado a partir de los datos de la dimensión fractal (H=2–D_m), haciendo referencia a una regularidad ya establecida (Carr, 1997; Balankin, 1997; Bresliny Belward, 1999; Malamudy Turcotte, 1999; Kanty Rangarajan, 2003), en cuanto menor es el valor del H para un conjunto, más rugoso es este último. En el patrón de porosidad mixta se presentó la rugosidad máxima (H=0.16) en cuanto a la distribución de poros a través de las imágenes tomográficas, mientras que el patrón de cavidades tuvo la rugosidad mínima (H=0.41), indicativa de la mayor homogeneidad de su patrón estructural.

Los 96 valores de la D_m, calculados a partir de las imágenes de los YNF, quedaron ubicados dentro de los límites topológicos establecidos para la dimensión fractal de masa Korvin, 1992), entre el cero (cuando el conjunto de interés no aparece en la imagen), y dos, cuando todo el espacio 2–D de la imagen está ocupado por el conjunto fractal. De la comparación de los valores de D_m arriba presentados, se deduce que la porosidad mixta, constituida por una combinación entre fracturas y cavidades, abarca un volumen máximo en el patrón estructural de los YNF. En el patrón de fracturas, el comportamiento de la distribución de la porosidad es intermedio, y la porosidad mínima se presenta en cavidades cuyos espacios porosos se ubican de manera más localizada, al interior de los núcleos de los YNF .

La prueba estadística de comparación múltiple demostró que las magnitudes de C1 varían en función del patrón de porosidad. A un nivel de confianza de 95%, se puede afirmar que el clasificador C1 permite diferenciar, de un modo estadísticamente significativo, entre los tres patrones de porosidad. En la Figura 4a se aprecian gráficamente los resultados de esta prueba, además aparecen las medias y los intervalos de variación de D_m para cada núcleo analizado, observándose que el único par de medias que muestra equivalencia es N–III y N–IV, que representan el mismo patrón de porosidad (mixta). Al mismo tiempo los núcleos N–I y N–II son estadísticamente diferentes entre sí y de N–III y N–IV.

Para definir matemáticamente el tipo de relación que existe entre Cl y la porosidad, se realizó un análisis de regresión simple. Al inicio, todos los valores de D_m calculados para los cuatro núcleos (96 datos en total) fueron analizados juntos, resultando la gráfica de la Figura 5a. Esta última muestra tres grupos (clusters) de datos claramente separados entre sí, que corresponden a los tres patrones característicos de porosidad: fracturas, cavidades y mixta. Al analizar en conjunto la D_m de los tres patrones de porosidad no se llegó a ninguna correlación estadística significativa entre las variables mencionadas.

Sin embargo, al efectuar posteriormente un análisis estadístico de cada patrón de porosidad en forma independiente, fueron obtenidas correlaciones positivas entre la dimensión fractal de masa y la porosidad del núcleo, con coeficientes de correlación altos (entre 0.87 y 0.99). En las gráficas b, c y d de la misma Figura 5 se aprecia que, a mayor porosidad, la dimensión fractal de masa del conjunto de poros es mayor, relacionándose directamente con la mayor y más heterogénea ocupación del espacio Euclidiano por ésta (la porosidad). El mejor ajuste lo presentó el patrón de fracturas (R²=0.99), seguido por el de cavidades (R²=0.98) y finalmente por el patrón mixto (R²=0.87). Las tendencias observadas coinciden con las reportadas por Anderson et al. (1996), y Oleschko et al. (2000), quienes indican que la dimensión fractal de masa es una variable de origen integral cuyos valores se correlacionan estrechamente con la naturaleza de la muestra y dependen no sólo de su porosidad total, sino también de la lagunaridad y el contenido de arcilla (Rieuy Sposito, 1991).

 

Dimensión espectral o fractón (C2)

La difusión de una partícula a través del espacio poroso Euclidiano sin restricciones al movimiento se describe teóricamente por una dimensión espectral máxima igual a 2, que corresponde al límite topo lógico superior y es un valor característico del fractón para el movimiento Browniano totalmente aleatorio. Mientras más tortuosa o menos continua se vuelve la red de poros, menor será su dimensión espectral, indicando mayores restricciones al avance de la partícula (Oleschko et al, 1998). Este segundo clasificador fractal permite estimar las características dinámicas de las redes fractales, generando información sobre el grado de fragmentación y continuidad del patrón de interés. Además, es un indicador cuantitativo y preciso del grado de impedimento que presenta una red de poros a la difusión de un fluido en una dirección determinada, así como de la continuidad del patrón de pixeles ocupados por el mismo tono de gris.

En los núcleos analizados, el mayor valor promedio de 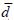, y por ende la mayor continuidad, se presentó en el patrón de porosidad mixta (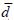=1.90±0.04 en N–III y 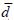=1.78 ± 0.09 en N–IV), seguido por el de fracturas (N–I) 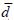=1.30±0.13 y finalmente las cavidades (N–II) 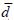=1.12±0.60. Estos resultados indican que la estructura del espacio poroso representada mediante la combinación de fracturas y cavidades facilita el desplazamiento de fluidos debido a una mayor conectividad y menor tortuosidad de la red de poros, lo que no ocurre al presentarse cada patrón por separado. En relación con la variabilidad de los datos de C2, se observó que ésta es inversa a la magnitud de la dimensión espectral. La menor variación se documentó para el patrón mixto, seguido por el de fracturas y el de cavidades. Dicha tendencia es similar a la variación documentada para C1 (Figura 4b).

La comparación entre los valores medios de C2 para los patrones de porosidad estudiados muestra diferencias estadísticamente significativas a un nivel de confianza de 95% entre los cuatro núcleos analizados (Figura 4b). De este análisis se concluyó que el clasificador C2 cuantifica de manera estadísticamente precisa la continuidad de los poros, que a su vez refleja la facilidad de desplazamiento de los fluidos a través de los YNF.

Al relacionar 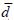vs. la porosidad estimada con las técnicas tradicionales, se observó para los 96 datos calculados un comportamiento similar al discutido anteriormente para C1 (Figura 6a). Los datos se distribuyen en tres áreas bien definidas, que corresponden a los patrones de porosidad estudiados. Se observa que el patrón mixto, con una porosidad similar a la de las cavidades, presenta mayor conectividad de los poros debido a que las cavidades están interconectadas por las fracturas, lo que asegura un movimiento más libre de los fluidos a través de este patrón estructural. Para el patrón de fracturas se observa que a pesar de los valores altos de porosidad, la conectividad entre los poros es baja, lo que limita el desplazamiento de los fluidos.

De las Figuras 6b a la 6d se muestran las correlaciones individuales obtenidas para cada patrón de porosidad específico. El ajuste más significativo correspondió al patrón de fracturas (R²=0.81), mientras que para el patrón de cavidades se obtuvo R²=0.71. En el caso del patrón mixto, no se observó una correlación significativa entre las variables de interés (R²=0.01). Este comportamiento se debe al hecho de que el clasificador C2 se relaciona no sólo con la magnitud de la porosidad (una característica estática), sino también proporciona información cuantificable sobre la facilidad de desplazamiento de los fluidos a través de la red de poros.

 

Exponente de Hurst (C3)

El clasificador C3 cuantifica la rugosidad de la distribución de los datos en el espacio (en el caso específico de las imágenes tomográficas los tonos de gris), vía el exponente de Hurst, que es un parámetro fractal característico de las curvas autoafines (Dougan et al, 2000). En la Figura 2 se muestra un ejemplo de las gráficas (firmagramas) a partir de las cuales, en el presente estudio, se extrajo este parámetro a nivel global, para los tres patrones de porosidad comparados. Estos firmagramas, provenientes de las imágenes con diferente porosidad, hacen visibles las diferencias en la densidad de distribución de los tonos de gris a través de las imágenes, lo que refleja la disparidad en la densidad de las muestras exploradas con rayos X. De este modo, la variación en la rugosidad de los tres patrones de porosidad comparados corresponde a la variación en las densidades de las distribuciones de los tonos de gris y es cuantificable en términos del exponente de Hurst. Resumiendo, se puede decir que el firmagrama es una firma fractal de la distribución de tonos de gris sobre una imagen, el cual permite cuantificar la distribución y rugosidad de la densidad de esta distribución y por ende de la porosidad interna de los YNF vía el exponente de Hurst.

Las magnitudes del clasificador C3 fueron mayores en el patrón de porosidad mixta (H=0.22±0.2) seguido por la porosidad de cavidades H=0.20±0.02 en N–II, siendo siempre menor para el patrón de fracturas (H=0.13±0.01). Comparando estos valores no hay que olvidar que H es el exponente de una ley de potencia, y por lo tanto, pequeñas variaciones en su magnitud resultan en cambios significativos de porosidad (Oleschko et al, 2004). Los resultados del presente estudio confirman que el patrón de porosidad mixto presenta una mayor rugosidad debido a la mayor heterogeneidad de su estructura interna. El comportamiento contrario se observó para las fracturas cuya distribución en el espacio poroso es más regular y homogénea.

La prueba de medias demostró que existen diferencias estadísticamente significativas a un nivel de 95% entre la rugosidad de los patrones de porosidad comparados para los YNF de interés (Figura 4c). Esto permite afirmar que H es un parámetro suficientemente sensible para cuantificar y distinguir entre los tres patrones estructurales de los YNF, por lo que es un clasificador útil para analizar la geometría interna de los yacimientos a partir de sus imágenes de tomografía.

Las correlaciones obtenidas entre C3 y la porosidad para los tres patrones evaluados fueron las menos significativas de los cuatro clasificadores evaluados (Figura 7), obteniendo valores de R² bajos (R²=0.61 en N–I, R²=0.53 en N–II y R²=0.52 al agrupar N–III y N–IV). Estos datos confirman una vez más la veracidad de nuestra hipótesis original en la que se plantea que la información extraída a partir de la imagen, vía el clasificador C3, está relacionada más con la geometría de la interfase sólido/poro que con el valor total de la porosidad.

Se puede concluir que la distribución completa de los tonos de gris (firmagrama) es un perfil exacto de la imagen, que muestra todos los cambios en la densidad de la distribución de la materia (y por ende de los poros) a través de un corte transversal del núcleo, con la precisión de un pixel.

El análisis visual de los firmagramas permite seleccionar aquellos segmentos o perfiles locales que sonde interés más específico por ser más o menos densos. Para un análisis posterior estos segmentos se extraen, llamándoles líneas de referencia, y su rugosidad se mide aparte en términos de #. Con esta técnica se obtiene la información sobre la variación local de los patrones de porosidad de los YNF en el espacio. En la Figura 3 se muestran los ejemplos de líneas de referencia ubicadas en el centro de cada imagen, extraídas para cada uno de los cuatro núcleos estudiados. La magnitud de C3 de las líneas de referencia (#) corresponde a la rugosidad local de cada parte de la imagen seleccionada (H=0.29 de N–I, H=0.60 en N–II, H=0.73 en N–III y H=0.65 en N–IV). En los estudios anteriores, Oleschko et al. (2004) han demostrado que esta información es representativa de toda la imagen, lo que se comprueba una vez más al comparar los resultados del análisis de las líneas de referencia con los extraídos a partir de los firmagramas completos. Los valores del exponente de Hurst de los firmagramas y las líneas de referencia, para los tres patrones de porosidad comparados siguen las mismas tendencias, a pesar de ser distintos sus valores puntuales.

 

Lagunaridad generalizada (C4)

El cuarto clasificador utilizado para catalogar a los patrones de porosidad en los YNF es la lagunaridad generalizada [Λ(r)]. Los valores más grandes de esta variable, extraídos tanto a partir de los firmagramas completos (análisis global) como de las líneas de referencia (nivel local), se documentaron para el patrón de fracturas (Λ= 1.23± 1.31), seguido por el de cavidades (Λ=1.10±1.14), y el patrón mixto (Λ=1.04±1.07 y Λ=1.05± 1.07 para N–III y N–IV, respectivamente). Estos resultados demuestran que la red de fracturas presenta una estructura definida por la presencia de espacios más amplios de diverso grosor entre los fragmentos, en comparación con los otros dos patrones. Las cavidades tienen un comportamiento intermedio entre los tres tipos de porosidad y, por último, el patrón mixto presenta una red interconectada más uniforme del espacio poroso, lo que confirma una vez más las regularidades documentadas para la dinámica de C1 y C2.

La prueba de medias muestra que el clasificador C4, evaluado a partir de los firmagramas, es estadísticamente diferente para los tres patrones de porosidad comparados en los YNF (Figura 4d).

En cuanto al análisis de correlación entre el clasificador C4 y la porosidad medida con las técnicas tradicionales al comparar los 96 datos en conjunto (Figura 8a) se muestra una tendencia lineal pero en tres áreas bien definidas que corresponden a los tres patrones evaluados. Al graficar por separado cada conjunto de poros se observaron correlaciones lineales positivas con los tres patrones de porosidad, obteniendo R²>89%, como se puede observar en la Figura 8. El mejor ajuste de este clasificador se obtuvo para cavidades con R²=0.96 (Figura 8c), seguido por el patrón mixto con R²=0.94 (Figura 8d) y el de fracturas, R²=0.89 (Figura 8b).

La relación que existe entre los clasificadores obtenidos a partir del análisis de las imágenes completas por el procedimiento tradicional de conteo de caja y los calculados a partir de los firmagramas se evaluó a través de un análisis de correlación lineal entre el clasificador C1 (D_m) y el calsificador C4 (Λ). En la Figura 9a se muestran las gráficas obtenidas del análisis de los 96 datos. Se aprecia que al igual que para la correlación entre la porosidad y los clasificadores fractales, la correlación de estos dos clasificadores entre sí permite agrupar los datos en tres clusters bien definidos, que corresponden a los tres patrones de la porosidad estudiados. El patrón de fracturas se caracteriza por valores altos de D_m y de Λ, indicando que las fracturas ocupan más espacio y sus aperturas son más grandes. Las cavidades se caracterizan por valores bajos de ambos clasificadores comparados, indicando que su distribución en el espacio es más restringida y más localizada. Por último, en el patrón mixto se aprecia un proceso aditivo entre las fracturas y las cavidades, por un lado abarca la mayor distribución en el espacio de los poros (mayores valores de D_m), y por otro la distribución del tamaño de estos poros es más uniforme.

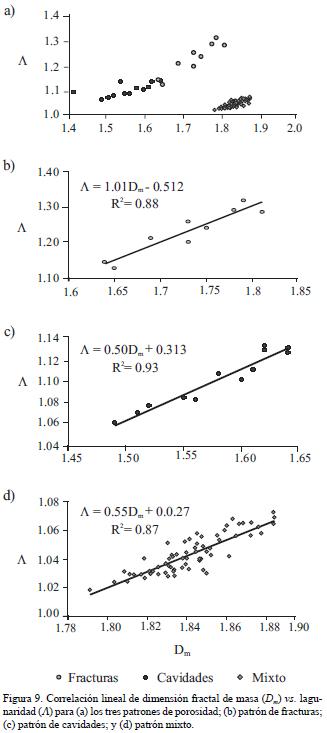
En las Figuras 9b a la 9d se muestran las correlaciones individuales para cada uno de los patrones de poros comparados, los coeficientes de correlación permiten afirmar que existe una estrecha relación entre ambos clasificadores, (R²=0.88 en fracturas, R²=0.93 en cavidades y R²=0.87 en porosidad mixta). Se puede concluir que al emplear ambas técnicas (imágenes y firmagramas) para el análisis fractal de la porosidad en YNF se llega a una caracterización más completa de la porosidad, permitiendo obtener clasificadores cuantitativos de la estructura y geometría de estos medios naturales.

 

CONCLUSIONES

El análisis fractal de imágenes digitales del tomógrafo de rayos X, tomadas de núcleos de yacimientos naturalmente fracturados, demuestra que la información extraída a partir de la distribución de los tonos de gris sobre la imagen original es estadísticamente representativa de su porosidad. Un análisis cuantitativo de esta información sirve de base para clasificar los patrones de porosidad de diversas formaciones geológicas según su geometría. En el presente trabajo se propone un esquema que utiliza cuatro clasificadores fractales para obtener de manera rápida y sencilla unas medidas precisas de los rasgos geométricos de los poros que constituyen los tres patrones distintos de porosidad (fracturas, cavidades y mixto) representativos de los YNF.

Los clasificadores propuestos proporcionan una información detallada sobre las características estáticas y dinámicas de la estructura de los núcleos, así como de la rugosidad de las interfases sólido/poro. Todos ellos son útiles para diferenciar, de manera estadística, entre los tres patrones de porosidad comparados, así como para cuantificar las diferencias en la homogeneidad de la distribución de los poros y su tamaño a través del espacio Euclidiano. Los firmagramas analizados, además de ser una fuente de información cuantitativa sobre la densidad de las muestras exploradas por los rayos X, permiten visualizar las diferencias que presentan las imágenes digitales de los núcleos en la densidad de la distribución de tonos de gris. El uso de los firmagramas y las líneas de referencia en el análisis fractal proporciona tanto información global como local sobre la rugosidad y lagunaridad de la porosidad.

El esquema de clasificación fractal propuesto abre un nuevo panorama para la evaluación y cuantificación de la estructura interna de los yacimientos naturalmente fracturados productores de hidrocarburos a partir de las imágenes tomográficas. Estas técnicas recientemente incorporadas permiten contar con una metodología moderna para caracterizar la geometría interna de estos medios porosos caracterizados como yacimientos, reto que se plantea en los numerosos estudios de caracterización de estos materiales.

 

AGRADECIMIENTOS

Se expresa un sincero agradecimiento al personal del IMP del grupo de YNF por el material proporcionado, sin el cual la realización de esta investigación no hubiese sido posible. Al Biól. Daniel Hernández Santiago por el apoyo en el trabajo de análisis y edición de las imágenes, a la Quím. Ana María Rocha por su apoyo técnico, y a Magdalena Alcayde por su colaboración en la edición del presente manuscrito. El financiamiento parcial que hizo factible la presente investigación proviene de los proyectos CONACYT 3309–Ay PAPIIT IN–102802, y del Programa de Apoyo a los Estudios de Posgrado, Tesis Doctorales 2004.

 

REFERENCIAS

Allain, C., Cloitre, M., 1991, Characterizing the lacunarity of random and deterministic fractal sets: Phyical Review A, 44, 3552–3558.        [ Links ]

Anderson, A.N., McBratney, A.B. FitzPatrick, E.A., 1996, Soil mass, surface, and spectral dimensions estimates from thin section photograph: Soil Science Society American Journal, 60, 962–969.        [ Links ]

Anderson, A.N., McBratney, A.B., Crawford, J.W., 1998, Applications of fractals to soil studies, en Sparks, D.L. (ed.), Advances in Agronomy, v. 63: San Diego, CA, Academic Press, 2–76.        [ Links ]

Antonellini, M., 1992, Geometry and distribution of deformation bands in porous sandstones, Delicate Arch area, Arches National Park, Utah, en Pollard, D.D., Aydin, A. (eds.), Rock Fracture Project, v. 3: Stanford, CA, Stanford University, A1–A7.        [ Links ]

Aviles, C.A., Scholz, C.H., Boatwright, J., 1987, Fractal analysis applied to characteristic segments of the San Andreas fault: Journal of Geophysical Research, 92(B1), 331–344.        [ Links ]

Babadagli, T., Develi, K., 2003, Fractal characteristics of rocks fractured under tension: Theoretical and Applied Fracture Mechanics, 39, 73–88.        [ Links ]

Babout, L., Maire, E., Buffiére, J.Y., Fougéres, R., 2001, Characterization by X–ray computed tomography of decohesion, porosity growth and coalescence in model metal matrix composites: Acta Materialia, 49(11), 2055–2063.        [ Links ]

Balankin, A.S., 1997, Physics of fracture and mechanics of self–affine cracks: Engineering Fracture Mechanics, 57, 135–203.        [ Links ]

Barton, C.C., Larsen, E., 1985, Fractal Geometry of two–dimensional fracture networks of Yucca Mountain, southwestern Nevada, en Stephansson, O. (ed.), Proceedings of the International Symposium on Fundamentals of Rock Joints, Bjorkliden, Suecia: Lulea, Suecia, Centek Publishers, 77–84.        [ Links ]

Berfield, W.C., 1994, Multifractal characteristics of natural fracture apertures: Geophysics Research Letters, 21(24), 2641–2644.        [ Links ]

Blunt, M.J., 1998, Physically–based network modeling of multiphase flow in intermediate–wet porous media: Journal of Petroleum Science and Engineering, 20, 117–125.        [ Links ]

Breslin, M.C., Belward, J.A., 1999, Fractal dimensions for rainfall times series: Mathematics and Computers in Simulation, 48, 437–446.        [ Links ]

Carr, J.R., 1997, Statistical self–affinity, fractal dimension, and geologic interpretation: Engineering Geology, 48, 269–282.        [ Links ]

Chilès, J. P., 1988, Fractal and geoestatistical methods for modeling of a fracture network: Mathematical Geology, 20(6), 631–654.        [ Links ]

Crawford, J.W., Sleeman, B.D., Young, I.M., 1993, On the relation between number–size distributions and the fractal dimension of aggregates: Journal of Soil Science, 44, 555–565.        [ Links ]

Cunningham, K.J., Carlson, J.I., Hurley, N.F., 2004, New method for quantification of vuggy porosity from digital optical borehole images as applied to the karstic Pleistocene limestone of the Biscayne aquifer, southeastern Florida: Journal of Applied Geophysics, 55, 77–90.        [ Links ]

Diego, P., Giampiero, P., 2000, Chaotic dynamics and fractals in magmatic interaction processes: a different approach to the interpretation of mafic microgranular enclaves: Earth and Planetary Science Letters. 175, 93–103.        [ Links ]

Dougan, L.T., Addison, P.S., McKenzie, W.M.C., 2000, Fractal Analysis of Fracture; A comparison of dimension estimates: Mechanics Research Communications, 27(4), 383–392.        [ Links ]

Falconer, K. 1990. Fractal Geometry; Mathematical Foundations and Applications: New York, Wiley, 288 p.        [ Links ]

Farber, L., Tardos, G., Michaels, J.N., 2003, Use of X–ray tomography to study the porosity and morphology of granules: Powder Technology, 132, 57–63.        [ Links ]

Feder, J., 1988, Fractals: New York and London, Plenum Press, 283 p.        [ Links ]

Gauthier, B.D.M., Lake, S.D., 1993, Probabilistic modeling of faults below the limit of seismic resolution in pelican field, North Sea, offshore United Kingdom: American Association of Petroleum Geologists Bulletin, 77(5), 761–777.        [ Links ]

Hewett, TA, 1994, Fractal Methods for fracture characterization, en Yarus, J.M., Chambers, R.L. (eds), Stochastic Modeling and Geostatistics; Principles, Methods, and Case Studies: Tulsa, Oklahoma, American Association of Petroleum Geologists, Computer Applications in Geology, 3, 379 p.        [ Links ]

Hernández, E.L., Martínez, A.R., 2001, Sistema de tratamiento de imágenes PROTOM 1.0: México, D.F., Instituto Mexicano del Petróleo (IMP), Informe técnico del proyecto D.01116 Caracterización de Núcleos Mediante Tomografía de Rayos X, 73 p.        [ Links ]

Hirata, T., 1989, Fractal dimension of fault systems in Japan; fractal structure in rock fracture geometry at various scales: Pure and Applied Geophysics, 131(1–2), 157–170.        [ Links ]

Instituto Mexicano del Petróleo (IMP), 2000, La investigación en el Instituto Mexicano del Petróleo, 35 Aniversario: México, Instituto Mexicano del Petróleo, 35–51.        [ Links ]

Kant R., Rangarajan, S.K., 2003, Effect of surface roughness on interfacial reaction–diffusion admittance: Journal of Electroanalytical Chemistry, 552, 141–151.        [ Links ]

Korvin, G., 1992, Fractal Models in the Earth Science: Amsterdam, Elsevier, 395 p.        [ Links ]

La Pointe, P. R., Hudson, J. A., 1985, Characterization and interpretation of rock mass joint patterns: Denver, Colorado, Geological Society of America, Special Paper, 199, 37 p.        [ Links ]

Long, J.C.S., Billaux, D.M., 1987, From field data to fracture network modeling; an example incorporating spatial structure: Water Resources Research, 23, 1201–1216.        [ Links ]

Malamud, B.D., Turcotte, D.L., 1999, Self–affine time series; measures of weak and strong persistence: Journal of statistical planning and interference, 80, 173–196.        [ Links ]

Mandelbrot, B.B., 1983, The Fractal Geometry of Nature: New York, W.H. Freeman and Company, 468 p.        [ Links ]

Marcelino, V., Stoops, G., 1996, A weathering score for sandy soil materials based on the intensity of etching of quartz grains: European Journal of Soil Science, 47, 7–12.        [ Links ]

Marret, R., Allmendinger, R.W., 1991, Estimates of strain due to brittle faulting; sampling of fault populations: Journal of Structural Geology, 13, 735–738.        [ Links ]

Martinez–Angeles, R., 2002, Metodología de caracterización estática mediante tomografía de Rayos X: México, D.F., Instituto Mexicano del Petróleo (IMP), Informe de Investigación, 103 p.        [ Links ]

Martínez–Angeles, R., Pérez–Rosales, C, 2000. Determination of basic geometrical characteristics of fractured porous media by X–Ray computerized tomography and digital photography: Society of Petroleum Engineers, Paper SPE 77780.        [ Links ]

Martínez–Angeles, R., Hernández–Escobedo, L., Pérez–Rosales, C, 2002. 3 D quantification of vugs and fractures networks in limestone cores: Society of Petroleum Engineers, SEP 74347.        [ Links ]

Mendoza, J.S., 1998, Computing petrophysical properties in porous rocks using a boundary–element technique: Mathematical Geology, 30(7), 889–909.        [ Links ]

Nieto–Samaniego, A. F., Alaniz–Alvarez, S. A., Toisón, G., Oleschko, K., Xu, S.–S., Pérez–Venzor, J. A., 2005, Spatial distribution, scaling and self–similar behavior of fracture arrays in the Los Planes Fault, Baja California Sur, Mexico: Pure and Applied Geophysics, 162, 805–826.        [ Links ]

Nolte, D.D., Pyrak–Nolte, L.J., Cook, N.G., 1989, The fractal geometry of flow paths in natural fractures in rock and the approach to percolation: Pure and Applied Geophysics, 131, 111–138.        [ Links ]

Oleschko, K., Figueroa, S., Miranda, M.E., Vuelvas, M.A., Solleiro, R., E. 2000, Mass fractal dimensions and some selected physical properties of contrasting soils and sediments of Mexico: Soil and Tillage Research, 55, 43–61.        [ Links ]

Oleschko, K., Parrot, J.F., Miranda, M.E. Taud, H., 1998, Análisis fractal comparativo de algunos suelos de México; un paso hacia la modelación de flujos, in Aldama, A.A., Aparicio, J., Berezowsky, M., Cruiskhank, C, Domínguez, R., Fuentes, R., Maza, J.A., Menéndez, C, Pérez–Franco, D., Sotelo, G. (eds.), XVIII Congreso Latinoamericano de Hidráulica, Oaxaca, México, 13–16 de octubre, Memorias, Resúmenes: International Association of Hydraulic Engineering and Research, Asociación Mexicana de Hidráulica, Instituto Mexicano de Tecnología del Agua, 757–765.        [ Links ]

Oleschko, K., Parrot, J.F., Shoba, S., Stoops, G., Marcelino, V., 2004, Weathering; toward a fractal quantifying: Mathematical Geology, 36(5), 607–627.        [ Links ]

Orbach, R., 1986, Dynamics of fractal networks: Science, 231, 814–819.        [ Links ]

Paredes, C., Elorza, F.J., 1999, Fractal and multifractal analysis of fractured geological media; surface–subsurface correlation: Computer and Geosciences, 25, 1081–1096.        [ Links ]

Parrot, J.F., 1997, Implementación y operación del algoritmo Fractal: México, D.F., Instituto de Geología, Universidad Nacional Autónoma de México, Informe Final Proyecto DGAPA, 35 p.        [ Links ]

Parrot, J.F., Taud, H., 1998, Implementación y operación del algoritmo Bromov: México, D.F., Instituto de Geología, Universidad Nacional Autónoma de México, Informe Final Proyecto DGAPA, 40 p.        [ Links ]

Piggott, A.R., 1997, Fractal relations for the diameter and trace length of disc–shaped fractures: Journal Geophysical Research, Solid Earth, 102(B8), 18121–18125.        [ Links ]

Rieu, M., Sposito, G., 1991, Fractal fragmentation, soil porosity and water properties, I. Theory: Soil Science Society of America Journal, 55, 1231–1238.        [ Links ]

Santos, L.O.E., Philippi, P.C., Damiani, M.C., Fernandes, C.P., 2002, Using three–dimensional reconstructed microstructures for predicting intrinsic permeability of reservoirs rocks based on a Boolean lattice gas method: Journal of Petroleum Science and Engineering, 35, 109–124.        [ Links ]

Seffens, W., 1999, Order from chaos: Science, 285, 1228.        [ Links ]

Turner, M.J., Blackledge, J.M., Andrews, PR., 1998, Fractal geometry in digital imaging: Cambridge, UK, Academic Press, 328 p.        [ Links ]

Van Dijk, I.P, Bello, M., Toscano, C., Versan A., Nardon, S., 2000, Tectonic model and three–dimensional fracture network análisis of Monte Alpi (southern Apennines): Tectonophysics, 324, 203–237.        [ Links ]

Velde, B., Dubois, J., Touchard, G., Badri, A., 1990, Fractal analysis of fractures in rocks; the Cantorr's dust method: Tectonophysics, 179, 345–352.        [ Links ]

Walsh, J.J., Watterson, J., Yielding, G., 1991, The importance of small scale faulting in regional extension: Nature, 351, 391–393.        [ Links ]