Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Sociedad Química de México
versión impresa ISSN 0583-7693
Rev. Soc. Quím. Méx vol.47 no.1 Ciudad de México ene./mar. 2003
Investigación
Modeling of the Free-Radical Copolymerization Kinetics with Crosslinking of Methyl Methacrylate / Ethylene Glycol Dimethacrylate Up to High Conversions and Considering Thermal Effects
Eduardo Vivaldo-Lima*, Rosalba García-Pérez, and Oswaldo J. Celedón-Briones
Departamento de Ingeniería Química, Facultad de Química, Conjunto E, Universidad Nacional Autónoma de México, Ciudad Universitaria, México D.F., CP 04510, México. Tel.: 5622-5256; Fax: 5622-5355. E-mail: vivaldo@servidor.unam.mx
Recibido el 13 de marzo del 2002.
Aceptado el 28 de enero del 2003.
Abstract
A mathematical model for the free radical copolymerization kinetics with crosslinking of vinyl / divinyl monomers is used to model the free-radical copolymerization of methyl methacrylate (MMA)/ethylene glycol dimethacrylate (EGDMA). Good agreement between model predictions and experimental data from the literature is obtained at low conversions, and low crosslinker concentrations. The agreement is also good at high conversions, and intermediate crosslinker concentrations, if thermal effects in ampoule copolymerization are incorporated into the model, through an energy balance. The thermal effects become important when ampoules greater than 0.5 mm in external diameter are used.
Keywords: Crosslinking, copolymerization, polymer network, MMA, EGDMA, mathematical modeling.
Resumen
Se usa un modelo matemático para copolimerización por radicales libres con entrecruzamiento para modelar el comportamiento del sistema de copolimerización metacrilato de metilo (MMA) / dimetacrilato de etilén glicol (EGDMA). Las predicciones del modelo se comparan contra datos experimentales de literatura, teniendo buena concordancia a bajas conversiones, y bajas concentraciones de agente de entrecruzamiento. Si se consideran en el modelo los efectos térmicos asociados a la polimerización con temperatura no uniforme en ampolletas de más de 0.5 mm de diámetro externo, la concordancia es aceptable aún a medias y altas conversiones, y a concentraciones medias de EGDMA.
Palabras clave: Entrecruzamiento, copolimerización, red polimérica, MMA, EGDMA, modelos matemáticos.
Introduction
Crosslinked polymers (polymer networks) are very important in technology, medicine, biotechnology, and agriculture (as construction materials, polymer glasses with high mechanical strength and high thermal stability, rubbers, ion-exchange resins and absorbents, insoluble polymer reagents, etc.). However, the treatment of polymer networks is difficult from any perspective. Polymer gels are difficult to handle experimentally, the characterization of their properties is a non-trivial subject, with several conventional theories being inapplicable to those materials. The modelling of polymer network formation is also a formidable task.
As explained in Penlidis et al. [1], a mechanistic process model is a mathematical form derived from consideration of a supposed mechanism. Mechanistic models are typically formulated in terms of differential equations, and are usually non-linear in the parameters. Judgement is needed in deciding when and when not to use mechanistic models. Mechanistic model development could be difficult and time consuming, and might be improvident if all that was needed might be achieved much more economically by empirical methods using factorials and response surface designs, i.e., empirical modeling. By contrast, a mechanistic approach is justified (a) whenever a basic understanding of the system is essential, or (b) when the state of the art is sufficiently advanced to make a useful mechanistic model easily available. Mechanistic models can contribute to scientific understanding, provide a basis for extrapolation and even interpolation, and provide a representation of the system's response function that is more parsimonious than that obtained empirically. A mechanistic model can suggest with greater certainty new sets of experimental conditions that are worthy of investigation.
In the case of production of polymer networks via free-radical copolymerization of vinyl / divinyl monomers, the complex and tedious experimental techniques can be reduced to the minimum necessary by using mechanistic mathematical models of intermediate degree of complexity. Material and process design, and even process operator training, can be facilitated by the use of mathematical models and process simulators based upon them.
There are several theories to explain gelation and polymer network formation. These theories are statistical or kinetic in nature, and have been known for decades. Reviews in this topic are available elsewhere [2,3]. However, the use of sound mathematical models with predictive capabilities has been very limited. In the context of free-radical copolymerization with crosslinking, quite complete and general kinetic models have been developed [4,5], but their application to actual systems require to make many assumptions and simplifications, which makes them lose their appeal.
Hutchinson [6] developed a mathematical model of intermediate degree of complexity based upon the method of moments. The model predicts the effect of branching on molecular weight development (molecular weight averages), including internal cyclization and diffusion-controlled termination. The model was validated using experimental data from the literature for the copolymerization of methyl methacrylate (MMA) / ethylene glycol dimethacrylate (EGDMA).
A similar model was developed by Vivaldo-Lima et al. [2], but it was validated using experimental data for the copolymerization of styrene / divinylbenzene. The main differences with the model of Hutchinson [6] are related to the calculation of cyclization, the equations used for diffusion-controlled reactions, and the fact of using different averages of the termination kinetic rate constant. The predictive power of the model of Vivaldo-Lima et al. [2] was demonstrated by using of the model to design a reaction recipe for a suspension copolymerization of styrene / divinylbenzene outside the ranges of variation of the operating variables used in the parameter estimation stage, and then running the experiments at the designed conditions [7].
Zhu and Hamielec [8] experimentally proved that "iso-thermal" ampoule copolymerizations of MMA / EGDMA present severe thermal effects, which manifest as the development of temperature profiles with a maximum of up to 20 deg Celsius above the controlled (wall) temperature, at the center of the ampoules. Vivaldo-Lima et al. [2] modeled these thermal effects coupling an energy balance to their kinetic model, and studied its effect on the copolymerization of styrene / divinylbenzene. Although there were no experimental data on temperature profiles in ampoule copolymerizations of styrene / divinylbenzene, their maximum temperatures at the center of the ampoules were in the same order of magnitude as the ones measured by Zhu and Hamielec for copolymerization of MMA / EGDMA, at similar concentrations of crosslinker (EGDMA) [8].
In this paper, the mathematical model of Vivaldo-Lima et al. [2] is used to model the copolymerization of MMA / EGDMA, using experimental data from the literature to validate the model for this application. Thermal effects are considered by coupling an energy balance to the kinetic and moment equations.
Highlights about the mathematical model
The reaction mechanism for free-radical copolymerization kinetics with crosslinking considered in this paper includes the following reactions: chemical initiation, inhibition, propagation, transfer to monomer, transfer to small molecules, transfer to polymer, transfer to initiator, crosslinking through radical attack to pendant double bonds, and radical termination by combination and disproportionation. The reaction scheme is shown below. Symbols are explained in the nomenclature.


The mathematical model developed by Vivaldo-Lima et al. [2] is based on the Tobita-Hamielec [5] model for crosslinking kinetics for the pregelation period, an improved version of the Marten-Hamielec model for diffusion-controlled kinetics in free-radical polymerization [9] (which incorporates the recommendations of Zhu and Hamielec [10] on the use of different number and weight average termination constants), and a simple phenomenological approach for the termination kinetic constant during the post-gelation period (although simple, this approach takes into account the unequal reactivity of vinyl groups and cyclization reactions). Some features and characteristics of the kinetic model are described below.
The model consists of a set of ordinary differential and algebraic equations that describe the most important reactions that take place during the copolymerization, according to the reaction scheme shown above. These equations are listed in Table 1. The most important equations dealing with diffusion-controlled reactions, pseudo-homopolymer approach, and behaviour during the post-gelation period are listed in Tables 2, 3, and 4, respectively.




The kinetic scheme can be treated as if it was a homopolymerization by making use of the "pseudo-kinetic rate constants method", developed by Hamielec and MacGregor [11]. The method of moments is used to follow the molecular weight development. Initiation, propagation and termination reactions are considered to be diffusion-controlled, and are modelled using a free-volume theory from the start of the polymerization. Two averages, number- and weight-average termination rate constants, are used to model the mechanism of bimolecular termination. The number average termination kinetic rate constant, ktn, is used to calculate polymerization rate and number average molecular weight. The weight average termination kinetic rate constant, ktw, is used to calculate the weight average molecular weight. These averages depend on polydispersity and conversion, and are defined in such a way that no additional parameters are needed in the model.
All diffusion-controlled reactions are modelled using a "series" structure for the effective kinetic rate constants, as opposed to the rather common "parallel" approach. The differences between these two modelling approaches are explained in detail in Vivaldo-Lima et al. [9]. The model equations can be solved using the steady-state-hypothesis (SSH) for polymer radicals, but this is reliable only during the pre-gelation period.
Cyclization reactions are modelled using the equations proposed by Tobita and Hamielec [5], although only average cyclization densities are calculated, instead of the full density distributions. Likewise, only the average crosslinking density as function of time is calculated. Tobita and Hamielec [5] generalized Flory's theory for the post-gelation period by using a crosslinking density distribution. Instead, in this paper the original Flory-Stockmayer equation for calculation of the sol fraction is used, but his simplifying assumptions regarding equal reactivity of double bonds, absence of cyclization and independence of double bonds were removed.
Results and discussion
Parameter Estimation Strategy
Whenever possible, kinetic rate constants were obtained from references where accepted experimental techniques were used (e.g., the "Pulsed Laser Polymerization", PLP, to measure propagation kinetic rate constants). In some cases, values estimated within the frame of a given model were used, provided that a clear description of the estimation procedure was available. For the situations where no experimental or reliable estimates were available, an accepted estimation procedure was used: the "error in variables method", EVM, which is a weighted non-linear multivariable regression procedure. More details on the use of this method are provided elsewhere [2,12]. Tables 5 and 6 provide a summary of the kinetic rate constants and other physical parameters, respectively.

Homopolymerization of MMA
The performance of the model was first tested using experimental data from the literature for the free-radical homopolymerization of MMA. An extensive study using 2,2'-azobis (isobutyronitrile) (AIBN) and benzoyl peroxide (BPO) as initiators (concentrations ranging from 0.006 to 0.042 mole / L), several temperatures: 45, 50, 60, 60, 70, and 90 °C, and bulk and solution (in benzene) processes, was carried out. Experimental data from different laboratories [16-24] were reproduced with the kinetic model described above, using zero as the initial concentration of crosslinker. The agreement between model predictions and experimental data is very good.
Fig. 1 shows a comparison of experimental data of Ito [20] versus predicted results for monomer conversion of MMA at 45 °C. As observed, the agreement is very good over all the range of AIBN initial concentrations. Similar results are observed in Figs. 2, 3, and 4, but at temperatures of 50, 60 and 70 °C, respectively. Experimental data of Figs. 2 and 4 are form Balke and Hamielec [21], and those of Fig. 3 from Carswell et al. [22].



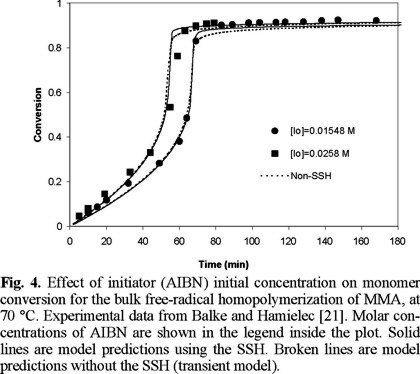
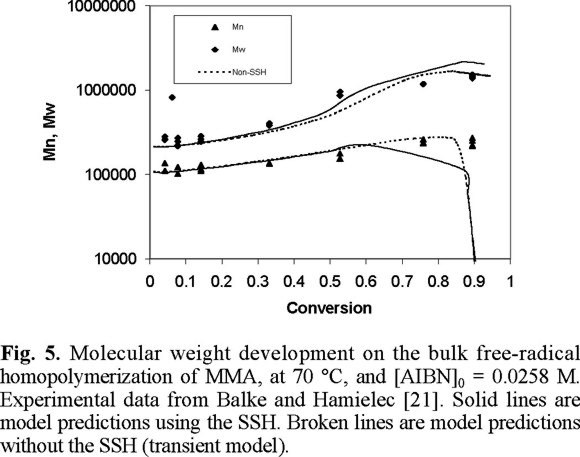
Fig. 4 shows a comparison of experimental data from Balke and Hamielec [21] and model predictions for number and weight average molecular weights at 70 °C, and [AIBN]0 = 0.0258 M. The solid lines are model predictions using the SSH, whereas the broken ones are model predictions without the SSH. The agreement is very good, except at very high conversions where model predictions of Mn drop more rapidly than the experimental values. Similar results were obtained at the other temperatures and initiator initial concentrations of Figs. 1 to 4 (2, 3).
The number average molecular weight in a free-radical polymerization is determined by the ratio of rate of propagation to rate of radical termination. Therefore, this ratio will depend on the ratio of kp[M] / (sqrt(kt*2*f*kd*[I])). The slow increase in Mn is caused by the auto-acceleration effect (the decrease in kt), but at high conversions the propagation reaction also becomes diffusion-controlled (kp decreases). The sharp decrease in Mn at very high conversions, shown in Fig. 5, may be caused by an exaggerated diffusion-controlled effect on kp, or a weak diffusion-controlled effect on the initiation reaction (a not enough decrease of f).
Figs. 6 and 7 show a comparison of experimental data by Balke and Hamielec [21] and model predictions, at 90 °C. The agreement is again very good, as in the previous cases at lower temperatures. Fig. 8 shows a comparison of experimental data and model predictions of total radical concentration versus time for the bulk free-radical homopolymerization of MMA, at 70 °C, and [AIBN]0 = 0.3 wt. %. The experimental data were obtained by Zhu et al. [23] using electro spin resonance (ESR). The agreement is very good, which shows some of the predictive capabilities of the model, given the fact that no fine tuning of the parameters was needed to reproduce the experimental data.



So far, all the cases shown here have been polymerizations carried out in bulk. Fig. 9 shows the performance of the model for polymerizations carried out in solution. The solvent used was benzene. The experimental data are from Schulz and Harborth [24]. The agreement is very good, and once again, no fine-tuning of parameters was needed.
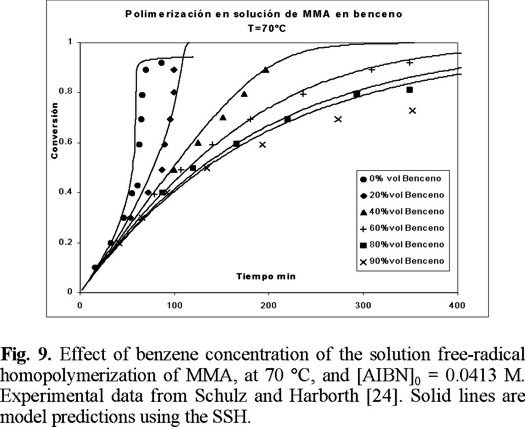
From Figs. 1 to 9 (2, 3, 4, 5, 6, 7, 8) it is observed that our model is very good for free-radical homopolymerizations, under a large range of temperatures, initiator initial concentrations, and solvent concentrations. This agreement provided confidence on the estimates of the kinetic rate constants for the homopolymerization situation. The only parameters that were estimated using the error in variables method (EVM) for the homopolymerization case were A and B (free-volume parameters for diffusion-controlled reactions), and ktn, the overall number average termination kinetic rate constant.
Copolymerization of MMA / EGDMA
With exception of the parameters mentioned before for homopolymerization of MMA, the only estimated parameters for the copolymerization situation were the crosslinking kinetic rate constants (k*ij). The main assumptions regarding the values of some of the kinetic parameters are summarized in Table 5.
Figures 10 to 12 (11) show a comparison of experimental data of Tobita [25] and model predictions for the bulk free-radical copolymerization of MMA / EGDMA at low concentrations of EGDMA: 0.3, 0.5 and 1 wt. %, respectively. The solid lines are model predictions using the SSH, and the broken lines are without the SSH. At 0.3 and 0.5 there is not significant difference between using or not the SSH, although the non-SSH simulations lie closer to the experimental data. At 1 wt. % of EGDMA, however, there is a larger difference between the simulations with and without using the SSH, and this time the SSH simulations lie closer to the experimental data. In the three cases the SSH simulations lie above the non-SSH ones. This behavior is explained by the fact that the model parameters estimated for MMA homopolymerization were obtained using a regression program with the SSH model implemented on it.



Fig. 13 shows a comparison of experimental data of Tobita [25] versus non-SSH model predictions for overall monomer conversion. The isolated circles, squares and triangles are experimental data at 1, 5 and 15 wt. % of EGDMA, respectively. Also shown in the plot are two sets of three lines. The three lines of one set are solid lines, and the other three lines of the second set are small symbols along solid lines. The solid lines are model predictions assuming that the process is isothermal. The lines with small symbols along them are model predictions assuming that temperature along the central line of the ampoules used by Tobita [25] (0.5 mm OD) is not constant. From the three solid lines, the one showing the slower polymerization rate at conversions higher than 0.5, corresponds to 1 wt. % of EGDMA. The line at an intermediate polymerization rate corresponds to 5 wt. % of EGDMA, an the one showing the fastest polymerization rate corresponds to 15 wt. % of EGDMA.

The qualitative behavior observed with the isothermal simulations is adequate; namely, polymerization rate increases with crosslinker initial concentration. The agreement between experimental data and isothermal model predictions is very good at low and intermediate conversions, and acceptable at higher conversions, for the case of 1 wt. % of EGDMA. However, in the cases of 5 and 15 wt. % of EGDMA, severe discrepancies are observed. Zhu and Hamielec [8] experimentally demonstrated that homopolymerizations of MMA and copolymerizations of MMA / EGDMA carried out in glass ampoules from 0.5 to 1 mm OD in controlled temperature bath circulators present severe thermal effects, manifested by increases in temperature along the central lines of the ampoules of about 20 °C higher than the controlled temperature at the walls of the ampoules. In the actual system, temperature profiles along the radial direction of the ampoules are developed, with a maximum at the center of the ampoule. This time and space-dependent, non-isothermal behavior causes the rate of polymerization to increase, and gelation to occur sooner.
To model that non-isothermal behaviour, an energy balance was coupled to the mass conservation equations (last row of Table 1). That energy balance assumes that the reaction takes place in a stirred tank reactor, with a jacket cooled with water at 20 °C. Temperature and concentrations are assumed homogeneous inside the tank reactor. It is also assumed that the maximum heat removal capacity of the cooling system is given by the maximum heat generation in a free-radical homopolymerization of MMA. When this maximum heat removal capacity is reached in the copolymerization case, temperature starts increasing.
The lines with small symbols are simulations with the previously explained energy balance incorporated into the mathematical model. These lines were obtained using a value of UA = 0; namely, adiabatic polymerization. Although there is a significant improvement over the isothermal simulations, the agreement with experimental data is not good enough. In the cases of 5 and 15 wt. % of EGDMA, the non-isothermal simulations show a quite faster polymerization rate, moving towards the experimental data, but not reaching them. For 1 wt. % of EGDMA, and for smaller concentrations of EGDMA, the isothermal simulations are good enough.
Fig. 14 shows a good agreement between predicted and experimental data for gelation point, as a function of crosslinker initial concentration. It is observed that the higher the crosslinker concentration, the sooner gelation takes place. This is reasonable, since more pendant double bonds accessible to crosslinking are present when the amount of EGDMA is higher.

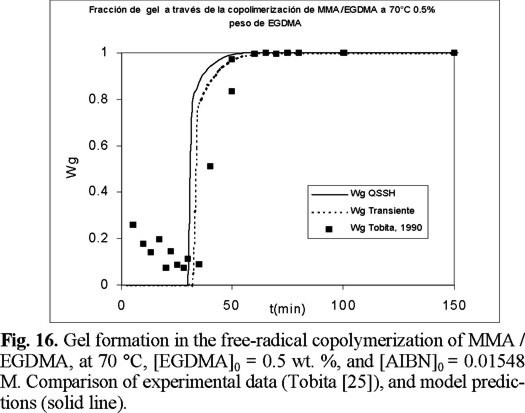
Figures 15 to 17 (16) show predicted calculations versus experimental data of weight fraction of gel, as function of time, at initial values of 0.3, 0.5, and 1 wt. % of crosslinker, respectively. The agreement is good, although the model predicts a faster gel formation than those experimentally observed. The non-SSH simulations show a better agreement than the SSH ones, although both can be considered good approximations to the experimental data.


The evolution of total radical concentration with time for copolymerizations started with 0.3 and 1 wt. % of EGDMA, is shown if Figs. 18 and 19. It is observed that the total radical concentration increases several orders of magnitude from the value at the onset of gelation until the end of the polymerization. The model captures quite nicely this behavior, which is manifested by the good agreement between model simulations and experimental data.


Finally, Figs. 20 and 21 show model predictions of number and weight average chain length versus time for the copolimerizations started with 0.3 and 1 wt. % of EGDMA, respectively. Unfortunately there were no experimental data available for molecular weight development for this system, but the profiles show the typical features of a crosslinking system. Weight average chain length increases exponentially up to the gelation point, and afterwards, the weight average chain length of the sol fraction decreases progressively due to sol consumption by the gel phase.


Concluding remarks
The mathematical model developed by Vivaldo-Lima et al. [2], which was originally validated for copolymerization of styrene / divinylbenzene, was proved to effectively explain and reproduce experimental data for the copolymerization of MMA / EGDMA. Model predictions at low crosslinker concentrations are reliable, although its behavior at high cross-linker concentrations, despite still being qualitatively correct, becomes less reliable.
It was demonstrated that heat effects are important in copolymerizations of MMA/ EGDMA, even if the experiments are carried out in thin ampoules immersed in controlled temperature baths. A first approach to model these effects by use of a simplified energy balance was presented in this paper. Although there was significant improvement over the isothermal model, the idealized situation is not yet a good enough representation of the actual reaction system in a glass ampoule with time-dependent temperature profiles in the radial direction.
Different experimental responses were simultaneously and effectively reproduced with the mathematical model, without having to perform extensive data fitting. Most of the model parameters were taken from the literature, and extra care was taken to obtain the most reliable estimates of those parameters. Whenever possible reliable experimentally measured values were used, and when not, an accepted statistical procedure was used (the "error in all variables model", EVM).
Acknowledgements
Financial support from Consejo Nacional de Ciencia y Tecnología (CONACYT), through research Projects I 30027A and 31170-U, and Dirección General de Asuntos del Personal Académico (DGAPA) of UNAM, through Project PAPIIT IN120599, is gratefully acknowledged.
Nomenclature
A Effectiveness factor to account for overlap of free-volume and separation of reactive radicals (or heat transfer area, m2, in Table 1).
C1 Empirical parameter to account for initiator efficiency decrease during the post-gelation period.
C2 Empirical parameter to account for propagation kinetic constant decrease during the post-gelation period.
C3 Empirical parameter to account for termination kinetic constant decrease during the post-gelation period.
Cp Heat capacity, J / K.
C°rd Parameter for reaction-diffusion termination.
D Effectiveness factor to account for overlap of free-volume and separation of fragment-radical molecules.
f, f0 Initiator efficiency (superscript "0" accounts for initial conditions).
f2, f20 Divinyl monomer molar fraction (also shown as f 0DVB).
F2 Instantaneous relative composition of monomer 2 in the polymer (accumulated composition if shown with an overline).
(−ΔH)r Heat of reaction, J / mol.
[I] Initiator concentration, mol / L.
kij Effective (diffusion-controlled) propagation kinetic constant for radical type i (i = 1, 2, or 3) and adding monomer unit j (j = 1, 2), L mol−1 s−1. Also represented as kpij.
k*i3 Effective (diffusion-controlled) propagation kinetic constant for addition of a pendant double bond (macromonomer) into a radical with end unit of monomer i, L mol−1 s−1. Also represented as kp*i3.
kcp Proportionality constant between primary cyclization density and mole fraction of divinyl monomer bound in the polymer chains.
kcs Proportionality constant between the average number of secondary cycles per crosslink and the fraction of "free" pendant double bonds in the primary polymer molecule.
kd Initiator decomposition kinetic constant, s−1.
kfI Pseudo-kinetic rate constant for chain transfer to initiator, L mol−1 s−1.
kfm Pseudo-kinetic rate constant for chain transfer to monomer, L mol−1 s−1.
kfp Pseudo-kinetic rate constant for chain transfer to polymer, L mol−1 s−1.
kfT Pseudo-kinetic rate constant for chain transfer to a small molecule T, L mol−1 s−1.
kfTi Kinetic constant for chain transfer of radical type i (i = 1,2 or 3) to a small molecule T, L mol−1 s−1.
kp Pseudo-kinetic propagation rate constant, L mol−1 s−1.
kp* Pseudo-kinetic rate constant for crosslinking reaction, L mol−1 s−1.
k0tc Intrinsic chemical kinetic constant for termination by combination, L mol−1 s−1.
k0td Intrinsic chemical kinetic constant for termination by disproportionation, L mol−1 s−1.
ktn Number average pseudo-kinetic rate constant for termination, L mol−1 s−1.
ktw Weight average pseudo-kinetic rate constant for termination, L mol−1 s−1.
m- Accounts for meta isomer.
[M] Total monomer concentration, mol/L.
M1, M2 Monomer molecules of MMA and EGDMA, respectively.
Mw Molecular weight, g mol−1.
n Molar mass, mol.
p- Accounts for para isomer.
Qi i-th moment of the dead polymer distribution, mol L−1.
r1 Reactivity ratio, k11 / k12.
r2 Reactivity ratio, k22 / k21.
[R*] Total polymer radical concentration (also shown as Y0), mol L−1.
R*in Molecule of primary radical.
R*n,m,i Molecule of a polymer radical with n units of monomer n, m units of monomer 2, and end unit type i (i may take the values 1, 2 or 3).
Pn,m, Inactive or "dead" polymer molecule with n units of monomer n, and m units of monomer 2.
T, Tw Temperature ("w" accounts for cooling water), °C or K. T can also represent a molecule of added chain transfer agent.
[T] Concentration of small molecule (either solvent of chain transfer agent), mol / L−1.
Tgi Glass transition temperature for species i, °C.
U Combined heat transfer coefficient, W m−2 K−1.
V Volume, L.
Vfcr2 Critical fractional free volume for glassy effect.
x Total monomer conversion.
Yi i-th moment of the polymer radical distribution, mol L−1.
Z Inhibitor.
Greek symbols
αi Expansion coefficient for species i °C−1.
β Ratio of rate of termination by combination to rate of propagation.
ρ Crosslink density.
τ Ratio of rate of termination by disproportionation plus rate of transfer reactions, to rate of propagation
φ*i Mol fraction of radical type i (i = 1, 2 o 3).
References
1. Penlidis, A.; Ponnuswamy, S. R.; Kiparissides, C.; O'Driscoll, K. F. Chem. Eng. J. 1992, 50, 95-107. [ Links ]
2. Vivaldo-Lima, E.; Hamielec, A. E.; Wood, P. E. Polym. React. Eng. 1994, 2, 87-162. [ Links ]
3. Capek, I. J. Disp. Sci. Technol. 1996, 17, 139-244. [ Links ]
4. Mikos, A. G.; Takoudis, C. G.; Peppas, N. A. Polymer 1987, 28, 998-1004. [ Links ]
5. Tobita, H.; Hamielec, A. E., in: Polymer Reaction Engineering, Reichert, K.-H., Geiseler, W., Eds., VCH Publishers, New York. 1989, 43-83. [ Links ]
6. Hutchinson, R. A. Polym. React. Eng. 1992-93, 1, 521-577. [ Links ]
7. Vivaldo-Lima, E.; Wood, P. E.; Hamielec, A. E.; Penlidis, A. J. Polym. Sci., Polym. Chem. 1998, 36, 2081-2094. [ Links ]
8. Zhu, S.; Hamielec, A. E. Polymer 1991, 32, 3021. [ Links ]
9. Vivaldo-Lima, E.; Hamielec, A. E.; Wood, P. E. Polym. React. Eng. 1994, 2, 17-85. [ Links ]
10. Zhu, S.; Hamielec, A. E. Macromolecules 1989, 22, 3093-3098. [ Links ]
11. Hamielec, A. E.; MacGregor, J. F., in: Polymer Reaction Engineering, Reichert, K.-H., Geiseler, W., Eds., Hanser Publishers, New York. 1983, 21. [ Links ]
12. García-Pérez, R., B. Sc. Thesis (Chem. Eng.), Facultad de Química, UNAM, 2000. [ Links ]
13. Marten, F. L.; Hamielec, A. E. ACS Symp. Ser. 1979, 104, 43-70. [ Links ]
14. Konstantinides, K.; Achilias, D. S.; Kiparissides, C. Polymer 1992, 33, 5019-5031. [ Links ]
15. Mao, R. Y.; Liu, Y.; Huglin, M. B.; Olmes, P. A. Macromolecules 1995, 28, 6739-6744. [ Links ]
16. Bevington, J. C.; Melville, H. W.; Taylor, R. P. J. Polym. Sci. 1954, 14, 463-476. [ Links ]
17. Landin, D. T.; Macosko, C. W. Macromolecules 1988, 21, 846-851. [ Links ]
18. Panke, D.; Stickler, M.; Wunderlich, W. Makromol. Chem. 1983, 184, 175. [ Links ]
19. Panke, D. Macromol. Theory Simul. 1995, 4, 759-772. [ Links ]
20. Ito, K. J. Polym. Sci., Polym. Chem. 1975, 13, 401-413. [ Links ]
21. Balke, S. T.; Hamielec, A. E. J. Appl. Polym. Sci. 1973, 17, 905-949. [ Links ]
22. Carswell, T. G.; Hill, D. J. T.; Londero, T. I.; O'Donnell. J. H.; Pomery, P. J.; Winzor, C. L. Polymer 1992, 33, 137-140. [ Links ]
23. Zhu, S.; Tian, Y.; Hamielec, A. E. Polymer 1990, 31, 1726-1734. [ Links ]
24. Schulz, G. V.; Harborth, G. Makromol. Chem. 1947, 1, 106. [ Links ]
25. Tobita, H. PhD Thesis, Department of Chemical Engineering, McMaster University, Hamilton, Ontario, Canada, 1990. [ Links ]
26. Li, W.-H.; Hamielec, A. E.; Crowe, C. M. Polymer 1989, 30, 1513-1517. [ Links ]














