Investigación

 

The Foundations of Density Functional Theory and Wave Quantum Mechanics

 

Jaime Keller

 

División de Estudios de Posgrado, Facultad de Química, and Facultad de Estudios Superiores-Cuautitlán, Universidad Nacional Autónoma de México, Apartado 70-528, 05410 México, D.F., México (permanent address) and Federal Institute of Technology (ETH), Festkoerperphysik ETH-Zürich, CH-8093, Switzerland. E-mail keller@servidor.unam.mx and keller@cms.tuwien.ac.at

 

Recibido el 21 de enero del 2000.
Aceptado el 24 de febrero del 2000.

 

Abstract

We analyze the notion of Density Functional Theory from the definition of a density of action over spacetime. We derive a theory to obtain the energy as a function of particle density, which contains the standard Density Functional Theory (DFT) and enlarges it by considering in one functional both the density of particles and the energy density per particle. The formulation presents a mathematical structure where the particle density is a factor of the energy per particle. The starting point is the definition of a global action density K(x) from which, by successive projections, the density K_j for a given type j of particles is projected. This density is then factorized into gauge dependent factors, which are shown to generate known relations and structures of quantum mechanics. Within DFT the minimization of the energy density functional, with respect to changes in the density, contains as a consequence two terms: the first corresponds to the standard density functional theory for non-interacting particles, and the second to the optimization of the kinetic and the interparticle interaction energy, terms that go beyond the standard DFT. We show explicitly the relation of the present approach to standard Wave Quantum Mechanics and show explicitly the reasons within space-time-action of several basic postulates of Quantum Mechanics.

Keywords: Density functional theory, fundations of quantum mechanics, principle of choice (PC).

 

Resumen

Analizaremos los fundamentos de la teoría de los funcionales de la densidad (DFT) a partir del concepto de una distribución de acción en el espacio-tiempo. Al hacerlo se aclaran sus principios y su relación con la Mecánica Cuántica formulada a partir de ecuaciones y funciones de onda. Se encuentra que en principio el concepto de DFT es más fundamental y como consecuencia que varias relaciones fundamentales de la mecánica cuántica están basadas en las propiedades de esta descripción. Proponemos y discutimos el principio de libertad para escoger descripciones aceptables equivalentes (principle of choice of acceptable equivalent description, in short, principle of choice, PC).

Palabras clave: Funcionales de la densidad, fundamentos de la mecánica cuántica, principio de selección.

 

Dedicated to the memory of Dr. Raúl Cetina Rosado

 

1. Introduction

The applicability of Quantum Mechanics to study the properties of matter at the level of nuclear, atomic, molecular and condensed matter physics is both universal and thus far unquestionable. Otherwise in the calculation of the properties of many particles systems the methods based on the use of the particle density as the basic variable have been specially successful. The method started with the suggestions of Thomas (1927) and of Fermi (1927, 1928) to use the density as the variable to compute the total energy as a functional of this density. The original idea was considered to be an approximated method where the guidance could come from wave functions quantum mechanics (see [1-8]). These ideas have also been extended to the calculation of transition probabilities and response functions. (see for example Parr and Yang and references therein [7] also [4]). In a series of papers [3] we have stated that the theory required a third theorem which introduces the correct boundary conditions and the poles of the Green's function of the system. Here we show the universality of DFT and in fact present it from first principles.

In practice the use of DFT has been very successful because, besides the use of the density functional equations, an auxiliary set of equations were introduced by considering that the density could have been constructed from a set of auxiliary functions and occupation numbers. The analysis of this procedure, now known as the Kohn-Sham equations, revealed that the set of eigenfunctions and eigenvalues are related to the elementary excitation of the system where one particle was removed at a time [2]. This is quite similar to the case of standard quantum mechanics with wave functions, where in the Hartree approximation the different states also are in one to one correspondence to the same type of excitations of the system or in the Hartree-Fock method where, according to the Koopmanns theorem, the eigenfunctions and the eigenvalues correspond to this, removal of one particle, elementary excitations of the system. It has been clear from the analysis of these cases that the inclusion of these excitations correspond to the more significant contributions to the density. Other elementary excitations contribute by amounts that are one or two orders of magnitude smaller, for example in the case of resonance energies and densities in polycyclic hydrocarbons [8].

In our present paper we will take a different starting point. The equations will be a systematic derivation from the consideration of the existence for any physical system of a density of action in spacetime and a theory relating that density of action (to the desired degree of complexity) to a representation of the physical system to which that action corresponds.

In section 2 we present the concept of a space-time-action geometry in a form suitable for our purposes. In section 3 we define the action distribution function and its main properties. In section 4 we derive the equations for the new description of matter and interactions fields. In section 5 we will analyze the procedure and in fact show that Space-Time-Action Relativity Theory (START) [9] contains a fundamental formulation of Quantum Mechanics and DFT.

 

2. Spacetime Action Geometry

In mathematical physics it is usual to consider spacetime as a frame of reference for the description of matter and the interaction fields, its use corresponds to postulating a specific approach to Geometry and in particular to Geometrical Analysis [10]. In fact spacetime, having a multivector structure and containing a spinor (and dual spinor) space, not only describes our perception of the physical nature but is also a powerful mathematical tool. Here we present both, a motivation for the use of a more general geometry, corresponding to space-time-action (STA) and the basic idea to describe matter in this geometry.

From a series of considerations [9,10], we have concluded that action has Spacetime Geometry pseudoscalar properties. Our analysis have shown that, if considered jointly with spacetime, this option is the more useful identification of the geometric properties of the action. Otherwise, when action is considered separately, it is always properly represented as a scalar quantity. The action constant is then, geometrically, both the constant relating energy-momentum to spacetime and the key to the construction of an unified geometry of space, time and action. The new geometry is derived from the introduction of an action coordinate x⁵ = a(x) 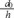where a is the density of action at a given point x of spacetime, h Planck's constant and d₀ an invariant basic length to be determined below, basically x⁵ = κa (x). We use the traditional indexes 0,1,2,3 for time and space and, also, the isomorphism between the Dirac gamma symbols γ_µ with the vectors in the geometry of spacetime.

In fact the special property of the pseudoscalar in space time (in the notation above e₅ = ie₀e₁e₂e₃) is that e₅e_µ = −e_µe₅ (from e_µe_ν = −e_νe_µ , µ ≠ ν) and then it has the same commuting properties with the generating vectors than the generating vectors among themselves. The linearly independent multivector e⁵ = iγ₅ is then the immediate candidate to introduce an additional basis vector, adding one more dimension and, through its use, obtain the five dimensional carrier space spanned by the basic vectors e_v , v = 0,1,2,3,5 with metric g_uv = diag (1,−1,−1,−1,1). Its use allows the construction of a geo metrical frame of work for the description of physical processes: a unified space-time-action geometry G_STA.

The product of e₅ = ie_ps with any element of the original Spacetime Geometry G_ST is a purely imaginary quantity with the result that the elements of the new (space-time-action) geometry are equivalent to G_STA = G_ST ⊗ C.

The value of d₀ we use (taken from the theory of the electron) is d₀ = r₀/2α, the Compton radius, where r₀ = e2/m₀c², the radius that relates the mass of the electron to an electromagnetic equivalent energy and also r₀ = µ/g_Dc the ratio of the electron magnetic moment to the Dirac monopole magnetic charge. With this choice the presentation of the theory will immediately be suitable for the study of elementary particles. Nevertheless we have shown that the same units are practical in the study of gravitational interactions.

There is a simple picture of STA: it consists of the space time continuum with an action density at every point of space time. This should be in fact the description of the space of physical phenomena. A full theory has been described elsewhere [10] as Space-Time-Action-Relativity-Theory (START). In spacetime, even if a geometrical unity has been achieved, space and time coordinates are not really equivalent for physical phenomena. While we can move in space in any direction and we can place systems in different points of space which can be changed according to the physical circumstances, time is always flowing, for all observers and systems, without any possibility of a back in time displacement. Even for an event as a light ray, where a congruence of points is defined from the property ds² = g_µνdx^µdy^ν = (ct)² − x² = 0, that is points where the spacetime distance vanishes, there is an evolution in time which can not be either put to zero or, even less, made negative. Then to have an action defined at every point of spacetime corresponds in practice to an energy ε defined at each point of space for a given observer, because the observer has to consider the local and relative rate of change of action A: ∂A/∂t = ε, as far as for it time is always flowing. A density of action in space time corresponds to a density of energy in space for a given observer. Of course density of action in spacetime is a relativistic covariant expression. In fact for another observer in relative motion with respect to the first the energy density will appear as a fourvector energy-momentum density.

Below we will call this density K = K(X, µ, ν) where the arguments of the function are the spacetime coordinates X, and two collective indexes, not used in this paper, for each one of the factors of action (energy-momentum) and (time-space). Here we should remind the reader that the Lagrangian function corresponds to the time-density of action, related but not equal to K(X).

 

3. Action Density Functional Theory and Wave Function Theory

In the space defined above we now introduce a dimensionless function K = K(X) defined at each point X of spacetime.

Here we have to make two crucial considerations about what we know about action and about quantum mechanics that will be basic for the systematic procedure presented in this section.

As we mention in the previous section for each observer the concept of action is locally the study of the energy attributed to physical phenomena. Relativity theory showed that an energy-momentum content in a given volume presents an inertia M, mass, through the basic relation M = E/c², this total energy content is independent of the form we have chosen to describe that matter. Let us for example start by considering that we have a free particle of a solid material. Which means that we have chosen a macroscopic point of view and a separation into the material itself and some external forces representing the mutual interaction between the material and the rest of the physical system. For some practical purposes this could be a sufficient degree of description where only shape and density will be required. We also know that if we consider that this piece of material is in movement relative to some measuring device, quantum mechanics can be applied to the material as a unit. Otherwise we may consider that the solid particle consists of molecules in interaction, and that there is an effective interaction potential between the molecules (this is a very common case in the study, for example, of rare gas solids). Quantum mechanics should be applied again for this system of interacting molecules. If our decision is to describe the material as electrons and nuclei we will again apply quantum mechanics at this level of detail in the description. The next steps, the study of the nucleus or the study of the nucleons are again admissible. In every case we will have a total energy which should be equal to the total energy of the previous steps and we will have the practical choice of separation at any degree of description into: constitutional energy or mass, kinetic energy and interaction energy.

That is: quantum mechanics is a universal description of the phenomena, valid for any degree of detail we might have chosen for the description and can not be a property of the components but a basic property for the description of nature. Action and spacetime are fundamental concepts in the description of nature and not concepts dependent on the system we are describing.

But, because particle density and density of action are gauge invariant physical quantities, we need to develop a procedure which can allow gaugefreedom, that is allow for arbitrary but correct and useful descriptions. This is possible with the introduction of the probability amplitude known as wave function ψ, required to contain the necessary information in a form compatible to the basic concept that the energy-momentum components are obtained by using the operator iħ∂_µ applied to the function which describes the splitting of the action density into a particle density ρ and the action per particle. The definition ρ = ψ 2 allows gauge independence. This procedure can be carried at any level of description, hence the universality of the possibilities to use Wave Equations in Quantum Mechanics.

Once we have established that we are: 1.- defining a density of action in spacetime which corresponds to an energy density in space E(x) = iħ∂ K(X)∂t for a fixed observer, for the reason to use i see below in this section, and 2.- the universality of the description, which allows a choice of the level of detail (for example: molecules → atoms → electron and nuclei to nucleons → quarks, provided that at each step the decision is formally made by selection of the type of "particle" and by the type of interaction between particle and the internal energy of the particles) we can now proceed to the steps creating a practical density functional theory:

The energy density is written as a product of a particle density and a (global) energy per particle.

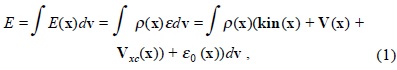
where we have defined the energy density E(x), the particle density ρ(x), the actual kinetic energy per particle kin(x), the external and average internal potential energy per particle V(x), the correction to the average kinetic and potential energy per particle arising from the statistics of the type of particles under consideration V_xc(x), and a local energy ε₀(x), basic term required to compensate for any difference in the sum of the previous terms with respect to the average energy per particle ε. Density functional theory describes the self organization of the system with density ρ (x).

The fact that we are arbitrarily defining the terms above requires the possibility of changing the description of the energy partitioning without changing the description of the density. That is that the density ρ (x) is required to be gauge invariant whereas the description of the energy (action) is gauge dependant. This is achieved by constructing the energy density as the product of two conjugated quantities Ψ(x) and Ψ^†(x) such that ρ (x) = Ψ^†(x) Ψ(x) is gauge invariant. Here we have defined an auxiliary quantity which can be essentially written in terms of the basic action a(x) and the action introduced by the gauge freedom ϕ (x) in units of ħ, as

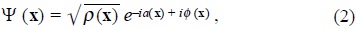
where we are restricted, by definition, to

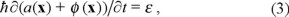
showing the gauge freedom of the description of the energy associated with the particle. In a sense at all position points x we have the same energy per particle ε which only in the simplest cases would be the sum of a kinetic and a potential energy part in the traditional sense. A well known example is the case of electron density functional theory where the kinetic energy is assumed the kinetic energy of the free electron gas and then our term ε₀(x) will contain, among other terms the difference between the actual kinetic energy and the free electron gas term. The term ε₀(x) exists either from the incomplete description of the other terms, the usual case, or from inaccuracies in the computational procedure. It acts locally to distribute the density in the form which minimizes the total energy and corresponds then to a variational procedure in the formulation of the theory. In the definition above if kin(x) + V(x) + V_xc(x)) + ε₀(x) are properly defined, then we should require that ∫ ρ(x)ε₀(x)dv = 0. The use of the Hohenberg-Kohn Theorems [1] and the Kohn-Sham minimization procedure [6] for the definition of this two terms

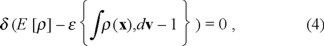
allows the direct self-consistent determination of ρ(x) and ε (see [2]).

In the formalism we have a very useful self-consistency relation

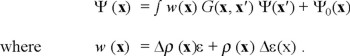
We have introduced both, the response function of the system G(x, x'), and the effective potential which would be caused either by fluctuations of the density or by differences in the local definition of energy per particle. This reaction would propagate to all points of the distribution to achieve stability. We have used elsewhere an approximation for the response function G(x, x') in terms of the lowest elementary excitations of an electron gas.

3.1 Restriction to Standard DFT

The auxiliary function Ψ in (1) is identical to the standard quantum mechanical ψ in the case of a "one" particle system, otherwise we should consider it as the function which represents the gauge dependent square root of the density of action, obeying the equations

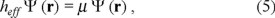
where we have defined an effective operator

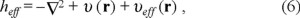
such that the system's energy

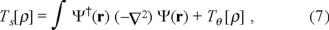
defining, variationally, the effective potential

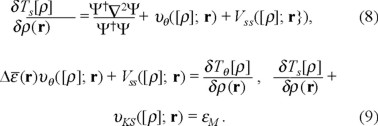
then (5) reads

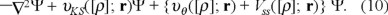
and

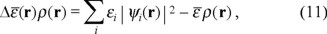
which is equivalent to the optimization of

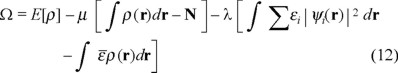
using a set of auxiliary functions ψ_i, with the index i running through all possible forms of extracting one particle from the system

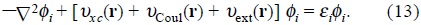
which will define the elementary excitations of the system corresponding to the removal of one particle with rate of change of the energy ε_i

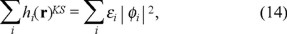
this is equivalent to the Kohn-Sham procedure and the use of the Kohn-Sham effective hamiltonian h_i(r)^KS

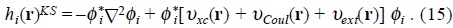
and then for the gauge dependent square root of the density auxiliary function (see [3,4a])

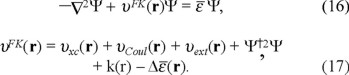
The last three terms correspond, the first two to the correct kinetic energy density and the last one, as above, the symmetry constraint potential arising from the actual values of the energy necessary to remove one electron from the system and the average energy per electron:

 

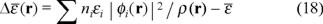
4. From Action Density Functional to Wave Mechanics

We now proceed formally to show that the procedure within START described here is equivalent to the usual postulation of the principles of the wave equation approach to quantum theory.

(1.) We have defined, for the representation of the physical system an (complex function) adimensional density of action K(X) at each space-time point X = γ_µ X^µ .

(2.) The action is factorized, for its study, into a carriers density n(X) and a local average action per particle k(X)

(3.) The energy of the system E(X) = iħ∂ K(X)/∂ t is obtained from this action density or in general

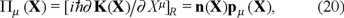
for the energy momentum four vector Π. This equation is in fact the defining equation for K.

(4.) To see the correspondence to the space-time-action geometry (STA) we remind the reader that the fifth axis of this geometry was labelled by iγ₅ and that γ₅ is the unit four-volume in spacetime, then the density

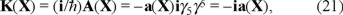
per unit spacetime volume. We see that this quantity is a pure imaginary complex number. Note that action acquires a negative sign from (iγ₅) (−iγ₅) = (γ₅)2 = −1

(5.) This action distribution representing the physical system has two sources of gauge dependence. (a) the dependence on the definition of the reference spacetime hypersurfaces in the STA space, a dependence related to gravitation, and (b) the dependence on the arbitrary (either by incomplete knowledge or by practical decision) choice of the type(s) of field(s) whose density is represented by n(X) and, by definition of the fields, their energy contributions. Here we should consider from very simple, one type of action carriers, to complicated cases like a system of an electron e⁻ and a W⁺ (which could also be a neutrino ν), where the description of the system should include the complete range of possibilities. To solve this description problem we now introduce a description and gauge dependent auxiliary function

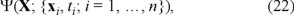
which allows to write for the action density

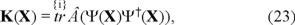
which for a single element n = 1 is

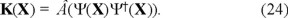
(6.) The self-consistent properties of Ψ(X; Çx_i, t_i; i = 1, ..., nç) from (19)-(24) are then

a.) From the simplest case, that of the homogeneous distribution of action with an assumed single carrier, where (defining k = Π/ħ

and therefore

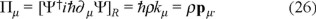
Now, defining the auxiliary reference energy-momentum m

then

where we have used the notation, in space-time-action geometry

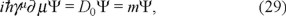
which shows that the auxiliary function Ψ has the same initial properties as the standard wave function in quantum mechanics. It is now immediate that the description freedom corresponds to the gauge theory approach, where the "Lagrangian" density is proportional to K(X), the Ψ are gauged and the D₀ operator is enlarged to the covariant derivative D, to keep K(X) gauge invariant.

b.) In the case of several identical among themselves carriers we can now construct the 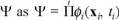and define the potentials V and V_xc accordingly or use a more complicated expression for Ψ and a (simpler) expression for V and V_xc. Otherwise a more complicated, interacting particles, definition of Ψ and V should contain the sum of the interparticle interactions. See next section.

c.) The case of several types of carriers corresponds to (sums and) products of descriptions of type b).

d.) The use of a description of an evolving system with changing types of carriers defines interaction Lagrangians where the sum of products of descriptions of type b) are used to represent our uncertainty in the actual distribution of action, keeping nevertheless the K(X) invariant.

All these descriptions obeying the principles above, show the intrinsic connection between the postulates of START and the structure and interpretation of wave quantum mechanics.

Description in Terms of Interacting Carriers

The basic description in terms of particles (particle fields in practice) is that of interacting carriers:

1) Each point of the particle field i is endowed of a self energy, expressed as its mass m_i, and spin s_i and a collection of charges {q_i^(g)}, one for every gauge field g,

2) all particles i are subjected to local external potentials V_i(x) representing the "rest of the universe" effects where

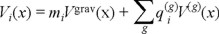
3) all particles i are supposed to have a kinetic energy contribution kin_i(x)

4) there is an interparticle pairwise potential energy

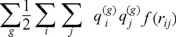
which is proportional to the products of the charges and to a function of the distances r_ij between points of the fields related to the particles, the basic example being the electromagnetic case q_i^(e)q_j^(e)/r_ij.

5) Other interaction terms, depending on the masses or spins of the particles. Until now there has been no practical use of more complicated terms, like terms depending on products of charges of different gauge fields q_i^(g)q_j^(g′). In practice, for non elementary particles, three body terms and "effective" charges have been used, this being perhaps a guide to establish that a particle is not elementary. When r_ij is large, with respect to a measure of the extent of the distribution of both the i and the j field, a center of distribution interdistance r^oij can be used in practice, fact that allows to consider the fields i and j as point-like objects.

The use of (at least) 1), 2), 3) and 4) induces either

a) the use of a non local Ψ_nl = Ψ_nl (Çx_iç) or

b) the local formulation obtained by the introduction of this non locality as a self consistent local potential (which requires for its calculation the knowledge of Ψ_nl, considered now as an auxiliary calculation procedure).

Case a) corresponds to standard quantum mechanics where the auxiliary function Ψ is constructed as sums of products of sums of basic functions. The last sum corresponds to an assumed distribution in space. The products to considering a set of those sums as an independent particle field scheme and the first sum to account both for the statistics of the auxiliary fields and for all possible forms of response of the system to the possibility of removing one particle from it.

Case b) corresponds to keeping the local Ψ(x) and introducing the result of the non local interaction as corrections to the kinetic energies obtained from ψ (x) and as an equivalent, average, local, interparticle potential where also the effect of the statistics and of the full response of the system are included. This last term is well known [5] as the local exchange-correlation potential in standard DFT. The remaining term was introduced [4] in the study of Ψ(x) for a many electron system.

This is not the only set of possibilities, a third major line of approach has been developed mainly in connection with high energy physics and the study of elementary particles. It consists in formulating an independent particle approach using an action related to the local effect of the gauge fields into the particle fields through terms q_i^(g)A_(g)(x).dx_i, the scalar product of the vector A_(g) and the vector dx_i. This is achieved at the expense of allowing independent existence to the gauge inter action fields. This has the advantage of allowing the possibility of describing the gauge fields independently of the source or target particle fields, introduce the quantization of this gauge interaction fields which carry energy-momentum, spin and geometrical information of the possible source or target fields. The gauge interaction fields are assigned a gauge independent field strength

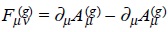
and a local action of the gauge field itself

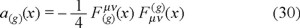
to be added to the particle's field action. The sum is a local action and a local energy-momentum by consequence. The pass from case 1) to case 3) is straightforward by partial integration using a source equation

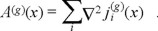
But it must be stressed that the energy related to (25) requires in general the integration over volumes much larger than those of the integration of ρ_i(x). Then in case 1) the energy related to external sources of gauge fields should be added, because only the action related to the system of particles {i} has been included.

There are many technical difficulties in this approach, which is in principle quantum field theory based in quantum electrodynamics as the simplest case and in the Maxwell theory in the classical formulation, some of them would disappear if a hybrid approach is taken, using 1) and allowing for (25) for the description of the external influences. The problems related to the non-abelian character of the gauge fields would require nevertheless the use of the special mathematical techniques now in use in the standard model of elementary particles. This considerations do not apply to the use of DFT to the many electron system, the most common example. Pairwise interactions and gauge fields are equivalent dual formulations which should be explicitly followed.

A note in the probabilistic interpretation of Ψ. Because the auxiliary functions describing the action contributions will either appear as products of functions φ₁φ₂... or as sums of functions ϕ₁ + ϕ₂ + ... the use of derivatives D as operators originate both a probabilistic interpretation and, in fact as a consequence, a systematic method to obtain Ψ.

In fact for a product φ₁φ₂, because D (aφ₁φ₂) = a[(Dφ₁)φ₂ + φ₁(Dφ₂)] the energy-momentum contributions will appear as sums of independent terms. Also, because D (aϕ₁ + ϕ₂) = aDϕ₁ + bDϕ₂, the energy contributions from a sum of functions appears as a weighted sum of dependent contributions. This is typical of probability theory and a probabilistic language will faithfully be useful to describe the total action.

An additional probabilistic concept, different from the one described above, arises from the algebra of the operators themselves, because the action being x^µp_µ, and its operator â = 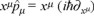, then we, from the chain rule for derivatives, obtain the operator

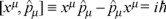
with the well known Heisenberg limitation, introducing an uncertainty in our possibilites to know (not the action but) the factors of the action, separately, for a given action distribution, up to the small but highly significant value of ħ. Because this is a fundamental restriction on the description of the action distribution as that of point like carriers this uncertainty is presented as a basic property of matter, independent from our choice to describe the matter.

We can then conclude that the action distribution in spacetime description of matter agrees, without actual limitations, with our present experimental and theoretical knowledge of matter and interaction fields.

In space-time-action geometry the main dynamical principle is that all trajectories should be minimal, then defining the (square of the) differential dS² = ds² − (da)², where dS² = g_µν dx^µdx^ν is the spacetime differential and (da)² the action differential. In a first, non united geometry, approximation the minimal principle

can be separated into the kinematical principle of (general) relativity

and the principle of minimum action

For some phenomena, light as the main example, (32) and (33) are separately obeyed given that (cdt)² − (dx)² = 0 and g_µνp^µx^ν = 0 because g_µν = diag(1, −1, −1, −1) and ε = pc = hν = hc/λ. Otherwise the principle of minimal action is universally accepted in the formulation of physical principles. If (31) is accepted a geometrical model for mass appears in our theory [9].

In relation to our construction of the auxiliary function Ψ we can then use a trial set of contributions to the action

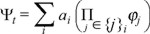
with the φ_j also a composition of functions representing some contributions to the action. A chain derivative

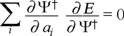
will allow the optimization of the description, then a variational principle for energy exists which is, in Action Density Functional Theory, the equivalent to the Hohenberg-Kohn Theorems [1].

 

Conclusions

We have presented an action-density functional formalism, developed it and shown that not only the standard density functional theory is recovered and that in a sense it is more fundamental than wave function wave mechanics, but also that the analysis of the mapping of the density matrix into a density allowable for density functional theory [11], requires the introduction of auxiliary terms which represent the internal symmetries of the system.

Several basic principles of quantum mechanics are shown to be natural structures in the approach developed here to describe matter as a distribution of action in space-time (energy distribution over space).

 

Acknowledgements

The author wants to thank Alejandro Keller for numerous profitable discussions as well as Mrs. Irma Vigil de Aragón for technical assistance. This paper was presented at the Foundations of Physics in the Threshold of the XXI Century Symposium, Naples, December 6-8, 1999. J.K. is a member of the Sistema Nacional de Investigadores, Conacyt, Mexico.

 

References

1. Hohenberg, P.; Kohn, W. Phys. Rev. 1964, 136, B864-B871.         [ Links ]

2. Janak, J. F. Phys. Rev. B 1978, 18, 7165-7168.         [ Links ]

3. Keller, J.; Flores, J. A.; Keller, A. Folia Chimica Theoretica Latina (Madrid) 1990, 18, 175-186.         [ Links ]

4. (a) Keller, J.; Gázquez, J. L. (Eds.) Density Functional Theory. Berlin, Springer-Verlag 1983, and references cited therein.         [ Links ] (b) Flores, J. A.; Keller, J. Phys Rev. A 1992, 6259-6262.         [ Links ]

5. Keller, J. Physics of Atomic Nuclei 1999, 62.         [ Links ]

6. Kohn, W.; Sham, L. J. Phys Rev. 1965, 140, A1133-A1138.         [ Links ]

7. Parr, R. G., Yang, W. Density Functional Theory of Atoms and Molecules. New York Oxford University Press. 1989, and references cited therein.         [ Links ]

8. Theophilou, A. J. Phys. C, 1978, 12, 5419-5430.         [ Links ]

9. Keller, J. Space-time-action geometrical unity as origin of a structural theory of matter. Proc. Int. Conf. Geometrization of Physics. Kazan State University, Kazan. October 4-8, 1999;         [ Links ] Keller, J. Turkish Journal of Physics 2000, in press.

10. Keller, J.; Winberger, P. Phil. Mag. 2000 (to be published).

11. (a) Keller, J. Int. J. Quantum Chem. Symp. 1986, 20, 767.         [ Links ] (b) Keller, J.; Ludeña, E. Int. J. Quantum Chem. Sym. 1987, 21, 171.         [ Links ]