Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Problemas del desarrollo
versión impresa ISSN 0301-7036
Prob. Des vol.52 no.205 Ciudad de México abr./jun. 2021 Epub 23-Ago-2021
https://doi.org/10.22201/iiec.20078951e.2021.205.69636
Articles
Economic growth and income distribution in Peru
aNational University of Piura, Peru. Email addresses: lvaronac@unp.edu.pe and jgonzalesc@unp.edu.pe, respectively.
This article analyzes the causal determinants of income distribution in Peru (IDP)during the period 1985-2017. There is empirical evidence suggesting that the GDP per capita and the slowed and unsustained economic growth of the economy have negatively impacted IDP. This can be conceptualized as a W-shaped causal relationship, in contrast to Kuznets' inverted-U hypothesis, thus reflecting a dual economy with productivity differences, low levels of human capital, and institutional weakness. This article contributes to the debate by making several recommendations, namely: balancing the market-state-society relationship with free-market and non-rentier economic policies, human capital investment policies, innovation and technology, and strengthening the social capital (geared towards endogenous economic growth) of inclusive and sustainable human development.
Keywords: Peru; economic growth; income distribution; Gini coefficient; 1985-2017
En el presente artículo se analizan los determinantes causales de la distribución del ingreso en Perú (DIP) durante el periodo 1985-2017. Se cuenta con evidencia empírica que apoya la hipótesis sobre que el nivel del PIB per cápita y el crecimiento económico ralentizado y no sostenido de la economía ha empeorado la DIP, reflejada en una relación de causalidad en forma de W, no cumpliéndose la hipótesis de U-invertida de Kuznets, que refleja una economía dual con diferencias de productividad, bajos niveles de capital humano y debilidad institucional. Se recomienda equilibrar la relación mercado-Estado-sociedad con políticas de economía de libre mercado y no rentistas, políticas de inversión en capital humano, innovación y tecnología, fortalecimiento del capital social -en la dirección del crecimiento económico endógeno- del desarrollo humano inclusivo y sostenible.
Palabras clave: Perú; crecimiento económico; distribución del ingreso; coeficiente Gini; capital humano 1985-2017
Clasificación JEL: C51; O11; O15; O41; O47
1. INTRODUCTION
Stylized facts show a reduction in poverty in Peru close to 34% compared to the level in 1985. Nevertheless, income distribution in Peru (IDP) has worsened by increasing the Gini (Gini) coefficient by an average of 0.11%. This scenario occurred in the period of 1985-2018, when the average annual economic growth rate was slow (1.98%).
According to Kuznets, income distribution (ID) should worsen at the beginning of economic development and, once the industrial sector employs the labor force with high-wages, inequality diminishes as a natural process (Kuznets, 1955 and 1963). However, Piketty (2014) considers state intervention a necessity to achieve equality in income distribution.
For Peru, works ranging from Figueroa’s and Webb’s (1975) seminal piece, through to later pieces such as Figueroa (1973, 1993, 2003 and 2010), Mendoza et al. (2011), Tello (2011), Yamada et al. (2016), Seminario and Zegarra (2016), Cruz-Saco et al. (2018) and, recently, Alarco et al. (2019), agree to present historical evidence on inequality in IDP.
Economic policies implemented in 1985-1990 and 1991-2017 did not fix the IDP. The State-planned Import Substitution Industrialization Development Strategy (ISIDS) gave way to the Neoliberal Development Strategy (NLDS), where the free market prevails. Both models fail to establish a sustained reversal of the IDP. As such, the following questions arise: what possible causes explain the IDP? What impact do economic growth and human capital levels have on the IDP? Does economic growth reduce IDP or is there growth without equality?
The objective of this research is to analyze the causal determinants of the IDP for the period of 1985-2017. The article is composed of seven sections. The second section is a review of the literature; while the third presents the stylized facts. The fourth section introduces the methodology used. The fifth shows the main results and the sixth the discussion, while the final section covers the conclusions.
2. REVIEW OF THE LITERATURE
The causal relationship between economic growth and ID continues to be debated theoretically and empirically. The classics, such as Smith (1776), consider it to be the specialization brought about by the division of labor that generates the increase in production and productivity that, on the one hand, generates workers’ higher wages and higher consumption and higher incomes for society. This, on the other hand, generates greater benefits for capitalists, allowing them to save, invest and accumulate capital, thus gaining greater income, wealth and economic growth for a nation. This process of generating wages and benefits is replicated in markets which lease individuals, who are guided as if by an “invisible hand” whilst seeking their own interests, to accrue benefits for a country. This implies that the market endogenizes ID among workers and capitalists through wages and benefits.
According to Ricardo (1817), ID is characterized by higher rental incomes from a fixed land supply to the detriment of workers’ wages and capitalist profits. Marx (1867) considers a living wage for workers given the “industrial reserve army” or unemployment, which is not due to marginal labor productivity, but can be political and institutional in origin. The appropriation of the surplus is not reflected in wages and is considered a benefit earmarked for investment and the accumulation of capital, affecting economic growth and worsening ID.
Marshall (1890) believes that supply and demand in markets determine the prices of goods, services and productive factors, therefore wages and interest rates do likewise in labor and capital markets, based on their marginal productivity. They thereby endogenously affect the allocation of productive factors and ID. He maintains that the state intervening with minimum wages in labor markets distorts the allocation of resources in the economy and creates unemployment, adversely affecting economic growth and ID.
Post-Keynesians such as Kaldor (1956), Kalecki (1954) and Pasinetti (1962) consider ID a function of aggregate demand. They argue that salaried employees, given their high propensity for consumption, spend a large proportion of their income on consumption, while capitalists, given their high propensity for savings, channel it into investing and accumulating capital. To sum up, aggregate demand expands and on both sides. Thus, unequal ID among capitalists and employees determines the level and composition of aggregate demand. As such, ID appears to be endogenous as a result of aggregate demand and economic growth.
For Lewis (1954), living wages exist due to overpopulation and, as such, the unequal ID is endogenous and can be explained by the growing benefits of capitalists, which are invested, accumulated and thought of as the driving force behind economic growth; an additional cause for unequal ID is stagnant living wages. He states that, in the long run, when overpopulation or unemployment eliminated, wages will grow and be paid according to marginal productivity, improving ID inequality and thus economic growth will eliminate the economy’s duality.
A pioneering work which presents empirical evidence and contrasts the relationship between economic growth and ID is that of Kuznets (1955), which finds in the case of the United States, England and Germany a worsening of ID in the early stages of development, only to later reach a turning point and improve. He demonstrates the presence of Kuznets’ inverted U Hypothesis (KUH) relationship between the two variables, which implies that there is a worsening of ID in the early stages of development in an agricultural economy. This is later reversed as economic growth improves ID, automatically trending towards ID equality in the market. According to Kuznets, ID obeys the imperfections present in labor markets, as well as the changes in productive structure and technological and productive differences.
Subsequent studies find empirical evidence which does and does not support a relationship between ID and per capita income or economic growth (Ahluwalia, 1976; De Gregorio and Lee, 2002; Deininger and Squire, 1998; Forbes, 2000; Gonzales-Castillo, 2009; Guiga and Rejeb, 2012; Heshmati, 2004; Knowles, 2005; Kuznets, 1963; Panizza, 2002; Papanek and Kyn, 1986; Ravallion, 2001; White and Anderson, 2001; Zanzzi et al., 2018).
These studies consider other causal determinants for ID in addition to economic growth. Ahluwalia (1976) explains the relationship between human capital (education) and its role as an equalizing mechanism for income. He argues that investing in human capital grows potential and improves skills and abilities which increase productivity and personal income, thereby promoting income equality in the long run. Likewise, De Gregorio and Lee (2002) find empirical evidence of a negative and statistically significant relationship between educational achievement and ID for countries in various parts of the world.
Likewise, there are authors who consider technology to be relevant, like Foellmi and Zweimüller (2017), who argue that vicious cycles caused by inequality in innovations due to the effects of price and market size create ID inequality. Perera-Tallo (2017) confirms that inequality is on the rise in many countries and associates it with technological change. He notes that technological change increases the share of the least equally distributed factor, exacerbating inequality along the growth path.
For Bourguignon and Morrisson (1990), mineral resource endowments and secondary education are the determinants in ID. For Forbes (2000) on the other hand, it is women’s and men’s education and public spending on education. De Gregorio and Lee (2002) believe that education makes economic growth more equal. For their part, Contreras and Ffrench-Davis (2012) recommend deep microeconomic reforms, which involves advancing the quality of education and public support for innovation in order to improve ID. Cheng and Wu (2016) research ID in China and find that this relationship was driven, due to low productivity, in agriculture in relation to the economy, secondary and higher education. Chong and Gradstein (2017) believe that ID is the combined effect of political and economic inequalities acting on redistributive taxes and institutional quality.
Other authors question the structure of the capitalist model due to the perverse results in ID (Alvaredo et al., 2013; Piketty, 1995, 2014 and 2015; Piketty and Saez, 2013). Piketty (2014) concludes that global capitalism provides a strong tendency towards a greater concentration of wealth and higher levels of inequality in ID, which put on display the only law governing capitalism: the capital return rate on capital “r”is higher than the economic growth rate “g”.
There is great diversity in cross-sectional and panel data studies. Nevertheless, time series studies on ID determinants and their relationship to economic growth are scarce, especially for Latin American (LA) countries or developing economies. One of the works which finds empirical evidence that proves the existence of inequality by means of KUH in Brazil is that of Keller (2012), as it demonstrates that human capital negatively explains ID.
Ranis (1980) understands that in Colombia ID is a measure of the success or failure of a society. To this end, he proposed that before resolving economic growth it should be equitable. He states that ID and growth are related and should be explained simultaneously in any theoretical context. In other words, measuring ID should not beex postthe equity with which the product was generated and distributed, but as an integral part of any positive development theory.
Ranis et al. (2000) find connections between economic growth and human development for a more global sampling of countries. Regressions among countries show a significant relationship in both directions, with public spending on health and education; and the investment rate and significant income distribution. This results in virtuous or vicious cycles, where good or poor performance in human development and economic growth reinforce each other. Ranis and Stewart (2002) replicate the previous methodology for a group of Latin American countries and the results bolster the trajectories of economic growth and ID. According to the four classification categories he suggests, Peru would be a country which went from a vicious cycle between growth and human development in the period of 1960-1990, to a more recent virtuous cycle of human development and economic growth in the period of 1990-2000.
Wahiba and El Weriemmi (2014) present empirical evidence indicating that economic growth exacerbates ID inequality in Tunisia and that the effects are accelerated by the process of trade liberalization. They find that human capital and financial development tend to counteract the perverse effects of economic growth by improving ID.
Nwosa (2019) finds empirical evidence that economic growth has a positive impact on ID inequality in Nigeria. He notes that the per capita GDP level positively affects ID, but is not statistically significant. He also finds that public spending and the population have direct impacts on ID, while market liberalization has a negative impact on ID.
In a study for Chile, Zanzzi et al. (2018) find evidence of KUH, in both growth rates and levels. He also demonstrates a negative relationship between poverty and ID, while human capital has a positive relationship, worsens ID, although it is not statistically significant.
In Peru, Figueroa and Webb (1975) analyze the impact of structural policies and reforms carried out by the government of General Juan Velasco (1968-1975). They argue that the very poor saw no significant improvement, due to both national income growth and the benefits of the steps the government has taken for redistribution. According to Figueroa (1993 and 2003), the Peruvian economy is in development and the classic, neoclassical and Keynesian economic models do not explain it. He claims that there is a capitalist economy and a peasant economy and proposes that the Peruvian economy is a stable system, but unable to eliminate dualism and the IDP. Figueroa (2010) argues that education is not an equalizing force for income and that this is explained by two factors: inequality in the initial distribution of political and economic assets among social groups and the provision of factors in society. Thus, these exogenous factors make the educational system continue to not be an equalizing force and one that creates uneven IDP.
Tello (2010 and 2011) focuses on the issue of IDP by approaching it from the dual economy or informal sector, in which much of the population’s income is generated. He asserts that improvements in the informal sector could lead to lower inequality for IDP and that economic growth does not generate a reduction in the informal sector’s size.
For Alarco et al. (2019), inequality in IDP is explained by the positive causal relationship between minimum wage and inflation; while the exchange rate and Brent oil price have a negative impact.
Finally, based on economic theory and empirical evidence, one can conclude and select as causal variables for ID inequality: per capita GDP levels, economic growth, human capital (education), natural resource endowment, productive structure, transfer mechanisms and tax policies, financial development, aggregate demand (public expenditure, savings and investment, exports) and productivity differentials and institutionality, in which technology plays an important role. Empirical evidence on the causal relationships of ID determinants is neither conclusive nor robust in developing economies.
3. STYLIZED FACTS
IDP inequality presents a persistent cyclical behavior. Figure 1 shows the evolution of the Gini coefficient for the period of 1985-2017, which ranges from 0.59 to 0.67, with periods of increase and decrease with an annual average of 0.63, implying that Peru has ID inequality far greater than countries with dynamic growth such as South Korea and Taiwan (0.28 and 0.38, respectively, according to Korzeniewicz and Moran, 2005).

Source: created by the authors. Hodrick-Prescott filter (HPF) was applied.
Figure 1 Evolution, trend and cycle of the Gini coefficient, for the period of 1985-2017. Base year 2010=100
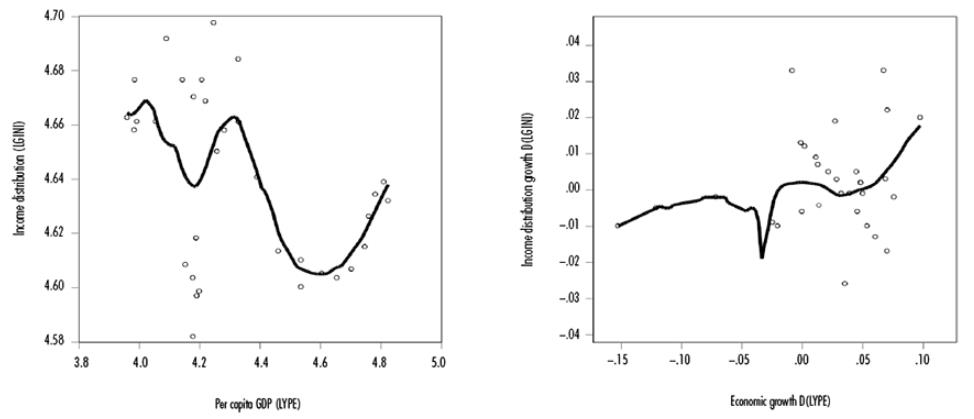
One can see that the Gini coefficient fluctuates around its average of 0.63, with a downward trend with zero order integration, I(0). Likewise, the per capita GDP level fluctuates around its average of $3,979 USD, and has zero order integration I(0) and a downward trend for the period of 1987-1992 and an upward trend in the period of 1993-2017.
It seems that in Figure 2A both variables progress together and manifest a long-term relationship. Moreover, Figure 2B shows the growth rates’ volatile evolution in both variables. It may therefore be inferred that neither economic growth nor Gini's growth rate is sustainable. Several factors had a causal role in the slow average annual economic growth of 1.98% and a trend towards inequality with an average annual Gini growth rate of 0.11%. These include a drop in international mineral prices; financial crisis (2008); public policies which do not mitigate the impact of oligopolistic power groups and institutional weakness; and expansionary monetary and fiscal policies for supply, which created hyperinflation and a recession.

Note: *indicates Gini growth rate. Source: created by the authors. Base year 2010=100.
Figure 2A-2B Evolution of income distribution and per capita GDP for the period of 1985-2017 (logarithm and first difference)
Table 1 shows descriptive statistics for the two variables relevant to the four periods analyzed. We have identified - as stylized facts - that the Peruvian economy for the period of 1985-2017 has a relative low average annual per capita income of $3,979 USD, while the Gini coefficient was 0.63, demonstrating that there is an inequality in ID. We also observed that the per capita income, due to its variation coefficient (28.6), was much more volatile than Gini (3.3). Likewise, volatilities were gradually reduced for both variables, tending to improve the IDP, with the exception of the boom period due to the export of natural resources (2002-2009), during which the per capita GDP level paradoxically increased and the IDP worsened, contrary to what was observed in most LA countries in that decade.
Table 1 Descriptive statistics for per capita GDP and Gini coefficient (level and first difference) 1987-2017
| Level | YPC$ | CG | YPC$ | CG | YPC$ | CG | YPC$ | CG | YPC$ | CG |
| Average | 3 979.0 | 0.6 | 3 112.8 | 0.6 | 3 165.9 | 0.6 | 4 007.1 | 0.6 | 5 731.8 | 0.6 |
| Standard deviation | 1136.9 | 0.02 | 446.4 | 0.02 | 198.9 | 0.02 | 508.5 | 0.02 | 430.9 | 0.01 |
| Variation coefficient | 28.6 | 3.3 | 14.3 | 2.8 | 6.3 | 3.5 | 12.7 | 3.5 | 7.5 | 1.5 |
| Observations | 33 | 33 | 8 | 8 | 9 | 9 | 8 | 8 | 8 | 8 |
| TCE | DLYPC$ | DLCG | DLPC$ | DLCG | DLYPC$ | DLCG | DLYPC$ | DLCG | DLYPC$ | DLCG |
| Average | 1.98 | 0.11 | -3.29 | 0.94 | 2.45 | 0.08 | 4.45 | -0.88 | 3.62 | 0.40 |
| Standard deviation | 5.40 | 2.44 | 8.72 | 2.65 | 3.68 | 3.46 | 2.49 | 2.10 | 2.02 | 0.58 |
| Variation coefficient | 272.0 | 2 218.1 | -265.0 | 281.0 | 150.5 | 4 325.0 | 55.8 | -238.6 | 55.8 | 145.0 |
| Observations | 32 | 32 | 7 | 7 | 9 | 9 | 8 | 8 | 8 | 8 |
| Period | 1985-2017 | 1985-1992 | 1993-2001 | 2002-2009 | 2010-2017 | |||||
Note: indicates Gini coefficient.
Source: Created by the authors
A volatile or unsustained behavior was identified as a stylized fact in Peru for the period of 1985-2017, both for economic growth and for IDP, with the volatility of economic growth being greater than the Gini in almost all periods.
We also saw for the period of 1985-1992 that economic growth was more volatile, with the average annual economic growth rate being -3.29%, associated with a worsening of the IDP with a Gini growth rate of 0.94. For the period 2002-2009 the opposite was observed with an average annual economic growth rate of 4.45%, associated with an improvement in the IDP, a Gini growth rate of -0.88% and with the IDP being more volatile in an economic environment created by the natural resources export boom.
Figure 3A shows the negative and statistically significant correlation at levels between LGINI and LYPE (r=-42%). Figure 3B presents in the form of growth rates a positive and statistically not significant association between DLGINI and DLYPE (r=18%).
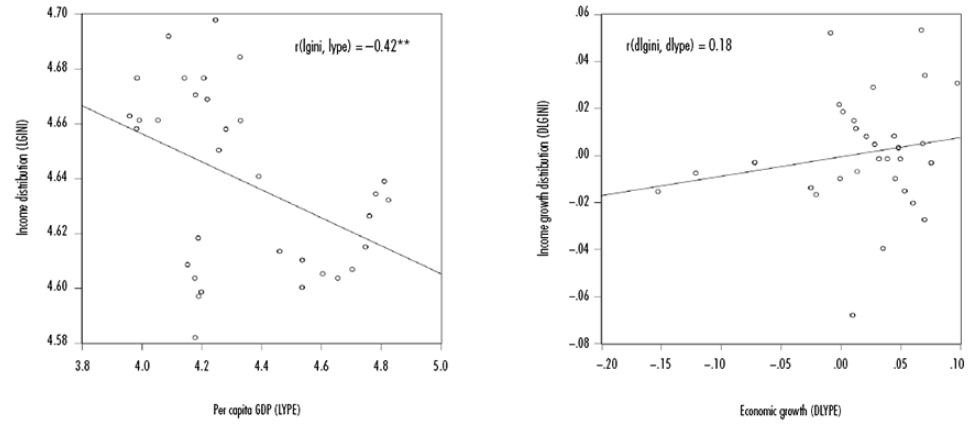
Source: created by the authors.
Figure 3A-3B Dispersion and correlation for income distribution index and per capita GDP(level and first difference)
Figure 4 A and 4B show the dynamic relationship between per capita GDP and Gini at growth rates and levels, indicating that rather than the KUH, there appears to be a W-curve (WCH) of the uneven IDP associated with cycles of unsustained economic growth and unequal IDP.
4. METHODOLOGY
Data
We used the per capita GDP growth rate for economic growth, the source of which is the Central Reserve Bank of Peru and the World Bank (WB)1. The Gini coefficient is an operational variable of the IDP developed by the National Statistical System (INEI)2. Some authors demonstrate that the data dismisses the real situation by undervaluing inequality in the IDP (Alarco et al., 2019; Cruz-Saco et al., 2018; Mendoza et al., 2011). The estimated model is an estimated time series based on Mendozaet al.(2011) together with Cruz-Sacoet al. (2018) and the WB (2018).
The INEI's Gini coefficients (GC) underestimate the inequality by excluding high-income households. The National Household Survey (ENAHO)3is shared with the WB which, like INEI, uses distribution without correcting for the missing residual from the upper part of the curve. The GC reported by the WB also underestimates inequality (Cruz-Saco et al., 2018). Mendoza et al. (2011) identify this characteristic, which coincides with the findings of Alarco et al. (2019), Figueroa and Webb (1975) and Yamada et al. (2016). Mendozaet al. (2011) use Figueroa’s methodology (1993) to determine ID.
Cruz-Saco et al. (2018) believe the income in the ENAHO only represents the first nine deciles of ID. Missing is the income from the upper decile (not represented in the ENAHO). As such, we get 12 income categories, ten deciles, the top 1% and the top 5% of the top 1%. Then, this author's estimate is used in order to determine the time series, as it takes into account the highest levels of wealthy households and has the most current data available for the period of 1997-2015. Mendoza et al.’s information (2011) is added according to growth rates for the period of 1985-1996.
The last two datums use the WB for the period of 2016-2017 (BM, 2018).
Method
The mathematical theoretical model is based on variables, identified in the empirical evidence and literature reviewed, which analyze the determinants of IDP while taking into account theoretical causalities. The hypothesis is that slow unsustained economic growth explains the uneven IDP in the period of 1985-2017, and that there are other theoretical factors that determine its behavior. According to the analysis, the theoretical function of income distribution would be:
where:
GINI t : income distribution,YPE t : per capita GDP level, andZ t are the exogenous and control variables: transfer mechanisms and tax policies operationalized as tax revenues as a percentage of GDP (ING), productive structure represented by the services sector as percentage of GDP (SSS), human capital represented by students in secondary education (EDU1) and natural resources endowment represented by income by the exploitation of natural oil resources (RRPP). Furthermore, the ENSO Phenomenon (el Niño and la Niña) is considered a variable, operationalized by the Multivariate ENSO Index (MEI) developed by the National Oceanic and Atmospheric Administration (NOAA). A dummy variable (DUM1) is employed for the change in economic growth and development strategy from 1991.
Using the theoretical function (1), an econometric model is specified by taking into account the determining variables of the IDP theoretical variable with its operational Gini variable. Subsequently, a model for testing KUH was considered. The econometric model is presented in the following linear equation (2):
For the econometric estimation of the parameters of the econometric model presented in linear equation (2), we use an ARDL model, which are linear models that analyze time series, where dependent and independent variables are related simultaneously through lag values according to Narayan (2004), Pesaran and Shin (1997) and Pesaranet al.(2001). The general ARDL model (p,q 1 ,q 2 ,q 3 ... q k ), is given by:y t which is an endogenous variable, and x1, x2, x3... xk, are exogenous variables, expressed in equation (3).
Where: ε t are innovations, α0is a constant term, α 1 is the coefficient associated with a linear trend, ψ i is the coefficient associated with lagsy t , and β j , lj are the coefficients associated with the lags from k regressorsx j,t forj= 1, 2, 3,..., k.
The starting point for ARDL applications is the intertemporal dynamics estimation. ARDL models are estimated with OLS using the endogenous variable based on exogenous variables and lags. The optimal combination is then established as the one which minimizes, in accordance with Schwarz’s (SC) criteria.
The short-term analysis finds a long-term cointegration relationship between exogenous variables and endogenous variables. We test to see if there is a long-term relationship between variables, using the limit test applied to the importance of parameters in the error correction model’s (EC) cointegration relationship. AnF-testis used with the null hypothesis that the variables are not cointegrated.
The test statistic is calculated and compared to two critical asymptotic values corresponding to cases where the variables are I(0) or I(1). When the test statistic is above the upper critical value, it rejects the null hypothesis (H0) and concludes that cointegration is possible and an EC model can be estimated.
According to Narayan (2004), the ARDL method estimates are unbiased and efficient given that they can be applied to studies with small samples like this one; they estimate the long- and short-term components of the model simultaneously, eliminating problems associated with omitted variables and autocorrelation, distinguishing between endogenous and exogenous variables.
5. RESULTS
The results suggest that the variables in first differences are stationary and ARDL estimation models can be applied. Table 2 shows the cointegration analysis of models with the limit test. The presence of a cointegration relationship in the long-term is demonstrated for all three models.
Table 2 Cointegration with the limit test, period of 1985-2017
| Model | Dependent Variable | Limit test | Cointegration | Procedure | |
| F-Statistic | t-Statistic | CP/LP | |||
| I | LGINI | 7.19 > 4.53*** | -3.91 > -3.43*** | Yes | ECM estimation |
| II | LGINI | 6.38 > 4.27*** | -4.01 > -3.43*** | Yes | ECM estimation |
| III | LGINI | 6.18 > 4.10*** | -4.37 > -3.43*** | Yes | ECM estimation |
Notes: *, **, ***; indicate statistical significance at 10%; 5% and 1%. Model uses equation (2); model II the quadratic equation, KUH (3) and model III the cubic equation, WCH (4).
Source: created by the authors.
Table 3 presents the results of estimating the ARDL model based on equation (2). In Model I there is evidence of a direct causal relationship between per capita GDP and IDP, being statistically significant at 1%. Model II contrasts KUH, achieving expected and statistically significant signs. Nevertheless, estimating model III results in a special case of the W-shaped curve. KUH is not met, which makes it possible to infer that the W curve (WCH) reflects the Peruvian economy with a slow and unsustained economic growth, with low levels of human capital and weak institutionality generated by cyclical IDP inequality.
Table 3 ARDL model estimate, period of 1985-2017
|
Method Variable |
Model I ARDL(1,2,1,1,2,0) |
Model II ARDL(1,1,1,1,1,0,0) |
Model III ARDL(1,1,0,0,1,1,0,0) |
| LGINI(-1) | 0.39** | 0.47*** | 0.42*** |
| - | (2.50) | (3.59) | (3.18) |
| LYPE | 0.41*** | 4.75** | 44.55** |
| - | (4.09) | (2.53) | (2.51) |
| LYPE(-1) | -0.20 | - 5.06** | -0.39*** |
| - | (1.42) | (2.46) | (3.93) |
| LYPE2 | - | - 0.51** | -10.27** |
| - | - | (2.33) | (4.50) |
| LYPE2(-1) | - | 0.55** | - |
| - | - | (2.25) | - |
| LYPE3 | - | - | 0.79** |
| - | - | - | (2.48) |
| LYPE(-2) | -0.22** | - | - |
| - | (2.20) | - | - |
| LING | -0.15*** | -0.10** | -0.12** |
| - | (3.29) | (2.25) | (2.73) |
| LING(-1) | -0.13** | -0.12** | -0.11** |
| - | (2.56) | (2.41) | (2.18) |
| LRRPP | 0.01 | -0.004 | 0.01 |
| - | (0.41) | (0.33) | (0.56) |
| LRRPP(-1) | 0.03** | 0.03** | 0.03** |
| - | (2.89) | (2.63) | (3.11) |
| LSSS | 0.03 | 0.38 | 0.29 |
| - | (0.06) | (1.14) | (0.87) |
| LSSS(-1) | -0.03 | - | - |
| - | (0.06) | - | - |
| LSSS(-2) | 0.75* | - | - |
| - | (1.89) | - | - |
| LEDU1 | - 0.16* | -0.19** | -0.16** |
| - | (2.05) | (2.52) | (2.14) |
| - | [0.06] | [0.02] | [0.05] |
| C | -1.14 | 3.03 | -61.47** |
| - | [0.46] | [0.34] | [2.47] |
| LMEI | -0.001 | -0.01 | -0.001 |
| - | [0.93] | [0.35] | [0.94] |
| DUM1 | 0.03 | 0.01 | 0.03 |
| - | [0.18] | [0.65] | [0.13] |
| Klein | 0.89>0.67 | 0.87 > 0.67 | 0.88 > 0.67 |
| Jarque-Bera | 1.56*** | 2.21*** | 0.50*** |
| - | [0.46] | [0.33] | [0.78] |
| LM test (1rez) | 4.36** | 4.23** | 4.36** |
| - | [0.054] | [0.055] | [0.052] |
| ARCH test | 1.64 | 0.09 | 2.28 |
| - | [0.21] | [0.76] | [0.14] |
| Ramsey test | 0.44 | 0.79 | 0.02 |
| - | [0.52] | [0.39] | [0.90] |
| R2 | 0.89 | 0.87 | 0.88 |
| F | 9.71*** | 9.47*** | 9.98*** |
| Schwarz C. | -4.63 | -4.61 | -4.66 |
| Sample range | 33 | 33 | 33 |
Notes: a lag. ( ), t. statistic [ ], probability. *, **, *** indicate statistical significance at 10°%, 5°% and 1°%. Contrast tests show that the models meet the criterion of the absence of a high degree of multicolinearity (R=0.89; 0.87; 0.88 > 0.67), normality (p=0.46; 0.33; 0.78 > 0.05), absence of serial correlation (p=0.054; 0.055; 0.052 > 0.05) and heteroskedasticity (p=0.21; 0.76; 0.14 > 0.05). Models are well specified at 5% significance (Model I, RESET statistic 0.44; F value (1,15) and p-value 0.52. Model II, RESET statistic 0.79, F value (1,17) and p-value 0.38. Model III, RESET statistic 0.016; F value(1,17) and p-value 0.90).
Source: created by the authors.
Model III also presents the impacts of a negative and statistically significant causality between human capital (education) and IDP, allowing one to infer that it tends to improve IDP inequality. Meanwhile, natural resource endowment tends to worsen the IDP through rents and a change in the productive structure due to services having an increased share of GDP.
Once cointegration was identified, the EC model was estimated, the results of which are presented in Table 4. Robust empirical evidence is found to support the hypothesis of a positive and statistically significant relationship, implying that with greater economic growth, there is a trend of greater IDP inequality (models I and III).
Table 4 EC model estimate (Model IV, V and VI), period of 1985-2017
| Variable |
Model IV CE(1,2,1,1,2,0) |
Model V CE(1,1,1,1,1,0,0) |
Model VI CE(1,1,0,0,1,1,0,0) |
| dlype | 0.41*** | 4.75*** | 44.94*** |
| (5.70) | (4.15) | (8.32) | |
| dlype(-1) | 0.21** (2.86) | ||
| d(lype2) | -0.51*** (3.85) | ||
| dling | -0.15*** | -0.10*** | -0.11*** |
| (5.05) | (3.46) | (4.18) | |
| dlrrpp | 0.01 | -0.004 | 0.01 |
| (0.65) | (0.52) | (0.98) | |
| dlsss | 0.02 (0.09) | ||
| dlsss(-1) | -0.74*** (2.94) |
- | - |
| C | 1.14*** | 3.03*** | -61.47*** |
| (7.63) | (7.84) | (8.28) | |
| LMEI | -0.001 | -0.01 | -0.001 |
| (0.15) | (1.49) | (0.12) | |
| DUM1 | 0.02** | -0.01 | 0.03*** |
| (2.39) | (1.09) | (3.27) | |
| ECM(-1) | -0.60*** | -0.52*** | -0.57*** |
| (7.52) | (7.72) | (8.28) | |
| R2 | 0.80 | 0.77 | 0.78 |
| Schwarz | -5.18 | -5.26 | -5.41 |
| F | 8.54*** | 12.08*** | 15.56*** |
Source: created by the authors.
According to Schwarz’s criterion and the empirical evidence acquired, models I, II IV, and V are discarded, leaving Model III and VI. These display a strong relationship in growth rates and levels between per capita GDP and IDP levels, behaving at levels as if it had a W-shaped curve. The chosen model passes normality, multicolinearity, serial correlation significance tests and the homoskedasticity test at 5% statistical significance.
In Table 4 one can see that in all models the error coefficient variable, ECM (-1) achieves a negative value and is statistically significant at 1%. This implies that the model’s variables cointegrate until they achieve a long-term balance and in the short term are corrected at an annual adjustment rate between 52 and 60%.
Likewise, in all models the growth rate for tax revenues has a negative causal relationship with a tendency to improve IDP inequality and is statistically significant at 1% (see Table 4). Growth in the services sector’s share of the GDP has negative causality and allows one to infer that it also tends to improve IDP, being statistically significant with a lag. The endowment of natural resources, operationalized by oil revenues, has a positive relationship and is not statistically significant, tending to increase IDP inequality, an outcome that is consistent with the resource curse, where an abundance of natural resources tends to reduce economic growth. The ENSO phenomenon, which destroys physical and human capital, does not exhibit the expected causality and is not statistically significant. The change in development strategy presents a negative causality, which implies that the change from the ISIDS, where the State prevails, to an NLDS, where the market prevails, has tended to worsen the IDP and is statistically significant.
6. DISCUSSION
Empirical evidence was found to support the hypothesis that the Peruvian economy’s per capita GDP level and slow and unsustained economic growth for the period of 1985-2017 has worsened and has failed to sustainably reverse IDP inequality, finding itself in a W-shaped causal relationship and not in Kuznet’s inverted U.
Table 5 presents the results of other works in order to compare the coefficients of per capita income and education. Model II has coefficients of 4.75 and -0.51 with the expected signs and is statistically significant at 5%, consistent and close to the results of Zanzzi et al. (2018). It estimates coefficients for both per capita GDP and its square, getting 3.08 and -0.17, which confirms KUH for Chile. Cheng and Wu (2016) get higher results than those found, 34.11 and -4.74, and also confirm KUH for China.
Table 5 Comparison of results with empirical evidence, ARDL models
| Author | Country | Method | pc GDP | (pc GDP)2 | EDU1 |
| Cheng y Wu (2016)a | China | ARDL (3,1,0) 1981-2011 |
β1 = 25.82*** p = [0.00] |
β2 = -4.01*** p = [0.00] |
ßh4 = 0.61*** p = [0.00] |
| ARDL (2,2,0) 1981-2011 |
β1 = 34.11* p = (0.06) |
β2 = -4.74* p = (0.063) |
ßs4 = 1.16 p = (0.24) |
||
| Zanzzi et al. (2018) | Chile | ARDL-MCE (1,0,0,0,0) 1984-2013 |
β1 = 3.08*** ts = (5.45) |
β2 = -0.17*** ts = (5.45) |
ßh4 = 0.01 ts = (0.38) |
| Nwosa (2019) | Nigeria | ARDL-MCE (1,1,1,1,1,1) 1981-2017 |
β1 = 1.55* ts = (2.25) p= [0.05] |
--- | --- |
Notes: (a) uses a Theil Inequality Index, with an economic activity proxy variable: urbanization; h, indicates higher education; s, secondary education.
Source: created by the authors.
Nwosa (2019) estimates an ARDL model with a linear model and the per capita GDP coefficient is 1.15, statistically significant at 10% for Nigeria, compared to the estimated basic model that achieves 0.41 at 1% significance.
The stylized facts and estimated ARDL models suggest a long-term cointegration relationship between the IDP and that the per capita GDP level, far from being a KUH, is rather a WCH, which drops until 2008 and starts a new IDP growth cycle starting in 2010. The relationship between per capita GDP and IDP in the W curve has the coefficients β1=44.5, β2=-10.2 and β3=0.78, respectively, and are statistically significant at 5% (Model III).
The results show that, for Peru, human capital (EDU1) tends to improve the IDP, demonstrating that education or investment in human capital is a mechanism for transferring benefits, not only for the economic growth and income level, but also improves distribution inequality in the IDP and achieves human development as it tends to be an equalizing force for opportunities and per capita income. Coefficients of -0.16, -0.19 and -0.16 were obtained for all three models, respectively, and these results match those of Keller (2012) in Brazil. According to Cheng and Wu (2016), the secondary education coefficient is 1.16 and not statistically significant, contrary to what has been found in the estimates. Zanzzi et al. (2018) found a low and not significant coefficient (0.01); they believe that human capital has not become a means to equalize ID in Chile.
An aggressive policy for investing in human capital is recommended, favoring quality in education, research, technological development, innovation and entrepreneurship(E+R+T+i+e).Investment in technology parks, business incubators and incubators specializing in biotech applied to the domestic biodiversity and promoting technological innovations with their ventures as the basis for truly sustainable endogenous economic growth and just improvements in uneven IDP, along with equalizing opportunities in order to achieve human development.
Investing in human capital through public health policies reduces diseases such as dengue, malaria, anemia and viral diseases, such as Covid-19, which affect human and social capital (Gonzales Castillo et al., 2020; Varona and Gonzales-Castillo, 2021), positively impacting the income level, economic growth, and tending to improve IDP inequality. Policies and reforms aimed at a knowledge economy based on production, distribution, use of knowledge and information, territorial and cluster configuration act as an agent for economic growth and human development (Tello, 2010).
Expanding tax revenues has a negative impact with a significant impact of 1%, reducing IDP inequality. Peru's tax system is characterized by being insufficient, incomplete, regressive, unfair and not ensuring the contribution of those with the most income and wealth. Furthermore, tax burdens are distorted or exempted, favoring sectors that enjoy privileged treatment through mercantilistic and rentier strategies imposed by powerful groups, with no direct taxes levied on their income and wealth. Another recommendation is to further the Tax Reform with policies that increase the tax base through a reduction or elimination of tax evasion, circumvention, or exemption and taxing wealth, generating higher income for financing which prioritizes investment in human capital, health, education and safety.
The services sector has an impact which reduces IDP inequality. The productive structure is characterized by a service sector which accounts for about 60% of GDP and much of the country’s informal workforce4, with low levels of productivity and income. The trend in Latin America and the world is to grow based on services, with high productivity and income, as they represent two thirds of the world’s total added value (Aboal et al., 2015). We recommend that the State promote, train and modernize the service sector in order to increase its productivity, helping it to stop being a dual stratum sector with low productivity and income (Figueroa, 1993 and 2003), and underemployment and informality (Tello, 2011). Likewise, policies should be implemented to diversify the economy by developing tourism, natural biodiversity, culture, gastronomy and IT and telecommunications-related services and to generate a decline in the size of the informal sector.
Peru has great potential in its natural resources. They generate income, taxes and mining and oil royalties (CRM). Historically, this wealth has not managed to sustainably reserve uneven IDP. Gonzales (2009) verifies the resource curse hypothesis in Peru. It is explained by the slow and unsustained economic growth generated by low levels of human capital, weak institutionality and corruption. CRM are also a direct mechanism for redistributing revenue and decentralizing investments in public services (health and education), through the central (40%), regional (25%) local (35%) governments. Therefore, reversing CRM's direct impact on the IDP makes it possible to recommend that contracts with companies should take into consideration subsidizing positive externalities and internalizing damages and negative externalities, as well as helping to examine whether CRM can essentially replace natural capital with human capital, seeking socio-economic and environmental profitability and to invest inE+R+T+i+eagents for future profits and sustainability.
We recommend promoting a new institutionality that involves the Central, Regional and Local Government correcting the “State’s Failures”, performing the functions which, by law, they are responsible for. At the market level, they can correct the “Market Failures” which implies that regulatory bodies are monitored and fulfill their functions related to promoting equal opportunities and businesses’ ability to compete. It is up to society to strengthen the country’s institutionality and social capital.
Economic policies and structural reforms brought about by a shift in growth and development strategies from ones where the state prevailed to a market economy, confirm that economic growth and improvement in the IDP tend not to be sustained. It also implies that the change in growth and development strategy helps reverse the trend exhibited by the per capita GDP and the course which economic growth was following since 1992. Nevertheless, it generates slowed and unsustained economic growth, being exogenous due to its response to fluctuating unsustained international demand for natural resources which have little added value, meaning the reversal in the uneven IDP has also been unsustained.
The uneven IDP fluctuates around stages of slow economic growth which are subject to international price cycles,supply shocks, natural disasters and macroeconomic policies, without seeking to achieve a country with equal sustained economic growth in the long run (Korzeniewicz and Moran, 2005). The process has not worked consistently and from Colonial times to the present there have been cycles with periods of intense progress followed by periods of setbacks. Cycles of convergence and divergence are caused by the relationships Peru and its different regions have with the world economy (Seminario and Zegarra, 2016). In line with the findings of Papanek and Kyn (1986), it is not possible to find arguments to support KUH, rather the relationship between economic growth and IDP growth is dynamic and for small and dependent economies such as Peru will fluctuate, following patterns affected by the international markets for commodities and natural resources.
According to Romer (1990), who argues that economic policy should prioritize investing in human capital for innovation, one should apply human capital, knowledge and innovation to abundant natural resources in order to stop being an economy which primarily exports raw materials and is subject to the whims of international markets; concurring with Tello (2011), Peruvian economic growth is based on the exploitation and export of natural resources, with human capital with low qualifications, low productivity and low income levels and is characterized by not creating a sufficiently powerful “trickle-down effect”. As a result, we have the dynamics of economic growth and development below the average annual rate of 2%, which does not sustainably reduce the inequality in the IDP. We recommend not changing the economic model but rather the opposite, namely to create a balance among the market, state and society, taking advantage of the large endowment of natural resources, especially its biodiversity, and investing in human capital through education. This would lead to expanding the domestic market, based on services and productive diversification with sustainable economic growth at rates greater than 5% per annum, seeking the improvement of inequality in IDP as a sustainable development goal.
7. CONCLUSIONS
There is empirical evidence which supports the hypothesis that the Peruvian economy’s per capita GDP level and its slow and unsustained economic growth for the period of 1985-2017 have worsened and have not sustainably reversed the IDP inequality reflected in a W-shaped causal relationship. As such it does not comply with KUH and reflects a dual economy with differences in income and productivity, with low levels of human capital and institutional weakness that generate or maintain cyclical and unequal IDP.
There are other determinants that explain the growth of IDP through inverse causality, tending to improve it, such as the growth of tax revenues, a highly productive services sector’s share of the GDP, investment in human capital, education, innovation and technology. Among other variables that explain a direct causality are the endowment of natural resources, the ENSO phenomenon and the change in growth and development strategy (ISIDS to NLDS).
The balance between market, state and society is necessary, along with policies that effectively correct the state’s, market’s and society’s failure to properly partake in strengthening social and institutional capital. These are proposals derived from the findings obtained that aim to achieve sustained and endogenous economic growth, which tends to reverse unequal IDP and bring about inclusive and sustainable human development.
REFERENCES
Aboal, D., Arias-Ortiz, E., Crespi, G., Garda, P., Rasteletti, A., Rubalcaba, L., Vairo, M. and Vargas, F. (2015).La innovación y la nueva economía de servicios en América Latina y el Caribe: retos e implicaciones de política. C. and R. Aboal (ed.). [ Links ]
Ahluwalia, M. S. (1976). Income distribution and development: Some stylized facts.The American Economic Review, 66(2). http://www.jstor.org/stable/1817209. [ Links ]
Alarco, G., Castillo, C. and Leyva, F. (2019). Desigualdad factorial, personal y de la riqueza en Perú, 1950-2016.Problemas del Desarrollo. Revista Latinoamericana de Economía, 50(197 ).http://dx.doi.org/10.22201/iiec.20078951e.2019.197.67473 [ Links ]
Alvaredo, F., Atkinson, A. B., Piketty, T. and Saez, E. (2013). The top 1 percent in international and historical perspective.Journal of Economic Perspectives, 27(3). https://doi.org/10.1257/jep.27.3.3 [ Links ]
Banco Mundial (BM) (2018). Índice Gini-Perú. https://datos.bancomundial.org/indicador/SI.POV.GINI?locations=PE [ Links ]
Bourguignon, F. and Morrisson, C. (1990). Income distribution, development and foreign trade: A cross-sectional analysis.European Economic Review, 34(6). https://doi.org/10.1016/0014-2921(90)90071-6 [ Links ]
Contreras, D. and Ffrench-Davis, R. (2012).Policy regimes, inequality, poverty and growth: The Chilean experience, 1973-2010. (2012/04). WIDER Working Paper. [ Links ]
Cruz-Saco, M. A., Seminario, B. and Campos, C. (2018). Desigualdad (Re) considerada Perú 1997-2015.Journal of Economics Finance International Business, 2(1). http://dx.doi.org/10.20511/je b.2018.v2n1.219 [ Links ]
Cheng, W. and Wu, Y. (2016). Understanding the kuznets process-an empirical investigation of income inequality in China: 1978-2011.Social Indicators Research, 134(2). https://doi.org/10.1007/s11205-016-1435-x [ Links ]
Chong, A. and Gradstein, M. (2017). Political and economic inequities and the shaping of institutions and redistribution.Southern Economic Journal, 83(4). https://doi.org/10.1002/soej.12206 [ Links ]
De Gregorio, J. and Lee, J. W. (2002). Education and income inequality: New evidence from cross-country data.Review of Income and Wealth, 48(3). https://doi.org/10.1111/1475-4991.00060 [ Links ]
Deininger, K. and Squire, L. (1998). New ways of looking at old issues: inequality and growth.Journal of Development Economics, 57(2). https://doi.org/10.1016/S0304-3878(98)00099-6 [ Links ]
Figueroa, A. (1973). El impacto de las reformas actuales sobre la distribución de ingresos en el Perú.Apuntes: Revista de Ciencias Sociales , (1). https://dialnet.unirioja.es/servlet/articulo?codigo=4998733 [ Links ]
______ (1993).Crisis distributiva en el Perú. PUCP. [ Links ]
______ (2003).La sociedad sigma: una teoría del desarrollo económico. PUCP. [ Links ]
______ (2010). ¿Mejora la distribución del ingreso con la educación? El caso del Perú.Revista CEPAL, 102. https://repositorio.cepal.org/handle/11362/11422 [ Links ]
Figueroa, A. and Webb, R. (1975).Distribución del ingreso en el Perú(1a. ed.). Instituto de Estudios Peruanos. [ Links ]
Foellmi, R. and Zweimüller, J. (2017). Is inequality harmful for innovation and growth? Priceversusmarket size effects.Journal of Evolutionary Economics,27(2). https://doi.org/10.1007/s00191-016-0451-y [ Links ]
Forbes, K. (2000). A reassessment of the relationship between inequality and growth.American Economic Review, 90(4). https://doi.org/10.1257/ aer.90.4.869 [ Links ]
Gonzales-Castillo, J. R. (2009).Recursos naturales y crecimiento económico en la economía peruana[Doctoral Thesis, Universidad Nacional Autónoma de México (UNAM)]. (Reg. 516). [ Links ]
Gonzales-Castillo, J. R., Varona-Castillo, L., Dominguez-Morante, M. G. and Ocaña-Gutierrez, V. R. (2020). Pandemia de la Covid-19 y las Políticas de Salud Pública en el Perú: marzo-mayo 2020.Revista de Salud Pública, 22(2). https://doi.org/10.15446/rsap.v22n2.87373 [ Links ]
Guiga, H. and Rejeb, J. B. (2012). Poverty, growth and inequality in developing countries.International Journal of Economics Financial Issues, 2(4). http://www.econjournals.com [ Links ]
Heshmati, A. (2004).Growth, inequality and poverty relationships. https://ssrn.com/abstract=602466 [ Links ]
Kaldor, N. (1956). Alternative theories of distribution.The Review of Economic Studies, 23(2). https://www.jstor.org/stable/2296292 [ Links ]
Kalecki, M. (1954).Theory of economic dynamics(1st. ed.). Routledge Library Editions. [ Links ]
Keller, Y. (2012).Inequality and economic growth in Brazil[Undergraduate thesis]. University of Zurich]. http://www.econ.uzh.ch/ipcdp/theses/ BA_YvesKeller.pdf [ Links ]
Knowles, S. (2005). Inequality and economic growth: The empirical relationship reconsidered in the light of comparable data. The Journal of Development Studies, 41(1). https://doi.org/10.1080/0022038042000276590 [ Links ]
Korzeniewicz, R. P. and Moran, T. P. (2005). Theorizing the relationship between inequality and economic growth.Theory and Society, 34(3). https://doi.org/10.1007/s11186-005-4575-6 [ Links ]
Kuznets, S. (1955). Economic growth and income inequality.The American Economic Review , 45(1). https://www.jstor.org/stable/1811581 [ Links ]
______ (1963). Quantitative aspects of the economic growth of nations: VIII. Distribution of income by size.Economic development cultural change, 11(2, Part 2). https://doi.org/10.1086/450006 [ Links ]
Lewis, W. A. (1954). Economic development with unlimited supplies of labour.Manchester Sch. Econ. Soc. Stud., 22. https://doi.org/10.1111/j. 1467-9957.1954.tb00021.x [ Links ]
Marshall, A. (1890).Principles of Economic(8a. ed.). McMillan. [ Links ]
Marx, K. (1867).El capital(vol. 1). Siglo XXI. [ Links ]
Mendoza, W., Leyva, J. and Flor, J. L. (2011). La Distribución del ingreso en el Perú: 1980-2010.Revista CIS, 9(15). http://www.untechoparachile.cl/cis [ Links ]
Narayan, P. (2004).Reformulating critical values for the bounds F-statistics approach to cointegration: An application to the tourism demand model for Fiji. https://core.ac.uk/download/pdf/36964011.pdf [ Links ]
Nwosa, P. I. (2019).Income inequality and economic growth in Nigeria: Implication for economic development. https://www.ceeol.com/search/article-detail?id=854033 [ Links ]
Panizza, U. (2002). Income inequality and economic growth: Evidence from American data.Journal of Economic Growth, 7(1). https://doi.org/10.1023/A:1013414509803 [ Links ]
Papanek, G. F. and Kyn, O. (1986). The effect on income distribution of development, the growth rate and economic strategy.Journal of Development Economics , 23(1). https://doi.org/10.1016/0304-3878(86)90079-9 [ Links ]
Pasinetti, L. L. (1962). Rate of pro t and income distribution in relation to the rate of economic growth. The Review of Economic Studies , 29(4). http://www.jstor.org/stable/2296303 [ Links ]
Perera-Tallo, F. (2017). Growing income inequality due to biased technological change.Journal of Macroeconomics, 52. https://doi.org/10.1016/j. jmacro.2017.02.002 [ Links ]
Pesaran, M. H. and Shin, Y. (1997).An autoregressive distributed-lag modelling approach to cointegration analysis. Paper presented at the Symposium at the Centennial of Ragnar Frisch, The Norwegian Academy of Science and Letters, Oslo, March 3-5, 1995. England. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.153.3246&rep=rep1&type=pdf [ Links ]
______, Shin, Y. and Smith, R. J. (2001). Bounds testing approaches to the analysis of level relationships.Journal of Applied Econometrics, 16(3). https://doi.org/10.1002/jae.616 [ Links ]
Piketty, T. (1995). Social mobility and redistributive politics.The Quarterly Journal of Economics, 110(3). https://doi.org/10.2307/2946692 [ Links ]
______ (2014).El capital en el siglo XXI(2a. ed.). Fondo de Cultura Económica. [ Links ]
______ (2015). About capital in the Twenty-First Century.American Economic Review, 105(5). https://doi.org/10.1257/aer.p20151060 [ Links ]
Piketty, T. and Saez, E. (2013). A theory of optimal inheritance taxation.Econometrica, 81(5). https://doi.org/10.3982/ECTA10712 [ Links ]
Ranis, G. (1980). Distribución del ingreso y crecimiento en Colombia.Revista Desarrollo y Sociedad, 3. https://revistas.uniandes.edu.co/doi/pdf/10.13043/dys.3.3 [ Links ]
Ranis, G. and Stewart, F. (2002). Crecimiento económico y desarrollo humano en América Latina.Revista CEPAL , 78. https://repositorio.cepal.org/handle/11362/10848 [ Links ]
______, Stewart, F. and Ramirez, A. (2000). Economic growth and human development.World Development, 28(2). https://doi.org/10.1016/S0305- 750X(99)00131-X [ Links ]
Ravallion, M. (2001). Growth, inequality and poverty: Looking beyond averages.World Development , 29(11). https://doi.org/10.1016/S0305-750X(01)00072-9 [ Links ]
Ricardo, D. (1817).On the principles of political economy and taxation. (3rd. ed., vol. 31). John Murray. [ Links ]
Romer, P. M. (1990). Endogenous technological change.Journal of Political Economy, 98(5, Part 2). https://doi.org/10.1086/261725 [ Links ]
Seminario, B. and Zegarra, M. A. (2016).La evolución de la desigualdad regional en el Perú, 1795-2007. Centro de Investigación de la Universidad del Pacífco. [ Links ]
Smith, A. (1776).An inquiry into the nature and causes of the wealth of nations . Printed byW. Strahan and T. Cadell. [ Links ]
Tello, M. (2010). Del desarrollo económico nacional al desarrollo local: aspectos teóricos.Revista CEPAL , 102. https://repositorio.cepal.org/handle/11362/11416 [ Links ]
______ (2011). Los efectos goteo (trickle down effects) del crecimiento: un análisis del desempeño económico del sector informal a nivel de regiones en el Perú, 2005-2009. In J. M. Iguíñiz and J. León (eds.).Desigualdad Distributiva en el Perú. Capítulos Libros PUCP. [ Links ]
Varona, L. and Gonzales-Castillo, J. R. (2021). Dynamics of the impact of COVID-19 on the economic activity of Peru.PLOS ONE, 16(1). https://doi.org/10.1371/journal.pone.0244920 [ Links ]
Wahiba, N. F. and El Weriemmi, M. (2014). The relationship between economic growth and income inequality.International Journal of Economics Financial Issues , 4(1). http://www.acarindex.com/dosyalar/makale/acarindex-1423903663.pdf [ Links ]
White, H. and Anderson, E. (2001). Growthversusdistribution: Does the pattern of growth matter?Development Policy Review, 19(3). https://doi. org/10.1111/1467-7679.00134 [ Links ]
Yamada, G., Castro, J. F. and Oviedo, N. A. (2016).Revisitando el coeficiente de Gini en el Perú: el rol de las políticas públicas en la evolución de la desigualdad. Documento de discusión CIUP (DD1606). Lima. [ Links ]
Zanzzi, P. F., Fernández, J. and González, V. H. (2018). Relación entre la desigualdad en el ingreso, el crecimiento económico, la educación y la pobreza: una explicación desde Kuznets para Chile.Revista Espacios, 39(44). http://www.revistaespacios.com/a18v39n44/a18v39n44p31.pdfpESA [ Links ]
Received: April 30, 2020; Accepted: November 17, 2020











 texto en
texto en