Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Problemas del desarrollo
versión impresa ISSN 0301-7036
Prob. Des vol.52 no.205 Ciudad de México abr./jun. 2021 Epub 23-Ago-2021
https://doi.org/10.22201/iiec.20078951e.2021.205.69620
Articles
Labor productivity and real wage: causal relationships in Venezuela
aLatinamerican Faculty of Social Sciences (FLACSO) - Ecuador, Department of Territory, Environment and Development, Ecuador. Email address: ivvera@flacso.edu.ed .
bVenanalytics, Economic Research Unit, Venezuela. Email address: jvera@venanalytics.com.
The discipline of economics has struggled to find a clear or well-established causal relationship between labor productivity and the real wage, despite the close statistical relationship and comovements that several studies report. The policy implications vary drastically depending on what causal link may exist between the two variables. Using conventional Granger causality tests and causality tests in a cointegration environment, with both annual and quarterly data for Venezuela, this article presents evidence showing that statistical causality runs from real wages to labor productivity, a finding which contrasts the orthodox thinking on the subject.
Keywords: Venezuela; labor productivity; wages; Granger causality tests
Para la disciplina económica no ha sido fácil encontrar una relación de causalidad clara o bien establecida entre la productividad laboral y el salario real, pese a la estrecha relación estadística y los comovimientos que varios estudios reportan. Las implicaciones de política pueden ser muy diferentes dependiendo del nexo causal que exista entre ambas variables. Usando pruebas de causalidad de Granger convencionales y pruebas de causalidad en ambiente de cointegración, tanto con datos anuales, como con datos trimestrales para Venezuela, este trabajo presenta evidencia que muestra, en contraste con el enfoque ortodoxo, que la causalidad estadística va de los salarios reales hacia la productividad laboral.
Palabras clave: Venezuela; productividad laboral; salarios; pruebas de causalidad de Granger
Clasificación JEL: C51; E24; E25; J24; J31; O47
1. INTRODUCTION
Over time economists have found various complex factors to explain changes in labor productivity. Smith (1776) became an undisputed success by highlighting the stellar role that the division of labor played in the free enterprise system while Ricardo (1817) and Marx (1867) took note of the influence had by machinery. Along with the potential effects that changes in the relative price of production factors can have on the mixture of capital and labor, there arose traits which were more neoclassical in nature. Other aspects, which nowadays are also considered as factors which influence the course of labor productivity, are the investment in next-generation equipment, acquisition of new knowledge, accumulation human capital and skills, along with information technologies.
Nevertheless, with regard to payment, or rather the incentive represented by real wages, economists have not found a clear or well-established relationship with labor productivity in spite of the close relationship reported between the two variables by many studies using statistical series.1One only needs to remember how Kaldor (1961) established the constant wages’ share of the GDP, a stylized fact which implicitly assumes and entails a long-term relationship between labor productivity and real wages. This means it is necessary to look into whether there is a causal link between these two variables, the crux which has divided theoretical and empirical literature.
There is an orthodox approach stemming from neoclassical distribution theory which thinks of the link between these two variables as one, in which the payment of factors is governed by productivity. This point of view believes real wages are adjusted in response to changes in marginal labor productivity and that only increases in labor productivity justify increases in wages. Likewise, it believes that drops in marginal labor productivity should force a decrease in real wages. If in the latter scenario there are impediments or resistance to the decrease, the adjustment is carried out by means of employment. Moreover, in a world of greater or growing global trade, keeping real wages under control and linked to increases in productivity is essential to maintaining international competitiveness.
Opposing this orthodox perspective there are other alternative approaches which reverse the causality between labor productivity and wages. The space has proven to be fertile ground for a wide variety of theories where changes in real wages may well cause the following: changes in the effort made by the workforce, changes in the relative cost of factors that affect the ratio of capital to labor, or stimuli for investing in the latest capital and technological changes (which subsequently generate changes in productivity), or variations in demand which impact the supply of innovations.
In the case of Venezuela, Baptista (2005) makes an interesting observation of how close the evolution of real wages and labor productivity was between 1950 and 2004. During that period, productivity grew at an annual rate of 1.34% while real wages grew at a rate of 1.22%. However, the author makes note of the inverted U-trajectory that these variables had taken over time and shows that starting in 1977 the upward trend reverses, so that both productivity and wages continuously drop. The growth phase (1950-1977) corresponds to a period in which Venezuela's GDP per capita doubles; while the downward trend (1977-2004) corresponds to one in which the per capita GDP at the end of the period is 25% below the initial per capita GDP. Without going too deep into the matter, Baptista (2005, p. 106) notes that the labor market in Venezuela is dominated by a “fundamental relationship” where “real wage variations always, in all cases, are adjusted in response to variations in productivity.” A large part of this work’s objectives will be to find out whether this statement can be supported empirically.
As we will see later on in detail, there are numerous empirical studies that try to determine in which direction causality flows between the real wage and labor productivity; however, most of them are aimed at contrasting this relationship in developed economies. This work presents evidence, with annual and quarterly data from both series for Venezuela, showing that the flow of causation goes from real wages to labor productivity.
Including the introduction, the study is divided into five parts: the second section presents a brief summary of the theoretical debate. The third presents empirical evidence reported by previous studies. The fourth section of the work uses the conventional Granger methodology (or test), as well as Granger's causality contrast in a cointegration environment to determine, with annual and quarterly statistical series, the flow of causation that the data shows for the Venezuelan economy. The study concludes with a few brief comments.
2. THEORETICAL DEBATE
Economic theory finds various explanations linking labor productivity to real wages. These explanations can in principle be divided into two groups: orthodox, or conventional theory that attempts to explain changes in real wages as a result of changes in labor productivity, and certain alternative theories which seek to reverse this causality by explaining changes in labor productivity as the result of changes in real wages. In truth, these theories differ not only in the order in which they establish causality between these two variables, but also in the mechanisms that explain this relationship.
The first explanation of the relationship between these two variables comes from orthodox microeconomic theory that establishes that the relationship between wages and productivity is through the labor demand curve, given the state of technology, the price of inputs, and the market price of the good produced. This approach is based on Clark’s early studies (1899) summed up in his well-known workThe Distribution of Wealth, according to which “under perfect conditions of competition, wages for all kinds of work tend to match the product which can independently be attributed to the work” (Ferguson and Gould, 1980, p. 372). Clark considers that this principle of marginal productivity determines wages. Thus, from a position of imbalance, if marginal labor productivity is higher than the real wage, companies would consider it profitable to hire more labor and put pressure against wage increases (and against a drop in labor productivity due to decreased output). Conversely, if marginal productivity is less than wages, companies will find it profitable to reduce labor, thereby generating downward pressures on wages (and upward on marginal productivity). The mechanism thereby creates a simple stability dynamic towards equilibrium.
The principle where wages are governed by productivity is so ingrained that it is not uncommon to find it in literature analyzing the labor market in developing and less developed economies. An influential study on productivity in Latin America, published by the Inter-American Development Bank (Banco Interamericano de Desarrollo [BID], 2010) describes the vicious cycle of labor productivity in the region by imposing order in this relationship in the following manner:
As less productivity results in lower real wages, it is understandable that governments try to improve workers’ standard of living with more social programs, especially for those in the informal sector. This, in turn, further widens the gap between the cost of formal and informal employment and results in more self-employed individuals and microenterprises that do not offer their workers health insurance. This trend generates more low-productivity jobs, reduces the labor supply for the most productive formal enterprises, and prevents real wage increases (BID, 2010, p. 14).
In its very recentWorld Economic Outlookreport for 2017, the International Monetary Fund (IMF) analyses the slow dynamics in global wage levels and summarizes this problem by noting:
Conversely, as productivity growth weakens, all else equal, profitability declines, along with firms’ ability to accommodate wage increases for their existing workers or their willingness to attract new workers with high wages. Thus, wage growth tends to weaken as productivity growth slows (International Monetary Fund [IMF], 2017, p. 75).
So, from the conventional perspective, the link that can be established between wages and productivity has been defined by a relationship where wages are governed by labor productivity. Among the most important policy implications arising from this vision is the impossibility of fostering wage increases which will not adversely affect employment levels if they are not linked to prior increases in labor productivity. On the other hand, regarding trade and positioning in the global economy, keeping real wages under control and tied to increases in productivity is essential to maintaining international competitiveness.
However, approached with a different logic, it is worth asking whether it is not wage increases that put pressure on productive units to increase productivity and remain competitive. There are, in fact, alternative approaches to orthodox economic theory that find it feasible to reverse the causality established between wages and labor productivity. In this setting, one can see a large set of arguments which point to and justify that increases (reductions) in real wages can have a positive (negative) impact on, and move, labor productivity.
Storm and Naastepad (2007) take on the well-known argument that arises from “efficiency wages” theories which argue that labor productivity depends positively on wage payment by increasing workers’ efforts when they are faced with a higher opportunity cost due to job loss. What happens when a worker is promoted, with a higher salary than they can earn in another job, is they try even harder to avoid being fired (Gordon, 1994). Others, such as Weisskopf et al. (1983), simply point out that substantial improvements in wages will result in greater effort and in workers cooperating to increase their productivity. Nevertheless, this relationship between wages and effort in efficiency wage models is not linear (marginal effort decreases with wages), which limits the impact which wage increases can have and leads companies to seek an optimal wage that minimizes efficient working hours (and does not exceed the market wage). Soo Khoon (2009) notes that economic effects along the lines of wage efficiency occur when increasing wages reduces the likelihood of workers quitting, allowing firms to retain a more experienced and productive human capital. On the other hand, there are those who emphasize a non-economic effect, estimating that when companies and employees operate under the restrictions of fairness, an increase in workers’ real wages will have a positive effect on labor productivity, as workers’ commitment to the company increases (Akerlof, 1982). Along these lines, Storm and Naastepad (2007) indicate that a firm which establishes wages below what is perceived to be a fair wage will in turn receive a lower level of effort from its personnel.
However, there is other literature which presents the relationship between real wages and labor productivity by calling upon the substitution effect between labor and capital goods. Veerger and Kleinknecht (2011), for example, point out that in achieving maximum profits, increases in wage costs lead firms to replace labor with capital until marginal labor productivity equals real wages. This adjustment will without a doubt be reflected in an increase in marginal labor productivity. Different authors agree with this vision. For example, Gordon (1987) and Sylos-Labini (1983) justify the relationship between real wages and labor productivity in this manner.
Sylos-Labini (1983), in particular, calls this substitution effect the “static effect” had by changes in wages on productivity, and argues that, given the technology and organization of the production process, variation in wages with respect to the price of capital goods generates a change in the ratio of labor to capital goods that subsequently leads to changes in factors’ productivity. He also engages a “dynamic effect” linked to the adoption of new technologies, in which varying relative wages stimulate technological and organizational changes; such dynamic substitution implies relative savings in the work factor. Along these lines, Marquetti (2004) starts with the hypothesis that changes in real wages pressure and reward businesses for finding and adopting new techniques with higher labor productivity, a stance quite similar to that proposed by Marx (1867) inCapitalon how increases in wage costs constitute an incentive for technological progress.
Increases in labor productivity, induced by wage improvements, can be thought of as the effect of adopting new capital. According to Madsen and Damania (2001), if wages increase and thereby bring about greater investment in fixed capital, the mere creation of a new generation of capital allows one to use the work factor in a more productive and efficient way. In a very similar vein, Veerger and Kleinknecht (2011) point out that more aggressive wage policies, adopted by trade unions and employers, will incentivize and bring about a much faster replacement of old capital with the next-generation, making the work factor much more productive.
Also, from a Schumpeterian perspective, Veerger and Kleinknecht (2011) point out that the process of creative destruction is accelerated within a context of higher real wages, which makes innovators take greater dominance of the market, thanks to the monopoly profit of their products and to a type of production process knowledge that create barriers to entry. Expelling less innovative businesses from the market results in an increase in average labor productivity at the industry level.
When wages change, there can likewise be an innovation effect thanks to demand, according to Schmookler's demand-pull theory (1966). As wages rise, effective demand rises through consumption, and increased demand for goods and services means more innovative activity. Therefore, a wage cost reduction strategy that leads to a drop in effective demand can impede the innovation process and labor productivity growth. Veerger and Kleinknecht (2014) remind us how similar this relationship between demand and productivity is to Schmookler's thesis, using the so-called Kaldor-Verdoorn Law. If a wage hike does cause a pull between demand and production, the Kaldor-Verdoorn mechanism would intervene to promote productivity gains through rising yields.
3. EMPIRICAL EVIDENCE
But what does the collected empirical evidence say about the causal relationship between real wages and labor productivity? Most known studies are aimed at contrasting this relationship in developed economies. Nayaran and Smyth (2009), for example, do so for the G7 economies (Canada, France, Germany, Italy, Japan, the United Kingdom and the United States) by looking at the contrast of unitary roots and cointegration in a panel data framework for the period of 1960-2004. The authors find that there is a single cointegration vector where productivity is the endogenous variable. The Fully Modified Ordinary Least Squares (FMOLS) estimator applied to the panel indicates (with the exception of the Canadian economy) that a 1% increase in real wages leads to an increase in labor productivity between 0.4 and 1.4%. Veerger and Kleinknecht (2011 and 2014) likewise use endogeneity-controlled panel data for 19 and 20 countries, respectively, in the Organisation for Economic Cooperation and Development (OECD) for the period of 1960-2004. These authors find in both endeavors that a change of 1% in the real wage’s growth rate produces a change in the range of 0.35-0.46% in labor productivity growth. Storm and Naastepad (2009) carried out the study for a group of 20 OECD countries during the period of 1984-2004, and found that the impact is approximately 0.3%. Madsen and Damania (2001) meanwhile use a cross-sectional data pool and time series for the manufacturing industry in 22 OECD countries and estimate a positive impact had by real wages on capital and labor productivity. Hein and Tarassow (2009) employ annual time series (1960-2007) for six OECD countries (Germany, France, the Netherlands, Austria, the United Kingdom and the United States) and in their regressions, using other control variables, find changes in real wages have a positive impact on productivity. The impact (depending on the economy) was found in the range of 0.54 to 0.23%.
One work that stands out among the studies for individual countries is that of Weisskopf et al. (1983) which uses annual data from the U.S. non-agricultural private sector for the period of 1948-1979 and finds, in time series regressions, that changes in labor productivity are influenced by wages, among other variables. At the same time, Sylos-Labini (1983) presented a study for the United States (1952-1981) and the Italian economy (1962-1980) where they use time series data for the economy as a whole and for the industrial sector in particular, thus corroborating the hypothesis of labor costs’ impact on labor productivity. Lucidi (2008) uses micro-data at the business level, acquired from the Italian Institute for Vocational Training, and attempts to replicate the Sylos-Labini specification (1983), finding for the Italian business sector an elasticity of labor productivity to labor costs that is positive and lower than the unit. While using annual time series data for Australia (1970-2001), Valadkhani (2003) acknowledges wage growth has a positive effect on productivity growth with a short-term elasticity of 0.22 in an error correction model. Upender and Sujan (2008) use aggregate data for India’s industrial sector and find, for the period of 1980-2005, a cointegration vector for average real wages and average labor productivity. An error correction model reveals that in the short term the elasticity of productivity to changes in real wages is 0.73. Yusof (2008) is among the few to have carried out a study using quarterly data (Q1 1992-Q3 2005), in this case for economy in Malaysia. The study finds a long-term relationship between labor productivity, employment and real wages. However, results stemming from a Vector Error Correction Model (VECM) show that the real wage is not a weakly exogenous variable, but rather is adjusted to maintain the cointegration relationship in the model.
There is also a large number of empirical studies which focus on contrasting the statistical causality between labor productivity and real wages. For example, Marquetti (2004) studies whether there is a long-term relationship between real wages and labor productivity in the US economy using data from 1869 to 1999. Cointegration tests indicate a long-term relationship between these variables, while Granger's causality tests in a cointegration environment indicate that real wages cause labor productivity. Strauss and Wohar (2004) use panel data for 459 sectors of the American manufacturing industry for the period of 1956-1996. Upon applying the same Granger test in a cointegration environment, they found in their results, a bidirectional causal link between real wages and labor productivity. Islam et al. (2015) led an annual time series study for Tanzania in the period of 1967-2010 with bivariate Granger causality tests which indicated that labor productivity statistically causes real wage movements. Kumar et al. (2012), for their part used annual time series data for Australia in the period of 1965-2007 to investigate the causality between labor productivity, the inflation rate and the real wage, using VECM, FMOLS and Autoregressive Distributed Lag (ARDL) estimators. They consistently found that the impact had by real wages changes on labor productivity is positive and with an elasticity between 0.5 and 0.8. Along the same lines, Yildrim (2015) applies a similar methodology (causality in a cointegration environment), but with quarterly data, for the Turkish manufacturing industry for the period between Q1 1988 and Q2 2012. Causality tests indicate that real wages actually cause labor productivity, but that productivity does not cause wages. Méndez and Hernández (2014) use the same methodology for panel data from 24 of Colombia’s departments and its manufacturing sector, though they do not find a long-term relationship between salary and productivity. As a result, the authors use a VAR model in differences. Causality tests in a VAR environment show that the relationship is bi-directional. Karaalp-Orhan (2017) investigates the relationship between labor productivity, average real wages and the unemployment rate, also for Turkey, using the bounds testing procedure in an ARDL model and applying the Toda-Yamamoto causality test with quarterly data for the period of Q1 2007 - Q4 2016. Their results find that even though the variables are cointegrated and real wages have an impact on labor productivity in the long-term, in the short term there is no statistical causality between these variables. Pyo (2018) used annual data for the economies of Japan, China and South Korea (1970-2014) and found a cointegration relationship between labor productivity and real wages in all three economies. The bivariate Granger causality test indicates that in South Korea and China real wages cause labor productivity but not in Japan. However, the reverse causality (from productivity to wages) does not appear to exist in any of these economies. Brida et al. (2010) used data from the Mexican tourism industry between 1970 and 2004. The authors found a long-term relationship between real wages and labor productivity and, in Granger causality tests with impulse response functions, confirmed that causality goes from real wages to productivity.
As a result, there are more than a few empirical studies that confirm that it is the real wage that drives changes in productivity and not the other way around.
4. EMPIRICAL TESTS FOR THE VENEZUELAN ECONOMY: DATA, METHODOLOGY AND RESULTS
To clear up the issue of the relationship between real wages and labor productivity, we used data from the Venezuelan economy and two statistical causality tests: the bivariate Granger test (1969) and the Sims test (1972), as well as the short-term causality test in a cointegration environment as suggested by Marquetti (2004) and Hossain (2005). In addition to time series with annual data for the period of 1967-2013, we also used quarterly data series for the period of Q1 1998 - Q4 2013.
Relationship with annual data
For the analysis with annual data, two statistical series will be used for the time being:
a) A real wage behavior index (RWI) for Venezuela, a series taken from the statistics provided by the Central Bank of Venezuela (CBV) for the years 1967-1998 and whose base year is 1984. From 1998 to 2013, it is joined with the annualized variation of the CBV’s real remuneration index series.
b) An indicator of average labor productivity (LP), calculated as the ratio of the annual GDP, in real terms as published by the CBV, to the employed population as reported by the National Institute of Statistics (INE in Spanish).
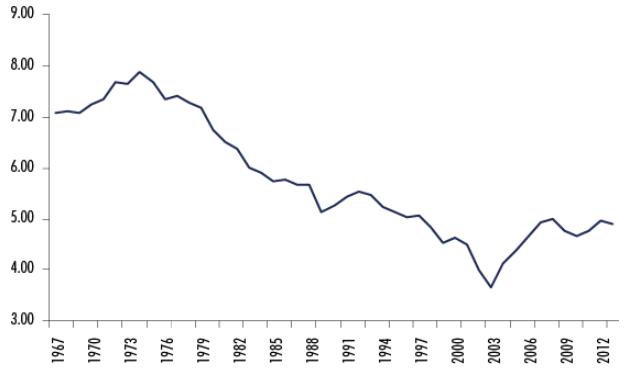
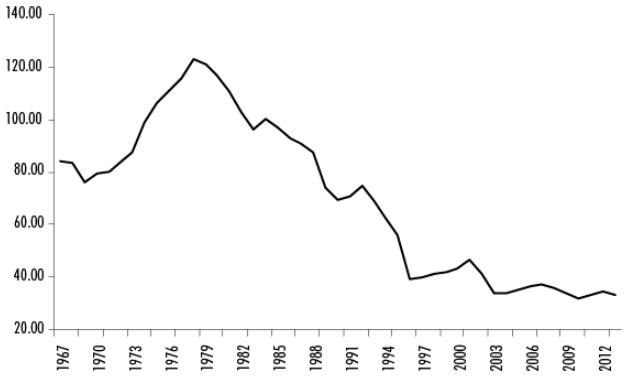
The behavior over time of these two variables expressed as a logarithm can be observed in Figures 1 and 2. The trajectory of both series is similar to the data reported by Baptista (2005) and it seems to be clear that after a period of ascent both variables reach a peak in the mid-1970s and experience a downward trend until the early 2000s, at which point productivity recovers slightly, which real wages do not. Nevertheless, it behooves us to point out the very high positive association between real wages and labor productivity in annual series, with a correlation index of 0.8719.
The Granger (1969) and Sims (1972) tests will be used to make an initial contrast of statistical causality. However, the variables need to be stationary to perform this causality test in order to avoid spurious results in regressions with non-stationary time series. As a result, the stationarity of the series will be analyzed by applying the more conventional Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) tests, as well as the Breakpoint Unit Root (BPUR) test which takes into account the possible presence of structural changes in the series. The hypothesis contrast for these tests is the same, both for the null hypothesis and for the alternative hypothesis. Essentially, a unit root process’s null hypothesis is contrasted with the alternate hypothesis which indicates that the data-generating process is a stationary process.
Table 1 shows the results of applying the two unit root tests to the real wage and LP series. For both variables at level, the values calculated by the ADF and PP tests, (sans intercept or trend), are greater than the critical values and the probabilities are all greater than 0.05, so they fail to reject the null hypothesis of the presence of a unit root. The BPUR test likewise rejects the null hypothesis of the presence of a unit root of the series at level. As such, LP and RWI variables are not stationary at level. Upon taking the variables at first difference, the calculated values of the tests are less than the critical values and the probabilities are all less than 0.05, so the null hypothesis that the variables are not stationary is rejected. In conclusion, both tests indicate that LP and RWI are stationary variables at first difference.
Table 1 Unit root tests (annual data)
| Variables | Augmented Dickey-Fuller test | DFA test critical values | Prob. | Phillips Perron test | P-P critical values | Prob. | Breakpoint Unit Root test | BPUR critical values | Prob. | Result |
|---|---|---|---|---|---|---|---|---|---|---|
| LnPL | -1.3228 | -1.9481 | 0.1694 | -1.1903 | -1.9481 | 0.2106 | -2.741 | -4.4436 | 0.8141 | p=1 |
| LnISR | -1.6159 | -1.9481 | 0.0993 | 1.4286 | -1.9481 | 0.1408 | -2.745 | -4.4436 | 0.8124 | p=1 |
| DLnISL | -4.5983 | -1.9483 | 0.0000 | -4.5983 | -1.9483 | 0.0000 | -5.9495 | -4.4436 | 0.0100 | p<1 |
| DLnPL | -4.9613 | -1.9483 | 0.0000 | -4.8830 | -1.9483 | 0.0000 | -6.0521 | -4.4436 | 0.0100 | p<1 |
Notes: LP-Labor Productivity; RWI-Real Wage Index; ADF and PP sans lag and without trend nor intercept. Breakpoint Unit Root with intercept and without lag.
Source: created by the authors
Knowing that both variables are I(1), the Granger causality test is then applied, consisting of running two dynamic regressions for the variablesX t andY t :
An unconstrained regression
A constrained regression
The squared sum of the residuals of each regression is used to calculate an F statistic to test whether the coefficients are significantly different from zero. If they are not, the hypothesis which states that “Xdoes not causeY” is rejected. Changing the variables (XtoY) we run similar regressions to test the hypothesis that says “Ydoes not causeX”.Note that the number of lags is arbitrary, so the test is usually run with different levels of lag. The Granger causality test is then applied to determine which variable has an impact or causes effects upon the other variable. We achieved this by contrasting the null hypotheses which establishes that “variableXdoes not cause variableY” and that “variableYdoes not cause variableX.”
Table 2 shows the results of applying the Granger causality test for annual data. The exercise was conducted at levels and differences, with two and three lags. The lag structure obeys the criterion of choosing only among those cases where errors are spherical (normal, homoscedastic and not correlated) in a VAR structure at levels containing both variables. The probabilities yielded by the causality test at levels using two lags are equal to 0.009 and 0.079, while using three lags yielded values equal to 0.003 and 0.53. This would indicate that, at levels, the RWI variable statistically causes or moves LP; there was greater failure in rejecting the null hypothesis that labor productivity does not cause the RWI. However, as Green (1997) and Wooldridge (2013) point out, if the variables in regressions (1) and (2) are not stationary, the coefficients will be biased and the validity of the statistical inference will be in doubt.
Table 2 Granger causality tests with annual data (1967-2013)
| Null hypothesis | Number of lags | F Statistic | Probability |
|---|---|---|---|
| LnRWI does not cause Granger LnLP | 2 | 5.24 | 0.009 |
| LnLP does not cause Granger LnRWI | 2 | 2.64 | 0.079 |
| LnRWI does not cause Granger LnLP | 3 | 5.29 | 0.003 |
| LnLP does not cause Granger LnRWI | 3 | 2.81 | 0.053 |
| DLnRWI does not cause Granger DLnLP | 2 | 7.77 | 0.001 |
| DLnLP does not cause Granger DLnRWI | 2 | 0.39 | 0.679 |
| DLnRWI does not cause Granger DLnLP | 3 | 4.74 | 0.007 |
| DLnLP does not cause Granger DLnRWI | 3 | 0.42 | 0.736 |
Notes: LP-Labor Productivity; RWI-Real Wage Index; ADF and PP sans lag and without trend or intercept; Breakpoint Unit Root with intercept and without lag.
Source: created by the authors.
Consequently, it is preferable to take the Granger test as valid, incorporating variables at differences in the regressions. We observed that with two and three annual lags, the probabilities yielded with the variables at differences essentially indicate the same thing. The null hypothesis that the RWI does not cause or has no effect on LP is rejected and we fail to reject the null hypothesis that LP does not cause the RWI.
In order to see how robust the results are, one can carry out a Granger causality contrast in a cointegration environment. One must clarify for the effects that the variables demonstrate a long-term equilibrium relationship in a bivariate form.
If the variables are I(1), as is the case in the study, it is possible that they are cointegrated and there is a long-term relationship between them. As such, the cointegration theory establishes that even when there are variables which are not stationary at level, there can be a stationary linear combination between them. To determine whether the real wage and labor productivity variables are cointegrated, and given that a bivariate relationship is present, we performed the Engle-Granger (1987) test which attempts to contrast the hypothesis that the regression residuals are stationary.2The contrast for determining whether or not regression residuals are stationary involves applying the ADF test to the estimated residuals.
Table 3 shows the value of estimators (coefficients) of LP regressions as a dependent variable and the RWI as an explanatory variable. It also shows the ADF test applied to the regression residuals and the probabilities of each contrast with a different number of lags. Here we see that the AFD test on regression residuals with one lag yields a probability of 0.058; this means that at 10% the null hypothesis that the residuals are non-stationary is rejected, while tests on regression residuals with two, three and four lags show probabilities of 0.045, 0.026 and 0.018, respectively, and are significant at 5%, which means they are stationary. As such, we can say that there is a long-term relationship between LP and RWI with annual data.3
Table 3 Residuals cointegration tests (annual data)
| Variable |
Regressor variable |
Coefficient | Beta |
Augmented Dickey- Fuller Test |
Number of lags |
Probability |
|---|---|---|---|---|---|---|
| LnLP | LnRWI | 13.959 | 0.384 | -1.876 | 1 | 0.058 |
| LnLP | LnRWI | 13.959 | 0.384 | -1.993 | 2 | 0.045 |
| LnLP | LnRWI | 13.959 | 0.384 | -2.232 | 3 | 0.026 |
| LnLP | LnRWI | 13.959 | 0.384 | -2.389 | 4 | 0.018 |
Source: created by the authors
If there is a long-term relationship between the two variables involved in the analysis, then a causal relationship also exists. However, the cointegration tests do not provide any information on the direction which causality flows. This is where Granger's causality tests in a cointegration environment can be of use. In the presence of cointegration, bivariate tests depend on the following error correction models:
Equations (3) and (4) indicate that changes in the dependent variableY t depend not only on changes inX t, but also on past imbalance (Y - kX) t-1 represented by the so-called error correction term.4According to Hossain (2005), two types of Granger causality tests, short and long term, can be done in a cointegration environment. Short-term causality is of particular interest. AnF-testof joint significance to the estimators Ʃαi, Ʃγi fori= 1,2..., in each of the equations above, allows us to determine whether or not there is a short-term causal link between the variables involved. There is causality flowing from the right-side variable to the dependent variable if the aforementioned regression estimators, together, are different than zero. Results for structures with one to four lags are presented in Table 4.5
Table 4 Error correction model with anual data
| Error correction model 1 with anual data | ||
|
| ||
| Number of lags | F Statistic | Probability |
| 1 | 5.3359 | 0.0087 |
| 2 | 3.4604 | 0.0253 |
| 3 | 2.9254 | 0.0337 |
| 4 | 2.2592 | 0.0699 |
| Error correction model 2 with anual data | ||
|
| ||
| Number of lags | F Statistic | Probability |
| 1 | 0.9677 | 0.3884 |
| 2 | 1.2623 | 0.3006 |
| 3 | 0.9424 | 0.4504 |
| 4 | 1.0243 | 0.4184 |
Source: created by the authors
To begin with, regression tests with up to three lags indicate that the estimators are not different from zero and that the RWI at first difference causes labor productivity growth. Only in a dynamic four-lag structure does wage growth not cause labor productivity growth (at 5% significance). In contrast, the evidence in a second case, as shown in error correction model 2, does not point to a causality from productivity to wages, as the null hypothesis of joint significance of parameters γican be rejected in a no lag structure.
Therefore, with annual data, robust results are obtained indicating that statistically and, most importantly in the case of the Venezuelan economy, if there is a causal relationship it goes from RWI to labor productivity.
Relationship with quarterly data
Quarterly data for the variables studied are taken from the longest period available which is from Q1 1998 to Q4 2013. It corresponds to 64 observations for each series. The series have been constructed as follows:
The RWI has been calculated as the costs between the remuneration index total that the CBV reported quarterly and the 2007 Consumer Price Index.
The LP has been calculated by dividing the quarterly GDP, which the CBV reports, by the employed population as reported each quarter by the INE.
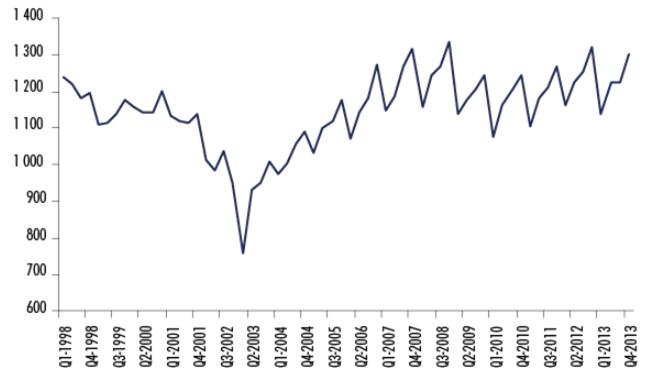
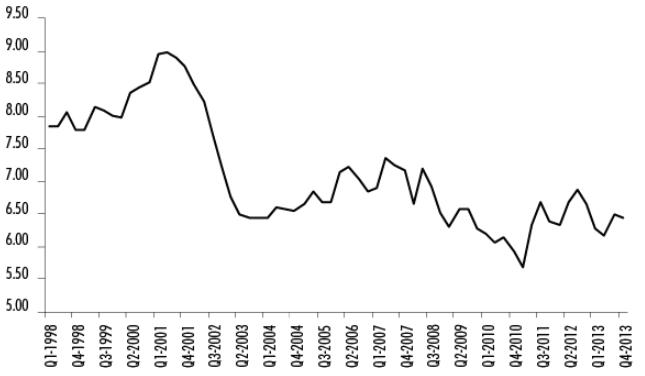
Figures 3 and 4, using quarterly data both for LP and the wage index for the period of 1998-2013, do not display a relationship over time. In fact, the correlation index yields a value of -0.0420. Labor productivity shows a downward trend since the beginning until 2002 when it suffers a sudden drop; since then the variable experiences an upward trend until it stabilizes near the end of the series. The RWI generally increases from the beginning until mid-2001, when it suffers a sharp decline. Starting in 2004, the real wage exhibits a slight recovery until 2008, when it experiences another downward trend and gains new momentum starting in 2010.
Before performing the Granger causality tests, the unit root tests need to be carried out. Table 5 shows the LP and RWI variables at level and first difference. The probabilities from the ADF, PP, and BPUR tests indicate that average productivity and RWI variables are stationary at first difference.
Table 5 Unit root tests (quarterly data)
| Variables |
Augmented Dickey- Fuller test |
DFA test critical values |
Prob. |
Phillips- Perron test |
P-P critical values |
Prob. |
Breakpoint Unit Root test |
BPUR Critical values |
Prob. | Result |
|---|---|---|---|---|---|---|---|---|---|---|
| LnLP | 0.2805 | -1.9464 | 0.7639 | 0.1410 | -1.946 | 0.7235 | -3.3183 | -4.4436 | 0.4932 | p=1 |
| LnRWI | -0.7264 | -1.9460 | 0.3980 | -0.7297 | -1.946 | 0.3965 | -4.2664 | -4.4436 | 0.0809 | p=1 |
| DLnISL | -6.8157 | -1.9461 | 0.0000 | -6.8318 | -1.9461 | 0.0000 | -6.9767 | -4.4436 | 0.0100 | p<1 |
| DLnLP | -3.3044 | -1.9464 | 0.0013 | -17.5496 | -1.9461 | 0.0000 | -6.8036 | -4.4436 | 0.0100 | p<1 |
Notes: LP-Labor Productivity; RWI-Real Wage Index; ADF and PP sans lag and without slope or intercept. Breakpoint Unit Root with intercept and without lag.
Source: created by the authors.
The next step was to carry out the causality tests. Table 6 shows Granger's causality for the average labor productivity and RWI variables but using quarterly data. The test is presented with variables at levels and differences with two and three lags, as they are the lag structures that guarantee spherical errors.
Table 6 Granger causality tests for LP and RWI (quarterly data)
| Null hypothesis | Number of lags | F Statistic | Probability |
|---|---|---|---|
| LnRWI does not cause Granger LnLP | 2 | 8.52 | 0.000 |
| LnLP does not cause Granger LnRWI | 2 | 2.14 | 0.126 |
| LnRWI does not cause Granger LnLP | 3 | 9.57 | 0.000 |
| LnLP does not cause Granger LnRWI | 3 | 1.13 | 0.345 |
| DLnRWI does not cause Granger DLnLP | 2 | 5.55 | 0.006 |
| DLnLP does not cause Granger DLnRWI | 2 | 1.09 | 0.342 |
| DLnRWI does not cause Granger DLnLP | 3 | 5.03 | 0.003 |
| DLnLP does not cause Granger DLnRWI | 3 | 1.90 | 0.139 |
Source: created by the authors.
If one focuses on the probabilities yielded by the test with data at difference and using two and three lags, the results are 0.006 and 0342; and 0.003 and 0.139, respectively. Therefore, the null hypothesis that the RWI does not cause or has no effect on average labor productivity is rejected, but it is not possible to reject the hypothesis that labor productivity dynamics do not cause wage dynamics in real terms.
As with the annual data, causality tests are then carried out in a cointegration environment, but with quarterly data. Given that a bivariate relationship is present, the Engle-Granger test is performed in order to determine if the variables when looking at quarters are cointegrated. The results are presented in Table 7.
Table 7 Cointegration tests using residuals (quarterly data)
| Variable |
Regressor variable |
Coefficient | Beta |
Augmented Dickey- Fuller Test |
Number of lags |
Probability |
|---|---|---|---|---|---|---|
| LnPL | LnRWI | 14.182 | -0.035 | -2.201 1 | 1 | 0.027 |
| LnPL | LnRWI | 14.182 | -0.035 | -1.695 2 | 2 | 0.085 |
| LnPL | LnRWI | 14.182 | -0.035 | -1.076 3 | 3 | 0.252 |
| LnPL | LnRWI | 14.182 | -0.035 | -1.960 4 | 4 | 0.048 |
Source: created by the authors.
Table 7 shows the regressions of average labor productivity using the RWI as an explanatory variable, as well as the results from the stationarity tests (with different numbers of lags) applied to the regression residuals with the goal of finding whether they are stationary and consistent. One can see that the ADF test on regression residuals indicates that the residuals are stationary at 5% significance for regressions with one and four lags. For two lags the results are significant at 10%. In general, the tests tend to confirm that the regression residuals are stationary and therefore it can be concluded, through the Engle-Granger approach, that the variables are cointegrated and form a long-term relationship.
Causality tests in a cointegration environment are reported in Table 8. One can see that regardless of the number of lags, the RWI causes labor productivity. However, the lack of causality from labor productivity to the RWI cannot be rejected, at least not when using two, three and four lags. While this does not refute the results found above, it introduces the possibility that with quarterly data causality is bi-directional.
Table 8 Error correction model with quarterly data
| Error correction model 1 with quarterly data | ||
|
| ||
| Number of lags | F Statistic | Probability |
| 1 | 7.1241 | 0.0017 |
| 2 | 5.4194 | 0.0024 |
| 3 | 6.0247 | 0.0004 |
| 4 | 5.0527 | 0.0008 |
| Error correction model 2 with quarterly data | ||
|
| ||
| Number of lags | F Statistic | Probability |
| 1 | 3.0902 | 0.0531 |
| 2 | 3.0776 | 0.0348 |
| 3 | 4.1201 | 0.0055 |
| 4 | 3.1536 | 0.0146 |
Source: created by the authors.
5. CONCLUSIONS
Vastly different ideas are employed in the analysis and design of policies aimed at the labor market depending on where the driving and causal force is found. Without a doubt, an approach where the idea that causality goes from productivity to wages will result in a system where wage increases are regulated by the course of productivity. In this approach it is then acceptable that productive units do not raise wages, even if their workers are disgruntled, as long as productivity does not increase. Otherwise, the increase in unit costs will impede competitiveness. But the fears cast by this logic are unfounded if, among a great number of variables and by the various means detailed herein, real wages constitute a source for engendering changes in labor productivity.
The results of this study for annual and quarterly data from the Venezuelan economy indicate, like other studies for developed and developing countries, that causality flows from real wages to labor productivity. As such, one should be leery, to say the least, of mandates who tend to impose restrictions on increases in real wages by tying them to increases in productivity.
REFERENCES
Akerlof, G. (1982). Labor contracts as partial gift exchange.Quarterly Journal of Economics,97(4).https://doi.org/10.2307/1885099 [ Links ]
Banco Interamericano de Desarrollo (BID) (2010).La era de la productividad: cómo transformar las economías desde sus cimientos .Banco Interamericano de Desarrollo. [ Links ]
Baptista, A. (2005). El capitalismo rentístico: elementos cuantitativos de la economía venezolana.Cuadernos del CENDES,22(60 ).http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1012-25082005000300005 [ Links ]
Brida, J. G., Risso, W. A. and Sanchez Carrera, E. J. (2010). Real wages as determinant of labour productivity in the Mexican tourism sector.European Journal of Tourism Research, 3(1).https://ssrn.com/abstract=1308577 [ Links ]
Clark, J. B. (1899).The distribution of wealth: A theory of wages, interest and profits. Macmillan. [ Links ]
Engle, R. F. and Granger, C. W. (1987). Cointegration and error correction: Representation, estimation, and testing.Econometrica,55(2).https://doi.org/10.2307/1913236 [ Links ]
Ferguson, C. and Gould, J. (1980).Teoría microeconómica. Fondo de Cultura Económica. [ Links ]
Fondo Monetario Internacional (FMI) (2017).World Economic Outlook, seeking sustainable growth: Short-term recovery, long-term challenges. Washington, DC, October. http://dx.doi.org/10.5089/9781484312490.081 [ Links ]
Gordon, D. M. (1994). Bosses of different stripes: A cross-national perspective on monitoring and supervision.The American Economic Review,84(2).https://www.jstor.org/stable/2117862 [ Links ]
Gordon, R. (1987). Productivity, wages, and prices inside and outside of manufacturing in the U.S., Japan, and Europe.European Economic Review,31(3).https://doi.org/10.1016/0014-2921(87)90089-4 [ Links ]
Granger, C. W. J. (1969). Investigating causal relation by econometric and cross-sectional method.Econometrica ,37(5).https://doi.org/10.2307/1912791 [ Links ]
Green, R. K. (1997). Follow the leader: How changes in residential and non-residential investment predict changes in GDP.Real Estate Economics,25(2).https://doi.org/10.1111/1540-6229.00714 [ Links ]
Hatanaka, M. (1996).Time-series-based econometrics. Oxford University Press. [ Links ]
Hein, E. and Tarassow. A. (2009). Distribution, aggregate demand and productivity growth: Theory and empirical results for six OECD countries based on a post-Kaleckian model.Cambridge Journal of Economics,34(4).10.1093/cje/bep066 [ Links ]
Hossain, A. (2005). The Granger-causality between money growth, inaction, currency devaluation and economic growth in Indonesia: 1954-2002.International Journal of Applied Econometrics and Quantitative Studies, 2(3).https://www.usc.gal/economet/reviews/ijaeqs234.pdf [ Links ]
Islam, R., Kiyondo, A. and Nganga, J. (2015). Real wages and labor productivity in Tanzania: How do they link?Journal of African Studies and Development, 7(3). http://hdl.handle.net/20.500.11810/4656 [ Links ]
Kaldor, N. (1961). Capital accumulation and economic growth. In F. Lutz, F. Hague (eds.).The theory of capital .St Martin’s Press. [ Links ]
Karaalp-Orhan, H. (2017). Labour productivity, real wages and unemployment: An application of bounds test approach for Turkey.Journal of Economic and Social Development, 4(2).http://www.jesd-online.com/dokumenti/upload/separated/Vol%204%20No%202_Paper2.pdf [ Links ]
Kumar, S., Webber, D. and Perry, G. (2012). Real wages, inflation and labour productivity in Australia.Applied Economics,22(23 ).https://doi.org/10.1 080/00036846.2011.568405 [ Links ]
Lucidi, F. (2008). Labour market exibility and productivity growth: New evidence from firm-level data. Preliminary Working Paper. “Sapienza” Università di Roma and Fondazione Giacomo Brodolini, Roma. http://www.aiel.it/Old/bacheca/BRESCIA/papers/lucidi.pdf [ Links ]
Madsen, J. and Damania, R. (2001). Labour demand and wage-induced innovations: Evidence from the OECD countries.International Review of Applied Economics ,15(3).https://doi.org/10.1080/02692170110052365 [ Links ]
Marquetti, A. (2004). Do rising real wages increase the rate of labor‐saving technical change? Some econometric evidence.Metroeconomica,55(4).https://doi.org/10.1111/j.1467-999X.2004.00201.x [ Links ]
Marx, K. (1967).Capital, vol. I. International Publishers. (Original publication in 1867). [ Links ]
Méndez, J. and Hernández, H. (2014). Relación de largo plazo y análisis de causalidad y sensibilidad entre los salarios reales y la productividad laboral en el sector manufacturero a partir de cifras de los departamentos en Colombia.Revista Finanzas y Política Económica, 6(2).http://www.scielo.org.co/pdf/fype/v6n2/v6n2a06.pdf [ Links ]
Nayaran, P. and Smyth, R. (2009). The effect of inflation and real wages on productivity: New evidence from a panel of G7 countries.Applied Economics ,41(10 ).https://doi.org/10.1080/00036840701537810 [ Links ]
Organisation for Economic Co-operation and Development (OECD) (2015). The labour share in G20 economies, report prepared for the G20 employment working group, Antalya, Turkey. https://www.OECD.org/g20/topics/employment-and-social-policy/e-Labour-Share-in-G20-Economies.pdf [ Links ]
Pyo, H. (2018). Labor productivity and a test of Kaldor-Verdoorn law in East Asia. In D. K. Das (eds.).Productivity dynamics in emerging and industrialized countries .Routledge India. 10.4324/9781351002547-8 [ Links ]
Ricardo, D. (2005).Principles of political economy and taxation. Barnes & Noble Books. (Original publication in 1817). [ Links ]
Schmookler, J. (1966).Invention and economic growth. Harvard University Press. [ Links ]
Sims, C. A. (1972). Money, income and causality.American Economic Review,62(4).https://www.jstor.org/stable/1806097 [ Links ]
Smith, A. (1776).An inquiry into the nature and causes of the wealth of nations, vols. I and II. Oxford University Press. [ Links ]
Soo Khoon, G. (2009). Is productivity linked to wages? An empirical investigation in Malaysia. CenPRIS Working Paper Series 102/09. https://mpra.ub.unimuenchen.de/18095/1/MPRA_paper_18095.pdf [ Links ]
Storm, S. and Naastepad, C. W. N. (2007). Why labour market regulation may pay off: Worker motivation, co-ordination and productivity growth. International Labour Organization, Economic and Labour Market Paper 2007/4. https://www.ilo.org/empelm/pubs/WCMS_113903/lang--en/in dex.htm [ Links ]
_______ and Naastepad, C. W. N. (2009). Labor market regulation and productivity growth: Evidence for twenty OECD countries (1984-2004).Industrial Relations: A Journal of Economy and Society,48(4).https://doi. org/10.1111/j.1468-232X.2009.00579. [ Links ]
Strauss, J. and Wohar, M. (2004). The linkage between prices, wages and labor productivity: A panel study of manufacturing industries.Southern Economic Journal,70(4).https://doi.org/10.2307/4135280 [ Links ]
Sylos-Labini, P. (1983). Factors affecting changes in productivity.Journal of Post Keynesian Economics, 6(2).https://www.jstor.org/stable/4537805 [ Links ]
Upender, M. and Sujan, M. (2008). Cointegration between labor productivity and wage rates: Empirical evidence from the Indian industries.The ICFAI Journal of Industrial Economics, 5(1).https://iupindia.in/208/IJIE_Coin-tegration_Labor_Productivity_Wage_Rates_39.html [ Links ]
Valadkhani, A. (2003). An empirical analysis of Australian labour productivity.Australian Economic Papers,42(3).10.1111/1467-8454.00199 [ Links ]
Veerger, R. and Kleinknecht, A. (2011). The impact of labor market deregulation on productivity: a panel data analysis of 19 OECD countries.Journal of Post Keynesian Economics ,33(2).10.2307/23035719 [ Links ]
_______ and Kleinknecht, A. (2014). Do labour market reforms reduce labour productivity growth? A panel data analysis of 20 OECD countries (1960- 2004).International Labor Review,153(3).https://doi.org/10.1111/ j.1564-913X.2014.00209.x [ Links ]
Weisskopf, T., Bowles, S. and Gordon, D. (1983). Hearts and minds: A social model of U.S. productivity growth.Brooking Papers on Economic Activity,14(2).https://doi.org/10.2307/2534294 [ Links ]
Wooldridge, J. (2013).Introductory econometrics: A modern approach. South- Western Cengage Learning. [ Links ]
Yildrim, Z. (2015). Relationships among labour productivity, real wages and inflation in Turkey.Economic Research-Ekonomska Istraživanja,28(1).10.1080/1331677X.2015.1022401 [ Links ]
Yusof, S. (2008). The long-run and dynamic behaviors of wages, productivity and employment in Malaysia.Journal of Economic Studies,35(3).https:// doi.org/10.1108/01443580810887805 [ Links ]
1This relationship continues to be positive even though in the last two years, studies for developed countries show that labor productivity indices went up more than real wage indices (OECD, 2015). This in effect is one of the many puzzles which analysts currently face.
2Hatanaka (1996) points out that this procedure is appropriate when dealing with two variables and a possible cointegration vector.
3The sign and value of the “beta” coefficient (0.38) indicates that there is a positive relationship in the long-term between variables but other factors can affect the behavior of labor productivity.
Received: April 21, 2020; Accepted: November 30, 2020











 texto en
texto en