Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Problemas del desarrollo
versión impresa ISSN 0301-7036
Prob. Des vol.50 no.196 Ciudad de México ene./mar. 2019
https://doi.org/10.22201/iiec.20078951e.2019.196.63004
Articles
Productivity and Rate of Surplus Value at International Level: An Empirical Evaluation
a Autonomous Metropolitan University (UAM), Iztapalapa, Mexico. *Email: bgloriamtz@gmail.com
b Faculty of Economics - National Autonomous University of Mexico (UNAM), Mexico. *Email: valle@unam.mx
c Central American University (UCA) José Simeon Cañas, El Salvador. *Emails: csanchez@uca.edu.sv
This paper examines the relationship between productivity and the rate of surplus value and seeks to establish if a higher rate of surplus value can be found in developed countries with higher productivity than in underdeveloped countries, a theory consistent with the Marxist conception of this relationship at international level.
A methodology was used which incorporated contingency tables, multivariate analysis using clusters and econometric analysis of fixed-effect panel data. The econometric analysis made use of a wide range of databases, with data from studies ranging from the post-war period to the first decade of the 21st century.
Key Words: Productivity; rate of surplus value; theory of accumulation; Marxist theory; econometric analysis
En el presente trabajo se examina la relación entre productividad y tasa de plusvalor, y si en los países desarrollados -con mayor productividad-, se verifica una tasa de plusvalor mayor a la correspondiente a los países subdesarrollados de acuerdo con la conjetura teórica marxista de dicha relación a nivel internacional. Para ello se emplearon tablas de contingencia, análisis multivariado mediante clústeres y análisis econométrico de datos de panel de efectos fijos. En este último se usaron diversas bases de datos cuyos periodos de estudio van desde la posguerra a la primera década del siglo XXI.
Palabras clave: productividad; tasa de plusvalor; teoría de la acumulación; teórica marxista; análisis econométrico
Clasificación JEL: C33; D24; D46; E11; O47
1. INTRODUCTION
This work provides core empirical results on Marxist theories on surplus value and accumulation. The relationship between some of the principal categories of accumulation, such as relative salary, productivity, rate of surplus accumulation and organic composition of capital, is presented in a concise manner. According to this theory, one should expect a link between productivity and organic composition of capital between countries as greater production follows the presence of more means of production per worker. Said link, in addition to a uniform tendency in median rates of profit between countries, dictates how much greater productivity is. This relationship was proposed by Marx (1980) and appears to be a necessary behavior of capitalist development.
What follows constitutes unexpected results. What should happen according to this theory is in contradiction with the results: surplus value rates in undeveloped, less productive, countries are not lower than those of more developed countries. Conjecture that between groups of countries, greater productivity corresponds to a lower surplus value rate, was partially corroborated. This core result is supported by research stemming from econometrics tests, based on proxy variables of the inverse of the surplus value rate with country samples from around the world.
The text starts with section 1 which is the introduction. Section 2 defines productivity at the level of individual goods and of a basket of goods, based on labor value theory, connecting surplus value rates with relative salary and argues why productivity’s impact on surplus value rate is positive, based on the general law of capitalist accumulation. Section 3 presents proof and empirical results. This last analysis is as much a review as a further development of the work of Figueroa and Amaya (2017), based on their estimations and complementing their econometric proof and constitutes an important contribution to empirical analysis of this theoretical problem. Section 4 provides conclusions.
2. THEORETICAL ASPECTS OF THE RELATIONSHIP BETWEEN PRODUCTIVITY AND SURPLUS VALUE RATE
Productivity
According to labor value theory, the productivity with which a commodity is made is reciprocal to the value of said commodity; when dealing with a basket of commodities it is a weighted average value of said commodities, based on the quantity of commodities contemplated.
The idea that productivity is reciprocal to value was developed by Valle (1998) despite being present in the works of other authors. Productivity is then the reciprocal of socially required labor time for producing some commodity. The production of a commodity i (
Where m i is the value amount of commodity i. At an aggregate level, analogous to the case of a good
This is based on the Marxist notion that value is past or indirect labor plus present or direct labor, M = MA+L and the consumable-product analysis: M = L (I-A)
-1
where A is the is the matrix of technical coefficients, a
ij
is the physical amount of commodity j required to produce a physical unit of commodity i; L row vector of simple labor coefficients whose elements are l
i
; M: row vector of elements m
i
, value amount of i
nth
commodity; X is a column vector of gross outputs; Y is a final demand column vector; Y
i
is a column vector with elements
This equation portrays direct and indirect labor as components of value according to the technical conditions of production; it allows one to see what would be the brute production necessary to produce one unit of final demand for a certain commodity; and supports equation (2), the productivity or the product of commodity i per worker or potential consumption per worker.
Valle (1998) establishes that the quotient of internal brute products per worker at current prices in a common currency is equal to the quotient of productivities.
y
A: column vector which denotes a basket of goods per worker in country A; y
B
: column vector which denotes a basket of commodities per worker in country B; P
A
row vector with prices of the basket yA; P
B
: row vector with the prices of basket y
B
; zc
BA
: exchange rate for purchasing power parity (PPP), defined in terms of a basket which is produced in A;
According to the previous equation, labor productivities can approach the GDP quotient per worker, as current prices approach value prices, as has been shown in various empirical works.1 The traditional comparisons of labor productivity which are justified for practical reasons, even in conventional literature, are well grounded in Marxist value theory. Further on we will use comparisons between PPP and productivities between countries and will analyze the relationship between said variable the surplus value rate.
Surplus Value Rate and Relative Salary
Said relationship is formed from the analysis of wages, not as an absolute value, but rather as a relative wage, in its relationship with capitalist profit. In Marx, we find the idea that capitalist accumulation produces two contrary phenomena: the growth of real wages and a reduction of relative wages, understood as the portion that said wages make-up of the social product generated.
The vital relationship which underlies this phenomenon is the surplus value rate’s tendency to grow. Wages received by the working-class, which in terms of values correspond to social variable capital, tend to be less in relation to profit, which in terms of value correspond to the socially produced surplus value. In a capitalist society only one part of value generated is new value, which was named value product by Marx and its money form is added value. One part of this replaces the value of labor power employed in the production process or variable capital and the rest constitutes excess or surplus value. The relationship between these two values gives the degree of exploitation of labor power. We define the surplus value rate as:
where: p is surplus value and v is variable capital.
“The rate of surplus-value is therefore an exact expression of the degree expectation of labor-power by capital, or of the laborer by the capitalist.” (Marx, 1887, p. 153).
Marx considered that p´ had a tendency to grow in capitalism. The numerator (surplus) as well as the denominator (variable capital), are elements of the value product, in such manner that the increase or decrease of the portion of one in said value product implies a decrease or increase of the other. This applies in a capitalist society in which one assumes the existence of only two social classes. Capital increases productivity of labor, decreases the value of labor power and increases surplus value at the same time. By increasing the productivity of labor the amount of use value produced increases but the unit value of each good decreases. The growing development of labor productivity in branches of production of goods for workers causes these to have less value, in other words these goods now contain less objective labor than they did before. The value of labor power becomes less which does not prevent the basket of workers’ means of subsistence from growing. This means that a contraction in the value of labor power stemming from an increase in labor productivity is far from resulting in a compression of real salary, but rather causes it to elevate.
We define relative salary as:
It would be the proportion between labor paid to the workers and the total living labor. Taking equation (5) we arrived at:
As such the movement of both variables is contrary. A growing surplus value rate corresponds to a decreasing relative wage, such that a decreasing surplus value rate would correspond to an increasing relative wage.
Productivity and the Surplus Value Rate According to the General Law of Accumulation
In capitalism, there is a dominating tendency in accordance with the general law of accumulation: growth in the organic composition of capital. As a result, the generation of an overpopulation, or a population excessive in relation to the needs of capital valuation. It is not a matter of a population which is excessive due to its absolute size but rather a relative overpopulation stemming from the fact that capitalism necessitates the separation of the rate of recrimination from the growth of the population. These topics are explored in detail in Valle (2005) and we will return to them later on. The concept manifests itself as a growth in the number of unemployed or tenuously employed workers, parallel to a growing investment in means of production, both in developed capitalist countries as well as in those which are underdeveloped. It is in the latter that the problems of employment and tenuous employment are the worst.
Growth in organic composition becomes an obstacle for accumulation, meanwhile there are subordinated counter tendencies which favor it, such as salaried labor and therefore variable capital; an absolute increase in constant capital; an increase in productivity; the devaluation of labor power and the increase on the surplus value rate, but also of real wages.
Literature on the general law of accumulation based on the works of Marx, such as Shaikh (1990), Guerrero (2006), Cockshott et al. (1995) and Valle (2005), has a tendency to espouse the idea of a growing organic composition, though they emphasize different aspects of the law such as generation of an excessive population, mechanization, concentration and centralization of capital, etc.
Valle’s interpretation (1998) supports capitalism’s need to separate accumulation from population growth and increasing productivity in a way that increases the composition of capital. As such the growing organic composition of capital (OCC) sets the limits of accumulation and other tendencies of the same process. Otherwise, the cheapening of means of productions resulting from growing productivity would lead to a given amount of capital needing ever more living labor for labor power merchandise whose rhythm of production escapes the bounds of capital. As such the rhythm of accumulation, by depending on the growth of labor power, would have to decrease.
According to Marx (1980), the logical choice of techniques is only that which maximizes earnings and raises organic composition. Consequently, the technical change which liberates the rhythm of accumulation from working population growth needs the technical composition of capital grow even more than the labor power and that the surplus value rate increase, as long as it allows the rate of earning to stay steady or grow.
It is from the interpretations of the general law of accumulation that the postulation arises known as the conjecture of Marx on productivity and the surplus value rate between countries: the accumulation of capital involves growth of productivity, organic composition and surplus value rate.
Capitalism needs an increase in OCC in order to grow, which entails an increase in the surplus value rate to counteract the negative effect of the OCC’s increase on the rate of profit. Most Marxist authors agree, some have even shown it via mathematical models, that the rate of profit is a direct function of the surplus value rate and inverse to the composition of capital. A variety of works provide empirical evidence of growing tendencies, both for composition of capital as well as the surplus value rate, and the decreasing tendency of the rate of profit (see Martinez, 2006).
As such, it is logical to expect a direct relationship between productivity and the surplus value rate as we can suppose that more productive countries possess a greater volume of means of production in value with respect to living labor. This demands a surplus value rate greater than the predominant one found in countries which are less productive and with a lower organic composition. In addition to this a greater OCC will, in general, signifies greater productivity which in turn allows for a higher wage along with greater exploitation.
3. EMPIRICAL RESULTS
Contingency Tables and ji Squared Test
Matrices are made with different levels of wage share in the rows, levels of productivity in the columns and countries’ frequencies are established according to the different combinations. High frequencies define groups of countries. We carried out ji squared tests of no association between productivity and wage share (as an approximate variable of the surplus value rate). The contrary result, of association, proves that the countries’ probability distribution is different and that a group of countries is statistically different from another due to its levels of productivity and wage share. We conjecture that the relationship between said variables is the following:
a. inverse between productivity and wage share in the groups of countries arranged according to productivity as a result of the direct relationship between productivity and surplus value rate
b. direct between productivity and wage share in the groups representing a higher level of worker exploitation in underdeveloped countries.
Variables and Sources
Wage share is calculated based on data for workers’ compensation and GDP to each country’s acquisition values, from the United Nations database (1978, 1999).
We used information from about 70 countries between 1960, 1970 and 1975 and about 60 countries between 1983 and 1994 after an initial filtering and making it compatible with the productivity information (available on Penn World Table Mark, PWTM). This source was chosen for it covers many countries and years with an acceptable level of homogeneity in the information; the choice of years follows the same logical criteria. The next section will see the testing of these variables updated and developed.
With productivity and par purchasing power, we used the RGDPW data (real gross domestic product per worker) from PWTM 5.6 and 6.1.
Results
Upon dividing the countries according to high or low productivity we have four groups: 1) countries with a high productivity and a high wage share; 2) with low productivity and low wage share; 3) with high productivity and low wage share and 4) with low productivity and high wage share. In Table 1 we see the frequencies according to said classification for each of the selected years (1960, 1970 and 1975, 1983 and 1994). For example, in 1994 the countries with high productivity and the high wage share were 24 while the countries with low productivity and low wage share were 23.
Table 1 Contingency Table: High and Low Productivity and Wage Share
| High productivity | low productivity | |
| 1960 (χ2 experim. vs. χ2 teór. (95%,1 g.l.), 1.67 < 3.84) | ||
| Low wage share | 13 | 11 |
| High wage share | 18 | 7 |
| 1970 (χ2 experim. vs. χ2 teór. (95%,1 g.l.), 11.20 > 3.84) | ||
| Low wage share | 11 | 24 |
| High wage share | 25 | 10 |
| 1975 (χ2 experim. vs. χ2 teór. (95%,1 g.l.), 4.96 > 3.84) | ||
| Low wage share | 13 | 16 |
| High wage share | 22 | 8 |
| 1983 (χ2 experim. vs. χ2 teór. (95%,1 g.l.), 13.77 > 3.84) | ||
| Low wage share | 8 | 22 |
| High wage share | 23 | 8 |
| 1994 (χ2 experim. vs. χ2 teór. (95%,1 g.l.), 15.24 > 3.84) | ||
| Low wage share | 8 | 23 |
| High wage share | 24 | 8 |
Source: created by the authors based on PWTM 5.1 and 6.1, <http://dc1.chass.utoronto.ca/pwt/> and United Nations (1978, 1999), <https://unstats.un.org/unsd/nationalaccount/data.asp>. The Null Hypothesis, Ho, is that of no association as is well-known. E.g. for 1994 the experimental value of ji squared is greater tan the theoretical at a 95% confidence level with 1° of freedom so that Ho is rejected.
The results confirm that countries with low productivity are countries with low wage share while countries with high productivity are countries with high wage share. We found with a 95% confidence level, with 1 degree of freedom, that there is a link between wage share and productivity, or that the probability distribution for high productivity countries is different than that of low productivity countries.
In 1960, based on 49 different observations, it was more common to find countries with high productivity and high wage share, followed by countries with high productivity but low wage share; while in 1970, based on 70 observations, a pattern arose with countries with high productivity and high wage share on one side and low productivity countries with low wage share on the other.
We should point out that countries like Uruguay, Chile, Mexico and Argentina appear in groups of countries with high productivity despite a low wage share. The productivity of these countries varies between 10 and 14 thousand dollars per person occupied/employed in the year. These numbers are markedly lower than countries such as Spain, Germany, Canada and even the USA, whose productivity was between 21 and 30 thousand dollars per person employed.
In 1975, based on 59 observations, the pattern outlined in 1970 was lost only to clearly resurface in the 1980s and 1990s. Nevertheless, in 1975, the highest frequencies correspond to countries with high productivity and high wage share, with countries with low productivity and low wage share taking second place. In 1983 and 1994, based on 61 and 63 observations, a pattern arose where the groups of countries are almost symmetrical.
The results create a pattern of differences in wage share between countries based on whether they were high or low productivity. Said pattern consists of: 1) countries with high productivity and highways share (or low surplus value rate), 2) countries with low productivity and low wage share (or high surplus value rate), 3) countries with high productivity and low wage share and 4) countries with low productivity and high wage share.
Cluster analysis
The sources and variables outlined in the previous section were employed. The corresponding distribution therein outlined passed the no homogeneity JI squared tests. In the cluster analysis, these economic criteria were not predefined. Nevertheless, there is a correspondence between both country groupings, especially when dealing with developed countries.
According to this analysis:
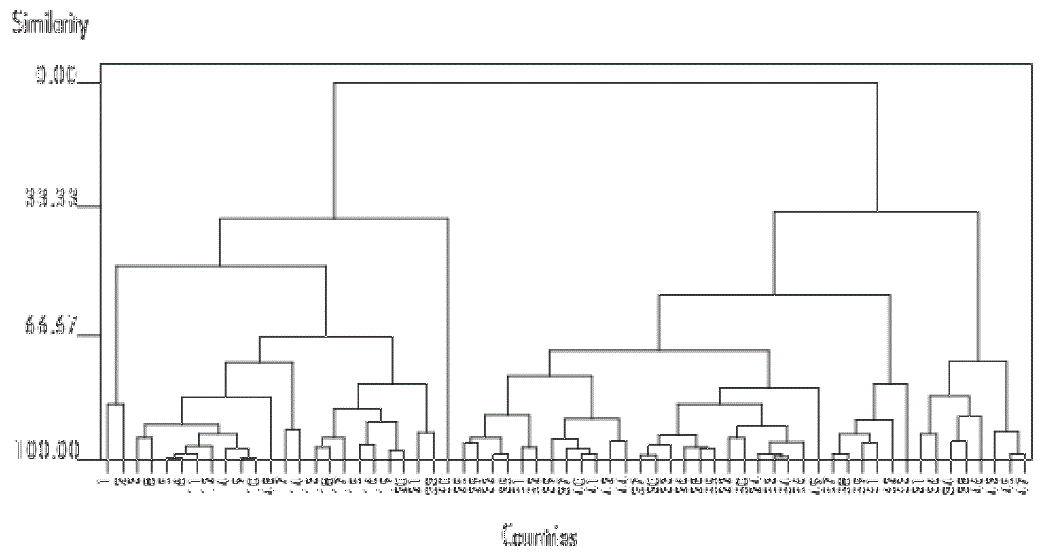
In 1983 and 1994 we were looking to find three clusters but the countries were concentrated in two groups with these two corresponding almost perfectly with the first two clusters: countries with high productivity and high wage share and countries with low productivity and low wage share (see Dendrogram 1 and Table 2) another outstanding fact is that the concentration of countries in each conglomerate is greater when there is a higher degree of similarity.
In 1960, 1970, 1975 and 1994 we found two clusters,2 in one we find countries with high productivity and high wage share and in the other countries with low productivity and low wage share, if we exclude from the analysis countries which combine high or low productivity with low or high wage share. Whereas if all countries studied are included, there is a correspondence albeit lower. Dendrogram 1 is one way to show these groupings while both groups of countries are displayed in Table 2. A convenient level grouping is made when countries which are far removed are separated into groups defined by the change of the coefficient of the conglomerates, or in other words when said change is significant. In the case of wage share and productivity variables for the countries listed, appropriate grouping is when groups one and two are precisely defined.
Table 2 Number of Countries Classified According to Productivity and Wage Share Levels, 1994.
| Countries with High Productivity and High Wage Share (24) | Countries with Low Productivity and Low Participation (23) |
| 1. Luxemburgo | 25. Botsuana |
| 2. Estados Unidos de América | 26. Túnez |
| 3. Bélgica | 27. Panamá |
| 4. Noruega | 28. Jordania |
| 5. Austria | 29. Fiyi |
| 6. Francia | 30. Namibia |
| 7. Suiza | 31. Ecuador |
| 8. Canadá | 32. El Salvador |
| 9. Australia | 33. Colombia |
| 10. Irlanda | 34. Tailandia |
| 11. Dinamarca | 35. Paraguay |
| 12. Israel | 36. Perú |
| 13. Reino Unido (RU) | 37. Rumania |
| 14. Suecia | 38. Filipinas |
| 15. Islandia | 39. Honduras |
| 16. España | 40. Bolivia |
| 17. Finlandia | 41. Papúa Nueva Guinea |
| 18. Japón | 42. Costa de Marfil |
| 19. Corea | 43. Sierra Leona |
| 20. Portugal | 44. Kenia |
| 21. Islas Caimán | 45. Nigeria |
| 22. Trinidad y Tobago | 46. Burundi |
| 23. Sudán | 47. Tanzania |
| 24. Uruguay | |
| Countries with high Productivity and Low Wage Share (8) | Countries with Low Productivity and Low Wage Share (8) |
| 48. Italia | 56. Polonia |
| 49. Grecia | 57. Turquía |
| 50. Mauricio | 58. Costa Rica |
| 51. México | 59. Bulgaria |
| 52. Venezuela | 60. Irán |
| 53. Nueva Zelanda | 61. Hungría |
| 54. Eslovenia | 62. Sri Lanka |
| 55. Rusia | 63. Guinea Francesa |
Source: Taken from Martínez (2006, Appendix 4).
The multivariate analysis results based on cluster or grouping are consistent with this; assuming that wage share is a variable approximate to the reciprocal of the surplus value rate the wage share is lower (or the reciprocal of wage share, the surplus value rate, is higher) in countries with low productivity than in countries with high productivity.
Another way of showing the paradoxical relationship between productivity and surplus value rate is shown in Figures 1 and 2 via the functions of productivity probability density and the surplus value rate of developed and undeveloped countries. A density function is a soft histogram, which allows one to identify forms and the dispersion of distribution of analyzed variables. Data from EPWT v.4 was used, covering a wide sample of 72 countries. The units for the variables are along the horizontal axis.

Note: Of the 72 countries, 28 are developed, according to their relative productivity and the global average. Source: Created by the authors. Productivity in thousands of 2005 USD/worker. Data from EPWT v.4, dollars from 2005.
Figure 1 Productivity (functions of density), 72 countries selected, 1995-2008.

Source: Created by authors with data from EPWT v.4.
Figure 2 Surplus Value Rate (functions of density). Profits/Wages 72 countries selected, 1995-2008.
The paradox is then set out as such: in 2008 the relationship between productivities between developed and undeveloped countries is 3:1 while the corresponding to exploitation is 1:1.80. As for the rest, the tendency and advance of the variables agrees with that set forth by the theory.
Now we will econometrically test if the idea proposed by Marx (1980), of a direct relationship between productivity and the surplus value rate, is correct if we consider the differential levels of the surplus value rates between country sub-groupings.
Fixed Effects Panel Analysis
Productivity and Surplus Value Rate
a) The problem, the variables and the sources
We will carry out an econometric analysis in order to answer the questions of whether the surplus value rate is higher in undeveloped countries with low productivity than in developed countries with high productivity and whether there is a positive relationship between productivity and the surplus value rate in each group of countries.
We used a fixed effects panel model as we considered it appropriate for the object of this study.3 The observations correspond to testing for a relationship between the dependent variable, surplus value rate (TP),4 and the independent variable, productivity (P).
We used estimates of the surplus value rate from different authors for the seven corresponding countries.5 These countries were elected in virtue of: 1) taking advantage of available estimates, 2) the compatibility of the different methods used to achieve these estimates and 3) the feasibility of including developed countries and undeveloped countries (see Martinez, 2006). Said estimates are compatible with the following definition of surplus value rate:
where: G is the surplus of exploitation; I are indirect taxes; Z are subsidies; s i he wages of unproductive workers; S the wages earned by productive workers.
In the second test, we have the cases of the surplus value rate in Mexico and Venezuela.
where: TP A is the unadjusted surplus value rate; Ita is the autonomous workers income (income of independent workers originally included in the operating surplus).6
This is owed to the fact that in undeveloped countries the problem of income from autonomous workers is more important due to its magnitude and it was not until very recently that this type of income was separated from the so-called operating surplus and national accounts. For these reasons, the surplus value rates were overestimated and as such required the aforementioned adjustment.
For indicators of productivity and purchasing power parity we use the RGDPPW series from the PWTM 5.6 and 6.3.
The time covered by the series varies from case to case within the period of 1950-2000.
So, for Mexico we have a period from 1960 to 2002 and for the United States from 1960 to 1993. Such is the case for every country in the sample. The model classifies the effects of changes in the surplus value rate in the country between 1950 and 2000 and the variation of the surplus value rate of the seven countries for each year.
For the fixed effects panel model, taking the cross-sections into account, we used the generalized least squares method (9), which corrects the estimate problems of autocorrelation and heteroskedasticity. The equation is:
This is the surplus value rate, TP, of country i in years t, is determined by productivity, P, of country i in year t. As was pointed out earlier, the fixed effect refers to a model presupposing an individual α for each country. In other words, it maintains an individual effect for each country based on the surplus value rate, not attributable to productivity.
The model in question puts out results on the relationship between productivity and the surplus value rate and the existence of a particular differential level of surplus value rate between countries which cannot be explained solely by productivity.
b) first test: panel data model without taking into account the problem of autonomous work in Mexico7
In this test i= the United Kingdom, United States of America, Canada, Japan, New Zealand and Mexico; t= 1950, 1951,…, 1990 and has a total of i x t = N = 170 panel observations. Surplus value rate estimates from different authors were used for the corresponding six countries.8
The results corroborate the positive relationship between productivity and the surplus value rate according to the Marxist theory of accumulation for the cases of Mexico, the United States of America, Canada, the United Kingdom, New Zealand and Japan; but do not corroborate the conjecture derived from the same theory which states that undeveloped countries, less productive countries, have a surplus value rate lower than that of more developed, more productive, countries. For the same country cases our conjecture is corroborated, according to which undeveloped countries, with a low productivity, have a high surplus value rate.
We found that the surplus value rate levels are individually differentiated, in particular regarding Mexico when compared to the rest of the countries.
The results show that:
1) An increase of a thousand dollars per person employed in the year increases the surplus value rate from 0.056 to 5.64%. The reason turns out to be statistically significant at a confidence level of 95% in order to explain the surplus value rate.
2) There is individual differentiation into surplus value rate levels attributable to the effects of each country expressed in αi, as can be seen in Table 3.
Table 3 Estimator (Intercept) of the Fixed Effects Panel with Cross-Sectional Weighting. Selected Countries, 1950-1990.
| Country i | USA | New Zealand | UK | Japan | Canada | Mexico |
| αi | 0.09 | 0.10 | 0.16 | 1.35 | 1.58 | 3.59 |
| αMex/αi | 36.63 | 34.19 | 22.02 | 2.66 | 2.26 | 1.00 |
Source: A1 (2006, Table 1 from Appendix 5)
This meant that supposing equal changes in TP before changes to P in each country, Mexico’s respective rate presents its own effect on its level which is considerably higher, compared to that of the other countries.
Knowing the estimators αi and β, and taking the corresponding productivity data from PWTM 5.6., the surplus value rates estimated for the United States of America and for Mexico in 1990 were determined in the following manner:
TPEUA,1990 = αEUA + βPEUA,1990 + εEUA,1990
= 0.09855 + 0.0564 (33.7710) - 0.0912 = 1.91 o 191%,
compared to an observed surplus value rate of 2.31 or 231% and
TP Méx,1990 = αMéx + βP Méx,1990 + εMéx,1990
= 3.5989 + 0.0564 (17.0120) + 2.1356 = 6.66 o 666%,
compared to an observed surplus value rate of 6.75 or 675%
In other words, Mexico’s surplus value rate is determined by the country’s productivity in 1990, multiplied by a coefficient common to Mexico and the rest of the sample countries, plus an individual term, representing a characteristic unique to Mexico, plus an error term.
Our own conjecture which states that undeveloped countries with low productivity have a high surplus value rate has been corroborated. In Martinez (1999a) one can see the current thinking of Marini via the presentation of the relationship between certain empirical evidence and his own aforementioned conjecture with the idea of super exploitation.
Next, we will show that the results hold when one does take into account the problem of income from autonomous workers. To do this we ran the same econometric model but using the adjusted surplus value rates for the cases of Mexico and Venezuela.
c) Second test. Panel data model including Mexico’s and Venezuela’s adjusted surplus value rates.9
This econometric test uses the same surplus value rates estimates from various authors as in the first test with the exception of Mexico; in their place, we use our own surplus value rate estimate adjusted by excluding the income, of autonomous workers from the operating surplus and we include the surplus value rate for Venezuela. In this case we made our own adjustment to said rate based on data from Mateo (2003).
We find a positive relationship between productivity and the surplus value rate in the group of countries examined. The productivity levels are individually differentiated. The results seen are:
An increase of a thousand dollars per person employed in the year increases the surplus value rate by 3.29%. Productivity results statistically significant at a confidence level of 95%.
There is individual differentiation in the surplus value rates of each country expressed in αi (see Table 4):
Table 4 Estimator (Intercept) of the Fixed Effects Panel with Cross-Sectional Weighting. Selected Countries, 1950-2000.
| Country i | USA | Canada | UK | New Zealand | Japan | Mexico | Venezuela |
| α | 0.47 | 1.81 | 0.35 | 0.47 | 1.40 | 2.39 | 0.66 |
| αMex/αi | 5.09 | 1.32 | 7.03 | 5.09 | 1.71 | 1.00 | 3.68 |
Source: A1 (2006, Table 2 from Appendix 5)
Based on the model (see Appendix) and taking the corresponding productivity datum from PWTM 6.3, the estimated surplus value rates of the United States of America and Mexico, for example, in 1993 within the period of 1950 to 2000 would be determined in the following manner:
TP EUA,1993 = α EUA + βP EUA,1993 + ε EUA,1993
= 0.475398 + 0.032956 (53.8669) - 0.0154 = 2.23 o 223%,
compared to an observed surplus value rate of 2.29 or 229% and
TP Méx,1993 = α Méx + βP Méx,1993 + ε Méx,1993
= 2.397509+ 0.032956 (21.8354) + 0.2693 = 3.39 o 339%,
compared to an observed progress at a rate of 2.78 or 278%.
This means that the results corroborate the positive relationship between productivity and the surplus value rate according to the Marxist theory of accumulation but do not corroborate the conjecture derived from the same theory which states that undeveloped, less productive, countries have a lower surplus value rate than more developed, more productive, countries. The results partially corroborate our own conjecture which states that undeveloped countries with lower productivity have a high surplus value rate as supported by the data from Mexico. The data from Venezuela only partially supports our conjecture as the results agree when compared to the USA, the UK and New Zealand but not with Canada and Japan.
Productivity and Wage Share: Global Sample
Variables and Sources
Figueroa and Amaya (2017) used the profits/wages ratio as an approximate variable of the surplus value rate and the productivity estimates from the EPWT v 4.0 of 79 countries for 1995 to 2008.10 This database allows aggregation given that it adjusts for PPP. It has estimates for wage share, employment and product. The regression equation used is:
ln(p')it = β1 ln(π)it + αi + uit
where: p´= profit/wages is a proxy variable of surplus value rate, π=GDP/employment which expresses productivity, i refers to the country and t to time. As such we have N=i x t= 79 x 14 = 1 106 observations.
The relationship is analyzed between productivity and surplus value rate both for the groups of countries as well as the individual subgroupings of developed countries and undeveloped countries, defined by their superior or inferior productivity, respectively, when compared to the average global productivity.11
Results
The authors establish the positive and direct relationship between productivity and surplus value rate, β=0.2223 both for the groups and the respective subgroupings of developed and undeveloped countries.
Groups of countries
ln( p' )it = 0.2222 ln(π )it − 1.7415 + uit
t-estad. (7.3689) (-5.8086)
F = 54.28, R 2 intra = 5%, R 2 inter = 49.5%, R 2 global = 45.7%, i = 79, t = 14, N = 1106
Developed countries
ln( p' ) it = 0.141ln(π)it − 1.5548 + uit ,
t-estad. (3.0163) (-2.9986)
F = 9.10, R 2 intra = 3%, R 2 inter = 6%, R 2 global = 5%, i = 28, t = 14, N = 392
Undeveloped countries
ln( p' ) it = 0.291ln(π)it − 2.07 + uit ,
t-estad. (7.6611) (-5.8275)
F = 58.68, R 2 intra = 9%, R 2 inter = 6%, R 2 global = 4%, i = 44, t = 14, N = 616
Given that the panel models are also log-log, the estimators obtained are also elasticities. We find that the developed countries’ productivity has a lesser effect on the surplus value rate, 51% less elasticity than undeveloped countries as it turns out that β11=0.141 < β12 = 0.291.
According to the results, increasing productivity by 10% would raise the surplus value rate by 2.2% for the countries as a group; 1.41% for the developed countries and 2.91% for the undeveloped ones.12 In any case, the relationship between the two variables is positive. If the study is extended in terms of time, it also suggests that the effect of productivity on the surplus value rate is greater in undeveloped countries.
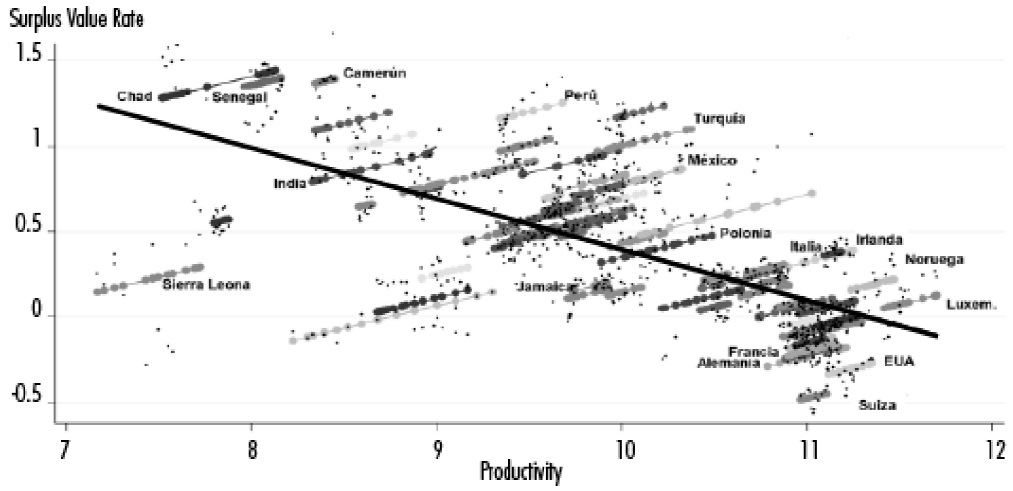
The estimates via the data of the panel are presented in Figure 3, where we can observe greater levels of exploitation of undeveloped countries and the correspondence to developed countries. The graphic also shows a very special relationship which is analyzed with data from the panel. The relationship between productivity and surplus value rate for the group of countries (a straight regression in a thick black line) turns out to be inverse to the behavior expected according to conjecture based on theory. But upon taking into account the fixed effect of each country’s slope we can observe underlying growth tendencies.13
4. CONCLUSIONS
The results of the tests presented in this work corroborate the positive relationship between productivity and the surplus value rate in accordance with the Marxist theory of accumulation. However, they do not corroborate the conjecture derived from this theory, according to which undeveloped, less productive, countries have a surplus value rate lower than more developed, more productive, countries. The results corroborate that undeveloped countries with low productivity have a surplus value rate higher than that corresponding to developed countries with high productivity.
According to the findings of a fixed effect panel econometric model that we presented here, the group of countries that is Mexico, Venezuela, the USA, the UK, New Zealand and Japan, the surplus value rate of undeveloped, less productive, countries is not lower than the corresponding rate of developed countries, with the exception of Japan and Canada when compared to Venezuela. JI squared test and cluster analyses of the relationship between productivity and a proxy inverse to the surplus value rate corroborate previous findings, according to which the surplus value rate is higher in undeveloped, less productive, countries.
Subsequent econometric tests prove that for a sample representative of all countries in the world, there is a positive relationship between productivity and a proxy of the surplus value rate, which agrees with the theory presented by Marx. The tests show that in undeveloped countries, although productivity is inferior to that in developed countries, it has a growth effect on the surplus value rate higher than that corresponding to that latter. It seems obvious that the greater productivity in countries can be explained in large part because they have more means of production with regards to living labor than countries which are less productive. As such, there seems to be no other option for the proper functioning of capitalism other than the increase of the surplus value rate as productivity grows. In other words, what should happen is that the greater productivity will present itself with an increase of organic capital composition and the necessary compensation with a greater surplus value rate. In Martinez and Valle (2011) we saw empirical evidence of a pattern of undeveloped countries with low productivity with a high composition of capital, due to said low productivity and their need to import means of production. These are elements which compel a high surplus value rate. The size of their industrial reserve force efficiently contributes to it. Undeveloped countries have a higher composition of capital than developed countries when they have a similar productivity average. As such they have a demand for a greater surplus value rate and it is driven as the increased difficulty in absorbing labor force produces a higher industrial reserve force.
REFERENCES
Cockshott, P., Cotrell, A. y Michaelson, G. (1995), “Testing Marx: Some New Results from UK Data”, Capital and Class, vol. 55, United Kingdom, Spring. [ Links ]
Cronin, B. (2001), “Productive and Unproductive Capital: a Mapping of the New Zealand System of National Accounts to Classical Economic Categories, 1972-1995”, Review of Political Economy, 13(3), DOI <https://doi.org/10.1080/09538250120055168> [ Links ]
Extended Penn World Table, versión 4 (EPWT v.4), <https://sites.google.com/a/newschool.edu/duncan-foley-homepage/home/EPWT>. [ Links ]
Figueroa, S. y Amaya, M. (2017), Análisis de la relación entre la tasa de plusvalía y la productividad laboral a nivel mundial, en el periodo de 1995-2008, Documento de trabajo, El Salvador, Universidad Centroamericana José Simeón Cañas. [ Links ]
Guerrero, D. (2006), La explotación. Trabajo y capital en España, Chap. I, España, Ed. Maia. [ Links ]
Kalmans, R. (1992), “The Political Economy of Exploitation: A Comparative Study of The Rate of Surplus Value in Japan and The United States, 1950-1980”, New York, Ph.D. dissertation, Department of Economics, New School for Social Research. [ Links ]
Levin, A., Lin, C.F. y Chu C. (2002), “Unit Root Tests in Panel Data: Asymptotic and Finite-Sample Properties”, Journal of Econometrics, vol. 108, núm.1, DOI <https://www.sciencedirect.com/science/article/pii/S0304407601000987?via%3Dihub> [ Links ]
Martínez González, B. G. (2006), “Diferencias de tasas de plusvalor entre países. Su relación con las diferencias de productividad” (Tesis doctoral), México, Doctorado en Ciencias Económicas, Universidad Autónoma Metropolitana. [ Links ]
__________ (2005), “Plusvalor, ingreso de trabajadores autónomos y diferencias nacionales de tasas de plusvalor”, Problemas del Desarrollo. Revista Latinoamericana de Economía, vol. 35, núm. 142, México, IIEc-UNAM, julio-septiembre. [ Links ]
__________ (1999a), “Algumas Evidências da superexploracao nos países subdesenvolvidos: a atualidade do pensamento de Marini”, Revista da Sociedade Brasileira de Economia Politica, núm. 4, junio. [ Links ]
__________ (1999b), “The Industrial Relative Wage in Mexico, 1960-1990”, International Journal of Political Economy, vol. 27, núm. 4. [ Links ]
Martínez González, B. G. y Valle Baeza, A. (2011), “Differences in Surplus Value Rates Between Developed and Underdeveloped Countries. An Analysis Based on Differences in Productivity and Capital Composition”, Marxism21 (korean review), vol. 21, Special Issue in English on Surplus-value Theory, Spring. [ Links ]
Marx, K. (1980) 1867, El capital, TI, secciones 2a., 3a., 6a. y 7a. caps. XXI- XXIII, T III, sección 3a., capítulos XIII a XV, México, Siglo XXI Editores. [ Links ]
Mateo, J. (2003), Análisis de la evolución y el papel de la relación salarial en la economía de Venezuela durante el periodo de crisis y reestructuración (1979-96), Reporte de investigación, España, Facultad de Ciencias Económicas y Empresariales, Universidad Complutense de Madrid. [ Links ]
Moseley, F. (1991), The Falling Rate of Profit in the Postwar United States Economy, chapters 2-4 and appendix B, New York, Macmillan. [ Links ]
Ochoa, E. (1989), “Values, Prices and Wage-profit Curves in the U.S. Economy”, Cambridge Journal of Economics, vol. 13. [ Links ]
Penn World Table Mark 5.2, 5.6, 6.1 y 6.3, <http://dc1.chass.utoronto.ca/pwt/> [ Links ]
Pindyck, R. S. y Rubinfeld, D. (2001), Econometría modelos y pronósticos, capítulo 9, México, McGraw Hill. [ Links ]
Sánchez, C. y Nieto, M. (2010), “Valores, precios de producción y precios de mercado a partir de los datos de la economía española”, Investigación económica, vol. 69, núm. 274. [ Links ]
Shaikh, A. (1990), Valor, acumulación y crisis, Bogotá, Tercer Mundo Editores. [ Links ]
__________ (1984), “The Transformation from Marx to Sraffa”, en Mandel and Freman (eds.), Ricardo, Marx, Sraffa: the Langston memorial Volume, London, Verso. [ Links ]
United Nations (1978), “Individual Country Data”, Yearbook of National Accounts Statistics, vol. I. [ Links ]
__________ (1999), National Accounts Statistics, vol. I y II. [ Links ]
Valle Baeza, A. (2005), “Por qué debe aumentar la composición de capital”, V Coloquio Latinoamericano de Economistas Políticos, Universidad Nacional Autónoma de México, México, octubre 27-29. [ Links ]
__________ (1998), “La productividad del trabajo al encuentro de la teoría marxista”, Revista da Sociedade Brasileira de Economía Política, 2, junio. [ Links ]
__________ (1994), “Correspondence Between Labor Values and Prices: A New Approch”, Review of Radical Political Economics, vol. 26, núm. 2. [ Links ]
Verbeek, M. (2000), A Guide to Modern Econometrics, cap. 10, 4th edition, John Wiley and Sons, Ltd., England. [ Links ]
1Among them Sánchez and Nieto (2010); Ochoa (1989); Shaikh (1984) and Valle (1994).
2
To create the clusters we used, for example, the Euclidean distance squared to calculate the similarity between variables of different countries, or the Ward method to make up the groups. These in turn determine a group called the centroid. The dendrogram is a tree diagram which is ideal for cases like these as it calculates the differences between the variables of the countries or the groups (see Pindyck and Rubinfeld, 2001, chap. 9). The number of groups is determined by the value of the coefficient of the conglomerates. The measure of similarities can be established for metric or binary variables. Instead Euclidean measure for the first:
where i and j are individual and xp did notice the variable. The similarity can be solved for K variables. The Euclidean similarities curve is:
Other measures are the Minkowski, Manhattan, etc. For binary variables, possible measures are: Euclidean; size, configuration, form differences (among others). While grouping methods are: centroid, closest neighbour, furthest neighbour, Ward, etc. The analysis of clusters or conglomerates can be done in a hierarchical or non-hierarchical manner. For the latter, the centroids must be known, and though they are usually not known, they can be estimated via a hierarchical approach.
3The panel models combine cross-sectional with time series analysis. Fixed effects refers to the model presupposing a coefficient, let us say alpha, unique to each unit of the cross-section. “When only a few observations are available for each individual it is very important to make the most efficient use of the data[… ]the individuals in the sample are ‘one of a kind’, and cannot be viewed as a random draw from some underlying population. This interpretation is probably most appropriate when i denotes countries, (large) companies or industries, and predictions we want to make are for a particular country, company or industry” (Verbeek, 2000b, p.351).
5Martínez (2006) for Mexico; Martínez (2006) and Mateo (2003) for Venezuela; Moseley (1991) for the United States; Murray (1993) for Canada; Cockshott et al. (1995) for the UK; Kalmans (1992) for Japan and Cronin (2001) New Zealand.
6To review discussions on unproductive labour and autonomous labour, as well as the role that their input plays in estimating the surplus value rate, see murkiness (1999b and 2006). In the case Venezuela, we took the surplus value rate excluding the oil industry as a way of omitting the service corresponding to foreign income. See further details murkiness (2006, chapter 5, paragraph 5).
10In this section we present a panel analysis which uses a widely known database, the EPTW v4. That analysis uses the work of Figuera and Amaya (2017) as a starting point as advised by Sanchez Perez. The results vary from those of the authors due to the adjustment of generalized least squares and the use of more econometric tests, like Levin-Li-Chu (2002), or autocorrelation and heteroskedasticity tests to check whether the model is sound.
11The Hausman test states that models must be made under fixed effects rather than random. There is no common source according to the Levin-Li-Chu test (2002), despite there being heteroskedasticity in the first model.
12The coefficient which links productivity and surplus value rate logarithms is the elasticity of the second in terms of the first; as such an increase of 10% in productivity becomes an increase of 2.2% in the surplus value rate. For example, the group of countries according to the regression model.
13In image three the thick black line estimated by MCO always suggest an inverse relationship. The black points are coordinates (πit, p’it), while the connect the dots are the estimates via fixed effects which show a direct relationship in most cases.
APPENDIX. REGRESSION, FIXED EFFECTS PANEL ON THE RELATIONSHIP BETWEEN PRODUCTIVITY AND SURPLUS VALUE RATE.
Image 1A. Estimates and diagnostic.Dependent variable: rate of surplus valueMethod: GLS (Cross Section Weights)Independent variable: productivity (P)Sample: 1950 2000Included observations: 51Number of cross-sections used: 7Total panel (balanced) observations: 182White Heteroskedasticity-Consistent Standard Errors & Covariance
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| P | 0.032956 | 0.001490 | 22.11974 | 0.0000 |
| Fixed Effects | ||||
| EUA-C | 0.475398 | |||
| CAN-C | 1.813681 | |||
| RU-C | 0.348390 | |||
| NZ-C | 0.470685 | |||
| JAP-C | 1.405849 | |||
| MEX-C | 2.397509 | |||
| VEN-C | 0.657718 | |||
| Weighted Statistics | ||||
| R-squared | 0.909785 | Mean dependent var. | 2.343662 | |
| Adjusted R-squared | 0.906155 | S.D. dependent var. | 1.544416 | |
| S.E. of regression | 0.473117 | Sum squared resid. | 38.94815 | |
| Log likelihood | - | |||
| 70.32730 | Durbin-Watson stat. | 0.193128 | ||
| Unweighted Statistics | ||||
| R-squared | 0.556934 | Mean dependent var. | 1.699236 | |
| Adjusted R-squared | 0.539110 | S.D. dependent var. | 0.778609 | |
| S.E. of regression | 0.528589 | Sum squared resid. | 48.61676 | |
| Durbin-Watson stat | 0.116717 | |||
Source: Created by the authors.
Received: January 10, 2018; Accepted: July 10, 2018











 texto en
texto en