Introducción
El problema inverso electroencefalográfico (PIE) consiste en determinar, a partir de mediciones electroencefalográficas sobre el cuero cabelludo, las fuentes bioeléctricas que generan dichas mediciones. Las fuentes representan grandes conglomerados de neuronas que trabajan de forma sincronizada para generar potenciales que puedan ser registrados en el cuero cabelludo a través de un electroencefalógrafo [1]. El PIE es un problema mal planteado en el sentido de Hadamard[2], esto es: Un problema es mal planteado si no tiene solución, o tal solución no es única ya que existen diferentes fuentes que pueden producir la misma medición, o presenta una inestabilidad numérica, que se refleja en el hecho de que pequeños cambios en la medición pueden producir grandes variaciones en la localización de la fuente. Para tratar esta inestabilidad se utilizan los llamados métodos de regularización [2], que permiten encontrar soluciones estables aproximadas a partir de la medición con error. Para el estudio del PIE, se requiere considerar el llamado problema directo, el cual consiste en determinar la medición cuando se conoce la fuente. A diferencia del problema inverso, el problema directo tiene buenas propiedades numéricas, es decir, si dos fuentes están cercanas, las respectivas mediciones también lo estarán. Esto se demuestra abajo cuando se llegue al planteamiento operacional del problema.
Las fuentes bioeléctricas pueden dividirse en corticales y subcorticales y su estudio puede hacerse por separado sin pérdida de generalidad. En este trabajo, sólo se considera el caso en el que la fuente se localiza sobre la corteza cerebral. En este caso, el problema de identificación de la fuente tiene solución única [3], por lo que el mal planteamiento del PIE está asociado con la inestabilidad numérica. Para manejar esta inestabilidad, se utiliza el método de regularización de Tikhonov [2], eligiendo el parámetro de regularización por medio del método de la curva L[4]. En este trabajo, se propone un algoritmo para identificar fuentes de corriente dipolar que modelan focos epilépticos. Las fuentes de corriente dipolar se definen por medio de la función delta de Dirac y el momento dipolar [5]. Para aproximar a la función delta de Dirac, se utilizan funciones campana. En el primer paso, el algoritmo identifica al centro de la función campana, con lo que se halla el centro de la función delta de Dirac. En el segundo paso, se determina el momento dipolar, con lo que se determinan los parámetros de la fuente de corriente dipolar. En ambos casos se utiliza el funcional de Tikhonov y se encontró que puede considerarse el mismo parámetro de regularización. El algoritmo propuesto es implementado en una geometría formada por dos círculos concéntricos, procediendo por dos caminos: 1) usando series de Fourier (armónicos circulares); 2) usando el método del elemento finito (MEF) y el Método de Gradiente Conjugado (MGC) [6]. En ambos casos se obtienen tanto el centro como el momento dipolar de la fuente y con ello se mostró que el algoritmo propuesto muestra buenos resultados. Los resultados son ilustrados a través de ejemplos sintéticos que muestran la factibilidad del algoritmo propuesto para determinar los parámetros de la fuente de corriente dipolar. Los dos métodos pueden extenderse al caso tridimensional y con ello, el algoritmo propuesto. Además, que el segundo camino puede utilizarse para geometrías irregulares.
Cabe destacar que el problema de identificar los parámetros de la fuente dipolar es no lineal y que se propone un algoritmo que encuentra dichos parámetros a través de dos problemas inversos lineales que utilizan el método de regularización de Tikhonov, y el parámetro de regularización se obtiene mediante el método de la curva L. Los resultados numéricos mostraron que puede elegirse el mismo parámetro de regularización para ambos problemas. Además, el primer paso del algoritmo puede aplicarse para fuentes más generales que las funciones campana, lo que podría permitir considerar otro tipo de actividad diferente a la epiléptica o aproximar a las fuentes de corriente dipolar por medio de otra clase de funciones.
Problema de Contorno Electroencefalográfico Cortical
Se considera a la cabeza
El estudio del problema de identificación de fuentes se realiza a través del siguiente problema de contorno [3]:
donde g es la fuente que representa a un foco epiléptico,
Llamaremos al problema (1)-(5), Problema de Contorno Electroencefalográfico Cortical (PCEC). Asociados al PCEC se tienen las siguientes definiciones.
Definición 1: Dada g definida sobre
S1, el problema directo consiste en hallar la
medición
Definición 2: Dada una función V definida sobre
S2, el problema inverso consiste en determinar
una fuente g definida sobre S1, tal
que la solución u del problema directo correspondiente a
g, satisfaga que
Solución del PCEC
Solución débil: Planteamiento operacional
Para el análisis de la solubilidad del PCEC se consideran los siguientes espacios funcionales:
Definición 3: Dada g ϵ F, a la función u ϵ U se le llama
solución débil del PCEC si para cada
El Teorema siguiente garantiza la existencia de solución débil del PCEC y permite realizar el planteamiento operacional del mismo.
Teorema 1: La condición (6) es necesaria y suficiente para la existencia de la solución
débil del PCEC. Hay una única solución débil
Se define el operador
Solución clásica
Definición 4:
El siguiente teorema garantiza la existencia y unicidad (salvo constantes) de la solución clásica del PCEC. La demostración utiliza las técnicas de la teoría de potencial, sistemas duales y los teoremas de alternativa de Fredholm[3].
Teorema 2: Dada g ϵ C (S1), la condición de compatibilidad (6), es necesaria y suficiente para la existencia y unicidad (salvo constantes) de la solución clásica del PCEC.
Para el caso de fuentes de tipo campana, con las que se aproximan a las fuentes dipolares, la solución clásica y la débil coinciden. Esto se debe a que dichas fuentes son infinitamente diferenciables con lo que satisfacen las hipótesis del Teorema 2 y a que la solución clásica satisface la relación (7). Por otra parte, para fuentes campana la solución débil pertenece al espacio de Sobolev H2(Ω) [3] con lo que satisface el problema de contorno en sentido clásico.
Solución del problema directo e inverso
Para hallar la solución del PCEC pueden emplearse diferentes métodos tanto analíticos como numéricos. Por ejemplo, el método de la matriz de tipo Green que generaliza al método de la función de Green, el método de las series de Fourier, el MEF, el método de diferencias finitas, entre otros. Se considera el MEF, el método de las series de Fourier y el caso bidimensional en una geometría simple para mostrar la factibilidad del algoritmo propuesto. Todos los resultados pueden extenderse al caso tridimensional. Claramente el problema directo tiene una solución única ya que el PCEC tiene solución única salvo constantes y en los espacios funcionales en los que se busca la solución, definidos anteriormente, se obvian las constantes. Para el problema inverso se tiene el siguiente resultado [3]:
Teorema 3: Dada una medición
En la Sección siguiente, se busca la solución de los problemas directo e inverso por medio de series de Fourier y del MEF. Estos métodos se usan para tener dos formas de validar el algoritmo propuesto, uno analítico y otro numérico.
Series de Fourier
Se considera que la región Ω está compuesta por dos círculos concéntricos centrados en el origen de radios R1 y, R2 es decir, Ω1 el círculo de radio R1, representa al cerebro y el resto de las capas que componen la cabeza Ω2 está representado por la región anular circular que se forma al hacer la diferencia del círculo de radio R2 con el de radio R1. La solución del PCEC se buscará usando el método de las series de Fourier. En particular, se usan los armónicos circulares los cuales forman una base para el espacio de las funciones armónicas. Para hallar la solución se supone que la fuente g puede desarrollarse en la forma:
donde los coeficientes
Para determinar los coeficientes de Fourier de u se utilizan las condiciones de contorno del PCEC. Después de laboriosos cálculos se halla que la solución del problema directo está dada por:
donde
Nótese que V representa a la medición sobre la frontera
Para el problema inverso se considera que
donde 𝛼(𝛿)>0 es el parámetro de regularización y
con
Se considera ahora que en vez de V, se tiene la medición con
error
Enseguida, se procede a buscar la solución de los problemas directo e inverso por medio de una combinación de dos métodos numéricos, a saber, el Método de Elemento Finito (MEF) y del Método de Gradiente Conjugado (MGC).
Método de Elemento Finito y el Método de Gradiente Conjugado
El MEF puede emplearse para resolver el PCEC tanto en geometría simple como
irregular. En ambos casos se considera la expresión para la solución débil (7). A fin de ilustrar el algoritmo
propuesto, sólo se desarrolla el caso de geometría simple, a saber, el caso en que
la región Ω se representa por medio de círculos concéntricos. Para
aproximar el espacio
U
, se considera una triangulación de elemento finito
Para hallar la solución del problema inverso, se debe minimizar el funcional de Tikhonov. Esto se realiza por medio del Método del Gradiente Conjugado (MGC) [8, 9, 10]. Para aplicar el MGC se utiliza el siguiente problema de valores en la frontera:
El cual es conocido como problema de contorno electroencefalográfico cortical
adjunto, denotado como PCECA. Con este problema se define el operador adjunto
A* : L2
(S2) → L2
(S1) con regla de correspondencia
Se propone una expresión para una fuente de corriente dipolar concentrada en la corteza cerebral, explicada en la siguiente Sección.
Fuentes dipolares corticales
La corriente total J en el cerebro consiste de la suma de dos corrientes J = Jp+ σi E, donde Jp es la corriente primaria o impresa y es debida a la actividad biológica de las neuronas; σi E, i = 1, 2, se llama corriente óhmica y es debida a la corriente eléctrica en el medio, donde σi representa la conductividad en cada región. La corriente Jp puede estar concentrada tanto en la corteza como en el volumen cerebral. En las regiones restantes que compone la cabeza sólo puede haber corrientes óhmicas.
Se considera que la fuente corresponde a un foco epiléptico ubicado sobre la
corteza cerebral. La representación matemática de este tipo de fuente, se hará
siguiendo la idea del caso en el que la fuente es subcortical, en el cual los
dipolos de corriente se representan a través de la función delta de
Dirac que es una función generalizada o distribución [1, 11, 12]. Más precisamente, se
considera que un foco epiléptico concentrado en el punto a ϵ
S1 puede representarse en la forma:
donde β es el ancho de la campana. Ahora, tomando en consideración que para los flujos de corriente en la frontera se considera la componente normal de las corrientes involucradas (óhmicas y primarias) se llega a que las fuentes corticales con la que se representan a los focos epilépticos tienen la forma:
donde n 1 representa la normal exterior sobre S1 y el término
se incluye para que se satisfaga la condición de compatibilidad (6) y representa la medida de S1 (longitud en el caso de dos dimensiones y área en el caso tridimensional).
El algoritmo propuesto se deduce en la siguiente Sección.
Algoritmo de identificación de los parámetros de la fuente
Como se ha mencionado anteriormente, el interés radica en el problema de
identificación de fuentes dipolares que representan a focos epilépticos. Por la
forma en que éstas se definen, se deben identificar los parámetros de las
mismas, a saber, el centro de la función delta de Dirac y el
momento dipolar. En [3], se presentó un
algoritmo para identificar a las fuentes
Se va a considerar el caso de círculos concéntricos. Cuando la solución se busca por medio de series de Fourier, una vez que se encontró el centro de la función campana [3], se utiliza (12) para definir
donde
y notando que en este caso
donde
con
Así, la solución del problema está dada por
Cuando se utilizan el MEF y el MGC, una vez que se determina el centro de la función campana [3], se determina el momento dipolar a través de:
con M= (m1,
m2) con
donde Mt denota la matriz transpuesta de M. Esta última metodología para determinar los parámetros del dipolo se puede aplicar también al caso de geometría irregular. Este caso no se aborda en este trabajo.
Resultados numéricos y discusión
En esta Sección, se presentan ejemplos numéricos para ilustrar el algoritmo
propuesto. Se considera que la región Ω está determinada por dos círculos
concéntricos centrados en el origen, es decir, Ω1 es un dominio circular
de radio R1 y Ω2 es un dominio anular con
radio interior R1 y radio exterior
R2, como se muestra en la Figura 1. Por simplicidad se consideran los siguientes valores
σ1 =3 y σ2=1. Los
ejemplos sintéticos son generados tomando una fuente superficial
gβ definida por (12); posteriormente se resuelve el
problema directo, es decir, se calcula
Primer paso: Determinar de manera estable el centro ɑ𝛼𝛿 de la función campana que define a g𝛼(𝛿),N (y con ello al centro aproximado de la función delta de Dirac) recuperada usando los métodos desarrollados en [3].
Segundo paso: Determinar el momento dipolar a partir de
Para determinar los parámetros de regularización
donde
En los ejemplos siguientes se consideran los errores absolutos EA(.,.) y relativos ER(.,.) en las normas de los espacios correspondientes.
Ejemplo 1 (Identificación de los parámetros de la fuente usando series
en armónicos circulares): Se considera que en la fuente de corriente dipolar
donde
para i = 1, 2 y para k = 1,2, …,
N. Después de aplicar el algoritmo para identificar una fuente
aproximada g𝛼(𝛿),N por el método
propuesto en [3], con 𝛼(𝛿) = 10-4
se obtiene el centro aproximado ɑ𝛼(𝛿) de la función
campana g𝛼(𝛿),N. En coordenadas
polares el centro exacto de la fuente exacta
gβ está dado para

Figura 2: (a) Fuente exacta gβ (línea punteada) y su aproximación por su serie de Fourier truncada gβ,N (línea continua). (b) Medición exacta V (línea punteada) y perturbada V𝛿 (línea continua). (c) Fuentes exacta gβ (línea continua) y recuperada g𝛼(𝛿) (línea punteada).
Para determinar el momento dipolar
Tabla 1 Resultados numéricos considerando el centro ɑ =
(0,1) y momento dipolar
| 𝛿 | 0 | 0.001 | 0.01 | 0.1 |
|---|---|---|---|---|
| EA(Vδ , V) | 0 | 1.1212×10-4 | 1.1594×10-3 | 1.1637×10-2 |
| ER(Vδ, V) | 0 | 5.6663×10-4 | 5.8590×10-3 | 5.8809×10-2 |
| α(δ) | 10-6 | 10-6 | 10-5 | 10-4 |
| ɑα(δ) | (-0.029, 0.999) | (-0.029, 0.999) | (-0.029, 0.999) | (-0.029, 0.999) |
| EA(ɑ, ɑα(δ)) | 2.9202×10-2 | 2.9202×10-2 | 2.9202×10-2 | 2.9202×10-2 |
| ER(ɑ, ɑα(δ)) | 2.9202×10-2 | 2.9202×10-2 | 2.9202×10-2 | 2.9202×10-2 |
| α1(δ) | 10-6 | 10-6/ | 10-5 | 10-4 |
|
|
(0.985, 0.999) | (0.984, 0.999) | (0.980, 1.000) | (0.883, 0.987) |
|
|
1.4929×10-2 | 1.5120×10-2 | 1.9765×10-2 | 1.1681×10-1 |
|
|
1.0556×10-2 | 1.0692×10-2 | 1.3976×10-2 | 8.2597×10-2 |
En este caso, el valor del parámetro de regularización de α(𝛿) y 𝛼1(𝛿)
es de
En la Tabla 2, se muestran los resultados de
la recuperación de los parámetros ɑ𝛼(𝛿) y
Tabla 2 Resultados numéricos considerando diferentes centros y momentos dipolares, para 𝛿 = 0.1.
|
ɑ
P |
(-1,0) (1,1) |
|
(1,0) (2,1) |
|---|---|---|---|
| EA(Vδ, V) | 9.7065×10-3 | 1.8806×10-2 | 2.0093×10-2 |
| ER(Vδ,V) | 4.9057×10-2 | 5.3766×10-2 | 5.0776×10-2 |
| α(δ) | 10-4 | 10-4 | 10-4 |
| ɑα(δ) | (-0.9824, 0.1862) | (0.6967, 0.7173) | (0.999, 0.029) |
| EA(ɑ, ɑα(δ)) | 1.8702×10-1 | 1.4601×10-2 | 2.9017×10-2 |
| ER(ɑ, ɑα(δ)) | 1.8702×10-1 | 1.4601×10-2 | 2.9017×10-2 |
| α1(δ) | 10-4 | 10-4 | 10-4 |
|
|
(0.9913, 0.9921) | (0.5764, 1.9505) | (2.0119, 1.0044) |
|
|
1.1751×10-2 | 9.1058×10-2 | 1.2751×10-2 |
|
|
8.3096×10-3 | 4.4169×10-2 | 5.7024×10-3 |
Ejemplo 2 (Identificación de los parámetros de la fuente usando el MGC y
el MEF): Se considera la misma región circular del ejemplo anterior con los mismos
valores para σ1, σ2, R1,
R2 y para los parámetros ɑ,
La Tabla 3 muestra los resultados numéricos
para el caso de datos perturbados V𝛿, para diferentes
valores de 𝛿, donde 𝛼(𝛿) es el parámetro de regularización, ε es
el criterio de paro (o tolerancia) del MGC, n es el número de
iteraciones del MGC para determinar la fuente superficial aproximada
Tabla 3 Resultados numéricos considerando el centro ɑ =
(0,1) y momento dipolar
| 𝛿 | 0 | 0.001 | 0.01 | 0.1 |
|---|---|---|---|---|
| EA(Vδ, V) | 0 | 1.0970×10-4 | 1.0481×10-3 | 1.0935×10-2 |
| ER(Vδ, V) | 0 | 1.5994×10-3 | 1.5281×10-2 | 1.5942×10-1 |
| α(δ) | 10-6 | 10-6 | 10-5 | 10-4 |
| ε | 10-3 | 10-3 | 10-3 | 10-3 |
| n | 5 | 5 | 5 | 6 |
| aα(δ) | (0.0006, 1) | (0.0006, 1) | (0.0006, 1) | (0.0006, 1) |
| EA(ɑ, ɑα(δ)) | 6.3075×10-4 | 6.3075×10-4 | 6.3075×10-4 | 6.3075×10-4 |
| ER(ɑ, ɑα(δ)) | 6.3075×10-4 | 6.3075×10-4 | 6.3075×10-4 | 6.3075×10-4 |
| α1(δ) | 10-6 | 10-6 | 10-/5 | 10-4 |
|
|
(0.978, 1.002) | (0.971, 1,002) | (0.937, 1.004) | (0.886, 1.046) |
|
|
2.2034×10-2 | 2.9282×10-2 | 6.2523×10-2 | 1.2239×10-1 |
|
|
1.5581×10-2 | 2.0706×10-2 | 4.4211×10-2 | 8.6545×10-2 |
La fuente dipolar superficial recuperada corresponde a ɑ
𝛼(𝛿) y
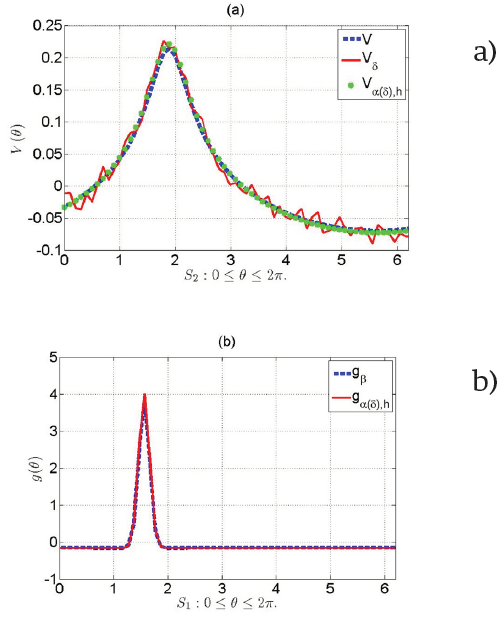
Figura 3 (a) Medición exacta (V, línea punteada), perturbada (
Se muestran resultados similares en la Tabla 4
para 𝛿 = 0.1 y diferentes valores del centro y del momento dipolar
Tabla 4 Resultados numéricos considerando diferentes centros y momentos dipolares con β = 0.1, para 𝛿 = 0.1, usando la malla M1 (774,1470) cuyo tamaño de malla es h = 0.1.
|
ɑ
P |
(-1,0) (1,1) |
|
(1,0) (2,1) |
|---|---|---|---|
| EA(Vδ, V) | 1.1258×10-2 | 1.9521×10-2 | 2.3167×10-2 |
| ER(Vδ, V) | 1.6138×10-1 | 1.6067×10-1 | 1.4192×10-1 |
| α(δ) | 10-4 | 10-4 | 10-4 |
| ε | 10-3 | 10-3 | 10-3 |
| n | 7 | 6 | 8 |
| ɑα(δ) | (-1, 0.0013) | (0.7073, 0.7069) | (1, -0.0024) |
| EA(ɑ, ɑα(δ)) | 1.2615×10-3 | 3.1537×10-4 | 2.4343×10-3 |
| ER(ɑ, ɑα(δ)) | 0.0013 | 3.1537×10-4 | 0.0024 |
| α 1(δ) | 10-4 | 10-4 | 10-4 |
|
|
(0.9885, 1.1042) | (0.4240, 2.0615) | (2.0065, 0.8816) |
|
|
1.0485×10-1 | 9.7728×10-2 | 1.1857×10-1 |
|
|
0.0707 | 0.0464 | 0.0541 |
Por lo tanto, se ha mostrado que el método propuesto recupera soluciones numéricas estables en el caso de datos con error Vδ, tal como se ilustra en la Figura 3.
En las ecuaciones (13) y (15), puede emplearse en vez de la medición Vδ , el potencial que corresponde a la solución encontrada en la primera parte del algoritmo. Ya que el método es estable se obtendrán resultados similares.
Conclusiones
Los resultados numéricos mostraron que el algoritmo propuesto es convergente, estable y que el parámetro de regularización de cada uno de los problemas en que se divide el algoritmo, puede elegirse igual (usando el método de la curva L) y el nivel de error es del orden del error de medición y con ello, la factibilidad del algoritmo propuesto. Entre las ventajas de este método para identificar de manera estable fuentes de tipo dipolar, se hallan que el problema no lineal se dividió en dos problemas lineales (para los cuales se pudieron aplicar algunos resultados conocidos) y que puede extenderse a geometrías complejas y tridimensionales. Sin embargo, debe analizarse su posible aplicación a fuentes más generales.
En un trabajo futuro, se explorará la posibilidad de aplicar el algoritmo a otro tipo de fuentes que se expresen por medio de un conjunto finito de parámetros, las cuales pueden representar diferentes tipos de actividad eléctrica; otra posibilidad es el de usar otro tipo de expresión para aproximar a la función delta de Dirac la cual pueda dar ventajas numéricas.











 nueva página del texto (beta)
nueva página del texto (beta)



