Introduction
Hearing loss may result from genetic causes, complications at birth, certain infectious diseases, chronic ear infections, the use of particular drugs, exposure to excessive noise and aging, which is represent a major global health problem. According to the World Health Organization (WHO), about 360 million people worldwide have disabling hearing loss, and 32 million of tríese are children [1]. There are many infections and contagious diseases related to hearing loss such as mumps. Mumps is an enveloped, single-stranded RNA virus belonging to the family paramyxoviridae and causes an acute infectious disease mainly in children and young adults [2]. Mumps is transmitted through infected respiratory secretions and is highly contagious [3]. The most common clinical manifestations of infection include a u-like illness and bilateral swelling of the parotid glands. Mumps infection occasionally induces the potential for complications such as pancreatitis, orchitis, ophoritis, aseptic meningitis, encephalitis and sensorineural hearing loss. Hearing loss due to mumps is thought to be unilateral and profound with rapid onset [4].
On the other hand, one of the most social factor of hearing loss is noise exposure (eg, through personal music players). This is a major cause of hearing loss worldwide [5]. In addition, the characteristic pathological feature of noise-induced hearing loss is the loss of auditory sensory cells in the cochlea. Because these hair cells cannot regenerate in mammals, no remission can occur, prevention of noise-induced hearing loss is the only option to preserve hearing [6].
Abnormalities or damage in the structure inside the inner ear can result by many diseases that can load to the hearing loss. An example of such a disease is the Alport syndrome [7] and Meniere's disease [8]. For these raisons, many mathematical models have been proposed to model the function and the dysfunction of the inner ear by using partial differential equation (PDEs) [7,8,9,10,11]. The epidemiological models in the beginning has started by Graunt [12] then described by Kermack and Mckendric [13] by considering the total population into three classes namely susceptible (S) individuals, infected (I) individuals and recovered (R) individuals which is known to us as SIR epidemic model [14,15,16]. Today, this SIR epidemic model is very important in analysis of many diseases. Referring to the simplest version of the most classical epidemiological model for directly-transmitted infectious diseases [17,18,19,20,21,22], as well as, the social and epidemiological factors of hearing loss existing in the biological studies and in the literature [23,24,25], we proposed a new mathematical model by using (ODEs) that describe the time dependence of the dynamics of hearing loss by considering the contagion factor is the mumps virus and the social factor is the exposure to noise. This model is described by the following system:
The population is divided into three epidemiological classes that are: H(t) is the number of susceptible individuals at time t (normal hearing), L(t) is the number of infected individuals at time t (loss of hearing), and R(t) is the number of removed individuals at time t (recovered hearing). Further Λ is the recruitment rate of the population, μ is the natural death rate of the population, β is the transmission rate due to social contagion of hearing loss (mumps), ε is the non-contagion risk of hearing loss due to noise exposure and γ is the recovery rate of the infective individuals.
The rest of paper is organized as follows. In the next section, positivity and boundedness of solutions are studied. In Section 3, the basic reproduction number is derived, also the local and the global asymptotic stability of the equilibria are analyzed. The numerical results are given in Section 4. Lastly, we give a conclusion of our results in Section 5.
Positivity and boundedness of solutions
In this section, we will establish the positivity and boundedness of solutions of model (1), which proves that our model is well posed.
PROPOSITION 2.1. All solutions starting from non-negative initial conditions exist for all t > 0 and remain bounded and non-negative.
PROOF. For the positivity, we show that any solution starting in non-negative
orthant,
This proves the positivity of solutions. Now, we prove that the solutions are bounded. We defined T(t)= H(t)+L(t) By non-negativity of the solution, it follows that;
Then
From the last equation (1) and since L is bounded, we deduce that R is bounded. This completes the proof.
Stability analysis of hearing loss model
Local stability of endemic equilibrium point for ε > 0
The following theorem presents the existence and uniqueness of endemic equilibrium if R0 > 1.
THEOREM 3.1. System (1) has a unique equilibrium point
PROOF. By equalizing to zero the rights members of the system (1), we find one endemic point that exists for above model:
Where
With
The Jacobian matrix of the system (1) is given by:
The characteristic equation of the endemic equilibrium point is given by;
Note that coefficient
are both positive if
From the Routh-Hurwitz theorem given in [26], all roots of equation (5) have negative real parts. Consequently E * is locally asymptotically stable whenever R0 > 1.
Global stability of endemic equilibrium point for ε > 0
The following theorem discusses the global stability of the endemic equilibrium.
THEOREM 3.2. The endemic equilibrium
PROOF. Consider the following Lyapunov functional;
Where
To simplify the presentation, we shall use the following notation: H=H(t) and L=L(t).
Note that
And
Hence,
Then, we obtain the following equation:
From equation (6), we have:
Since,
We have
Thus
if and only if H =
From LaSalle invariance principle [27], we conclude that
Stability analysis for special case ε = 0
Notice that the system (8) has a basic reproductive number
R0 represents the average number of secondary infections caused by an infective individual introduced into a group of susceptible. By equalizing to zero the rights members of the system (8), we find two equilibrium points that exists for above model:
The endemic equilibrium point exist only when
i.e the infection rate must be greater than the death rate of the infected individuals or R0 > 1.
Local stability of equilibria
The following theorems discuss the local stability of the equilibrium point.
THEOREM 3.3.
1. If R0 < 1, then the disease-free equilibrium, Ef is locally asymptotically stable.
2. If R0 > 1, Ef is unstable.
PROOF. The Jacobian matrix evaluated in the disease-free equilibrium
is given by
Whose eigenvalues are
then R0 < 1 and therefore Ef is locally asymptotically stable.
The disease-free equilibrium point is unstable if
which translate into R 0 > 1.
Now, we focus on local stability of the endemic infection equilibrium E * .
THEOREM 3.4.
1. If R0 > 1, E* is locally asymptotically stable.
2. If R0 < 1, then the endemic equilibrium E* does not exist.
PROOF. By substituting the endemic equilibrium E*= (H*, L*, R*) in the Jacobien matrix of the system (8)
The characteristic equation of the endemic equilibrium point is given by
Clearly when R0 > 1, both
And
then all roots of the characteristic equation have negative real parts. Consequently E* is locally asymptotically stable.
Global stability of equilibria
In this section, we establish the global stability of the equilibria. Firstly, we have the following
THEOREM 3.5. The disease-free equilibrium Ef is globally asymptotically stable when R0 < 1.
PROOF. Consider the following Lyapunov functional
Where
and calculating the time derivative of V1(t) along the positive solution of system (8), we get;
Where
Since R0 ≤ 1, we have
Thus, the disease-free equilibrium Ef is stable, and
if and only if H = Hf and L(R0-1)=0. We discuss two cases:
Then βHfL = 0, Hence L = 0.
From LaSalle invariance principle [27], we conclude that Ef is globally asymptotically stable.
Note that the disease-free equilibrium Ef is unstable when R0 > 1.
Now, we establish a set of conditions which are sufficient for the global stability of the endemic equilibrium E*.
THEOREM 3.6. The endemic equilibrium E* of the system (8) is globally asymptotically stable.
PROOF. See the proof of theorem 3.2, and we replace ε by zero, we conclude that E* is globally asymptotically stable.
Numerical simulations
In this section, we show the numerical simulations and the graphs of system (1) to illustrate the different result obtained for each of the two cases ε > 0 and ε = 0 previously analyzed.
We choose the following data set of system (1) as follows: Λ= 0.5, μ= 0.1 and γ= 1/17. By using the values of Λ, μ,
γ
and ε= 0.0025 > 0 [28], we find β= 0.1433 for R0 > 1 already defined for mumps disease [29]. Therefore, according to Theorem 3.2, the system (1) has a unique endemic equilibrium which is globally asymptotically stable. So, the solution of system (1) is persistent in population and converge to
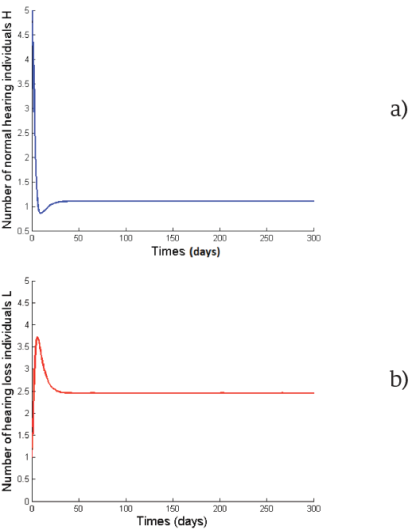
Figure 1 Normal hearing (a) and loss of hearing (b) individuals as function of time in the case of ε = 0,0025 and R0>1.
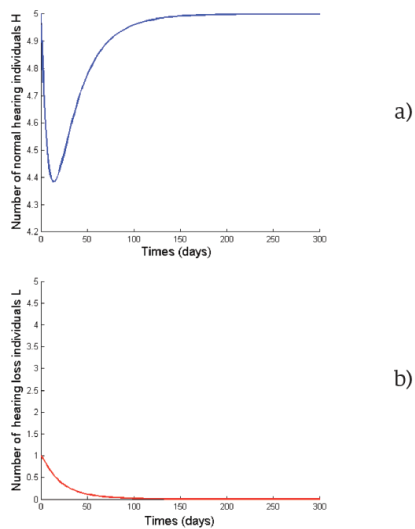
Figure 2 Normal hearing (a) and loss of hearing (b) individuals as function of time in the case of ε = 0 and R0 < 1.

Figure 3 Normal hearing (a) and loss of hearing (b) individuals as function of time in the case of ε = 0 and R0 > 1.
Conclusions
In this paper, we have presented a mathematical model of hearing loss based on a nonlinear system of differential equations. We analysis the hearing loss resulting from two factors, the first factor is contagious due to Mumps disease and the second is social caused by exposure to noise. By analysis the model, we have proved the existence, positivity and the boundedness of solutions of the problem, which implies that the model is well posed. We have shown in the case of ε = 0 that the disease free equilibrium is globally asymptotically stable if the basic reproductive number R0 < 1 and the endemic point is globally asymptotically stable when R0 > 1. In the case of hearing loss with the both factors mumps and noise ε > 0 the system has a unique endemic point exists and is globally asymptotically stable, which means that the disease persists in the population. In addition, the simulation of this model provides that the number of individuals with hearing loss increase when we introduce the risk factor noise.











 nueva página del texto (beta)
nueva página del texto (beta)



