INTRODUCCIÓN
Los métodos de árboles de decisión inductivo se introdujeron por primera vez con el concepto de Sistema de aprendizaje en la década del sesenta[1][2]. Desde entonces, se han seguido desarrollando y aplicando estudios para clasificar objetos.
De hecho, métodos importantes incluyen particiones recursivas de algoritmo[3], y la técnica de Iterative Dichotomiser 3 (ID3)[4][5]. La estructura de un árbol de decisión comienza con un nodo raíz, a partir del cual, todas las ramas se originan. Una rama toma la forma de una serie de nodos donde las decisiones sobre los valores de atributo de condición se realizan en cada nodo, lo que permite la progresión a través del árbol. Una progresión se detiene en un nodo hoja, donde se da una clasificación de decisión. Esto se basa en la regla asociada con la rama completa desde el nodo raíz al nodo de hoja individual[6].
Una característica clave de estos métodos tradicionales de árboles de decisión inductivos, es que las decisiones de un nodo son clásicos (crisp). Por ejemplo, las sentencias relativas a valores de atributos 'menos que', 'igual' o 'mayor que', que indican el camino por el árbol.
El resultado de los árboles de decisión es categórico; por ello, no cubren la incertidumbre que pudiera existir en la clasificación[7]. Éstos han tenido una serie de alteraciones para tratar con el lenguaje y las incertidumbres de medición, con el objetivo de combinar los árboles simbólicos de decisión con el razonamiento aproximado ofrecido por la representación difusa. La intención es aprovechar las ventajas complementarias de ambos: la popularidad en las aplicaciones para aprender de los ejemplos y la comprensión del conocimiento de los árboles de decisión, y la capacidad de tratar con información inexacta e incierta de la representación difusa[28]. En este contexto, Yuan y Shaw[8], consideran que en las sentencias clásicas, realizar pequeños cambios en los valores de los atributos de un objeto pueden llevar a repentinas variaciones para la decisión de asignar a una clase determinada. Por lo tanto, para superar estas deficiencias, Quinlan[7] sugiere un método probabilístico para construir árboles de decisión como clasificadores probabilísticos. En ese sentido, para suavizar los límites de los nodos del árbol de decisiones, se han desarrollado varias técnicas dentro de un ambiente difuso. Por ejemplo, el análisis de ID3 se ha extendido para incluir medidas de entropía difusa[9] [10], cuyo objetivo es determinar el nivel de incertidumbre de un conjunto difuso.
Yuan y Shaw[8] introdujeron un método de inducción de un árbol de decisión difusa. El trabajo expone esta técnica en un contexto antropométrico para la salud del escolar. Una de las razones para el uso de la teoría de conjuntos difusos es su simplicidad y su similitud con el razonamiento humano[11]. Esta similitud incluye el uso de términos lingüísticos asociado al conjunto de las reglas difusas a través de la utilización de las funciones de pertenencia específicas a un conjunto difuso. Una característica importante del método de Yuan y Shaw[8] es que permite el uso de atributos de condición continua y nominal, donde las funciones de pertenencia convierten los atributos continuos en valores ordinales con términos lingüísticos asociados.
De otro lado, los árboles de decisión difusa se pueden utilizar como parte de modelos híbridos que mejoren los resultados esperados. Mao[31] propone un forma de sistema de inferencia difusa basado en la estructura de árboles adaptativos mostrando que se requiere menor cálculo y tiene una alta exactitud. Fan[32] desarrolla un modelo híbrido integrando un método de agrupación de datos basado en casos y un árbol de decisiones difuso para la clasificación de datos médicos.
En general, un conjunto de reglas difusas (lingüísticas) es construido a partir de un árbol de decisión difusa, que describe la variación en los atributos antropométricos de una determinada muestra. Desde esa perspectiva el análisis del árbol de decisión difuso se puede aplicar en un contexto de exceso de peso y obesidad de escolares mediante el análisis de los atributos antropométricos que la muestra refleja. Pues las variables antropométricas, por lo general son utilizadas para analizar el estado nutricional, el crecimiento físico y la composición corporal del ser humano.
La valoración del exceso de peso está dada por las recomendaciones que brinda la Organización Mundial de la Salud[12] y la IOFT[13]. Estos organismos basan la clasificación en función del Índice de Masa Corporal [IMC= peso (kg)/estatura (m2)]. En ese contexto, algunos estudios han desarrollado aproximaciones hibridas usando árbol de decisión, Na'ive Bayes, distancias medias y euclidiana y minería de datos para la predicción del exceso de peso en niños y adolescentes[14]; sin embargo, hasta donde se sabe no hay estudios que investiguen la exactitud para determinar la clasificación del exceso de peso corporal en escolares entre los 6 a 17 años de edad. Esta información podría facilitar la clasificación, especialmente cuando se trata de diagnosticar grandes muestras de datos. Por lo tanto, el objetivo de este estudio fue analizar la precisión de la clasificación del exceso de peso de escolares mediante la aplicación de un árbol de decisión difusa, utilizando una base de datos de Itaipú, Paraná (Brasil). Esta información podría auxiliar a los profesionales de las ciencias de la salud, con lo cual, podrían clasificar el exceso de peso de forma rápida y precisa, en especial al identificar casos específicos en grandes poblaciones.
MÉTODOS
Para los datos antropométricos de los estudiantes se efectuó un estudio de tipo descriptivo-comparativo (survey). La muestra seleccionada fue de tipo probabilística (estratos). Se evaluó a 5962 estudiantes (3024 del sexo femenino y 2938 del sexo masculino) El rango de edad oscila entre los 6 a 17 años de edad. El tamaño y las características de la muestra estudiada se observa en la Tabla I.
Tabla 1 Características de los escolares estudiados.
| Variables | fi | % |
|---|---|---|
| Sexo | ||
| Femenino | 3024 | 50,72 |
| Masculino | 2938 | 49,28 |
| Total | 5962 | 100 |
| Edad (años) | ||
| 06 - 09 | 1775 | 29,77 |
| 10 - 13 | 2378 | 39,89 |
| 14 - 17 | 1809 | 30,34 |
| Todos | 5962 | 100 |
Fuente: Propia
Los datos antropométricos de los estudiantes han sido recolectados en la región de Paraná (Brasil). La Base de datos está a cargo de la Red Iberoamericana de Investigación en Desarrollo Biológico Humano.
Se seleccionó un total de 34 escuelas aledañas a la región. Todo el procedimiento de recolección de datos estuvo a cargo de 10 profesionales capacitados en técnicas antropométricas, quienes efectuaron la recolección de datos. Los datos cuentan con los consentimientos informados que los padres y/o responsables de los menores firmaron, en el que autorizan la realización de las medidas antropométricas en los niños y adolescentes de ambos sexos.
Las variables antropométricas evaluadas fueron el peso (kg) y la estatura (cm). Se adoptó el protocolo estandarizado por Ross, Marfell-Jones[15]. Se calculó el Índice de Masa Corporal (IMC) [IMC= peso (kg)/estatura (m2)] y fueron utilizados los puntos de corte para clasificar en Normal, Sobrepeso, Obesidad y Exceso de Peso (Sobrepeso+Obesidad), equivalentes a 18,5; 25 y 30 en adultos, según IOTF[13]. El estudio utilizó las variables: Estatura, Peso, Edad e IMC por tener presencia difusa.
La metodología utilizada es la de Knowledge Discovery in Databases (KDD). Este es un proceso no trivial que sirve para identificar patrones valiosos, novedosos, potencialmente útiles y en última instancia, comprensibles a partir de los datos [16]. Las fases adoptadas en el estudio se detallan a continuación.
Identificación de objetivos
Esta fase inicial se enfoca en entender los objetivos y requerimiento del proyecto convirtiendo esto en la definición del problema de minería de datos.
a) Determinación de objetivos
El estudio se realiza para:
› Clasificar a los estudiantes según su peso con imprecisiones cognitivas.
› Utilizar las herramientas de minería de datos con manejo de datos difusos.
› Determinar la exactitud de la clasificación en relación al exceso de peso en los niños y adolescentes.
b) Evaluación de la situación
Los datos muchas veces son tratados sin considerar los inciertos cognitivos como la vaguedad y la ambigüedad que están asociados a la percepción y el pensamiento humano. La incertidumbre cognitiva puede ser bien representado por la teoría de conjuntos difusos de Zadeh[1]. Algunos conceptos básicos se resumen a continuación.
Sea U una colección de objetos denotados genéricamente por {u}. U se llama el universo del discurso y u representa el elemento genérico de U.
Un conjunto difuso A en un universo de discurso U se caracteriza por una función de pertenencia nA, que toma valores en el intervalo [0, 1].
Para u U, µA(u)= 1 significa que u es definitivamente un miembro de A y µA(u)= 0 significa que u no es definitivamente un miembro de A, y 0<µA(u)<1 significa que u es parcialmente miembro de A. Si µA(u)= 0 o µA(u)= 1 para todo u U, A es un conjunto clásico.
Un universo de objetos o casos U= {u} son descritos por una colección de atributos A= {A1,..., Ak}. Cada atributo Ak mide algunas características importantes de un objeto y está limitado a un pequeño conjunto de términos lingüísticos discretos T(Ak)= Tk1, ... , TkSk. T(Ak) es, en otras palabras, el dominio de un atributo Ak. Cada objeto u en el universo se clasifica por un conjunto de clases C= {C1,..., CL}. Una regla de clasificación puede ser escrita como en la Ecuación 1:
Un conjunto de reglas de clasificación puede ser inducido usando un método de máquina de aprendizaje de un conjunto de entrenamiento de objetos cuyas clases es conocida. Las reglas de clasificación pueden ser utilizadas para clasificar objetos basados en los valores de sus atributos.
La vaguedad o imprecisión de un conjunto difuso se pueden medir con una entropía difusa[17], similar a la medida de la entropía de Shannon de aleatoriedad[18].
La medida de vaguedad se define como: Sea A un conjunto difuso sobre el universo U con una función de pertenencia µA(u) para todo u U. Si U es un conjunto discreto U= {u1, u2,...., um} y µi= µA(u), la vaguedad del conjunto difuso A se define por la Ecuación 2:
La ambigüedad o falta de especificidad de una distribución de posibilidad pueden ser definidos de acuerdo a Higashi y Klir[19] de la siguiente manera.
Sea π= (π(x)lx∈X) denotan una posibilidad de distribución normalizada de Y sobre X= {x1, x2,...,xn}, La medida posibilista de ambigüedad se define como se muestra en la Ecuación 3:
Donde π*= {π*1, π*2,..., π*n} es la permutación de la distribución de posibilidad π= {π(x1), ϖ(x2),..., π(xn),}, ordenados tal que π*i ≥ π*i-1 para i= 1,..., n, y π*n+1= 0.
La clasificación de ambigüedad con particionamiento difuso P={E1, E2,...,Ek} en una evidencia difusa F, denotado como G(P|F) es el promedio ponderado de la clasificación de ambigüedad con cada subconjunto de la partición, como se aprecia en la Ecuación 4:
Donde G(Ei∩F) es la clasificación de ambigüedad con evidencia difusa Ei∩F, W(Ei|F) es el peso que representa el tamaño relativo al subconjunto Ei∩F en F.
c) Determinación de los objetivos de la Minería de datos
Objetivo de minería de datos: Dar soporte mediante técnicas de Minería de datos a los objetivos de la investigación:
› Fusificar de los datos de entrenamiento.
› Inducir de un árbol de decisión difusa,
› Convertir el árbol en un conjunto de reglas.
› Aplicar las reglas difusas para clasificación.
Conocer estos objetivos permitirá determinar de una mejor manera la realidad del exceso de peso de los escolares y llevar un control pudiendo realizar la prevención de la obesidad.
Selección de los datos
Se analizaron las variables antropométricas que provienen de las evaluaciones realizadas a los escolares. Existen varios métodos de selección de variables independientes que se puede elegir para un modelo de regresión, el de mayor aceptación es el método de selección por pasos (stepwise).
Por ese motivo, se ha aplicado el Análisis de Regresión por Pasos (SRA, por sus siglas en inglés) para elegir los datos de entrada con mayor significado entre las variables. Se ha utilizado el software estadístico SPSS para realizar dicha tarea.
El análisis de regresión por pasos se utiliza para determinar el conjunto de variables independientes que más cercanamente afectan la variable dependiente. Esto se logra repitiendo el procedimiento de selección de variable.
Las entradas importantes seleccionadas por SRA se muestran en la Tabla 2.
Tabla 2 Variables seleccionados mediante SRA.
| Factores de entrada | Variables |
|---|---|
| Mediante regresión por pasos |
|
Fuente: Propia
Para lo cual, se tomaron y analizaron los siguientes atributos, por presentar comportamiento difuso:
Las variables se observan en la Tabla 3.
Tabla 3 Atributos seleccionados para evaluar.
| Campos | Tipo de datos |
|---|---|
| Estatura | Double |
| Peso | Double |
| Edad | Tiny |
| IMC (Índice Masa Corporal) |
Double |
Fuente: Propia
a) Describir los datos
La mayoría de problemas de clasificación asume que cada objeto toma uno de los valores mutuamente exclusivos para cada atributo y cada objeto se clasifica en una sola clase mutuamente exclusiva[4]. En este caso un objeto de estudio puede tener cuatro atributos: Clasificar a los estudiantes según su peso con imprecisiones cognitivas.
Y cada atributo tiene los valores:
Estatura= {Bajo, Normal, Alto},
Peso= {Bajo, Normal,
Alto}, Edad= {Niño, Adolescente},
IMC= {Bajo, Normal, Alto},
La clasificación que tiene el escolar es:
Los atributos y clasificaciones representan los deseos y percepciones humanas, hay vaguedad por su naturaleza. Para una instancia, las percepciones de estatura de un estudiante bajo, normal o alto es vago y no hay un límite clásico (crisp) entre ellos. Aunque la vaguedad de la estatura puede evitarse mediante una medida numérica, una regla puede inducir con un árbol de decisión clásico puede luego tener un límite clásico artificial, tal como "SI estatura >= 1.75 THEN Alto". Pero ¿Qué pasa cuando la estura es 1.74? ¿La persona no es alta? Obviamente los limites artificiales clásico no son siempre deseables. Aunque puede no haber vaguedades.
b) Explotar los datos
Al llevar a cabo la exploración de los datos, se identifica que a la base de datos se puede introducir el concepto difuso al problema clásico si los objetos o clases son difusas[20].
Un objeto se dice que es difuso si al menos una de sus características (atributos) es difuso, para ello se empezó incorporando las etiquetas lingüísticas mostradas por cada atributo en el punto anterior.
c) Construir datos
La construcción de los datos ha permitido generar el conjunto de registro de datos que se va a utilizar en la herramienta para la inducción del árbol de decisión difusa, para ello se ha generado el correspondiente archivo fuente con los siguientes atributos:
Posteriormente se ha utilizado la función trapezoidal con los promedios y desvíos para determinar sus funciones de pertenencia de los atributos difusos. Los valores de la estadística descriptiva se muestran en la Tabla 4. Para clasificar el exceso de peso de los niños y adolescentes se han utilizado los puntos de corte de la IOTF[13].
Tabla 4 Valores medios y desviación estándar para el peso, estatura e IMC de niños y adolescentes de ambos sexos.
| Peso (kg) | Estatura (cm) | IMC (kg/m2) | ||||
| X | DE | X | DE | X | DE | |
| Masculino | ||||||
| 6 | 21.02 | 6.29 | 115.55 | 5.19 | 15.67 | 1.63 |
| 7 | 23.50 | 7.60 | 121.83 | 5.56 | 15.85 | 1.84 |
| 8 | 26.01 | 4.23 | 127.62 | 5.83 | 16.03 | 1.86 |
| 9 | 29.51 | 5.99 | 133.15 | 6.08 | 16.63 | 2.43 |
| 10 | 32.67 | 6.73 | 138.25 | 7.09 | 17.12 | 2.57 |
| 11 | 36.84 | 7.66 | 143.49 | 6.74 | 17.87 | 2.90 |
| 12 | 41.23 | 9.82 | 149.67 | 7.68 | 18.44 | 3.36 |
| 13 | 46.42 | 15.24 | 156.64 | 8.14 | 18.91 | 3.10 |
| 14 | 53.33 | 11.63 | 163.56 | 8.71 | 19.88 | 3.41 |
| 15 | 58.69 | 11.62 | 169.52 | 7.73 | 20.51 | 3.24 |
| 16 | 63.64 | 11.76 | 172.85 | 7.13 | 21.25 | 3.25 |
| 17 | 67.74 | 12.15 | 175.71 | 7.74 | 21.91 | 3.37 |
| Femenino | ||||||
| 6 | 20.82 | 3.60 | 115.12 | 5.38 | 15.63 | 1.86 |
| 7 | 22.87 | 3.90 | 120.91 | 5.57 | 15.60 | 1.79 |
| 8 | 25.84 | 4.68 | 126.78 | 6.10 | 16.04 | 2.07 |
| 9 | 29.59 | 6.17 | 132.86 | 6.42 | 16.79 | 2.67 |
| 10 | 33.38 | 7.69 | 138.34 | 6.87 | 17.36 | 2.96 |
| 11 | 37.50 | 8.18 | 144.76 | 7.29 | 17.96 | 3.03 |
| 12 | 43.63 | 11.54 | 151.55 | 7.69 | 18.90 | 3.44 |
| 13 | 49.19 | 10.84 | 157.48 | 6.85 | 19.80 | 3.70 |
| 14 | 52.71 | 11.18 | 160.05 | 6.37 | 20.56 | 3.95 |
| 15 | 55.16 | 11.06 | 161.85 | 6.56 | 21.04 | 3.66 |
| 16 | 57.16 | 10.76 | 163.17 | 6.24 | 21.43 | 3.71 |
| 17 | 57.90 | 12.17 | 162.60 | 6.55 | 21.95 | 4.24 |
Fuente: Propia
Para los puntos de corte de la edad, se consideró como niños aquellos entre las edad de 6 a 10 y como adolescentes de 12 a 17 años, dejando a los escolares de 11 años como una transición entre niños y adolescentes.
Transformación
a) Selección de la técnica de modelado
Antes de escoger el modelo apropiado, debemos de enfocarnos en nuestro objetivo: ¿qué propósito buscamos? Lo que se busca es la clasificación de los estudiantes asociados con la percepción y pensamiento humano mediante técnicas de clasificación de minería de datos.
A continuación se ecidió el tipo de clasificación más apropiado, que será la de las técnicas de clasificación de minería de datos que clasifique la categoría o clase (Bajo, Normal, Exceso) que se obtendrá como resultado de la ejecución del clasificador. Entonces nuestro clasificador (modelo) elegido ha salido como resultado de una evaluación de algoritmos evaluados (de clasificador K-NN, árboles de decisión y red bayesiana) según[21], del cual se pudo obtener como resultado que el mejor clasificador fue el del árbol de decisión para identificar sobre peso en estudiantes.cEste método es similar al método de inducción árbol de decisión no difusa como ID3[22] donde el uso de información de la entropía como el criterio de inducción heurística se sustituye por la medición de la ambigüedad de clasificación.
Hay varias diferencias entre el enfoque utilizado y otros enfoques basados en ID3[23]. En el enfoque presentado se puede manejar los problemas de clasificación con dos atributos difusos y las clases difusas representados en términos difusos lingüísticos.
También puede manejar otra situación de una manera uniforme, donde los valores numéricos se pueden fusificar a términos difusos y las categorías clásicas pueden tratarse como un caso especial de términos difusos con cero borrosidades. La principal diferencia entre el enfoque utilizado y otra de ID3 difusa es el uso de la ambigüedad clasificación como entropía difusa. La ambigüedad de clasificación mide directamente la medida de la calidad de clasificación en el nodo de decisión. Puede calcularse bajo la partición difusa y múltiples clases difusos y sin ninguna restricción. Otra ventaja es el uso de nivel de evidencia y el umbral del nivel de verdad que proporciona un control efectivo durante el proceso de inducción.
b) Generación de la prueba de diseño
Se define el conjunto de datos que se utilizará como datos de entrenamiento como una clasificación conocida que consta de los 2938 registros para los estudiantes del sexo masculino y de 3024 registros para los estudiantes del sexo femenino; y otro conjunto de datos de similar cantidad de registros con el que se construirá el clasificador con reglas de aprendizaje para poder determinar la exactitud de clasificación obtenida.
c) Construcción del modelo
En el problema de clasificación, los datos de entrenamiento pueden ser en forma ya sea categórica o numérica. Por ejemplo, los datos numéricos del peso pueden ser percibidos en términos lingüísticos, tales como alta, media y baja. Las funciones de pertenencia se pueden determinar aproximadamente basándose en la opinión de expertos o la percepción común de la gente. Alternativamente, la función de pertenencia se puede derivar a partir de datos estadísticos[24][25].
Se utiliza un simple algoritmo para generar la función de pertenencia trapezoidal en los datos numéricos. Supongamos que el atributo A tiene un valor numérico x. Los valores numéricos del atributo A para todos los objetos u ∈ U a continuación, puede ser representado por X = {x(u), u ∈ U}. Queremos agrupar X a k términos lingüísticos Ti, i = 1,..., k. Cada término lingüístico Ti tiene una función de pertenencia trapezoidal.
Los atributos, con sus correspondientes puntos de corte, generan la función de pertenencia que se ha obtenido para niños y adolescentes. En la Figura 1, se muestra la función de pertenencia para el grupo de niños de 6, 10, 14 y 17 años, siendo similares para otras edades y para las niñas. Los valores de cada atributo se han codificados en un formato específico CSV, que es un tipo de documento en formato abierto sencillo para representar datos en forma de tabla, en la que las columnas se separan por comas y las filas por saltos de línea.
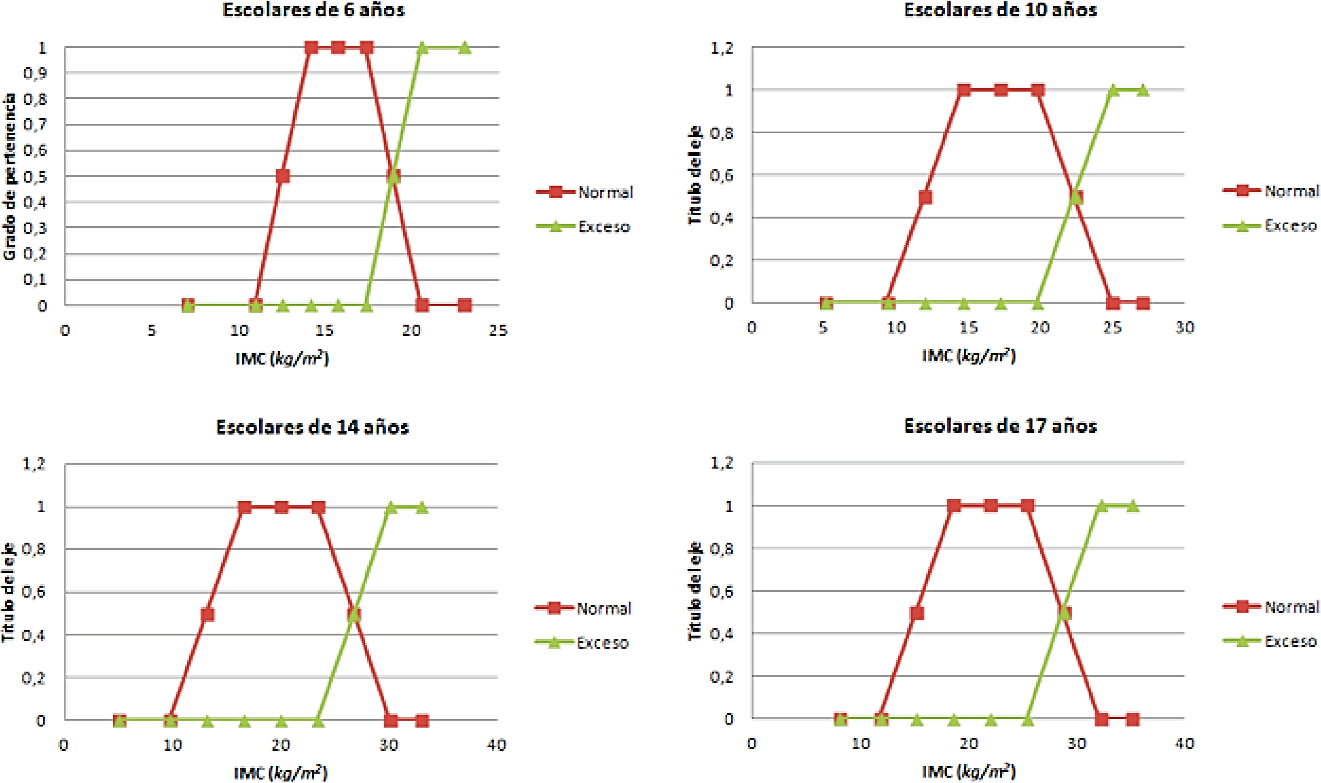
Figura 1 Función de pertenencia de los atributos Peso, Estatura e IMC para niños de 6, 10, 14 y 17 años.
Los valores obtenidos de la función de pertenencia para la clasificación del método difuso y clásico con sus respectivas categorías (Normal y Exceso), se muestran en la Tabla 5 y la Tabla 6.
Tabla 5 Clasificación difusa y clásica en escolares ambos sexos.
| Clasificación Difusa | Clasificación Clásica | ||||||||||||
| Edad | Normal | Exceso | Normal | Exceso | |||||||||
| Total | n | X | DE | n | X | DE | n | X | DE | n | X | DE | |
| Masculino | |||||||||||||
| 6 | 284 | 193 | 0,675 | 0,289 | 91 | 0,325 | 0.417 | 241 | 0.849 | 0.359 | 43 | 0.151 | 0.359 |
| 7 | 222 | 160 | 0,715 | 0,289 | 62 | 0,285 | 0.421 | 186 | 0.838 | 0.369 | 36 | 0.162 | 0.369 |
| 8 | 210 | 125 | 0,576 | 0,294 | 85 | 0,424 | 0.460 | 159 | 0.757 | 0.430 | 51 | 0.243 | 0.430 |
| 9 | 227 | 134 | 0,591 | 0,295 | 93 | 0,409 | 0.463 | 175 | 0.771 | 0.421 | 52 | 0.229 | 0.421 |
| 10 | 236 | 146 | 0,627 | 0,282 | 90 | 0,373 | 0.456 | 178 | 0.754 | 0.431 | 58 | 0.246 | 0.431 |
| 11 | 244 | 168 | 0,685 | 0,279 | 76 | 0,315 | 0.450 | 183 | 0.750 | 0.434 | 61 | 0.250 | 0.434 |
| 12 | 297 | 203 | 0,681 | 0,33 | 94 | 0,319 | 0.446 | 221 | 0.744 | 0.437 | 76 | 0.256 | 0.437 |
| 13 | 354 | 210 | 0,596 | 0,319 | 144 | 0,404 | 0.468 | 274 | 0.774 | 0.419 | 80 | 0.226 | 0.419 |
| 14 | 326 | 240 | 0,731 | 0,366 | 86 | 0,269 | 0.426 | 270 | 0.828 | 0.378 | 56 | 0.172 | 0.378 |
| 15 | 241 | 171 | 0,71 | 0,357 | 70 | 0,29 | 0.437 | 205 | 0.851 | 0.357 | 36 | 0.149 | 0.357 |
| 16 | 167 | 126 | 0,744 | 0,289 | 41 | 0,256 | 0.423 | 135 | 0.808 | 0.395 | 32 | 0.192 | 0.395 |
| 17 | 130 | 97 | 0,744 | 0,396 | 33 | 0,256 | 0.416 | 104 | 0.800 | 0.402 | 26 | 0.200 | 0.402 |
| Femenino | |||||||||||||
| 6 | 241 | 181 | 0,731 | 0,213 | 60 | 0,269 | 0.373 | 195 | 0.809 | 0.394 | 46 | 0.191 | 0.394 |
| 7 | 203 | 132 | 0,636 | 0,268 | 71 | 0,364 | 0.446 | 156 | 0.768 | 0.423 | 47 | 0.232 | 0.423 |
| 8 | 170 | 117 | 0,676 | 0,251 | 53 | 0,324 | 0.438 | 129 | 0.759 | 0.429 | 41 | 0.241 | 0.429 |
| 9 | 218 | 143 | 0,649 | 0,275 | 75 | 0,351 | 0.435 | 176 | 0.807 | 0.395 | 42 | 0.193 | 0.395 |
| 10 | 276 | 176 | 0,638 | 0,291 | 100 | 0,362 | 0.452 | 216 | 0.783 | 0.413 | 60 | 0.217 | 0.413 |
| 11 | 323 | 245 | 0,759 | 0,215 | 78 | 0,241 | 0.429 | 245 | 0.759 | 0.429 | 78 | 0.241 | 0.429 |
| 12 | 311 | 255 | 0,82 | 0,193 | 56 | 0,18 | 0.385 | 255 | 0.820 | 0.385 | 56 | 0.180 | 0.385 |
| 13 | 337 | 273 | 0,81 | 0,197 | 64 | 0,19 | 0.393 | 273 | 0.810 | 0.393 | 64 | 0.190 | 0.393 |
| 14 | 332 | 266 | 0,801 | 0,2 | 66 | 0,199 | 0.400 | 266 | 0.801 | 0.400 | 66 | 0.199 | 0.400 |
| 15 | 276 | 240 | 0,866 | 0,362 | 36 | 0,134 | 0.325 | 238 | 0.862 | 0.345 | 38 | 0.138 | 0.345 |
| 16 | 198 | 173 | 0,878 | 0,388 | 25 | 0,122 | 0.313 | 165 | 0.833 | 0.374 | 33 | 0.167 | 0.374 |
| 17 | 139 | 123 | 0,873 | 0,379 | 16 | 0,127 | 0.305 | 115 | 0.827 | 0.379 | 24 | 0.173 | 0.379 |
Tabla 6 Comparación de la clasificación original y reglas aprendidas entre escolares del sexo masculino y femenino.
| Clasificación | Ambigüedad | Clasificación correcta |
Clasificación incorrecta |
Exactitud |
|---|---|---|---|---|
| Original (Masculino) |
0.06 | 2471 | 467 | 84% |
| Reglas aprendidas (Masculino) |
0.04 | |||
| Original (Femenino) |
0.04 | 2688 | 336 | 89% |
| Reglas aprendidas (Femenino) |
0.01 |
Minería de datos
La minería de datos se realizó utilizando la propuesta de Yuan[8], con la herramienta de árboles de decisión difusa adaptada para el ingreso de los datos de origen basado en la reducción de ambigüedad de clasificación con evidencia difusa.
Los pasos de inducción del árbol de decisión difuso se llevan a cabo a un nivel significativo α. Un objeto pertenece a una rama sólo cuando la función de pertenencia correspondiente es mayor que α.
La medida de ambigüedad también se calcula a nivel significativo α. El parámetro α juega un papel muy importante en el filtrado de evidencias insignificantes, por tanto, elimina las ramas y hojas insignificantes.
El umbral de nivel de la verdad β controla el crecimiento del árbol. Un bajo β puede conducir a un árbol más pequeño pero con una menor exactitud (precisión) de la clasificación. Un alto β puede conducir a un árbol más grande con una mayor exactitud (precisión) de la clasificación. La selección de: α y β depende en situación individual.
Se analizó la estadística descriptiva de media aritmética, desviación estándar y rango. Para contrastar la precisión entre métodos, se usó el análisis de las curvas ROC (receiver operating characteristics). Tal cálculo permite derivar un valor de corte para la evaluación de la precisión diagnóstica de una variable que discrimine entre la ausencia y la presencia de un estado de salud (sobrepeso o peso normal). Se calculó también la sensibilidad y especificidad para ambos métodos y sexos.
RESULTADOS
Se ilustra el proceso de inducción mediante el uso de los datos de entrenamiento con 2938 registro para escolares del sexo masculino y 3024 registro para escolares del sexo femenino tanto para el archivo de entrenamiento como de prueba. Dado la evidencia con nivel significativo α= 0,5, y el umbral de nivel de la verdad β= 0,82. Realizado el cálculo de la clasificación de ambigüedad con cada atributo, se obtiene:
Y se genera el árbol de decisión difusa mostrado en la Figura 2.
Con las ocho reglas de clasificación derivada y simplificada (Figura 3), se muestra que de los 2938 casos de entrenamiento, 2471 están clasificados correctamente y 467 lo están incorrectamente. La exactitud es de 84% y la ambigüedad es de 0,04, menor que la original 0.06.
En la Figura 4 se muestra el árbol generado para los 3024 registros de escolares mujeres. Dada la evidencia con nivel significativo a= 0,5, y el umbral de nivel de la verdad p= 0,82. Realizado el cálculo de la ambigüedad de la clasificación con cada atributo, tenemos
Con las diez reglas de clasificación, derivada y simplificada (Figura 5), se muestra que entre los 3024 casos de entrenamiento, 2688 están clasificados correctamente y 336 lo están incorrectamente. La exactitud es de 89% y la ambigüedad es de 0,01, menor que la original 0.04.
Los resultados del conjunto de entrenamiento entre los escolares (del sexo masculino y femenino) en relación a la clasificación correcta e incorrecta se muestran en la Tabla 5.
Después de la simplificación, las reglas ya no corresponden a las del árbol original. La simplificación de las reglas sin comprometer su exactitud es deseable porque una regla simplificada con menos condiciones es más general y probable para clasificar más objetos; además, es más propensa a tolerar la falta o datos imprecisos. La colección de reglas simplificadas se puede almacenar en una base de reglas en un sistema experto difuso.
La tabla comparativa de clasificación original y de reglas aprendidas entre los dos conjuntos de datos de los escolares (Masculino y Femenino) en relación a la ambigüedad y la exactitud se muestra en la Tabla 6.
Los valores de la curva ROC (Receiver operating characteristics) entre ambos métodos de clasificación se observan en la Tabla 7. Los resultados muestran diferencias significativas entre ambos métodos. El método difuso evidenció mayor exactitud en los escolares de ambos sexos (Masculino 0.983 y femenino 0.965) en relación al método clásico (Masculino 0.804 y Femenino 0.895). Además, las curvas ROC evidenciaron altos valores de sensibilidad en ambos sexos (93 a 97%) y similares valores de especificidad (100%).
Tabla 7 Valores del Área Bajo la Curva (Receiver operating characteristics) del método difuso y clásico.
| Métodos | ABC (Área bajo la curva) |
EE (Error estándar) |
Intervalo de confianza (95%) |
p-Valor |
|---|---|---|---|---|
| Masculino | ||||
| Método Clásico | 0,804 | 0,01 | 0,785-0,824 | <0,05 |
| Método Difuso | 0,983 | 0,003 | 0,977-0,990 | |
| Femenino | ||||
| Método Clásico | 0,895 | 0,004 | 0,878-0,913 | <0,05 |
| Método Difuso | 0,965 | 0,005 | 0,954-0,975 | |
DISCUSIÓN
Los resultados muestran que la exactitud en la clasificación de niños y adolescentes de ambos sexos con exceso de peso oscilan entre 84% a 89%. Además, el método difuso puede emplearse con razonable éxito y precisión según las curvas ROC para clasificar a niños y adolescentes de 6 a 17 años. La aplicación de árboles de decisión difusa mostró ser ligeramente más precisa en mujeres. De hecho, estudios previos con la misma técnica, pero diferente temática, han reportado valores del 75% de la exactitud en referencia a los antecedentes de pagos por auditoría[6] y, en el caso de Ebadi et al[26], mostraron resultados aceptables basados en el coeficiente de determinación para la predicción de la precipitación de asfaltenos por el agotamiento natural; además, Fan et al[27] con un modelo híbrido para clasificación de datos médicos, alcanzaron un promedio de exactitud del 81.6% para desórdenes hepáticos, evidenciando resultados similares frente al presente estudio.
La representación de la incertidumbre cognitiva en el problema de clasificación del exceso de peso de la muestra refleja la exactitud en la clasificación, pues estos resultados podrían proveer mayor información en la toma decisiones respecto a los niveles de verdad de las reglas y la membresía de la clasificación del exceso de peso en niños y adolescentes.
La ventaja del uso de árboles de decisión difusa radica en la facilidad de comprensión para tratar con el lenguaje natural y la incertidumbre[28], creando un marco que implica la comprensión de conocimiento[8]; por tal motivo, es de gran aceptación para resolver problemas con incertidumbre y falta de exactitud de datos. En tal sentido, el uso de la teoría de conjuntos difusos sirve para ofrecer etiquetas difusas y construir árboles de decisión difusos que generen bases de reglas difusas. Esto puede mejorar en gran medida la inteligibilidad de los especialistas de las ciencias de la salud, específicamente para comprender las correlaciones entre la descripción de los pacientes y sus clasificaciones[29].
En ese contexto, algunos autores, como Khan et al [30], encontraron que la clasificación de árboles de decisión difusa hibrida es más robusta y balanceada que la aplicación clásica independiente para el diagnóstico de cáncer de mama con factores de riesgo, como la obesidad.
En general, estos resultados sugieren que al utilizar los árboles de decisión difusa son una buena alternativa para la clasificación en cuanto al exceso de peso y peso normal de niños y adolescentes de la región Itaupú, Paraná (Brasil), sin embargo, se sugiere efectuar otros cálculos estadísticos que tengan que ver con la precisión y exactitud a través de métodos estadísticos convencionales y comparar con la técnica de árboles difusos. Esta información podría ofrecen ventajas en la toma de decisiones para efectuar las clasificaciones en grandes bases de datos de otras poblaciones escolares.
Para futuros estudios, se deben tomar en consideración la afinación de las funciones de pertenencia. Una forma es agregando modificadores lingüísticos como "muy", "más o menos", "Entre", etc., para términos lingüísticos durante el proceso de inducción. Otra forma es la de convertir funciones de pertenencia y reglas difusas en las redes neuronales y utilizando el mecanismo de aprendizaje de las redes neuronales para afinar la función de pertenencia.
CONCLUSION
Los árboles de decisión difusa ofrecen una forma comprensible del análisis para problemas orientados a la clasificación y predicción con un grado de exactitud aceptable, en ese contexto, basado a los resultados obtenidos se obtuvo las reglas de decisión que se fundamentan a dos resultados, identificando las clases de normal y alto en relación al exceso de peso de los escolares. Para ello se utilizó un árbol de decisión difuso que mostró como exactitud en escolares del sexo masculino 84%, mientras que en el sexo femenino la exactitud fue 89%. La ambigüedad obtenida de las reglas aprendidas en el sexo masculino fue 0.04 y en escolares del sexo femenino fue ligeramente inferior (0.01). Además, los valores del ABC del método Difuso fueron más altos respecto al método clásico. Por lo tanto, estos resultados sugieren el uso del árbol de decisión para clasificar el exceso de peso de grandes grupos de datos de niños y adolescentes. Esta técnica puede ahorrar tiempo a la hora de analizar el estado nutricional de niños y adolescentes, al menos entre los 6 a 17 años.











 nueva página del texto (beta)
nueva página del texto (beta)







