Introducción
La intención de este texto es presentar un estimador alterno para calcular la exactitud de las encuestas electorales,1entendiendo por tal la proximidad entre los valores medidos y los observados. Con esta propuesta se busca atenuar problemas detectados en las opciones actualmente disponibles. Ello, sabiendo que no existe actualmente un estimador de la exactitud de las encuestas exento de problemas que limiten su uso y, por ende, el entendimiento del fenómeno bajo observación.
En el desarrollo de este texto se buscó que su contenido pueda ser entendido por cualquier persona con conocimientos medios de matemática, pero expuesto con el rigor requerido para eliminar cualquier ambigüedad. Por ello, se explicita y formaliza cada paso dado, pues se trata no sólo de proponer un nuevo estimador, sino de generar el algoritmo que lo calcule apegado al criterio que se define para su estimación. Por ende, en lo posible se siguen las normas convencionales de tipografía y notación matemática, usando una única letra, generalmente cursiva, para etiquetar un símbolo.2
Respecto al carácter novedoso del estimador propuesto, para su construcción se recurre a procedimientos convencionales de normalización a intervalos unitarios de estimadores previamente existentes, lo que facilita la comparabilidad entre medidas y otorga un significado más preciso al concepto mismo de error o exactitud, asumiéndolo como la diferencia respecto a una norma pertinente. Tras una revisión de la literatura en el tema, no se encontró evidencia de que este procedimiento de estimación haya sido previamente utilizado como tal para los fines planteados; pero, dado que la ausencia de evidencia nunca es evidencia de ausencia, siempre es posible que haya antecedentes al respecto desconocidos por el autor.
Los estimadores disponibles
En una colaboración anterior se efectuó la exposición y evaluación de los diversos métodos para el cálculo del error de las encuestas electorales, postulados originalmente por Mosteller.3
Recordando lo dicho al respecto en forma resumida: un primer método, la diferencia porcentual entre la proporción prevista para el ganador y la proporción obtenida respecto al total de votos emitidos, es el más simple e intuitivo posible. Empero, como Mitofsky advierte,4 resulta artificial, sobre todo cuando el líder cuenta con menos de la mitad de los votos, por existir terceros contendientes relevantes.
Otra opción es tomar la diferencia porcentual entre las proporciones predichas y reales de votos recibidos por los dos mayores contendientes, pudiendo adoptarse para casos de multipartidismo la diferencia absoluta entre lo previsto y lo observado para los dos mayores contendientes respecto al total de votos emitidos. Este indicador suele ser el más usado por los comunicadores y en la literatura científica tradicional, pero atiende a una evaluación propia de un sistema bipartidista, sin atender los problemas de concentración-fragmentación del voto restante.
El objetivo primordial de Mosteller -como de fondo lo es también de nuestra propuesta- es la construcción de una base de datos homogénea, lo que para el caso estadounidense se logra cuando se consideran sólo dos componentes, excluyendo o colapsando en lo posible opciones cuyo peso electoral es absolutamente marginal. Sin embargo, esta no es la realidad de la mayoría de los sistemas electorales.
Por ello, una alternativa más utilizada en casos de sistemas de múltiples partidos es la desviación media en puntos porcentuales entre lo previsto y lo observado para la totalidad de contendientes, sin tener en cuenta el signo. Empero, este procedimiento no sólo no permite una comparación diáfana cuando el número de partidos es variable, sino que impide reconocer el sesgo en la medición y asume un valor absoluto, por lo que puede derivar en cálculos reducidos de error al incluir a diversos componentes menores que contribuyen escasamente al voto, pero cuya estimación suele presentar divergencias absolutas pequeñas.
Para superar este problema, puede tomarse la media de las desviaciones de la razón entre la proporción prevista y la observada para todos los candidatos. Sin embargo, ello lleva a un problema inverso al anterior, pues este método tiende a dar un peso muy elevado a desviaciones en componentes menores.
Otras opciones, como tomar la diferencia máxima observada entre lo previsto y lo observado para cualquiera de los contendientes, resultan confusas y equívocas. Métodos más sofisticados, como la prueba estadística chi cuadrado (
Así, la lista original de indicadores propuestos y analizados por Mosteller ha resultado a todas luces insatisfactoria. Ante esta situación, recientemente se presentó la propuesta de un nuevo estimador del error en las encuestas respecto al resultado,5 que busca resolver el problema de tratamiento de los casos no definidos mediante la eliminación de todo efecto del mismo en el cálculo y avanzar en la disposición de un estimador universal del error entre encuestas y resultados.
Empero, esta propuesta es una medición adecuada solamente para sistemas bipartidistas, no para multipartidista; e incluso uno con características muy peculiares, que se encuentran en muy pocos sistemas: la constancia temporal de la condición de dos partidos específicos como las opciones efectivamente competitivas, pues asume que existen dos partidos que son siempre los primeros lugares en una elección y, presumiblemente, en toda encuesta (1.1).
Y, en todo caso, asigna una condición de tercer contendiente a cualquier otro participante en una elección, por lo que
Esta propuesta parte del reconocimiento de que, si bien la diferencia entre las proporciones estimadas considerando o excluyendo casos indefinidos no son iguales, sí lo son las razones entre las mismas proporciones (1.2).
Donde
Asumiendo lo anterior, se construye un estimador del error (A) que toma el logaritmo natural del cociente de la razón entre las proporciones estimadas y la razón de las proporciones reales para dos partidos (1.3).
Con ello, los autores de esta propuesta eliminan el problema derivado de la adopción de cualquier método de asignación o supresión del segmento indefinido, pues carece de relevancia para el cálculo; permiten la detección simultánea de la magnitud y el sentido del error en la estimación, pues si su valor es cero supone la coincidencia en el peso relativo entre los dos contendientes considerados, si el valor es positivo corresponderá a una sobrestimación del partido cuyo error se calcula y si es negativo supondrá una subestimación.
Además, disponen de un estimador de la varianza (
Empero, no incluye alguna estimación relacionada con terceros contendientes. Como solución propuesta al respecto, se plantea la disposición de un cálculo suplementario e independiente del error, llamado A’ (1.5).
Pero ello no responde a la inquietud, pertinente y propia de los análisis para sistemas multipartidarios, de disponer de un estimador agregado de la exactitud de las mediciones, que dé cuenta del fenómeno considerando todos los componentes, o al menos los relevantes. Así que el problema existente se perpetúa hasta ahora.
Un estimador alterno
Para entrar en la propuesta propia, se ha de partir del reconocimiento de que los estadísticos para medir la exactitud en las encuestas electorales suelen aportar estimadores de la distancia, sin reparar en su relación con la desviación esperada en las estimaciones. Generar un estimador que sí lo haga pudiera lograrse mediante la introducción en el algoritmo de un procedimiento de normalización convencional.
Esto se consigue generando un estimador del error que dependa no de la magnitud absoluta de la diferencia entre lo estimado y lo observado, o de su cociente, sino de la magnitud relativa de esta diferencia con el error esperado, tomando como medidor de dicho error esperado la desviación estándar de las proporciones estimadas (
Estrictamente hablando, este estimador de la dispersión de los datos sólo es pertinente cuando se trata de un muestreo aleatorio simple. Sin embargo, dado que este es el método con mínimas restricciones en el proceso de selección, suele ser utilizado como punto de referencia para evaluar la eficiencia de otros diseños por la simplicidad de su cómputo, al costo de ignorar que regularmente no fue el diseño usado -lo que debiera normalmente ser declarado de manera explícita-, e incluso para estimar un error esperado de manera genérica en un experimento.
Este error esperado es básico para el cálculo del margen de error para un estimador de proporción (
Donde
El error esperado disminuye a medida que aumenta el tamaño de la muestra disponible. Igualmente, es menor a medida que la proporción de ocurrencia de un evento se aleja del inverso del número de resultados posibles. Empero y como es bien sabido, estos cambios no son lineales, sino parabólicos, con diferente escala según el tamaño de la muestra de la que se derivan.
A partir del cálculo del margen de error, puede establecerse un intervalo dentro del cual es esperable hallar el parámetro con cierta probabilidad predeterminada (2.3), siendo 1 - α el nivel de confianza o probabilidad de éxito en la estimación y alfa el nivel de significación o probabilidad máxima de que se rechace siendo verdadera la hipótesis de que el parámetro se encuentra dentro del intervalo estimado:
Cabe recordar que el nivel de confianza y la amplitud del intervalo varían conjuntamente, de forma que un intervalo más amplio y menos preciso tendrá más posibilidades de acierto, mientras que un intervalo menor, que ofrece una estimación más precisa, aumenta las posibilidades de error.
Si los contendientes son sólo dos, el error esperado con un muestreo aleatorio simple es el máximo posible (2.4):
Por lo que también se alcanza el margen de error máximo (2.5):
Con base en este margen de error máximo suele reportarse un margen de error genérico para una encuesta (2.6):
Cabe aclarar que existe una fórmula sencilla que permite incorporar el efecto del diseño en el cálculo del error cuando se trata de un muestreo en dos etapas, cuando las unidades primarias de muestreo son elegidas con probabilidad proporcional a tamaño y las secundarias de manera aleatoria simple o sistemática, aunque no profundizaremos en este desarrollo. En el caso en cuestión, la varianza total puede aproximarse por6 (2.7):
Siendo “
El error máximo posible correspondiente a eventos dicotómicos cuando es igualmente probable su ocurrencia o no, se asume también como el error medio esperable para un conjunto de estimadores cuya suma sea unitaria, como son las proporciones para los diversos contendientes en una elección (lo que no es estrictamente correcto, pues lo pertinente sería mudarse del modelo binomial al multinomial, pero esto casi nadie lo hace en la práctica, por razones de sencillez). Luego, lo que se hace es lo siguiente:
El error medio para un conjunto de estimadores (
Con un margen de error medio (
El error medio máximo para ese conjunto de estimadores sería entonces (2.11):
Con un margen de error medio máximo de (2.12):
Así, aunque de manera imprecisa, se concluye que el margen de error medio máximo esperado para un grupo de estimadores de proporciones cuya suma sea igual a la unidad será equivalente al margen de error máximo de una estimación cualquiera cuando se trata de eventos dicotómicos, asumiendo que de lo contrario, como en el caso de contiendas multipartidarias, este margen será crecientemente menor a medida que aumente el número de contendientes. Así (2.13):
Si m = 2, entonces
Si m
Disponiendo de un margen de error tolerado a un nivel de confianza dado, para cada estimación particular producto de una encuesta pudiera verse si su diferencia con el resultado estuvo dentro o fuera de lo esperado (
Esto supone ver cómo cumple la condición siguiente (2.14):
Puede también calcularse la dispersión de las proporciones estimadas para un componente en un conjunto de estimaciones dado (
Nuevamente, de aquí puede calcularse el margen de error para un conjunto de estimaciones de un componente (
Dado que (2.17)
Es posible detectar con lo anterior las estimaciones particulares que resultan significativamente diferentes al grueso de estimaciones y, por ende, determinar las estimaciones atípicas dentro de una colección, asumiendo como tales a aquellas que presenten desviaciones por encima del margen de error tolerado. Esto supone considerar como típica una estimación (
Lo anterior no puede presuponer nada más allá del propio carácter atípico asignado a la estimación, pues asumir que ello es indicativo de un determinado error esperable respecto a cualquier parámetro externo a las propias mediciones, como es el resultado registrado, implica considerar como dada una distribución normal de las diversas estimaciones colectadas y la inexistencia de un sesgo implícito que afecte al conjunto de mediciones, aspectos que tendrían que validarse externamente.
Además, el hecho mismo de detectar una estimación como atípica no puede derivar en su exclusión de un cálculo de tendencia central para un conjunto de estimaciones dadas con el fin de supuestamente robustecerlo, sin evaluar antes la pertinencia del procedimiento de exclusión y, en su caso, constatar el cumplimiento de otras condiciones demandadas conforme los diversos criterios de eliminación de casos extremos disponibles en la literatura. Lo que es más: es deseable analizar la relación empírica entre el cumplimiento de la condición de haber sido una estimación típica o atípica respecto a un conjunto de estimaciones (
Regresando a la argumentación central, y partiendo de la definición del error esperado para una estimación, es posible calcular un error normalizado de dicha estimación respecto al dato real (
Que correspondería al estimador de la magnitud relativa del sesgo con sentido más comúnmente empleado en estadística.
La generación de este estimador demanda la disposición de un dato adicional para cada unidad analizada a los requeridos para el cálculo del error en estimadores previamente disponibles: el tamaño efectivo de la muestra o la proporción de casos asignados a algún contendiente respecto del total de casos observados en una encuesta. Empero, este aumento de la información demandada para el cálculo se premia con la disposición de un estimador que no se afecta sustancialmente por el número de contendientes involucrados en cada elección.
De hecho, al amortiguar los efectos relacionados con el peso relativo de las proporciones correspondientes, al darles una ponderación ajustada a una relación cuadrática, permite que la eventual agregación o diferenciación de contendientes menores no propicie una importante sobreestimación o subestimación del error calculado; esto es: se logra disponer de un estimador del error que no sea sensible a valores extremos estimados. Por ende, su cálculo no sólo puede realizarse para todo contendiente del que exista un reporte diferenciado de proporciones observadas, sino que su estimación resulta coherente y comparable sin importar el peso relativo de los componentes.
Es posible calcular el error normalizado de la diferencia entre las estimaciones para un par de componentes respecto a los valores realmente observados. Esto resulta del encuentro de la desviación estándar de la estimación de la diferencia (
Que supone considerar para el cálculo del error en una diferencia los errores en las estimaciones para cada una de las proporciones consideradas. Así, el margen de error esperado para la estimación de una diferencia entre dos contendientes cualesquiera ( 𝜉 𝑖−𝑗 𝑠 ) vendrá dado por (2.21):
Por lo que el intervalo de la estimación estaría definido como (2.22):
Realizando el procedimiento de normalización para el cálculo del error de la diferencia (
Que correspondería al mejor estimador para medir el error de una diferencia estimada de la magnitud relativa del sesgo, asignando sentido al mismo. Cabe recordar que la desviación de una muestra particular puede afectarse por el diseño adoptado. Técnicas de estratificación o división de la población de estudio en grupos que se suponen homogéneos con respecto a alguna característica a estudiar suelen aumentar la precisión, misma que disminuye cuando se recurre a la selección de conglomerados, como es usual y por lo general necesario por razones prácticas en encuestas electorales.7 Cabe mencionar que los métodos directos para computar las varianzas de muestras complejas son tediosos, por lo que suelen usarse procedimientos abreviados que no miden la incertidumbre sobre sesgos o errores de respuesta y, por tanto, son estimaciones del error mínimo involucrado en la medición.8
Para medir el efecto del diseño se calcula el número de casos bajo un diseño de muestra aleatoria simple que sería equivalente a la muestra actual bajo el diseño muestral específico adoptado. En el caso de diseños de muestras complejas, el tamaño real de la muestra se determina multiplicando el tamaño efectivo de la muestra por el efecto de diseño, entendido como la razón de la varianza verdadera de un estadístico construido tomando en cuenta el diseño muestral respecto de la varianza para una muestra aleatoria simple con el mismo número de casos.
El estadístico comúnmente usado para el cálculo del efecto de diseño (
Siendo ρ el coeficiente de correlación intraclase, que de manera simplificada y correspondiente de nuevo sólo a la primera etapa del diseño, correspondería a (2.25):
Y
La desviación al interior de las clases (
El coeficiente de correlación intraclase es una medida de la homogeneidad de los elementos dentro de los agrupamientos, que tiene un valor máximo de uno cuando hay una completa homogeneidad dentro de los grupos y un valor mínimo de cero, que se alcanza cuando existe una heterogeneidad extrema dentro de los grupos (2.28):
Con base en el efecto de diseño, idealmente calculado para todas las etapas del mismo, se puede estimar el tamaño de muestra equivalente al que con un muestreo aleatorio simple lograría la misma precisión, el cual será distinto para cada componente que se estime según la particular diferencia entre e intra clase (2.29):
Claro que lo relevante en el caso de encuestas electorales es el tamaño de la muestra asignada que corresponde al número de casos disponibles para lograr una precisión con un muestreo aleatorio simple (2.30):
Con base en el número de casos ajustado por el efecto de diseño, es posible establecer un error esperado para la muestra asignada equivalente a un muestreo aleatorio simple (
O bien, un margen de error esperado para la muestra asignada incluyendo el efecto de diseño para hacerla equivalente a un muestreo aleatorio simple (
Con base en lo cual puede establecerse el intervalo de la estimación para la muestra asignada, incluyendo el efecto de diseño, equivalente a un muestreo aleatorio simple (2.33):
Y calcular el error normalizado de dicha estimación respecto al dato real (
Este es el estadístico más exacto para el cálculo del error normalizado de una estimación que permite establecer su magnitud y sentido. Basados en él, debiera analizarse la existencia o no de un sesgo adicional al error aleatorio esperado en la medición.
Sin embargo, su cálculo lleva incorporado el efecto del diseño como parte del error estocástico, además de que los efectos de diseño son diferentes para distintos subgrupos poblacionales y respuestas a reactivos, por lo que no existe un efecto genéricamente aplicable a la totalidad de datos producto de una encuesta.9
Por lo anterior, la adopción de este estimador para fines comparativos entre estudios tendería a premiar los diseños menos eficientes y castigar aquellos que hubieran tenido mayor eficiencia en su arranque.
Es por ello que resulta preferible, en aras de la comparabilidad entre estudios y adicionado al problema de disposición de los datos requeridos para una estimación más exacta para cada estudio, establecer un estimador del error normalizado de las mediciones que dé cuenta del error estadístico observado cual si se tratara de muestreos aleatorios simples en todos los casos, como procedimiento para dotar de uniformidad a la base para la estimación y, dado que es el método con restricciones mínimas, usarlo como punto de referencia para evaluar la eficiencia de los diseños y la presencia potencial de sesgos adicionales.
Retomando entonces el estimador orientado de la magnitud relativa del sesgo normalizada (εi), se enfrenta nuevamente el problema de que su suma aritmética no permite la estimación de un valor que dé cuenta de la magnitud agregada del error, pues solamente arrojaría un dato relacionado con el tamaño de las salientes en un sentido u otro que fuera predominante en un conjunto de estimaciones dado.
Por ello, nuevamente puede adoptarse la estrategia de calcular la distancia euclidiana (De) de los errores normalizados (2.35):
E idealmente hacerlo calculando la raíz cuadrada de la mitad de la suma de los cuadrados de los errores normalizados (D), para evitar la duplicidad de contabilidad de errores, dado que las salientes que se tengan provocan entrantes de similar magnitud (2.36):
Este estadístico del error normalizado agregado de las estimaciones producto de una encuesta adquiere valores que van de cero, cuando existe perfecta coincidencia entre las proporciones observadas y las reales, hasta cerca de infinito (2.37).
Otra manera de resolver el problema de cómo arribar a una estimación agregada es calcular los valores absolutos del error normalizado (
Lo que en el caso de la estimación de la diferencia de dos contendientes se calcularía por (2.39):
La propuesta alternativa de estimador del error entre las proporciones arrojadas por una encuesta y las proporciones observadas parte precisamente de obtener los valores absolutos de los errores normalizados de la estimación para cada contendiente y luego extraer su promedio, que llamaremos E, (2.40):
Siendo “k” el número de componentes considerados o computados.
Haciendo esto, y debido al comportamiento parabólico del error esperado para un tamaño de muestra dado, se disminuye de manera significativa el efecto que puede tener el número o tamaño de los componentes considerados para fines de estimación del error medio, siendo poco sensible a decisiones de separación o agrupamiento de contendientes por problemas en los reportes de resultados.
Este estimador, al igual que D, adquiere valores que van de cero, cuando existe perfecta coincidencia entre las proporciones observadas y las reales, hasta cerca de infinito (2.41).
E incluso adquiere los mismos valores que D cuando se calcula para los datos de elecciones con dos contendientes, aunque difiere cuando los contendientes son más de dos (2.42).
Si
(2.42)
Si
Como siempre, es viable calcular el error absoluto normalizado de la estimación de la diferencia entre dos contendientes cualesquiera (2.43), lo que en el caso de los dos componentes mayores dará cuenta del error normalizado para la estimación del margen de victoria.
Existe una familia completa de estimadores derivados que pudieran extraerse de este estimador. Uno sería el cálculo de la media de los errores normalizados para un nivel de confianza dado (
Como resultado de este ejercicio, se tendría un estimador que tomaría valores por debajo de 1 cuando la media del error normalizado de sus estimaciones se encontrara por debajo del margen de error tolerado y por encima de 1 cuando fuera más elevada, diferenciando los casos dentro y fuera del margen esperado (2.45).
Incluso, podría sacarse la diferencia de
Que sería un estimador del error excedente al teóricamente tolerado, dada la precisión pretendida en el ejercicio de medición, aunque los valores posibles de
Lo anterior permite considerar la posibilidad de incluir esta variable en modelos o pruebas referidas a conjuntos de estudios cuando sea deseable y considerando sus particulares características.
Adicionalmente, es posible extraer el logaritmo natural de
Este estimador es simétrico y toma valores que van de menos infinito en la cota inferior, cuando existe perfecta coincidencia entre proporciones estimadas y observadas, hasta infinito en la cota superior (2.49).
Dado que la probabilidad de una posible concordancia entre un valor estimado y el real es mayor a cero, resulta imposible evitar que en algunos casos el valor de L alcance la cota inferior de −
Al igual que
Poniendo frente a frente a E y L, se descubre que ventajas de uno son carencias de otro y viceversa, por lo que pudieran considerarse dos formulaciones alternas cuyas virtudes y limitaciones habría que analizar más a fondo. El carácter no simétrico de E puede ser un aspecto negativo para el uso de este indicador, aunque al pasar a L se está modificando la distribución del estimador y se generan dificultades para la interpretación inmediata de los resultados de su aplicación.
Asimismo, esta propuesta permite la detección simultánea de la magnitud y el sentido del error en la estimación y, por su similitud con la lógica empleada para el cálculo de A, goza de las mismas ventajas, por las que este estimador, recientemente desarrollado, goza cada día de mayor aceptación por la academia estadounidense, pero sin tener el problema de responder solamente a una realidad bipartidista, para proporcionar los mismos beneficios pero en el análisis, cualquiera que sea el formato prevaleciente en un sistema. Sería luego de esperarse que esta propuesta tuviera también una aceptación potencial en medios académicos y especializados.
Estimadores complementarios
Como un paso adicional, es posible construir una variable dicotómica que dé cuenta de la condición de exactitud de un estudio (
Luego, el valor medio de
Desde luego, para la condición de un estudio, de haberse encontrado dentro de los márgenes de error correspondientes a una colección de encuestas relacionadas, puede construirse una variable dicotómica que dé cuenta de su tipicidad (
Ello partiría de estimar el grado de tipicidad de una encuesta respecto a un conjunto elegido (
Observando entonces el cumplimiento de la condición de tipicidad (3.3):
Con ello puede analizarse la relación empírica entre el cumplimiento de la condición de haber sido una encuesta con estimaciones típicas o atípicas respecto a un conjunto de estimaciones (
Hay un punto adicional a desarrollar: aunque el indicador propuesto, al igual que el error medio en puntos porcentuales para todos los componentes propuesto por Mosteller,10 arroja estimaciones del error homogéneas y normalizadas para cada ejercicio de medición, que permiten la comparabilidad entre estudios y en distintas elecciones del mismo tipo en una democracia, sería al menos impropio asumir sus resultados como indicadores que permitan la comparación directa entre elecciones de distinto tipo o por diferentes cargos y menos aún entre distintas naciones.
Ello, dadas las características peculiares que presenta la competencia electoral en cada nivel, tipo, nación o estado. Estas diferentes condiciones de competencia pudieran estimarse mediante el empleo de indicadores agregados y la determinación de la capacidad de las encuestas preelectorales para la detección anticipada de los cambios.
En específico, la sugerencia sería estimar la proporción de cambio en el sentido del voto que se registra realmente, conforme los resultados oficiales de las elecciones, contra la proporción de cambio en el voto prevista por las mediciones por encuesta publicadas antes en dichas elecciones.
Universalmente, se ha tomado como estimador del cambio entre elecciones el índice de Pedersen,11 calculado como (3.4):
Que estima el saldo de las ganancias y pérdidas acumuladas entre todos los contendientes. P (anotado en redondas sólo para evitar confusión con el símbolo de probabilidad) es luego la volatilidad o proporción de cambio en las preferencias entre el periodo t y el anterior (t − 1). El saldo de los cambios en distintos componentes se divide entre dos, debido a que la proporción ganada por algún contendiente es necesariamente
Empero, para fines de homogeneidad en los procedimientos y para dotar de comparabilidad los datos de elecciones de distinto tipo o en diferentes naciones, lo ideal no es tomar la volatilidad total que se registra, sino un cálculo que parta de estimar la volatilidad para cada componente utilizado para fines de estimación. Así, la volatilidad entre elecciones para un componente dado (t ) se calcularía simplemente como (3.5):
Luego, la volatilidad promedio para los distintos componentes (t) se calcularía con base en los valores absolutos de la volatilidad de cada uno, puesto que la suma de los valores con signo daría necesariamente cero (3.6):
A semejanza, puede calcularse la volatilidad implícita en la estimación de la proporción del voto atribuida por una encuesta a un componente dado (
Con esto puede estimarse la volatilidad promedio implícita en la estimación producto de una encuesta (
Empero, lo relevante para fines de comparación entre estudios es el cálculo de la diferencia entre la volatilidad estimada por componente y la volatilidad realmente registrada, que resulta idéntica al cálculo del error absoluto de la medición, dado que (3.9):
Lo que se buscaría entonces es calcular el promedio resultante del cotejo del error en la volatilidad implícita de la estimación para cada componente conforme la encuesta versus la volatilidad oficialmente observada (3.10):
Para el cálculo de la proporción media del error de la estimación respecto a la volatilidad registrada, debieran luego promediarse los valores absolutos del error relativo a la volatilidad en cada componente (3.11):
Este estimador toma un valor de cero cuando el error en la estimación es nulo; es decir: cuando la medición advierte una volatilidad para cada componente idéntica a la registrada y, por ende, presenta total concordancia con el resultado. En el otro extremo, el estimador puede alcanzar un valor próximo a infinito, siendo posible evitar este límite en la medida que se aproxime el cálculo de la volatilidad a su valor exacto, sin redondeo, salvo en las excepcionales ocasiones en que las proporciones para todo componente resultan ser idénticas a las previamente registradas (3.12):
Una forma alterna de presentar este cálculo es obtener la estimación de la proporción de la volatilidad anticipada por la medición (u), resultado de restar a la unidad el error relativo promedio en la medición de la volatilidad (3.13):
Este cálculo daría una magnitud y un sentido al estimador de la relación entre la medición y la volatilidad registrada (3.14).
Entre mayor es el valor de u que se obtenga, más cercana a la realidad fue la volatilidad implícita en las estimaciones producto de la encuesta. Cuando alcanza un valor igual a la unidad, muestra la absoluta concordancia entre las estimaciones y el resultado. Entre cero y uno, estaría mostrando la mejoría de la estimación producto de la encuesta respecto al empleo alternativo del resultado previo como estimador del resultado por venir. Cuando toma un valor igual a cero, refleja una identidad entre el error observado y la volatilidad registrada, lo que significa que la medición es tan próxima al resultado como el dato de la elección previa. Finalmente, cuando el valor es negativo, informa que el resultado electoral previo resulta mejor estimador del resultado actual que la propia medición por encuesta, lo que contradice el sentido mismo de realizar un ejercicio por muestreo sobre las preferencias previo a una elección.
Es de apuntar que el cálculo de u adopta el error absoluto en la medición propuesto por Mosteller como estimador del error en una encuesta, no el estimador propuesto en este ensayo. Ello debido a que en principio lo que se coteja son cambios absolutos entre resultados en dos momentos separados en el tiempo, por lo que no resulta conveniente incorporar en el cálculo un estimador del error normalizado de la medición y cotejarlo contra el cambio registrado entre elecciones.
Es viable generar un estimador que muestre la proporción de encuestas cuyas estimaciones resultaron más próximas al resultado que lo que hubiera sido la simple disposición de los datos del evento anterior como estimador del estado de las preferencias esperables. Ello podría calcularse como (3.15):
Este estimador ϖ debiera idealmente alcanzar un valor unitario, pues la función de las encuestas en un proceso electoral es precisamente aproximarse al conocimiento actualizado de las preferencias y, con ello, aumentar la información disponible para el elector respecto a la existente sin el recurso a esta herramienta. Si la razón de tomar en ejercicios de evaluación las últimas mediciones es su proximidad al evento y, por consecuencia, se asume que una medición posterior tenderá, ceteris paribus, a presentar una mayor exactitud respecto al resultado, ello se aplicaría también, y casi como exigencia, a la expectativa de proximidad entre una estimación por encuesta cercana a una elección y el dato oficial correspondiente a la elección anterior.
Un ejercicio de aplicación
Para ver el comportamiento del nuevo estimador del error en encuestas es conveniente tomar como un caso empírico las estimaciones finales y los resultados oficiales de las elecciones presidenciales en México durante el presente siglo, que incluyen tres eventos: 2000, 2006 y 2012.
Ello por diversas razones, dos de ellas vinculadas con la disposición de datos: primera, se trata de elecciones para las que se cuenta con cómputos oficiales de sencillo acceso, referidas a listados bloqueados de contendientes registrados; y segunda, por regulaciones nacionales se dispone de un inventario con los datos relevantes producidos en las diversas encuestas, incluyendo el tamaño de la muestra, la proporción de no respuesta a la pregunta electoral y, desde luego, las proporciones observadas de preferencias para cada contendiente; inventario que, además, permite acotar con certidumbre el universo de mediciones a considerar. Estos datos están disponibles en publicaciones del Instituto Federal Electoral de México y, para las últimas dos elecciones, en el sitio de la propia institución. Pero existe otra razón relacionada no con la accesibilidad a los propios datos, sino con características propias del sistema electoral: se trata de un sistema multipartidario, donde la reducción de los datos a la pareja de competidores mayores no solamente no aportaría información completa sobre la exactitud de las mediciones difundidas, sino que derivaría en la consideración de conjuntos distintos de contendientes en cada elección, pues entre un evento electoral y otro ha habido cambios en el ordenamiento de los contendientes que provocan la inaplicabilidad de soluciones óptimas para la medición de la exactitud de encuestas en sistemas bipartidistas estables, como el estadounidense.
Este hecho se refleja en la presencia de muy elevados niveles de volatilidad, que durante el presente siglo han alcanzado una media próxima a los 18 puntos, más de cinco veces superior a lo que se registra en Estados Unidos. Esto quiere decir que entre una elección presidencial y la siguiente, cerca de la quinta parte de los electores mexicanos cambian el sentido de su sufragio.
Para este análisis se parte de considerar a M3 como el indicador más válido y pertinente, dentro de los previamente existentes, para la medición de la divergencia entre encuestas y resultados en una realidad multipartidaria, cotejable luego con el estimador propuesto Ez, simple de calcular y diáfano, y con L, el indicador más complejo que se propone en este ensayo, que tiene la ventaja de ser simétrico.
Para fines de comparar lo similar y no enfrentar problemas adicionales, se consideran únicamente ejercicios nacionales que hayan tenido por finalidad estimar las preferencias en torno a la disputa del Ejecutivo federal. Se excluye luego toda medición referida a posiciones legislativas, cuya lógica de decisión del voto atiende a elementos diversos a los propios de una elección por un cargo único, personal. De igual manera, no se consideran elecciones para niveles estatales ni mediciones que no correspondan a una cobertura nacional, eliminando posibles efectos derivados de características particulares del electorado o la competencia en cada unidad menor.
Dado lo anterior, existe una constancia en el reporte para los contendientes mayores, para los cuales invariablemente se reporta una estimación separada. Para el resto de competidores existen casos de reportes en que los datos se presentan por separado para cada uno y casos de reportes en que su proporción se agrega. Es por ello obvio que el cálculo del error en las encuestas debe considerar, en el caso mexicano, lo cercano de la estimación para los tres partidos mayores. Lo que no resulta tan claro es si el remanente, que corresponde a uno o varios contendientes que pueden ser distintos en cada ocasión, debe ser incluido como un componente único, producto del colapso de los datos sobre cada cual que pudieran haber sido reportados por separado, si debe incluirse respetando el agrupamiento o separación de opciones hecha en cada reporte, o si debe ser francamente excluido de los cálculos.
En aras de la completitud del cálculo, no pareciera prudente excluir un componente que pudiera ser depositario de un error mayor o menor en cada caso. Pero su inclusión debe preservar la homogeneidad entre los datos tratados. Por ello, en el análisis que nos ocupa, se ha decidido tomar a los contendientes distintos a los tres mayores como uno único, agregando las proporciones correspondientes a los distintos contendientes menores cuando hubieran sido reportadas por separado. Con ello, además, se evita en parte el problema apuntado por Mosteller de reducir artificialmente el nivel de error calculado, al promediar unidades con divergencias esperadas menores con las mayores, dado que no serán varios sino sólo uno el componente susceptible de presentar dicho comportamiento y de que su inclusión regular en los cálculos permite la comparabilidad de las magnitudes de error registradas por las diversas encuestas en los distintos momentos bajo observación.
En el caso de la dicotomía entre proporciones efectivas derivadas de la observación y repartos de proporciones según algún modelo de votantes probables, pueden presentarse diferencias significativas entre ambas salidas. Por ello, en algunos análisis se incorporan dos registros para una misma encuestadora, correspondientes a los reportes de preferencias efectivas y de votantes probables. Empero, ello resulta cuando menos inequitativo, puesto que no todas las encuestadoras presentan ambos resultados, bien sea porque no realizan un ejercicio con la pretensión de detectar los probables votantes, bien por privilegiar las estimaciones derivadas del modelo de propensión al sufragio sobre el reparto directamente observado.
En el caso que nos ocupa, se toman dos decisiones: primera, homologar los datos arrojados por las distintas encuestas, excluyendo de los repartos los casos no definidos, lo que en la mayoría de ocasiones significa tomar el dato correspondiente al reporte generado por la propia casa, y que en cualquier caso implica un tratamiento homogéneo y sistemático de los datos; y segunda, tomar un único dato para cada encuestadora en cada ocasión, que no sólo corresponde a la última estimación hecha pública, sino que privilegia repartos producto de modelos de votante probable sobre las preferencias efectivas, asumiendo que la encuestadora responsable optó por aproximarse a una estimación del resultado mediante una estrategia de decantación de votantes entre los electores, desechando con ello toda presunción de correspondencia entre las preferencias efectivas y los resultados por venir.
Esto implica una responsabilidad última de quien es responsable del análisis sobre el proceso de homologación y selección de datos a considerar. Algunas veces, la carencia de un ejercicio de exclusión de casos no definidos por alguna encuestadora obligó a efectuar cálculos sobre los datos brutos aportados. En otras, se tuvo que elegir entre varias posibles distribuciones de preferencias que fueron reportadas por una misma casa, para lo cual se privilegió el reparto de votantes probables cuando se presentaba como tal y no solamente como producto de un ejercicio de segmentación que no presuponía una aproximación al resultado esperado.
Igualmente, tuvo que definirse bajo qué principios incluir o excluir una estimación particular. Desde luego se consideró únicamente la última encuesta publicada por cada firma, pero bajo la condición de que el dato correspondiera a un ejercicio cuya toma de datos en campo hubiera concluido dentro de la ventana de cinco semanas previas a la elección y no con anterioridad. Además, no se consideraron ejercicios con muestras menores al millar de casos.
Con ello, se trata de equilibrar en lo posible las condiciones externas a la generación de las estimaciones, evitando cotejar datos que fueran caducos o cuya proximidad con los resultados pudiera cuestionarse. La disposición de una ventana temporal definida reduce asimismo la posibilidad de que las diferencias entre estimaciones puedan atribuirse al momento de terminación del proceso de acopio de datos, reconociendo que el lapso entre una medición y el evento electoral es una fuente primordial de diferencia de las encuestas con los resultados, como demuestra un conocido estudio sobre el tema.12
Finalmente, en el ejercicio dejamos fuera las encuestas realizadas que incluyen entrevistas por vía telefónica, pues de acuerdo con los cánones internacionales no resulta pertinente efectuar ejercicios por este medio en México, dada la relativamente reducida cobertura del sistema telefónico, que no alcanza dos tercios del electorado. Dadas las decisiones anteriores, se dispone de un total de 42 mediciones, catorce para cada una de las tres elecciones. Cabe reconocer que este recuento no resulta original, pues es imposible reinventar la historia y conformar series nuevas de mediciones antaño hechas del dominio público.13 Tampoco lo es la toma de criterios que, al partir de ciertos principios lógicamente sustentables, dan lugar a una selección. Luego, lo novedoso de este artículo no será el recuento de mediciones, sino el tratamiento que de ellas se hace, poniendo énfasis en la propuesta de nuevos estimadores.
Los datos correspondientes serían los siguientes, ordenando las encuestas finales de mayor a menor exactitud en cada elección:
Cuadro 1 Estimaciones por encuesta y resultado oficial de la elección presidencial de México en 2000
| 2000 | Casos | Válidos | VFQ | FLO | CCS | Otros | M3 | E | L |
| ARCOP | 1400 | 1204 | 42.5 | 38.1 | 16.7 | 2.7 | 0.65 | 0.51 | -0.29 |
| GEA-ISA | 2400 | 1481 | 40.5 | 38.2 | 18.0 | 3.3 | 1.50 | 1.47 | 0.17 |
| Democracy Watch | 1542 | 1496 | 41.0 | 36.0 | 20.0 | 3.0 | 1.70 | 1.62 | 0.21 |
| GAUSSC | 1500 | 1337 | 40.6 | 38.5 | 19.1 | 1.8 | 1.85 | 1.88 | 0.27 |
| Demotecnia | 2054 | 1150 | 44.0 | 34.0 | 16.0 | 6.0 | 1.95 | 2.05 | 0.31 |
| Grupo Reforma | 1545 | 1251 | 39.0 | 42.0 | 16.0 | 3.0 | 2.75 | 2.18 | 0.34 |
| MERCAEI | 1316 | 1316 | 38.4 | 42.9 | 16.1 | 2.6 | 3.00 | 2.27 | 0.36 |
| AC Nielsen | 2489 | 2016 | 39.0 | 42.0 | 16.0 | 3.0 | 2.75 | 2.76 | 0.44 |
| Consultores y MP | 1800 | 1472 | 38.0 | 41.0 | 19.0 | 2.0 | 3.05 | 2.79 | 0.45 |
| Zogby | 1330 | 838 | 40.7 | 43.6 | 14.5 | 1.2 | 3.35 | 2.83 | 0.45 |
| Alduncin y Asoc. | 2095 | 1676 | 40.5 | 34.6 | 20.3 | 4.6 | 2.65 | 2.94 | 0.47 |
| Pearson | 1590 | 1399 | 38.6 | 43.2 | 14.8 | 3.4 | 3.55 | 3.12 | 0.49 |
| CEO | 2423 | 2205 | 38.9 | 42.7 | 15.3 | 3.1 | 3.15 | 3.38 | 0.53 |
| MUND | 1362 | 1253 | 35.1 | 36.2 | 26.6 | 2.1 | 4.80 | 3.92 | 0.59 |
| Promedio | 1911 | 1546 | 39.8 | 39.5 | 17.7 | 3.0 | 1.86 | 1.69 | 0.23 |
| Resultado | 43.5 | 36.9 | 17.0 | 2.6 | 2.62 | 2.41 | 0.38 |
Fuentes: cálculos del autor a partir de IFE, El papel de las encuestas en las elecciones federales. Memorias del Taller Sumiya 2000, IFE-AMAI-Colegio Nacional de Actuarios, México, 2001; e INE, Atlas de resultados de las elecciones federales 1991-2015 [http://www.siceef.ine.mx/atlas.html?página=1#siceen].
Cuadro 2 Estimaciones por encuesta y resultado oficial de la elección presidencial de México en 2006
| 2006 | Casos | Válidos | FCH | RMP | AMLO | Otros | M3 | E | L |
| GEA-ISA | 1600 | 1403 | 38.0 | 23.0 | 36.0 | 3.0 | 0.55 | 0.71 | -0.15 |
| ARCOP | 1400 | 1204 | 37.0 | 25.0 | 34.0 | 4.0 | 1.15 | 0.93 | -0.03 |
| Consultores y MP | 1200 | 1013 | 36.8 | 25.8 | 33.9 | 3.5 | 1.40 | 1.06 | 0.02 |
| Grupo Reforma | 2100 | 1721 | 34.3 | 25.3 | 36.4 | 4.0 | 1.31 | 1.26 | 0.10 |
| El Universal | 2000 | 1220 | 34.0 | 26.0 | 36.0 | 4.0 | 1.60 | 1.28 | 0.11 |
| Parametría | 1000 | 823 | 33.0 | 27.0 | 37.0 | 3.0 | 2.35 | 1.68 | 0.23 |
| BGC Ulises Beltrán | 1200 | 1032 | 34.3 | 26.3 | 34.3 | 5.1 | 2.30 | 1.85 | 0.27 |
| Consulta Mitofsky | 2800 | 1590 | 33.0 | 27.0 | 36.0 | 4.0 | 2.10 | 1.89 | 0.28 |
| CEO | 2000 | 1738 | 33.5 | 25.3 | 35.8 | 5.4 | 1.95 | 2.15 | 0.33 |
| Zogby | 1000 | 870 | 35.0 | 28.0 | 31.0 | 6.0 | 3.60 | 2.64 | 0.42 |
| Alduncin y Asoc. | 2046 | 1733 | 35.0 | 29.0 | 32.0 | 4.0 | 3.10 | 2.86 | 0.46 |
| INDEMERC | 1500 | 990 | 32.3 | 28.2 | 33.5 | 6.0 | 3.70 | 2.88 | 0.46 |
| Demotecnia | 2000 | 1240 | 30.5 | 29.6 | 35.4 | 4.5 | 3.65 | 2.96 | 0.47 |
| GAUSSC | 3250 | 2990 | 34.6 | 28.8 | 33.7 | 2.9 | 2.90 | 3.90 | 0.59 |
| Promedio | 1793 | 1398 | 34.4 | 26.7 | 34.6 | 4.2 | 2.09 | 1.82 | 0.26 |
| Resultado | 36.9 | 23.0 | 36.3 | 3.8 | 2.26 | 2.00 | 0.30 |
Fuentes: cálculos del autor a partir de IFE, Memoria del seminario: encuestas y elecciones2006, IFE-AMAI-Wapor-Consejo de Investigadores de la Opinión Pública, México, 2010; e INE, Atlas de resultados de las elecciones federales 1991-2015 [http://www.siceef.ine.mx/atlas.html?página=1#siceen].
Cuadro 3 Estimaciones por encuesta y resultado oficial de la elección presidencial de México en 2012
| 2012 | Casos | Válidos | JVM | EPN | AMLO | GQT | M3 | E | L |
| MERCAEI | 1200 | 899 | 27.2 | 38.5 | 31.0 | 3.3 | 1.05 | 0.94 | -0.03 |
| Covarrubias y Asoc. | 1500 | 1410 | 26.0 | 40.0 | 30.0 | 4.0 | 1.25 | 1.48 | 0.17 |
| IPSOS-BIMSA | 1000 | 648 | 24.6 | 44.1 | 29.5 | 1.8 | 2.45 | 1.49 | 0.17 |
| Demotecnia | 1500 | 975 | 22.9 | 40.2 | 32.4 | 4.5 | 1.60 | 1.58 | 0.20 |
| Consulta Mitofsky | 1000 | 864 | 24.1 | 44.5 | 29.4 | 2.0 | 2.65 | 1.77 | 0.25 |
| Grupo Reforma | 1616 | 1293 | 24.0 | 41.0 | 31.0 | 4.0 | 1.75 | 1.82 | 0.26 |
| BGC Ulises Beltrán | 1200 | 996 | 25.0 | 44.0 | 28.0 | 3.0 | 2.75 | 2.06 | 0.31 |
| ARCOP | 1200 | 984 | 31.0 | 39.0 | 27.0 | 3.0 | 2.80 | 2.14 | 0.33 |
| Parametría | 1000 | 810 | 23.6 | 43.9 | 28.7 | 3.8 | 3.10 | 2.23 | 0.35 |
| GEA-ISA | 1144 | 964 | 22.4 | 46.9 | 28.5 | 2.2 | 3.85 | 2.61 | 0.42 |
| Berumen y Asoc. | 3480 | 2791 | 22.4 | 41.7 | 34.0 | 1.9 | 2.05 | 2.67 | 0.43 |
| Con Estadística | 1150 | 943 | 24.7 | 44.4 | 26.7 | 4.2 | 3.55 | 2.77 | 0.44 |
| Buendía & Laredo | 2000 | 1752 | 24.4 | 45.0 | 27.9 | 2.7 | 3.10 | 2.94 | 0.47 |
| INDEMERC | 2000 | 1805 | 22.8 | 47.2 | 27.1 | 2.9 | 4.30 | 4.18 | 0.62 |
| Promedio | 1499 | 1224 | 24.7 | 42.9 | 29.4 | 3.1 | 2.24 | 1.93 | 0.29 |
| Resultado | 26.1 | 39.2 | 32.4 | 2.3 | 2.59 | 2.19 | 0.34 |
Fuentes: cálculos del autor a partir de INE, "Séptimo informe que presenta la Secretaría Ejecutiva al Consejo General del Instituto Federal Electoral respecto del cumplimiento del Acuerdo CG411/2011", México, 26 de julio de 2012; e INE, Atlas de resultados de las elecciones federales 1991-2015 [http://www.siceef.ine.mx/atlas.html?página=1#siceen].
Como se podrá observar en estos cuadros, M3 (la media por componente de las diferencias entre estimaciones y resultado) suele resultar un poco más elevada en valor que
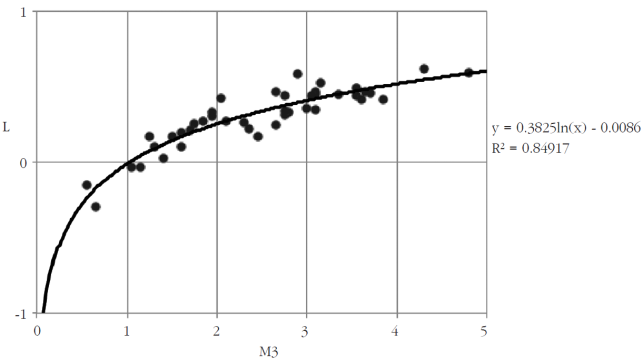
En cambio, como se ve en la Gráfica 2, resulta obvio que L es una simple conversión a escala logarítmica de
Conclusiones
Existe una demanda pública que implica disponer de un estimador agregado que dé cuenta de la exactitud de las encuestas. Esto ha sido atendido desde hace décadas mediante diversos medidores, todos éstos con limitaciones y sin lograrse un consenso en el campo sobre cuál estimador usar.
Pareciera claro que adoptar un estimador determinado para evaluar el nivel de exactitud de las encuestas respecto a los resultados de una elección tiene impacto significativo en las conclusiones a las que se llegue en un análisis. Asumir en realidades multipartidarias métodos reductivos del número de componentes, además de ser algo artificial, genera estimaciones distintas respecto de la distancia entre estimaciones por encuesta y resultados oficiales a cuando se considera al grueso de contendientes.
Existen limitaciones claras de los estimadores disponibles para medir la exactitud de las encuestas electorales, entendida como el contraste entre las estimaciones producidas y los resultados oficiales. Estas limitaciones son de dos tipos: las derivadas de la ambigüedad en los conceptos y procedimientos para su cálculo, y las relativas a su sensibilidad al cambio en la cantidad de componentes involucrados en su estimación.
Lo anterior, sin olvidar que la robustez de los estimadores no depende total ni únicamente de los algoritmos utilizados o las consideraciones o características incluidas en su construcción, puesto que un aspecto fundamental en cualquier ejercicio de estimación de parámetros es la disposición y empleo de un apropiado marco muestral y de la muestra en sí, por lo que deben evitarse en lo posible sesgos de selección y otros problemas comunes a las mediciones mediante encuesta.
Por lo anterior, resulta pertinente definir de manera operativa los conceptos que las encuestas intentan medir y proponer un mecanismo que reduzca el efecto de los problemas detectados en las opciones disponibles para calcular la exactitud de las encuestas electorales.
La vía para restringir el impacto de la inclusión o exclusión de componentes en el cálculo de la exactitud de las encuestas es la ponderación de las diferencias entre estimaciones y resultados según la proporción estimada del voto para cada competidor. Ello se logra mediante el ajuste del valor de las diferencias absolutas según el error estadístico de las estimaciones y, para permitir un comportamiento simétrico del indicador, convertirlo en su logaritmo. Esta fue la ruta tomada en este ensayo para construir un estimador alterno para medir la exactitud de las encuestas electorales.
En forma complementaria, es posible disponer de diversos estimadores que den cuenta de manera agregada de la exactitud en colecciones de encuestas bajo análisis y que arrojen datos sobre la proporción en que el ordenamiento resultante corresponde con el resultado, en que las estimaciones se encuentren en promedio dentro o fuera del margen de error para cada una de ellas, o que cuantifiquen la relación entre la exactitud del conjunto de encuestas y la volatilidad interelectoral.
Este nuevo estimador aporta una medición de la diferencia entre estimaciones producto de encuestas y resultados oficiales que permita dilucidar rápidamente la significación del error estimado para una encuesta o colección de encuestas. Los estimadores agregados propuestos permiten además una profundización en el dimensionamiento del fenómeno. La expectativa del autor es que estos estimadores aporten una herramienta útil para futuros análisis sobre la exactitud de las encuestas preelectorales.











 text new page (beta)
text new page (beta)