Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Política y cultura
versión impresa ISSN 0188-7742
Polít. cult. no.23 México ene. 2005
Matemáticas y ciencias sociales
Symmetries and exchange relations
Paul Cockshott*
* Universidad de Glasgow, Reino Unido.
wpc@dcs.gla.ac.uk
Recepción del original: 30/06/04
Recepción del artículo corregido: 10/01/05
Resumen
Este artículo presenta un análisis de la forma del valor basada en ideas de espacios métricos y operaciones de preservación de la simetría en estos espacios. Esto se relaciona con el concepto de la simetría en sistemas regidos por leyes de conservación.
Palabras clave: relaciones de intercambio, teoría del valor, espacios métricos, simetrías y sistemas
Abstract
The paper presents an analysis of the value form based in ideas of metric spaces and symmetry preserving operations in these spaces. This is related to the concept of symmetry in systems governed by conservation laws.
Key words: Exchange relations, value theory, metric spaces, symmetries and systems
THE FORMAL PROPERTIES OF EXCHANGE
The first chapter of Marx's Capital is concerned with an analysis of the commodity. It is a somewhat difficult chapter to read, but it is considered by many scholars to be essential to understanding his whole conceptualization of capitalism. It is a relatively formal text but not in the sense that we would now describe a scientific or mathematical text as being formal. Instead of mathematics or modern formal logic, it uses Hegelian logic to analyze the form assumed by value.
Since the mid 19th century the study of formal systems has advanced tremendously in its scope and the tools available for constructing formalisms have multiplied. In this paper we want to construct an analysis of the value form using some modern conceptual tools. The possibility of doing this is predicated on the fact that value and money are in the strict sense formal systems. They are systems of symbols whose time evolution is governed by formal rules analogous to termrewrite rules. We will first attempt to identify what those rules are and their necessity.
Legally independent owners-economic subjects
Commodity exchange presupposes the existence of economic subjects. An economic subject is an abstract category that encompases both people and social organisations that engage in trade. The reason why economic subjects exist is two fold:
- The units of production in a society are not self sufficient.
- There exists no overall system of social direction of labour.
In capitalism a unit of production is an enterprise, a technical unit of production and an economic subject. It can own, buy and sell things. Such subjects are the result of technology and a social division of labour. Capitalist production is social. Enterprises in contrast with the "natural economy" of the peasant household, produce for society not themselves. Technology compells each to produce just a few types of goods, while consuming many types, which necessitates a circulation of products. As enterprises are property owners, how can circulation take place without a loss of property? The only possible way is the exchange of equivalents. An economic subject, appears juridically as a legal person. In law it seems that the attributes of a person that are projected onto firms. But look at it the other way round-our attributes as legal personalities came from the needs of the enterprise system. Once, most enterprises were sole proprietorships, and the rights of the sole proprietor shaped the concepts of capitalist law. These proprietors were faces for units of production. The reproduction of these units of production by trade required their representatives to own and dispose of property. These requirements shaped our outlook on 'natural' / 'human' rights.
This juridical relation, which thus expresses itself in a contract, whether such a contract he part of a developed legal system or not, is a relation between two wills, and is but a reflex of the real economic relation between the two. It is this economic relation that determines the subject matter comprised in each such juridical act. The persons exist for one another merely as representatives and therefore, as owners of, commodities. In the course of our investigation we shall find, in general, that the characters who appear on the economic stage are hut the personification of the economic relations that exist between them.1
People have not always been legal personalities. To the framers of the US constitution certain rights appeared self evident, but self evident only as the rights of white property owners. Slaves were 'self evidently' not the bearers of such rights. Go back further. Members of a hunter-gatherer family were not economic subjects. Money constitutes people as economic subjects. Today, technology forces capitalist enterprises to be inter-dependent. But this is not the aboriginal condition. The aboriginal condition is self sufficiency, of household economy or village community. The existence of commodities and money could not originally spring from their current reproductive roles.
FIGURE 1. Symmetries and exchanges

An artwork on the subject of this paper, featuring the monetary system introduced by the British
colonialists to Nigeria, the Kola nut, and its most famous commodity derivative. Produced by symmetries
within the Poincare disk of hyperbolic geometry.
Lydia
Orthodox economic theory says money came from barter, with one commodity was set aside as a means of exchange. Typically this commodity is said to have been gold or silver, standardised units of which served as the unit of account. Coin is explained as disinterested state production of standardised weights of gold. This fable projects Newton's gold standard back to the early history of money. Were it true, we would expect a stage in which privately issued gold weights circulated as money, then a period when private gold weights circulated alongside state issued coins. What we see is a sudden issue of coins by Lydia in the 7th century B.C. These are a standard weight the stater, roughly 220 grams, but, far from being of pure gold were a debased alloy of gold, silver and copper.2 The addition of copper meant that they still looked golden, instead of the whitish look that a simple gold/silver alloy would have had. If they were supposed to be standard ingots of pure gold, then the Lydia was defrauding its public. If they were for day to day purchases in markets, why were they so heavy and valuable that were they worth a month's subsistence?3
An alternative is that Lydian coins were designed to pay taxes. This interpretation which ties the origins of money to the development of class society and the state is currently defended by writers such as Wray, Ingham and Forstater,4 , 5 , 6 building on a tradition established by Knapp and Innes.7 , 8 According to this State or Chartalist theory, the State calls money into being by levying taxes in it. At an earlier stage - for example early Egypt, taxes were in labour or produce. By levying taxes in coin, and paying his servants coin, the King forced the coin's currency. The Lydian stater were to costly for day to day transactions but a month's subsistence would be a reasonable minimal unit of annual tax.
If the King forced his subjects to pay tax in coin, then they must either have worked for him - building roads, acting as soldiers etc., or, produced commodities to sell to soldiers road builders, etc. It is the coercive power of the State that called commodity production into being. Adam Smith called money the "power to command the labour of others". This power, in aboriginal form, belongs to the state. By issuing coins stamped with a royal emblem, the state delegates this command over labour to those who hold the coins. A coin in my hand shows either that I have personally served the King as a soldier etc., or have done so indirectly by providing commodities to the soldiery. Money comes from appropriating a surplus product. States, first appropriators of a surplus, by commuting of taxes in kind to taxes in money, forced an initially self-sufficient peasantry to produce for the market and thus engendered civil society.
The use of precious metal was incidental. Wray emphasises that in Britain up to the 19th century the predominant form of state money was actually the tally stick not the gold coin:
Originally, the money liability was always in terms of a unit of account as represented by a certain number of grains of wheat or barley. In fact, all the early money units were weight units for grain -the mina, the shekel, the lira, the pound. Once the State has imposed the tax liability, the taxed population has got to get hold of something the State will accept in payment of taxes. This can be anything the State wishes: It can be clay tablets, hazelwood tallies, iron bars, or precious metal coins. This, in turn, means the State can buy whatever is offered for sale merely by issuing that thing it accepts in payment of taxes. If the State issues a hazelwood tally, with a notch to indicate it is worth 20 pounds, then it will be worth 20 pounds in purchases made by the State so long as the State accepts that same hazelwood stick in payment of taxes at a value of 20 pounds. And that stick will circulate as a medium of exchange at a value of 20 pounds even among those with no tax liability so long others need it to pay taxes. The matching of those with tallies but no taxes with those who have tax liabilities but no tallies is accomplished by bankers -who have always been the agents of government precisely to accomplish such matching.
[...]
A tally was simply "a stick of squared hazel-wood, notched in a certain manner to indicate the amount of the purchase or debt", with the name of the debtor and the date of the transaction written on two opposite sides of the stick (Innes, 1913, p. 394). After notching, the stick was split down the middle in such a way that the notches were cut in half. The split was stopped about an inch from the base, with the longer piece (called the stock, from which our term "capital stock" derives) retained by the creditor, with the "stub" (a term still used as in "ticket stub") held by the debtor. The two pieces of the tally would be matched later (most significantly at the time of settlement) to verify the amount of the debt. Importantly, governments spent by raising a "tallia divenda" on the exchequer, issuing tallies for payment for goods and services delivered to the court (after 1670, wooden tallies were supplemented by paper "orders of the exchequer", although tallies were still held in the English House of Commons until 1834) [Wray, 2004].
Money is a formal system consisting of a binary relation9 associating with each juridical subject an integer number. Each historical form of money is a step in the development of the technologies of record supporting this binary relation. Coins maintain the relation by possession. The number associated with each individual is encoded in the coins they carry. Coin is an imperfect technology of record: it can only record positive numbers. You can not have £-50 in your pocket. Coins and paper notes are token based methods of record keeping. They are abbacic i.e., correspond to abbacus based systems of calculation. A change of state is achieved by the physical movement of tokens.
Tallys, double entry account books, decks of punched cards or computerised relational databases are more sophisticated monetary technologies to associate with a legal person a credit or debit state. Tallys are a specialised token system. The other technologies are algorithmic. A change of state is achieved by the writing down or recording of symbols.
A key concern of all monetary technologies is their integrity of record. They must provide some protection against falsification. It is in this light that the use of precious metal for coins should be seen. States have always enacted severe penalties for the fraudulent issue of coin. But penalties would be ineffective if the issue of fraudulent coin is made too easy. Beyond legal prohibitions on forgery, State coin had two distinct protection mechanisms.
1) The coin is made by stamping from a master, one of the basic copying technologies. Unless one has access to the master it is difficult to make accurate copies of the coin. Reasonably good copies may however pass without notice. To do this one has to replicate the master, which can in principle be done by taking an impression of the coin, using this to make a mould and from that cast a new die. Until the invention of iron casting, this process was technically infeasible, since dies made from softer castable metals like bronze would not have the toughness required to stamp out coin. Note that there are 3 copying stages between the coin used as a model and the new forged coins. Errors in copying accumulate exponentially so it is very difficult to get forgeries of acceptable quality.
The remaining forgery techniques were to hand carve a new die, or to use an existing coin to make negative moulds from which coin could be cast rather than stamped. These are relatively expensive processes and would only be worth while for high denomination coinage.
2) Whilst low denomination coins were made from copper or copper alloys, and protected against forgery by the method above, high denomination coins required additional protection. This could be done by forging them from expensive materials like gold and silver. Provided that the nominal value of the coins was not hugely in excessive of the value of the metal they contained, this, in conjunction with the inherent difficulties of accurate copying, reduced the profits to be made from forgery.
The use of gold or silver is not essential to money tokens, as is shown by their abandonment in favour of the use of paper money printed using sophisticated techniques that make it difficult to copy. The use of bullion was a low-tech anti-forgery expedient.
As the State commutes taxes in kind to money taxes it moves from the direct real appropriation of the surplus product to a symbolic appropriation. In levying a money tax, the State symbolically asserts its right to a portion of society's labour. When it spends the tax money purchasing goods and labour, it performs a real appropriation of a surplus product. Civil society acts as an intermediary transfering labour from those who paid the tax, to those who provide the actual services to the State.
The essential interdependence of State and money is particularly clear in the history of empires. On conquering Africa, the Europeans face the problem that
if the subsistence base was capable of supporting the population entirely, colonial subjects would not be compelled to offer their labor-power for sale. Colonial governments thus required alternative means for compelling the population to work for wages. The historical record is clear that one very important method for accomplishing this was to impose a tax and require that the tax obligation be settled in colonial currency. This method had the benefit of not only forcing people to work for wages, but also of creating a value for the colonial currency and monetizing the colony. In addition, this method could be used to force the population to produce cash crops for sale. What the population had to do to obtain the currency was entirely at the discretion of the colonial government, since it was the sole source of the colonial currency [Forstater, 2003].
The State, of course, predates commodity producing society and has a primordial power to appropriate part of society's labour time. In the early empires of Mesopotamia and Egypt, or the later Inca empire this appropriation was performed directly. All peasants had a duty to provide either time or crops to the State. Some of the crops would be consumed by priests or State officials, another portion would be stockpiled against drought and redistributed to the working population in times of scarcity. This form of economy was termed redistributive by Polanyi.10 Such a system requires the development of information technology-systems of writing down and recording numbers. Thus the Mesopotamian civilisations developed cuniform numbers and later, developed writing. The Incas developed quipu, a numerical notation based on knotted strings. Such systems of record had to:
- Keep track of physical stocks of crops held by the state or temples;
- Keep track of the deliveries made by individuals and groups subject to tribute deliveries;
- Track the tribute obligations of such groups.
These require a recording technology, standardised systems of measurement and a reliable arithmetic. The State had to associate numbers with tax-payers and types of products. It had to measure the grain delivered. It had to add up tribute delivered by groups to know what total it had in stock -a reliable technique for adding large numbers was needed. In order to determine if a group had met their tribute obligations, a technique of subtraction was required, taking away their deliveries from their obligations.
The Summerian civilisations developed a sophisticated system of written numerals, using a place notation similar to that we use today. The key difference was the number base. Our place notation, deriving originally from India, uses base 10, the Summerians used base 60. Place notation is concise and allows large numbers to be readily manipulated. It was also a written notation, lending itself to the recording of tables of tax deliveries. Without this technology for recording and processing information the social complexity of the early empires would not have been feasible. In all but the simplest social systems, social relations are embodied in information technology. For example, without a technique for recording debts, the social relation of creditor/debtor can not persist.
FIGURA 2

Code of Hammurapi cited in J. N. Postgate, Early Mesopotamia, London, Routledge, 1992.
Different subjects of the empire would deliver different crops depending on their circumstances. Some might deliver barley, some dates, some dried fish, or a mixture of such products might be delivered. It is thus necessary to determine if a farmer delivering a basket of dates and three gur of barley has met his tax obligations. The solution was to define the tax obligation in terms of barley and for the State to then define how much fish, dates etc. would be required to meet this obligation in terms of barley. The standard volumetric unit of barley, the gur, about 300 litres, then became the unit in which deliveries of other products were measured. The gur of barley had an equivalent in silver the shekel, defined as silver to the weight of 240 grains of barley. It appears that this then became the basis for a purely accounting based monetary system. The sheckel/gur was never issued as a coin, it existed only as entries in accounting records on clay tablets. This notional quantity of barley then acted as a generalised way of measuring values and obligations. From regulating obligations to the State, it moved to being the unit in which credit relations between private individuals were expressed.
FIGURA 3

Opening section of Esnunna Law Code, cited in Postgate, 1992
Such a system of credit based accounting was only possible thanks to there being a literate and numerate class of scribes. The place based number system and algorithmic calculation underlay it. If you are to become profficient in a place based number system you need to spend childhood years learning by rote your tables. You have to learn to memorise the addition, subtraction and multiplication tables. This is a hard enough task using base 10. With a base 60 number system it would have been more difficult. A naive estimate indicates that the size of the tables to be learned is 36 times as great as for our school children. To operate an accounting based monetary system required an expensively educated class lacking in the petty kingdoms who first introduced coinage. Coins allowed monetary relations to operate in societies which lacked a class of numerate scribes.
EXCHANGE IS VALUE CONSERVING
We have asserted that the operations of payment and commodity transfer are conservative, in the sense that the amount of money and commodites is unchanged after them. We will now look at what it means to say that commodity exchange, that is to say linked pairs of payment and commodity transfer are value conserving as well as conserving commodities and money.
METRIC SPACES
We have been talking about commodity-money space. We will now try and characterise this as a mathematical space. To do this we introduce the mathematical notion of a metric space. This is a generalisation of the properties of the real space that we live in, to various more abstract spaces.
A metric space (S,d) is a space S together with a real-valued function 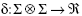 ,which measures the distance between pairs of points p,
,which measures the distance between pairs of points p, 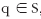 , where d obeys the following axioms:
, where d obeys the following axioms:
1. Commutation: What this says is that the distance from p to q is the same as the distance from q to p, the distance from Paris to London is the same as the distance from London to Paris.
d(p,q) = d(q,p)
2. Positivity: This says that distances between places are always positive. It does not make sense to talk of somewhere being -4 miles away.
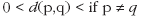
3. Self-identity:
d(p,p) = 0.
A place is no distance at all away from itself.
4. Triangle inequality: This why it is never shorter to go from London to Birmingham by way of Beach Head. It is nearly always shorter to go directly from London to Birmingham. The only exception would be if Beachy Head lay on the straight line between them, then it would make no difference going via Beachy Head.
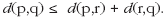
In the formula London = p, Birmingham = q and Beachy Head = r.
Examples of metric spaces
Euclidean 2-space. This is the familiar space of planar geometry. It is the space defined by perfectly flat blackboards or flat sheets of paper. If p and q are two points on a sheet of graph paper, with coordinates (p1, p2) and (q1, q2) respectively, then the distance between these points is derived from the rule of Pythagoras
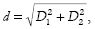 (1)
(1)
where Di = pi-qi, i = 1, 2
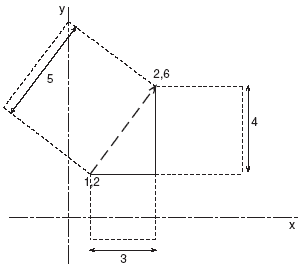
Consider the example in figure 4. Suppose we have two points on a sheet of graph paper, the point at x, y coordinates (1, 2) and the point at
(2, 6). Thus the distance between them is 5, since
FIGURE 4. Use of Pythagoras's rule to work out straight line distance between points on a grid
This method of calculating distances extends to multidimensional vector spaces such as three dimensional space or more abstract vector spaces. To measure distances in an n dimensional Euclidean space you can use the formula:

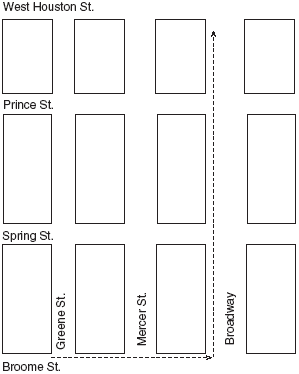
Manhattan space. So-called after the Manhattan street plan,11 the metric is simply the sum of the absolute distances in the two dimensions. It specifies the distance that you have to walk between two points in a city with a grid street layout. Consider the example in figure 5. We want to go from Greene and Broome to West Houston and Broadway. We have to go the distance in the x direction from Broome St to Broadway, added to the distance from Greene St to West Houston St. The distance will be the same so long as our route stays in the rectangle formed by the four streets. The distance formula is:

FIGURE 5. Getting from Greene and Broome to West Houston and Broadway in Manhattan
Equality operations in metric spaces
We now introduce the concept of positions in a metric space being in some way equivalent. Let us define two points q,  so be equal with respect to p if they are equidistant from p under the metric d. Formally,
so be equal with respect to p if they are equidistant from p under the metric d. Formally,
q = pr if d(p,r) = d(p,q) (5)
Given an equality operator E and a member q of a set S, we can define an equality subset, that is to say, the set whose members are all equal to q under E. The equality set of q under = p using the Euclidean 2-space metric is shown in figure 6, while figure 7 shows the corresponding equality set under the Manhattan metric.
FIGURE 6. Equality set in Euclidean space
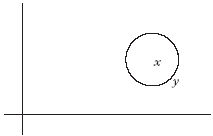
FIGURE 7. Equality set in Manhattan space
Commodity-money space
What, it may be asked, has all this to do with value? Well, value is a metric on commodities. To apply the previous concepts, we define commodity-money space as follows: a commodity-money space of order n is the set of tuples (am, q1 C1, q2 C2, ... qn Cn) where qi Ci stands for quantity i of commodity i.
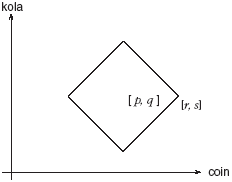
Consider, for example, the commodity-money space of order 1 composed of tuples of coin and kola. The set of all points equidistant with (e coin, f kola) from (a coin, b kola) under the Manhattan metric is shown in figure 8.
FIGURE 8. Points equidistant with (e coin, f kola) from (a coin, b kola) in Manhattan space
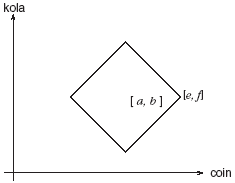
We have a distinct equality operator, =p , for each point p = (p1 coin, p2 kola) in our kola-coin space. Let us consider one particular equality operator, which defines the equality set of points equidistant from the origin, = (0, 0). Whichever metric we take, so long as we use it consistently each point in the space belongs to only one such equality set under the given metric. These equality sets form an ordered set of sets of the space.
If all that value involved was assigning relative orderings to bundles of commodities, then it would not matter what metric we used to model commodity money space.
This is shown in figure 9. Both the diamonds and the conventional circles are, in the relevant space, circles: the diamonds are circles in Minkowski or Manhattan space. Each metric defines a collection of concentric circles around the origin. Any combination of commodities we have will fall onto one of these circles, and we can thus order bundles of commodities in terms of value.
FIGURE 9. The ordering of equality sets under possible metrics
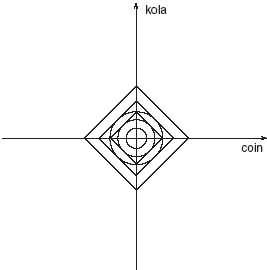
If the elements of a set of commodity-money tuples are mutually exchangeable then they form an equality set under some metric. By examining the observed equality sets of commodity-money tuples we can deduce the properties of the underlying metric space.
The metric of commodity-money space
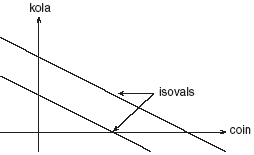
What is the metric of commodity-money space? The observed sets of exchangeable tuples constitute the isovalent contours, or isovals, in commodity-money space. We find, in practice, that they are straight lines -known to economists as budget lines (see figure 10). Note that these extend beyond the axes. Why, we may ask, are they not circles centered on the origin? Commodity-money space clearly has a non-Euclidean, and for what it is worth, a non-Manhattan geometry, but why? Before attempting an answer to this question it will be useful to make some preliminary points.
FIGURE 10. Observed form of the isovals in commodity-money space
We will call commodity-money spaces obeying the observed metric of exchange- value, as displayed in the economist's budget lines, commodity value space, whereas a commodity bundle space obeying a Euclidean metric we will call commodity vector space. (Although our examples have applied to spaces of order two, the argument can be extended to arbitrary hyperspaces.) There is something very particular about the metric of commodity value space, namely d = |aDx + bDy| where a and b are constants. This metric occurs elsewhere -for instance, in energy conservation.
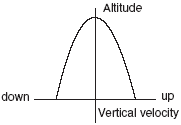
Consider figure 11, the graph of position versus velocity for a body thrown up and then falling. All points on the trajectory are "freely exchangeable" with one another in the course of the time-evolution of the system: an equivalence set.
FIGURE 11. Points in phase space traversed by a projectile thrown upward in a gravitational field
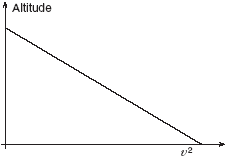
The graph does not look like the equivalence set of commodity value space until we square the velocity axis. This yields the diagram in figure 12, much like the budget line in figure 10. By squaring the velocity axis we obtain a measure proportional to kinetic energy. But kinetic energy is only revealed through its exchange relation with height. Physics posits a one-dimensional "substance", energy, whose conservative exchange between different forms underlies the phenomena.
FIGURE 12. Points in the space of (altitude, velocity squared) traversed by the particle shown in previous figure
Conjugate isovals
Looking more closely at the metric we have deduced for commodity value space, we can see that our representation of the equality sets as budget lines is only half the story.
FIGURE 13. Conjugate pairs of isovals
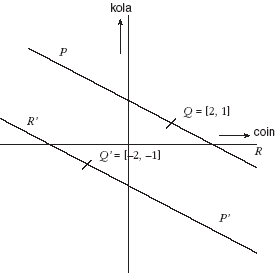
Let a =1 and b = 2 in the metric d = |aDx + bDy|. Taking the point Q = (2, 1) in figure 13, we can show its equality set with respect to the origin as the line PQR along with its extension in either direction. All such points are at distance 4 from the origin. But by the definition of the metric, the point Q' = (-2, -1) is also at distance 4 from the origin. There thus exists a second equality set on the line P'Q'R' on the opposite side of the origin. In general, for a commodity bundle space of order n there will be a conjugate pair of isovals forming parallel hyperplanes of dimension n -1 in commodity vector space.
If the positive isoval corresponds to having positive net wealth, its conjugate corresponds to being in debt to the same amount. There is an obvious echo of this in the practice of double-entry bookkeeping, the effect of which is to ensure that for every credit entry there exists a conjugate debt entry.
Points on an isoval and its conjugate are equidistant from the origin, but not exchangeable with one another. If I have a credit of 1 dollar, I will not readily exchange it for a debt of 1 dollar. Points on an isoval may not be continuously deformed to a point on its conjugate isoval, but may be continuously deformed within the isoval. Thus the isovalent set is topologically disconnected.
Contrast this with what occurs on a Euclidean metric. The points Q = (2, 1) and Q' = (-2, -1) lie on a circle of radius 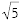 , along which we may uninterruptedly move from one to the other. The disconnected character of the isovalent set in commodity value space becomes understandable once we realize that this space is a projection of a one dimensional space into an n dimensional one. As such, its unit circles comprise disjoint planes corresponding to the two disjoint points of the unit circle in one-space. The property of being multidimensional projections of one-space marks conservative systems.
, along which we may uninterruptedly move from one to the other. The disconnected character of the isovalent set in commodity value space becomes understandable once we realize that this space is a projection of a one dimensional space into an n dimensional one. As such, its unit circles comprise disjoint planes corresponding to the two disjoint points of the unit circle in one-space. The property of being multidimensional projections of one-space marks conservative systems.
Implications for value theory
If value just a matter of providing an ordering combinations of goods, then an Euclidean metric would pass muster. It is some additional property of the sys-tem of commodity production that imposes this specific metric characteristic of a system governed by a conservation law. This fits in rather nicely with the labour theory of value, where social labour would be the embodied substance conserved during exchange relations, which in turn provides us with some justification for casting the law of value in the form of a classical conservation law.
This is a formal argument: the form of the phenomena is consistent with a conservation relation.
WHY COMMODITY-VALUE SPACE IS NON-EUCLIDEAN
Spatial metrics are so much part of our mode of thought that to imagine a different metric is conceptually difficult. Most of us have difficulty imagining the curved space-time described by relativity theory, Euclidean metrics being so ingrained in our minds. Conversely, when looking at commodities, a non-Euclidean metric is so ingrained that we have difficulty imagining a Euclidean commodity space. Try to imagine a Euclidean commodity space: a commodity vector space.
The implicit contradictions of this idea, give a better idea why value takes the metric form that it does.
Is an Euclidean metric for commodity space internally consistent? In commodity bundle space of order 2 the Euclidean isovals take the form of circles centered on the origin, in higher-order spaces, spheres or hyperspheres. (We assume that some linear scaling of the axes converts them into a common set of units.) Let us suppose that the economic meaning of these isovals is that given any pair of points p, q on an isoval, the bundle of commodities represented by p will be equivalently exchangeable with the bundle q.
If the state of an economic agent is described by her position in this commodity bundle space, then the set of permissible moves that can be made via equivalent exchanges is characterized by unitary operators on commodity vector space. The set of equivalent exchanges of p is {|p| u such that |u|=1}, i.e. the radius-preserving rotations of p. Mathematically, this is a consistent system.12 Economically, such a system would break down. It says that I can exchange one unit of kola for one unit of coin, or for any equivalent combination such as
( 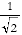 coin,
coin, 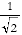 kola). But then what is to stop me carrying out the following procedure?
kola). But then what is to stop me carrying out the following procedure?
- Exchange my initial 1 unit of kola for
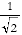 coin plus
coin plus 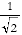 kola.
kola. - Now sell my
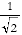 coin for kola, giving me
coin for kola, giving me 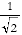 kola.
kola. - Add my two bundles of kola together, to give a total of
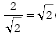 of kola in total.
of kola in total.
I end up with more kola than I had at the start, so this cannot be a set of equivalent exchanges. The second step is illegal within the context of the Euclidean metric, since it involves operating upon one of the coordinates independently. But in the real world, commodities are physically separable, allowing one component of a commodity bundle to be exchanged without reference to others. Physical separability of the commodities makes the observed metric the only consistent one.
A commodity-producing society, in which the individual components of the wealth held by economic agents can be independently traded, selects out of the possible value metrics one consistent with the law of value.
CONSERVATION LAWS AND SYMMETRY
There is an underlying relationship between conservation laws and symmetry. The notion of symmetry is familiar. We know that people with beautiful faces, tend to have symmetrical faces. This means that their face will look the same whether we look at the original or look at it in a mirror. Another type of symmetry is rotational symmetry. A starfish looks the same if we rotate it by 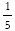 of a circle.
of a circle.
If we chose the right representation, many processes governed by conservation laws posess symmetry. Consider the projectile thrown upwards, and falling freely to earth. We plotted its velocity against its height in figure 11. We then showed that by translating this to a graph of height against velocity squared we got a straight line in figure 12. This illustrated that there was a conserved value, energy, operating in the process. But we could equally well have transformed the graph as shown in figure 14.
FIGURE 14. Points traversed by the particle in space v, 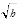
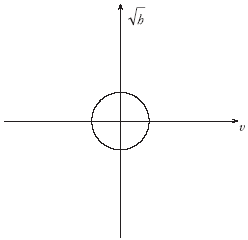
In this case our orbit is a circle in the space (v2, h). It is clear that this has to be the case since the height is proportional to potential energy whereas kinetic energy is proportional to the square of velocity. We have the relation v2 + h = k where k is the conserved energy per unit mass. Since the equation for a circle is of the form x2 + y2 = k for some constant k, then if we set x = v, y = 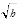 we will get an orbit that lies on a circle in the new space. In this space, the path enforced by the conservation of energy has rotational symmetry. The conservation law reflects itself in the constant radius of the orbit: proportional to the conserved energy.
we will get an orbit that lies on a circle in the new space. In this space, the path enforced by the conservation of energy has rotational symmetry. The conservation law reflects itself in the constant radius of the orbit: proportional to the conserved energy.
We can specify these rotational symmetries in terms of operations which turn things but don’t change their size. This is done by applying a unitary rotation matrix to the co-ordinates of the system.
Rotations
FIGURE 15. Illustration of the effect of rotations by  on the unit vectors
on the unit vectors
x =[1, 0], y = [0, 1].
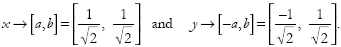
The result is that
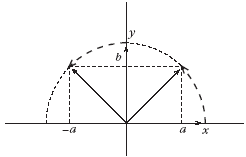
Figure 15 illustrates the effect of rotating unit vectors aligned with the x and y axes by 45°. Any point in the plane P = [x,y] can be treated as the sum of two vectors [x,0] + [0,y] with one aligned with the x axis and the other with the y axis. These in turn are scalar multiples of the unit vectors [1,0], [0,1] aligned the axes. These unit vectors are the basis of the 2D vector space. We can thus decompose P into x[1,0] + y[0,1]. The numbers x, y specify the amplitude of the point P with respect to these basis vectors.
We know what the effect of the rotation of these unit vectors by 45° will be,
namely: 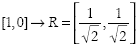 whereas
whereas 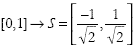 . We can therefore
. We can therefore
achieve the effect of rotating P by first rotating the unit vectors, multiplying them by their original amplitudes in P and summing the result:  . So it follows that a rotation by 45° will map a point
. So it follows that a rotation by 45° will map a point 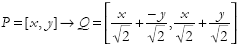 .
.
We can express this as a matrix calculation TP = Q with
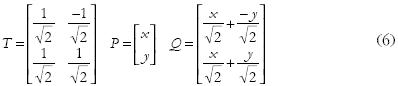
More generally we can express any 2D rotation of a point P in terms of operating on P with an appropriate transformation matrix T. This generalises to 3D points and higher.
Because of its metric, commodity money space is not a vector space and we can not apply rotation matrices directly to it. However it is possible to posit an underlying linear vector space of which commodity space is a representation. This is done by a trick similar to the one we did in figure 14.
COMMODITY AMPLITUDE SPACE
We now develop the an underlying space, commodity amplitude space, which can model commodity exchanges and the formation of debt. Unlike commodity space itself, this space, is a true vector space whose evolution can be modeled by the application of linear operators. The relationship between commodity amplitude space and observed holdings of commodities by agents is analogous to that between amplitudes and observables in quantum theory.
Let us consider a system of n agents and m commodities, and represent the state of this system at an instance in time by a matrix A, where aij represents the amplitude of agent i in commodity j. The actual value of the holding of commodity j by agent i, we denote by hij an element of the holding matrix H. This is related to aij by the equation aij= 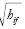 .
.
Commodity sales
TABLE 1. Table of money and commodity holdings by agents
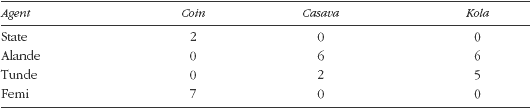
Suppose we start off with table 1 as our holding matrix H. We can generate the matrix A as shown in table 2.
TABLE 2. Table of money and commodity amplitudes of agents following table 1
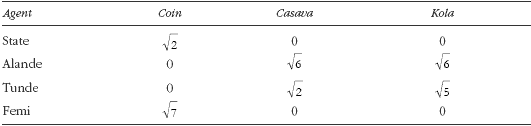
This gives us a matrix pair of the form
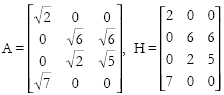
Commodity sales have to respect two conservation laws:
1. The total quantity of a commodity in existence is unchanged by the act of sale.
2. The value of each agents holdings of money plus commodities are unchanged by an act of sale.
After a sale has taken place commodities may appreciate or be consumed so that neither of these constraints holds outside the sale itself. The transfer of 6 kola nuts from Alande to Femi changes the column 3 of the
A matrix as follows shown below:

This implies that the sum of the squares of the amplitudes in the column remain unchanged at 11 before and after, so a transfer is a unitary rotation of one of the amplitude columns.
At the same time we have payment of 3 coins from Femi to Alande which in coin amplitude space is:
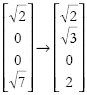
Since the sum of the squares in coin amplitude space remain equal to 9, we also have a unitary rotation in this space.
The transfer and payment operation affects two rows, those refering to the asset holdings of Femi and Alande (rows 2 and 4). Can we represent this as a unitary rotation as well? Since only Alande and Femi's rows are affected and only the kola and money columns are involved, we will simplify the argument by looking at the 2 by 2 sub matrix of these rows and columns. We have the transform

It is clear that the tranformation is not a unitary rotation on the rows of the matrix. The length of the first row is 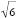 before the sale and
before the sale and 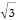 afterwords. But this is because our matrix is in terms of disparate units -kola nuts and coins. To we need to change the original holdings matrix so that instead of being denominated in material units it is denominated in money units. If the price of a kola nut is 1/2 a coin, we must multiply the kola holding column by a half prior to obtain a value matrix V.
afterwords. But this is because our matrix is in terms of disparate units -kola nuts and coins. To we need to change the original holdings matrix so that instead of being denominated in material units it is denominated in money units. If the price of a kola nut is 1/2 a coin, we must multiply the kola holding column by a half prior to obtain a value matrix V.
Let us illustrate this with a new and simpler example. We have two columns, column 1 for money, column 2 for kola nuts.
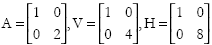
Where agent one has 1d of coin and no kola, and agent two has no coin and 8 kolas worth 4d. We can model the purchase of 2 kolas worth 1d by agent one from agent two by the evolution of A to:

which corresponds to final holdings of:
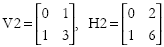
Note that the operation on amplitude space is a length preserving rotation on both the rows and the columns. The lengths of the row zero and column zero in A2 are 1 the lengths of row and column one is 2 just as it was for A. This operation can be effected by the application of an appropriate rotation matrix so that A2 = M.A. A matrix which produces this particular set of rotations is:
Price changes
Price movements are scaling operations modeled by the application of diagonal matrices. Thus a 50% fall in the price of kola in our model would be represented by the application of the matrix 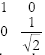 to the current commodity amplitude matrix. Scaling operations are not length preserving.
to the current commodity amplitude matrix. Scaling operations are not length preserving.
Modeling Debt
We have already said that accounts based monetary systems are capable of recording both positive and negative amounts of money. This is required to represent debt. Can we model this in amplitude space?
Suppose that starting from holdings V agent zero buys 2d of kola from agent one. Since agent zero only has 1d in money to pay for it, the transaction leaves the following holdings:
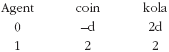
The corresponding amplitude matrix is
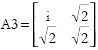
In this 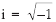 thus it follows that commodity amplitude space is complex valued. It is interesting that this too is the result of applying a unitary rotation operator to the original amplitude vector since the length of row zero
thus it follows that commodity amplitude space is complex valued. It is interesting that this too is the result of applying a unitary rotation operator to the original amplitude vector since the length of row zero 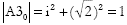 , likewise the lengths of all other rows and columns are preserved. The linear operator required to create debts has itself to be complex valued, thus if A3 = NA we have
, likewise the lengths of all other rows and columns are preserved. The linear operator required to create debts has itself to be complex valued, thus if A3 = NA we have
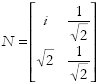
The rule for small loans made by moneylenders who start out with much more money than the person they are lending to is that the loan does not alter the Manhattan separation13 of the agents, i.e., the operation is conservative.
Proof: Manhattan separation only grows when loans are made to richer agents. Let us consider two agents Ajit and Rakesh, and consider only holdings of money and the mutual debts between the agents. Let us describe the initial situation by Ajit = A = [a,b,c], Rakesh = R = [d,e,f], with a, d representing the original cash holdings of the two. Rakesh lends x to Ajit. The situation is now:
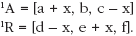
We want to show that dm(A R) = dm ( 1A - 1R) . This translates to
|a - d| + |b -e| + |c -f| = |a -d + 2x| + |b -e -x| + |c -f -x| (1)
Because the terms f and b represent Rakesh and Ajit's debts to themselves we can assume these terms are zero. We can also assume e = -c, since these terms are the credit and debit sides of Rakesh and Ajit's pre-existing mutual debts.
We can thus simplify to:
|a - d|+|c|+|c|=|a - d + 2x| + |c - x|+|c - x| (2)
If we are dealing with a loan rather than a loan repayment then Ajit can not have been a creditor of Rakesh so we have e = c. We also have x > 0 or Rakesh would not be making a loan. From this it follows that |c - x| = |c|+ x. So we still have to prove that:
|a – d| + 2|c|=|a – d + 2x| + 2|c|+ 2x (3)
or that |a - d| - 2x =|a - d + 2x|. Clearly this will be true if d > a + 2x that is to say if Rakesh starts out and finishes out with more cash than Ajit.
This means that the two agents are the same distance apart after the loan as before it.
Symmetry breaking
If we consider the obverse relationship, where an agent with a small amount of cash lends some to an agent with much more cash, we find that the agents move appart in Manhattan space.14 An agent with a small amount of money making a loan to an agent that is much richer is what happens when an individual makes a deposit with a bank. This symmetry breaking is the ability of banks to create credit money.
CONCLUSION
We related the value form to the chartalist theory of money and to formal properties of conservation laws. We view money as essentially a technology of record driven by formal rules that govern permisable state transitions in the monetary economy. We suggest tools used to characterize conservation laws in physics: rotational symmetries in abstract spaces are applicable to analyzing such state transitions. The abstract space proposed, is, like that of quantum mechanics, a complex valued Hilbert space. State transitions arising from exchange relations but not banking can be modeled by unitary operators on this space.
1 Karl Marx, Capital I, London, Lawrence and Wishart, 1970, p. 84. [ Links ]
2 Sture Bolin, State and Currency in the Roman Empire to 300 A.D., Stockholm, 1958. [ Links ]
3 Ian Carradice, and Martin Price, Coinage in the Greek World, London, Seaby, 1988. [ Links ]
4 R. Wray, "The Credit Money and State Money Approaches", in Credit and State Theories of Money: The Contributions of A. Mitchell Innes, Cheltenham, Edward Elgar, 2004, pp. 79-98. [ Links ]
5 G. Ingham, The Nature of Money, London, Polity, 2004. [ Links ]
6 M. Forstater, "Taxation: A Secret of Colonial Capitalist (so-called) Primitive Accumulation", Center for Full Employment and Price Stability, Working Paper No. 25, May 2003. [ Links ]
7 G. F. Knapp, "The State Theory of Money", Clifton, Augustus M. Kelley, 1973 [1924]. [ Links ]
8 A. M. Innes, "What is Money?", Banking Law Journal, May 1913, pp. 377-408. [ Links ]
9 We use the term relation in the strict logical sense of set of tuples defining the extent of logical predicate. The predicate in the case of money has the form x is credited with y: x Juridical Subjects, y
Juridical Subjects, y integers.
integers.
10 M. Polanyi (ed.), Trade and Market in Early Empires. [ Links ]
11 This is also known as a Minkowski metric.
12 A very similar model is used in one of the standard formulations of quantum theory to describe possible state transformations.
13 Note that distances in Manhattan space serve as duals for the norms of vectors in amplitude space .














