Matemáticas y ciencias sociales

 

Indecomposability and Primitivity of Nonnegative Matrices

 

Takao Fujimoto*
Fumiko Ekuni**

 

*University of Kagawa, Japón
takao@ec.kagawa-u.ac.jp

** Shikoku-Gakuin Junior College, Japón
fmkekn@sg-u.ac.jp

 

Recepción de original: 01-03-04
Recepción de artículo corregido: 05-04-04

 

Resumen

El artículo aborda aspectos relativos a la relación entre la “indescomponibilidad” (“conectabilidad”) y la “primitividad” de matrices cuadradas no negativas. El teorema principal es que una matriz no negativa es primitiva si y sólo si su késima potencia es indescomponible para cualquier entero positivo k. Este resultado remite a Frobenius. Se presentan dos aplicaciones: una es el modelo de Leslie sobre dinámica de poblaciones y la otra es el análisis de redes sociales.

Palabras clave: indescomponibilidad, primitividad, matrices no negativas, Frobenius, modelo de Leslie.

 

Abstract

This paper deals with the propositions concerning the relationship between the indecomposability and the primitivity of nonnegative square matrices. The main theorem is that a nonnegative matrix is primitive if and only if its k-th power is indecomposable for any positive integer k. This result dates back to Frobenius. Two applications of the result are given, one is to Leslie model of population dinamycs and the other to social network analysis.

Keywords: indecomposability, primitivity, nonnegative matrices, Frobenius, Leslie model.

 

1. INTRODUCTION

In Leontief models, the concepts of indecomposability and primitivity play an important role with the former meaning the interconnectivity among industries and the latter meaning dynamic stability of given models. In this paper, we restate a proposition due to Frobenius, which has not been presented in the textbooks on linear algebra. We also explain about two applications of this proposition to population dynamics by Leslie and to social networks. In Section 2, we define indecomposability and primitivity of nonnegative matrices, and give our main proposition on a characterization of primitivity in terms of indecomposability. Section 3 is devoted to Leslie model of population dynamics, and Section 4 to the concepts of degree of connection and fragility of social networks. The last Section 5 includes some remarks.

2. INDECOMPOSABILITY AND PRIMITIVITY

We first explain our notation. The symbol Rⁿ means the Euclidean space of dimension n(n>=2), is the nonnegative orthant of Rⁿ, and A is a given n×n nonnegative matrix. Let a_ij be the (i, j)-element of the matrix A, and x_j the j-th entry of the vector . The symbol N stands for the index set . For vector comparison, we use the following inequality signs.

Now we define

Definition 2.1. A nonnegative matrix A is decomposable iff there exist two nonempty subsets I and J of the index set N such , and .1

A nonnegative matrix A is indecomposable iff it is not decomposable. Equivalently, however, we may define the indecomposability as
Definition 2.2. A nonnegative matrix A is indecomposable iff for any two nonempty subsets I and J of the index set N such that , we have

(Ax)_i >(Ay)_i in at least one

for arbitrary two vectors x and y in such that x_i = y_i for and x_j >y_j for .

Definition 2.3. A nonnegative matrix A is primitive when there exists a positive integer k such that A^k >> 0 . Otherwise it is imprimitive.2

It is well known that a nonnegative matrix which is indecomposable and has at least one positive diagonal element is primitive. This is obvious from another well-known characterization of indecomposable imprimitive matrices explained, e.g., in Nikaido (1963, Theorem 8.2, p. 117) or Nikaido (1970, Theorem 21.1, p. 142).3 This proposition dates back to G. Frobenius.4 A direct and combinatorial proof is given in a forthcoming book by Krause, even in a nonlinear setting.5 In this paper, a direct and simple proof is presented, which can be used also in nonlinear generalizations.

Let us consider the following 2×2 matrix A

.

This is indecomposable. When we make the second power of A,

,

which is decomposable. Thus, we need an additional condition to guarantee the indecomposability of the power of an indecomposable matrix.

We first state a lemma.

Lemma 2.1. If A is indecomposable and has at least one positive diagonal element, then A^k is also indecomposable for any integer k > 0.

Proof. We prove this lemma using mathematical induction. First for k = 1, the proposition is obvious. We assume this lemma holds for (k – 1) with k>= 2 . Let us also assume without losing generality that a₁₁ > 0.

Suppose to the contrary that A^k be decomposable and we have two nonempty subsets I and J of the index set N such that , and for and . Here, means the (i, j)-element of the matrix A^k. Among possible bipartitions between I and J, we adopt as I the one with the minimum number of rows. When 1 is in the index set I, we split A^k as A · A^k-1 . Since a₁₁>0,
a_ij^k-1=0 for . Now because of the supposition of mathematical induction, there should be at least one positive entry among a_ij^k-1 for and , say for some when , where because for . We will consider the index set (I – H) and . (The index subset H is assumed to be maximal in the sense that for any pair (i, j) such that for and .) It is clear that a_ih = 0 for any pair (i, h) such that and : otherwise we would have a_ij ^(k) > 0 for that and some since
A^k = A · A^k-1, thus yielding a contradiction. Then, from another relationship that A^k = A^k-1 · A, we have a_ih^(k) = 0 for any pair (i, h) such that for and . This implies that we have two nonempty subsets and of the index set N such that and a_ij ^(k) = 0 for and , a contradiction to the supposed minimality of the index set I. Hence, A^k is shown to be indecomposable when .

When , we first split A^k as A^k-1 · A, and in the second stage as A · A^k-1, looking for positive entries column-wise rather than row-wise. The above proof can proceed mutatis mutandis. QED.

Now we prove our main proposition.

Proposition 2.2. A given nonnegative matrix A is primitive if and only if A^k is indecomposable for any positive integer k.

Proof. First, let us prove the ‘only if’ part. Suppose that there is a positive integer p such that A^p becomes decomposable. Then we can find a vector x with at least one zero element such that for any positive integer q, A^pq·x keeps zero elements in the same positions. This is a contradiction to the fact that A^k >> 0 for some integer k > 0, and so A^r >> 0 for any integer r > k.

Now we proceed to the ‘if’ part. Let us adopt the absolute sum norm 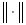in the n-dimensional Euclidean space Rⁿ, and we consider the subset . All we have to show is that starting from an arbitrary point x on the boundary of S, bd(S), a sequence of vectors , comes into the interior of S, int(S). Suppose to the contrary that this sequence remains on the boundary for ever, starting from a certain vector x. Indecomposability by Definition 2.2 requires that in the vector series X, there can be no two points on the same sub-simplex facet of the boundary bd(S). Otherwise x and A^kx for some integer k > 0, has the same sign pattern, contradicting the assumed indecomposability of A^k. There are, however, only a finite number of facets on bd(S). Hence, the vector sequence X has to enter the interior of S. QED.

Corollary 2.3. If a given indecomposable matrix has its trace positive, then it is primitive.

Proof. It is obvious from Lemma 2.1 and Proposition 2.2. QED.

 

3. LESLIE MODEL OF POPULATION DYNAMICS

3.1. Leslie Model

We are ready to apply our results in the previous section to Leslie’s model of population dynamics, which is a discrete version of Lotka’s model.6 This model consists of n age groups and it is represented by a nonnegative n×n(n>=2) matrix A, which shows the survival ratios of age groups after one period, let us say an ‘year’, and reproduction ratios (or birth rates) for some age groups. (We assume away the differences between males and females.) More specifically, the matrix A is written as

The entry a_k,k+1>0 means the survival ratio from the age group (k + 1) to that of k, while if a_n,k> 0 , then this implies the age group k is reproductive. The dynamics of population is described by the following difference equation:

,

where is the vector of population distribution among age groups at period t.

We make

Assumption 3.1. In the bottom row of A, there are at least two positive entries, i.e., a_n,k > 0 and with , and a_i,i+1> 0 for all i such that 1 <=i <= (n-1) .

We assume in addition that a_n,k> 0 is the left-most entry in the bottom row of A. It is clear that the matrix A above is decomposable if 1 < k, and yet when we consider the submatrix A_y of the younger groups including all the reproductive ones, i.e.,

this is indecomposable. This means that if there are at least two age groups which are reproductive, the matrix A_y is primitive. To prove this, consider

that is, the elements a_n,j in A_y are set to zero for j such that (k+1) <= j <= (n-1). It is well known that the matrix A_y0 is indecomposable, and its power A_y0^p is also indecomposable except when p is a multiple of (n - k + 1) . Now suppose with in A_y. Then, the
-th power of A_y, , is indecomposable because , and there is a positive entry on the diagonal at the -position. Thus, by Corollary 2.3, is primitive, and accordingly A_y is shown to be primitive. The older age groups have no influence on the population of the younger groups. Primitivity implies strong ergodicity, hence we have

Proposition 3.1. When Assumption 3.1 is satisfied, converges to a unique stable distribution x*. (The symbol means the absolute sum norm.)7

It is important to note that this proposition holds good even when the model is generalized to a nonlinear case. That is, the survival ratios and reproduction rates can depend on the distribution vector x itself. Moreover, these ratios can change through time, thus covering the Coale-Lopez theorem.8

3.2. A Numerical Example

In this subsection, we raise a numerical example of Leslie model. Let there be six age groups in our society, and the survival-birth ratio matrix is given as follows:

With this matrix, we have

 

In fact, among eigenvalues of A, there exists a unique positive eigenvalue, , called the Frobenius root of A, with which a strictly positive eigenvector is associated:

= 1.05, and its eigenvector x= (0.04 0.24 0.35 0.39 0.42 0.74)’.

Starting from an arbitrary initial vector of distribution, the relative age distribution gets near the above eigenvector, and the rate of growth approaches to 5% because in the limit the population dynamics is described by the equation,

, where c is a certain positive scalar.

4. CONNECTIVITY AND FRAGILITY OF SOCIAL NETWORKS9

4.1. A Long-Run Degree of Friendship Connection

We proceed to the second application of our results in Section 2. The topic is the degrees of connection and fragility of social networks. In the standard literature of social network analysis (SNA), a degree of connection is normally defined using the adjacency matrix of a social network.10 Although indirect connections or chains among members are taken into consideration in the works so far made, the adjacency matrix or binary relationships are left static, and a measure is constructed supposing these basic structures remain unchanged.

In reality, however, an indirect connection today often turns into a direct one tomorrow. We may think of a network of friendship among members. Thus, degrees proposed in the literature have to undergo quick revisions as time goes on. Here in this section, we go to the other extreme, and define a degree of connection as if all sorts of efforts have been done to make indirect connections direct: a friend of my friend today is my direct friend tomorrow. This supposition is not so awkward when we consider particularly ‘affectionate’, ‘benign’, or ‘cheerful’ relationships among the members of a network. In this context, we can also propose an ‘efficient’ way to raise the degree of connection of a network, and a new concept, ‘degree of fragility’.

Let us consider a human network consisting of n persons. Each person may be called a member or a node. First, we take up a normal n×n adjacency matrix A, in which each entry is either unity or zero. When the (i, j) entry is unity, member i likes member j, while in the case of zero, member i has no particular feeling toward member j. We do not assume the reciprocity or the reflexivity in this relationship, though it seems quite natural to observe mutual affectionate feeling in this sort of relationship when we consider a network consisting of self-conscious people. What we assume away is a psychological phase of a ‘stalker’ where love and hatred are two sides of a thin paranoiac sheaf of feeling. In other words, what we deal with is a very simple feeling of liking or love toward another member, and an important assumption we make is that when member i likes member j, who in turn likes member k, then after a short while member i starts to like member k. And in this section, the intensity of feeling is not discussed: either one likes someone else or not, one or zero relationships. As mentioned above, reciprocity is not required. The reader can, however, include it when it is desirable to do so.

Let us define our concept of degree of connection, given a usual adjacent matrix, A. To make our story simple, we assume

Assumption 4.1. All the diagonal elements of A are unity.

That is, every member likes himself/herself. Note that this assumption is mathematically an extreme opposite to the Leslie model where all the diagonal elements can be zero. Let us define the ad-square (or adjacency square), A⁽²⁾, of matrix A. In plain words, the (i, j) element of A⁽²⁾ is unity when its corresponding element of the ordinary square A² is positive, and otherwise 0. In a recursive way we can define A^(k), i.e., A to the ad-power of k. Formally,

Here a_ij^(k) is the (i, j) entry of A^(k), and a_ij^(k-1) is the (i,j) entry of A^(k-1). Since the number of positive entries monotonically increases with a higher ad-power by Assumption 4.1, certainly there exists the limit

We propose

Definition 4.1. The F-degree(or friendship-degree) of connection of a given nxn adjacency matrix A is the ratio of positive entries in off-diagonal elements of against n(n –1) possible one-way relationships.

This may seem artificial. The identity matrix, however, gives degree 0. It is not difficult to compute F-degrees once the adjacency matrix is available. It is well known that by a suitable renumbering of members, any nonnegative matrix is divided into the indecomposable submatrices, each of which is aligned along the diagonal of the original n×n matrix.

Each A_i, i = 1 to s, is indecomposable, and its size is m_i. The index set (members in the subnetwork A_i) for A_i, i = 1 to s, is written as I_i, i = 1 to s.

Our Corollary 2.3 tells us that any indecomposable nonnegative matrix with al least one positive entry on its diagonal is primitive and some power of this matrix becomes strictly positive. Thus, in the limit, those indecomposable submatrices are all positive while the remaining entries are filled with zero if we in addition assume that the submatrices represented by * in the above adjacency matrix A are all zero matrix, i.e., the friendship feeling is reciprocal. Our Fdegree of connection, F, in a social network is thus computed as

(when n is large)

In general, when the submatrices represented by * include non-zero entries, the F-degree falls in the region

When n is large, these bounds can be approximated as

In a completely isolated society in which the adjacency matrix is represented by the n×n identity matrix, our degree gives 0, as noted above. Being different from the degrees previously proposed, our F-degree gives 1, a perfect connection, for the following adjacency matrix A4.

This matrix, when multiplied by itself for three times, becomes strictly positive. Likewise, if a given adjacency matrix is given as A8 below, our
F-degree is again 1 while traditional degrees may give a low magnitude because there are many zeros in the matrix. This matrix turns to be

strictly positive after multiplication of itself 7 times: A⁷ > 0. Note that this A is not symmetric.

The reader may have observed that a perfect degree is to be obtained when a series of direct ‘friendships’ are started among couples of members, each of which consists of members from the subnetworks A_i and A_i+1. (It is understood that A_s+1 stands for A₁.) Thus, in order to realize perfect degree of connection in a network, it is necessary to create only one friendship between so far isolated subnetworks arranged in a serial way. Though our degree is special and limited, this efficient way to enhance mutual connection may be telling us something useful. In terms of mathematics, the condition is

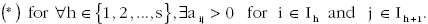
The above 8 8 × example of A8 is constructed so that it satisfies this condition.

It is not difficult to prove this by the method of ad absurdum. Suppose to the contrary, that is, the network adjacency matrix is not primitive even if the above condition is satisfied. Then, the matrix must be decomposable because we have positive entries all along the diagonal. We now have two index sets I and J such that

.

These two sets I and J cannot divide each subnetwork because each subnetwork is known to be indecomposable. Thus, each subnetwork either belongs to I or to J. Then, there exists at least one pair of subnetworks, A_i and A_i+1, such that

This, however, contradicts the condition (*) stated above.

4.2. Fragility of Social Networks

Our fragility of social networks is the Marshallian elasticity of the F-degree of connection with respect to the size of a network. In more detail, when the number of members decreases by 1 percent (%), we calculate the maximum percent decrease of our F-degree of connection, which is our definition of fragility of social networks. When 1% means a fractional number, e.g., 9.7 persons, we may take the arithmetic average of the two cases: the decrease of 9 and that of 10 members. On the other hand, when the withdrawal of 1 member means x% decrease, we divide the percent decrease of F-degree by x. Thus, in the above example of the adjacency matrix A8, the withdrawal of the first member decreases

the F-degree from 1 to , while the membership diminishes by 1/8, making

the fragility .

When the adjacency matrix is the identity matrix, i.e., a completely isolated society, the withdrawal of an arbitrary number of members, so long as it is fewer than the total, does not affect the F-degree, and leaves it always 0. Hence, the fragility is also 0, and this makes sense.

5. CONCLUDING REMARKS

It should be emphasized once more that the Leslie model can be generalized in two directions: one is that both the reproduction (or birth) and the survival ratios can depend upon the population distribution, and the other is those ratios change with time. The former is a nonlinear generalization, and the latter an extension to the inhomogeneous case. In more detail, to make a nonlinear extension, one simple way is to consider the elements, a_ij(X), of a given matrix are functions of the distribution itself:

In order to make the transformation Ax ray-preserving, we assume a_ij(x)’s are all homogeneous of degree 0.

The inhomogeneous case comes out when a_ij(x, t)’s are functions of time or period as well as distribution. Weak ergodicity remains to be valid under some conditions, thus starting from two different initial distributions, two dynamic paths get nearer to each other as time goes on, though they may not converge to a ray and continue to fluctuate or even run chaotic.

It is clear from our mathematical arguments in Section 2 that we do not need in Section 4 the Assumption 4.1 that every member likes himself/herself. All we need is at least one person in each indecomposable subnetwork likes himself/ herself. The center of networks can also be defined in our own way. The reader is referred to our paper in the footnote 9.

Hatred can hardly be treated by our method. This feeling is often hidden and unidirectional. Hatred is not a quick transitive relationship: it is not easily made a direct relation from member i to k when member i hates member j and member j hates member k. Member i may even like member k because the latter is hated by member j.

Acknowledgments: The authors are grateful to the referees for suggestions to improve this paper. Thanks are also due to Professor Alejandro Valle Baeza who introduced this journal to the authors.

 

1 An interesting history of terminology about ‘indecomposability’ is given in A. Brauer, “On the Theorems of Perron and Frobenius on Nonnegative Matrices”, in Solomon G. Szego et al. (eds.), Studies in Mathematical Analysis and Related Topics, Stanford, Stanford University Press, 1962, pp. 48-55.         [ Links ]

2 T. Fujimoto and U. Krause, “Strong Ergodicity for Strictly Increasing Nonlinear Operators”, Linear Algebra and Its Applications, vol. 71, 1985, pp. 101-112.         [ Links ]

3 H. Nikaido, Convex Structures and Economic Theory, Nueva York, Academic Press, 1968;         [ Links ] H. Nikaido, Introduction to Sets and Mappings in Modern Economics, Nueva York, Academic Press, 1970. (The original Japanese edition in 1960.)         [ Links ]

4 G. Frobenius, “Über Matrizen aus nicht-negativen Elementen”, Sitzungsberichte der Kgl. Preussischen Akademie der Wissenschaften zu Berlin, 1912, pp. 456-477.        [ Links ]

5 U. Krause, Positive Discrete Dynamical Systems: Theory, Models, and Applications (to appear in 2004).        [ Links ]

6 P. H. Leslie, “On the Use of Matrices in Certain Population Mathematics”, Biometrika, vol. 33, 1945, pp. 183-212;         [ Links ] P. H. Leslie, “Some Further Notes on the Use of Matrices in Population Mathematics”, Biometrika, vol. 35, 1948, pp. 213-245,         [ Links ] and A. J. Lotka, Elements of Physical Biology, Baltimore, Williams and Wilkins, 1925. (Reprinted in 1956: Elements of Mathematical Biology, New York, Dover Publications.         [ Links ]) See also J. H. Pollard, Mathematical Models for the Growth of Human Populations, Cambridge, Cambridge University Press, 1973.        [ Links ]

7 See for similar theorems E. Seneta, Non-negative Matrices and Markov Chains, 2nd ed., Springerverlag, 1981.         [ Links ] T. Fujimoto and U. Krause, “Strong Ergodicity for Strictly Increasing Nonlinear Operators”, Linear Algebra and Its Applications, vol. 71, 1985, pp. 101-112.         [ Links ]

8 T. Fujimoto and U. Krause, 1985, in footnote 7. See also T. Fujimoto and U. Krause, “Asymptotic Properties for Inhomogeneous Iterations of Nonlinear Operators”, SIAM Journal on Mathematical Analysis, vol.19, 1988, pp. 841-853,         [ Links ] and J. H. Pollard, 1973, in footnote 6.

9 A portion of this section comes from F. Ekuni and T. Fujimoto, “Degrees of Connection in Social Networks: A Long-Run Analysis of Friendship”, Treatises (Shikoku-Gakuin), vol. 113, 2004, pp. 59-66.         [ Links ]

10 J. P. Scott, Social Network Analysis: A Handbook, 2nd ed., Sage Publications, 2000 (the 1st ed. in 1991);         [ Links ] S. Wasserman and K. Faust, Social Network Analysis: Methods and Applications, Cambridge, Cambridge University Press, 1994,         [ Links ] and R. Hanneman, Introduction to Social Network Methods, 2001, online text at http://www.analytictech.com/networks.pdf or http://faculty.ucr.edu/~hanneman/SOC157/TEXT/Textindex.html.        [ Links ]