1. Introducción
En otro lugar hemos propuesto una unión del sistema Term Functor Logic (Sommers, 1967, 1982; Sommers y Englebretsen, 2000; Englebretsen, 1987, 1996; Englebretsen y Sayward, 2011) con la silogística intermedia (Peterson, 1979; Thompson, 1982). Dicha unión estaba motivada porque si bien el sistema Term Functor Logic (TFL) ofrece una aproximación algebraica para la silogística, desafortunadamente, no modela casos de razonamiento en lenguaje natural con cuantificadores no clásicos como “muchos”, “la mayoría”, o “pocos”; mientras que, por otro lado, la silogística intermedia extiende el alcance de la silogística mediante la adición de cuantificadores no clásicos pero carece de un tratamiento algebraico. De la unión de estos sistemas resultó la Intermediate Term Functor Logic (TFL+), un sistema capaz de modelar inferencia silogística con las ventajas de un enfoque algebraico (i.e., la reducción de conjunto de reglas complejas a un sistema simple, formal y unificado) y las ventajas de una teoría silogística con cuantificadores no clásicos (i.e., la evaluación de una amplia gama de patrones inferenciales en lenguaje natural que extiende las capacidades de la silogística apodíctica tradicional) (Castro-Manzano, 2019). Adicionalmente, en otro lugar hemos propuesto un método analítico de árboles para el sistema TFL. Este método de árboles estaba motivado porque no existía un sistema de árboles para TFL capaz de preservar la riqueza expresiva y el poder inferencial del álgebra de Sommers y Englebretsen (cfr. D’Agostino et al, 1999; Sommers y Englebretsen, 2000, pp. 183 y ss.; Priest, 2008). Esta propuesta resultó en un método de prueba que reduce el número de reglas de inferencia y preserva las capacidades expresivas e inferenciales de TFL para la silogística básica, la silogística relacional y la lógica proposicional (Castro-Manzano, 2018).
Dados estos resultados previos, en este trabajo proponemos, a modo de síntesis, un método de árboles para la silogística intermedia usando las nociones del álgebra de TFL; en otras palabras, presentamos un método analítico de árboles para el sistema TFL+. El resultado es un método de árboles capaz modelar inferencia en silogística básica, relacional y, por supuesto, silogística intermedia. Para alcanzar este resultado procedemos de la siguiente manera. Primero presentamos de manera breve los sistemas lógicos previamente mencionados (con 212 J. Martín Castro-Manzano especial énfasis en la silogística), posteriormente introducimos nuestra contribución y, al final, mencionamos algunos posibles usos de este método.
2. Silogística, TFL, silogística intermedia y TFL+
2.1 Aspectos generales de la silogística
La silogística es una lógica de términos que tiene sus orígenes en los Primeros Analíticos de Aristóteles y que estudia la relación de inferencia entre proposiciones categóricas. Una proposición categórica es una proposición compuesta por dos términos, una cantidad y una cualidad. El sujeto y el predicado de una proposición se llaman términos: el término-esquema S denota el término sujeto de la proposición y el término-esquema P denota el predicado. La cantidad puede ser universal (Todo) o particular (Algún) y la cualidad puede ser afirmativa (es) o negativa (no es). Estas proposiciones categóricas se denotan mediante una etiqueta (a (para la universal afirmativa, SaP), e (para la universal negativa, SeP), i (para la particular afirmativa, SiP), y o (para la particular negativa, SoP)) que nos permite determinar una secuencia de tres proposiciones categóricas que se conoce como modo. Un silogismo categórico, entonces, es un modo ordenado de tal manera que dos proposiciones fungen como premisas y la última como conclusión. Al interior de las premisas existe un término que ocurre en ambas premisas pero no en la conclusión: este término especial, usualmente denotado con el término-esquema M, funciona como un enlace entre los términos restantes y es conocido como término medio. De acuerdo con la posición del término medio se pueden definir cuatro arreglos o figuras que codifican los modos o patrones silogísticos válidos (Cuadro 1 1).
2.2 Term Functor Logic
Para estudiar la relación de inferencia es costumbre hacer uso de lenguajes de primer orden. Ası́, por ejemplo, la lógica proposicional, la lógica de primer orden y la lógica de primer orden con identidad son sistemas lógicos definidos mediante lenguajes de primer orden: {p, q, r, ..., ¬, ⇒}, {a, b, c, ..., x, y, z, ..., f, g, h, ..., A, B, C, ..., ¬, ⇒, ∀, ∃} y {a, b, c, ..., x, y, z, ..., f, g, h, ..., A, B, C, ..., ¬, ⇒, ∀, ∃, =}, respectivamente. El origen de esta costumbre está relacionado con las ventajas de orden representativo que los lenguajes de primer orden ofrecen frente a sistemas más tradicionales. Russell (1937), por ejemplo, popularizó la idea de que las limitaciones del programa lógico tradicional, i.e. silogı́stico, se debían al análisis de las proposiciones en clave terminista como triadas de términos sujeto y predicado unidos por una cópula. Carnap (1930) generalizó esta consideración a toda la lógica tradicional al sostener que la única sintaxis disponible en este tipo de lógica es predicativa.
Ciertamente, la sintaxis de términos ternaria (sujeto-cópula-predicado) de la silogística tradicional es limitada y sus restricciones generan dificultades para representar proposiciones singulares, relacionales o compuestas (cfr. Geach, 1980, p. 64 y 1962, p. 54). Sin embargo, desde finales de la década de los 60’s, Fred Sommers defendió una revisión y una revitalización de la sintaxis ternaria, a la luz de lo que llamamos “el reto de Bar-Hillel”,2 mostrando que ninguna de estas limitaciones es de tipo knock-out. Como resultado de esta revisión, el proyecto filosófico de Sommers se diversificó en tres grandes líneas de investigación en ontología, semántica y lógica (cfr. Sommers, 2005) que se sistematizaron, respectivamente, en una teoría de categorías, una teoría de la verdad y un sistema lógico que hoy conocemos como Term Functor Logic (Sommers, 1967; Sommers, 1982; Sommers y Englebretsen, 2000; Englebretsen, 1987; Englebretsen, 1996; Englebretsen y Sayward, 2011).
El sistema Term Functor Logic representa la silogística usando términos en lugar de elementos lingüísticos de primer orden como variables individuales o cuantificadores3. De acuerdo con esta álgebra, las cuatro proposiciones categóricas pueden representarse mediante la siguiente sintaxis:4
•SaP := -S+P = -S-(-P) = -(-P)-S = -(-P)-(+S)
•SeP := -S-P = -S-(+P) = -P-S = -P-(+S)
•SiP := +S+P = +S-(-P) = +P+S = +P-(-S)
•SoP := +S-P = +S-(+P) = +(-P)+S = +(-P)-(-S)
Dada esta representación, TFL ofrece un método de decisión correcto, completo y simple para la silogística: una conclusión se sigue TFL-válidamente de un conjunto de premisas si y sólo si i) la suma de las premisas es algebraicamente igual a la conclusión y ii) el número de conclusiones con cantidad particular (viz., cero o uno) es igual al número de premisas con cantidad particular (cfr. Englebretsen, 1996, p. 167). Así, por ejemplo, si consideramos un silogismo válido, digamos un silogismo tipo aaa-1, podemos ver cómo la aplicación de este método produce la conclusión correcta (Cuadro 2).
Cuadro 2 Un silogismo tipo aaa-1
| Proposición | Representación | |
| 1. | Todos los mamíferos son animales. | -M+A |
| 2. | Todos los perros son mamíferos | -P+M |
|
|
Todos los perros son animales | -P+A |
En el ejemplo anterior podemos ver claramente cómo funciona este método: i) si sumamos las premisas obtenemos la expresión algebraica (−M+A)+(−P+M)=−M+A−P+M=−P+A, de tal modo que la suma de las premisas es algebraicamente igual a la conclusión, y la conclusión es igual a −P+A, en lugar de +A−P, porque ii) el número de conclusiones con cantidad particular (cero en este ejemplo) es igual al número de premisas con cantidad particular (cero en este ejemplo).
Esta aproximación algebraica es capaz de representar y modelar proposiciones relacionales, singulares y compuestas sin perder su motivación principal, a saber, que una inferencia es un proceso que ocurre entre términos. Así, por ejemplo, los siguientes casos ilustran cómo representar y modelar inferencias con proposiciones relacionales (Cuadro 3), singulares5 (Cuadro 4) o compuestas6 (Cuadro 5).
Cuadro 3 Ejemplo con proposiciones relacionales
| Proposición | Representación | |
| 1. | Algunos caballos son más rápidos que algunos perros. | +C1+(+R12+P2) |
| 2. | Los perros son más rápidos que algunos hombres. | -P2+(+R23+H3) |
| 3. | Lo que es más rápido que lo que es más rápido que los hombres, es más rápido que los hombres.7 | -(+R12+(+R23+H3))+(+R13+H3) |
|
|
Algunos caballos son más rápidos que algunos hombres | +C1+(+R13+H3) |
Cuadro 4 Ejemplo con proposiciones singulares
| Proposición | Representación | |
| 1. | Todo hombre es mortal | -M+L |
| 2. | Sócrates es hombre | +s+M |
|
|
Sócrates es mortal | +s+L |
2.3 Silogística intermedia
Peterson (1979) y Thompson (1982) desarrollaron extensiones para la silogística (SYLL+) añadiendo cuantificadores no clásicos como “la mayoría” (para proposiciones mayoritarias), “muchos” (para proposiciones comunes) y “pocos” (para proposiciones predominantes).8 Ası́, la silogı́stica intermedia añade las siguientes proposiciones intermedias: p es la predominante afirmativa (Pocos S no son P), b es la predominante negativa (Pocos S son P), t es la mayoritaria afirmativa (La mayorı́a de S es P), d es la mayoritaria negativa (La mayorı́a de S no es P), k es la común afirmativa (Muchos S son P) y g es la común negativa (Muchos S no son P).
Dadas estas nuevas proposiciones, SYLL+ añade las siguientes suposiciones de distribución: las proposiciones universales distribuyen su término sujeto; las negativas distribuyen su término predicado; y las proposiciones predominantes, mayoritarias y comunes distribuyen su término sujeto si y sólo si dicho término sujeto es el término menor. Con estas suposiciones básicas, decimos que una conclusión se sigue SYLL+- válidamente de un conjunto de premisas si y sólo si:
1. Reglas de distribución.
El término medio está distribuido por lo menos en una premisa.
Todo término distribuido en la conclusión está distribuido en las premisas.
2. Reglas de cualidad.
Existe por lo menos una premisa afirmativa.
Si la conclusión es negativa, por lo menos una premisa es negativa.
Si una premisa es negativa, la conclusión es negativa.
3. Reglas de cantidad.
Si una premisa es predominante, la conclusión no es universal.
Si una premisa es mayoritaria, la conclusión no es universal o predominante.
Si una premisa es común, la conclusión no es universal, predominante o mayoritaria.
Con estos elementos SYLL+ nos permite extender la silogística básica para lidiar con un rango más amplio de inferencias, tanto válidas (Cuadro 6) como inválidas (Cuadro 7). Además, como es de esperarse, la adición de p, t, k, b, d y g incrementa el número de inferencias válidas (Cuadro 8).
Cuadro 6 Un razonamiento válido: att-1
| Proposición | Representación | |
| 1. | Los humanos son mortales. | HaM |
| 2. | La mayoría de griegos son humanos. | GtH |
|
|
La mayoría de griegos son mortales. | GtM |
Cuadro 7 Un razonamiento inválido: tta-1
| Proposición | Representación | |
| 1. | La mayoría de humanos son mortales. | HtM |
| 2. | La mayoría de griegos son humanos. | GtH |
|
|
Los griegos son mortales. | GaM |
Cuadro 8 Extensión de los silogismo válidos en SYLL* (adaptado de (Thompson, 1982))
| Figura 1 | Figura 2 | Figura 3 | Figura 4 | |
| Con “mayoría” | aat att ati ead atd ato |
aed add ado ead etd eto |
ati eto tai dao |
aed eto tai |
| Con “muchos” | aak atk aki akk eag etg eko ekg |
aeg adg ago agg eag etg eko ekg |
aki eko kai gao |
aeg eko kai |
| Con “pocos” | aap app apt apk api eab apb epd epg epo |
aeb abb abd abg abo eab epb epd epg epo |
pai epo bao api |
aeb pai epo |
2.4 Intermediate Term Functor Logic
Hasta este momento es claro que el tratamiento algebraico de TFL provee un método simple y correcto para modelar la inferencia silogística; sin embargo, desafortunadamente, este tratamiento no incluye inferencias con cuantificadores no-clásicos como “la mayorı́a”, “muchos”, o “pocos.” Por otro lado, como hemos visto, aunque la silogı́stica intermedia, SYLL+, ofrece un rango más amplio de inferencias, carece de un procedimiento algebraico. Dado este estado de cosas, en esta sección exponemos brevemente algunos detalles del sistema Intermediate Term Functor Logic (TFL+). Para exponer este sistema proponemos una modificación de la sintaxis de TFL con el fin de representar los cuantificadores adicionales de SYLL+ y posteriormente mostramos el método de decisión de TFL+.
Así pues, para representar las proposiciones intermedias p, t, k, b, d y g dentro del marco de TFL consideremos la sintaxis del Cuadro 9.
Cuadro 9 Sintaxis de TFL+
| Proposición | Representación | Proposición | Representación | |||
| SaP | := | -S0+P0 | SeP | := | -S0-P0 | |
| SpP | := | +S3+P0 | SbP | := | +S3-P0 | |
| StP | := | +S2+P0 | SdP | := | +S2-P0 | |
| SkP | := | +S1P0 | SgP | := | +S1-P0 | |
| SiP | := | +S0+P0 | SoP | := | +S0-P0 |
La razón detrás de esta propuesta sintáctica es simple: de acuerdo con el marco lógico de SYLL+, las proposiciones intermedias p (b), t (d) y k (g) son particulares hasta cierto punto, tal como lo son las proposiciones tipo i (o), lo cual nos obliga a elegir, siguiendo la sintaxis de TFL, una combinación +/+ de términos para las proposiciones afirmativas; y una combinación +/− para las negativas. Sin embargo, esto no es suficiente porque, de acuerdo con SYLL+, las proposiciones p (b), t (d) y k (g) no son convertibles,9 y por tanto, no son equivalentes a proposiciones de tipo i (o), lo cual nos obliga a usar algún tipo de bandera para denotar explícitamente este hecho: nosotros proponemos el uso de superíndices.
Ahora, de acuerdo con SYLL+, los nuevos cuantificadores implican un cierto orden (p (b) implica t (d), t (d) implica k (g) y k (g) implica i (o)) y por ende los superı́ndices se usan no sólo como banderas, sino como niveles ordenados de cuantificación. Esta elección sintáctica tiene las siguientes caracterı́sticas: las proposiciones tipo a, e, i y o tienen nivel 0 para denotar el hecho de que se comportan de manera usual, como si no se hubieran hecho modificaciones; los superı́ndices se añaden a cada término con la finalidad de especificar el detalle de que las proposiciones tipo p, t, k, b, d y g no son convertibles; y además, estos ı́ndices nos permiten inducir un orden (3≥2≥1≥0) que indica que a (e) no entraña p (b), t (d), k (g), i (o); pero p (b), t (d), k (g) sı́ entrañan i (o). 10
Dada esta representación, la modificación del método de decisión es como sigue: una conclusión se sigue válidamente de un conjunto de premisas si y sólo si i) la suma de las premisas es algebraicamente igual a la conclusión, ii) el número de conclusiones con cantidad particular (viz., cero o uno) es igual al número de premisas con cantidad particular, y iii) el nivel de cuantificación de la conclusión es menor o igual que el máximo nivel de cuantificación de las premisas. Para ejemplificar este procedimiento consideremos un par de ejemplos, uno válido (Cuadro 10), uno inválido (Cuadro 11).
Cuadro 10 Un razonamiento válido: att-1
| Proposición | Representación | |
| 1. | Los humanos son mortales. | -H0+M0 |
| 2. | La mayoría de griegos son humanos. | +G2+H0 |
|
|
La mayoría de griegos son mortales. | +G2+M0 |
Cuadro 11 Un razonamiento inválido: tta-1
| Proposición | Representación | |
| 1. | La mayoría de humanos son mortales. | +H2+M0 |
| 2. | La mayoría de griegos son humanos. | +G2+H0 |
|
|
Los griegos son mortales. | -G0+M0 |
Para ilustrar las ventajas de TFL+ frente a TFL y SYLL+ consideremos algunos ejemplos que ilustran el balance entre la complejidad de las reglas de SYLL+ y el poder expresivo de TFL (Cuadros 13, 14, 15, 16). Notemos además que, como es de esperarse, la adición de p, t, k, b, d y g incrementa el número de modos correctos y permite las inferencias válidas del Cuadro 12.11
Cuadro 12 Extensión de los silogismos válidos en TFL+
| Figura 1 | Figura 2 | Figura 3 | Figura 4 | |
| Con “mayoría” | att ati etd eto |
add ado etd eto |
ati eto tai dao |
eto tai |
| Con “muchos” | atk aki akk etg eko ekg |
adg ago agg etg eko ekg |
aki eko kai gao |
eko kai |
| Con “pocos” | app apt apk api epb epd epg epo |
abb abd abg abo epb epd epg epo |
pai epo bao api |
pai epo |
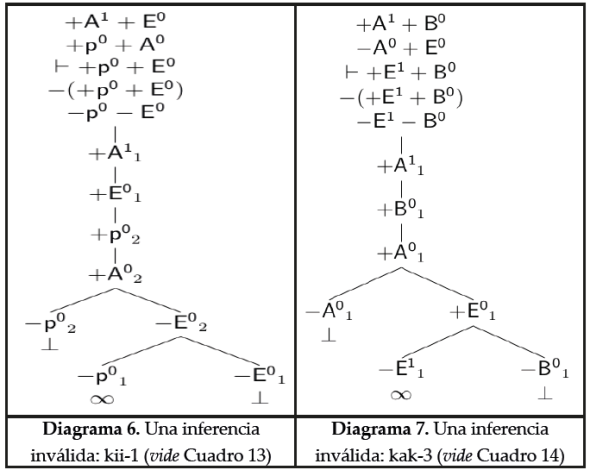
Cuadro 13 Una inferencia inválida: kii-1
| Proposición | Representación | |
| 1. | Muchos ancianos están enfermos. | +A1+E0 |
| 2. | Esta persona es anciana. | +p0+A0 |
|
|
Esta persona está enferma. | +p0+E0 |
Cuadro 14 Una inferencia inválida: kak-3
| Proposición | Representación | |
| 1. | Muchos alemanes son blancos. | +A1+B0 |
| 2. | Todos los alemanes son europeos. | -A0+E0 |
|
|
Muchos europeos son blancos. | +E1+B0 |
Cuadro 15 Una inferencia válida: bao-3
| Proposición | Representación | |
| 1. | Pocos autos son híbridos. | +A3-H0 |
| 2. | Todo auto es caro. | -A0+C0 |
|
|
Algunos autos caros no son híbridos. | +C0-H0 |
Cuadro 16 Una inferencia válida: etg-2
| Proposición | Representación | |
| 1. | Ningún tonto es ciudadano. | -T0-C0 |
| 2. | La mayoría de votantes son ciudadanos. | +V2+C0 |
|
|
Muchos votantes no son tontos. | +V1-T0 |
Así pues, como se puede observar, TFL+ es un sistema que, además de ser confiable, tiene las ventajas algebraicas de TFL y las ventajas expresivas de SYLL+.
Con estos elementos estamos en condiciones para introducir, a modo de síntesis, un método analítico de árboles para TFL+.
3. Árboles para TFL+
Como es usual, y siguiendo a D’Agostino et al (1999; Priest, 2008), decimos que un árbol es un grafo conectado acíclico definido por nodos y vértices. El nodo superior es la raíz. Los nodos inferiores son puntas. Cualquier camino desde la raíz hasta una punta es una rama. Para probar la validez de una inferencia se construye un árbol que comienza con una única rama cuyos nodos son premisas y la negación de la conclusión: esta es la lista inicial. Entonces se aplican las reglas que nos permiten extender la lista inicial:
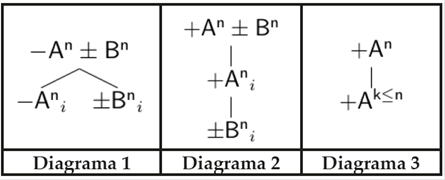
El Diagrama 1 ilustra la regla para las proposiciones de tipo universal; el Diagrama 2, la regla para las proposiciones intermedias; y el Diagrama 3, la regla de ordenamiento para los términos positivos, con n,k ∈{0, 1, 2, 3}. Notemos, además, que después de aplicar una regla introducimos un subíndice i∈{1, 2, 3, ...}. Para las proposiciones universales el subíndice puede ser cualquier número natural; para las proposiciones intermedias, el subíndice tiene que ser un nuevo natural si dichas proposiciones no tienen ya un subíndice asociado. Adicionalmente, y siguiendo los principios de TFL, asumimos las siguientes reglas de negación: −(±A) =∓A, −(±A±B)=∓A∓B y −(−−A−−A)=+(−A)+(−A).
Como es costumbre, decimos que un árbol es completo si y sólo si toda regla que puede ser aplicada ha sido aplicada. Una rama es cerrada si y sólo si hay términos de la forma ±An i y ∓An i en dos de sus nodos; de otro modo es abierta. Una rama cerrada se indica escribiendo ⊥ en su punta; una rama abierta se indica escribiendo ∞. Un árbol es cerrado si y sólo si todas sus ramas son cerradas; de otro modo es abierto. Así, de nuevo como es usual, A es una consecuencia lógica de un conjunto de premisas Γ (i.e., Γ⊢A) si y sólo si existe un árbol completo y cerrado cuya lista inicial incluye a Γ y la negación de A (i.e., Γ∪{−A}⊢⊥).
De acuerdo con esta propuesta, a continuación mostramos que el método funciona probando algunas formas válidas (Diagramas 4 y 5) e inválidas (Diagramas 6 y 7) de TFL+. Adicionalmente, a modo de ejemplo, mostramos algunos casos particulares de silogística básica y relacional. Y por último, ofrecemos algunos elementos para concluir que el método es confiable.
3.2 Ejemplos de silogística básica
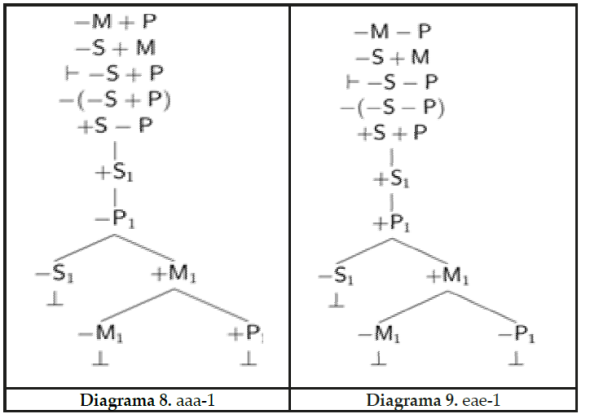
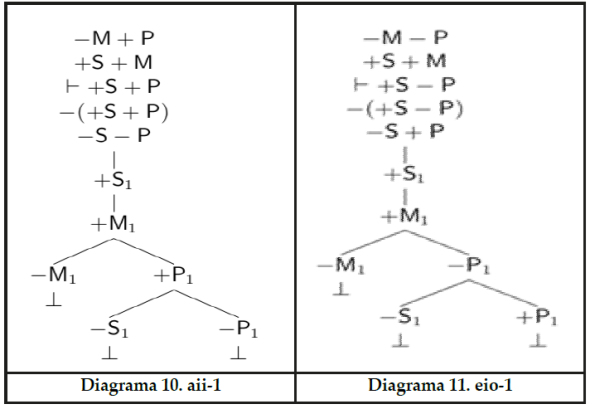
Cuando no usamos superíndices para representar niveles de cuantificación, el método nos permite lidiar con la silogística apodíctica tradicional o básica (Diagramas 8-11).
3.3 Ejemplos de silogística relacional
El método, también, preserva inferencias con proposiciones relacionales. Consideremos, a continuación, el árbol del Diagrama 12 que corresponde al ejemplo del Cuadro 17 (aquí, de nuevo, no necesitamos superíndices para representar niveles de cuantificación).
Cuadro 17 Ejemplo de silogística relacional (adaptado de Englebresten (1996, p. 172))
| Proposición | TFL | |
| 1. | Todo niño ama alguna niña. | -B+(+L+G) |
| 2. | Toda niña adora algún gato. | -G+(+A+C) |
| 3. | Todo gato es sarnoso. | -C+M |
| 4. | Quien adora algo sarnoso es tonto. | -(+A+M)+F |
|
|
Todo niño ama algo tonto | -B+(+L+F) |
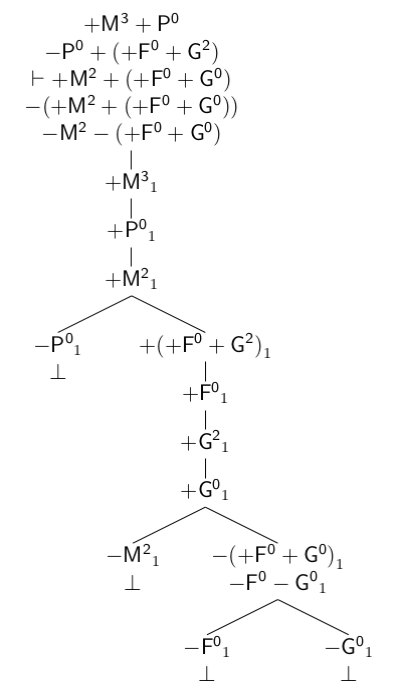
Consideremos, por último, el árbol del Diagrama 13 que corresponde a un silogismo relacional con cuantificadores no clásicos (Cuadro 18).
Cuadro 18 Ejemplo de silogística intermedia relacional
| Proposición | TFL+ | |
| 1. | Pocos mexicanos no son populares. | +M3+P0 |
| 2. | Las personas populares favorecen a muchos gobiernos. | -P0+(+F0+G2) |
|
|
La mayoría de mexicanos favorece a algunos gobiernos. | +M2+(+F0+G0) |
3.4 Confiabilidad
Adicionalmente, podemos comentar que este método de árboles es confiable en la medida en que preserva las inferencias de TFL+, es decir, es confiable en el sentido de que toda inferencia TFL+ válida produce árboles completos y cerrados; y viceversa, toda inferencia que produce un árbol completo y cerrado es una inferencia TFL+ válida.
Proposición 1. Toda inferencia TFL+ válida produce un árbol TFL+ completo y cerrado.
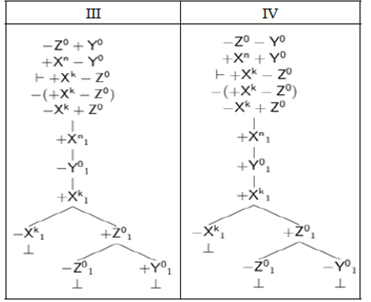
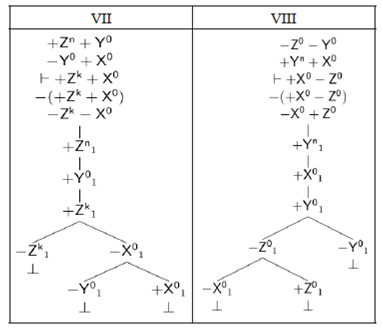
Para probar esta proposición consideremos un esquema general con todas las inferencias TFL+ válidas que aparecen en el Cuadro 12 (Cuadro 20). Al aplicar las reglas de los árboles a las inferencias del Cuadro 20 obtenemos árboles completos y cerrados (Cuadros 21 y 22).
Cuadro 20 Inferencias válidas en TFL+ para 𝑘≤𝑛
| I | II | III | IV | V | VI | VII | VIII | |
| 1. | -Y0+Z0 | -Y0+Z0 | -Z0+Y0 | -Z0-Y0 | -Y0-Z0 | -Y0-Z0 | +Zn+Y0 | -Z0Y0 |
| 2. | +Xn+Y0 | +Xn+Y0 | +Xn-Y0 | +Xn+X0 | +Yn+X0 | +Y0+X0 | -Y0+X0 | +Yn+X0 |
|
|
+Xk+Z0 | +Xk-Z0 | +Xk-Z0 | +X0-Z0 | +X0-Z0 | +Zk+X0 | +Zk+X0 | +X0-Z0 |
Proposición 2. Toda inferencia que produce un árbol TFL+ completo y cerrado es una inferencia TFL+ válida.
Para probar esta proposición supongamos que existe una inferencia que produce un árbol TFL+ completo y cerrado pero que no es una inferencia TFL+ válida. Entonces existe un árbol completo y cerrado cuya lista inicial incluye un conjunto de proposiciones, digamos Γ, y la negación de la conclusión, pero de Γ no podemos construir una prueba de la conclusión usando las condiciones de validez de TFL+, es decir, a partir de Γ, o bien la suma de las premisas no es algebraicamente igual a la conclusión, o el número de conclusiones con cantidad particular no es igual al número de premisas con cantidad particular, o el nivel de cuantificación de la conclusión es mayor que el máximo nivel de cuantificación de las premisas.
Para este caso, considerando únicamente las inferencias TFL+ válidas que aparecen en el Cuadro 12, existen dos formas generales de conclusión a considerar, a saber, +Xk±Z0 y +X0±Z0. Ahora, como el árbol es completo, las reglas para generar dicho árbol deben haber sido aplicadas; y como el árbol es cerrado, cada árbol debe ser de una de las siguientes siguientes formas (Diagramas 14 y 15):
Supongamos, entonces, que tenemos una instancia del árbol del Diagrama 14 pero que su correspondiente inferencia no es válida, es decir, donde Γ+=Γ∪{-Xk∓Z0}, Γ+⊢⊥, pero la aplicación de las condiciones de inferencia de TFL+ a Γ no nos permite producir +Xk±Z0, con k<n. Ahora bien, siguiendo las ramas del árbol del Diagrama 14 observamos que las puntas están cerradas, por lo que en nodos previos el árbol tiene que incluir algo de la forma +Xk y ±Z0, es decir, Γ={…, +Xk, ±Z0, …}. Pero si esto es así, si aplicamos la regla i) (i.e. la suma) a Γ obtenemos algo de la forma +X±Z, y no al revés, por la condición ii) (cantidad de particulares); y por último, por la condición iii) (nivel de cuantificación), la conclusión tiene que ser algo de la forma +Xk±Z0 con k<n. Sin embargo, esto último contradice la suposición de que no podemos construir una prueba de tal conclusión usando las condiciones de inferencia de TFL+. Lo mismo ocurre para el árbol del Diagrama 15 que es un caso particular del Diagrama 14 cuando k=0.
4. Conclusiones
En esta contribución hemos intentado ofrecer un método analítico de árboles para el sistema TFL+. Como consecuencia de esta meta podemos extraer las siguientes observaciones:
El método de árboles que hemos propuesto evita la condición ii) (y iii)) del método de decisión de la silogística básica, relacional (e intermedia), a saber, que el número de premisas particulares debe ser igual al número de conclusiones particulares. Esto posibilita la aplicación general del método para cualquier número de premisas y niveles de cuantificación.
El método preserva el poder de TFL con respecto a inferencias relacionales, transformaciones de voz activa-pasiva, cambios asociativos y simplificaciones poliádicas, lo cual le da a este procedimiento una ventaja competitiva sobre (los árboles de) la lógica clásica de primer orden.
El método preserva el poder de TFL+ para lidiar con inferencias con cuantificadores no clásicos, lo cual le da una ventaja competitiva no sólo sobre (los árboles de) la lógica clásica de primer orden, sino sobre (los árboles de) TFL.
Debido a la peculiar álgebra de TFL, no necesitamos usar reglas de cuantificación ni skolemización, lo cual puede ser útil en relación con la programación lógica y la resolución.
El número de reglas de inferencia se reduce a un conjunto más pequeño, simple y uniforme de reglas que preserva las capacidades de TFL y TFL+ en diferentes contextos inferenciales (silogística básica, silogística relacional, silogística intermedia y lógica proposicional12).
Por todas estas razones, creemos que este método no es sólo novedoso, sino también prometedor, no nada más como otra herramienta didáctica, sino como un dispositivo de investigación:
1. Por ejemplo, el método puede ser útil para estudiar razonamiento modal, probabilista o numérico en la medida en que puede ser usado para representar silogística modal (cfr. Englebretsen, 1988; Thom, 1996; Rini, 1998; Malink, 2006), probabilística (cfr. Thompson, 1986) o numérica (cfr. Murphree, 1998).
2. El método, además, contribuye al estudio del razonamiento visual en tanto que encuentra un lugar natural dentro de un proyecto de razonamiento diagramático (cfr. Englebretsen, 1991; Englebretsen, 1996; Castro-Manzano y Pacheco-Montes, 2018).
3. Como el método puede ser útil para el estudio psicológico de la inferencia puede usarse para aproximar una descripción psicológica más rica del razonamiento en lenguaje natural (cfr. Keil, 2005; Khemlani y Johnson-Laird, 2012).
4. Además, en la medida en que puede utilizarse para adaptar o modificar motores inferenciales para bases de datos aristotélicas (cfr. Mozes, 1989), el método tiene impacto en la programación lógica (cfr. Castro-Manzano, Lozano-Cobos y Reyes-Cárdenas, 2018).
5. Por último, el estudio de este método tiene relevancia para la historia y la filosofía de la lógica en tanto que promueve una revisión de las lógicas de términos (cfr. Veatch, 1970; Sommers, 1982; Englebretsen, 1996; Englebretsen y Sayward, 2011) como herramientas que pueden ser más interesantes y poderosas de lo que originalmente podríamos creer (cfr. Carnap, 1930; Geach, 1962 y 1980).











 nueva página del texto (beta)
nueva página del texto (beta)