Introducción
La interferometría de corrimiento de fase (PSI, por sus siglas en inglés) es una técnica bien establecida para el análisis de franjas en interferometría óptica (Bruning et al., 1974; Malacara, Servin & Malacara, 2005; Rastogi & Hanck, 2015), la cual está caracterizada por su gran precisión y su amplia utilización para la reconstrucción de frentes de onda, medición de elementos ópticos, aplicaciones de deflectometría (Canabal & Alonso, 2002) y, recientemente, en perfilometría mediante proyección de franjas (Gorthi & Rastogi, 2010). La PSI está caracterizada por requerir de una serie de mediciones de intensidad llamados patrones de interferencia, los cuales son corridos en fase con ciertos valores predeterminados. A fin de estimar el mapa de fase que contiene los datos de la medición (área, distancia, temperatura, etc.), diversos esquemas numéricos se han empleado para demodular dichos patrones (Canabal & Alonso, 2002; Gorthi & Rastogi, 2010; Malacara et al., 2005; Rastogi & Hanck, 2015; Schreiber & Bruning, 2007; Servin, Quiroga & Padilla, 2014).
En la literatura se ha propuesto una gran variedad de métodos para la demodulación de patrones de interferencia corridos en fase (phase-shifting algorithm [PSA]) (Bruning et al., 1974; Guo, Zhao & Chen, 2007; Kulkarni & Rastogi, 2017; Morgan, 1982; Schreiber & Bruning, 2007; Servin et al., 2014; Surrel, 1996; Wang & Han, 2004;). En particular, las propuestas realizadas en Bruning et al. (1974), Morgan (1982) y Surrel (1996) confluyen a la estimación de fase mediante un esquema basado en el principio de los mínimos cuadrados. Estos tipos de PSA han sido desarrollados y analizados ampliamente debido a su buena relación señal a ruido y su capacidad de eliminación de armónicos, dos de las figuras de mérito principales para PSA (Servin et al., 2014). Sin embargo, en dichos métodos no se consideró que los corrimientos pudiesen estar desintonizados con respecto del PSA, esto es la tercera figura de mérito llamada detuning error. De hecho, en la práctica, los corrimientos presentan cierto error de calibración debido a problemas vibracionales, turbulencia y otros factores. Servin et al. (2014) y Wang & Han (2004) propusieron un esquema que transforma el problema no-lineal en un problema lineal iterativo por bloques para estimar la fase envuelta y los corrimientos no-uniformes. Recientemente, Kulkarni & Rastogi (2017) abordaron la estimación de la fase como un problema de mínimos cuadrados no lineales empleando el esquema de Levenberg-Marquardt. Los resultados obtenidos son satisfactorios y tiene como principal ventaja que el estimador no lineal obtiene la fase desenvuelta. Sin embargo, los autores omitieron el análisis exhaustivo de los resultados obtenidos con su propuesta.
En el presente artículo, se realiza un estudio numérico exhaustivo entre dos esquemas contemporáneos para la estimación de fase en esquemas de proyección de franjas y PSI empleando patrones sinusoidales. Los algoritmos analizados han sido desarrollados desde la perspectiva de mínimos cuadrados lineales (Wang & Han, 2004) y bajo el enfoque de mínimos cuadrados no-lineales (Kulkarni & Rastogi, 2017). El análisis considera datos sintéticos para estimar el orden de convergencia de ambos métodos, su precisión numérica y la respuesta a corrimientos desintonizados. Esta caracterización de ambos esquemas nos permitirá conocer bajo qué criterios es preferible el método de AIA vs. LM.
En la sección siguiente se introduce el modelo matemático de los patrones de franjas, así como la demodulación de ellos mediante un esquema lineal y no-lineal. En la sección 3, se realiza el análisis comparativo con datos sintéticos. Finalmente, en la sección 4, se describen las conclusiones principales.
Teoría
En PSI el modelo matemático que representa los patrones de interferencia se puede expresar como:
donde I(x,y,k) representa la intensidad capturada en el instante temporal k definido en el rango k∈(1,M), siendo M el total de patrones capturados. La iluminación o intensidad de fondo y el contraste de franjas están determinados por α(x, y) y β(x, y), respectivamente. En el caso de interfeometría, la función ϕ(x, y) contiene la fase introducida por la diferencia de camino óptico, y corresponde a la información de la superficie a recuperar; δ es el corrimiento de fase introducido y, finalmente, η(x, y, k) es ruido blanco aditivo.
Mínimos Cuadrados Lineales
El método iterativo propuesto por Wang & Han (2004) consiste en transformar el problema no-lineal que plantea la ecuación (1) en un problema lineal iterativo por partes. Primero, se estima la función de fase (espacial) y, posteriormente, se determinan los corrimientos de fase (temporal). En este esquema se considera que los desplazamientos θ(x, y) permanecen constantes espacialmente y, por ende, solo representan un cambio de fase en la parte temporal.
Estimación de la fase ϕ. Se considera que la intensidad de fondo y la modulación de la amplitud se mantienen constantes temporalmente, solo varían espacialmente. Con estas consideraciones se tiene la expresión siguiente:
donde
donde
Estimación del corrimiento δ Considerando que los términos a, b de la ecuación (1) solo presentan variaciones temporales y no espaciales. Además, conociendo la estimación de la fase ϕ, se plantea una función de error a minimizar cuya incógnita principal es el factor de corrimiento para cada imagen. Lo anterior queda expresado como:
donde N es la cantidad de pixeles y
El esquema iterativo representado esquemáticamente por las ecuaciones (4) y (6)
genera una sucesión de aproximaciones que convergen a la solución, siendo la
condición de paro
El algoritmo descrito permite estimar el mapa de fase y los corrimientos de forma envuelta (módulo 2π). El mapa de fase desenvuelto se puede obtener mediante una técnica de desenvolvimiento de fase (phase unwrapping) (Ghiglia & Romero, 1994). Al ser un esquema iterativo, se requiere un punto inicial, y en la práctica el número de iteraciones depende de dicha selección. Recientemente, en Ordoñes, Muñoz, de la Fuente & Flores (2016) se desarrolló un esquema para estimar un punto inicial de forma eficiente para reducir drásticamente el número de iteraciones requeridas para que el método converja.
Mínimos Cuadrados No-Lineales
La estimación de los parámetros empleando mínimos cuadrados no-lineales fue propuesta recientemente por Kulkarni & Rastogi (2017), basado en el esquema de Levenberg-Marquardt (Levenberg, 1944; Marquardt, 1963). Por completez en la exposición, se reprodujo el planteamiento del primer artículo citado. Para ello, se considera que en el modelo matemático espacio-temporal de la ecuación (1) no se tienen variaciones temporales en la amplitud y la intensidad de fondo ha sido removida. Con base en dichas suposiciones, el modelo de la ecuación (1) se puede reducir a la expresión siguiente:
donde los parámetros a estimar son la amplitud b, el corrimiento θ y la fase ϕ. Por simplicidad, se omite la notación (x, y), en lo sucesivo. La ecuación anterior es un problema no-lineal que puede ser planteado en el sentido de mínimos cuadrados. Sea p[b, ϕ, θ] el vector de parámetros a estimar en cada pixel de la imagen. Por consiguiente, definimos la función objetivo como la suma de los cuadrados de los errores entre el dato observado y el modelo, es decir:
donde Ik es el dato observado,
donde J representa la matriz Jacobiana, el superíndice indica la transpuesta, Δp es el término de corrección a estimar, y λ es el factor de amortiguamiento. En la ecuación anterior, el término J T J corresponde a la aproximación del Hessiano, y el término I d corresponde a la matriz identidad. La corrección en la estimación se realiza mediante:
donde el superíndice denota la iteración. Al ser un esquema iterativo se requiere de punto inicial p(0) para cada pixel en la imagen. La idea es inicializar el esquema con la solución obtenida en un pixel vecino. Los detalles del esquema de inicialización se muestran en Kulkarni & Rastogi (2017).
El Jacobiano de la ecuación (9) es de dimensión M×3 y queda expresado como:
para la estimación de las derivadas se emplea un esquema de diferencias finitas
de segundo orden con un tamaño de paso
El factor de amortiguamiento λ es la clave en el éxito en el método Levenberg-Marquardt, este se ajusta dinámicamente acorde al valor previo del incremento/decremento de la función objetivo, ecuación (8). Si bien la selección de este factor de amortiguamiento no es óptimo en algún sentido, su dinámica es de tipo heurístico, el cual funciona muy bien en la práctica (Nocedal & Wright, 2006). Aunado a ello, el esquema numérico puede ser considerado como una combinación de un método de segundo orden tipo Newton cerca del punto óptimo y como un esquema de primer orden al inicio de las iteraciones. Esta versatilidad permite a LM ser un esquema predilecto en la estimación de los parámetros. Cabe resaltar que la característica principal del esquema planteado en esta sección radica en recuperar la fase en forma desenvuelta.
Resultados Númericos
Con el fin de comparar la estimación de la fase empleando el esquema no-lineal de Levenberg-Marquardt con el esquema de mínimos cuadrados por bloques de AIA, se realizaron diversas simulaciones numéricas.
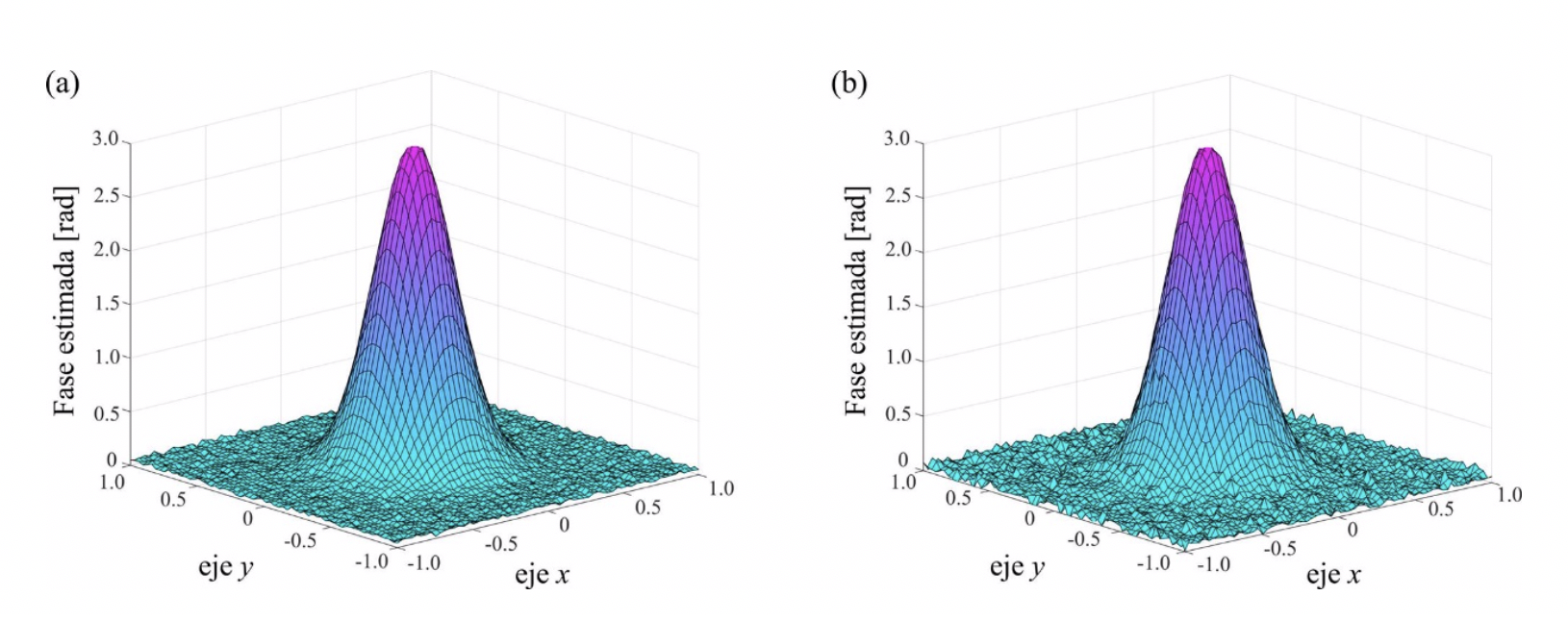
En este primer caso de estudio, se investigó si ambos esquemas convergen a una solución similar. Para ello se considera que la fase a estimar es una función Gaussiana bidimensional, la amplitud de las franjas fue unitaria y se emplearon tres corrimientos de fase uniformes con δ=2π⁄3, (ecuación 1). Los corrimientos iniciales fueron perturbados con un corrimiento del orden 2×10-1 [radianes] para ambos métodos. En la simulación, se agregó ruido aditivo blanco Gaussiano con una desviación estándar de σ=0.015. En la Figura 1 se muestra la fase recuperada empleando ambos esquemas; con el esquema de AIA se observa una menor variación en la zona plana, esto indica una mejor estimación. El error cuadrático medio (rms) obtenido es: (a) rms = 0.0123 y (b) rms = 0.0248, para el esquema de AIA y LM, respectivamente. La mayor diferencia entre ambos métodos radica en la forma de estimar los datos. Para el método de AIA se utilizaron los datos de una imagen n x n para estimar un corrimiento y tres datos para estimar cada pixel de la fase, mientras que con el método de LM se emplean tres observaciones para estimar la fase y el corrimiento. La ventaja del método de LM radica en entregar la fase desenvuelta, pero el costo computacional es 10 veces mayor que el tiempo requerido con AIA.
Fuente: Elaboración propia.
Figura 1 a) Fase estimada con el esquema de AIA, y b) fase estimada con el método de Levenberg-Marquardt.
En este segundo análisis, se estudia numéricamente la atenuación del ruido con respecto al número de patrones empleados. Es decir, se investiga el orden de convergencia de ambos métodos, AIA y LM. Para ello, se simularon patrones de franjas con la función Peaks de Matlab como función de fase. El mapa de fase es de 128×128 pixeles y está definido en el rango (-0.8π,0.8π). La señal portadora es una función rampa en la dirección x tal, que las franjas son abiertas con periodo de 16 pixeles. Ambos algoritmos se evaluaron empleando M=3,4…20 patrones de franjas, con corrimientos equi-espaciados δ=2π⁄M. Se agregó ruido blanco con una desviación estándar de σ=0.020. La desviación del ruido corresponde a 2.55 niveles de gris para una imagen codificada en 8 bits.
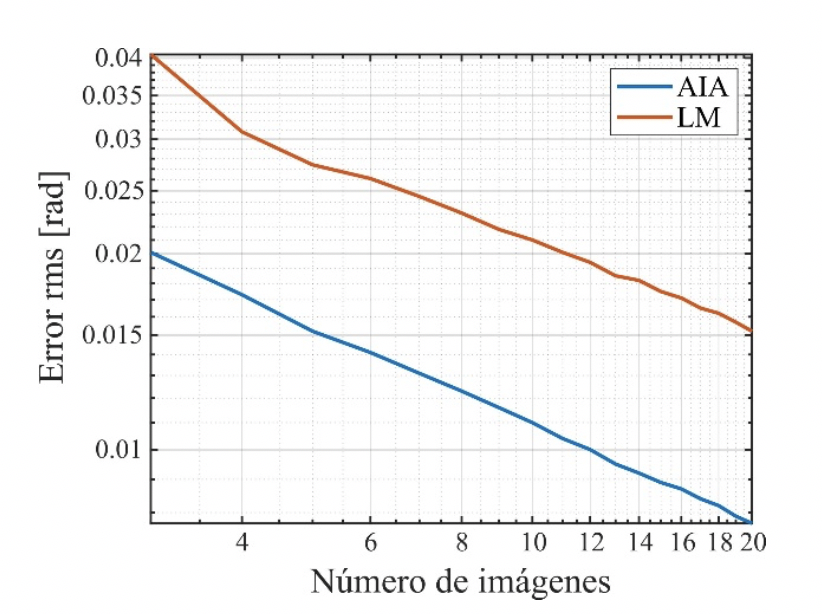
En la Figura 2 se muestra -en escala loglog- el error de la fase estimada para cada esquema numérico. Las gráficas mostradas representan claramente un par de líneas rectas paralelas, lo cual indica que ambos métodos comparten un comportamiento similar. Es decir, conforme el número de imágenes se incrementó, se observa un decrecimiento lineal en el error para el método de AIA y LM. Esto lo podemos expresar en la notación de Landau O(q(1/2)), con q=1⁄k siendo k el número de imágenes. Hasta donde tenemos conocimiento, no se había reportado en la literatura el orden de convergencia para cualquiera de estos esquemas en recuperación de fase.
Fuente: Elaboración propia.
Figura 2 Convergencia lineal O(h1/2), O(q1/2) para el esquema de AIA y LM, respectivamente.
Por los datos mostrados en la Figura 2, se observa que con el método de AIA se obtiene una mejor precisión. De hecho, el error obtenido con AIA es la mitad del error obtenido con el esquema de LM. Fijando un valor de error (rms = 0.0152) con el esquema de LM se requieren 20 patrones de franjas para alcanzar esa precisión, mientras que con el método de AIA solo se requieren cinco.
Como tercer caso de estudio, se considerarán patrones de interferencia con dos
franjas cuya fase de prueba sigue una función cuadrática bidimensional. Esta
distribución de intensidades es típica cuando se emplea un interferómetro tipo
Michelson. En la literatura de algoritmos de corrimiento de fase se ha reportado que
el esquema AIA no obtiene una buena estimación cuando el número de franjas es
pequeño -dos franjas o menos- (Xu, Jin, Chai &
Xu, 2011); por ello, el objetivo de esta simulación es mostrar que este
esquema converge a la solución exacta -en ausencia de ruido- a pesar de que los
datos tengan pocas franjas. Además, se analizó el esquema LM con error de
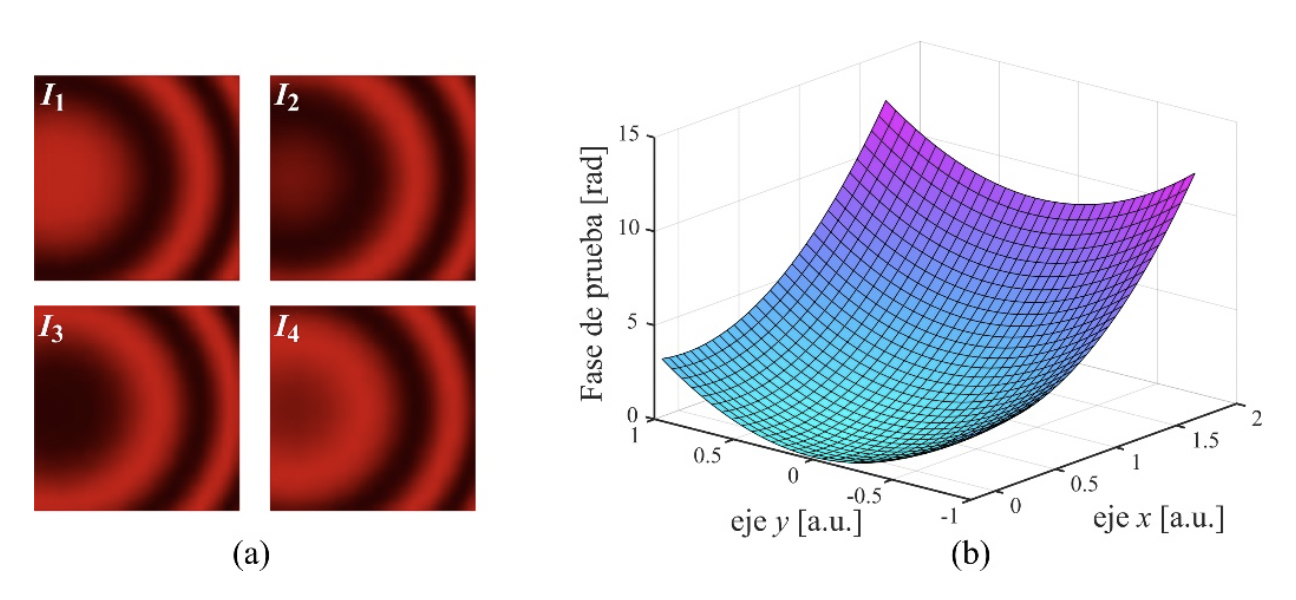
desentonamiento (detuning error) (Servin et al., 2014). La Figura 3 muestra los datos simulados con corrimientos de fase
Fuente: Elaboración propia.
Figura 3 (a) patrones de franjas simulados con corrimientos de fase
En la Figura 4 se muestran los resultados obtenidos de la simulación numérica. En (a) se muestra el perfil del error de fase obtenido por utilizar el esquema AIA. Este error sinusoidal con amplitud de 6×10-7 radianes corresponde con el error típico de desentonamiento, debido a que la oscilación es dos veces mayor que la frecuencia espacial de los patrones de franjas (Figura 4). De aquí, podemos inferir que el esquema AIA no estimó de forma exacta los corrimientos (Ordones et al., 2019). Sin embargo, dicho error del doble de la frecuencia puede ser omitido debido al rango de su amplitud. Por otro lado, en (b), se muestra el perfil de error de fase obtenido con el esquema LM; como en el caso anterior, el error es periódico con una amplitud de 7×10-3, es decir, cuatro órdenes de magnitud mayor que el error obtenido con AIA. Además, el tipo de oscilación del error no corresponde únicamente con el error de desentonamiento, sino que contiene más de una frecuencia espacial. Debido a que el esquema LM consiste en un proceso de optimización no lineal, se debe esperar que el error por desentonamiento sea no lineal. No obstante, la amplitud de este error sinusoidal es también pequeña.
Conclusiones
En el presente trabajo, se realizó una comparación numérica exhaustiva entre dos esquemas contemporáneos para la extracción de la fase en patrones de franjas con corrimientos de fase aleatorios. Los esquemas analizados abordan la estimación desde una perspectiva de mínimos cuadrados lineales y un enfoque no-lineal de Levenberg-Marquardt. El interés surge porque con LM se obtiene la fase desenvuelta y al ser un proceso no-lineal se requiere investigar su precisión numérica para este campo de aplicación. Numéricamente hemos demostrado que ambos métodos convergen linealmente conforme incrementamos el número de patrones de franjas, el orden de convergencia es: O(q1/2), donde q=1⁄k y k representa el número de imágenes. Sin embargo, el método de LM es la mitad de preciso que el esquema de AIA. Desde el punto de vista de desempeño computacional, el método de AIA es 10 veces más rápido que el esquema de LM. Además, hemos mostrado que el método AIA converge a la solución aun cuando los interferogramas tienen muy pocas franjas, el cual es un resultado novedoso. Finalmente, en este trabajo se muestra el tipo de error obtenido por ambos métodos en presencia de errores de calibración en los pasos. El error correspondiente en AIA es del tipo denominado en inglés detuning lineal, que se presenta como el doble de la frecuencia espacial de las franjas del interferograma, mientras que para el esquema de LM se observó una frecuencia secundaria adicional, la cual tiene la misma frecuencia espacial que las franjas del interferograma. El resultado con AIA supera en cuatro órdenes de magnitud lo obtenido con LM.
Considerando los resultados obtenidos, el método de AIA tiene un mejor desempeño en precisión y tiempo de procesamiento que lo obtenido con el esquema de Levenberg-Marquardt.











 nueva página del texto (beta)
nueva página del texto (beta)



