Introduction
The result of the 2016 presidential election in the United States brought about a combination of events that reconfigured many aspects of international life and coexistence. In the context of cooperation, the global economy is facing a new paradigm of neo-protectionism on the part of the country, which, until that moment, had been recognized as the protagonist of world capitalism. But in the present, it has delegated its leadership. In this scenario, the tendency toward the integration of economic and commercial blocks for competition among them has been affected by the new proposal of the United States of signing bilateral agreements, with the premise of America First.
Likewise, the Asia-Pacific region manifests itself as an area of interest because it involves countries such as Japan, China, Australia and the United States, whose economic activities are characterized by their levels of growth, development and their economic and commercial influence. In this context, the proposal of the formation of the TransPacific Partnership (consisting of 12 countries in the region, including the United States) emerged, which was described as an innovative agreement, considering aspects such as intellectual property, free mobility of business persons, democracy, as well as the alternative of arbitration by multilateral organizations in judicial litigation.
However, the United States withdrawal from the Trans-Pacific Partnership has brought about its reconfiguration by the other 11 countries that have decided to remain in it, leading to the Comprehensive and Progressive Agreement for Trans-Pacific Partnership, CPTPP, or TPP-11. This interest in maintaining the agreement motivates researchers and analysts to investigate the effects that it could have in the future for the economies that have signed it, and for those that do not belong to the agreement. Therefore, the objective of this research is to analyse the effect of the integration of the CPTPP on the convergence in technical efficiency of the countries that signed it, along with a forecast for the year 2020.
To achieve this objective, in section two the theoretical foundation is presented in order to obtain the efficiency through a stochastic frontier analysis. In section three, a revision is made of the recently incipient scientific literature about the agreement. In section four, the methodology of Battese & Coelli (1995) is presented to be used and to obtain the technical efficiency, which makes use of econometrics with panel data. In section five, the results obtained about the efficiency of the TPP-11 countries are presented, in which they are identified with cooperation. This can increase and accelerate the convergence among them in terms of a better use of production factors. Finally, the main conclusions obtained from the analysis are presented. So, theoretically, this study is founded in the technical efficiency concept of Farrell (1957)) and its empirical application in the stochastic frontier analysis.
Theoretical foundation
The optimal use of production factors is a fundamental condition for economic growth and development, as well as to elevate the quality of life of society, because the best practices are being done within the economic system. However, empirical studies demonstrate that this does not occur in reality in that there are circumstances that can remove production from its potential path, provoked by inefficiencies in the use of the factors. Because of this, it is important to have measurements for the way in which these factors are being used within the economic system.
In this sense, the theoretical proposal regarding the Farrell (1957) technical efficiency contributes elements for its conceptualization and foundation, which is used for later empirical developments for its measurement, leading to two great slopes. The first is related to lineal programming techniques, known as data envelopment analysis, DEA. The second, identified in the literature as stochastic frontier analysis, SFA, makes use of econometric tools for its implementation.
In this research, an approximation of stochastic frontier production technologies is made in order to theoretically delimit the central elements of the stochastic frontier production functions, which, at the same time, allow to theoretically base an estimate of technical efficiency. Particularly, the input-oriented technical efficiency is analysed, which permits the identification of how much the output can be raised without raising the input.
In the context of the economic science, Greene (1993) defines production as a process of transforming a set of x inputs that belong to a k-dimensional space, in the field of real non-negative numbers, in a set of y outputs that belong to an m-dimensional space, in the field of real non-negative numbers. This production process can be characterized as a set of input requirements in the following way:
This set does not refer to efficiency nor does it define the production function per se, but rather what it does indirectly in the measure is that it defines a set of inputs that is insufficient to produce y (id est), the complement of L(y) and, therefore, defines the limits of the producer’s capacities. The production function is defined by the isoquant
This isoquant defines the frontier of the set of requirements of inputs. So, a more general definition is the efficient subset in the following:
Also, Greene (1993) expresses that Shephard’s (1953) distance function is:
If D I (x,y)≥1 and the isoquant is the set of the x s, for which D I (x,y)=1; therefore, the measurement of technical efficiency oriented to the Debreu (1951)-Farrell (1957) input is
From these definitions, it follows that if TE≤1 and that TE(y,x) = 1/DI(x,y) the Debreu-Farrell measurement contributes a starting point for analysing the efficiency. If this is defined in terms of production, it refers to technical efficiency.
Hence, if y≤f(x), it defines the production function with only one output, so a measurement of technical efficiency based on production of the Debreu-Farrell type is:
which for i companies can be written as:
where TEЄ(0,1], β is a parameter vector, and i refers to the i-esima analyzed firm.
The production model will generally be lineal and in logarithms of the variables, so the empirical counterpart will be in the form
where -u i ≥ 0 is a measurement of technical inefficiency, because:
bearing in mind that TE I = EXP (-ui).
The above constitutes a fundamental theoretical basis for the econometric production models that have technical efficiency in consideration.
Empirically, this refers to Aigner, Lovell & Schmidt (1977) and Meeusen & Van den Broeck (1977), who specify a stochastic frontier function for a cross-section of a data set in which they break down the component of error. One considers the random effects, and the other considers the technical efficiency. The proposed model has the following representation:
where Yi is the production or its logarithm for the i-esima firm;
xi is a vector of size (kx1) for the input quantities of i-esima
firm; β is a parameter vector; the Vi are random variables that are
supposedly independent or identically distributed, i.i.d.,
In 1995, a similar model was proposed, but for a data panel structure, suggested by Battese & Coelli (1995), which is used for the empirical application in this research.
Background
The reconfiguration of the TPP after the withdrawal of the United States from the Transpacific Agreement has caused the 11 remaining countries to decide to maintain it, making the necessary adjustments, among them, clauses for its implementation. Because of the self-exclusion of the United States, the new standard is being adapted in order to consider that this can be put into force 60 days after six of its members sign it, which has always superseded the legislative process within the countries. In accordance with the Gilberto Bosques Center for International Studies (2017), it is hoped that the CPTTP can enter into force by 2019.
There are few studies about the CPTPP, due to the recent transition of the TPP-12 to the CPTTP-11. However, works such as that of Muhammad, Zada & Mukhopadhyay (2018) analyse the economic implications for Pakistan as a non-member country, arguing that the agreement is a threat to countries like Pakistan, because a deviation of commerce in textiles and garments could occur in favor of the CPTTP members, negatively affecting the GDP of this country. Because of this, the alternative is to follow the agreement, whose effects could be beneficial to the economy, because of its geographic and strategic location and its potential to be a transit economy in the confluence of southern Asia, western Asia, and central Asia.
Another work about the CPTPP is that of Ciuriak, Xiao & Dadkhah (2017), who suggest that the CPTPP without the United States could be better for countries in the Americas that participate in the agreement. The results also suggest that eleven parties are better for implementing the CPTPP, leaving aside the controversial elements of governance, whose implications for national interests are not clear.
Methodology
Starting from the theoretical framework proposed by Debreu (1951)-Farrell (1957), with the theoretical-mathematical formulation of Greene’s (1993) stochastic frontier production function, allows the contextualization of the methodology used, which is confined to the slope of the stochastic frontier analysis for estimating the production function and the inefficiency equation, as well as obtaining the technical efficiency, which is oriented to the use of econometrics with panel data, proposed by Battese & Coelli (1995), which permits the simultaneous estimation of the stochastic frontier production function and the inefficiency equation.
For the empirical application of this research, Battese & Coelli’s (1995) model was specifically used, whose stochastic frontier production function for panel data is the following:
The Y i variable represents the output of the i-th firm in time t; x i,t is a vector of the size (1xk) of the inputs and other explanatory variables associated with the signature i in the moment t. β is a parameter vector.
In this structure, the V
i,t
are random variables that are supposedly independent or identically
distributed, i.i.d. with a normal distribution
Following Battese & Coelli (1995), equation 1) specifies the stochastic frontier production function in function of the original production values. However, the effects of inefficiency, the U i,t , supposedly are a function of the set of explanatory variables, the zi,t, and a vector coefficient, δ. The explanatory variables in the inefficiency model can include some input variables in the stochastic frontier, always providing the inefficiency effects are stochastic. In this application, a globalization variable is included as a proxy of cooperation among countries.
The effects of technical inefficiency, the U i,t in the stochastic frontier model of model 1), are specified as:
where the random variable
For the simultaneous estimation of the stochastic frontier parameters and the technical inefficiency model, the method of maximum likelihood was used. The likelihood function and its partial derivatives regarding the model’s parameters are presented in Battese & Coelli (1993).
The technical efficiency of the production of the firm i, in the moment t of time, is obtained through the equation:
In this way, through equations 1) and 2), the stochastic frontier production function and the inefficiency equation1 are obtained; and based on this, the technical efficiency of the economies that signed the CPTTP are obtained. In the following section, the results are presented.
Results
For the empirical application, information from the World Bank Group (2017) database about production, investment, and employment was used. The globalization indicator came from Gygli, Florian & Jan-Egbert (2018), Dreher (2006), and Dreher, Gaston & Martens (2008). The proxy variables that were used for estimating the production function and the inefficiency equation are the Gross Domestic Product (constant 2010 USD), gross fixed capital formation (constant 2010 USD), and labour force total, as well as the de facto Economic Globalization Index, respectively. When necessary, each variable was forecasted using the methodology for the construction of univariate models, proposed by Box & Jenkins (1976) and Box, Jenkins & Raisel (1994) and, when opportune, simple and exponential forecasting and smoothing techniques were used to complete some time series.
For choosing an adequate functional form, in Appendix A-1 a set of likelihood contrasts is presented, in which it can be seen that a Cobb Douglas function is adequate for estimating the ex ante production function, which is to say, one that does not consider the globalization variable. In appendix A-2 the contrasts for the ex post production function are presented, in which it can be seen that the trans-logarithmic production function is adequate and that, in the inefficiency equation, the globalization variable was taken into account in order to identify its effect on the technical inefficiency of the CPTPP countries. Also, the variables suggested for the inefficiency equation are adequate in both contrasts because the proposed null hypothesis is rejected, as can be seen in appendices A-1 and A-2.
Once the adequate function form was chosen, along with the variables to be included in the inefficiency equation, the equations 1) and 2) were simultaneously estimated with the maximum likelihood method. In appendix A-3, the results of the estimation of the ex ante and ex post production function parameters are reported, which permitted the technical efficiencies of the countries in the agreement to be obtained.
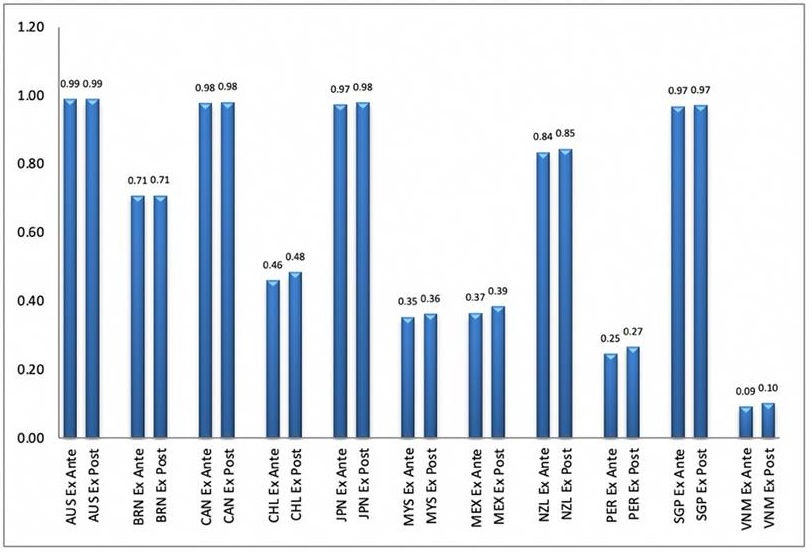
Once the technical efficiency of the countries that signed the CPTPP was estimated, the results are presented in appendices A-4 and A-5 for the ex ante and ex post production functions, which are analysed in this section. The data permitted the average behaviour of the efficiency index of the 11 participating economies to be obtained. As can be observed in Figure 1, considering the geometric mean of efficiency during the study period, it was identified that Australia reaches levels close to optimum efficiency, as this is at 0.96, which in terms of percentages equals 96%, followed by Canada, whose indicator is at 93%.
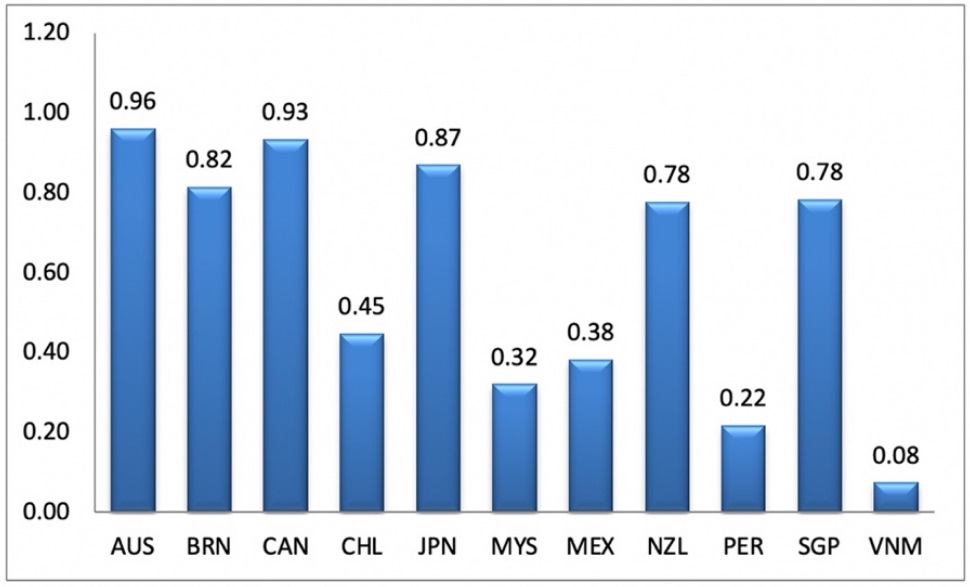
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 1 CPTPP: Geometric mean of the countries’ efficiency, 1990-2020.
Mexico achieved a level of 38%, meaning that it has broad possibilities for improvement, because it has an inefficiency of 62%. Vietnam is the country with the lowest indicator from the group of analysed economies, with barely 8% on average. High-income countries with elevated levels of technical efficiency stand out.
The result of the mean temporal evolution is presented in Figure 2. It can be seen that it has not passed 50% throughout the years. It shows that in the year 2020 it will barely be at 52 percentage points, which means that, as a group, the economies at a little below 50% can improve by making a better use of their production factors.
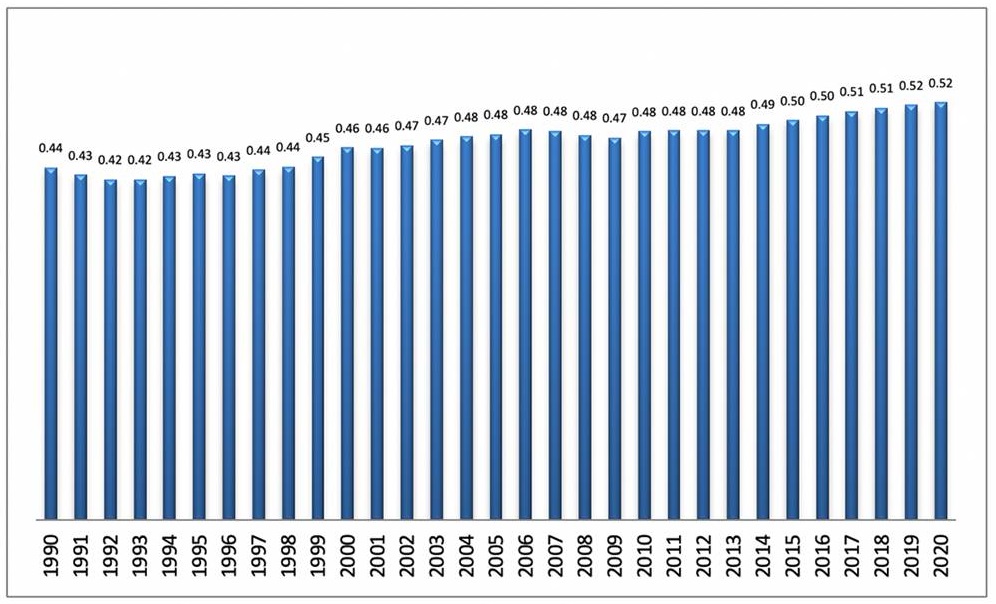
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 2 CPTPP: Temporal evolution of the geographic mean of the efficiency of the countries, 1990-2020.
Even though the countries present a medium level of efficiency, little over 50%, in the individual analysis of the CPTPP countries, each of them report differentiated and disparate behaviour among their efficiency levels. Figure 3 shows the particularities among them. Also, in the case of Australia, a tendency to growth is observed in its efficiency levels, even reaching an index of 99% for the year 2020. The behaviour of the evolution for Japan, Canada, and Singapore is similar to that of Australia and New Zealand, with levels around 80%. In the cases of Chile, Mexico, and Peru, although their tendency is toward growth, their efficiency is found at medium levels, while in Brunei and Malaysia the temporal evolution of their efficiency is more erratic, with ups and downs throughout the study period.
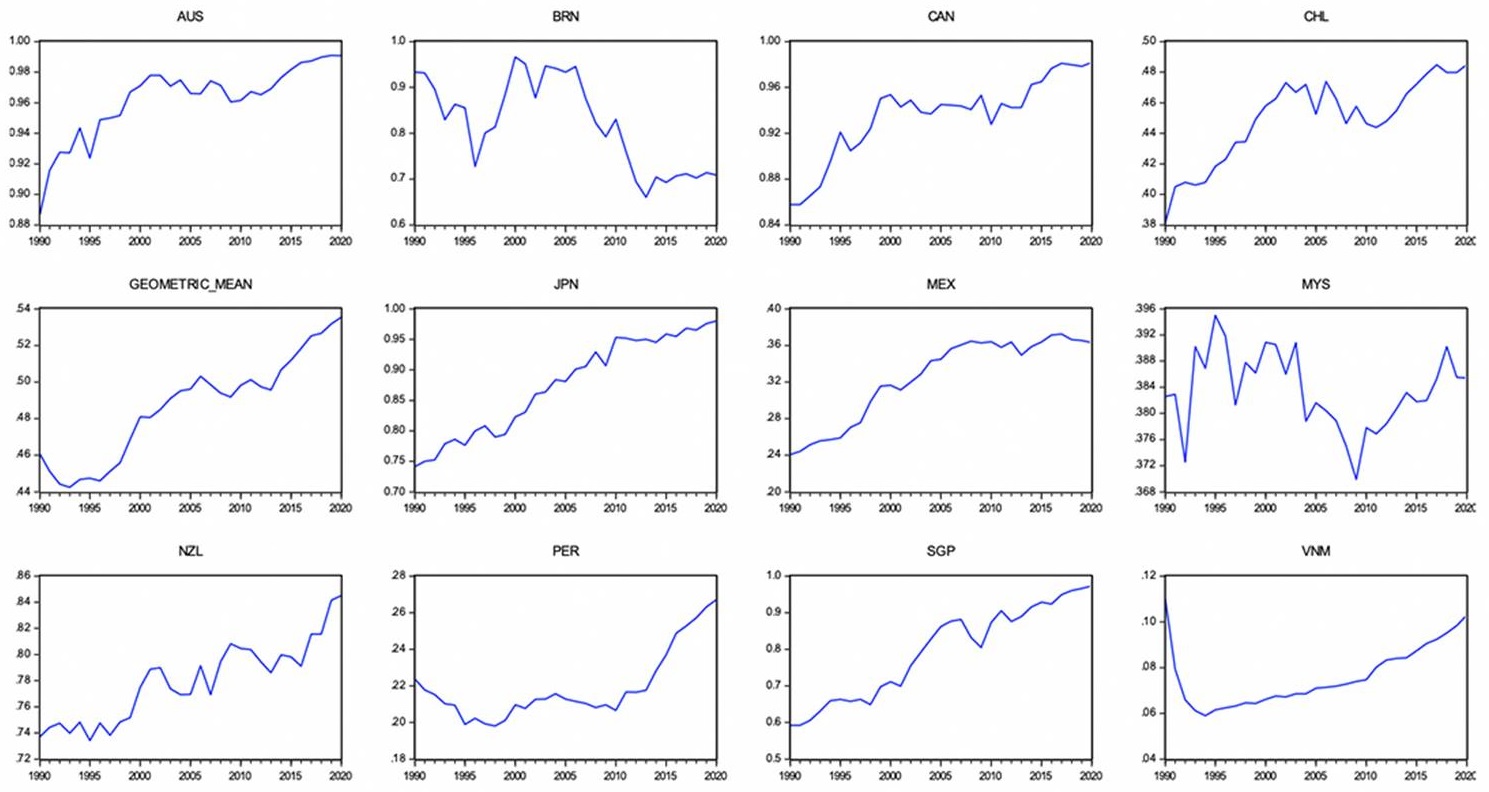
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 3 CPTPP: Temporal evolution of individual efficiency, 1990-2020.
In order to compare the effect of cooperation among countries, two estimates of technical efficiency have been obtained for the group of countries that signed the CPTPP. The first is under the assumption that they will act independently among themselves in commerce (ex ante efficiency). The second incorporates a globalization index, which can be assumed to be a proxy variable to the economic cooperation derived from the signing of the CPTPP (ex post efficiency). The results are presented in figure 4. As can be seen with these assumptions, the countries would have a profit efficiency of around 1.5% with cooperation, which in terms of improvements means that they could raise their production by approximately 1.5 percentage points with the collaboration among countries.
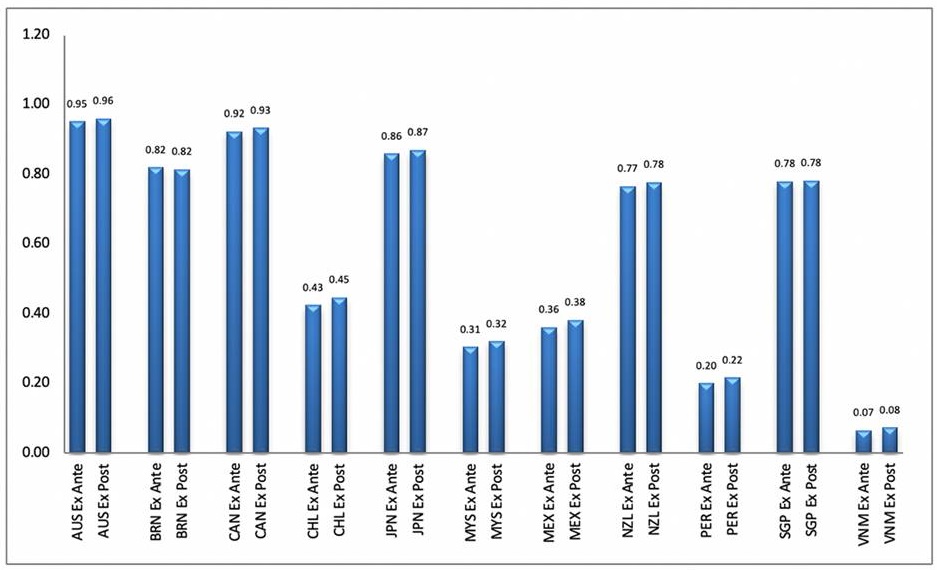
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 4 CPTPP: Geometric mean of the ex ante, ex post efficiency, 1990-2020.
Upon individually analysing the change in efficiency of the CPTPP countries, ex ante and ex post, it is observed that most of them, with the exceptions of Brunei and Singapore, present positive results when the globalization index in the inefficiency equation is considered, assuming that this contributes to reducing it. However, as can be seen in Figure 5, for this to be true, it is necessary that positive values are observed in the figure. The individual vision for the countries shows that each of them, except for Brunei, presents positive values, indicating profits with cooperation within the economic block. The forecast for the year 2020 is that, with the signing and implementation of the CPTPP, the signatory countries will obtain profit efficiency.
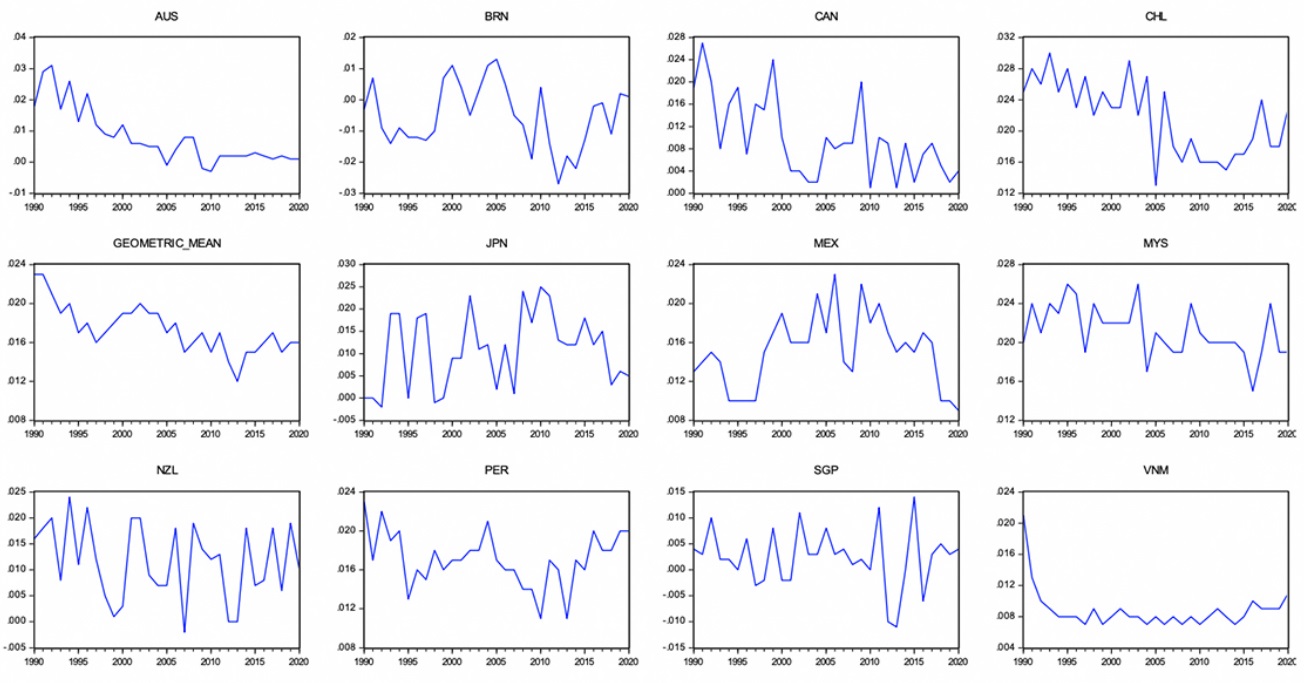
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 5 CPTPP: Individual profit efficiency because of globalization.
Figure 6 shows the profit efficiency that will be achieved by the year 2020. As can be seen, in a vision forecast, the countries with lower income within the block will be those that obtain higher profit efficiency for the year 2020.
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 6 CPTPP: Profit efficiency because of globalization in the year 2020.
The use of the variation coefficient permitted the analysis of the existent disparities among the group of individuals. A higher value of the variation coefficient has more heterogeneity among them, and a lower coefficient, more homogeneity, which is the same as expressing that it is causing a convergence process if this diminishes through time. That is to say, there is a process of reduction in the disparities in efficiency among the countries in the group. So, Figure 7 shows the temporal evolution of the ex ante and ex post efficiency of the CPTPP countries. As can be observed, this presents a decreasing tendency through time in both indicators, demonstrating that a process of convergence in efficiency is present among economies, because of which the disparities among them could be reduced once it is put into operation, after its signing, as the decreasing temporal evolution is less than the ex post variation coefficient, along with reporting that the decreasing tendency is also less than the ex ante indicator, causing the inference that with cooperation among countries, the disparities in their levels of technical efficiency are reduced more quickly.
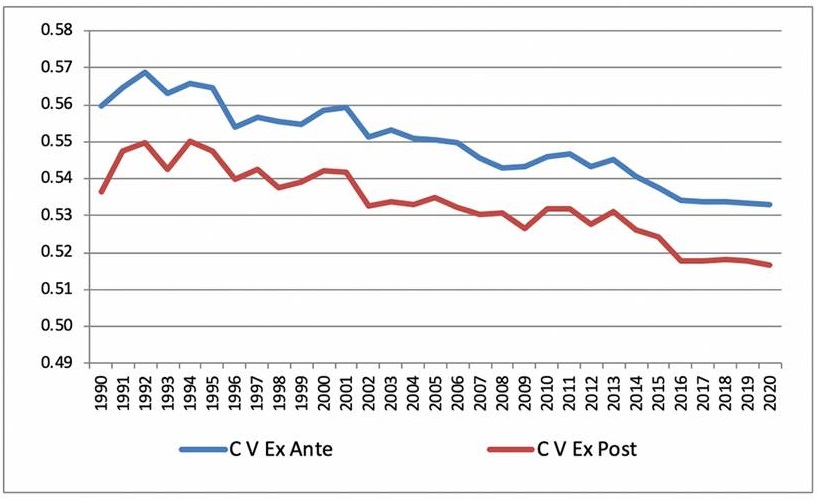
Source: Authors’ own elaboration with data from the World Bank Group (2017).
Figure 7 CPTPP: Temporal evolution of the coefficient of variation in technical efficiency, ex ante, ex post. 1990-2020.
These results permitted the construction of a set of conclusions which will be presented below.
Conclusions
Having databases, such as that of the World Bank, and a globalization indicator such as that of the KOF, has allowed to estimate the technical efficiency of the group of countries that signed the CPTPP. The results show that high-income economies also have high average levels of efficiency. It has been observed that, through time, at the end of the period of analysis the signers of the agreement, also on average, have broad possibilities for improving the use of their production factors. However, when the evolution of the indicator is analysed individually, it is identified that most of them present tendencies toward growth in their levels of efficiency, which translates to improvements in the use of their production factors.
In addition, making ex ante and ex post estimates has allowed to identify that there are profit efficiencies when a globalization factor is considered an enhancing factor for efficiency within the group of countries, which is corroborated by observing the individual evolution of each country.
The construction of a scenario of efficiency for the year 2020 has demonstrated that middle-income countries are those that obtain a greater benefit in terms of the better use of production factors. Finally, obtaining an indicator to analyse convergence indicates that with globalization, as an additional variable in the model used, contributes to the process of convergence in efficiency, reducing the disparities that exist among countries.
Derived from the previous, the signing, ratification, and implementation of the CPTPP would contribute to the improvement and reduction of the disparities in the use of the production factors of the countries that signed it, as shown in the indicator in the scenario for the year 2020.











 nueva página del texto (beta)
nueva página del texto (beta)


