Introducción
La educación es un aspecto muy importante en el desarrollo de un país, ya que el capital humano es un factor determinante en el crecimiento económico. La política nacional de los últimos diez años ha dado mayor énfasis al fomento de la calidad académica, de ahí que muchos centros educativos hayan incorporado exámenes de selección para el ingreso y pongan en práctica proyectos de modernización de la infraestructura institucional y de innovación educativa, así como tareas de actualización de programas y formación del personal académico (Rodríguez, 2014).
La política educativa del país ha tenido como prioridad elevar la calidad educativa en sus diferentes niveles, instrumentando diversos programas para otorgarles infraestructura, mejorar los cuadros docentes, así como la calidad de su formación y su desempeño. Específicamente, el análisis de la educación superior ha ido tomando fuerza, por lo que se han venido implementado algunas estrategias del Plan Nacional de Desarrollo para evaluar los programas educativos, con la finalidad de aumentar su nivel (López, Rodríguez & Ramírez, 2008).
México cuenta actualmente con un sistema de educación superior amplio y diverso, que incluye instituciones de educación superior públicas y particulares, tales como universidades, institutos tecnológicos, universidades tecnológicas, universidades politécnicas, universidades pedagógicas, universidades interculturales, centros de investigación, escuelas normales y centros de formación especializada (Secretaría de Educación Pública [SEP], 2014). La importancia de tener herramientas que ayuden a evaluar el nivel de eficiencia está siendo determinante para una adecuada implementación de políticas educativas que fortalezcan al sector en su nivel superior. Es en esta dirección que el presente estudio tiene como objetivo utilizar el análisis de la envolvente de datos (DEA, por sus siglas en inglés) en la evaluación de la eficiencia en las universidades públicas de México en el 2012.
En la revisión de la literatura se encontraron diversos trabajos para medir la eficiencia en las universidades con la metodología DEA. Entre los más relevantes se encuentran: Guccio, Martorana & Mónaco (2014), quienes evalúan la eficiencia de la enseñanza de las universidades italianas y su efecto de las reformas educativas durante el periodo 2000-2010, utilizando DEA con el estadístico bootstrap. Nazarko & Šaparauskas (2014) realizan un estudio comparativo de eficiencia de 19 universidades en Polonia a través de un modelo DEA con rendimientos de escala constante, determinando los elementos que permiten mejorar la eficiencia en el gasto de la educación. Ramírez & Alfaro (2013) estimaron la eficiencia de las universidades chilenas, basando su estudio empírico en los datos financieros y de matrícula del 2011 y en los resultados obtenidos solo tres universidades fueron eficientes.
Kipesha & Msigwa (2013) evalúan la eficiencia de siete universidades públicas en Tanzania, donde se encontró que las universidades públicas son ineficientes en la generación de ingresos de consultorías, investigación, tasas de inversiones. Cunha & Rocha (2012) revisan la eficiencia de las instituciones públicas de educación superior de Portugal, encontrando que la mayoría de las instituciones están trabajando de manera ineficiente, lo que contribuye a una pérdida significativa de recursos. Wolszczak-Derlacz & Parteka (2011) analizan la eficiencia y productividad total de los factores (PTF) con el índice Malmquist de 266 instituciones públicas de educación superior (IES) de siete países europeos en el periodo 2001-2005, de las 266 universidades europeas examinadas, solo cuatro registraron mejoras anuales consistentes en la PTF y presentaron aumentos en los cambios de la eficiencia técnica.
Tzeremes & Halkos (2010) utilizan el DEA con la técnica bootstrap para determinar los niveles de rendimiento de los 16 departamentos de la universidad pública de Tesalia en Grecia, encontrándose una mala asignación de recursos e ineficiencias entre los departamentos de esta universidad. Agasisti & PérezEsparrells (2010) realizan un análisis de eficiencia de las universidades de Italia y España, donde, según los resultados, se tiene en general un promedio elevado de eficiencia en las universidades de ambos países; también realizan una medición de la productividad con el índice Malmquist, y en Italia el cambio en la productividad está dado por el cambio tecnológico, a diferencia de España, que fue el cambio en la eficiencia técnica lo que determinó la productividad en las universidades.
Kantabutra & Tang (2010) examinan el funcionamiento de las universidades públicas de Tailandia en términos de eficiencia; analizan dos modelos: el modelo de enseñanza y el modelo de investigación. Los resultados indican que las universidades autónomas superan a las universidades del gobierno en cuanto a la eficiencia de la investigación; además, las universidades en áreas provinciales y las facultades del grupo de ciencias de la salud son eficientes en términos de enseñanza.
Thanassoulis, Kortelainen, Johnes & Johnes (2009) analizan la eficiencia en las instituciones de educación superior en Inglaterra y evalúan su estructura de costos, la eficiencia técnica y la productividad; los resultados revelan que para la mayoría de las instituciones tienen ineficiencia económica, y en cuanto a la productividad no existe crecimiento en el periodo de estudio. Athanassopoulos & Shale (1997) comparan 45 instituciones de educación superior en el Reino Unido, donde revisan la eficiencia técnica, obteniendo en la mayoría de las universidades una mala optimización de los recursos, por lo que realizan propuestas para maximizar la cantidad de alumnos graduados, así como mayor número de publicaciones de los profesores. Sinuany-Stern, Mehrez & Barboy (1994) ejecutaron un estudio de caso donde se evaluaron los departamentos académicos en la Universidad Ben-Gurion, a través del DEA, utilizando el modelo de Charnes, Cooper y Rhodes (CCR); se aplicó también un análisis de cluster para dividir los departamentos en varios conjuntos, observando que las áreas de ciencias sociales son más eficientes. Beasley (1990) hace una medición de la eficiencia en las universidades del Reino Unido en el área de investigación y de enseñanza en los departamentos de física y química, encontrándose que estos departamento son de mayor el nivel de eficiencia en la investigación en la mayoría de las universidades.
La hipótesis del presente trabajo es que durante el 2012, las universidades públicas de nivel superior en México no fueron eficientes debido a que no se utilizaron de manera óptima el financiamiento para elevar la matrícula, los doctores, el número de doctores pertenecientes al Sistema Nacional de Investigadores (SNI), las publicaciones de artículos indexados en la base del portal Web of Knowledge, Institute for Scientific Information (ISI) y los graduados totales.
Materiales y Métodos
Para determinar la frontera eficiente y así poder conocer las universidades ineficientes, su grado y origen, se pueden utilizar métodos paramétricos (modelos econométricos) y no paramétricos (programación matemática) (Ahn, Charnes & Cooper, 1988).
La frontera se construye a través de la comparación de cada observación con la mejor práctica observada (la frontera), por lo que se desarrollan conceptos como la eficiencia técnica, que es la capacidad de utilizar insumos de manera tal que se maximiza la cantidad producida. La frontera se construye a partir de funciones de producción y su estimación informa sobre la ineficiencia técnica (Coelli, 1996).
El análisis de la envolvente de datos (DEA)
La eficiencia analizada bajo el método no paramétrico del DEA fue iniciada por Farrell (1957) y reformulada como un problema de programación matemático por Charnes, Cooper & Rhodes (1978). Dado un número de unidades de producción, que son las unidades de manejo decisión (DMU, por sus siglas en ingles), se construye una frontera de eficiencia de la muestra de unidades de producción.
La metodología DEA pertenece al grupo de los denominados métodos de frontera, en los cuales se evalúa la producción respecto a las funciones de producción, donde por función de producción se entiende el máximo nivel de output alcanzable con una cierta combinación de inputs, o bien, el mínimo nivel de inputs necesario en la producción de un cierto nivel de outputs (Coelli, 1995).
La eficiencia de Farrell (1957), basada en la entrada o simplemente en la eficiencia de entrada de un plan de (x, y) con relación a una tecnología T, se define como:
Asimismo, la producción basada en la eficiencia de Farrell (1957) o salida de eficiencia se define como:
Farrell (1957) centró el problema de la eficiencia en su estimación a partir de los datos observados en las unidades productivas, dotando de un marco analítico al concepto neoclásico de eficiencia paretiana. En su trabajo diferenció entre eficiencia técnica y eficiencia asignativa. En todo proceso de producción, la eficiencia técnica orientada a los inputs viene dada por el consumo de inputs mínimo necesario para lograr un determinado volumen de outputs. Por otra parte, una empresa es eficiente en precios o asignativamente cuando combina los inputs en la proporción que minimiza sus costos. En la primera se comparan los inputs y los outputs en unidades físicas, y en la segunda se añaden los precios de los factores de producción. La combinación de estos dos indicadores proporciona una medida de la eficiencia denominada económica o global.
Los modelos DEA pueden clasificarse en función de:
El tipo de medida de eficiencia que proporcionan modelos radiales y no radiales.
La orientación del modelo input orientado, output orientado o input-output orientado.
La tipología de los rendimientos a escala caracteriza la tecnología de producción entendida como la forma en que los factores productivos pueden caracterizarse por la existencia de rendimientos a escala: constantes o variables.
Eficiencia técnica
La literatura sobre la eficiencia técnica tiene su origen en los primeros años de la década de los cincuenta. La primera definición formal de la eficiencia técnica se debe a Koopmans (1951): “es aquella en donde un incremento en cualquiera de los outputs, exige una reducción en al menos de uno de los restantes o el incremento de alguno de los inputs”. La primera medida de la eficiencia técnica es propuesta por Debreu (1951) y Shephard (1953), aunque con diferente orientación (output e input, respectivamente).
El estudio de Farrell (1957) se complementa con los trabajos de Charnes et al. (1978), que partían de rendimientos de constantes a escala (CRS, por sus siglas en inglés) de forma tal que un cambio en los niveles de inputs conlleva a un cambio proporcional en el nivel del output, el cual requiere tantas optimizaciones como DMU. Puede escribirse el modelo DEA en términos generales en tres formas: fraccional, multiplicativa y envolvente. El modelo CRS en su forma envolvente es el siguiente:
Donde θ indica la distancia en inputs a la envolvente de datos, es decir, la medida de eficiencia. X es la matriz de inputs, Y es la matriz de outputs, λ es el vector de pesos o intensidades, Xi , Yi representan los valores de inputs y outputs, respectivamente.
Posteriormente, Banker, Charnes & Cooper (1984) extendieron el modelo original para incluir rendimientos variables a escala (VRS, por sus siglas en inglés), considerando que diversas circunstancias como la competencia imperfecta, las restricciones en el acceso a fuentes de financiación, etcétera, pueden provocar que las unidades no operen a escala óptima. Este modelo propone una modificación al programa lineal original a la cual se le agrega una restricción:
N1 es vector unitario N × 1, λ es el vector de las intensidades donde se restringe el rango de valores que pueden tomar los componentes del vector de manera que sumen uno.
Esta restricción permite que una unidad ineficiente solo sea comparada con unidades productivas de su mismo tamaño. Sin esta restricción, las unidades evaluadas pueden ser comparadas con otras unidades mayores o menores.
El modelo con orientación input en su forma envolvente es el siguiente:
A la eficiencia técnica medida bajo rendimientos variables se le designa también eficiencia técnica pura, porque no se incluye en esta medición ningún efecto de escala (Thanassoulis, 2001). Por lo que a partir de la propuesta de Banker et al. (1984) se puede descomponer la eficiencia de la siguiente manera:
Eficiencia técnica global:
Eficiencia de escala (EE)
La eficiencia de escala mide el impacto del tamaño de la escala en la productividad de una DMU. Para poder realizarlo se deben calcular los dos modelos: CRS y VRS con los mismos datos; si existe una diferencia para las dos mediciones para una DMU en particular, entonces significa que esa DMU posee ineficiencia de escala y que el valor de ineficiencia es la diferencia entre la medición CRS y VRS (Coll & Blasco, 2006).
La eficiencia técnica global (ETG) puede ser descompuesta en eficiencia técnica pura (ETP) y eficiencia de escala (EE).
Por lo tanto, la ETG = ETP * EE.
Asimismo, la eficiencia de escala se puede definir de la siguiente manera:
Análisis estadístico bootstrap para los modelos DEA
Una de las críticas al modelo DEA es que asume que todas las distancias entre las eficiencias observadas y la frontera eficiente reflejan ineficiencia. De cualquier manera, la distancia de una observación de la frontera eficiente muestra ineficiencia y ruido. Esto es porque la observación input-output debería estar normalmente sujeta al error.
El bootstrap es una herramienta estadística que fue introducida por Efron (1979) para analizar la sensibilidad de las medidas de eficiencia a una muestra de variación. Posteriormente, Simar (1992) proporcionó la primera aplicación que, en un contexto de frontera, se sirvió del bootstrap al incorporarlo a la estimación semiparamétrica de modelos de datos de panel. Sin embargo, la adaptación consistente del bootstrap a estimaciones del DEA fue formulada por primera vez por Simar & Wilson (1998).
El DEA, en lo que llamamos el mundo real, estima, mediante la muestra, una frontera de producción, y respecto a ella obtiene las medidas de eficiencia. Esta frontera, sabemos, que por construcción se va a situar en el interior del verdadero conjunto de posibilidades de producción. Es decir, entre la verdadera función de producción y la estimada por el DEA va a existir un sesgo. Este sesgo va a ser diferente en cada empresa, y es el que vamos a aproximar con el bootstrap.
Para ello se necesita generar una muestra con la que se pueda obtener una estimación del verdadero valor de la función de la frontera y así poder determinar el sesgo que cada empresa puede tener, restando a la eficiencia estimada con el DEA original la obtenida con el bootstrap. Si repetimos este proceso varias veces, tendremos infinitas fronteras bootstrap que se comparan siempre con la misma frontera verdadera. Para cada empresa, por tanto, tendremos infinitas mediciones de eficiencia bootstrap, y si hemos estimado con propiedad el proceso generador de datos, la distribución del sesgo bootstrap de cada empresa debe ser similar al que se presenta en el mundo real (Simar & Wilson, 2004).
La eficiencia bootstrap que nos interesa es aquella eficiencia que se observa para la empresa de la muestra original, que hemos denominado (x0; y0), con respecto a esta nueva estimación. Es decir:
La resolución con programación lineal de la eficiencia bootstrap θ ∗ ( x 0 y 0 ) RVS es entonces:
donde se observa como el único punto desde donde medimos la eficiencia (x0y0 ), y esta eficiencia se observa en referencia a la frontera construida con la muestra especificada.
Desarrollo del modelo
Se desarrolla un modelo DEA para calcular la ETG, la ETP y EE con rendimientos de escala constantes CRS y rendimientos de escala variables VRS con orientación input.
Posteriormente, para darle robustez a los cálculos de eficiencia, se aplica la técnica bootstrap. Para ello se genera una muestra de los resultados obtenidos en los cálculos de eficiencia técnica y se repite el procedimiento un elevado número de veces para asegurarnos que el sesgo calculado con la muestra bootstrap corresponda con la frontera real. Simar & Wilson (2000) recomiendan remuestrear 2000 interacciones, por lo que en el caso de esta investigación se realizó esta cantidad de interacciones para tener resultados más fidedignos.
Para la selección de los DMU se identificaron 32 universidades públicas de México para el 2012, utilizando como criterio aquellas que recibieron financiamiento federal o estatal, quedando la muestra en la Tabla 1.
Tabla 1 Universidades públicas de México.
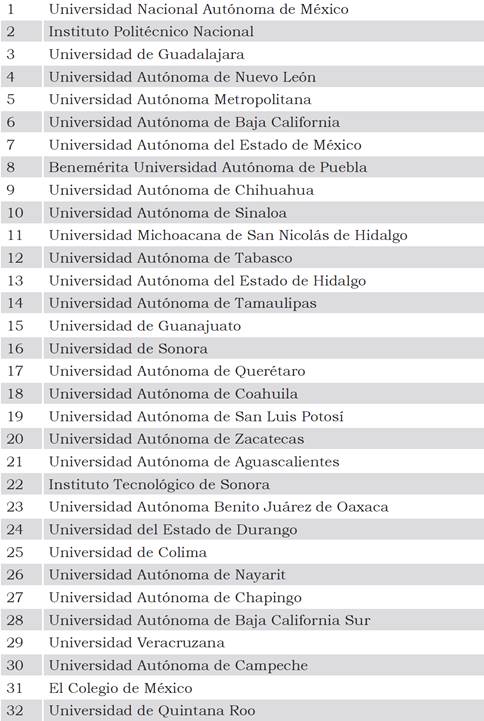
Fuente: Elaboración propia con base en Estudios Comparativos de Universidades Mexicanas (ECUM), 2014.
Selección de inputs y outputs
De acuerdo con la revisión de la literatura realizada, se encontraron los siguientes autores que han utilizado como input el financiamiento: Athanassopoulos & Shale (1997), Beasley (1990), Cunha & Rocha (2012), Nazarko & Saparauskas (2014), Ramírez & Alfaro (2013), Sinuany-Stern et al. (1994), Thanassoulis et al. (2009), Tomkins & Green (1988). La selección de este input se hizo con la finalidad de saber qué tan eficientemente se utilizaron los recursos financieros en las universidades.
En cuanto a los outputs, diversos autores han contemplado variables relativas a la enseñanza y la investigación. La mayoría de los estudios que analizan la parte de la enseñanza de las universidades se centran en el número de graduados a nivel licenciatura y a nivel de posgrado, como en el caso de Agasisti & Pérez-Esparrells (2010), Johnes (2008), Kantabutra & Tang (2010) y Wolszczak-Derlacz & Parteka (2011). Otra variable utilizada en el área de la enseñanza es la cantidad de alumnos matriculados a nivel licenciatura o posgrado, lo que se encuentra contemplado en los trabajos de Agasisti & Dal Bianco (2009), Beasley (1990), Ramírez & Alfaro (2013), Thanassoulis et al. (2009), Tomkins & Green (1988).
En el área de investigación, las variables más utilizadas son la publicación de artículos en revistas con factor de impacto, número de profesores y número de profesores con grado de doctor, considerado por autores como Ramírez & Alfaro (2013) y Daghbashyan (2009).
El modelo DEA queda estructurado de la siguiente manera:
Inputs:
• Financiamiento.
Outputs:
• Matricula total (total de alumnos de licenciatura y posgrado).
• Graduados total (total de alumnos graduados a nivel licenciatura y posgrado).
• Docentes (total de profesores docentes en las universidades).
• Doctores (total de profesores con grado de doctor).
• Doctores en el SNI (número de académicos que participan en el SNI del Consejo Nacional de Ciencia y Tecnología [Conacyt]).
• Publicación de artículos ISI (número de artículos registrados en el índice bibliográfico ISI-Thomson).
Para la parte de financiamiento, se contemplan los siguientes rubros: subsidio ordinario federal, subsidio ordinario estatal, subsidio extraordinario federal y subsidio extraordinario estatal. De esta manera, las universidades consideradas en la presente investigación fueron aquellas que cumplieron con este criterio. Cabe aclarar que en México el presupuesto de las universidades públicas se integra a partir de varias fuentes de financiamiento: las aportaciones suministradas por el gobierno federal, a través del presupuesto aprobado por el Congreso; las aportaciones de los gobiernos estatales; los recursos extraordinarios provenientes de diversos fondos y programas de los gobiernos federal y estatal; y los recursos autogenerados de las instituciones (ECUM, 2014).
Resultados
Se observa en los resultados, mostrados en la Tabla 2, que el promedio de la eficiencia técnica con rendimientos variables del modelo original es de 0.87, y con la aplicación del bootstrap es de 0.77, y en el caso de la eficiencia con rendimientos constantes el modelo original tuvo un promedio de eficiencia del 0.80 y con el bootstrap aplicado fue de 0.71.
Tabla 2 Eficiencia en las universidades públicas de México, 2012.
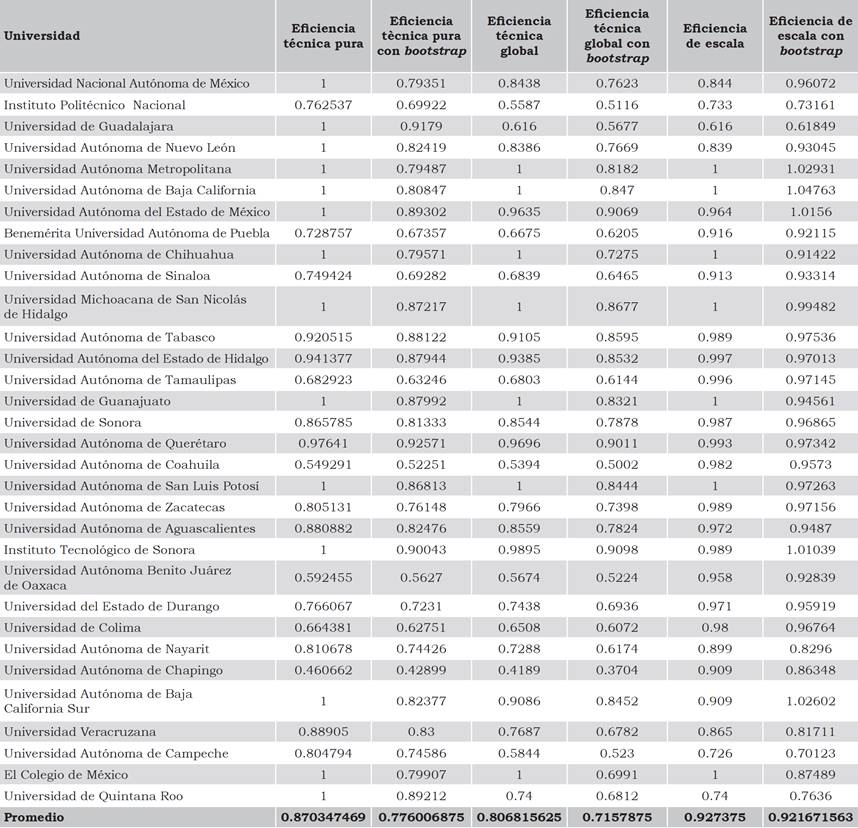
Fuente: Elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
Después de haber aplicado la técnica bootstrap en los modelos VRS y CRS, ninguna de las universidades obtuvo un valor eficiente, sin embargo, la Universidad Autónoma de Querétaro fue la que alcanzó el valor más cercano al óptimo 0.93, en el lado opuesto la Universidad Autónoma de Chapingo fue la menos eficiente. En cuanto a la Universidad Michoacana de San Nicolás de Hidalgo, se ubicó en el lugar 9° con un 0.87 de eficiencia.
Los resultados de la eficiencia de escala fueron los mayores con un promedio de eficiencia ya ajustado (una vez aplicado el bootstrap) de 0.94, lo que significa que la mayoría de las universidades tuvieron una escala de producción óptima. Sin embargo, se tiene que técnicamente no son eficientes debido a que de las 32 universidades analizadas, el 0.78 pueden operar con menos insumos, es decir, requieren de menos financimiento en proporción a la matrícula, doctores, doctores en el SNI, publicaciones, graduados que actualmente están manejando. En el caso específico de la Universidad Michoacana de San Nicolás de Hidalgo puede ser eficiente con $91.46 millones de pesos menos de los que está recibiendo en proporción a los productos ya mencionados.
Discusión
Se han desarrollado diversos estudios sobre eficiencia en las universidades utilizando la metodología del DEA, midiendo la eficiencia con rendimientos constantes, rendimientos variables y en algunos casos utilizan el estadístico bootstrap, pero todos ellos difieren del trabajo que se está presentando porque se realiza la medición de la eficiencia técnica pura, técnica de escala y técnica global con bootstrap, utilizando como input financiamiento y como outputs: docentes, matrícula total, doctores, doctores en el SNI, publicación de artículos ISI y graduados total.
Los siguientes autores calculan la eficiencia técnica, pero ninguno de ellos utiliza el estadístico bootstrap. Ramírez & Alfaro (2013) estimaron la eficiencia técnica con rendimientos constantes a escala de las universidades chilenas para el 2011, utilizando como inputs los gastos operativos y como outputs publicaciones ISI y número de estudiantes matriculados. También Cunha & Rocha (2012) hacen un análisis de la eficiencia técnica con rendimientos constantes a escala de las instituciones de educación superior en Portugal en el 2008, usando como inputs el total de financiamiento por estudiante, el total de gasto por estudiante y el personal académico por estudiante, y como output el total de estudiantes graduados, el total de estudiantes graduados de doctorados premiados y el número total de cursos.
Kipesha & Msigwa (2013) evaluaron la eficiencia técnica con rendimientos constantes a escala, eficiencia técnica con rendimientos variables a escala y eficiencia de escala, de siete universidades públicas que operan en Tanzania. Utilizan tres modelos: en el primero los inputs son la matrícula total, personal académico, el total de personal no académico, y utilizan como outputs número de graduados universitarios, licenciados y titulados de postgrado de manera conjunta; el segundo modelo considera las mismas variables de entrada y como output la recaudación interna generada; en el tercer modelo, de igual manera, tiene las mismas variables de entrada, pero para los outputs combina las variables de salida de los dos primeros modelos.
En los siguientes casos, los autores calculan la eficiencia técnica utilizando bootstrap, pero en ninguna situación se presentan los resultados desagregados como en esta investigación. Nazarko & Saparauskas (2014) realizaron un estudio de las universidades de Polonia, midiendo la eficiencia técnica con rendimientos constantes a escala aplicando el estadístico bootstrap. Considerando como inputs: presupuesto, número de profesores, número de empleados; y como outputs: número de estudiantes de tiempo completo, número de estudiantes de doctorado de tiempo completo, porcentaje de estudiantes internacionales, porcentaje de estudiantes con beca, porcentaje de estudiante con beca de gobierno, preferencia del empleador para contratar egresados, evaluación paramétrica de los logros académicos de la facultad.
Tzeremes & Halkos (2010) hicieron un estudio para medir la eficiencia técnica con rendimientos constantes a escala y rendimientos variables a escala con bootstrap, con el fin de determinar los niveles de rendimiento de 16 departamentos de la universidad de Grecia, utilizaron como inputs personal académico, personal auxiliar, número de estudiantes, recursos para investigación; y como outputs número de graduados y número de publicaciones. También los autores Guccio et al. (2014) realizan una investigación donde calculan la eficiencia con rendimientos a escala constantes y rendimientos a escala variables con bootstrap de las universidades italianas, utilizando variables de enseñanza e investigación
Como se puede observar, todos los modelos son diferentes al estudio que aquí se presenta, ya que en ninguno se calcula de manera integral la eficiencia técnica con rendimientos constantes, la eficiencia técnica con rendimientos variables, la eficiencia de escala y la instrumentación del bootstrap en los tres casos. Asimismo, existen diferencias en los inputs y outputs considerados entre este trabajo y los modelos revisados. Es decir, esta investigación comprende un análisis más completo de eficiencia, que permite identificar si se tiene una adecuada utilización de los recursos en el sector educativo. De tal forma, que a partir de ello se puedan planear y organizar los recursos humanos -docentes y estudiantes- y financieros, con la finalidad de fortalecer la docencia y la investigación en las universidades de México.
Conclusiones
En el documento se presenta la medición de la eficiencia técnica en las universidades públicas de México en el 2012, a través del modelo de DEA, aplicando la técnica bootstrap para darle robustez a los datos.
Para el cálculo de la eficiencia DEA se desarrolla un modelo de rendimientos constantes a escala y rendimientos variables a escala con orientación input. Los DMU que se utilizaron fueron 32 universidades públicas del país, utilizando como input el total de financiamiento recibido federal y estatal y como outputs la matrícula total, el número de doctores que son docentes, el número de doctores en el SNI, las publicaciones de artículos ISI y el total de graduados.
Los modelos DEA VRS y CRS con bootstrap tuvieron un nivel de ineficiencia de 22% y 28%, respectivamente. Por lo que la hipótesis se cumple, ya que los resultados dan cuenta de que las universidades públicas de nivel superior de México no fueron eficientes durante el 2012, debido a que no se utilizó de manera óptima el financiamiento para elevar la matrícula, el número de doctores, el número de doctores pertenecientes al SNI, las publicaciones de artículos ISI y los graduados totales.
Con respecto a las diferentes investigaciones que se han efectuado en las mediciones de la eficiencia en las universidades, se observa que en este trabajo se presenta un mayor nivel de desagregación al considerar la EFP, de EE, ETG y la aplicación del bootstrap. Esta última técnica no ha sido contemplada en otros estudios en el ámbito educativo en su nivel superior en México.
La evaluación de la eficiencia de las universidades a través la metodología no paramétrica del DEA permitió calcular la eficiencia técnica con rendimientos constantes, la eficiencia técnica con rendimeintos variables y la eficiencia de escala. De esta manera, se pudo determinar qué tan eficiente utilizaron los recursos financieros las universidades, en función de los alumnos matriculados, de los alumnos graduados, de los profesores con grado de doctor, de los profesores en el SNI y de las publicaciones en revistas con factor de impacto. Estos resultados proporcionan elementos para la implementación de políticas educativas que fortalezcan en específico a cada universidad, y así eleven su nivel educativo y formen recursos humanos que fomenten el desarrollo social y económico de su estado.
Con los resultados obtenidos y la revisión bibliográfica realizada se identifican más áreas que permiten fortalecer este tipo de estudios, como es el uso de otras metodologías con fronteras estocásticas, así como el análisis de más instituciones de educación superior, como puede ser el ampliar las investigaciones a otros países de America Latina, de Europa y de Asia.











 nueva página del texto (beta)
nueva página del texto (beta)



