Introducción
La formabilidad es el alargamiento que puede ser deformado un material en un proceso particular, antes del inicio de falla. Las láminas de aleación de aluminio usualmente fallan durante el formado, ya sea por encuellamiento localizado o por fractura dúctil. El encuellamiento es gobernado por las propiedades del material, tales como el endurecimiento por trabajo y deformación-velocidad de endurecimiento; además, depende críticamente de la trayectoria seguida por el proceso de formado. La fractura dúctil ocurre como resultado de la nucleación y enlace de huecos microscópicos en las partículas, así como de la concentración de deformaciones en bandas estrechas de cortante (Semiatin, 1996).
La inestabilidad plástica o encuellamiento localizado es un tema importante en el formado de láminas de metal, donde los diagramas límite de formado (Forming Limit Diagram [FLD]) son usualmente usados para caracterizar la formabilidad del material (Xu & Weinmann, 2000). Diferentes criterios de cedencia han sido propuestos para representar las características anisotrópicas de láminas de metal, hechas de aceros avanzados de alta resistencia y aleaciones de aluminio. Se ha mostrado que los coeficientes anisotrópicos y leyes de endurecimiento tienen efectos considerables en la predicción de deformación plástica y formabilidad (Uthaisangsuk, Panich, Suranuntchai & Jirathearanat, 2014). Entre los criterios comúnmente estudiados se encuentran el de cedencia de Hill, el cual es un criterio generalizado de Huber-Misses-Hencky con anisotropía en tres planos ortogonales; y el de Barlat, que modela láminas con materiales anisotrópicos bajo diferentes condiciones de esfuerzo (Hussaini, Krishna, Gupta & Singh, 2015).
Mohr, Dunand, Maertens & Luo (2012) realizaron experimentos uniaxiales y biaxiales involucrando cargas combinadas normal y cortante de una aleación de aluminio. Los resultados de cinco experimentos los usaron para calibrar un modelo de plasticidad anisotrópico, el cual compararon con la función Yld2000-2d de Barlat, una regla de flujo asociado y la ley de endurecimiento de Swift. El error relativo máximo que obtuvieron fue de 4.5%. La validación del modelo fue implementada en el programa de Elemento Finito ABAQUS®.
Los criterios de cedencia de von Misses, Hill 48 y Barlat Yld2000-2d fueron considerados en combinación con las leyes de endurecimiento de Swift y Voce en el trabajo reportado por Uthaisangsuk et al. (2014). Las pruebas de tensión de muestras con diferentes tipos de muescas y pruebas de extensión de barreno fueron realizadas experimental y numéricamente, para verificar los modelos de cedencia y endurecimiento con respecto a la distribución de esfuerzo de formación local. Los valores obtenidos por medio de elemento finito con el modelo Yld2000-2d tuvieron una mejor aproximación a los resultados experimentales. El material bajo estudio fue una lámina de acero avanzado de alta resistencia.
Hussaini et al. (2015) obtuvo FLD teóricos a través de un análisis de Marciniak-Kuczynski con los criterios de cedencia de Hill y Barlat, a una temperatura de 300 °C para un acero inoxidable austenítico 316. Los FLD experimentales se obtuvieron a partir de pruebas con punzón semiesférico en muestras de diferente ancho a esa temperatura. Los resultados obtuvieron un factor de correlación de 0.887 con la predicción de Barlat, mostrando una mejor aproximación con los FLD obtenidos experimentalmente.
Sin embargo, Lin, Hu, Yuan & He (2015) consideran que los materiales presentan diferentes propiedades mecánicas y que las relaciones esfuerzo-deformación, resultado de diferentes estados de esfuerzo, no pueden ser definidas siguiendo una sola fórmula empírica, como la ley de potencia comúnmente aplicada. En su trabajo desarrollaron un modelo constitutivo de segundo y uno de cuarto orden, los cuales se pueden ajustar a diferentes relaciones experimentales de esfuerzo-deformación que permiten el cambio de la razón de deformación transversal/espesor.
De acuerdo con lo mencionado anteriormente, existen diferentes modelos para el ajuste de los coeficientes anisotrópicos y obtención de FLD en el formado de láminas de metal, entre estos destaca el modelo de Barlat con buenas aproximaciones en las curvas experimentales. Por ello, el objetivo del presente trabajo es obtener los coeficientes anisotrópicos para una aleación de aluminio, aplicando el modelo de cedencia de Barlat. Se utilizó el programa LS-DYNA® en la generación de un código fuente para el módulo de optimización LSOPT®, donde se optimiza el ajuste de los parámetros de Barlat, y con esto se obtenga un mejor ajuste de dicho modelo a los resultados experimentales.
Parámetros anisotrópicos experimentales
Para realizar un análisis completo de una parte formada, las propiedades mecánicas específicas deben ser consideradas. La prueba de tensión es usada para determinar las propiedades reportadas comúnmente (módulo de elasticidad, resistencia última a la tensión, esfuerzo de cedencia, elongación), así como dos propiedades especialmente importantes en el formado: exponente de endurecimiento por deformación n y la relación de deformación plástica r.
Donde σ es el esfuerzo real, ε es la deformación real y K es una constante de proporcionalidad. La relación de deformación plástica, r, describe la resistencia del material al adelgazamiento durante las operaciones de formado, y es la razón de la deformación verdadera en la dirección del ancho (∈w ) a la deformación verdadera en la dirección del espesor (∈t ) de una lámina deformada plásticamente.
La orientación de la dirección de laminado en una pieza, relativa a la dirección de la deformación crítica, puede ser la diferencia entre producir una buena parte o producir desechos (Semiatin, 1996).
Las propiedades mecánicas de una lámina de aleación de aluminio, objeto del presente estudio, se obtienen de una prueba de tensión uniaxial. Esta se lleva a cabo en una máquina de tensión universal, con la configuración mostrada en la Figura 1, cuyos resultados permiten construir las curvas de esfuerzo real-deformación real que se presentan en la Figura 2. Las probetas utilizadas se obtuvieron cortando la geometría a 0°, 45° y 90° respecto a la orientación de laminado del aluminio, y de cada una se probaron 10 especímenes.

Fuente: Elaboración propia.
Figura 1 Configuración de la probeta en la prueba de tensión experimental.

Fuente: Elaboración propia.
Figura 2 Comparación de curvas esfuerzo real-deformación real a 0°, 45° y 90° de la dirección de rolado.
El valor de n se calcula por medio de regresión lineal en la zona del rango plástico de las curvas mostradas en la Figura 2, aplicando la norma ASTM E 646-00 (ASTM, 2000b) para cada una de las probetas (o para cada una de las direcciones de rolado).
Las ecuaciones para el cálculo del coeficiente K se presentan a continuación.
Los valores de r para cada orientación de laminado se obtienen aplicando la norma ASTM E 517-00 (ASTM, 2000a), en la que se considera que el volumen de la probeta permanece constante conforme las cargas son aplicadas.
Donde w0 y wf son el ancho inicial y final, l0 y lf son la longitud inicial y final de la zona calibrada. En la Tabla 1 se resumen las propiedades mecánicas de la aleación de aluminio y los valores de los parámetros calculados a partir de las curvas experimentales.
Modelo de LS-DYNA® con parámetros de Barlat
Para generar el código con el que trabaja el optimizador, es necesario tener una simulación en el programa LSDYNA® de la prueba a tensión (tres códigos, uno para cada dirección de laminado) equivalente a la que se realiza de manera experimental. Para las tres simulaciones, con base en la norma ASTM E 8M-04 (ASTM, 2004) se toman las dimensiones de la probeta tipo plana (sheet type), para la longitud de 200 mm. Las dimensiones relevantes para la prueba son: espesor de la lámina 0.92 mm, longitud de la sección calibrada 50 mm, ancho de la sección calibrada 12.5 mm, longitud de la sección de sujeción 50 mm y ancho de la sección de sujeción 20 mm. La norma estipula las velocidades a las cuales se debe de deformar la probeta; en este caso, se toma el rango máximo de 0.25 mm/mm por minuto, equivalente a una velocidad de desplazamiento de las mordazas de 0.208 mm/s. Se generan 1881 nodos, de los cuales son de interés aquellos que representan los puntos en los cuales toma medición el extensómetro en la prueba de tensión experimental. El tipo de elemento es SHELL163 con 5 puntos de integración a través del espesor y el modelo de material es no lineal inelástico de tres parámetros de Barlat. En la Figura 3 se muestra la configuración de la prueba a tensión en la simulación.

Fuente: Elaboración propia.
Figura 3 Configuración de la prueba a tensión en la simulación en software LS-DYNA®.
Se llevan a cabo tres optimizaciones en total, una para cada dirección de laminado del material. Como se menciona, para cada una debe existir una simulación de la prueba a tensión y, por supuesto, el código de la misma en el lenguaje de LS-DYNA®. Para cada simulación se alimenta el modelo de material con las constantes obtenidas de la curva experimental correspondiente a la dirección de laminado, es decir, la prueba experimental para la dirección de laminado a 0° alimenta las constantes del modelo de material para la generación de los códigos de la simulación y optimización de la prueba de tensión a 0°. Los valores de las constantes del modelo de material para cada dirección se resumen en la Tabla 1.
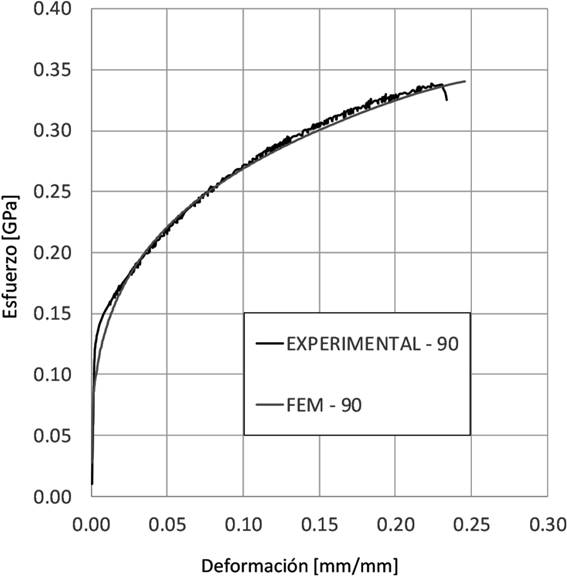
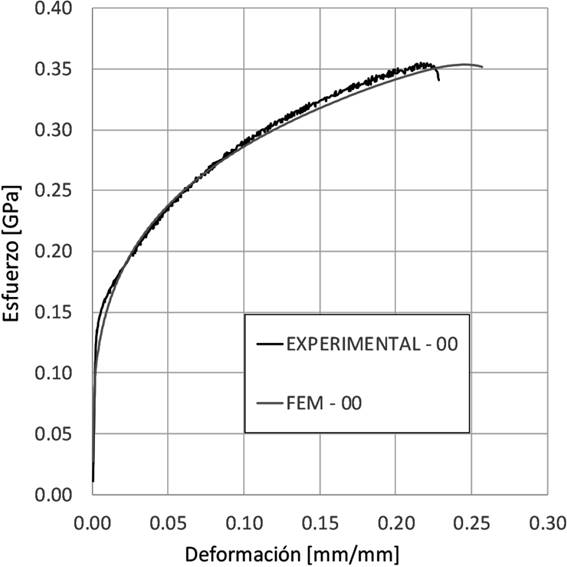
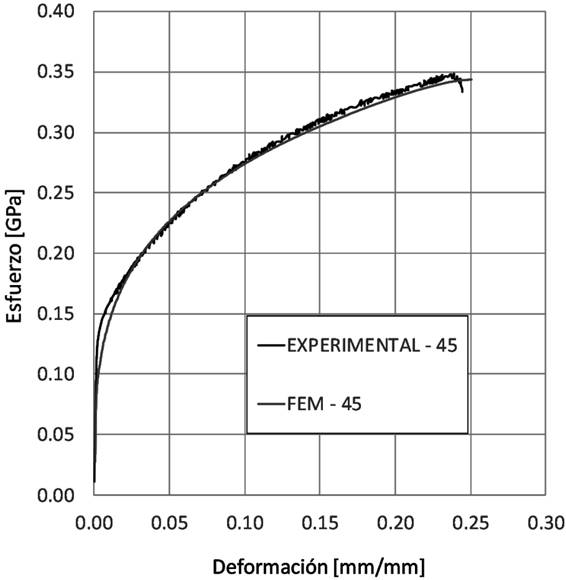
Una vez que se tienen las simulaciones en LSDYNA® de las pruebas de tensión, se compara la curva deformación real-esfuerzo real de las pruebas experimentales contra la equivalente obtenida de la simulación para cada dirección de laminado, así se observa la diferencia que existe entre la respuesta que tiene el modelo de elemento finito con respecto al comportamiento verdadero. En las Figuras 4, 5 y 6 se muestran las curvas experimentales y de simulación para las direcciones de laminado 0°, 45° y 90°, respectivamente, donde se observa una diferencia significativa para el comportamiento del modelo de elemento finito en la zona de transición de la parte lineal a la no lineal, y una diferencia apenas perceptible en la curva a partir de una deformación del 10% hasta el final de la curva, debido a que los parámetros son obtenidos mediante una aproximación al comportamiento general de la curva experimental de cada caso.
Fuente: Elaboración propia.
Figura 4 Curva real y de modelo de elemento finito del comportamiento esfuerzodeformación para la dirección 0°.
Fuente: Elaboración propia.
Figura 5 Curva real y de modelo de elemento finito del comportamiento esfuerzodeformación para la dirección 45°.
Modelo de LS-OPT® con parámetros de Barlat
En el enfoque de diseño convencional, un diseño se mejora mediante la evaluación de su respuesta al hacer cambios basados en la experiencia o la intuición del mismo. Esta aproximación no siempre lleva al resultado deseado, dado que los objetivos del diseño están algunas veces en conflicto, y no siempre es claro cómo cambiar el diseño para lograr el mejor arreglo de los objetivos; un enfoque más sistemático puede ser obtenido usando un proceso inverso para especificar primero los criterios y posteriormente definir el “mejor” diseño.
El procedimiento por el cual los criterios de diseño, procesos de manufactura y técnicas de análisis, se incorporan como objetivos y restricciones en un problema de optimización que posteriormente se resuelve, se conoce como diseño óptimo. Los métodos computacionales han tenido un reciente avance para la solución de problemas no-lineales complejos que pueden ser analizados mediante el uso de rutinas (Stander et al., 2013).
En numerosas aplicaciones industriales y de investigación, LS-DYNA® ha demostrado ser eficiente y confiable, especialmente en casos de comportamiento no-lineal. Este éxito de simulaciones numéricas ha propiciado que incluso se pueda utilizar en sustitución de experimentos físicos en el diseño, y con ello se ha acelerado el desarrollo de herramientas de optimización basadas en simulación tales como LS-OPT®, desarrollada por Livermore Software Technology Corporation (LSTC®).
En lo que respecta a la identificación de parámetros, un modelo computacional es calibrado con resultados experimentales. Estos últimos son fijados como valores-objetivo, aunque también se pueden especificar restricciones. La metodología para obtener parámetros de un material a partir de resultados experimentales es conocida como identificación de parámetros del material. Ejemplos representativos son el uso de funciones compuestas y problemas no restringidos.
LS-OPT® usa simulaciones paramétricas en combinación con el programa LS-DYNA® para realizar una calibración automática de datos experimentales. El objetivo es minimizar el error entre las simulaciones numéricas y experimentales con respecto a variables definidas por el usuario (Gladman, 2007).
Los parámetros de Barlat a optimizar con el módulo LS-OPT® en el presente trabajo son:
Relación de deformación plástica r, en las tres direcciones de laminado como en la prueba uniaxial (r00, r45 y r90).
Constante de proporcionalidad K.
Exponente de endurecimiento por deformación n.
Para cada optimización se requiere de un archivo que contenga una base de datos tabulada de la curva experimental desplazamiento-fuerza axial, ya que el módulo LS-OPT® en cada iteración genera una curva desplazamiento-fuerza axial del modelo de elemento finito y lo compara con la curva experimental que se le proporciona. El optimizador asigna valores a las variables, resuelve la simulación de la prueba a tensión y calcula la curva desplazamiento-fuerza axial de la simulación y la compara contra la experimental en cada iteración. El programa tiene establecido una corrida de 10 iteraciones, y en cada iteración se resuelven 10 simulaciones de la prueba a tensión con valores que se asignan mediante un diseño factorial. En la Figura 7 se muestra el diagrama de flujo que se sigue en el proceso de optimización descrito. Los valores obtenidos para el diseño factible en cada una de las tres direcciones de laminado se presentan en la Tabla 2.
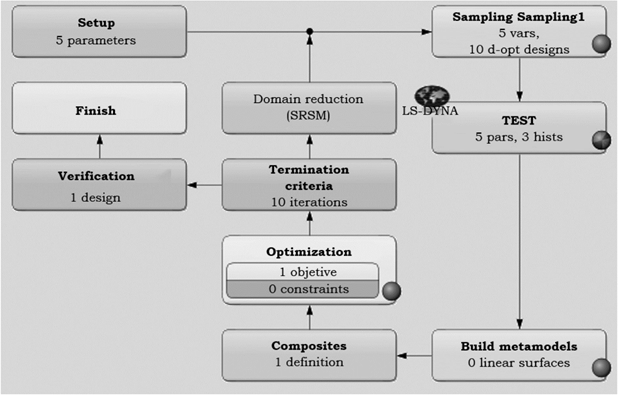
Fuente: Elaboración propia.
Figura 7 Diagrama de flujo en el proceso de optimización en módulo LS-OPT®.
Tabla 2 Parámetros de Barlat para el diseño factible en las direcciones de laminado.

Fuente: Elaboración propia.
Una vez que se tienen los valores de los parámetros del mejor diseño obtenido para cada dirección de laminado, con ellos se alimentan los códigos de las simulaciones de las pruebas a tensión de LS-DYNA® y se vuelven a correr las simulaciones, obteniendo con ello nuevas curvas de deformación-esfuerzo por el método de elemento finito.
En las Figuras 8, 9 y 10 se muestran las curvas deformación-esfuerzo con los valores optimizados para el modelo de material, para las direcciones 0°, 45° y 90°, respectivamente, comparados contra las curvas experimental y la obtenida por simulación antes de la optimización de los parámetros.
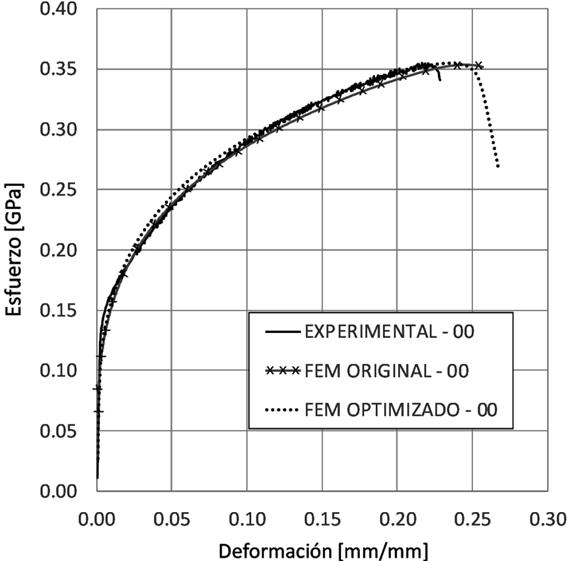
Fuente: Elaboración propia.
Figura 8 Curva deformación-esfuerzo, experimental, simulación por elemento finito y simulación por elemento finito con parámetros optimizados para la dirección 0°.
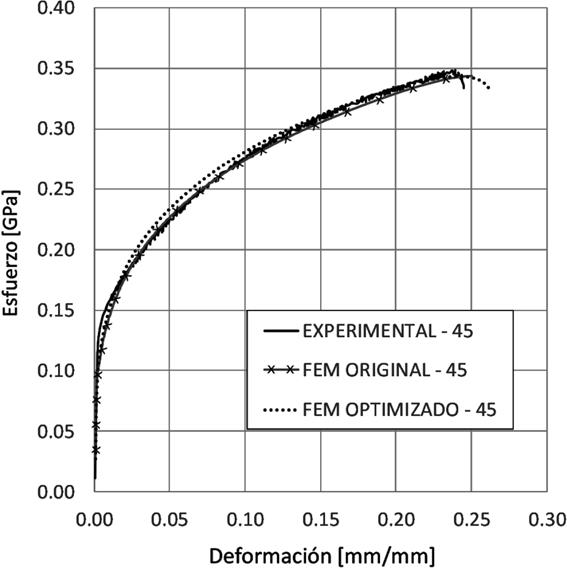
Fuente: Elaboración propia.
Figura 9 Curva deformación-esfuerzo, experimental, simulación por elemento finito y simulación por elemento finito con parámetros optimizados para la dirección 45°.
Discusión
En la Figura 2 se puede observar que en la curva deformación-esfuerzo de las pruebas experimentales existe diferencia entre los valores obtenidos para las tres direcciones de laminado, lo cual es esperado, ya que las propiedades del material real cambian dependiendo de la orientación que se elija para el análisis.
En las Figuras 3, 4, y 5 se observan las curvas experimental y de simulación por elemento finito antes de la optimización para cada dirección de laminado. Además de la diferencia de valores obtenidos en la zona de transición y en gran parte de la zona plástica, no existe la parte de la curva que representa el rompimiento de la probeta en las curvas de las simulaciones, es decir, no se aprecia que exista un esfuerzo a la ruptura.
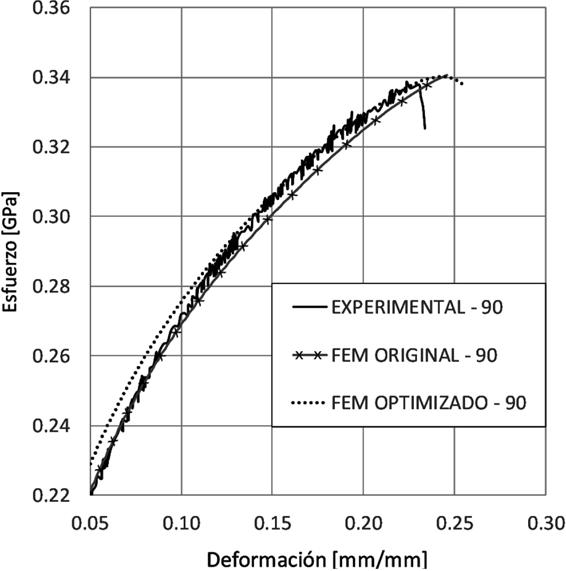
En las Figuras 8, 9 y 10 se observan las curvas experimental y de simulación con parámetros optimizados. Se identifica una diferencia mayor de los valores obtenidos de la simulación después de la optimización en la zona de transición lineal-no lineal. Sin embargo, en la zona plástica, aproximadamente a partir de un 0.10 de deformación, se reduce esa diferencia, además de que las curvas ya presentan la zona de la ruptura. En las Figuras 11, 12 y 13 se muestra a detalle la zona plástica de las curvas para las diferentes direcciones de laminado.
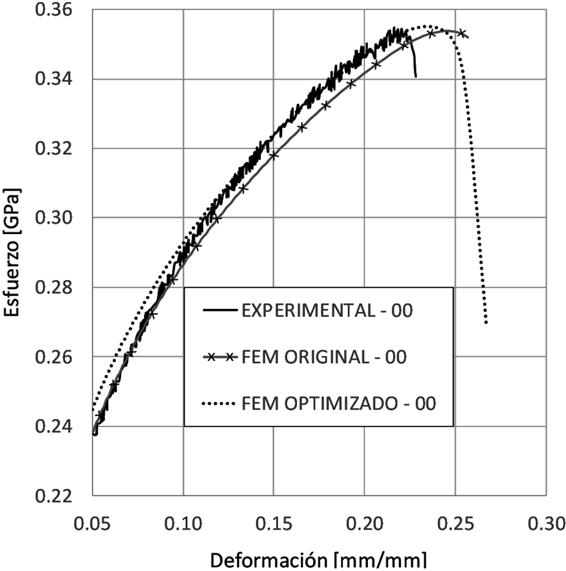
Fuente: Elaboración propia.
Figura 11 Curva deformación-esfuerzo, experimental, simulación por elemento finito y simulación por elemento finito con parámetros optimizados para la dirección 0° en la zona plástica.
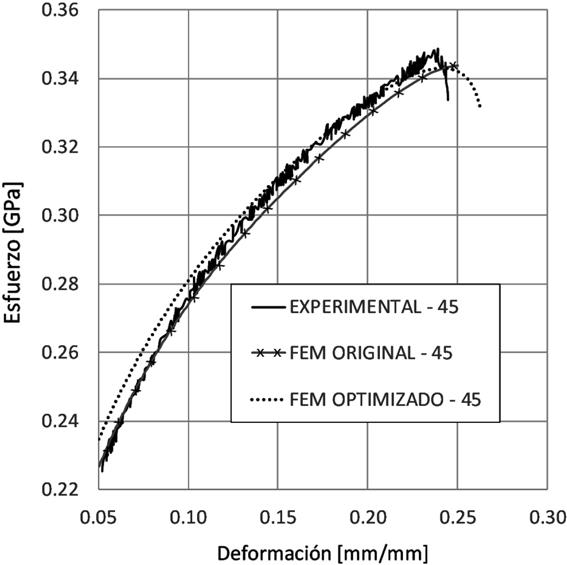
Fuente: Elaboración propia.
Figura 12 Curva deformación-esfuerzo, experimental, simulación por elemento finito y simulación por elemento finito con parámetros optimizados para la dirección 45° en la zona plástica.
Conclusión
En este trabajo se describe el procedimiento para hacer la caracterización de una aleación de aluminio laminado, con base en las normas ASTM aplicables. También se describe la metodología aplicada para hacer la identificación de los parámetros del modelo de material propuesto y la optimización de su ajuste a los resultados experimentales obtenidos.
Una vez analizadas las curvas deformación-esfuerzo (experimental, simulación y simulación con parámetros optimizados) se concluye que las curvas con los parámetros optimizados se ajustan mejor a los resultados experimentales en la zona plástica inicial, aunque a partir de 0.15 de deformación muestran ligeras diferencias, el ajuste es aceptable para cada dirección de laminado. Asimismo, resalta la presencia de la zona de ruptura, aunque la deformación a la cual aparece es mayor, específicamente a un valor positivo de máximo 0.05 mm/mm de deformación respecto a las curvas experimentales para las tres curvas.
El modelo de material de 3 parámetros de Barlat es utilizado en el modelado de fenómenos de alta plasticidad, por lo tanto, haber obtenido un mejor ajuste en la zona plástica es un resultado importante del procedimiento descrito en el presente trabajo. Una vez que se han mostrado sus ventajas, es posible usar este procedimiento con más iteraciones para evaluar si los valores de los parámetros que se optimizan cambian de manera significativa con respecto a los obtenidos con las 10 iteraciones inicialmente designadas. Así también trabajos futuros pueden incluir un criterio de ruptura, con el cual se mejoren los resultados hacia el final de la curva esfuerzo-deformación real.











 nueva página del texto (beta)
nueva página del texto (beta)