Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Acta universitaria
versión On-line ISSN 2007-9621versión impresa ISSN 0188-6266
Acta univ vol.25 no.2 México mar./abr. 2015
https://doi.org/10.15174/au.2015.688
Ciencias exactas e ingenierías
El cálculo diferencial e integral fraccionario y sus aplicaciones
The differential and integral fractional calculus and its applications
M. Guía-Calderón*, J. J. Rosales-García*, R. Guzmán-Cabrera*, A. González-Parada*, J. A. Álvarez-Jaime*
* Departamento de Ingeniería Eléctrica, División de Ingenierías, Campus Irapuato-Salamanca, Universidad de Guanajuato. Carretera Salamanca-Valle de Santiago km. 3.5 + 1.8 km, comunidad de Palo Blanco, Salamanca, Guanajuato, México, C.P. 36885. Tel.: (464) 6479940, ext. 2369 y 2464. Correos electrónicos: guia@ugto.mx; rosales@ugto.mx; guzmanc@ugto.mx
Recibido: 23 de noviembre de 2014.
Aceptado: 12 de marzo de 2015.
Resumen
Durante los últimos 20 años, el cálculo de orden arbitrario (mejor conocido en la literatura como cálculo de orden fraccionario) se ha desarrollado de manera impresionante. Sin embargo, en México no hay grupos consolidados en el estudio y su aplicación. El objetivo de este trabajo es dar a conocer los orígenes y el desarrollo del cálculo fraccionario, con la finalidad de motivar a los futuros investigadores a incursionar en esta área tan interesante del análisis matemático no convencional. Finalmente, como ejemplo, se analiza el movimiento vertical de una partícula en el seno de un medio donde la resistencia es proporcional a la velocidad.
Palabras clave: Derivadas e integrales fraccionarias; ecuaciones diferenciales fraccionarias.
Abstract
Over the last 20 years arbitrary order calculus (better known in the literature as fractional calculus) has been developed impressively. However, in Mexico there are no solid groups devoted to its study and applications. The objetive of this work is to present the origins and development of fractional calculus, in order to encourage future researchers to venture into this very interesting area of unconventional mathematical analysis. Finally, as an example, vertical motion of a particle within a medium where resistance is proportional to speed is analized.
Keywords: Fractional differentias and integrals; fractional differential equations.
INTRODUCCIÓN
En el estudio del cálculo se aprenden algunos métodos de derivación e integración, así como la gran importancia que tienen estas herramientas matemáticas en la ciencia e ingeniería. Se aprende, de igual forma, que la derivación y la integración son operaciones inversas una de la otra y difieren en una o varias constantes, dependiendo del orden de la derivada. Si (dn/dxn) f (x) = Dn f (x) representa la n-ésima derivada de la función f (x) con respecto a x, con n = 1, 2, entonces In f (x) = ∫f (x)dx = D-n f (x) representará la n-ésima integral o integral iterada de la misma función f (x). Sin embargo, los operadores de derivación e integración vistos en los cursos universitarios han sido de orden entero n = 1, 2, .... Esto es lo que conocemos como cálculo diferencial e integral ordinario o de orden entero. Aquí surgen algunas preguntas: ¿por qué debe ser n = 1, 2, 3, ¿existirá la posibilidad de que sea n = 1/2, 1/3, ... ?
El objetivo principal de este trabajo es, además de dar a conocer la historia del cálculo de orden fraccionario desde las fuentes históricas originales, completar ciertas expresiones escritas en libros y artículos cuando tratan sobre la historia y origen del cálculo de orden fraccionario. Por ejemplo, la expresión "Así se tiene que d1:2x será igual a  " no muestra el razonamiento de Leibniz (1859) para establecer la derivada fraccionaria de orden un medio de x; o bien, "La referencia a una derivada fraccionaria en un libro de texto aparece por primera vez en 1819 en el libro del matemático francés S. F. Lacroix (1765-1843). El libro, de casi 700 páginas, dedica dos páginas [...]", que sin ver si quiera el índice del libro de Lacroix (1819) le atribuyen la definición de la derivada de orden fraccionario un medio; otra expresión común es: "Euler solo menciona pero no da ejemplos ni aplicaciones de la derivada de orden fraccionario", sin leer en realidad el texto completo del documento a que se hace referencia en este mismo trabajo (Euler, 1738). Por tal motivo, se considera importante en este trabajo dar un poco más de información sobre los documentos originales donde quedó escrito el pensamiento de Leibniz, Euler, Liouville y Riemann. Se presenta, además, una aplicación con la que se analiza el movimiento vertical de una partícula en el seno de un medio donde la resistencia es proporcional a la velocidad (Rosales, Guía, Martínez & Baleanu, 2013), con el propósito de motivar al lector para que se inicie en el estudio del cálculo de orden fraccionario.
" no muestra el razonamiento de Leibniz (1859) para establecer la derivada fraccionaria de orden un medio de x; o bien, "La referencia a una derivada fraccionaria en un libro de texto aparece por primera vez en 1819 en el libro del matemático francés S. F. Lacroix (1765-1843). El libro, de casi 700 páginas, dedica dos páginas [...]", que sin ver si quiera el índice del libro de Lacroix (1819) le atribuyen la definición de la derivada de orden fraccionario un medio; otra expresión común es: "Euler solo menciona pero no da ejemplos ni aplicaciones de la derivada de orden fraccionario", sin leer en realidad el texto completo del documento a que se hace referencia en este mismo trabajo (Euler, 1738). Por tal motivo, se considera importante en este trabajo dar un poco más de información sobre los documentos originales donde quedó escrito el pensamiento de Leibniz, Euler, Liouville y Riemann. Se presenta, además, una aplicación con la que se analiza el movimiento vertical de una partícula en el seno de un medio donde la resistencia es proporcional a la velocidad (Rosales, Guía, Martínez & Baleanu, 2013), con el propósito de motivar al lector para que se inicie en el estudio del cálculo de orden fraccionario.
Breve historia del cálculo fraccionario
El nacimiento del cálculo de orden fraccionario tuvo lugar después de la publicación, en 1675, de un documento de G. W. Leibniz, donde aparecía el símbolo dny/dxn, el cual se refiere a la derivada de orden n de la función y respecto de x, donde n es un número natural. Sin embargo, ¿tendrá sentido extender los valores de n al conjunto de los números racionales, irracionales o complejos?
G. W. Leibniz (1646-1716), al responder a una carta de G. F. Antoine, marqués de l'Hôpital (1641-1704), cuestiona sobre qué sucedería si n fuera 1/2. El 30 de septiembre de 1695 contesta de manera intuitiva: "esto conduciría aparentemente a una paradoja de la cual algún día serán extraídas consecuencias muy útiles" (Leibniz, 1859). En esta misma carta, Leibniz da una aproximación a lo que podría ser una derivada fraccionaria, poniendo como ejemplo la derivada 1/2 de x. El razonamiento de Leibniz es el siguiente: "Sea dada la ordenada x en progresión geométrica de modo que si se tiene una constante dβ sea dx = xdβ: α, o (sustituyendo α por la unidad) dx = xdβ, ahora ddx será  y d3x será =
y d3x será =  etcétera y dex =
etcétera y dex =  . Y de esta forma el exponente diferencial es cambiado por exponente potencia reemplazando dx: x por dβ se tendrá dex =
. Y de esta forma el exponente diferencial es cambiado por exponente potencia reemplazando dx: x por dβ se tendrá dex = 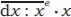 . Así se tiene que d1:2x será igual a
. Así se tiene que d1:2x será igual a  (Leibniz, 1859)1.
(Leibniz, 1859)1.
En notación actual, la definición que propone Leibniz para la derivada de orden fraccionario de x está dada por:

y para el caso particular e = 1/2 se tendrá:

Sin embargo, la primera referencia a una derivada fraccionaria aparece, por primera vez, en un artículo escrito por Leonhard Euler (1707-1783) entre 1729-1730 y publicado en 1738, donde aplica su fórmula de interpolación del factorial entre números enteros positivos para dar una definición de la derivada de orden fraccionario. El razonamiento de Euler es el siguiente: se trata de investigar la relación entre dn(ze) y dzn con dz constante. Supone primero que n es un entero y si n = 1, ez e-1 = [1-2-3...e/1-2-3...(e -1)]z e-1, si n = 2, e(e -1)z e-2 = [1-2-3...e/1-2-3...(e -2)]z e-2 si n = 3, e(e -1)(e -2)z e-3=[1-2-3...e/1-2-3...(e -3)] z e-3, en general, dnze/dzn= [1-2-3...e/1-2-3...(e -n)]z e-n. Pero 1-2-3...e =∫dx(-1x)e y 1-2-3...(e-n) = ∫dx(-1x)e-n, por lo tanto:

donde los límites de integración son x = 0 como límite inferior y x = 1 como límite superior. En (2) deberá actualizarse la simbología 1n para 1. Después de Andrien-Marie Legendre (1752-1833) se usa la notación Γ(e + 1) para la integral del numerador y Γ(e — n + 1) para la integral del denominador.
Es posible realizar algunas operaciones algebraicas con (2) para comparar la definición de la derivada de una función potencia con definiciones más recientes y, a la vez, para hacer notar la diferencia con la definición propuesta por Leibniz (1859). La ecuación dada por (2) también puede ser escrita como:

equivalente a escribir:

Multiplicando numerador y denominador de (4) por Γ(-n) ≠ 0 se obtiene:

donde B(e + 1, - n) = B(-n, e + 1) es la función beta, definida por:

Sustituyendo (6) en (5) y haciendo zt = u se obtiene:

Si n no es un entero, entonces (7) es la fórmula de Euler (1738) para una derivada fraccionaria de una función potencia, y quedaría como sigue:

La existencia de la derivada fraccionaria de orden α está determinada por la convergencia de la integral en (8). Euler (1738) también da un ejemplo para e = 1 y n = 1/2 y obtiene, en la simbología actual:

donde A es el área de un círculo de diámetro igual a la unidad. También se puede utilizar la ecuación (4) para obtener:

Para finalizar, Euler (1738) propone la siguiente ecuación diferencial fraccionaria para determinar la forma de la curva dada por la ecuación:

la curva buscada se obtiene de la siguiente manera:

En el libro de S. F. Lacroix mencionado antes se incluye el artículo publicado por Euler, en el cual se define la derivada de orden fraccionario de una función potencia. Así, pues, se puede decir que a Euler se le debe la primera fórmula para la derivada fraccionaria de una función potencia.
En 1822, en su libro Théorie Analytique de la Chaleour (1822), Jean-Baptiste Joseph Fourier (1768-1830) indica que diferenciales e integrales de orden arbitrario i pueden ser obtenidas a partir de la ecuación:

y observando que la i-ésima derivada de la función coseno difiere sólo en el signo y en el factor pi, se obtiene:

donde i puede ser cualquier cantidad: positiva o negativa. Así, pues, Fourier (1822) presenta una fórmula general para la derivación e integración fraccionaria. Una función tendrá derivada o integral fraccionaria si las integrales impropias convergen. Sin embargo, no presenta ejemplos de aplicación ni desarrolla un tratado completo sobre el cálculo integro-diferencial de orden fraccionario. Indica, además, en el mismo libro, que sus resultados sobre las derivadas e integrales de orden fraccionario ya los había publicado con anterioridad en una "Mémoire sur les vibrations des surfaces élastiques, lu à la séance de l'Académie des Sciences, le 6 juin 1816 (art. VI, § 10 et 11, et art. VII, § 13 et § 14)" (Fourier, 1822).
Una de las primeras aplicaciones a la física es proporcionada por Niels Henrik Abel (1802-1829). El problema consiste en encontrar la forma de la curva sobre un plano vertical, tal que un objeto, al deslizarse sin fricción sobre ella, llegue al final de su recorrido en un tiempo que sea independiente del lugar en que comience el movimiento. Si el tiempo de caída es una constante conocida, la ecuación integral de Abel (1839a) tiene la forma:

En realidad, Abel estudió ecuaciones integrales con núcleos de la forma (x — t)α (Abel, 1839b), siendo la ecuación (14) un caso particular cuando α = 1/2. Para determinar la función desconocida f(x) en (14), Abel (1839a) escribió la parte derecha de (14) como:

Después, tomando la derivada 1/2 en ambos lados de la ecuación obtuvo:

ya que los operadores fraccionarios (derivadas e integrales con ciertas condiciones sobre f) satisfacen la propiedad D1/2 D-1/2 f = D0 f = f. Entonces, calculando la derivada de orden 1/2 de la constante k en (16) se determina la función f(x). Este resultado de Abel (1839a) se considera un gran logro para el desarrollo posterior del cálculo de orden fraccionario. Es importante hacer notar que la derivada de orden fraccionario de una constante no siempre es cero.
Derivada fraccionaria de Liouville
Joseph Liouville (1832) hace referencia, en Mémoire sur questions de Geométrie et de Mécanique..., a los trabajos de Euler, Laplace, Fourier y al libro de cálculo de Lacroix; también hace referencia a la cuarta carta de Leibniz a Wallis (Leibniz, 1832), aunque se basa más en los trabajos de Laplace (1812) y Fourier (1822) para hacer su desarrollo del cálculo integro-diferencial de orden fraccionario. Liouville (1832) parte de la derivada de orden entero de la función exponencial, esto es:

donde indica que m puede ser cualquier número real o complejo, positivo (indicando la derivación) o negativo (indicando la integración). Partiendo, pues, de esta definición de la derivada, y suponiendo que una función y se puede desarrollar en una serie de exponenciales, establece una fórmula general para la derivada. Primero desarrolla y en serie de exponenciales:

y deriva término a término esta serie para obtener:

A la expresión (19) se le conoce como la primera definición de derivada fraccionaria de Liouville. En la misma memoria, Liouville (1832) da dos ejemplos, que algunos historiadores han llamado como la segunda definición de Liouville. El primer ejemplo es para la función y = 1/ x, en tanto que el segundo es una generalización del primero y = 1/ xn, esto es:

Es importante notar que (20) no es más que la transformada de Laplace (1812) de la función escalón unitario en la que se ha cambiado s por x. Partiendo de (20), Liouville (1832) utiliza la fórmula para la derivada de orden fraccionario y obtiene:

Para el segundo ejemplo, define:


A continuación, Liouville (1832) da una expresión para la integral fraccionaria de una función arbitraria, pero con restricciones:

donde μ > 0 y si φ(.)= ΣAm emx y m debe ser menor que cero o si es de la forma m = -p + q , p debe ser mayor que cero. Al final de cuentas lo que se trata es de cuidar la convergencia de la integral impropia de la derecha en (24), que se logra cuando el integrando se anula en ∞, de acuerdo con Liouville (1832).
, p debe ser mayor que cero. Al final de cuentas lo que se trata es de cuidar la convergencia de la integral impropia de la derecha en (24), que se logra cuando el integrando se anula en ∞, de acuerdo con Liouville (1832).
Para obtener la derivada de φ(x), Liouville (1832) hace μ = n - p, donde n es el menor entero positivo mayor que μ, con lo que obtiene:

Liouville (1832) ha llegado a la misma conclusión a la que había llegado Fourier (1822) dieciséis años antes: la derivada de orden fraccionario es una integral definida, esto conducirá, como se verá más adelante, a un nuevo punto de partida en la definición de la derivada de orden fraccionario. Liouville (1832), en la misma memoria, aplica la fórmula para resolver varios problemas de eletrodinámica, geometría y mecánica.
Antes de continuar con este nuevo enfoque que trata a la derivada de orden fraccionario como una integral, seguiremos al enfoque propuesto por Grünwald-Létnikov.
Derivada fraccionaria de Grünwald-Létnikov
Anton Karl Grünwald (1838-1920), en 1867, y Aleksey Vasilievich Létnikov (1837-1888), en 1868, proponen la definición de la derivada fraccionaria, partiendo de la definición básica de la derivada de orden entero; esto es:

donde

Haciendo algunas operaciones aritméticas se llega a las siguientes fórmulas de la derivada fraccionaria de Grünwald-Létnikov:


Las fórmulas (27) y (28) son muy útilies en el cálculo numérico de la derivada de orden fraccionario; en estas fórmulas a < x es el punto desde donde se calculará la derivada correspondiente al punto x.
Otro punto de partida para definir la derivada de orden fraccionario fue propuesto por Liouville (1832), quien, partiendo de la integral del orden fraccionario, obtiene:

donde α < x. La ecuación se puede obtener de (8) haciendo uβ = f (t), sustituyendo α por -α y u por t. Ahora bien, si n -1 < α < n se puede hacer α = n -v, entonces se tiene:

La derivada fraccionaria está definida, en este caso, si la integral converge, debido a que, según se vio al inicio de esta sección, Liouville (1832) desarrolla f(t) en una serie de exponenciales. La integral en (30) converge si α = —∞, las partes reales de las potencias de e son mayores que cero y x > 0.
Derivada fraccionaria de Riemann
Bernhard Riemann (1826-1866), en un manuscrito del 14 de enero de 1898, en su época de estudiante y publicado en forma póstuma, propone:

Para la fórmula (31), Riemann (1898) desarrolla f(t) en una serie de potencias, por lo que el límite inferior en este caso es k = 0. A la ecuación:

Se le llama fórmula para la derivada de orden fraccionario de Riemann-Liouville, para c = 0 y para c = —∞, respectivamente.
Derivada fraccionaria de Caputo
En 1969, el físico matemático italiano Michele Caputo dio una nueva definición de derivada de orden fraccionario que permitía interpretar físicamente las condiciones iniciales de los cada vez más numerosos problemas aplicados que se estaban estudiando. Caputo (1969) definió la derivada fraccionaria como:

donde n - 1 < α < n y f(n) es una derivada ordinaria. La relación entre ambas definiciones (32) y (33) de la derivada de orden fraccionario está dada por:

Se puede notar que la definición de la derivada de orden fraccionario propuesta por Michele Caputo (1969) es más restrictiva que la de Riemann-Liouville, ya que en el primer caso la función debe ser derivable, lo que no requiere la segunda definición.
La transformada de Laplace de la derivada fraccionaria de Riemann-Liouville (32) y de Caputo (33) están dadas por las expresiones:


donde F(s) es la transformada de Laplace de f(t). Observe que la expresión (35) contiene condiciones iniciales fraccionarias, lo cual tiene dificultades de interpretación en la aplicación a problemas físicos, mientras que la expresión (36) tiene condiciones iniciales ordinarias, es decir, no fraccionarias, ya que f(k)(0) son derivadas ordinarias (k = 1, 2, 3,...). Ésta es una de las razones por las cuales en los problemas de aplicación se usa frecuentemente la derivada fraccionaria de Caputo (1969) (36).
Existen, actualmente, dos aplicaciones principales del cálculo de orden fraccionario: aplicaciones al control y aplicaciones de modelado matemático. Esta última aplicación incluye el análisis, simulación, diseño, etcétera. Cuando se habla de modelado matemático se incluyen, preferentemente, aquellos fenómenos cuyos modelos de orden entero no satisfacen los datos experimentales, por ejemplo fenómenos de difusión anómala: sub-difusión y super-difusión, viscoelasticidad, superconductividad, cáncer, etcétera.
En este punto surgen algunos cuestionamientos: ¿cuál es la interpretación física de una derivada y/o integral fraccionaria?, ¿por qué hay diferentes definiciones de derivada e integral fraccionaria? En el cálculo ordinario, estas preguntas están bien claras y tienen una interpretación muy elegante geométrica y físicamente. Sin embargo, en el caso del cálculo fraccionario aún estas preguntas no están completamente resueltas, así que hay mucho trabajo por hacer. En la siguiente sección damos un ejemplo sencillo y detallado de aplicación del cálculo fraccionario.
Movimiento vertical en un campo gravitacional
Se analizará, como un ejemplo de aplicación del cálculo fraccionario, el caso de una partícula en movimiento vertical en el seno de un medio, donde la resistencia es proporcional a la velocidad. Supóngase que una partícula se lanza hacia abajo con una velocidad inicial υ0 desde una altura h en un campo gravitacional constante. La ecuación de movimiento es entonces (Thornston & Marion, 2004):

donde k es una constante positiva responsable de la fuerza de resistencia con unidades de segundos inversos, s-1, y -mkv representa una fuerza dirigida hacia arriba, ya que tomamos z y υ = ż positivos en ese sentido, y el movimiento se dirige hacia abajo; o sea υ < 0 de forma que -mkv > 0. Si la condición inicial se considera υ(0) = υ0, donde υ0 es la velocidad inicial del cuerpo cayendo, la solución es:

Dado que υ= dz/dt se integra una vez más, tomando en cuenta la condición inicial z(0) = h, como resultado se obtiene:

La expresión (38) indica que a medida que el tiempo crece (t → ∞), la velocidad se va aproximando al valor υ(t) → -g / k, la cual es llamada velocidad final o velocidad terminal υf . Por otro lado, se ve en la ecuación (37) que cuando en ella se hace υ = -g / k, se consigue el mismo resultado, pues entonces la fuerza se anula y desaparece la aceleración. Cuando el módulo de la velocidad inicial sea mayor que el de la velocidad final, el cuerpo comenzará a moverse perdiendo velocidad y υ tenderá hacia el valor de la velocidad final desde el sentido contrario.
Ahora se analizará el problema anterior desde el punto de vista del cálculo fraccionario. Para ello se harán algunas modificaciones, como se muestra en (40), antes de pasar a la ecuación diferencial de orden fraccionario, a partir de (37). Estas modificaciones consisten en normalizar las variable υ y t tomando como base de normalización -g/ k y 1/ k para la velocidad y el tiempo, respectivamente, de forma que dividiendo υ entre -g/ k :

Esta ecuación diferencial se puede escribir también en función de una nueva variable dependiente y adimensional, representada por u, mientras que la variable temporal, adimensional, independiente es τ = kt. Se tiene, entonces:
![]()
En esta ecuación diferencial de orden fraccionario, las variables u y τ son adimensionales.
Aplicando la transformada de Laplace (Podlubny, 1999; Samko, Kilbas & Marichev, 1993) con la condición u(0) = u0 y 0) = -υ (0)k/g, obtenemos:

Resolviendo respecto a U(s) resulta:

Ahora, aplicando la transformada inversa de Laplace (Podlubny, 1999; Samko, Kilbas & Marichev, 1993) se tiene:
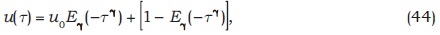
donde se han usado las fórmulas (Monje, Chen, Vinagre, Xue & Feliu-Batle, 2010)


Volviendo a las variables υ(t) y t se tiene:

Ahora, suponiendo que:

donde

Sustituyendo U(s) de (48) en (43) y resolviendo para W(s) se tiene:

Finalmente, se aplica la transformada inversa de Laplace (1812) a (49) y se realizan las operaciones necesarias para volver a las variables, t y z.

donde 0< β, γ ≤ 1.
Si en (50) se dan valores de 1 a β y γ, se recupera (39).
Si en (50) se hace β = γ, se obtiene:

Hoy en día, el cálculo fraccionario se ha aplicado en diferentes áreas de las ciencias e ingenierías, física, biología, química, geología, teoría de control, electromagnetismo, eléctrica, circuitos eléctricos, procesamiento de imágenes y señales, óptica, etcétera, y existen excelentes libros que tratan sobre su reciente desarrollo y aplicaciones como son: Baleanu, Günvec & Tenreiro (2010), Diethelm (2010), Duarte (2011), Mainardi (2010) y Tarasov (2010).
CONCLUSIÓN
En este trabajo se han presentado las distintas definiciones de la derivada e integral de orden fraccionario. Estas diferentes definiciones existen por no haber un consenso generalizado sobre qué son la derivada e integral de orden fraccionario de una función; es decir, no hay una interpretación física y geométrica consistente sobre ellas. Sin embargo, los modelos descritos por ecuaciones diferenciales de orden fraccionario, con las propiedades de no localidad y memoria, representan en forma más adecuada sistemas complejos heterogéneos que los modelos de orden entero, como se muestra en el ejemplo presentado para el movimiento vertical en un campo gravitatorio.
REFERENCIAS
Abel, N. H. (1839a). Resolution d'un problème de mécanique. Oeuvres Complètes (tomo premier, pp. 27-30). Gröndah: Christiana. [ Links ]
Abel, N. H. (1839b). Sur quelques intégrales defines. Oeuvres Complètes (tomo second, pp. 93-102). Gröndah: Christiana. [ Links ]
Baleanu, D., Günvec Z. B. & Tenreiro, M. J. A. (2010). New Trends in Nanotechnology and Fractional Calculus Applications (544 pp.). Dordrecht Heidelberg London New York: Springer. [ Links ]
Caputo, M. (1969). Elasticità e Dissipazione. Bologna: Zanichelli. [ Links ]
Diethelm, K. (2010). The Analysis of Fractional Differential Equations (248 pp.). Dordrecht Heidelberg London New York: Springer. [ Links ]
Duarte, O. M. (2011). Fractional Calculus for Scientists and Engineers (114 pp.). Dordrecht Heidelberg London New York: Springer. [ Links ]
Euler, L. (1738). De progressionibvs transcendentibvs, sev qvarvm termini generales algebraice dari neqvent, Commentarii Academiae Scientiarvm Imperialis PetropolitAn Ae (tomo V, pp. 36-57). San Petersburgo. [ Links ]
Fourier Joseph, J. B. (1822). Théorie Analytique de la Chaleur (pp. 561-562). Paris: Chez Firmin Didot, Père et fils. [ Links ]
Grünwald, A. K. (1867). Ueber, Begrenzte, Derivationen und Deren Anwendung, Zeitschrift für Mathematik und Physik, 12, 441-480. [ Links ]
Lacroix, S. F. (1819). Traité du calcul différentiel et du calcul intégral. Second édition, reveu et augmentée (pp. 409-410). Paris: Courcier. [ Links ]
Laplace, P. S. (1812). Théorie Analytique des Probabilities. M. V. Councier, Libraire pour les Mathématiques, quis des Agustins, 57. Paris: Imprimeur. [ Links ]
Leibniz, G. (1859). Mathematische Schriften. Berlin: Verlag von A. Asher & Comp. [ Links ]
Leibniz, G. (1832). Cuarta carta a Wallis. Oeuvres completes (tome III, 105 pp.). Paris. [ Links ]
Létnikov, A.V. (1868). Theory of differentiation of an arbitrary order Mat. Sb., 3, 1-68. [ Links ]
Liouville, J. (1832). Mémoire sur questions de Geométrie et de Mécanique, et sur un nouveau genre de Calcul pour résoudre ces Quesions. Journal de l'Ecole Polytechnique, 21(13), 1-66 y 67-163. [ Links ]
Mainardi, F. (2010). Fractional Calculus and Waves in Linear Viscoelsticity (368 pp). Ed. Imperial College Press. [ Links ]
Monje, C. A., Chen, Y., Vinagre, B. M., Xue, D. & Feliu-Batle, V. (2010). Fractional Order Systems and Controls, Fundamentals and Applications. Londres: Springer-Verlag London Limited. [ Links ]
Podlubny, I. (1999). Fractional Differential Equations. San Diego: Academic Press. [ Links ]
Rosales García, J. J., Guía Calderón, M., Martínez Ortiz, J. & Baleanu, D. (2013). Motion of a Particle in a Resisting Medium Using Fractional Calculus Approach. Proceedings of the Romanian Academy, 14(1), 42-47. [ Links ]
Riemann, B. (1898). Oeuvres mathématiques de Riemann. Paris: Gauthiervillar. [ Links ]
Samko, S. G., Kilbas, A. A. & Marichev, O.I. (1993). Fractional Integrals and Derivatives, Theory and Applications. Langhorne, PA: Gordon and Breach Science Publishers. [ Links ]
Tarasov, V. E. (2010). Fractional Dynamics; Applications of the Fractiona Calculus to Dynamics of Particles, fields and Media (522 pp.). Dordrecht Heidelberg London New York: Springer. [ Links ]
Thornston, S. T. & Marion, J. B. (2004). Classical Dynamics of Particles and Systems. Ed. Thomson Brooks/cole. [ Links ]
1 "Car soyent les ordenées x en progression Geometrique en sorte que prenant une constante dβ soit dx = xdβ: α, ou (prenant α pour l'unité) dx = xdβ, alors ddx sera  , et d3x sera =
, et d3x sera =  etc. et dex =
etc. et dex = . Et par cette adresse l'exposant differentiel est changé en exposant potentiel et remettant dx: x pour dβ, il aura dex=
. Et par cette adresse l'exposant differentiel est changé en exposant potentiel et remettant dx: x pour dβ, il aura dex= 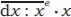 . Ainsi il s'ensuit que d1:2x sera egal ὰ
. Ainsi il s'ensuit que d1:2x sera egal ὰ .
.














