Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigaciones geográficas
versión On-line ISSN 2448-7279versión impresa ISSN 0188-4611
Invest. Geog no.85 Ciudad de México dic. 2014
https://doi.org/10.14350/rig.36934
Geografía física
Evaluación de la exactitud posicional vertical de una nube de puntos topográficos lidar usando topografía convencional como referencia
Vertical positional accuracy assessment of a topographic lidar point cloud using conventional surveying as reference
Wilver Enrique Salinas Castillo* Cutberto Uriel Paredes Hernández* Xicoténcatl Martínez Becerra** y Francisco Guevara Cortina**
* Instituto de Ingeniería y Ciencias, Facultad de Ingeniería y Ciencias, Universidad Autónoma de Tamaulipas, Centro de Gestión del Conocimiento, Centro Universitario Victoria, 87149, Ciudad Victoria, Tamaulipas, México. E-mail: wsalinas@uat.edu.mx; cparedes@uat.edu.mx
** GeoExpert S.C., Normal Superior 182, Col. Adolfo López Mateos 2A Etapa, 87025, Ciudad Victoria, Tamaulipas, México. E-mail: xicotencatl_mtz_b@hotmail.com; fgcortina@hotmail.com
Recibido: 26 de julio de 2013.
Aceptado en versión final: 3 de octubre de 2013.
Resumen
La exactitud vertical de datos lidar es normalmente establecida por proveedores comerciales en un EMC máximo de 0.150 m. Sin embargo, los resultados de evaluaciones de exactitud en las que se han utilizado datos de campo por lo menos tres veces más exactos que los datos lidar, sugieren que dicha exactitud se observa solo cuando la densidad de los datos lidar es mayor a un punto sobre el terreno por metro cuadrado. Desafortunadamente, el número de estos estudios es limitado y se requiere de la elaboración de otras evaluaciones que confirmen dicha hipótesis. En este estudio se evaluó la exactitud vertical de una nube de puntos topográficos lidar de una densidad de 1.02 puntos sobre el terreno por metro cuadrado, usando como referencia datos recolectados en campo mediante una estación total. Los resultados coinciden con aquéllos de estudios previos, por lo que se sugiere establecer la EPV de la nube de puntos topográficos lidar en 0.200 m para terreno mixto y de cambios constantes y en 0.150 m para terreno con cambios topográficos gentiles. Sin embargo, la EPV no refleja la magnitud del 95% de los errores bajo la presencia de errores sistemáticos, por lo cual es necesario incluir el percentil 95 de los errores en la documentación de datos lidar.
Palabras clave: Lidar, nube de puntos, exactitud posicional vertical (EPV), error medio cuadrático (EMC).
Abstract
Lidar is an active remote sensing technology that reduces the cost and time required to collect topographic data. The vertical accuracy of lidar data is normally set by commercial data providers at a maximum root mean square error of 0.150 m. However, the results of accuracy assessments where field data at least three times more accurate than lidar data have been used suggest that that accuracy is only met when the density of the lidar data is higher than 1 ground points per square meter. Unfortunately, the number of these studies is limited and more accuracy assessments are needed in order to establish the vertical accuracy of lidar data. In this paper, the vertical accuracy of a topographic lidar cloud point with a density of 1.02 ground points per square meter is assessed for different types of terrain. Reference data was collected on the field using a total station with millimeter accuracy in order to meet the ASPRS requirements for the accuracy assessment of lidar data. The results suggest that the vertical accuracy of topographic lidar data exceeds the accuracy specifications of commercial data providers and, also, are consistent with previous studies where the vertical accuracy of lidar was assessed under similar conditions. Therefore, it is suggested to set the vertical positional accuracy (EPV, after its Spanish acronym) of the lidar point cloud in 0.200 m for mixed terrain with constant changes and in 0.150 m for areas with smooth topographic changes. However, under the presence of systematic errors, the EVP does not convey the magnitude of 95% of the vertical errors, as intended; therefore, it is recommended to include the 95th error percentile in the documentation of lidar data.
Key words: Lidar, point cloud, vertical positional accuracy (EPV), root mean square error (RMSE).
Introducción
La elevación es una variable crítica para las bases de datos geográficas utilizadas por la comunidad científica, la iniciativa privada y agencias gubernamentales en proyectos ambientales y de ingeniería. Algunas aplicaciones prácticas de dicha variable, como la identificación de zonas inundables, la planificación regional y la selección de sitios para la construcción de nueva infraestructura, requieren de datos exactos para la generación de resultados confiables (Jensen, 2007). La magnitud de la exactitud requerida por cada aplicación varía, por lo cual los usuarios de datos de elevación deben verificar que la exactitud de los datos utilizados cumpla con los requerimientos mínimos de sus proyectos (Darnell et al., 2008). Desafortunadamente, en la mayoría de los casos, los usuarios de datos de elevación no cuentan con los recursos para obtener datos de mayor calidad y evaluar la exactitud de los productos de elevación que utilizan (Wechsler, 2003), por lo que deben recurrir a evaluaciones elaboradas por otros usuarios o investigadores para determinar la idoneidad de los datos para sus proyectos (Heuvelink et al., 1989). Del mismo modo, cuando aparecen nuevas tecnologías en el mercado, los usuarios de datos de elevación con recursos limitados dependen de las especificaciones emitidas por los proveedores de datos.
En el caso de lidar (Light Detection and Ranging), un sistema relativamente nuevo para la recolección de datos topográficos de alta precisión y alta densidad, los proveedores de datos especifican un error medio cuadrático (EMC) vertical máximo de 15 cm cuando se emplean sistemas aerotransportados (Bluesky, 2013; MAPA, 2013; Sanborn, 2013). Sin embargo, en la mayoría de los casos, los proveedores de datos no especifican en la documentación de sus productos si el EMC especificado proviene de las características técnicas del equipo lidar utilizado o de evaluaciones realizadas por organizaciones financieramente independientes de los mismos, como lo recomienda la Sociedad Americana de Fotogrametría y Percepción Remota (ASPRS, 2004). Consecuentemente, en varios estudios se ha intentado documentar la exactitud de los datos topográficos lidar. Desafortunadamente, debido al alto costo de los datos topográficos de alta precisión, la mayoría de los investigadores se han visto forzados a recurrir a técnicas como la validación cruzada (Isaaks y Srivastava, 1989) para establecer la exactitud vertical de los datos lidar (Lloyd y Atkinson, 2002; Anderson et al., 2005; Bater y Coops, 2009; Guo et al., 2010); con lo cual se corre el riesgo de que los resultados alcanzados reflejen únicamente la incertidumbre de los métodos de interpolación (Pérez y Mas, 2009; Paredes et al., 2013) utilizados y no la exactitud vertical de los datos lidar (Anderson et al., 2005).
En aquellos estudios en los que ha sido posible contar con datos de campo con una exactitud vertical al menos tres veces superior a la de lidar, como lo recomienda la ASPRS (2004), se han observado resultados que exceden la exactitud vertical especificada por los proveedores de datos cuando la densidad de puntos lidar sobre el terreno es de al menos un punto por metro cuadrado (Hopkinson et al., 2004; Aguilar y Mills, 2008; Schmid et al., 2011). No obstante, cuando se han evaluado productos lidar con una menor densidad de puntos sobre el terreno, los resultados sugieren que no se cumple con la exactitud vertical normalmente atribuida a los datos lidar (Hodgson y Bresanahan, 2004; Su y Bork, 2006; Aguilar y Mills, 2008), debido principalmente a la variabilidad del terreno no capturada por los datos lidar. Sin embargo, considerando que el número de estudios en los que se ha contado con datos de campo para evaluar datos lidar con una densidad superior a un punto por metro cuadrado es limitado, es necesaria la elaboración de otros estudios que coadyuven a establecer la exactitud vertical de los datos topográficos lidar.
Este estudio pretende, por lo tanto, contribuir a mejorar el conocimiento de la exactitud vertical de dichos datos y reducir la incertidumbre asociada con la utilización de los mismos por otros usuarios, estableciendo la exactitud posicional vertical (EPV) para los datos topográficos lidar de acuerdo con las definiciones del Instituto Nacional de Estadística y Geografía de México (INEGI, 2010) y de la ASPRS (2004). Para lograr dicho objetivo se presenta a continuación la evaluación de una nube de puntos topográficos lidar, precedida por la descripción de la tecnología lidar utilizada en este estudio, del área en estudio y de los materiales y métodos empleados para evaluar la exactitud vertical y establecer la EPV alcanzada. Finalmente, se presenta una discusión de los resultados y las conclusiones que surgen de los mismos.
Lidar Topográfico Aerotransportado
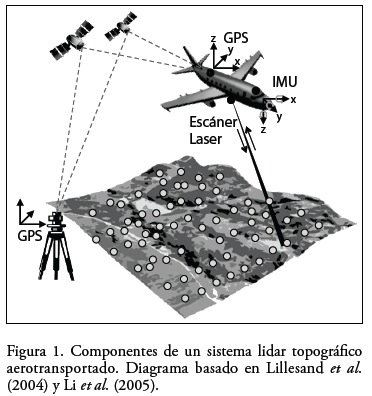
Lidar es una tecnología de percepción remota activa que cuenta con su propio sistema (un escáner láser) para iluminar y medir la superficie terrestre (Lillesand et al., 2004). En un sistema de lidar topográfico aerotransportado (Figura 1) se emiten pulsos o haces de luz láser dirigidos hacia la superficie terrestre y se registra la energía que es reflejada hacia el escáner láser por los objetos existentes sobre la superficie y por el terreno natural (Jensen, 2007). Adicionalmente al escáner láser, un sistema topográfico lidar también se compone de dos GPS de doble frecuencia (uno aerotransportado y otro terrestre) y una unidad de medición inercial (inertial measurement unit; IMU) que permiten documentar la ubicación exacta y el balanceo (roll), cabeceo (pitch) y desvío (yaw) de la aeronave en los momentos en que un pulso láser es emitido y recibido por el escáner láser (Ibid.). Por lo que es posible, mediante software especializado, combinar la información de estos cuatro componentes (escáner láser, IMU, GPS aerotransportado y GPS terrestre) para asignar coordenadas x,y,z de alta precisión a cada retorno de luz láser registrado por el escáner láser (Li et al., 2005).
A partir de dichos retornos con coordenadas x,y,z se conforma una nube (o conjunto) de puntos lidar (Figura 2) que contiene mediciones de la elevación del terreno natural, vegetación, edificios y otros objetos que se encuentren sobre la superficie terrestre (Aguilar y Mills, 2008). Dependiendo del escáner lidar utilizado, es posible que la nube de puntos contenga múltiples retornos por cada pulso láser que fue emitido debido a la interacción de la luz con los objetos sobre el terreno (Lillesand et al., 2004). Por ejemplo, en zonas boscosas normalmente se obtienen cuatro o más retornos por cada haz láser que incide sobre un árbol (Figura 2a). En estos casos, el primer retorno se puede asociar con la copa de los árboles, los retornos intermedios con la interacción del láser con la estructura (tallo, ramas y hojas) de los árboles y el último retorno con el terreno natural (Jensen, 2007). Por lo tanto, para la generación de productos topográficos lidar, es necesario descartar de la nube de puntos aquellos retornos que no pertenecen al terreno natural (Figura 2b) mediante una combinación de a) algoritmos semiautomáticos y b) edición manual (Raber et al., 2007).
El uso de la tecnología lidar permite reducir el costo y el tiempo requerido para la recolección de datos topográficos, tanto en terreno abierto como en terreno con vegetación densa o inaccesible para los topógrafos (Jensen, 2007). Sin embargo, diferentes factores, como la exactitud de los equipos GPS e IMU, introducen errores posicionales en los productos lidar, por lo que es necesario evaluar la exactitud de los mismos. Desafortunadamente, la distribución de los puntos sobre el terreno es aleatoria, por lo que no es posible la medición directa de coordenadas x,y,z conocidas (Hodgson y Bresanahan, 2004). Debido a lo anterior, cuando se efectúan evaluaciones de la exactitud de los datos lidar existentes, usando datos de campo como referencia, es necesario recurrir a técnicas de interpolación para determinar la elevación reportada por la nube de puntos topográficos lidar en los puntos x,y,z medidos en campo (Hopkinson et al., 2004). Tal es el caso de este estudio, por lo que en la siguiente sección se presentan los métodos de interpolación utilizados para estimar la elevación lidar y evaluar la exactitud vertical de los mismos, así como la descripción de las diferentes fuentes de datos utilizadas.
Materiales y métodos
Lidar topográfico
La nube de puntos topográficos lidar fue recolectada sobre el municipio de Actopan, Veracruz, México usando el laboratorio aerotransportado de la Universidad Autónoma de Tamaulipas, el cual cuenta con un sensor lidar Leica Geosystems ALS50-II montado en una aeronave tipo Cessna. El área evaluada (Figura 3) se delimita por las coordenadas UTM WGS84 de la Zona 14 Norte (760 840 E; 2 1687 325 N) en la esquina superior izquierda y (761 720 E; 2 166 225 N) en la esquina inferior derecha; es decir, conforma un rectángulo con una superficie de 968 000 m2 (880 x 1 100 m). En la nube de puntos lidar original para dicha área de estudio existen 3 568 349 retornos con coordenadas x,y,z (aproximadamente 3.69 puntos por m2); de los cuales 993 078 fueron clasificados como puntos sobre el terreno (1.02 puntos sobre el terreno por m2), (Figura 4) usando una combinación de algoritmos semiautomáticos implementados en el software de gestión de datos lidar Merrick MARS (Merrick, 2013) y posterior edición manual en el mismo paquete informático.
Datos topográficos convencionales
Para la evaluación de la exactitud vertical de datos lidar, la ASPRS (2004) recomienda que los datos utilizados como referencia sean por lo menos tres veces más exactos que los datos lidar. Atendiendo esta recomendación, para la recolección de los datos topográficos de referencia se utilizó una estación total Sokkia Set 1030R3; la cual tiene una exactitud de ±(2 mm + 2 ppm x D) mm cuando se utilizan prismas topográficos (Sokkia, 2005). En total se recolectaron 306 puntos sobre el terreno para ser utilizados como referencia, distribuidos en dos perfiles (Figura 3 y 5) representativos de los tipos de terreno observados por topógrafos durante proyectos de construcción de infraestructura. El Perfil 1 (Figura 5a y 5b), con una longitud de 1050.10 m y elevaciones mínimas de 153.53 m y máximas de 202.92 m, representa terreno con cambios gentiles de topografía sobre distancias largas en áreas de escasa vegetación y terreno abierto. En contraste, el Perfil 2 (Figura 5c y Figura 5d), con una longitud de 862.57 m y elevaciones mínimas de 154.00 m y máximas de 192.93 m, muestra cambios bruscos de topografía en distancias cortas con algunas aéreas de vegetación densa. Para el Perfil 1 se recolectaron 151 puntos sobre el terreno distribuidos entre las coordenadas UTM de Zona 14 Norte (761 303.97 E; 2 167 299.97 N) y (761 335.39 E; 2 166 250.34 N) y para el Perfil 2 un total de 155 puntos distribuidos entre las coordenadas (760 847.84 E; 2 166 735.96 N) y (761 702.81 E; 2 166 850.21 N).

Métodos de interpolación
Dada la distribución aleatoria de los retornos registrados en la nube de puntos lidar (Hodgson y Bresanahan, 2004), fue necesario recurrir a métodos de interpolación recomendados para la interpolación de datos lidar (Lloyd y Atkinson, 2002; Guo et al., 2010) para estimar la elevación reportada por la nube de puntos topográficos lidar en las coordenadas x,y,z de los puntos sobre el terreno recolectados usando la estación total. Los métodos de interpolación utilizados en este estudio son: el vecino más cercano (NN, Nearest Neighbour), red irregular de triángulos (TIN, Triangulated Irregular Network), ponderación en función inversa de la distancia (IDW, Inverse Distance Weighting), Kriging ordinario (OK, Ordinary Kriging) y Kriging con un modelo de tendencia (KT, Kriging with a Trend model). Una descripción detallada de dichos métodos se puede encontrar en Isaaks y Srivastava (1989), Goovaerts (1997) y Paredes et al. (2013). A continuación se presenta una breve descripción de los mismos:
– El vecino más cercano (NN) consiste en encontrar en la nube de puntos lidar el retorno más cercano a las coordenadas x,y,z de los puntos de referencia e interpretar la elevación de dicho retorno como el valor reportado por los datos lidar para dichas coordenadas.
– La red irregular de triángulos (TIN) es una forma de representar la superficie terrestre mediante triángulos continuos usando los puntos en la nube de datos lidar como nodos.
La elevación para cada dato de referencia es interpolada linealmente usando los tres nodos del triángulo en el cual se localiza dicho dato.
– El método de ponderación en función inversa de la distancia (IDW) consiste en asignar pesos a los n puntos lidar más cercanos a cada dato de referencia con base en el inverso de la distancia a estos últimos para promediar el valor de la elevación en las coordenadas x,y de cada punto sobre el terreno usado como referencia. IDW fue aplicado con una potencia de 2 para ponderar las distancias.
– Kriging es el nombre genérico para una familia de métodos de interpolación geoestadísticos basados en la teoría de variables regionalizadas, la cual asume que la variación espacial es homogénea en el área en estudio. Kriging Ordinario (OK) asume que la media de la nube de puntos lidar varía a través del área en estudio, pero es constante en el vecindario local usado para la interpolación. En contraste, Kriging con un modelo de Tendencia (KT) asume que la media varía en cada vecindario local de interpolación. En ambos casos se utilizaron modelos gaussianos para definir la variación espacial en el área en estudio.
Con la finalidad de reducir la incertidumbre respecto a la influencia de los métodos de interpolación en la exactitud calculada para la nube de puntos topográficos lidar, los métodos IDW, OK y KT se aplicaron con vecindarios de 6, 12, 24 y 48 puntos para estimar y comprar la elevación lidar en las coordenadas x,y,z de los datos topográficos de referencia.
Evaluación de la exactitud vertical
Para evaluar la exactitud vertical de los datos lidar se calculó la diferencia (o error) entre la elevación reportada por los datos lidar eLidar para cada método de interpolación utilizado y la elevación obtenida en campo mediante topografía convencional eEstaciónTotal:
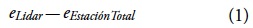
Con base en dichas diferencias se generaron estadísticas descriptivas de error (media, desviación estándar, valores mínimos y máximos y percentiles) y se calculó el error medio cuadrático (EMC) de las mismas (Hodgson y Bresanahan, 2004):

donde n es el número de puntos sobre el terreno usados como referencia (eEstaciónTotal).
El EMC y las estadísticas descriptivas de error detallan la dispersión y distribución de los errores en la nube de puntos. Sin embargo, los proveedores de datos lidar documentan sus productos únicamente con el EMC (MAPA, 2013; Bluesky, 2013; Sanborn, 2013). Por lo que diferentes organizaciones encargadas del manejo de datos geográficos (ASPRS, 2004; INEGI, 2010), reconociendo las limitantes del EMC para describir la distribución de los errores en los datos geográficos (Fisher y Tate, 2006) y la dificultad de obtener datos de campo para estimar la distribución de los errores, recomiendan documentar la exactitud de los datos con un intervalo de confianza del 95%. Con tal propósito, usando las estadísticas de error generadas se calculó la exactitud posicional vertical (EPV), la estadística definida por el INEGI (2010) para indicar el intervalo de confianza del 95%, de los datos topográficos lidar:

donde σ es la desviación estándar de los errores en la nube de puntos lidar.
Asimismo, atendiendo las directrices de la ASPRS (2004) para la evaluación de datos lidar, se calculó el percentil 95 de los valores absolutos de los errores en los datos lidar y la Exactitud(z), ya que dichas estadísticas, al igual que la EPV, indican que el 95% de los errores tendrán una magnitud menor o igual a las mismas. Exactitud(z) se define como (Ibid.):

Dado que el EMC es igual a la desviación estándar cuando la media de los errores es igual a 0 (Stewart et al., 2009), la EPV definida por el INEGI (2010) y la exactitud vertical ASPRS (2004) pueden ser considerados como equivalentes si se asume que los datos lidar se encuentran libres de errores sistemáticos y que siguen una distribución normal (INEGI, 2002).
Resultados
Los resultados aquí presentados se reportan en metros con tres cifras decimales. Debido a que la exactitud vertical de los datos lidar se estima normalmente en 0.15 m (EMC), las dos primeras cifras usadas para reportar los resultados pueden ser consideradas positivas (verdaderas) y la tercera estimativa (dudosa) y, consecuentemente, cuestionable (INEGI, 2002; Schofield y Breach, 2007).
Para reducir la incertidumbre asociada a la influencia de los métodos de interpolación en el análisis de la exactitud vertical de la nube de puntos topográficos lidar, se comparó el EMC estimado usando diferentes tamaños de vecindario en la aplicación de los métodos de interpolación IDW, OK y KT. Los resultados (Tabla 1) sugieren que la incertidumbre introducida por dichos métodos de interpolación es mínima cuando se evalúan datos lidar que representan únicamente terreno con cambios gentiles de topografía (Perfil 1) o, bien, que contengan datos de dichas características (Nube de puntos lidar) que compensen los errores introducidos en áreas de cambio frecuente (Perfil 2); en cuyo caso es necesario aplicar los métodos de interpolación cuidadosamente, ya que debido a la variabilidad espacial de la elevación se pueden generar estadísticas de error que reflejen la inestabilidad de los métodos de interpolación y no la de los datos lidar (Anderson et al., 2005). Tal es el caso de IDW 48 y KT 06, los cuales indican que el EMC de los datos lidar es igual o mayor a 0.150 m. En contraste, cuando los métodos de interpolación se aplican con un tamaño de vecindario apropiado para evaluar datos lidar, el EMC estimado para la nube de puntos es menor a 0.150 m.
En consecuencia, para llevar a cabo la evaluación de los datos lidar, se seleccionó un tamaño de vecindario de 12 puntos lidar (IDW 12, OK 12 y KT 12), ya que este tamaño de vecindario muestra resultados estables en los tres tipos de terreno evaluados (mixto, cambios gentiles y cambios bruscos; véase Tabla 1). En el caso del método NN no se requiere la definición de un vecindario y en el caso TIN el vecindario se define por los tres nodos del triángulo dentro del cual se ubica el punto sobre el terreno usado como referencia. Los resultados de la evaluación se presentan para la totalidad de los puntos de referencia recolectados mediante la estación total (terreno mixto; Tabla 2) y para cada uno de los perfiles topográficos recolectados: para terreno con cambios gentiles de topografía (Tabla 3) y para terreno con cambios de elevación en distancias cortas (Tabla 4).
La evaluación sobre el terreno mixto indica que la exactitud vertical de los datos lidar excede las especificaciones normalmente publicitadas por proveedores comerciales. En todos los casos el EMC se encuentra por debajo de los 0.150 m y únicamente cuando se utilizó el método NN el EMC excedió los 0.100 m (Tabla 2). Sin embargo, en todos los casos se observa que la nube de puntos topográficos lidar subestima ligeramente la elevación del terreno, ya que la media es diferente a 0 en todos los casos por aproximadamente -0.020 m; lo cual en turno causa pequeñas diferencias entre la desviación estándar de los errores y el EMC. En cuanto a la distribución de los errores en este tipo de terreno, el método NN generó los errores de mayor magnitud, mientras que el resto de los métodos (TIN, IDW 12, OK 12 y KT 12) generó errores mínimos y máximos de magnitud similar. Sin embargo, dicha diferencia es únicamente observable para el 2.5% de los errores en cada extremo de la distribución, es decir, para los errores extremos de cada método de interpolación. Si se descartan dichos errores (2.5% en cada extremo), la distribución de los errores verticales en la nube de puntos es muy similar en todos los casos evaluados.
En el caso de la evaluación sobre terreno con cambios gentiles de topografía y escasa vegetación (Tabla 3), los resultados obtenidos muestran que el EMC vertical es de aproximadamente 0.069 m sobre este tipo de terreno para los métodos TIN, IDW, OK y KT. Dicho EMC sugiere que la exactitud vertical de los datos lidar sobre este tipo de terreno duplica la exactitud esperada de los datos lidar comerciales. Sin embargo, el EMC estimado usando el método NN es de 0.114 m; lo cual realza la importancia de seleccionar y aplicar cuidadosamente un método de interpolación para la evaluación de los datos lidar. Sobre este tipo de terreno no se observó la presencia de errores sistemáticos, por lo que la media de los errores es muy cercana a 0 y, por ende, la desviación estándar muy similar al EMC. Asimismo, la magnitud de los errores máximos y mínimos se redujo con respecto a la evaluación sobre terreno mixto (a excepción del ya mencionado caso del método NN). Sin embargo, una vez descartados el 2.5% de los errores en cada extremo de la distribución, la magnitud de los errores sobre terreno con cambios gentiles es similar a la observada sobre terreno mixto.
En la evaluación de los datos lidar sobre terreno con cambios de elevación en distancias cortas y vegetación densa (Tabla 4) los resultados muestran que el EMC sobre este tipo de terreno es inferior a 0.150 m. Sin embargo, la magnitud del mismo varía dependiendo el método de interpolación seleccionado para su estimación; siendo los métodos TIN, OK y KT los que mejores resultados producen (EMC ~0.110 m). No obstante, la subestimación de la elevación, indicada por medias negativas, sobre este tipo de terreno es observada en todos los casos con magnitudes similares y sugiere que la nube de puntos contiene errores sistemáticos en este tipo de terreno, causados posiblemente por la presencia de vegetación, como ha sido observado en otros estudios (Hodgson y Bresnahan, 2004; Hopkinson et al., 2004). Respecto a la distribución de los errores, la magnitud de los errores extremos sobre este tipo de terreno coincide con aquéllos observados en la evaluación de terreno mixto, indicando el origen de los mismos en dicho tipo de terreno y exaltando la importancia de incluir terreno con cambios constantes de elevación en la evaluación de datos lidar.
Por último, utilizando los resultados del análisis descriptivo del error, discutido arriba, se generaron las estadísticas definidas por el INEGI (2010) y la ASPRS (2004) para documentar el intervalo de confianza del 95% de los datos. Los resultados (Tabla 5) sugieren que es factible establecer la EPV (Ecuación 3) y la Exactitud(z), (Ecuación 4) de la nube de puntos topográficos lidar en el orden de los 0.200 m sobre terreno mixto y sobre terreno con cambios de elevación en distancias cortas y en el orden de los 0.150 m si únicamente se representa terreno con cambios gentiles en la topografía y con escasa vegetación. No obstante, en aquellos casos en los que se observaron errores sistemáticos en la nube de puntos, el orden sugerido para la EPV y la Exactitud(z) no reflejan la magnitud del 95% de los errores, como se observa en la Tabla 5. Asimismo, la distribución espacial de la magnitud de los errores (Figura 6) sugiere la presencia de una cantidad importante de los mismos no capturados por la magnitud de la EPV cuando se evalúan datos lidar sobre terreno con cambios constantes de topografía. Por lo tanto, adicionalmente a la EPV o Exactitud(z), en caso de contar con datos de campo con la exactitud requerida para evaluar datos lidar, es importante también incluir el estadístico del Percentil 95 en la documentación de la nube de puntos topográficos lidar.

Conclusiones
En este estudio se evaluó la exactitud vertical de una nube de puntos topográficos lidar de una densidad de 1.02 puntos sobre el terreno por metro cuadrado. Los datos de referencia fueron recolectados utilizando una estación total de una exactitud milimétrica, cumpliendo así los requisitos de exactitud de la ASPRS (2004) para evaluar datos lidar. Para estimar y comparar la elevación reportada por los datos lidar en las coordenadas x,y,z de los puntos sobre el terreno de referencia se utilizaron diferentes métodos de interpolación con la finalidad de reducir la influencia de los errores por interpolación en los resultados de la evaluación de los datos lidar.
Los resultados del estudio muestran que en todos los casos evaluados la exactitud vertical de la nube de puntos cumple con las especificaciones publicitadas por los proveedores de datos lidar; ya que el EMC observado no superó los 0.150 m, a excepción de los casos IDW 48 y KT 06 en los que los métodos de interpolación fueron aplicados con parámetros no apropiados para datos lidar.
Sin embargo, al aplicar los diferentes métodos con tamaños de vecindarios apropiados, el EMC vertical de la nube de puntos fue estimado en la región de los 0.069 m para áreas con cambios gentiles de topografía y escasa vegetación; en 0.111 m para terreno con cambios constantes de topográfica en distancias cortas y vegetación densa; y en 0.100 m para terreno mixto. Por lo tanto, la evaluación aquí presentada coincide con las evaluaciones de Hopkinson et al. (2004), Aguilar y Mills (2008) y Schmid et al. (2011), y sugiere que la exactitud vertical de los datos lidar excede aquella publicitada por los proveedores de datos lidar comerciales cuando la densidad de puntos es de por lo menos un punto sobre el terreno por metro cuadrado.
Sin embargo, dado que el EMC indica únicamente la dispersión de los errores en la nube de puntos, se calcularon también las estadísticas definidas por la ASPRS (2004) y el INEGI (2010) para documentar el 95% de los errores verticales. En el estudio se estableció que la nube de puntos lidar tiene una EPV (INEGI, 2010) o Exactitud(z) (ASPRS, 2004) en el orden de los 0.200 m sobre terreno mixto y sobre terreno con cambios de elevación en distancias cortas, y en el orden de los 0.150 m si únicamente se representa terreno con cambios gentiles en la topografía. Sin embargo, si la nube de puntos lidar contiene errores sistemáticos, EPV y Exactitud(z) no capturan el 95% de los mismos. Por lo cual se considera necesaria la inclusión del percentil 95 de los errores en la documentación de los datos lidar.
Finalmente, los resultados de la evaluación aquí presentada sugieren que la utilización de datos lidar puede ser preferible a la utilización de topografía convencional para la generación de productos de elevación sobre grandes áreas, si se considera que el EMC y la EPV de la nube de puntos son similares a los errores introducidos por los métodos utilizados para interpolar los puntos sobre el terreno recolectados mediante topografía convencional (Paredes et al., 2013) y, además, se reduce el costo y tiempo requerido para la recolección de datos topográficos (Jensen, 2007). No obstante, en aquellos casos en los que se requiere información puntual y no sea necesario recurrir a métodos de interpolación, la utilización de topografía convencional es preferible a la de los datos lidar, debido a los errores observados en el estudio.
Referencias
Aguilar, F. J. and J. P. Mills (2008), "Accuracy assessment of lidar-derived digital elevation models", The Photogrammetric Record, no. 23, pp. 148-169. [ Links ]
Anderson, E. S., J. A. Thompson and R.E. Austin (2005) "Lidar density and linear interpolator effects on elevation estimates", International Journal of Remote Sensing, no. 26, pp. 3889-3900. [ Links ]
ASPRS (2004), ASPRS Vertical Accuracy Reporting for Lidar Data, American Society of Photogrammetry and Remote Sensing, ASPRS Lidar Committee. [ Links ]
Bater, C. W. and N. C. Coops (2009), "Evaluating error associated with lidar-derived DEM interpolation", Computers & Geosciences, no. 35, pp. 289-300. [ Links ]
Bluesky (2013), Lidar Height Data [http://www.blueskyworld.com/products/lidar/: 12 de febrero de 2013] [ Links ].
Darnell, A. R., N. J. Tate and C. Brunsdon (2008), "Improving user assessment of error implications in digital elevation models", Computers, Environment and Urban Systems, no. 32, pp. 268-277. [ Links ]
Fisher, P. F. and N. J. Tate (2006), "Causes and consequences of error in digital elevation models", Progress in Physical Geography, no. 30, pp. 467-489. [ Links ]
Goovaerts, P. (1997), Geostatistics for Natural Resources Evaluation, Oxford University Press, Nueva York. [ Links ]
Guo, Q., W. Li, H. Yu and O. Álvarez (2010), "Effects of topographic variability and lidar sampling density on several DEM interpolation methods", Photogrammetric Engineering & Remote Sensing, no. 76, pp. 701-712. [ Links ]
Heuvelink, G. B. M., P. A. Burrough and A. Stein (1989), "Propagations of errors in spatial modelling with GIS", International Journal of Geographical Information Systems, no. 3, pp. 303-322. [ Links ]
Hodgson, M. E. and P. Bresnahan (2004), "Accuracy of airborne lidar-derived elevation: Empirical assessment and error budget", Photogrammetric Engineering & Remote Sensing, no. 70, pp. 331-339. [ Links ]
Hopkinson, C., L. E. Chasmer, G. Zsigovics, I. F. Creed, M. Sitar, P. Treitz and R. V. Maher (2004) "Errors in lidar ground elevation and wetland vegetation height estimates", en ISPRS Archives – Volume XXXVI-8/W2 Láser-Scanners for Forest and Landscape Assessment, Freiburg, Alemania, 3-6 octubre de 2004 [http://www.isprs.org/proceedings/XXXVI/8–W2/HOPKINSON.pdf: 31 de enero de 2013] [ Links ].
INEGI (2002), Tratamiento de Errores en Levantamientos Topográficos, Instituto Nacional de Estadística, Geografía e Informática, Aguascalientes, México. [ Links ]
INEGI (2010), "Norma técnica de estándares de exactitud posicional", Diario Oficial de la Federación, 23 de diciembre de 2010, Instituto Nacional de Estadística, Geografía e Informática, México. [ Links ]
Isaaks, E. H. and R. M. Srivastava (1989), An Introduction to Applied Geostatistics, Oxford University Press, Oxford, London. [ Links ]
Jensen, J. R. (2007), Remote Sensing of the Environment: An Earth Resource Perspective, 2a. ed., Prentice Hall, New Jersey. [ Links ]
Li, Z. Q. Zhu and C. Gold (2005), Digital terrain modeling. Principles and Methodology, CRC Press, Florida, USA. [ Links ]
Lillesand, T. M., R. W. Kiefer and J. W. Chipman (2004), Remote sensing and image interpretation, John Wiley & Sons, Massachusetts. [ Links ]
Lloyd, C. D. and P. M. Atkinson (2002), "Deriving DSMs from lidar data with Kriging", International Journal of Remote Sensing, no. 23, pp. 2519-2524. [ Links ]
MAPA (2013), Lidar [http://www.mapamerrick.com.mx/ lidar.html: 12 de febrero de 2013] [ Links ].
Merrick (2013), MARS Software [http://www.merrick.com/Geospatial/Services/MARS–Software: 31 de enero de 2013] [ Links ].
Paredes Hernández, C. U., W. E. Salinas Castillo, X. Martínez Becerra y S. B Jiménez Hernández (2013) "Evaluación y comparación de métodos de interpolación determinísticos y probabilísticos para la generación de modelos digitales de elevación", Investigaciones Geográficas, Boletín, núm. 82, Instituto de Geografía, UNAM, México, pp. 118-130. [ Links ]
Pérez Vega, A. y J. F. Mas (2009), "Evaluación de los errores de modelos digitales de elevación obtenidos por cuatro métodos de interpolación", Investigaciones Geográficas, Boletín, núm. 69, Instituto de Geografía, UNAM, México, pp. 53-67. [ Links ]
Raber, G. T., J. R. Jensen, M. E. Hodgson, J. A. Tullis, B. A. Davis and J. Berglund (2007), "Impact of lidar nominal post-spacing on DEM accuracy and flood zone delineation", Photogrammetric Engineering and Remote Sensing, no. 73, pp. 793-804. [ Links ]
Sanborn (2013), Sanborn Lidar Products [http://www.sanborn.com/sites/default/files/files/SANBORN_LIDARv4_0.pdf: 12 de febrero de 2013] [ Links ].
Schmid, A. K., B. C. Hadley and N. Wijekoon (2011), "Vertical accuracy and use of topographic lidar data in coastal marshes", Journal of Coastal Research, no. 27-6A, pp. 116-132. [ Links ]
Schofield, W. and M. Breach (2007), Engineering Surveying, 6a. ed., Elsevier, Oxford. [ Links ]
Sokkia (2005), Sokkia Series 030R Product Brochure [http://www.sokkia.com/Products/Detail/attachment.axd?id=48: 31 de enero de 2013] [ Links ].
Stewart J. P., J. Hu, R. E. Kayen, A. J. Lembo Jr., B. D. Collins, C. A. Davis and T. D. O'Rourke (2009), "Use of airborne and terrestrial lidar to detect ground displacement hazards to water systems", Journal of Surveying Engineering, no. 135, pp. 113-124. [ Links ]
Su, J. and E. Bork (2006), "Influence of vegetation, slope and lidar sampling angle on DEM accuracy", Photogrammetric Engineering and Remote Sensing, no. 72, pp. 1265–1274. [ Links ]
Wechsler, S. P. (2003), "Perceptions of digital elevation model uncertainty by DEM users", Urban and Regional Information Systems Association Journal, no. 15, pp. 57-64. [ Links ]
Cómo citar: Salinas Castillo, W. E., C. U. Paredes Hernández, X. Martínez Becerra, F. Guevara Cortina (2014), "Evaluación de la exactitud posicional vertical de una nube de puntos topográficos lidar usando topografía convencional como referencia", Investigaciones Geográficas, Boletín, núm. 85, Instituto de Geografía, UNAM, México, pp. 5-17, dx.doi.org/10.14350/rig.36934