Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigaciones geográficas
versión On-line ISSN 2448-7279versión impresa ISSN 0188-4611
Invest. Geog no.69 Ciudad de México ago. 2009
Geografía física
Evaluación de los errores de modelos digitales de elevación obtenidos por cuatro métodos de interpolación
Error assessment of digital elevation models obtained by interpolation
Azucena Pérez Vega* Jean François Mas*
* Centro de Investigaciones en Geografía Ambiental, Universidad Nacional Autónoma de México, Antigua Carretera a Pátzcuaro No. 8701, Col. Ex Hacienda San José de la Huerta, 58190 Morelia, Michoacán. E–mail: azuperezvega@yahoo.com.
Recibido: 21 de enero de 2008.
Aceptado en versión final: 27 de junio de 2008.
Resumen
Son pocos los estudios enfocados en la evaluación de los errores inherentes a los modelos digitales de elevación (MDE). Por esta razón se evaluaron los errores de los MDE obtenidos por diferentes métodos de interpolación (ARC/INFO, IDRISI, ILWIS y NEW–MIEL) y con diferentes resoluciones, con la finalidad de obtener una representación del relieve más precisa. Esta evaluación de los métodos de interpolación es crucial, si se tiene en cuenta que los MDE son la forma más efectiva de representación de la superficie terrestre para el análisis del terreno y que son ampliamente utilizados en ciencias ambientales. Los resultados obtenidos muestran que la resolución, el método de interpolación y los insumos (curvas de nivel solas o con datos de escurrimientos y puntos acotados) influyen de manera importante en la magnitud de la cantidad de los errores generados en el MDE. En este estudio, que se llevó a cabo con base en curvas de nivel cada 50 m en una zona montañosa, la resolución más idónea fue de 30 m. El MDE con el menor error (Error Medio Cuadrático –EMC– de 7.3 m) fue obtenido con ARC/INFO. Sin embargo, programas sin costo como NEW–MIEL o ILWIS permitieron la obtención de resultados con un EMC de 10 m.
Palabras clave: Modelos digitales de elevación, error, interpolación, relieve.
Abstract
There have been few studies focused on assessing the errors inherent of digital elevation models (DEM). For this reason, the errors of DEM obtained by different programs of interpolation (ARC/INFO, IDRISI, ILWIS and NEW–MIEL) and with different resolutions, were evaluated in order to obtain a more precise representation of the relief. This evaluation of the methods of interpolation is crucial, because DEMs are the most effective representation of the terrestrial surface for terrain analysis and are widely used in environmental sciences. The results show that the resolution, the interpolation algorithm and the inputs (contours only or along with streams and points) influence the amount of error importantly. In the present study, carried out with 50 m contour data in a mountainous area, the most suitable resolution was 30 m. The MDE with the minor error (Root Mean Square Error –RMSE– of 7.3 m) was obtained by ARC/ INFO. Nevertheless, free programmes such as NEW–MIEL or ILWIS allowed obtaining result with a RMSE of 10 m.
Key words: Digital elevation model, error, interpolation, relief.
INTRODUCCIÓN
Los Modelos Digitales de Elevación (MDE) son definidos como una estructura numérica de datos que representan la distribución espacial de la altitud en la superficie terrestre, almacenados en una base de datos digital, georreferenciada en un sistema de proyección cartográfica (Felicísimo, 1994). Es llamado modelo porque, a través de algoritmos matemáticos, los datos altitudinales pueden ser modelados automáticamente en una computadora y así lograr analizar la superficie terrestre en un modelo en tres dimensiones (Maune, 2001).
Actualmente los MDE constituyen una herramienta fundamental sobre todo en estudios para describir rasgos topográficos. Los MDE permiten de forma fácil la representación de las formas del relieve, la producción de cortes transversales y la creación de animaciones en tres dimensiones. Además, el almacenamiento de la información digital no sufre deformaciones como sucede con los mapas convencionales; la integración y actualización de información adicional es realizada con menor trabajo y tiempo y la representación multiescalar y en diferentes resoluciones se realiza fácilmente (Li et al., 2005).
Existen diferentes nombres para designar a estos modelos: Modelo Digital de Terreno (MDT), Modelo Digital de Alturas (MDA); Modelo Digital de Suelo (GDM en inglés) y Modelo Digital de Elevación del Terreno (MDET), aunque en general son utilizados como sinónimos. Algunos textos determinan diferencias como es el caso del MDT, que además de presentar la información altitudinal incluye otros rasgos geográficos tales como pendiente, forma de la pendiente, escurrimientos, cuerpos de agua, línea de costa, vías de comunicación y asentamientos humanos, entre otros (Ibid.).
Otros autores consideran que el término más adecuado debería ser Datos de Elevación Digitales (DED), ya que dichos datos sirven para generar posteriormente el modelo. Sin embargo, debido al uso generalizado del término "MDE" en la literatura y para evitar mayor confusión, algunos autores han optado por conservarlo, lo cual se hizo también en este trabajo (Maune et al., 2001).
Los datos de elevación digital pueden ser divididos básicamente en tres grupos de acuerdo con su estructura: a) datos vectoriales: líneas y puntos (curvas de nivel y puntos acotados) obtenidos a partir de mapas topográficos; b) red irregular de triángulos construidos a través de la unión de tres puntos adyacentes (TIN) y c) datos en formato de celdas (raster), los cuales representan el valor medio de unidades elementales con una distribución regular (datos matriciales). Estos últimos fueron ampliamente utilizados en la última década debido a su simplicidad y facilidad de almacenamiento y procesamientos de la información (Wilson y Gallant, 2000).
La información altitudinal que conforma un MDE es obtenida a través de sistemas pasivos o activos, o bien por mediciones directas. Los métodos pasivos como la interpretación de pares estereoscópicos de fotografías áreas fueron los pioneros en la construcción de la información topográfica. Esta información fue posteriormente digitalizada y es la más frecuente en muchas partes del mundo, ya que puede fácilmente ser incorporada en un sistema de información geográfica (SIG). En el caso de México, curvas de nivel digitalizadas en formato vector (escalas 1:50 000 y 1:250 000) han sido generadas por el INEGI y están disponibles para la totalidad del territorio. Sin embargo, dicha información altitudinal no es continua, por lo que dichos datos requieren de métodos de interpolación para generar información altitudinal continua como se presentará a continuación. Recientemente, ciertos sensores a bordo de satélites como ASTER (Advance Space Borne Thermal Emisión and Reflection Radiometer) o SPOT (Système Probatoire d 'Observation de la Terre) tienen la capacidad de tomar pares estereoscópicos de imágenes, lo cual permite generar un MDE.
Desde hace algunos años se desarrollaron sistemas activos como el Radar (Radio Detection and Ranking) y el Lidar (Laser Imaging Detection and Ranging) que permiten adquirir información topográfica. Estas tecnologías hacen posible determinar la distancia desde un emisor a un objeto o superficie utilizando una señal de radar o laser. La distancia al objeto se determina midiendo el tiempo de retraso entre la emisión del pulso y la detección de la señal reflejada. Por ejemplo, sistemas de radar como el Shuttle Radar Topographic Mission (SRTM), producen MDE para el mundo entero con una resolución cercana a los 30 m. Una versión con una resolución de 90 m está disponible para el público y es considerada uno de los mejores medios de información topográfica en la actualidad (Geoscience Australia, 2005). El Lidar permite generar modelos de elevación muy detallados pero no está aún aplicado en México y es costoso.
Finalmente, la obtención directa de datos altitudinales en el terreno a través de equipos topográficos como estaciones totales o GPS (Global Positioning System) es laboriosa y costosa, por lo cual no es práctica para generar MDE sobre grandes extensiones.
En México, la información más susceptible de ser utilizada para generar MDE detallados a bajo costo es, por tanto, la información topográfica vectorial del INEGI a escala 1:50 000. Para generar un MDE en formato de celdas, esta información debe ser interpolada. Los métodos de interpolación utilizados para elaborar MDE consisten en la estimación altitudinal, a través de datos conocidos, discontinuos y en la mayoría de los casos distribuidos irregularmente, los cuales sirven para generar un nuevo conjunto de puntos localizados en los nodos de una red regular y continua, utilizando algoritmos matemáticos (Felicísimo, 1994). Los métodos de interpolación usados comúnmente son: ponderación en función inversa de la distancia, superficies de tendencia, kriging, triangulación, interpolación de parches locales, y rasterización adaptada localmente (locally adaptive gridding). Debido a que los modelos son una descripción aproximada de la realidad, y se construyen aplicando supuestos más o menos apegados a la realidad, nunca pueden ser exactos; por tanto, la utilización de modelos conlleva diferentes fuentes de error donde las imprecisiones son inherentes (Ibid.).
Existen diferentes fuentes de error en los MDE. El primero concierne a errores en los insumos utilizados para generar dichos MDE; por ejemplo, los errores posicionales (deficiente localización geográfica) de los puntos acotados o de la trayectoria de la curva de nivel, que afectan la información en XY. Otro tipo de errores son los valores de altitud erróneos. Existen también los errores relacionados con el proceso de interpolación. Los errores más comunes son relacionados con la creación de hoyos ("pits") o depresiones, éstos son áreas rodeadas por celdas con mayor altitud y de picos ("peaks"), las cuales se encuentran rodeadas por áreas o celdas con altitudes más bajas. Con el fin de sistematizar estos errores, el Departamento de Investigaciones Geológicas de Estados Unidos (U.S. Geological Survey) reconoce que produce tres tipos de errores en los MDE: a) errores garrafales (blunders), b) sistemáticos y c) no sistemáticos (aleatorios). Los blunders son errores verticales asociados al proceso de colección de datos, son identificados y corregidos antes de llegar a los usuarios. Los errores sistémicos son resultado del procedimiento o sistema utilizado en el proceso de la generación de los MDE; en general, presentan ciertos patrones que siguen un arreglo y pueden producir un sesgo en el producto final. Cuando la causa es conocida, los errores sistémicos son eliminados o reducidos. Por lo regular, los errores aleatorios permanecen en los MDE ya que su naturaleza y localización es poco entendida (Wechsler y Kroll, 2006).
Diferentes autores han propuesto métodos y técnicas para evaluar estos errores y eventualmente aminorarlos o corregirlos (Guercio y Soccodato, 1996; Jenson y Domingue, 1988; Hutchinson 1988, 1997; Martz y Garbrecht, 1998 y Rieger, 1998). Sin embargo, los usuarios de los MDE frecuentemente no evalúan los efectos de los errores de los MDE (Wechsler, 2003) y los métodos para disminuir los errores no han sido sistemáticamente integrados a los programas de SIG (Wechsler y Kroll, 2006).
Generalmente, la evaluación de la calidad de los MDE se hace a través de la medición de error medio cuadrático (EMC) entre la elevación estimada por el MDE y mediciones muy precisas. Por ejemplo, Erten et al. (2005) realizaron una evaluación de la calidad de los MDE obtenidos con imágenes ASTER y Shuttle Radar Topography Mission (SRTM) contra MDE generados a partir de curvas de nivel a escala 1:25 000. La precisión de los MDE Aster fue mayor que los del SRTM en comparación con los datos altitudinales extraídos de los mapas topográficos, teniendo una máxima diferencia de 16 m en ASTER y 28 m en SRTM. Carlisle (2005) resaltó la importancia de ubicar espacialmente los errores de los MDE y realizó un modelado espacial del error, cuestionó la utilización de un único índice de error como el error medio cuadrático y la desviación estándar para describir los errores en los MDE. Wechsler y Kroll (2006) desarrollaron una metodología para evaluar la confiabilidad de los parámetros derivados de los MDE e integrar dicha metodología en un sistema de información geográfica (SIG) para usuarios.
Otros autores se enfocaron en comparar el desempeño de diferentes métodos de interpolación (Krajewski y Gibbs, 1994; Morillo et al., 2002). En primer lugar se demostró que la resolución del MDE interpolado tiene una influencia muy importante sobre su calidad. Otros trabajos mencionan que resoluciones bajas producen bajos gradientes de pendiente sobre pendientes fuertes y fuertes gradientes de pendiente sobre áreas planas. Sin embargo, también concluyen que resoluciones altas no necesariamente implican modelos de terreno más útiles (Thompson et al., 2001). Kienzle (2004) establece que los valores de atributos como: elevación, pendiente, exposición, curvatura en planta y perfil y el índice de humedad, se modifican al cambiar el tamaño de la malla (resolución espacial del MDE).
Por otro lado, la determinación de la resolución en un MDE no puede establecerse como una regla general para todos los estudios relacionados con el relieve, ya que ésta dependerá del tipo de relieve en estudio (planicies, montañas, valles, barrancos, etc.; Theobald, 1989; Wood, 1994;WeibelandBrándli, 1995, entre otros) y de la escala original de los datos altitudinales. Hengl et al. (2004) proponen que la resolución de un MDE debe ser la mitad de la distancia promedio entre curvas de nivel. Hutchinson (1996) propone un método gráfico para determinar la resolución óptima para llevar a cabo la interpolación. Este método se basa en la medición del error medio cuadrático de la pendiente a diferentes resoluciones, siendo la resolución idónea aquella que no presenta una reducción importante de este error en comparación con el modelo de resolución más baja.
Finalmente, existen algunas técnicas para mejorar los MDE. Una de las más comunes consiste en aplicar filtros que reducen la magnitud de los errores, al identificar condiciones anisotrópicas (donde la variación en una dirección es distinta en otra dirección) y establecer una homogeneidad con el conjunto que los rodea (Brown y Bara, 1994).
Este estudio pretende comparar cuatro programas que permiten interpolar la información altitudinal vectorial para generar un MDE, determinando cuál de ellos obtiene una mayor precisión, además de establecer la resolución más adecuada para el manejo y análisis del relieve en la zona en estudio. El proceso antes mencionado es de crucial importancia, ya que a partir de la generación de un MDE con alta calidad, es posible producir mapas de pendientes, curvatura, exposición, etc., que contengan información confiable y por lo tanto útil, para la correcta interpretación del relieve.
ÁREA DE ESTUDIO
La zona en estudio forma parte de una microcuenca de 570 km2, la cual desemboca en la subcuenca del río Tepalcatepec, que a su vez forman parte de la gran cuenca del río Balsas. La microcuenca presenta un gradiente altitudinal que va desde 200 hasta 2 200 msnm y fisiográficamente pertenece a la provincia montañosa de la Sierra Madre del Sur (Figura 1). El origen de esta sierra es muy complejo, ya que presenta rocas de diversos orígenes y tipos, destacando rocas volcánicas intrusivas del Eoceno–Mioceno (batolito granítico); rocas volcánicas extrusivas del Eoceno–Oligoceno (andesitas, tobas ácidas y tobas ácidas–brechas volcánicas); rocas metamórficas (esquistos); y rocas sedimentarias del Albiano–Cenomaniano o Turoniano (calizas, areniscas–conglomerado y lutitas–areniscas; Garduño et al., 1999). La regionalización geomorfológica (Bocco et al., 1999) describe a la zona en estudio con tres geoformas principales: lomeríos bajos, lomeríos altos y sierra.
MATERIALES Y MÉTODOS
Se utilizó un Modelo Digital de Elevación derivado de imágenes del sensor ASTER con una resolución de 30 m como modelo de referencia. El DEM se genera con base en un par estereoscópico de imágenes tomadas en el visible e infrarrojo cercano por dos telescopios a bordo del sensor: uno mirando al nadir, el otro hacia atrás (USGS, 2006).
Los programas utilizados para llevar a cabo las interpolaciones fueron ARC/INFO, IDRISI, ILWIS y NEW–MIEL (Tabla 1).
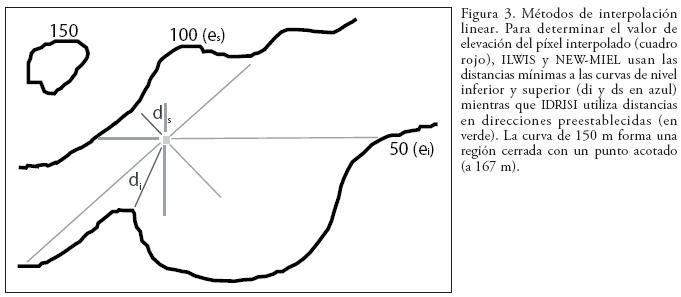
Se generaron curvas de nivel y puntos acotados a partir del MDE Aster con una separación entre curvas de nivel de 50 m, considerando la resolución del MDE que es de 30 m. Esta información fue utilizada para llevar a cabo la interpolación en los diferentes programas, a las diferentes resoluciones y utilizando diferentes insumos (curvas de nivel únicamente, con puntos acotados y/o escurrimientos superficiales), los cuales constituyen las opciones disponibles para que el usuario personalice el proceso de interpolación. Finalmente se comparó el MDE ASTER original con los diferentes MDE obtenidos (Figura 2). Los métodos de interpolación de ILWIS y NEW–MIEL se basan en una interpolación linear con base en la elevación de las dos curvas de nivel más cercanas. Para cada píxel ubicado entre dos curvas, el algoritmo determina las distancias mínimas que lo separan de la curva inferior y superior. La elevación de este píxel se estima como se indica a continuación (Ecuación 1 y Figura 3).
donde:
ep es el valor de la elevación del píxel objeto de la interpolación,
di y ei son, respectivamente, la distancia mínima a la curva de elevación inferior y el valor altitudinal de dicha curva,
ds y es son, respectivamente, la distancia mínima a la curva de elevación superior y el valor altitudinal de dicha curva.
Para los píxeles ubicados en una curva de nivel cerrada (polígono), ILWIS le asigna el valor de elevación de la curva de nivel a todos los pixeles (formación de un plateau) dentro del polígono, mientras que NEW–MIEL utiliza un algoritmo de dilatación de curvas (Taud et al., 1999) para calcular estos valores si existe un punto acotado.
El método de interpolación de IDRISI es una modificación de CONSURF (Douglas, 2000), también basado en una interpolación linear entre puntos que pertenecen a curvas de nivel. En este algoritmo, en vez de calcular la distancia más corta a las curvas de nivel, se construyen perfiles verticales, horizontales y en diagonal (Figura 3) . La elevación que se retiene es aquella que corresponde al perfil con más pendiente.
El algoritmo de interpolación de ARC/INFO (TOPOGRID) es un método de interpolación diseñado específicamente para la creación de modelos digitales del terreno. Está basado en el algoritmo ANUDEM desarrollado por Hutchinson (1988). Es un método de interpolación multiresolución, empieza con un raster de baja resolución y continúa hasta la resolución predefinida por el usuario. Este procedimiento de interpolación cuenta con las ventajas de aquellos algoritmos locales, como el gravitacional (Inverso del Cuadrado de la Distancia), y la de los algoritmos globales de las curvas adaptativas (splines). En resumen, la técnica de interpolación desarrollada está basada en el método de curvas adaptativas (thin plate splines) modificado en cuanto al cálculo de la rugosidad para conseguir que el modelo se ajuste a los bruscos cambios de pendiente. Admite utilizar curvas de nivel, puntos acotados y datos de corrientes, permitiendo así que la interpolación respete la red de drenaje.
Se compararon los resultados obtenidos por la interpolación de los cuatro programas (ARC/INFO, ILWIS, IDRISI y NEW–MIEL) con cinco diferentes resoluciones (20, 30, 50, 70 y 100 m) con el MDE de referencia que se utilizó para generar las curvas de nivel (Figura 2).
La interpolación para generar el MDE en los diferentes programas se llevó a cabo básicamente con dos tipos de información: a) curvas de nivel y b) curvas de nivel más puntos acotados. El programa ARC/INFO permitió llevar a cabo la interpolación agregando información de las corrientes fluviales (información vector, INEGI). Al contrario, con ILWIS sólo se puede realizar la interpolación con una sola capa de información (curvas de nivel).
La determinación de la resolución más adecuada para la representación del relieve se realizó a través de la representación gráfica del error medio cuadrático, obtenido de la diferencia altitudinal entre cada DEM obtenido por interpolación y el DEM de referencia. El error medio cuadrático (véase ecuación 2) es la raíz cuadrada del promedio de las diferencias entre los dos MDE al cuadrado (MDE de referencia y generado en cada programa a cada resolución).
donde:
ei es la elevación en la localización i del MDE obtenido por interpolación y,
Ei es la elevación en el modelo de referencia para la misma localización i.
n es el número total de puntos analizados.
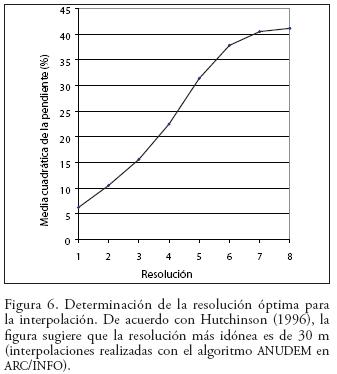
A través de los EMC obtenidos en los diferentes programas se determinó la resolución óptima del DEM. Otra alternativa en la determinación de la mejor resolución fue obtenida a través del método de Hutchinson (1996). Este método se basa en el hecho de que los MDE realizados con una baja resolución agrupan y promedian los valores de elevación de diferentes curvas o puntos acotados y, en consecuencia, tienden a subestimar la pendiente. El método consiste en realizar la interpolación a diferentes resoluciones y observar el comportamiento de la pendiente (a través del error medio cuadrático de la misma) en función de la resolución. Según Hutchinson (op. cit.), esta curva presenta un quiebre que permite identificar la resolución idónea para la interpolación (Figura 4). Hutchinson y Gallant (2000) aplicaron este método pero no encontraron una curva muy fácil de interpretar.
Posteriormente se realizaron comparaciones entre las interpolaciones obtenidas por cada programa con la resolución más adecuada y el MDE de referencia, pretendiendo con ello visualizar la distribución espacial del error de los MDE y observar si los errores están asociados a determinadas formas del relieve.
Para elaborar los mapas de error, se agruparon los valores del error con base en la desviación estándar del mismo. Los errores cercanos a los valores del MDE de referencia (menos de una desviación estándar) se consideraron aceptables. Los valores de error más grandes (error superior a una desviación estándar) negativos y positivos, se agruparon en dos niveles cada uno (error bajo y alto).
Posteriormente se elaboró un perfil, el cual cruzó el área con los errores más altos y con una mayor superficie con la finalidad de entender el comportamiento de los diferentes algoritmos de interpolación en el área en estudio.
Finalmente, seleccionando tanto la resolución más adecuada como el programa de interpolación con mayor precisión, se elaboraran los diferentes mapas de representación del relieve (altitud, pendiente, exposición y curvatura en planta). Sin embargo, estos mapas sólo tendrá sentido su elaboración en función de los resultados del capítulo siguiente, donde se determinarán los atributos del relieve que resulten con un relación entre los atributos del relieve y la distribución del BTSC en la zona en estudio.
RESULTADOS
El cálculo del error medio cuadrático de los MDE obtenido por interpolación en cada uno de los cuatro programas (ARC/INFO, NEW–MIEL, IDRISI e ILWIS) a diferentes resoluciones (Figura 5), mostró que en los programas ARC/INFO y NEW–MIEL fue posible determinar que las resoluciones entre 20 y 30 m son las más adecuadas. Dichas resoluciones permitieron obtener errores menores que las resoluciones más gruesas. La reducción del error con una resolución de 20 m en vez de 30 m es mínima. La gráfica para IDRISI es muy diferente y muestra mayor error en la resolución más fina (20 m). En cuanto al programa ILWIS, la curva no tiene una estabilización clara para alguna de las resoluciones; sin embargo, el error mostrado en una resolución de 20 m, lo coloca en el segundo más bajo después de ARC/INFO. El método de Hutchinson (1996), por su parte, mostró que la resolución, para la cual el aumento del error medio cuadrático de la pendiente presenta un quiebre, está alrededor de 30 m, siendo ésta la resolución más adecuada para interpolar los datos (Figura 6).
Para ARC/INFO e IDRISI, el desempeño de la interpolación fue mejor al utilizar sólo la información de las curvas de nivel (EMC de 8.3 y 10 m, respectivamente) que agregando la información de los puntos acotados (EMC de 10.3 y 11.8 m; Figura 7). Sólo el programa NEW–MIEL tuvo un mejor resultado al utilizar los datos de curvas y los puntos acotados (EMC de 10.0 m con curvas y puntos contra 10.8 m con curvas únicamente). El resultado obtenido con ILWIS dio un EMC de 11.3 m, siendo el mayor error en comparación con los demás programas aunque con la resolución de 20 m presenta resultados similares a los obtenidos por NEW–MIEL. Por otro lado, ARC/INFO tiene la posibilidad de insertar información de las corrientes fluviales para llevar a cabo la interpolación, lo cual redujo el error hasta 7.3 m (Figura 7).
Los valores del EMC fueron agrupados en cinco rangos para visualizar espacialmente los errores. Para ello se tomaron en cuenta los errores de la interpolación sólo con curvas de nivel y a una resolución de 30 m. La fijación de los umbrales de los valores se hizo con base en la desviación estándar del error, la cual determinó los errores aceptables, siendo éstos inferiores a 10 m (tanto positivos y negativos). Los otros cuatro rangos fueron establecidos considerando los valores máximo y mínimo, los cuales fueron de 46.1 y –49.8 m, (Tabla 2). Se consideran los errores positivos y negativos cuando el MDE interpolado está, respectivamente, por arriba y por debajo de la elevación real (Figura 8).
Los errores se ubicaron principalmente en las zonas con pendiente muy baja (planicies y planicies aluviales) y en las cimas. En las zonas con pendiente moderada a fuerte (laderas) los errores son mínimos (en blanco), aunque el programa ILWIS fue el único que presentó errores negativos bajos (azul claro) en zonas de laderas (Figura 9).
En ARC/INFO los errores positivos moderados y altos (colores naranja y rojo) se ubican predominantemente en la planicie (porción noreste de la zona), y es muy evidente que al agregar los datos de los puntos acotados en la interpolación, en esta misma zona aumentan de forma considerable las superficies de error positivo.
La distribución espacial del error al utilizar la información de las corrientes fluviales para ARC/INFO, muestra una disminución importante de los errores positivos (naranja y rojo), de forma considerable en la zona de la planicie y las planicies aluviales, mostrando ARC/INFO el menor error en comparación con los otros programas.
Los errores positivos en IDRISI y NEW–MIEL (naranja y rojo) ocupan mayor superficie en la zona de la planicie noreste y las planicies aluviales en comparación con ARC/INFO e ILWIS (Figura 9). Sin embargo, en la interpolación de NEW–MIEL al utilizar los puntos acotados y las curvas de nivel, la superficie de dichos errores disminuye para la porción de la planicie noreste cercana al punto acotado. En contraste, IDRISI mantiene casi las mismas superficies de error para ambos tipos de interpolación. En este programa son notables los artefactos en forma de estrella producidos por el método de búsqueda de las curvas vecinas en direcciones predeterminadas (Figura 3).
El perfil se ubicó en la planicie aluvial ubicada en la porción noreste de la zona en estudio, con la finalidad de cruzar la región con mayor error (Figura 10).
El perfil para ARC/INFO (Figura 11) mostró que el algoritmo utilizado para interpolar curvas y puntos acotados, trata de generar perfiles que pasen por los puntos cuya elevación es conocida (curvas y puntos acotados) con poca curvatura. La introducción del punto acotado incrementó considerablemente los errores, con un error positivo que alcanzó hasta 60 m (con la interpolación sólo con curvas este error máximo era de 21 m) y un error negativo de hasta –22 m mientras los producidos sólo con la interpolación con curvas de nivel fue –9 m (Figura 11).
La gráfica correspondiente a IDRISI muestra cómo de forma general los errores de los MDE producidos con curvas de nivel y curvas de nivel más puntos son muy parecidos. Sin embargo, el algoritmo de IDRISI realiza una corrección de la elevación a partir de puntos acotados, pero únicamente si éstos coinciden con las direcciones de búsqueda. De manera general, el perfil presenta cambios abruptos que no corresponden a la realidad y que corresponden a los defectos en forma de estrella que se observan en la Figura 9. Por su parte NEW–MIEL, al llevar a cabo la interpolación con curvas de nivel y puntos, disminuye los errores al crear líneas rectas entre los puntos cuya altura es conocida. Es el único programa que disminuyó los errores utilizando los datos de puntos acotados. Por último, en ILWIS sólo se presentan los datos con curvas de nivel, porque como se mencionó anteriormente, solo es posible interpolar con curvas de nivel. ILWIS generó una superficie sin desniveles bruscos más elevada que la real debido a la ausencia de curvas de nivel a 200 m.
DISCUSIÓN Y CONCLUSIONES
La evaluación de los errores inherentes a los procesos de interpolación así como la determinación de la resolución adecuada, son aspectos de suma importancia en la representación del relieve. En este estudio la resolución más adecuada utilizando curvas de nivel cada 50 m fue de 30 m. El método de Hutchinson (1996) permitió definir la resolución más idónea para llevar a cabo la interpolación.
Para este trabajo los programas que presentaron menor error medio cuadrático fueron ARC/INFO y NEW–MIEL en relación con el MDE de referencia (imágenes ASTER), siendo este último el único programa que mejoró sus resultados al agregar la capa de información de puntos acotados.
Por otro lado, los mejores resultados fueron obtenidos con el programa ARC/INFO, utilizando la información de los escurrimientos (y omitiendo los puntos acotados), lo cual permitió reducir de manera importante los errores en la zona de planicies. Sin embargo, ARC/INFO es un sistema de información con un alto costo de adquisición a diferencia de NEW–MIEL que es gratuito y disponible en línea.
La distribución espacial del error que mostraron los diferentes programas depende del algoritmo de interpolación utilizado. En el caso de IDRISI, el MDE presenta errores muy burdos. ARC/INFO al generar perfiles con una curvatura reducida en los puntos de elevación conocida, produce una superficie curveada entre formas de laderas y planicies, lo cual provoca resultados con errores de importante magnitud.
Los cuatro programas utilizados presentan los mayores errores en superficies de baja pendiente (planicies y cimas) con errores positivos; de forma opuesta las superficies con pendientes fuerte (laderas) mostraron un error muy bajo, excepto para el programa ILWIS.
El análisis y comparación de los errores en los MDE muestra un rango de error entre 7.3 a 11.3 m para los cuatro paquetes utilizados con la combinación de las diferentes capas que fueron interpoladas, y permite observar que los algoritmos utilizados para dicho fin todavía requieren de un mayor perfeccionamiento para lograr sobre todo que las superficies planas y de baja pendiente sean representadas con una mayor calidad.
Finalmente, es notable que la elaboración de MDE sin búsqueda de la resolución más idónea y el uso de los MDE sin ningún análisis de la calidad de los mismos, genera errores importantes, los cuales representan formas del relieve ajenas a la realidad.
REFERENCIAS
Bocco, G., M. Mendoza, A. Velázquez y A. Torres (1999), "La regionalización geomorfológica como una alternativa de regionalización ecológica en México. El caso de Michoacán de Ocampo", Investigaciones Geográficas, Boletín, núm. 40, Instituto de Geografía, UNAM, México, pp. 7–21. [ Links ]
Brown, D. B. and T. J. Bara (1994), "Recognition and reduction of systematic error in elevation and derivate surfaces from 7 ½– minute DEMs", Photogrammetric Engineering and Remote Sensing, vol. 60, pp. 189–194. [ Links ]
Carlisle, B. (2005), "Modelling the spatial distribution of DEM Error", Transactions in GIS, vol. 9, núm 4, pp. 521–540. [ Links ]
Douglas, D. H. (2000), "CONSURF, the Douglas contour to grid methodology" (http://www.hig.se/~dds/research/consurf/consur1.htm: 10 de octubre 2007). [ Links ]
Erten, E., N. Musaoglu and A. Hervía (2005), "Quality assessment of digital elevation model produced from ASTER images", Proceedings of the 6th Geomatic Week, Barcelona, 8–11 February 2005. [ Links ]
Felicísimo, A. (1994), "Modelos Digitales de Terreno. Introducción y aplicación en las ciencias ambientales" (http://www6.uniovi.es/~feli/pdf/libromdt.pdf: 14 de enero 2008). [ Links ]
Garduño, V. H., P. Corona, I. Israde, L. Mennella, E. Arreygue, B. Bigioggero y S. Chiesa (1999), Carta Geológica del Estado de Michoacán, escala 1:250 000, Universidad Michoacana de San Nicolás de Hidalgo, Instituto de Investigaciones Metalúrgicas, Morelia, Michoacán, México. [ Links ]
Geoscience Australia (2005), "Geodata 9 Second DEM Version 2" (http://www.ga.gov.au/nmd/products/digidat/dem_9s.htm: 14 de enero de 2008). [ Links ]
Guercio, R. and F. M. Soccodato (1996), "GIS Procedures for automatic extraction of Geomorphological Attributes from TIN–DTM", HydroGIS 96: Application of Geographic Information Systems in Hydrology and Watershed Resources Management (Proceedings of the Vienna Conference, April 1996), IAHS Publ. no. 235, pp. 175–182. [ Links ]
Hengl, T., S. Gruber and D. P. Shrestha (2004), "Reduction of errors in digital terrain parameters used in soil–landscape modeling", International Journal of Applied Earth Observation and Geoinformation, no. 5, pp. 97–112. [ Links ]
Hutchinson, M. F. (1988), "Calculation of hydrologically sound digital elevation models", Proceedings of the Third International Symposium on Spatial Data Handling, August 17–19, Sydney, International Geographical Union, Columbus, Ohio, pp. 117–133. [ Links ]
Hutchinson, M. F. (1996), "A locally adaptive approach to the interpolation of digital elevation models", Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling, Santa Fe, NM, January 21–26, 1996. Santa Barbara, CA: National Center for Geographic Information and Analysis. [ Links ]
Hutchinson, M. F. (1997), ANUDEM. Versión 5.2, Centre for Resource and Enviromental Studies, Australian National University, Camberra, Autralia (http://cres.anu.edu.au/outputs/anudem.php: 14 de enero de 2008). [ Links ]
Hutchinson, M. and J. Gallant (2000), "Digital elevation models and representation of terrain shape" in Terrain Analysis. Principles and Applications, Ed. Wilson y Gallant, John Wiley & Sons, Inc. New York, USA. [ Links ]
Jenson, S. K. and J. O. Domingue (1988), "Extracting topographic structure from Digital Elevation Data for Geographic Information System analysis", Photo–gramm. Eng. Rem. S. 54, pp. 1593–1600. [ Links ]
Kienzle, S. (2004), "The effect of DEM raster resolution on first order, second order and compound terrain derivatives", Transactions in GIS, vol. 8, no. 1, pp. 83–11. [ Links ]
Krajewski, S. A. and B. L. Gibbs (1994), "Computer contouring generates artifacts", Geotimes, no. 39, pp. 15–19. [ Links ]
Li, Z., Q. Zhu and C. Gold (2005), Digital Terrain Modeling. Principles and Methodology, CRC Press, Boca Raton Florida, USA. [ Links ]
Martz, L. W. and J. Garbrecht (1998), "The treatment of flat areas and closed depressions in automated drainage analysis of raster digital elevation models", Hydrological Processes 12, pp. 843–855. [ Links ]
Maune, D. F. (ed.; 2001), Digital Elevation Model Technologies and Applications: the DEM Users Manual, The American Society for Photogrammetry and Remote Sensing, USA. [ Links ]
Morillo, J., J. Pozo, F. Pérez, M. C. Rodríguez, F. Gordillo y J. Rebollo (2002), "Análisis de calidad de un modelo digital de elevaciones generado con distintas técnicas de interpolación", XIV Congreso Internacional de Ingeniería Gráfica, Santander, España, 5–7 junio de 2002 (http://departamentos.unican.es/digteg/ingegraf/cd/ponencias/11.pdf: 14 de enero de 2008). [ Links ]
Parrot, J. F. y V. Ochoa–Tejeda (2005), Generación de Modelos Digitales de Terreno Raster, Método de Digitalización, Geografía para el Siglo XXI, Serie Textos Universitarios, núm. 2, Instituto de Geografía, UNAM, (http://www.igeograf.unam.mx/instituto/publicaciones/libros/manual mde/index.html: 10 de octubre de 2007). [ Links ]
Rieger, W. (1998), "A phenomenon–based approach to upslope contributing area and depressions in DEMs", Hydrol. Processes, no. 12, pp. 857–872. [ Links ]
Taud, H., J. F. Parrot y R. Álvarez (1999), "DEM generation with contour line dilation", Computers and Geosciences, vol. 25, no. 7, pp. 775–783. [ Links ]
Theobald, D. M. (1989), "Accuracy and bias issues in surface representation", in Goodchild, M. F. and S. Gopal (eds.), The Accuracy of Spatial Databases, London, Taylor and Francis, pp. 99–106. [ Links ]
Thompson, J. A., J. C. Bell and C. A. Butler (2001), "Digital elevation model resolution: effects on terrain attribute calculation and quantitative soil–landscape modeling", Geoderma, no. 100, pp. 67–89. [ Links ]
USGS (2006), "ASTER Digital Elevation Model" (http://edcdaac.usgs.gov/aster/ast14dem.asp: 14 de enero de 2008). [ Links ]
Wechsler, S. (2003), "Perceptions of digital elevation model uncertainty by DEM users", Urban and Regional Information Systems Association Journal, vol. 15, no. 2, pp. 57–64. [ Links ]
Wechsler, S. (2003), "Perceptions of digital elevation model uncertainty by DEM unser", Urban and Regional Information Systems Association Journal, vol. 15, no. 2, pp. 57–64. [ Links ]
Wechsler, S. and C. Kroll (2006), "Quantifying DEM Uncertainty and its effect on topographic parameters", Photogrammetric Engineering and Remote Sensing, vol. 72, no. 9, pp. 1081–1090. [ Links ]
Weibel, R. and M. Branli (1995), "Adaptive methods for the refinement of digital terrain models for geomor–phometric applications", Zeitschrift and Geomorpho–logie, no. 11, pp. 13–30. [ Links ] Weibel, R. and M. Heller (1991), "Digital terrain modeling", in Maguire, D. J., M. E Goodchild and D. W. Rhind (eds.), Geographic Information Systems, vol. 1: Principles. Harlow: Longmanv, London, UK, pp. 269–97. [ Links ]
Wilson, J. P. and J. C. Gallant (2000), Digital Terrain Analysis. Terrain Analysis. Principles and Applications, Ed. Wilson y Gallant, John Wiley & Sons, New York, USA. [ Links ]
Wood, J. D. (1994), "Visualising contour interpolation accuracy in digital elevation models", in Herarnshaw, H. M. and D. J. Unwin (eds.), Visualization in Geographical Information Systems, John Wiley & Sons, Chichester, UK, pp. 168–180. [ Links ]