Introducción
Como pieza clave de la estrategia de liberalización comercial emprendida por México desde mediados de los años ochenta de la pasada centuria, el TLCAN (Tratado de Libre Comercio de América del Norte) ha contribuido significativamente en los cambios observados en las estructuras de la oferta y la demanda agregadas de la economía mexicana. Este acuerdo regula las relaciones comerciales entre Canadá, Estados Unidos de América (EUA) y México, desde el 1 de enero de 1994.
Si bien en los 30 años transcurridos entre 1985 y 2015 las tasas de crecimiento real del producto interno bruto (PIB) de la economía mexicana fueron modestas (2.3 por ciento), en ese mismo periodo, los coeficientes de exportaciones e importaciones respecto al PIB pasaron del 15.3 al 35.2 por ciento y del 7.5 al 33.8 por ciento, respectivamente. De esta forma, el grado de apertura de la economía de México despegó del 22.8 al 69 por ciento, convirtiéndose en pocos años en una de las economías más abiertas del mundo (Dávila y Valdés, 2016).
Por su parte, las exportaciones petroleras disminuyeron aceleradamente su importancia relativa (del 68.2 al 6.2 por ciento), en tanto las no petroleras alcanzaron el 93.8 por ciento de las ventas totales en el 2015. En este último grupo, sobresalieron los productos manufactureros, concentrando el 95.1 por ciento. A lo largo de esas tres décadas, el valor real de las exportaciones manufactureras se multiplicó por 31, es decir, experimentaron una tasa media de expansión anual del 12.1 por ciento, cinco veces mayor a la registrada por el PIB nacional esos mismos años (Dávila y Valdés, 2016).
El valor de las exportaciones de mercancías está fuertemente concentrado en los EUA (80.9 por ciento en 2016)1 y en un puñado de productos. Así, el 60.5 por ciento de las ventas internacionales de manufacturas en 2015 correspondieron a tres de los 97 capítulos del Sistema Armonizado de Designación y Codificación de Mercancías: el 87, Vehículos terrestres y sus partes (23.7 por ciento del total); el 85, Máquinas y material eléctrico (21.3), y el 84, Aparatos mecánicos, calderas y sus partes (15.5). A nivel de fracciones arancelarias, 11 de las 599 del Sistema Armonizado concentraron el 50.6 por ciento de las exportaciones de bienes de ese año: automóviles tipo turismo (8.6 por ciento); partes y accesorios de vehículos (6.6 por ciento); vehículos para transporte de mercancías (6.6 por ciento); petróleo crudo (4.9 por ciento); máquinas para el procesamiento de datos (4.8 por ciento); televisores (4.4 por ciento); aparatos eléctricos de telefonía o telegrafía (4.2 por ciento); otras máquinas y material eléctrico (3.1 por ciento); conductores aislados para electricidad (3 por ciento); otros aparatos mecánicos y partes (2.9 por ciento), y tractores (2.3 por ciento) (Dávila y Valdés, 2016).
Dadas estas tendencias, cualquier cambio cualitativo en el marco normativo del comercio exterior con Canadá y, muy especialmente, con los EUA, reviste importancia estratégica para la economía mexicana. Desde esta perspectiva, y bajo la iniciativa del gobierno norteamericano, se iniciaron las renegociaciones del TLCAN, que podrían desembocar ya sea en un tratado modificado, en la continuidad del actual o en la eventual salida del mismo por parte de los EUA.
La hipótesis central del trabajo es la existencia de una acentuada interdependencia estructural de la economía mexicana con la de los EUA, lo cual la hace muy sensible a las fluctuaciones significativas en la demanda por sus exportaciones de bienes y servicios a Norteamérica.
En este contexto, los objetivos del ensayo son los siguientes:
Construir la Matriz de Contabilidad Social (MCS) de la economía mexicana para el año 2013.
Elaborar y resolver, con la base de datos del punto previo, el modelo de producción ampliado de Leontief, así como calcular los multiplicadores de la producción bruta, el empleo, el salario y el valor agregado.
Con el modelo de producción y mediante la técnica de extracción de las exportaciones de la demanda final exógena, cuantificar la importancia de las ventas internacionales para los principales agregados de la economía mexicana.
Posteriormente, los multiplicadores son utilizados como insumos para el cómputo de las elasticidades totales, aplicando para tal efecto el procedimiento propuesto por Stone (1985). Al hacerlo podremos determinar la sensibilidad de las principales variables de la economía mexicana ante fluctuaciones unitarias en el valor de su demanda final exógena en general y de sus exportaciones internacionales en particular.
A continuación, se aplican las técnicas de descomposición aditiva (Stone, 1985, citado en Miller y Blair, 2009) para determinar el peso de los efectos inicial, directos, indirectos e inducidos, en las elasticidades totales.
Finalmente, se cuantifican los efectos de variaciones unitarias en las exportaciones de las actividades productivas sobre la asignación del ingreso primario y el consumo privado de los hogares.
Consecuentemente, el trabajo aborda un tema de importancia estratégica en la actual coyuntura de replanteamiento de las relaciones comerciales en la región de Norteamérica. Para tal efecto, se emplea una versión ampliada del modelo de Leontief la cual, al utilizar una base de datos generada con una MCS, nos permite abordar el tema no sólo desde una perspectiva multisectorial, sino adicionalmente soporta la integración de los flujos de generación, asignación, distribución y utilización del ingreso, así como de sus vínculos estructurales con los sectores productores de bienes y servicios.
En la siguiente sección (I) haremos una breve recapitulación de los orígenes, características, desarrollo y aplicaciones de las MCS y de los modelos lineales multisectoriales construidos con su información. El siguiente apartado (II) lo dedicamos a la descripción del proceso de construcción de la MCS de la economía mexicana, así como a la presentación del modelo de producción derivado de la misma. A continuación (epígrafe III), mediante la aplicación de la técnica de extracción de las exportaciones de la demanda final exógena, se resuelve el modelo ampliado de producción y se comparan los resultados con los del escenario base para medir la importancia de las ventas internacionales en la determinación de los principales agregados de la economía mexicana. Posteriormente (apartado IV), se describe la metodología de cálculo de las elasticidades totales desarrollada por Stone (1985) para, en el inciso posterior (V), utilizarla en el análisis de la sensibilidad de la economía mexicana ante fluctuaciones en sus exportaciones, presentando y discutiendo los resultados obtenidos. Finalmente, el ensayo cierra con la derivación de las conclusiones más relevantes.
I. Origen, características, desarrollo y aplicaciones de matrices de contabilidad social, así como de los modelos ampliados de Leontief construidos con éstas
I.1. Origen y características generales de las matrices de contabilidad social
Erik Thorbecke (1998) describe a las MCS como sistemas de datos completos, consistentes, desagregados y comprehensivos que hacen posible capturar la interdependencia existente en un sistema socioeconómico. Las MCS constituyen la base para la construcción de versiones ampliadas de los modelos lineales de producción y precios de Leontief, de sus multiplicadores, de los métodos de descomposición estructural, multiplicativa y aditiva de éstos, así como para la elaboración y la calibración de los modelos de equilibrio general aplicado.
El mismo autor agrega que las MCS son sistemas de datos: 7) comprehensivos y desagregados porque incluyen estimaciones de las transacciones entre sectores productivos, instituciones y agentes económicos; 2) consistentes, en el sentido de que cada ingreso debe ser equivalente a los gastos, y 3) completos en virtud de que las dos facetas de cada transacción (compra y venta, envío y recepción) deben identificarse. Por lo anterior, proporcionan una imagen integral del sistema socioeconómico en el periodo temporal examinado.
Richard Stone (1962) fue el autor del trabajo seminal en este campo de especialización económica al formular la primera MCS para el Reino Unido. Su metodología fue adoptada por los modernos sistemas de contabilidad social de la Organización de las Naciones Unidas,2 los cuales aplican las agencias estadísticas de muchos países y regiones del mundo. Una característica central de su planteamiento es que permite la fusión consistente, en un solo marco contable, de las matrices de insumo producto, los sistemas de cuentas nacionales y las cuentas de los sectores institucionales. La relevancia de sus contribuciones lo hizo acreedor al Nobel de Economía en 1984.
Partiendo de los conceptos básicos del flujo circular de ingreso y gasto de una economía simplificada, la cual es gradualmente modificada mediante la integración de agentes y mercados adicionales, Miller y Blair (2009) brindan una descripción didáctica del proceso de construcción de las MCS resultante de la articulación de los tres sistemas de información referidos arriba (cuentas nacionales, matrices de insumo producto y cuentas por sectores institucionales). Los autores retoman el formato de las MCS propuesto por Holland y Wyeth (1993), el cual constituye una extensión del modelo básico de Leontief. En el apartado 3 del trabajo se describirá puntualmente este enfoque, pues se utilizó para la conformación de la MCS de la economía mexicana. Previamente haremos una revisión de literatura sobre la evolución de las MCS y de las aplicaciones con modelos económicos lineales construidos con sus bases de datos.
I.2. Desarrollo y aplicaciones de las matrices de contabilidad social para la construcción de modelos económicos lineales multisectoriales
La revisión de literatura se centra en la conformación de las MCS, en su uso para la construcción de modelos lineales multisectoriales ampliados tipo Leontief, así como en sus aplicaciones en el análisis económico. No se abordan los temas de matrices y modelos de insumo producto de Leontief, ni los modelos de equilibrio general computable (mega) de precios flexibles. De hecho, con la información de las MCS, el modelo de Leontief puede formularse como un caso especial del mega, en el cual se aplican los mismos supuestos del modelo de insumo producto (coeficientes técnicos y proporciones fijas, no sustitución de bienes ni de insumos, rendimientos constantes a escala y precios fijos) (Sobarzo, 2011).
1.2.1. Desarrollo metodológico
Stone (1978, citado en Defourny y Thorbecke, 1984), así como Pyatt y Round (1979, citado en Miller y Blair, 2009), analizaron los multiplicadores en el marco contable de una MCS, los cuales son similares a los del modelo clásico de Leontief, con la significativa diferencia de que integran el flujo completo de ingreso-gasto de un sistema económico.
Por su parte, Defourny y Thorbecke (1984) propusieron una metodología de análisis estructural que da seguimiento detallado a la senda de transmisión de un impacto exógeno sobre un sistema económico lineal modelado con una MCS.
Las técnicas de descomposición multiplicativa fueron desarrolladas por Pyatt y Round (1985) y Round (1985) (ambos referidos por Miller y Blair, 2009). Esta herramienta analítica permite descomponer las matrices de multiplicadores construidas con MCS en tres matrices cuyo producto reproduce el valor de los efectos totales. De esta forma, es posible diferenciar los efectos directos e indirectos al interior de los grupos, los impactos extra grupo (también denominados de open loop) y los de retroalimentación (cross or closed loop).
Ese mismo año, Richard Stone (1985, citado en Miller y Blair, 2009), formuló la descomposición aditiva de los multiplicadores, facilitando la interpretación de cada uno de los efectos, cuya agregación simple da cuenta del cambio total en la variable analizada. El mismo autor (Stone, 1985) desagregó la cuenta de los hogares en el sistema de cuentas nacionales y en las MCS.
Roland-Holst y Sancho (1995) ampliaron el horizonte analítico al formular un modelo de precios en el marco contable de una MCS, lo que les permitió investigar la interdependencia entre las actividades productivas, los hogares y los factores de producción. Adicionalmente, aplicaron las técnicas de descomposición estructural referidas previamente, a fin de rastrear los efectos de las presiones en los costos sobre el equilibrio general subyacente.
1.2.2. Aplicaciones en México y en el extranjero
Las aplicaciones de modelos lineales de producción y precios construidos con MCS han sido abundantes y variadas. Desde el punto de vista espacial, este enfoque analítico ha sido muy flexible, pues lo mismo puede emplearse en el estudio de pequeñas economías locales o comunitarias, o en el ámbito regional, interregional, meso regional, nacional e incluso supra nacional.
De igual forma, los campos temáticos han sido muy diversos, destacando el análisis estructural. Sobre el particular, se refieren los trabajos de Holland y Wyeth (1993), para la economía de los EUA; Hajnovičová (1994) en el caso de Eslovaquia; en Bolivia, Alarcón, Van Heemst y De Jong (1997); Roberts (1998 y 2003), quien en el primer trabajo realizó un análisis interregional para economías del noreste de Escocia, en tanto que en el segundo se enfocó en un estudio similar en la región de las islas occidentales de ese mismo país; Resosudarmo y Ditya (2005) también aplicaron un enfoque interregional para Indonesia; Pasaltopoulos, Balamou y Skuras (2009) lo hicieron para seis regiones rurales de la Unión Europea, y Alikaj y Alexopoulos (2014) en la región occidental de Grecia.
Los estudios sobre los cambios en la distribución del ingreso de los hogares ante variaciones en la demanda final exógena, o en las transferencias unilaterales de ingreso, también han sido copiosos. Se pueden citar las contribuciones de Bottiroli y Targetti (1988) para Italia; en España, a nivel nacional, las aportaciones de Polo, Roland-Holst y Sancho (1990), así como la de Llop y Manresa (2003) para Cataluña y las de Vélez y Pérez (2006), y De Miguel y Pérez (2010) para la región de Extremadura; para Vietnam, Civardi, Vega y Targetti (2010), y, en el caso de Hawái, Arita, et al. (2013).
En el plano sectorial, se pueden enumerar investigaciones para el sector agrícola y pesquero: Roberts (1994); Sayan y Tin (1998); Bautista (2001); Seung y Waters (2006), así como; Psaltopoulos, Balamou y Thomson (2006).
De igual forma, estos modelos han sido utilizados para analizar temas tan variados como el impacto del cambio tecnológico en algunos sectores económicos sobre los agregados macroeconómicos, el nivel y la distribución del ingreso, así como la composición de la producción y el empleo (Khan y Thorbecke, 1989); o sobre impacto ambiental, al cuantificar el consumo de energía y las consecuentes emisiones equivalentes de gases de efecto invernadero (Chang-Gui y Kihoon, 2013; Manresa y Sancho, 2004); las finanzas públicas y el endeudamiento en la economía de Portugal (Santos, 2004); las tendencias económicas y su impacto en la urbanización en los Países Bajos (Cohen, 1996); estimar los efectos de las políticas de fomento a las actividades culturales en Corea y su difusión sobre el resto de las actividades y agentes económicos (Yong, 2010); los resultados de la transición económica en países de Europa del Este, como Polonia y Hungría (Braber et al, 1996); la derivación de los agregados contables marxistas, partiendo de MCS, para calcular el excedente económico (Olsen, 2011); la endogenización de la cuenta del sector externo para modelar el impacto de variaciones en el tipo de cambio sobre la economía española (Mainar et al, 2012); la endogenización de la cuenta de capital en un modelo de precios de la economía de Cataluña, con el propósito de modelar la reacción de los precios a los cambios exógenos en el ahorro y la inversión, así como para desentrañar el efecto global de los precios mediante la aplicación de técnicas aditivas de descomposición (Llop, 2012); o, finalmente, los modelos de oferta, tipo Ghosh, adoptados para analizar el sector pesquero en Alaska (Seung y Waters, 2006) y Galicia (Fernández et al, 2008).
En México, transcurrieron más de dos décadas sin matrices nacionales de insumo producto generadas mediante la aplicación de encuestas y siguiendo los lineamientos metodológicos de la onu (Organización de las Naciones Unidas). Hacia fines de 2008, el INEGI liberó la correspondiente al año 2003, cuatro años más tarde, divulgó la de 2008 y posteriormente una actualización al 2012 obtenida mediante la aplicación del método RAS. Por último, en octubre de 2017, se publicó la matriz de 2013. Así pues, los especialistas tienen a su disposición la información necesaria para construir las MCS de la economía mexicana. Como resultado de lo anterior, se aceleró rápidamente la producción de literatura especializada en la materia.
A pesar de la penuria de información durante los años aludidos, el campo de especialidad se mantuvo activo al menos por dos razones: 7) la actualización de matrices de insumo producto (MIP), ya sea mediante el procedimiento de ajuste biproporcional RAS o del método de entropía cruzada, y 2) la generación directa de información a partir del levantamiento de encuestas para el análisis económico de pequeñas comunidades.
Sobre este último punto, destacan los trabajos pioneros de Adelman, Taylor y Vogel (1987), así como de Yúnez y Taylor (1999). Estas aplicaciones se han enfocado en el análisis estructural de estas comunidades, así como en los efectos de las transferencias de ingreso ligadas a la migración (nacional e internacional), o a los programas públicos de combate a la pobreza, o bien, otras iniciativas, como la diseñada para apoyar al campo (Procampo). Además de los trabajos ya mencionados, se pueden referenciar las contribuciones de: Bracamonte y Méndez (2004); Núñez y Mendoza (2008); González y Fuentes (2010); González (2012); Arellano-González (2015), y Vuelvas (2015).
El despacho de Consultoría Internacional Especializada, S.A. de C.V. (1996), generó actualizaciones de la MIP de 1980 (la última disponible previa a la de 2003) para los años de 1990, 1993, 1996 y 2000. Con estas estimaciones y la información de cuentas nacionales y cuentas por sectores institucionales, distintos analistas construyeron MCS para realizar ensayos de carácter nacional y regional. Se pueden apuntar las aportaciones de Rodríguez (1995)); Núñez (2003); Blancas (2006); Bravo y Castro (2006); Chapa, Rangel y Ramírez (2008); Domínguez (2009); Aguayo et al. (2009); Chapa y Rangel (2010); Núñez y Polo (2010).
Por su parte, Barboza-Carrazco et al. (2009) aplicaron el método de entropía cruzada para construir una MCS con datos de México para el año 2004. Vázquez-Alvarado et al. (2008) utilizaron esta base de datos para calcular el efecto multiplicador de las remesas en la economía mexicana y González et al. (2011) incorporaron las cuentas ecológicas y de servicios ambientales a esa MCS.
Finalmente, utilizando la información de las nuevas matrices de insumo producto publicadas por el INEGI, se elaboraron MCS con datos de 2003 (Núñez, 2014; Sobarzo, 2011 y Casares et al., 2017) y de 2008 (Beltrán, 2015 y Beltrán et al., 2016).
De igual forma, Albornoz (2015) utilizó técnicas de entropía cruzada para confeccionar una matriz híbrida de contabilidad social para el estado de Yucatán, con datos de 2008. En tanto que, Martínez-Prats et al. (2016) realizaron un análisis de la balanza comercial del estado de Tabasco, utilizando para tal efecto una MCS con información de 2008, la cual fue regionalizada mediante la aplicación del RAS.
No se encontró en la revisión de literatura una aplicación de las elasticidades totales propuestas por Stone (1985) para determinar su sensibilidad ante cambios en la demanda final exógena o en las exportaciones en modelos lineales multisectoriales ampliados.3
II. Matriz de contabilidad social de la economía mexicana
Pasamos ahora a describir el proceso de construcción de la MCS de la economía mexicana. Las principales fuentes de información fueron la matriz homogénea de insumo producto, formato producto por producto; las cuentas por sectores institucionales, la encuesta de ingreso y gasto de los hogares y el PIB de las entidades federativas de México. En todos los casos se trabaja con cifras correspondiente a 2013 (INEGI, 2017). La MCS se desagrega en 31 sectores de actividad productiva y cuatro sectores institucionales (sociedades, hogares, gobierno y resto del mundo). A su vez, los hogares se desglosan en 10 estratos, conformados por sus rangos de ingreso.
A fin de expresar sintéticamente la MCS y sus aplicaciones, se hace uso de algunas de las convenciones del álgebra matricial. Específicamente, todas las letras empleadas son resaltadas mediante el uso de negritas, las mayúsculas corresponden a matrices de dimensión n x n, en tanto que las minúsculas indican vectores de dimensión n x 1. El apóstrofe se emplea para señalar la transposición del vector, mientras que el acento circunflejo (^) significa que los elementos del vector correspondiente se ordenan en una matriz diagonal. Por último, la letra "i", colocada a la derecha de una matriz, especifica la suma de los valores de sus renglones, en tanto que ubicada a la izquierda, denota la agregación de los elementos de las columnas. Cuando se emplea la barra sobre un vector o una matriz, esto revela que se trata de una matriz o vector particionado.
Como se explicó en el apartado previo, para la presentación formal de la MCS, su solución y el análisis de sus multiplicadores, utilizamos la notación propuesta por Holland y Wyeth (1993), posteriormente retomada por Miller y Blair (2009, pp. 514-555).
De esta forma, las transacciones económicas realizadas en la economía mexicana durante el año
2013, valuadas en millones de pesos constantes, se presentan en la MCS (
Por su parte, la integración de la matriz
También es necesario definir los vectores
El siguiente paso es la definición de la matriz de coeficientes de
Asumiendo que las particiones de las matrices
La formulación básica del modelo de producción de la MCS puede expresarse de la siguiente forma:
Y su solución:
III. ¿Qué tan importantes son las exportaciones para la economía mexicana?
El modelo ampliado de producción y la técnica de extracción de las exportaciones internacionales del vector de demanda final exógena fueron utilizados para abordar esta interrogante. Los resultados obtenidos se contrastaron con los del modelo base. En 2016 las exportaciones totales ascendieron a 373,939.2 millones de dólares, de ese monto, el 83.7 por ciento se colocó en América del Norte, especialmente en los EUA que, como ya se señaló, concentró el 80.9 por ciento de las ventas foráneas de la economía mexicana. El 3.4 por ciento restante se dirigió a Canadá.
El 43.7 por ciento de la producción bruta total se basa en las actividades de exportación. La participación en el empleo es 7.5 puntos menor, lo cual indica que los sectores exportadores son más intensivos en capital con respecto al promedio de la economía en su conjunto. El aporte relativo en el caso de los componentes del valor agregado fluctúa entre el 32.9 por ciento para las remuneraciones a los asalariados, el 39.1 por ciento en los impuestos indirectos a la producción y el 43.6 por ciento en el excedente bruto de operación. En el caso del PIB, el 40.5 por ciento depende del sector externo.
Los modelos ampliados construidos con MCS vinculan la generación primaria del ingreso, con su asignación y redistribución entre los diferentes sectores institucionales (hogares, empresas, gobierno), así como la utilización del ingreso disponible de estos últimos en sus diferentes usos (consumo privado doméstico, consumo privado importado, pago de impuestos y ahorro privado en el caso de los hogares). Gracias a lo anterior, se puede cuantificar el impacto de las ventas internacionales en el ingreso medio de los hogares mexicanos en un 39.7 por ciento. Esta participación aumenta con el nivel de ingresos. Como se trata de un modelo de proporciones fijas también en el consumo privado, el impacto en esta variable es equivalente al del ingreso, en tanto que su magnitud absoluta depende de la participación del consumo privado doméstico en la asignación del ingreso disponible para los hogares de distintos rangos, así como de las estructuras de sus canastas de consumo. Estos aspectos serán analizados con mayor detalle en los siguientes apartados.
IV. Cálculo de las elasticidades totales
En el modelo ampliado de Leontief, las elasticidades se obtienen al computar el cociente de cambios porcentuales unitarios en la demanda final exógena y sus efectos relativos en la variable endógena estudiada (en nuestro caso: producción bruta, empleo, salario y valor agregado).
Se trata de un indicador de gran utilidad, pues permite ponderar los efectos generados por cambios en la demanda final, cuantificados a través de los multiplicadores, por la dimensión de cada una de las actividades productivas. El ponderador utilizado para tal efecto es el cociente del valor de la demanda final exógena de un sector (fj) dividido entre el producto bruto total de la economía analizada (i'x):
Utilizando la notación de Miller y Blair (2009), la elasticidad total de producción de un sector se define así:
Donde: oej =elasticidad de la producción bruta del sector "j " y m(o)j = multiplicador de la producción bruta del sector "j"
De forma equivalente se calculan las elasticidades totales del empleo (t), los salarios (w) y el valor agregado (va).10
A su vez, los multiplicadores de producción de cada actividad productiva se obtienen de sumar los elementos de las columnas de la inversa de Leontief vinculados con la submatriz A (de dimensión 31x31), de la matriz S descrita en la ecuación 4.
Entonces:
Para calcular los multiplicadores del resto de las variables (empleo, salarios y valor agregado), la inversa de Leontief se premultiplica por matrices diagonales con los coeficientes correspondientes y ceros en el resto de las posiciones.
Sí, por ejemplo, t es un vector columna con los coeficientes de empleo por sector, entonces:
Como el modelo ampliado de Leontief incorpora el ingreso y gasto de los hogares, se trata de multiplicadores totales truncados, y en el caso de las variables distintas a la producción, de multiplicadores tipo II, los cuales son ponderados por el valor de sus coeficientes respectivos a fin de obtener variaciones normalizadas.
V. Análisis de resultados
En la versión estándar del modelo de producción construido con las MCS, el ingreso y el consumo de los hogares se integran a sus variables endógenas. Por lo anterior, a diferencia de un modelo básico de insumo producto, el gasto en bienes de consumo privado se excluye de la demanda final exógena, quedando esta última conformada solamente por el consumo de gobierno, la inversión y las exportaciones.
Como se apuntó en la introducción, la rápida apertura de la economía mexicana permitió la expansión acelerada de las exportaciones. De manera que, aún sin considerar el consumo privado, la participación de la demanda final exógena en el producto bruto total generado por la economía mexicana fue apenas inferior a un tercio del total (32.3 por ciento) y de este porcentaje, las exportaciones absorbieron más de la mitad (55 por ciento).
Considerando estas características y los propósitos del ensayo, se decidió realizar el análisis de las elasticidades totales en dos modalidades: la primera, considerando cambios en la totalidad del vector de la demanda final exógena por sector y, la segunda, simulando el efecto de variaciones únicamente en el componente de las exportaciones. Por limitaciones de espacio, en este documento se presentan los principales resultados. El lector interesado puede pueden acceder al detalle de éstos en el anexo referido en la nota 4.
V.1. Sensibilidad ante cambios en la demanda final exógena
A manera de ilustración, analizaremos las elasticidades totales de la producción bruta ante cambios unitarios en la demanda final exógena del sector Maquinaria y Equipo (subsectores 333 a 336 del código SCIAN -Sistema de Clasificación Industrial de América del Norte-). La elección no es casual, pues se trata de la actividad económica con la mayor elasticidad total en tres de las cuatro variables incluidas en nuestro análisis. Así, por ejemplo, el cambio unitario en el valor de la demanda final exógena de ese sector produce una variación del 0.2505 en la producción bruta total de la economía mexicana.11
La elasticidad total del empleo de este sector (0.6488) mide el cambio porcentual en esta variable en toda la economía, resultante de un aumento en la demanda final capaz de ampliar el valor de la producción bruta en esta actividad en una magnitud suficiente para generar un aumento unitario del empleo. La interpretación es similar en el caso del salario (0.4012) y el valor agregado (0.5164).
Claramente es el sector cuyos cambios en la demanda final exógena generan las mayores repercusiones en la economía nacional.
Solamente la minería petrolera (21p), en la cual se reportan las actividades de extracción de petróleo y gas, obtuvo una elasticidad total superior en el caso del empleo (1.2485). Sin embargo, al discutir los efectos sobre la economía mexicana de una alteración normativa en nuestras relaciones comerciales con Canadá y los EUA, decidimos excluirlo por dos razones: 7) no está considerado en el tratado comercial vigente, y 2) es un sector que, pese a la reforma energética, aún presenta rigideces importantes, especialmente en el ámbito laboral.
Dados los objetivos planteados en este trabajo, resulta de mayor interés calcular la sensibilidad de la economía nacional ante fluctuaciones en sus exportaciones, las cuales constituyen el componente más importante del vector de la demanda final exógena en el modelo construido para México.
V.2. Sensibilidad ante cambios en las exportaciones
El Cuadro (1) presenta los ocho sectores cuyas variaciones en sus exportaciones tienen las mayores repercusiones en las variables estudiadas para el conjunto de la economía mexicana. Sombreados en gris se muestran los cinco valores más elevados de cada categoría. En el caso de los primeros tres, además del sombreado, se utilizan negritas. Los cinco renglones inferiores de la tabla exhiben, para cada variable y respectivamente: 7) las elasticidades totales de los sectores computados; 2) las de los cuatro sectores con los montos más elevados en cada categoría; 3) la participación porcentual de estos últimos en el total; 4) las elasticidades totales acumuladas de las ocho actividades con mayor impacto, y 5) la participación de este último subconjunto en las elasticidades totales.
Cuadro 1 Economía mexicana: sectores con las mayores elasticidades totales de la producción bruta, el empleo, el salario y el valor agregado por cambios en las exportaciones internacionales de cada actividad productiva. 2013 (%)
| MÉXICO | |||||
| Producción Bruta | Empleo | Salarios | Valor Agregado | ||
| Oj | Tj | Wj | Vaj | ||
| 333-336 | Maquinaria y equipo. | 0.2204 | 0.5709 | 0.3530 | 0.4544 |
| 43-46 | Comercio. | 0.0560 | 0.0445 | 0.0704 | 0.0470 |
| 331-332 | Industrias metálicas. | 0.0376 | 0.0810 | 0.0808 | 0.0649 |
| 324-326 | Petroquímica, del plástico y del hule. | 0.0354 | 0.1575 | 0.0811 | 0.0851 |
| 48-49 | Transportes, correo y almacenamiento. | 0.0152 | 0.0208 | 0.0142 | 0.0154 |
| 11 | Prima rio. | 0.0135 | 0.0066 | 0.0179 | 0.0134 |
| 311 | Industria alimentaria. | 0.0139 | 0.0337 | 0.0350 | 0.0203 |
| 339 | Otras manufacturas. | 0.0097 | 0.0094 | 0.0095 | 0.0174 |
| ELASTICIDAD TOTAL (Todos los sectores, excepto Minería Petrolera). | 0.4399 | 0.9898 | 0.7171 | 0.7707 | |
| SUBTOTAL 4 SECTORES CON MAYOR ELASTICIDAD TOTAL. | 0.3495 | 0.8539 | 0.5853 | 0.6514 | |
| Participación en el cambio global en la elasticidad total. | 79.4% | 86.3% | 81.6% | 84.5% | |
| SUBTOTAL 8 SECTORES CON MAYOR ELASTICIDAD TOTAL. | 0.4096 | 0.9301 | 0.6698 | 0.7293 | |
| Participación en el cambio global en la elasticidad total. | 93.1% | 94.0% | 93.4% | 94.6% | |
Fuente: matriz de contabilidad social de la economía mexicana. Elaborada por los autores con base a la metodología descrita en este documento con información del INEGI (Matriz Homogénea de Insumo Producto 2013 de la economía doméstica en formato producto por producto, Cuentas por Sectores Institucionales y Encuesta de Ingreso Gasto de los Hogares).
Las elasticidades totales de las exportaciones de las 30 actividades productivas consideradas (como ya se indicó, se excluyeron las de la minería petrolera) aparecen en el primer renglón de la parte inferior de la tabla. Un ajuste del uno por ciento en las exportaciones de ese grupo de sectores produciría variaciones acumuladas en la economía mexicana del 0.4399 por ciento en su producción total. Por su parte, las fluctuaciones en el empleo, los salarios y el valor agregado serían de 0.9898, 0.7171 y 0.7707, respectivamente.
La mayor exposición de la economía mexicana ante cambios en sus exportaciones está determinada por el sector de maquinaria y equipo (códigos 333 a 336 del SCIAN), el cual concentra el 50.11 por ciento de las elasticidades totales de las exportaciones en el caso de la producción bruta, el 57.6 por ciento de las del empleo, el 49.2 por ciento de las relativas a los salarios y el 60 por ciento de las relacionadas con el valor agregado.
Además de la fabricación de maquinaria y equipo, las manufacturas con derivados del petróleo y carbón; la industria química, del plástico y del hule (subsectores 324 a 326 del SCIAN), así como las industrias metálicas (básicas y no básicas, es decir, los subsectores 331-332) registran las elasticidades totales más altas en tres de las cuatro variables (empleo, salarios y valor agregado). Si añadimos el comercio (sectores 43 a 46), que consigna la tercera posición en la elasticidad total de las exportaciones sobre la producción bruta, se conforma un subconjunto que concentra entre el 79.4, el 86.3, el 81.6 y el 84.5 por ciento del impacto total sobre cada variable para la economía nacional.
Si a este grupo se yuxtaponen los aportes a las elasticidades totales de la industria alimentaria (311); los transportes, correos y almacenamiento (48-49); otras industrias manufactureras (339), y el sector primario (11), se alcanzan índices de concentración que fluctúan entre el 93.1 por ciento, en el caso de la producción bruta, y el 94 por ciento en el empleo, en tanto que los valores para los salarios y el valor agregado ascienden al 93.4 y el 94.6 por ciento, respectivamente.
V.3. Descomposición aditiva de las elasticidades totales de las exportaciones
Cuando se registra un cambio en la demanda final exógena de un sector de actividad, el efecto inicial es una alteración equivalente en la demanda de su bien o servicio. Los requerimientos de insumos intermedios que realiza este sector se adaptan a la nueva circunstancia (efecto directo) y esta señal es posteriormente transferida a todas las actividades productoras de bienes y servicios intermedios vinculadas directa e indirectamente con aquél (efectos directos e indirectos). La magnitud del impacto dependerá de las características estructurales del sector de origen, así como de la mayor o menor densidad del tejido productivo de la economía doméstica. Posteriormente, los efectos inicial, directo e indirecto, repercuten en la demanda de factores primarios, así como en las remuneraciones que reciben sus propietarios y, consecuentemente, en los ingresos de los sectores institucionales. Entre los mismos se destacan los hogares. Los ajustes en el ingreso disponible de los hogares influyen a su vez en sus niveles de consumo, lo cual finalmente repercute en variaciones adicionales en la demanda de bienes y servicios registradas por las actividades productivas (efectos inducidos).12
Como observamos en el Cuadro 1, el cambio unitario en las exportaciones de los 30 sectores generó una elasticidad total en la economía mexicana de 0.4399 en la producción bruta. Un subconjunto de ocho actividades acumuló 0.4096, es decir, el 93.1 por ciento del cambio total en esa variable. La gráfica de barras acumulativas (Gráfica 1) muestra la descomposición aditiva de la elasticidad total de siete de esos sectores. A la derecha de la barra aparece la etiqueta con la elasticidad total de cada sector, en tanto que cada barra contiene cuatro segmentos con diferente color para cada componente: efectos iniciales (negro), directos (gris oscuro), indirectos (gris claro) e inducidos (líneas diagonales grises). En la gráfica se sobrepone un cuadro con el peso relativo de cada uno de esos factores en la elasticidad total de cada sector y al final el promedio simple de cada componente en estas siete actividades productivas.

*Nota: eliminando la actividad 21P-Minería petrolera.
Fuente: ídem.
Gráfica 1 Economía mexicana: elasticidades totales de las exportaciones. 2013.
Además de destacarse la gran relevancia de las variaciones de las exportaciones de la producción de maquinaria y equipo en la economía mexicana, sobresale el peso relativo de los efectos inducidos, cuyo promedio simple alcanzó el 51.3 por ciento. Por su parte, los efectos iniciales explican poco menos de un tercio de las elasticidades totales de las exportaciones de este subconjunto de actividades, mientras que los efectos directos lo hicieron con el 11.7 por ciento y los indirectos con el 5.6 por ciento. Los datos muestran la relevancia de los efectos inducidos como mecanismo de difusión de un shock en las exportaciones sobre la economía mexicana. Los impactos inicial, directo e indirecto inciden sobre la demanda de factores primarios y, consecuentemente, sobre los ingresos de sus propietarios. A su vez, las fluctuaciones del ingreso primario afectan las distribuciones primaria y secundaria del ingreso, así como los niveles del ingreso disponible ajustado y el consumo privado doméstico, lo cual produce un segundo shock de demanda que desencadena efectos multiplicadores a través del flujo circular de la economía.
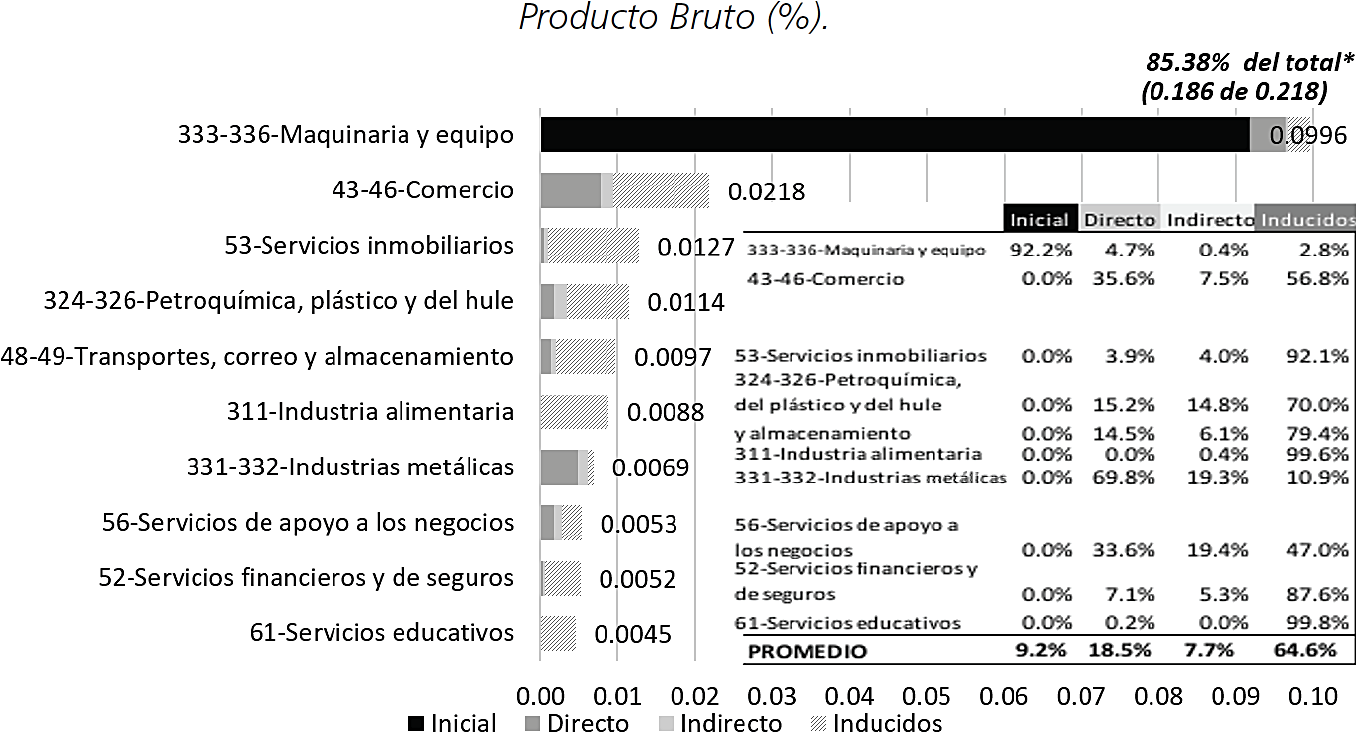
Dada la relevancia de las actividades exportadoras de la fabricación de maquinaria y equipo en la elasticidad total de la economía mexicana, conviene analizar con mayor detalle el desglose sectorial de la elasticidad total de esta actividad productiva. Ese es el propósito de la Gráfica 2, la cual permite apreciar que las transacciones intrasectoriales explican cerca de la mitad (49.5 por ciento) de la elasticidad total. Al agregar el aporte de otras ocho actividades productivas, se obtiene un porcentaje acumulado del 85.38 por ciento del total de la elasticidad del subsector 333-336-Maquinaria y equipo.
*Nota: eliminando la actividad 21 P-Minería petrolera.
Fuente: ídem.
Gráfica 2 Economía mexicana: distribución sectorial de la elasticidad total de las exportaciones del sector maquinaria y equipo. 2013.
Al enfocar nuestro análisis en la elasticidad total del sector maquinaria y equipo, sobresalen los efectos iniciales en el mismo. En el resto de las actividades visibles en el gráfico, sólo figuran los efectos directos, indirectos e inducidos asociados a un cambio unitario en las exportaciones de maquinaria y equipo. En este caso, todos los aportes a la elasticidad total de la producción bruta de la economía mexicana se miden como proporción de ese agregado. En la tabla incluida en la gráfica, se computan las aportaciones relativas de cada uno de los efectos. Sobresalen dos aspectos:
1. El poco peso relativo de los impactos directos e indirectos, lo cual se explica por la reducida densidad de la cadena de valor de insumos de origen doméstico en el sector. Sólo en dos actividades los impactos directos e indirectos superan el promedio (industrias metálicas y servicios de apoyo a los negocios). Por su parte, el comercio únicamente rebasa la media en el caso de los efectos directos, en tanto que la petroquímica, en los indirectos.
2. La elevada participación de los efectos inducidos, los cuales contribuyen con cerca de dos tercios de la elasticidad total del sector. Recordemos que en este caso la cadena de transmisión del impacto inicial pasa por la demanda y remuneración de factores primarios, la asignación, distribución y redistribución del ingreso, sus consecuencias en el consumo privado y su efecto de retorno sobre los niveles de actividad del sector que experimentó el shock en sus exportaciones (maquinaria y equipo). Así pues, los sectores cuya demanda de bienes de consumo privado de origen doméstico es más sensible a un choque exportador del sector de maquinaria y equipo son: industria alimentaria, servicios inmobiliarios, servicios financieros, transporte, petroquímica, comercio y servicios de apoyo a los negocios.
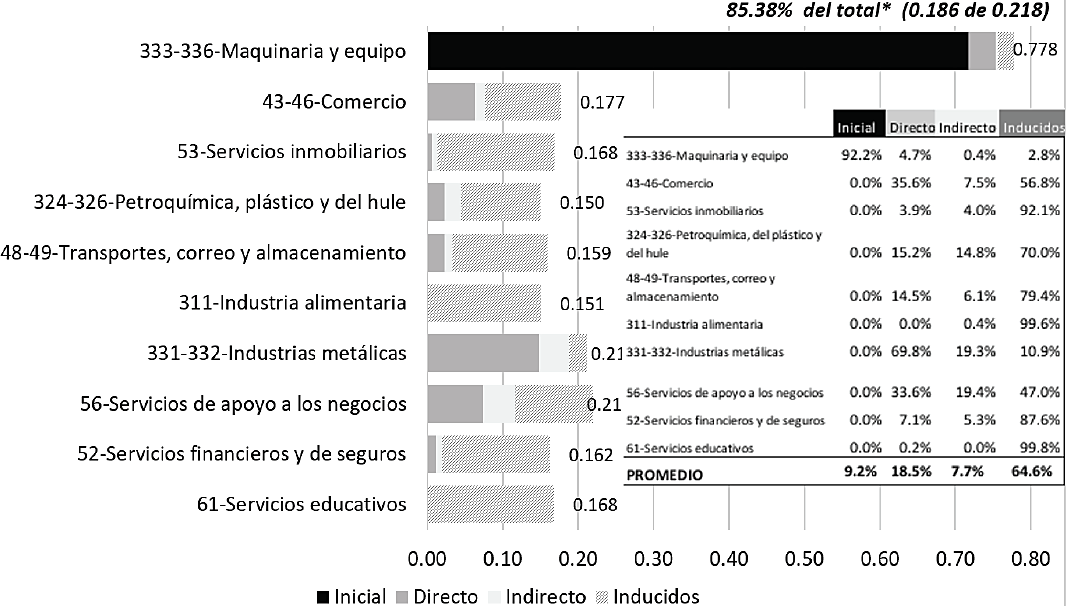
Dado que el aporte a las elasticidades totales se mide como porcentaje del cambio en la producción bruta de toda la economía, los valores son muy pequeños y no permiten apreciar el efecto de un choque exportador sobre la producción bruta del propio sector. Para lograr lo anterior, se usa el modelo de producción, y el vector de demanda final exógena se modifica introduciendo en el valor de referencia un incremento unitario en las exportaciones del sector estudiado, en este caso el de maquinaria y equipo. Posteriormente, se comparan los resultados de esta simulación con el escenario base a fin de medir las repercusiones sobre la producción bruta en cada uno de los sectores involucrados. Los resultados se muestran en la Gráfica 3. La estructura de distribución de la descomposición aditiva de cada sector es la misma que en el ejercicio previo, pero ahora los efectos de un cambio unitario en las exportaciones del sector de maquinaria y equipo se comparan contra el valor de la producción bruta de cada sector.
*Nota: eliminando la actividad 21 P-Minería petrolera.
Fuente: ídem.
Gráfica 3 Economía mexicana: variaciones en la producción bruta de cada sector derivadas de un cambio unitario en las exportaciones del sector maquinaria y equipo. 2013. (%).
Esta simulación revela la excesiva dependencia del sector de maquinaria y equipo de sus propias exportaciones, pues éstas explican casi cuatro quintas partes (0.778) del impacto sobre el valor de su producción bruta. Aunque en menor magnitud, el cambio en las exportaciones de maquinaria y equipo también produce alteraciones significativas en la producción bruta de las otras actividades que aparecen en la gráfica (las cuales fluctúan entre el 0.15 y el 0.219).
Si generalizamos el ejercicio anterior y cuantificamos las consecuencias de un cambio unitario en las exportaciones de todos los sectores (salvo el ya mencionado de minería petrolera) sobre sus niveles de producción bruta, se identifican las 10 actividades más sensibles a un choque generalizado en las exportaciones: maquinaria y equipo (81 por ciento); otras manufacturas (80 por ciento); industrias metálicas (67 por ciento); fabricación de insumos textiles (65 por ciento); fabricación de prendas de vestir (59 por ciento); minería no petrolera (55 por ciento); petroquímica (51 por ciento); industria del papel (50 por ciento); agropecuario (49 por ciento), y bebidas y tabaco (46 por ciento).
V.4. Impactos sobre el ingreso y el consumo de los hogares
Al integrar los flujos de ingreso y gasto en un sistema económico, los modelos construidos con MCS permiten captar los efectos directos, indirectos e inducidos de alteraciones en las variables exógenas. De esta forma, los multiplicadores totales de las cuatro variables estudiadas incorporan los impactos del cambio inicial sobre la generación del ingreso, su gasto en consumo privado y sus repercusiones de retorno sobre las actividades productivas. Por tanto, estos multiplicadores permiten capturar los efectos de difusión hacia otras actividades económicas.
Prácticamente el 90 por ciento del valor de las exportaciones realizadas por la economía mexicana se genera en actividades de los sectores primario y secundario, por lo que el efecto inicial simulado en este trabajo se concentra en éstas. Sin embargo, una vez que los efectos iniciales se propagan por medio de las articulaciones productivas intersectoriales, la generación y el gasto del ingreso, así como las demandas adicionales del consumo sobre las actividades productivas, las variaciones en la producción bruta se generalizan y alcanzan a las actividades terciarias. En estas últimas, los componentes del valor agregado tienen un peso relativo mucho más importante. Asimismo, se caracterizan por ser intensivas en trabajo, de manera que el efecto sobre la asignación primaria del ingreso a los hogares se amplifica.
Para el análisis sobre el ingreso y el consumo centramos nuestra atención en los pagos a los factores primarios; remuneraciones a los asalariados y excedente bruto de operación, que conforman el PIB y constituyen las fuentes del ingreso primario asignado a los sectores institucionales domésticos: hogares, empresas y gobierno. Después de realizarse la asignación primaria, la distribución secundaria y las transferencias, puede determinarse el ingreso disponible ajustado de los hogares. Un choque unitario generalizado en las exportaciones de las actividades productivas produce un cambio del 0.457 en el ingreso disponible ajustado de los hogares. Si dejamos fuera de la simulación la minería petrolera, el impacto es del 0.385.
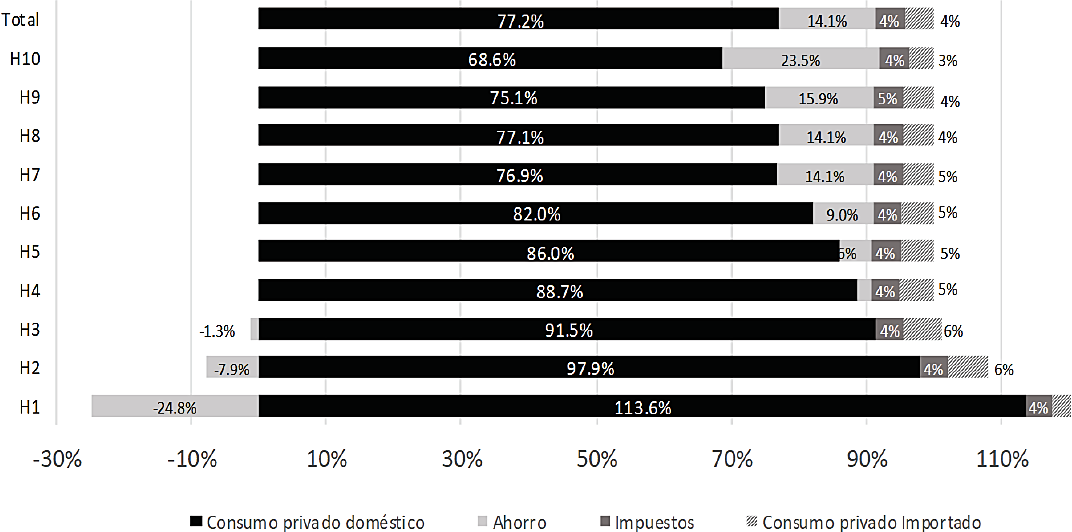
Los hogares utilizan estos recursos para el consumo privado final, doméstico y foráneo, el pago de impuestos y el ahorro privado. Los porcentajes de distribución difieren dependiendo del rango de ingreso. La estructura de asignación derivada de la MCS se presenta en la Gráfica 4. A nivel agregado, el consumo privado doméstico y el ahorro privado concentran el 91.3 por ciento del ingreso disponible, el resto se distribuye en proporciones muy similares entre el pago de impuestos al consumo y las importaciones para el consumo privado, sin embargo, estas proporciones difieren en los distintos rangos de ingreso.
Fuente: ídem.
Gráfica 4 Economía mexicana: estructuras de asignación del ingreso disponible en los hogares por rangos de ingreso y total. 2013 (%).
En el caso de la economía mexicana, los primeros tres deciles registraron ahorro negativo y el consumo privado doméstico acaparó el grueso del ingreso e incluso superó el ingreso disponible de los hogares más pobres. A medida que los rangos de ingreso son mayores, el porcentaje dedicado al consumo privado doméstico se reduce gradualmente, mientras que ocurre lo contrario con el coeficiente destinado al ahorro.
Las cuentas de ingreso y consumo del modelo ampliado de Leontief comparten las características establecidas en el modelo base para las actividades productivas; específicamente, las proporciones se mantienen fijas. Al estimar las consecuencias de cambios en las exportaciones sobre el ingreso disponible y el consumo, se mantienen constantes las cuotas del ingreso disponible asignadas por cada grupo de hogares al consumo, así como la estructura de distribución del consumo entre los distintos bienes y servicios domésticos, es decir, la canasta de bienes y servicios consumidos también se mantiene inalterada.
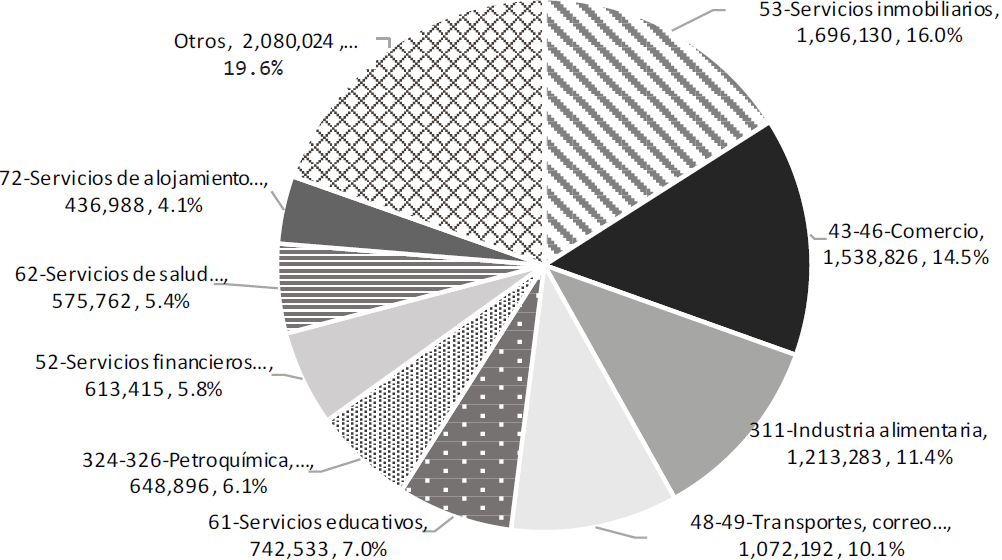
La Gráfica 5 nos muestra el valor y la estructura de consumo privado doméstico para el conjunto de los hogares del país. Los principales bienes y servicios domésticos consumidos son: servicios inmobiliarios (16 por ciento), comercio (14.5 por ciento), industria alimentaria (11.4 por ciento), transportes (10.1 por ciento), servicios educativos (7 por ciento), petroquímica y sus derivados (6.1 por ciento), servicios financieros (5.8 por ciento) y servicios de salud (5.4 por ciento). En estas ocho actividades productivas se concentra el 80.4 por ciento del consumo privado de origen doméstico. Los 23 sectores restantes aportan la diferencia (19.6 por ciento).
Fuente: ídem.
Gráfica 5 Economía mexicana: valor y estructura de consumo privado doméstico. 2013. Millones de pesos y (%).
Finalmente, la Gráfica 6 contiene la información de las estructuras de consumo privado doméstico de los hogares mexicanos de los 10 rangos de ingreso considerados en el ensayo. El porcentaje de gasto en servicios educativos, financieros y de alojamiento crece a medida que lo hace el ingreso de los hogares. Lo contrario ocurre en: comercio, transportes e industria alimentaria. La participación de los gastos en servicios de salud decrece con el ingreso hasta el decil tres y luego se invierte la tendencia. En la parte derecha de esa misma Gráfica (6), aparece la información del monto absoluto destinado por los hogares de cada estrato al consumo privado doméstico, así como la participación de cada decil en el total nacional de esta variable. Solamente los tres grupos de ingresos superiores tienen una participación en el consumo privado mayor al nivel de equidistribución (10 por ciento) y su consumo acumulado alcanzó el 58.7 por ciento del total.
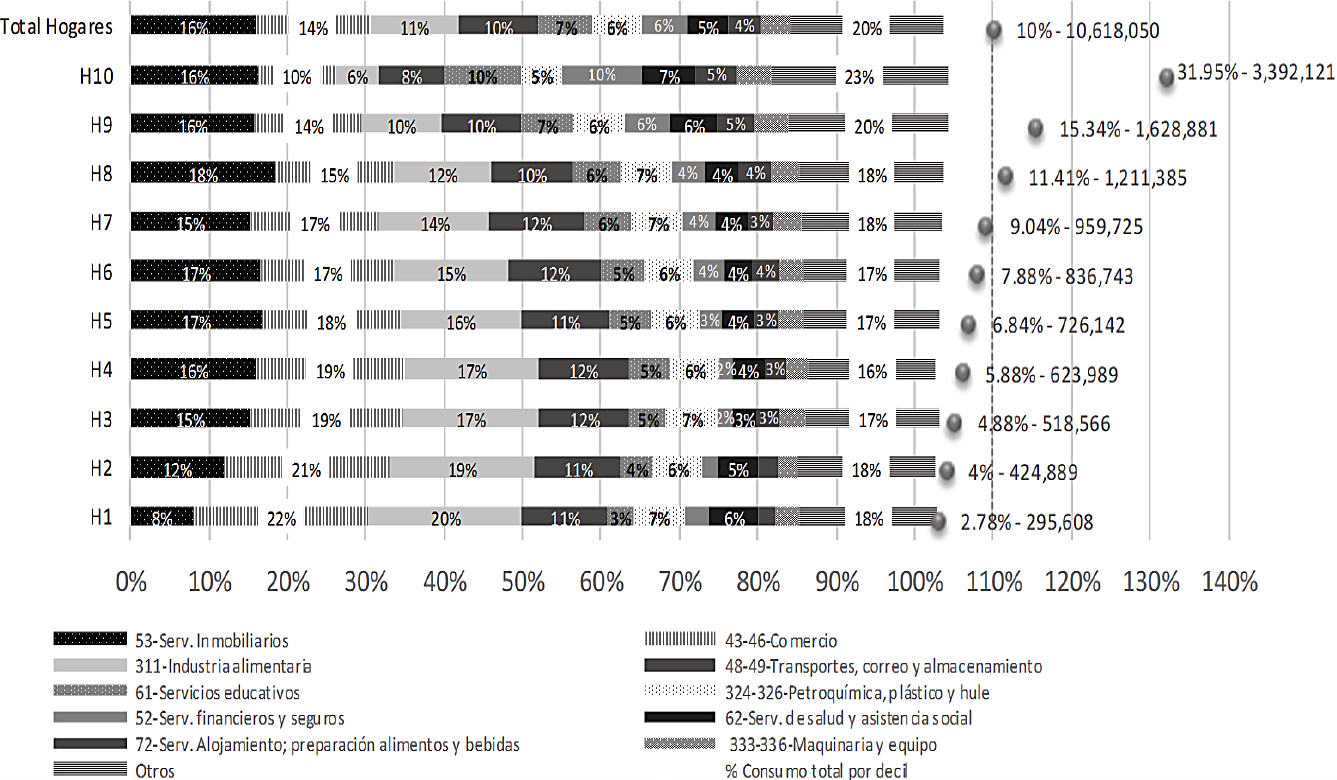
Fuente: ídem.
Gráfica 6 Economía mexicana: estructura de consumo privado doméstico de los hogares por rangos de ingreso y total. 2013. (%).
Ahora contamos con todos los elementos para medir el impacto sobre el consumo privado doméstico de una variación unitaria en las exportaciones de todos los sectores. Como ya apuntamos, bajo este escenario el ingreso disponible ajustado cambia en 0.457. Ponderando este factor por el peso del consumo privado en el ingreso disponible ajustado (0.771), la fluctuación sería de 0.352. Ésta se distribuye proporcionalmente entre los distintos bienes y servicios considerando la canasta de consumo nacional y puede desagregarse utilizando el mismo criterio para los hogares de distintos estratos ingreso.
La variación del consumo privado doméstico en el escenario alternativo (en el cual no cambian las exportaciones petroleras) sería igual a 0.385 (cambio en el ingreso disponible ajustado) por 0.771 (participación del consumo privado doméstico en el gasto de los hogares), es decir, de 0.297. De igual forma, para la apertura por tipo de bien y rangos de ingreso, se utilizan las estructuras de las canastas correspondientes. Estas características estructurales de la economía mexicana son las que definen los efectos inducidos presentados en los apartados previos.
Conclusiones
La economía mexicana es muy vulnerable a un choque en su sector externo, especialmente al nivel de sus exportaciones hacia los EUA: el ajuste de un punto porcentual en las ventas foráneas de sus actividades productivas (exceptuando la extracción de petróleo y gas, por las razones apuntadas en el documento) se traduciría en un impacto del 0.44 por ciento en el valor de la producción bruta total. Las elasticidades totales de las otras tres variables también son considerablemente elevadas.
Además, como las exportaciones están fuertemente concentradas en el mercado de los EUA y en un pequeño grupo de productos, tan sólo cuatro de 30 actividades productivas explican cerca de cuatro quintas partes de las elasticidades totales ante fluctuaciones en las exportaciones de todos los sectores. Una sola actividad, la fabricación de maquinaria y equipo, concentra un porcentaje superior al 50 por ciento de las elasticidades totales en las cuatro variables estudiadas.
A pesar de esta acentuada focalización sectorial, el impacto de un choque externo en las exportaciones rápidamente se extiende al resto de la economía nacional. Las correas de transmisión son las compras intermedias de insumos (directas e indirectas), los ingresos primarios obtenidos por los proveedores de factores de producción de todos los sectores afectados por los efectos mencionados y la manera como las variaciones del ingreso inciden en el consumo de bienes y servicios y, por ende, en un componente fundamental de su demanda.
Los ajustes en el consumo privado doméstico dependen de las canastas de los hogares de los distintos estratos de ingreso. Sobresalen las variaciones en el consumo privado de bienes y servicios en: servicios inmobiliarios, comercio, industria alimentaria, transportes, petroquímica y sus derivados, servicios educativos, financieros y de salud.
Dadas las características estructurales de su economía, así como sus escasas posibilidades reales de diversificar sustancialmente su mercado externo en el corto plazo, México enfrenta la renegociación del TLCAN desde una posición vulnerable.
Finalmente, se apunta la conveniencia de ahondar el análisis del tema, incorporando la dimensión de sus impactos regionales, así como mediante la aplicación de modelos de equilibrio general computables.











 nueva página del texto (beta)
nueva página del texto (beta)



