La forma triangular de la matriz de Leontief

 

Alberto Benítez*

 

* Profesor de Economía de la Universidad Autónoma Metropolitana, Unidad Iztapalapa. Correo electrónico: besa@xanum.uam.mx.

 

Resumen

En este artículo presento algunos comentarios sobre la forma triangular del modelo de Leontief. Entre ellos, propongo una demostración alternativa de la equivalencia entre la existencia de una solución viable para el modelo y la condición de Hawkins y Simon (H-S). Además, expongo el peculiar significado económico de los coeficientes de la diagonal principal en la forma triangular de la matriz de Leontief, lo cual permite, entre otras cosas, apreciar la estrecha relación entre las condiciones económicas y las matemáticas en la solución del modelo. También identifico algunas proposiciones matemáticas equivalentes a (H-S) que poseen interés económico.

Número de clasificación: JEL: C390, C670.

Palabras clave: Leontief, Hawkins and Simon, insumo-producto, matriz no negativa.

 

Abstract

In this article, I present some comments related to the triangular form of Leontief's system. Among them, I propose an alternative proof of the equivalence between the existence of viable solutions to the model and the Hawkins and Simon's condition (H-S). In addition, I expose the peculiar economic significance of the coefficients in the principal diagonal of the triangular form of Leontief's matrix, which permits us, among other things, to appreciate the tight relation between the economic and the mathematical conditions in the solution to the model. Moreover, I identify some other mathematical propositions equivalent to (H-S) possessing economic interest.

Classification number: JEL: C390, C670.

Key words: Leontief, Hawkins and Simon, input-output, non-negative matrices.

 

Introducción

Los sistemas lineales de ecuaciones de producción se convirtieron en un tema relevante para la economía a partir de la publicación del libro de Leontief (1941), ya que en él se establecieron las bases para el desarrollo del campo de investigación conocido como análisis de insumo-producto.¹ En este artículo presento algunos comentarios relacionados con la interpretación económica de las condiciones matemáticas requeridas para que exista una solución viable en su modelo básico, mismo que expongo brevemente en la sección I. Allí también, una vez ordenado por columnas el sistema de ecuaciones correspondiente, formulo la condición establecida por Hawkins y Simons (1949) —que representaré con la notación (H-S)— de acuerdo con la cual cada uno de los menores principales de la matriz de Leontief es mayor que cero.

En el estudio del modelo de Leontief, el método de Gauss ha sido usado principalmente para probar que (H-S) es una condición necesaria y suficiente para la existencia de una única solución no negativa. Con el propósito de establecer este resultado, es suficiente llevar a cabo una sola eliminación gaussiana para proceder enseguida, mediante la inducción matemática, como en Nikaido (1970), o bien considerar algunas propiedades del proceso completo de triangulación, como en el artículo de Hawkins y Simon recientemente citado. En la sección II llevo a cabo la triangulación completa del sistema de ecuaciones a fin de explorar en la siguiente algunos aspectos del sistema resultante que tienen interés económico.

Las pruebas que conozco de la equivalencia entre (H-S) y la existencia de una solución no negativa para el modelo omiten indicar en qué forma las cantidades mayores que cero y las nulas se distribuyen entre los distintos bienes. Como es natural, se espera que las primeras cantidades correspondan a los bienes producidos en excedente así como a aquellos que son requeridos para producirlos y que las segundas sean asignadas a los demás bienes. Por esta razón, en la sección III estudio esta distribución y muestro que el modelo de Leontief tiene una solución con la propiedad que acabo de mencionar si y sólo si satisface (H-S). Esto me permite formular la relación entre la existencia de una solución viable para el modelo y (H-S) de una forma detallada y también exponer una prueba alternativa para el resultado fundamental mencionado al principio del párrafo precedente.

Por otra parte, la interpretación económica de (H-S) señala que para producir una unidad de un bien, la cantidad requerida del mismo bien en cualquier grupo de industrias es menor a una unidad. Sin embargo, la relación entre las cantidades consumidas de esta manera y la magnitud de los determinantes concernidos no es directa. A consecuencia de esto, aunque la interpretación es correcta, no es muy sencillo percibir el lazo entre (H-S) y su significado económico. A este respecto, la forma triangular de la matriz de Leontief facilita las cosas.

En efecto, en la sección IV establezco el significado económico de los coeficientes situados sobre la diagonal principal de dicha matriz. La base de la interpretación es la igualdad entre el coeficiente que resta en la última ecuación y la cantidad del bien correspondiente que se produce en excedente después de descontar la cantidad total que se consume en la producción de una de sus unidades, lo cual me permite expresar directamente en términos matemáticos el significado económico de (H-S). Por tanto, puedo decir que una virtud del estudio de esta forma triangular consiste en que identifica una condición matemática equivalente a (H-S), cuya interpretación económica es inmediata.

En la sección V utilizo la misma propiedad para formular (H-S) de una manera más precisa que como se hace habitualmente en el caso de las matrices de Leontief, señalando una cota superior para las magnitudes de los menores principales así como también una jerarquía entre las mismas. Finalmente, en los teoremas 2, 3 y 6 establezco proposiciones matemáticas que son equivalentes a (H-S), mientras que en el lema 1 presento una proposición que es equivalente a (H-S) en el caso particular de las matrices de Leontief; el interés económico se señala en cada caso. Respecto a estos resultados, es conveniente recordar que un número considerable de condiciones matemáticas ya conocidas son equivalentes a (H-S). Las exposiciones mas completas de las mismas que consulté son las que se presentan en Takayama (1985) y en Berman y Plemmons (1994).

 

I. El modelo básico de Leontief

En lo que sigue hablaré de la producción de un cierto bien haciendo alusión a la producción bruta y habré de especificar cuando me refiera a la producción neta. La economía considera n ramas industriales que llevan a cabo simultáneamente procesos de producción de igual duración; cada rama produce un bien particular al cual corresponde un índice representado por i o por j de tal forma que i, j = 1,2,...,n. Me referiré a un conjunto {j1,j2,..., jd,..., jD} como un conjunto D si éste contiene D bienes diferentes y, para simplificar, hablaré de los índices también como bienes. Para cada i, la notación x_i. representa la cantidad del bien i producida en la industria correspondiente y c_i. la diferencia entre ésta y el monto del mismo bien que se consume en el sistema industrial durante el periodo. Además, para cada par (i,j), el coeficiente técnico a_ij., representa la cantidad de i que es consumida directamente (en la rama que produce j durante el periodo considerado) en la producción de una unidad de j.² Supongo que a_ij ≥ 0 ∀ (i, j). Hay rendimientos constantes a escala de tal forma que los coeficientes son independientes de las cantidades producidas. Un bien i produce al bien j (no necesariamente distinto) directamente si a_ij > 0 e indirectamente si hay un conjunto D que no contiene a i ni a j y que verifica la desigualdad a_i,j1a_j1,j2a_j2,j3...a_jD,j > 0.

De acuerdo con las definiciones precedentes, las relaciones entre las cantidades consumidas y las producidas de cada bien definen el siguiente sistema de ecuaciones:

Después de ordenarlo por columnas, es posible escribir este sistema como sigue:

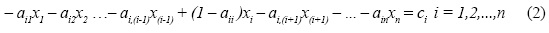
Para simplificar, cambiaré la notación de los coeficientes que están en el lado derecho del sistema introduciendo la variable no negativa r que será igual a cero en este capítulo pero adoptará también otros valores en los siguientes. Para cada par (i, j), sea b_ij igual a: -a_ij (1 + r) si i ≠ j y a 1 - a_ij(1 + r) si i = j; esto me permite escribir (2) bajo la forma siguiente:

Supondré que este sistema tiene las propiedades siguientes:

La segunda desigualdad se debe a que los coeficientes técnicos no son negativos mientras que la primera y la tercera son necesarias para producir al menos las cantidades consumidas de cada bien, respectivamente en cada industria y en el conjunto de las industrias.

Introduciendo la matriz B = [b_ij] de n X n y las matrices x = [x_i] y c = [c_i] de n X 1, el sistema (3) puede representarse mediante la ecuación matricial:

Esta fórmula resume las condiciones que deben ser satisfechas por el programa de producción x a fin de producir como excedente el conjunto de bienes c usando la tecnología definida por B.³ Es importante identificar las condiciones matemáticas que garantizan la validez de la proposición siguiente:

⁴

Con este propósito, es útil representar, para cada j, el determinante del j-ésimo menor principal de B con la notación D_j. Dicho menor es la matriz formada por la intersección de las primeras j columnas con las primeras j hileras de B. La relación entre estos determinantes y la proposición precedente se establece enseguida.

Teorema 1. La proposición (6) y la condición siguiente son equivalentes:

La equivalencia significa que cada proposición implica a la otra.⁵ El hecho de que una matriz de Leontief satisfaga (H-S) —o cualquier otra condición matemática equivalente— ha sido interpretado económicamente, señalando que en este caso la tecnología correspondiente es "autosustentable", un concepto definido a continuación.

Definición 1. Una tecnología es "autosustentable" si cualquier conjunto de industrias que produce una unidad de un bien consume en este proceso, en forma directa e indirectamente (a través de los bienes producidos por el conjunto) en total menos de una unidad del mismo bien.

Esta definición está basada en la interpretación económica de (H-S) presentada en el trabajo ya mencionado de Hawkins y Simons (1949, p. 248), en Takayama (1985, p. 361) y en Dorfman, Samuelson y Solow (1987, p. 215). En la sección V presento algunos resultados que permiten apreciar de manera directa dicha interpretación.

Además del (4), el sistema (5) también satisface la condición siguiente:

debido a la misma razón que justifica (4 b). Sin embargo, el teorema 1 es válido para todos los sistemas de tipo (5) que satisfacen (4) aun si no verifican (7). Para identificar cada caso, hablaré del sistema (5) y de la matriz B para referirme al último caso y reservaré las expresiones "matriz de Leontief y "sistema de Leontief para los sistemas de tipo (5) que verifican (4) y (7). Por ejemplo, el sistema (6) x = 1 satisface (H-S) pero (6) no es una matriz de Leontief.

 

II. Triangulación del sistema (3)

Como es bien sabido, el método de Gauss para resolver (3) consiste en eliminar los términos situados bajo la diagonal principal procediendo sucesivamente por columnas a partir de la primera de ellas. Con este propósito, para cada columna j, la ecuación correspondiente se divide por su coeficiente en la diagonal principal (si no es cero), luego se multiplica por el coeficiente de coordenadas (i, j) que debe ser eliminado y la ecuación resultante se sustrae de la ecuación i. Después de proceder en la primera columna del sistema (3), resulta el sistema siguiente:

A fin de simplificar, introduciré el superíndice t (t = 1,2,...,n), el cual indica, si t = 1, que el coeficiente original (identificado en cada caso por los dos subíndices) no ha sido modificado. Si t > 1, dicho coeficiente habrá sido modificado por medio de las operaciones lineales requeridas para la eliminación de los términos situados bajo la diagonal principal en las primeras t - 1 columnas. Es conveniente observar que, para cada t > 1, las eliminaciones en la columna t - 1 afectan (además de los términos eliminados) sólo los coeficientes cuyos dos subíndices son mayores que t - 1. De acuerdo con esto, para cada t, los coeficientes b_ij^t y c_i^t están definidos sólo si t ≤ (i, j) y, por otra parte, si t > 1 debe ocurrir que b_t-1,t-1^t-1 ≠ 0. En este caso:

Por tanto, suponiendo que b_tt^t ≠ 0 para cada t < n, la eliminación en las primeras n - 1 columnas tiene como resultado el sistema siguiente:

Los coeficientes de esta matriz presentan la relación expuesta a continuación.

Teorema 2. Las dos proposiciones siguientes son equivalentes:

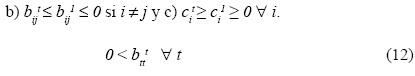
Prueba. Obviamente (11 a) implica (12). Por otra parte (12), junto con (4 b) y (4 c) implica que (11) también se verifica en la primera ecuación de (10). El supuesto de que esto no es así en al menos una de las otras ecuaciones lleva a una contradicción. En efecto, sea t la primera ecuación de (10), en el orden natural, para la cual (11) no es verdad; entonces (11) es válida para t - 1. Como t ≤ (i, y) tenemos t - 1 ≠ (i, j) de tal manera que b_i,t-1^t-1 ≤ 0 y b_t-1,j^t-1 ≤ 0 de acuerdo con (11 b); por tanto, se sigue de (9 a) que b_ij^t-1 ≤ b_ij^t-1. Este resultado y el hecho de que (11) es válida para t - 1 implica (11 b) y la primera desigualdad en (11 a), la segunda desigualdad de (11 a) se debe a (12), lo cual demuestra que (11) se verifica en el lado izquierdo de la t-ésima ecuación. En forma análoga, la validez de (11) para t - 1 implica que -b_it1^t-1c_t-1^t-1/b_t-1t-1^t-1 ≥ 0 por lo cual c_t¹≥c_i^t-lde acuerdo con (9 b). Este resultado y el hecho de que (11 c) es válida para t - 1 implica que (11 c) es válida para t, contradiciendo el supuesto de que (11) no se cumple, con lo que termina la prueba.

 

III.Coordenadas nulas y superiores a cero en la solución de (3)

Dado un c particular, sólo se debe de producir aquellos bienes requeridos para obtener en excedente exactamente el vector c. Por esta razón, como ya indiqué anteriormente, es de esperarse que en la solución del sistema (5), las cantidades mayores que cero correspondan a los bienes producidos en excedente y también a aquellos necesarios para la producción de éstos, mientras que los ceros quedan asignados a los demás bienes. Sin embargo, el teorema 1 dice solamente que hay una solución no negativa para (5), sin especificar la asignación de los dos tipos de cantidades entre los distintos bienes.

En esta sección voy a presentar un procedimiento original para demostrar una proposición que implica el teorema 1. Dicho procedimiento permite al mismo tiempo verificar que la solución matemática corresponde a la intuición económica, cuyo contenido se enuncia en la proposición siguiente.

Para cada:

Con ese propósito, probaré enseguida un resultado equivalente al teorema 1 siguiendo un procedimiento original.

Teorema 3. Las proposiciones (11) y (13) son equivalentes.

Prueba. I) Probaré que (13) ⇒ (11) mediante inducción sobre el índice t. Para ello, consideraré un c > 0 particular tal que, de acuerdo con (13 a), el sistema (3) correspondiente posee una solución única x > 0. I a) (11) es válida para t = 1: (11 b) y (11 c) son verificadas respectivamente por (4 b) y (4 c). Estos resultados y los supuestos de que c₁ > 0 y x > 0 implican que b₁₁ > 0 según la primera ecuación de (10), lo cual demuestra (11 a). I b) Si (11) se verifica para un t - 1 tal que 1 ≤ t - 1 < n entonces también es válida para t: como t ≤ (i,j) tenemos que t-1 # (i,j) por lo que b_1,t-1^t-1 ≤ 0 y b_t-1j^t-1 ≤ 0 de acuerdo con (11 b), también debido a (11 a) tenemos b_t-1,t-1^t-1 > 0 y de (11 c) se infiere que c_t-1^t-1≥ 0. Entonces, se concluye de (9 a) y (9 b) respectivamente que b_ij^t ≤b_ij^t-1 j^-1 y c^t_i≥ c_i^t-1. A su vez, estos resultados y el supuesto de que (11) es verificado por t - 1 implican (11 b) y (11 c) para el índice t. Por tanto, como x > 0 y c_t > 0 podemos comprobar por medio de la t-ésima ecuación de (10) que b_tt^t > 0, lo cual valida (11 a).

 

II) Probaré que (11) = (13) mediante inducción sobre el índice n. II a) Si n = 1, (11 a) ⇒ b₁₁ > 0 lo que permite escribir (3) bajo la forma x₁ = c₁ lb₁₁, con ello se puede verificar (13) fácilmente. II b) Si (11) ⇒(13) en un sistema con n - 1 ecuaciones en el cual 1 ≤ n - 1 < n, entonces esto ocurre también en un sistema con n ecuaciones. En efecto, si (3) verifica (11) tenemos b₁₁¹ > 0, de tal forma que se puede realizar la primera eliminación gaussiana. Esto implica que (3) es equivalente al sistema integrado por su primera ecuación y por el sistema formado por las restantes n - 1 ecuaciones (S_n-1), que no contienen la variable x₁, mismo que se presenta en (8). El sistema (10) muestra que si (3) satisface (11) también lo hace S_n-1. Debido a ello, puedo suponer que S_n_₁ verifica (13) por lo que esta proposición se ve satisfecha por cada i > 1. Para probar que esto implica que el índice i = 1 verifica (13) podemos escribir la primera ecuación bajo la forma x₁ = (c₁ -∑_i=₂ⁿb_hx)/b ₁₁. Dado que (13) se verifica en S_n-1, el numerador en el lado derecho de la ecuación es mayor que cero si el primer índice satisface (13 a). También si sólo satisface (13 b): en este caso b_1i > 0 para al menos un i > 1 que verifica (13 a) o (13 b), así que b_1i x_i< 0. En consecuencia, en ambos casos x₁ > 0. Finalmente, si el primer índice satisface (13 c) se tiene que b_1i= 0 para cada i > 1 que valida (13 a) o (13 b) (de otra forma el índice 1 comprobaría 13 b). Además, c₁ = 0 y x₁= 0 para cada i > 1 que no verifica (13 a) ni tampoco (13 b). En consecuencia, el numerador que se acaba de mencionar es igual a cero de tal manera que x₁ = 0. Por tanto, (11) ⇒ (13), con lo que termina la prueba.

Las proposiciones (6), (H-S), (11), (12) y (13) son equivalentes, como se puede establecer a partir de los teoremas 1, 2, 3 y de la proposición siguiente.

Teorema 4. (H-S) es equivalente a (12).

Prueba. El determinante del primer menor es igual al único coeficiente del mismo, mientras que, si (12) se verifica, el determinante de cada uno de los otros menores principales de B es igual al producto de los coeficientes de la diagonal principal de la forma triangular del menor concernido. En consecuencia,

En consecuencia (12) ⇒ (H-S). Por otra parte, si se verifica (H-S) ocurre lo mismo con (14 b) y, además:

esta proposición y (14 a) muestran que (H-S) ⇒ (12), terminando la prueba.⁶

 

IV. Tecnologías "autosustentables" y la condición (12)

Dada una matriz de Leontief B, para cada j sea c (j) la matriz de n X 1 en la que c_j = 1 y c_i= 0 ∀ i ≠ j. Por otra parte, sea x (j) = (x_ij) la matriz de n X 1 que satisface la ecuación:

Para cada j esta ecuación matricial corresponde a un programa de producción que obtiene a su término exactamente la colección de bienes invertida al principio excepto por la cantidad de j que aumenta en una unidad. Esta observación me permite formular las conclusiones siguientes: i) si i ≠ j, la cantidad total de i requerida para producir x_jj unidades de j es x_ij, y ii) la cantidad total de j requerida para producir x_jj unidades de j es x_jj - 1.

De acuerdo con la sección III, las tecnologías "autosustentables" verifican (13). Esta proposición y la j-ésima ecuación del sistema (16j) implica que x_jy ≥ 1 y también que la igualdad se verifica sólo si j no se produce a sí mismo. Entonces, de ii) y del supuesto de rendimientos constantes a escala, se infiere que para cada j, la cantidad total de j requerida para producir una unidad de j es (x_jj- 1) /x_jj = 1 - 1/x_jj . En consecuencia, la cantidad de j producida en excedente (después de descontar la cantidad consumida de j) en la producción de una unidad de j es determinada por 1 - (1 -1/x_jj= 1/x_jj . Concluyo, por tanto, que en estas tecnologías:

Que es equivalente a:

La estrecha relación entre las condiciones (12) y (18) en una matriz de Leontief puede ser apreciada en el teorema siguiente y en su corolario. Conviene mencionar que el teorema es válido para todos los bienes porque el último índice puede ser asignado a cualquier bien.⁷

Teorema 5. En la forma triangular de una matriz de Leontief, el coeficiente del lado izquierdo en la última ecuación es igual a la cantidad del bien correspondiente, obtenida como excedente después de remplazar la cantidad total de este bien consumida en la producción de una de sus unidades.

Prueba. Consideraré la forma (10) correspondiente al sistema (16 n), a fin de mostrar que:

Con este propósito es conveniente verificar que c_nⁿ = 1: si n = 1, entonces c_nⁿ = c(1) = 1 y si n > 1, el supuesto de que c_nⁿ≠ 1 implica una contradicción. En efecto, sea i el primer índice en el orden natural que satisface c_i^t ≠ c_i^t-1 para un cierto t > 1; de acuerdo con (9 b), esto es posible sólo si c_t-1^t-1≠ 0. Sin embargo, c_i^t esta definido sólo si t ≤ i; de ahí que t - 1 < i. Como t - 1 < n, c_t-1¹ = 0 por lo que c_t-1^t-1 ≠ c_t-1¹ en contradicción con el supuesto hecho sobre i. Por tanto, sustituyendo c_nⁿ por 1 en la última ecuación del sistema (10) correspondiente y resolviendo para b_nnⁿ da como resultado (19), terminando la prueba.

De acuerdo con (19) y (17), si la tecnología es "autosustentable", entonces:

La estricta desigualdad y la igualdad en el lado derecho de (20) se verifican respectivamente si n se produce y si no se produce a sí misma. Además, si b_nnⁿ ≤ 0, para obtener una unidad del bien correspondiente el consumo del mismo bien tendría que ser al menos igual a una unidad.

El teorema 5 permite interpretar económicamente cada uno de los coeficientes en la diagonal principal (10). Con este propósito, es útil considerar para cada t el sistema de ecuaciones (21 t), el cual resulta después de borrar en (16 t) todos los términos en los que aparece al menos uno de los últimos n - t índices. Este sistema representa una economía que produce en excedente una unidad de t y cero unidades de los primeros t - 1 bienes (si t > 1). Es conveniente observar que la forma triangular de (21 t) es el sistema que resta después de borrar la últimas n - t filas y las últimas n - t columnas en la forma triangular correspondiente al sistema (16 t). Esto significa que el sistema resultante es similar al sistema (10) que corresponde a (15 n), excepto por el hecho de que el último tiene n ecuaciones en vez de t. En consecuencia, el teorema 5 es también válido para (21 t), de tal forma que si se verifica (H-S) obtenemos:

La desigualdad de la izquierda se debe al teorema 4. Bajo estas condiciones, de acuerdo con el teorema 5, b_tt^t es igual a la cantidad de t obtenida como excedente después de remplazar la totalidad de este bien consumida en la producción de una de sus unidades en (21 t). La diferencia entre esta cantidad y el monto total de t consumida en las primeras t industrias en (16 t) consiste en la cantidad de t consumida por este conjunto de industrias a partir de los últimos n - t bienes, ya que ellos no existen en (21 t). Llegamos así a la conclusión siguiente.

Corolario al Teorema 5. Para cada t, b_tt^t es igual a la cantidad de t obtenida en excedente en la producción de una unidad de t, después de remplazar el monto del mismo bien consumido en las primeras t industrias, cuando la cantidad consumida a través de las últimas n - t industrias no está incluida.

Este resultado permite calcular, dado un conjunto D, el monto de cada j cuyo índice pertenece a D, que es consumido para producir una unidad de j en las D industrias que producen este bien, independientemente de la cantidad de j consumida en las otras n - D industrias. Es suficiente asignar los primeros D índices a los bienes en D y, sucesivamente, el índice D a cada uno de estos bienes, realizando cada vez la triangulación correspondiente. La cantidad consumida en este caso es igual a 1 - b_DD^D.

Por tanto, como (22) puede escribirse en la forma 1 > 1 - b_tt^t > 0 ∀ t, el corolario permite expresar la definición 1 en términos matemáticos mas directamente que (H-S).

 

V. Otra formulación de (H-S)

La proposición siguiente presenta una propiedad particular de las matrices de Leontief.

Lema 1. Una matriz de Leontief verifica (H-S) si y sólo si:

Prueba. Si una matriz de Leontief satisface (23), también verifica (H-S). En este caso, la desigualdad del extremo derecho es válida y, con base en (14) y (22) podemos inferir la primera desigualdad (empezando por la izquierda) en (23), mientras que las otras son establecidas sucesivamente a partir de t = 2 sobre la base de (15) y (22), terminando la prueba.

Como D₁ = 1 - a₁₁ mientras que (15) se verifica para cada t > 1, se sigue que (23) es necesaria para (22), una condición cuya interpretación económica es presentada en el corolario al teorema 5. Por esta razón, también se puede decir que (23) es necesaria para que en la producción de cada bien t la cantidad total del bien consumido en las primeras t industrias (sin considerar el consumo realizado en las otras n - t industrias) es menos de una unidad.

La siguiente proposición es similar a (23), pero es válida para todas las matrices de tipo B y no solamente para las matrices de Leontief.

Teorema 6. Sea k = max {1,b₁₁ ,b₂₂ ,.. .,b_nn}. (H-S) es equivalente a:

Prueba. Puesto que k > 0, (24) implica (H-S). Multiplicando B por 1/k resulta la matriz B* = [b_ij*], en la cual b_ij * = (1/k) b_ij ∀ (i, j). Es conveniente observar que B* satisface (4 a), (4 b) y (7). Para cada j, sea D_j* el j-ésimo menor principal de B*. Puesto que el determinante de una matriz de j X j, multiplicado por un número (1/k), es igual al determinante de la matriz original multiplicado por (1/k)^j, obtenemos:⁸

Entonces, si B satisface (H-S), también lo hace B*. Por esta razón, dadas las otras propiedades ya mencionadas, B* satisface las condiciones del lema 1. En consecuencia, 1 ≥ D₁* ≥ D₂*...≥ D_n *. Una vez hechas en esta fórmula las correspondientes sustituciones de acuerdo con (25), se obtiene (24), terminando la prueba.

El lector puede observar que (24) implica que k^j es una cota superior para la magnitud de los primeros j menores. Sin embargo, se sigue de (17) y de la definición de k que b₁₁b₂₂...b_jj. es otra cota superior no mayor que k.

 

Conclusiones

Este artículo no toma en cuenta ciertos aspectos de las actividades económicas, como su dimensión ecológica, cuya inclusión en el análisis podría eventualmente conducir a establecer algunas restricciones en los resultados. Sin embargo, el enfoque exclusivo en el modelo de Leontief está justificado, desde mi punto de vista, en la medida en que los resultados obtenidos tienen interés económico. En esta sección agregaré a los argumentos ya expuestos algunos comentarios que pueden resultar útiles para esclarecer este punto.

Puesto que todo proceso de producción emplea trabajo, junto con ciertos bienes consumidos como insumos, la condición (6) caracteriza a un conjunto de tecnologías que encuentro apropiado llamar viables. Éste contiene todas las tecnologías que permiten obtener cualquier excedente dado, después de remplazar los bienes consumidos como insumos. La definición 1 indica una condición necesaria y suficiente para que una tecnología pertenezca a este conjunto, que también permite definir a la misma como "autosustentable". Cuando nos referimos al sistema industrial en su conjunto, el sentido de esta definición se establece en (18): la cantidad total de cada bien consumida en la producción de una unidad del mismo bien es menor que una unidad.

Para reconocer la necesidad de la condición establecida en la definición 1 para que una tecnología sea viable, es suficiente considerar el caso recientemente mencionado. Si un cierto bien no cumple la condición, entonces no es posible producirlo en excedente, remplazando al mismo tiempo la cantidad total del mismo bien consumida en el proceso. La suficiencia de la condición, probada en el teorema 1, puede ser apreciada más fácilmente con la ayuda del corolario al teorema 5, ya que éste permite apreciar el significado económico de una condición equivalente a (H-S).

Por otra parte, el artículo desarrolla una prueba original de la equivalencia entre la condición (H-S) y el carácter "autosustentable" de una tecnología de Leontief lo cual aporta una vía alternativa para el estudio de la misma. Comparada con los procedimientos ya publicados (entre los cuales el más citado aparece en el libro previamente señalado de Nikaido)⁹ presenta las siguientes ventajas: a) los instrumentos matemáticos empleados son más sencillos debido a que la prueba está basada en el método de Gauss; b) el resultado contiene más información porque permite identificar la distribución de los dos tipos de coordenadas (nulas y mayores que cero) en la solución, y c) la forma triangular del modelo de Leontief permite presentar el significado económico de las condiciones matemáticas involucradas más directamente.

Tal como se indica en la introducción, también añadí a las ya conocidas dos nuevas condiciones matemáticas equivalentes a (H-S) que -hasta donde sé-no han sido publicadas anteriormente. Además, identifico otras dos condiciones equivalentes a (H-S) en el caso particular de las matrices de Leontief. En mi opinión, es conveniente publicarlas porque permiten apreciar algunos aspectos matemáticos del modelo de Leontief y también debido a las implicaciones económicas señaladas en cada caso.

Finalmente, la definición del significado económico de los coeficientes en la diagonal principal de la forma triangular de la matriz de Leontief puede facilitar algunos estudios comparativos con otras disciplinas. Para ilustrar este punto, refiero al lector a la interpretación de los mismos coeficientes hecha en el libro ya citado de Gantmatcher (1960, pp. 28-31).

 

Referencias bibliográficas

Berman, A., y R. J. Plemmons (1994), Nonnegative Matrices in the Mathematical Sciences, Philadelphia, SCIAM .         [ Links ]

Bidard, C. (2004), Prices, Reproduction, Scarcity, Cambridge, Cambridge University Press.         [ Links ]

Chenery, H. B., y P. G. Clark (1959), Interindustry Economics, Nueva York, Wiley.         [ Links ]

Dorfman, R., Samuelson P., y R. M. Solow (1987), Linear Programming and Economic Analysis, Nueva York, Dover Publications, Inc.         [ Links ]

Gale, D. (1960), The Theory of Linear Economic Models, Chicago, The University of Chicago Press.         [ Links ]

Gantmatcher, F. R. (1960), The Theory of Matrices, Nueva York, Chelsea Publishing Company.         [ Links ]

Georgescu-Roegen, N. (1950), "Leontief's System in the Light of Recent Results", Review of Economics and Statistics, XXXII.         [ Links ]

---------- (1966), Analytical Economics, Cambridge, Harvard University Press.         [ Links ]

Goldberg, J. L. (1991, Matrix Theory with Applications, Nueva York, McGraw Hill, Inc.         [ Links ]

Hawkins, D. (1948), "Some Conditions of Macroeconomics Stability", Econométrica, núm. 16, pp. 309-322.         [ Links ]

----------, y H. A. Simon (1949), "Note: Some Conditions of Macroeconomics Stability", Nueva York, Econométrica, núm. 17, pp. 245-248.         [ Links ]

Leontief, W. (1941): The Structure of the American Economy 1919-1929, Cambridge, Cambridge University Press.         [ Links ]

---------- (1966), Input-Output Economics, Nueva York, Oxford University Press.         [ Links ]

McKenzie, L. W. (1960), "Matrices with Dominant Diagonals and Economic Theory", en K. J. Arrow, S. Karlin, y F. Suppes (comps.), Mathematical Methods in the Social Sciences. Stanford, Stanford University Press.         [ Links ]

Nikaido, H. (1970), Introduction to Sets and Mappings in Modern Economics. Ámsterdam, North Holland Publishing.         [ Links ]

Seneta, E. (1973), Non-Negative Matrices, Nueva York, John Wiley and Sons.         [ Links ]

Takayama, A. (1985), Mathematical Economics, Cambridge, Cambridge University Press.         [ Links ]

Ten Raa, T. (2005), The Economics of Input-Output Analysis, Cambridge, Cambridge University Press.         [ Links ]

Uribe, P. (1977), Análisis de actividades y teoría del capital, Guadalajara, Universidad de Guadalajara.         [ Links ]

 

Notas

¹ Chenery y Clark (1959) describen los 20 primeros años de este desarrollo; ten Raa (2005) ofrece una exposición actualizada de los usos del modelo de Leontief.

² En las aplicaciones empíricas a_ij representa el monto gastado en el bien i para obtener una unidad de valor en la industria j. Dado que en la economía considerada aquí se produce un solo bien en cada industria, se puede obtener cada coeficiente técnico a partir del coeficiente en valor multiplicando este último por el cociente p₁/p_j Véase sobre este punto Bidard (2004, pp. 26-28). Tanto la restricción al caso de la producción simple como la interpretación de a_ij adoptada aquí se debe a que ambas cosas forman parte del modelo de referencia utilizado originalmente por Hawkins y Simon y, después de ellos, por los autores que se han ocupado de la condición (H-S) citados en este trabajo. Por otra parte, Dorfman et al. (1987, p. 208) justifican la interpretación aludida como un requisito para pasar de un procedimiento descriptivo a un instrumento analítico.

³ Hawkins (1948) y Leontief (1966) llegan a un sistema de ecuaciones similar a (5), estudiando el costo de producción. McKenzie (1960) y Gale (1960) presentan varias aplicaciones de este tipo de sistemas.

⁴ Para simplificar, si y es un vector, escribo y ≥ 0 para indicar que y. ≥ 0 ∀ i y digo que se trata de un vector no negativo.

⁵ Hawkins y Simon publicaron la primera prueba de este teorema en el texto ya citado. Casi al mismo tiempo, Georgescu-Roegen (1950) publicó un resultado equivalente que alcanzó de manera independiente y, en otra publicación, Georgescu-Roegen (1966) indica algunos defectos presentes en la prueba propuesta por los dos autores citados aunque también defiende la originalidad de sus contribuciones respecto a ciertos trabajos publicados con anterioridad.

⁶ Gantmatcher (1960, p. 26) establece que (15) es válida para los sistemas lineares de n ecuaciones con n incógnitas, en los que todos los coeficientes de la diagonal principal en la forma triangular correspondiente son diferentes de cero.

⁷ Reasignar los índices de los bienes no afecta a la solución del sistema, como se demuestra en la sección 1.2 de Seneta (1973).

⁸ Véase el ejemplo 1.6.4 en Goldberg (1991).

⁹ Por ejemplo, en el libro ya citado de Takayama (p. 359). También en Uribe (1997, p. 104).