Artículos

 

Aplicaciones de índices de poder en dos universidades argentinas

 

Indexes of power applications in two argentinian universities

 

Jesús Francisco Aguirre,* María Laura Ivanissevich,** Jorge Armando Oviedo,*** Luis Guillermo Quintas****

 

*Licenciado en Ciencias de la Computación, Universidad Nacional de San Luis. Jefe de Trabajos Prácticos en el Departamento de Informática de la Facultad de Ciencias Físico-Matemáticas y Naturales, Universidad Nacional de San Luis. Dirección: Ejército de los Andes 950 (D5700) San Luis, Argentina. Tema de especialización: Desarrollo de software. Teléfono: 54652-422803. Fax: 54652-430724. Correo electrónico: <jaguirre@unsl.edu.ar>.

**Magister en Ciencias de la Computación, Universidad de Cantabria, España. Profesor asociado regular con dedicación completa en la Unidad Académica Río Gallegos, Universidad Nacional de la Patagonia Austral. Tema de especialización: Matemática para las Ciencias de la Computación. Dirección: Lisandro de la Torre 1070 (Z9400), Río Gallegos, Santa Cruz, Argentina. Teléfono: 542966-442319. Fax: 542966442620. Correo electrónico: <mivanissevich@uarg.unpa.edu.ar>.

*** Doctor en Matemáticas, Universidad Nacional de San Luis. Profesor Titular en el Departamento de Matemáticas, Instituto de Matemática Aplicada San Luis (IMASL). Tema de especialización: Teoría de Juegos. Dirección: Ejército de los Andes 950 (D5700), San Luis, Argentina. Teléfono: 54652-422803. Fax: 54652-430224. Correo electrónico: <joviedo@unsl.edu.ar>.

**** Doctor en Managerial Economics and Decision Sciences, Kellogg Graduate School of Management, Northwestern University, Estados Unidos. Departamento de Matemáticas-Instituto de Matemática Aplicada San Luis (IMASL), Consejo Nacional de Investigaciones Científicas y Técnicas (Conicet), Facultad de Ciencias Físico-Matemáticas y Naturales, Universidad Nacional de San Luis. Tema de especialización: Teoría de Juegos. Dirección: Ejército de los Andes 950 (D5700), San Luis, Argentina. Teléfono: 54652-4. Fax: 54652-430724. Correo electrónico: <lquintas@unsl.edu.ar>.

 

Recibido: 4 de junio de 2003.
Aceptado: 20 de enero de 2005.

 

Resumen

El trabajo analiza los índices de poder: el valor de Shapley y el índice de Coleman-Banzhaf con el fin de estudiar la distribución de poder en las elecciones para elegir autoridades en dos universidades argentinas. Se aplica un sistema de computación desarrollado para calcular los índices de poder. El sistema permite introducir restricciones (incompatibilidades) entre algunas coaliciones. El estudio concluye que los índices de poder con incompatibilidades dan una mejor aproximación de la distribución real del poder que la proporción de votos que cada grupo tiene en los Consejos Universitarios.

Palabras clave: teoría de juegos cooperativos; índices de poder; incompatibilidades.

 

Abstract

In this article we present the Shapley Value and the Banzhaf-Coleman index of power so as to analyze the power allotment in the authorities "electoral" system for two Argentinian universities. We work with a computational system developed to estimate the indexes of power. The system allows to introduce restrictions (incompatibilities) among some coalitions. The results show that the indexes of power with incompatibilities turn out to be a better model to approach the real allotment of power than the share of votes that each group has in our scenarios.

Key words: cooperative games theory; indexes of power; incompatibilities.

 

I. INTRODUCCIÓN

En este trabajo se analiza el poder que tienen los distintos grupos en dos universidades argentinas en la elección de autoridades, la cual se lleva a cabo bajo sistemas electorales indirectos. Así, la autoridad electa (decano o rector) resulta elegida por mayoría simple en cuerpos colegiados cuyos miembros han sido elegidos por votación directa.

Las universidades argentinas están típicamente integradas por Facultades. Se trata de unidades administrativas y de gobierno con funciones académicas, de docencia e investigación (Estatuto universitario, 1990). Cada Facultad está regida por un decano, elegido usualmente de manera indirecta por el Consejo Directivo (CD),¹ el cual se halla integrado por representantes de los claustros docentes, los alumnos, los no docentes y los graduados. Los miembros de los CD son elegidos por votación directa en el claustro correspondiente.

La Asamblea Universitaria (AU), que elige al rector de la Universidad, está integrada por los miembros de los CD.

Así, a primera vista, se podría pensar que los grupos de docentes, alumnos, no docentes o graduados, con mayor cantidad de representantes en los cuerpos colegiados (CD o AU) que eligen a las autoridades universitarias, tendrían mayores posibilidades de imponer a sus candidatos. Sin embargo, los porcentajes de votos que tienen las distintas agrupaciones, habitualmente no coinciden con el poder real que tienen a la hora de elegir a las autoridades. Ello se debe a que, en muchos casos, para imponer a una autoridad es necesario contar con el apoyo (y los votos) de representantes de distintos sectores, y a que suele haber grupos antagónicos que apoyan a distintos candidatos (a veces con posiciones irreconciliables) que por sí solos no forman mayorías en los cuerpos colegiados. De este modo, grupos con menor cantidad de representantes suelen desempeñar roles más importantes que otros que cuentan con mayor cantidad de representantes a la hora de reunir a las mayorías necesarias para elegir a las autoridades universitarias. Por ello resulta necesario contar con otra medida, distinta del simple porcentaje de representantes, a la hora de modelizar el poder real que cada grupo posee. Esto se hace mediante los llamados "índices de poder".

Los índices de poder son valores numéricos que intentan reflejar el poder real que tiene cada agrupación. Los más conocidos son el valor de Shapley (Shapley, 1953), y el índice de Coleman-Banzhaf (Coleman, 1971; Banzhaf, 1965; Banzhaf, 1968; Dragan, 1996).

Una situación estratégica con algunas características similares a la aquí planteada ocurre en los Parlamentos de distintos países; allí también es modelizado el poder de cada agrupación mediante índices de poder (Garrett y Tsebelis; 1999; Katz, Gelman, y King, 2002; Stromberg, 2002; y otros).

En el presente trabajo aplicamos los índices de poder: valor de Shapley así como el índice de Coleman-Banzhaf, para estudiar la distribución de poder en la elecciones de autoridades en dos universidades argentinas: la Universidad Nacional de San Luis (UNSL) y la Universidad Nacional de la Patagonia Austral (UNPA). La primera está ubicada en el centro de Argentina (en la provincia de San Luis) y la segunda, en el sur de Argentina (en la provincia de Santa Cruz). Se analizan los sistemas electorales de estas dos universidades, los cuales son similares a otras universidades argentinas. Los estudios realizados, con pocas modificaciones, podrían adaptarse a otras universidades de la región.

Asimismo, se analizan las posibles alianzas (coaliciones) e incompatibilidades entre los sectores en pugna, y se concluye que los índices reflejan adecuadamente la distribución de poder.

 

II. JUEGOS COOPERATIVOS, ÍNDICES DE PODER E INCOMPATIBILIDADES

La teoría de juegos es una teoría matemática que sirve para modelizar interacciones entre agentes en situaciones de conflicto estratégico. Un juego es una situación en la cual dos o más personas interactúan. Esto incluye la modelización de las interacciones de grupos en distintos escenarios (académicos, políticos, económicos, y así por el estilo).

Cada jugador tiene un control parcial de la situación; pero, en general, ningún jugador la controla totalmente. Cada jugador o grupo de jugadores tiene ciertas preferencias personales sobre el conjunto de resultados posibles y trata de obtener una que le favorezca. Estas preferencias pueden ser descritas por alguna función de utilidad, en la cual cada jugador es caracterizado por una función numérica.

Los juegos pueden ser divididos en dos categorías: "no cooperativos" y "cooperativos". En la primera de ellas, solamente el egoísmo es asumido. En la segunda, si bien los agentes pueden mantener una actitud egoísta, se considera la posibilidad de formar coaliciones, y los grupos de jugadores pueden actuar de manera cooperativa con el propósito de obtener mejores resultados.

En el presente artículo trabajaremos solamente con juegos cooperativos. Así, la elección de autoridades se puede representar por un conjunto de votantes N = {1, 2,..., n; éstos son los miembros de los CD o AU, y por una función V (función característica) definida en los subconjuntos S de N, cuyo resultado es 0 si S pierde la elección y 1 si gana. En este último caso diremos que S es una coalición ganadora. En una elección por mayoría simple, para que S gane la elección debe contar con más de la mitad de los votos; así:

Donde |S| indica la cantidad de miembros que tiene el conjunto S.

En la elección de autoridades universitarias, el conjunto N se conforma por grupos de electores que corresponden a agrupaciones provenientes de los claustros respectivos. Los denominamos "coaliciones básicas". Puede haber varias coaliciones básicas de docentes, alumnos, no docentes y graduados. Estos grupos, a su vez, pueden unirse con otros grupos para intentar imponer a un candidato (decano o rector) y conformar una coalición ganadora. Para ello hace falta obtener más de la mitad de los votos del CD o AU.

Un vector de pago en un juego cooperativo es un n-vector donde cada componente es lo que obtiene cada jugador como resultado del juego. Cada componente debe ser mayor o igual que v({i}): lo que obtendría cada jugador por sí mismo. Además, la suma de las componentes es igual a v(N). Así, un vector de pago aporta una manera posible de distribuir la cantidad total v(N) provista por la coalición N de todos los jugadores. La teoría de juegos cooperativos estudia qué vectores de pagos pueden surgir como resultado del juego y qué características deben poseer. Dan una medida del poder de cada jugador. Una solución para un juego cooperativo es un vector o conjunto de vectores de pago que cumple determinadas propiedades. Los juegos cooperativos admiten diferentes tipos de soluciones; las más conocidas son: el valor de Shapley, el índice de Coleman-Banzhaf, el Core y el nucleolo (en Owen, 1995, se detallan características de estos conceptos).

Como dijimos anteriormente, en este trabajo usaremos el valor de Shapley (Shapley, 1953), y el índice de Coleman-Banzhaf (Coleman, 1971; Banzhaf, 1965; Banzhaf, 1968; Owen, 1978). Éstos dan en cada caso un (único) vector que constituye una medida aproximada del poder de cada jugador. Usaremos una herramienta computacional desarrollada para analizar los índices de poder (Aguirre y otros, 2001). El sistema permite introducir restricciones (incompatibilidades) entre algunas coaliciones.

En muchos casos hay grupos antagónicos que no forman coaliciones entre sí. De este modo se tienen incompatibilidades. Supongamos que dos grupos, S1 y S2, están enfrentados entre sí. Entonces la coalición que se integraría si ambos grupos se unieran (S1 È S2), ya no resulta factible. El sistema desarrollado permite definir los grupos incompatibles entre sí (de a pares) y redefine automáticamente la función característica v, asignándole a S1 È S2 el máximo valor entre v(S1) y v(S2). Esto indica que S1 È S2 no es considerada como la unión de S1 y S2 sino como las coaliciones S1 y S2 por separado. De tal modo se modeliza la incompatibilidad entre S1 y S2, y se obtienen los índices teniendo en cuenta esta nueva situación. Ello facilita una tarea que sería engorrosa de realizar de manera manual.

El estudio realizado revela características importantes de las estructuras de poder al tomar en cuenta las incompatibilidades entre grupos antagónicos y los diferentes sectores que conforman los Consejos Universitarios (CD y AU).

 

III. EL VALOR DE SHAPLEY

Dado un juego cooperativo (que denotamos G = (N, v)), el valor de Shapley está dado por un n-vector φ(v) = (φ1(v),φ2(v),..., φn(v)), tal que:

φi(v) es la componente i-ésima del valor de Shapley y da un promedio de las contribuciones marginales del jugador i, a todas las posibles coaliciones en las que puede participar. Así, la fórmula anterior puede interpretarse de la manera que se explica a continuación.

Supongamos que los jugadores (elementos de N) arribaran en diferentes tiempos conformando coaliciones S (cuya cardinalidad es s). Cuando el jugador i se incorpora a la coalición S, se forma la coalición S È {i}, y su aporte es v(SÈ {i}) - v(S). Como hay s jugadores que llegaron antes que el jugador i, los órdenes (permutaciones) en que pueden arribar son s! (aquí s! es el producto de 1, 2, 3,. . . s-1, s). En la fórmula anterior también aparece el término (n-s-1)! para indicar las permutaciones de los (n-s-1) jugadores que arriban después del jugador i. Finalmente, se divide por n! (permutaciones de los n jugadores) ya que todos los órdenes de llegada para los n jugadores tienen la misma probabilidad de ocurrir.

El valor de Shapley está caracterizado por una serie de axiomas que justifican adecuadamente su uso para medir distribuciones de poder (Shapley, 1953).

 

IV. EL ÍNDICE DE COLEMAN-BANZHAF

Un segundo índice de poder fue estudiado por Banzhaf (Banzhaf, 1965), y por Coleman (Coleman, 1971).

Este índice es definido sobre juegos simples normalizados a (0, 1). (N, v) es un juego simple normalizado a (0, 1), si los resultados del juego son 0 o 1.

El índice de Coleman-Banzhaf se basa en contar, para cada jugador, la cantidad de coaliciones para las cuales él es decisivo para ganar. Una coalición S es ganadora cuando v(S) = 1. Para cada coalición S ganadora, cuando v(S-{i}) = 0, es un swing para el jugador i (nótese que el jugador i la convierte en ganadora).

Dado un juego (N, v), supongamos que si (N, v) es el número de swings para i, y que

es el número total de swings de todos los jugadores que participan en el juego. Luego definimos el índice normalizado de Coleman-Banzhaf por:

Este índice puede ser generalizado para juegos generales (owen, 1978) por la siguiente fórmula:

Así, el valor de Shapley y el índice de Coleman-Banzhaf dan promedios de las contribuciones de los jugadores al ingresar en cada coalición S; difieren sólo en el coeficiente con que se promedian dichas contribuciones. En muchas aplicaciones ambos índices dan valores similares, y eso es justamente lo que ocurre en este trabajo.

 

V. CÁLCULOS DE ÍNDICES DE PODER EN DOS UNIVERSIDADES ARGENTINAS

En esta sección analizaremos los índices de poder en los Consejos Universitarios (CD y AU) de la Universidad Nacional de San Luis (UNSL) y la Universidad Nacional de la Patagonia Austral (UNPA). Así se pueden analizar aspectos importantes de la distribución de poder entre grupos y sectores que conforman los organismos de gobierno, los cuales tienen como primera decisión que tomar, la elección de la autoridad máxima de la Facultad o Unidad Académica (el decano) o del rector de la Universidad (Asamblea Universitaria). El análisis aquí presentado es común a otras universidades argentinas y podría extenderse sin mayores cambios a otras universidades de la región.

 

A. Universidad Nacional de San Luis

En la Universidad Nacional de San Luis se decidió la modificación del Estatuto Universitario (Estatuto Universitario, 1990). Al igual que varias otras universidades argentinas, la que nos ocupa inició un cambio de su sistema electoral: pasó de uno indirecto a un método directo de elección de las autoridades universitarias. Con este nuevo método, las autoridades son elegidas por votación directa, con un sistema proporcional donde los votos recibidos se pesan según del estamento de donde provengan (docentes, alumnos, graduados y no docentes). Para la elección de los miembros de los Consejos (Consejo Superior, Consejos Directivos y Consejos Departamentales), se propuso aplicar el sistema proporcional de D'Hont. La aplicación de este cambio de sistema de votación exigió cambios en la distribución de poder.

En el sistema indirecto, para el caso de la elección del decano de una Facultad, es necesario obtener una mayoría de votos en el Consejo Directivo de la correspondiente Facultad, el cual está formado por 17 electores que consisten en seis grupos básicos:

1 - Profesores (mayoría) = siete votos

2 - Profesores (minoría) = tres votos

3 - Estudiantes (mayoría) = cuatro votos

4 - Estudiantes (minoría) = un voto

5 - Empleados administrativos = un voto

6 - Graduado = un voto

Es necesario obtener nueve votos (mayoría simple) para decidir la elección del decano de la Facultad. Se trata de una configuración típica, la cual fue resultado real de varias elecciones recientes en una de las cuatro Facultades que tiene la Universidad Nacional de San Luis (la Facultad de Ciencias Físico-Matemáticas y Naturales). Las otras Facultades muestran escenarios similares, pero los estudiantes tienen en algunos casos distribuciones de tres y dos votos; o de tres, uno y un voto. (Éstas podrían ser otras configuraciones que dan situaciones alternativas similares a la aquí estudiada.)

Si los profesores integran una coalición entre ellos (sumando los votos de la mayoría y la minoría), reúnen diez votos, con lo cual podría parecer que tendrían el control total de la situación. Si bien en ciertos casos ello ocurre (en tal circunstancia suele haber una sola lista conjunta cuya función característica será v(S) = 1), lo más común es que pertenezcan a diferentes grupos y no formen coaliciones entre ellos (luego se analizará más en detalle cuándo se introducen incompatibilidades entre grupos). Para conocer el poder electoral de cada grupo, calcularemos el valor de Shapley y el índice de Coleman-Banzhaf.

A continuación se muestra el índice de Coleman-Banzhaf b(v), calculado con la ayuda del sistema computacional (Aguirre et al., 2001). Calcular los índices sin este sistema podría resultar dificultoso porque son 26 = 64 coaliciones las que han de ser consideradas.

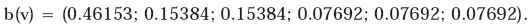
De manera similar, podemos computar el valor de Shapley y obtenemos:

En este caso, ambos índices arrojan valores similares. Notamos que no se corresponden exactamente con la fracción de votos que los grupos tienen en el Consejo Directivo. Por ejemplo, la mayoría de profesores tiene 7/17 = 0.41176 de los votos, pero los índices de poder son más grandes: 0.46667 y 0.46153. También notamos que grupos con diferentes números de votos tienen el mismo índice de poder: en este caso, los grupos 2 y 3 tienen tres y cuatro votos, respectivamente; pero tienen el mismo poder electoral porque cuentan con las mismas posibilidades de conformar una mayoría simple que los incluya.

Como se indicó anteriormente, en la práctica algunos grupos podrían oponerse entre sí y, de ese modo, no formarían una coalición. Se trata de una situación típica entre la mayoría y la minoría de los profesores. Así podemos recalcular los índices con incompatibilidades y obtenemos los siguientes valores.

El valor de Shapley está dado por:

(El índice de Coleman-Banzhaf arroja valores similares.)

Lo anterior parece estar más ligado a la situación real. En tal caso, la mayoría de los estudiantes tiene un poder grande y la minoría de los profesores tiene poco poder. Ello resulta consistente con la realidad pues, de hecho, usualmente la mayoría de los profesores y la mayoría de los estudiantes se juntan para formar la coalición ganadora y elegir al decano de la Facultad.

También observamos que la mayoría de los profesores generalmente impone al representante de los graduados. En este caso tenemos solamente cinco coaliciones básicas:

1 - Profesores (mayoría) = ocho votos

2 - Profesores (minoría) = tres votos

3 - Estudiantes (mayoría) = cuatro votos

4 - Estudiantes (minoría) = un voto

5 - Empleados administrativos = un voto

Ahora bien, si no ponemos condiciones sobre las coaliciones (en este caso permitimos a cualquier grupo juntarse con otro, incluso ambos grupos de profesores), tendríamos los siguientes índices:

El valor de Shapley está dado por

y el índice de Coleman-Banzhaf está dado por

Si nuevamente imponemos la restricción de que ambos grupos de profesores provienen de sectores opuestos, y de este modo no pueden armar una coalición, tenemos los siguientes índices:

El valor de Shapley está dado por

y el índice de Coleman-Banzhaf está dado por

Es interesante comparar el resultado de los índices de poder con los porcentajes de representantes en el CD y el nuevo sistema proporcional.

Esto se muestra en la figura 1. Allí may p es la mayoría de los profesores; min p es la minoría de los profesores; may e es la mayoría de los estudiantes; min e es la minoría de los estudiantes; y no doc corresponde al sector de empleados administrativos (no docentes).

La fracción de votos de la minoría de los profesores: 3/17 (aproximadamente 18%) no se corresponde con los índices de poder. Estos índices —la segunda componente de j(v) y b(v)— son mucho más chicos que las fracciones de votos correspondientes y se hallan entre 0.043478 y 0.05 (o sea entre 4% y 5%). Dichos resultados son consistentes con la siguiente observación.

En las elecciones de las últimas 48 autoridades: decanos y vicedecanos (en seis elecciones de dos autoridades en cada una de las cuatro Facultades), solamente en dos casos (entre 4% y 5% de las veces) la autoridad fue elegida con la adhesión de los profesores de la minoría y sin el apoyo de los profesores de la mayoría.

Así, los últimos índices calculados con incompatibilidades entre grupos, parecen una mucha mejor aproximación a la distribución del poder real de cada grupo que las fracciones de votos correspondientes. Resulta claro que no se trata de contar cuántos votos tiene cada grupo, sino de entender para qué sirven dichos votos.

 

B. Universidad Nacional de la Patagonia Austral

En esta sección analizamos el sistema electoral de la Universidad Nacional de la Patagonia Austral (UNPA). En primer lugar, nos concentramos en la distribución de poder en una de sus Unidades Académicas, aunque el mismo tipo de estudio puede hacerse de manera similar para otras unidades académicas. También estudiamos la estructura de la Asamblea Universitaria, la cual consta de representantes de diferentes sectores y allí se elige al rector, máximo directivo de la Universidad.

Hay cuatro unidades académicas en la UNPA: Unidad Académica Río Gallegos (UARG), Unidad Académica Caleta Olivia (UACO), Unidad Académica Río Turbio (UART) y Unidad Académica San Julián (UASJ). cada Unidad Académica se halla presidida por un decano, y tiene un consejo que forma su estructura de gobierno. La primera decisión de dicho consejo es elegir al decano mediante mayoría simple de votos.

El Consejo de la UARG está formado por 12 electores: seis representantes de los profesores, cinco estudiantes y un administrativo (no docente). Así se obtiene la siguiente estructura:

1 - Profesores = seis votos

2 - Estudiantes = cinco votos

3 - No docentes = un voto

Se necesitan siete votos para elegir al decano. A primera vista parecería que tanto los profesores como los estudiantes se hallan en buenas condiciones de imponerse pues sólo les falta uno y dos votos, respectivamente, para formar la mayoría. sin embargo, el índice de poder muestra que los profesores tienen más y que los estudiantes tienen el mismo que el sector no docente, pues entre estos dos últimos reúnen sólo seis votos y no forman mayoría. El valor de Shapley es

suele ocurrir que los representantes de los profesores —al igual que los estudiantes— pertenecen a distintos sectores; así se tiene la siguiente situación típica:

1 - Profesores (A) = tres votos

2 - Profesores (B) = tres votos

3 - Estudiantes (A) = tres votos

4 - Estudiantes (B) = dos votos

5 - No docentes = un voto

Fue un resultado que se ha observado en varias elecciones en la UARG (otras unidades académicas tienen escenarios similares).

Así podemos calcular los índices de poder de cada grupo. Lo hacemos primero sin considerar incompatibilidades entre ellos y luego considerando estas incompatibilidades dentro de cada estamento (lo cual lleva a sostener distintos candidatos para decano).

Cuando tomamos en cuenta las incompatibilidades entre grupos (lo cual refleja una situación que usualmente ocurre en la práctica), se obtienen los índices de poder que aparecen a continuación.

Aquí se observa que el grupo de la mayoría de los estudiantes (grupo 3) desempeña ahora un papel muy importante (índices cercanos a 0.5, aproximadamente la mitad del poder), pues se halla en muy buenas condiciones de ser parte de una coalición que elija al decano dado que ahora los profesores están divididos, y sin el voto de este grupo no pueden formar mayoría.

También podemos recalcular los índices de poder luego de la elección del decano cuando el mismo se agrega y vota en el consejo. De hecho el decano pertenece a un grupo de profesores (supondremos que es el primer grupo de profesores, por ello se lo suma a dicho grupo) y preside el consejo.

Los últimos cuadros revelan que con el agregado del decano, ahora el grupo de profesores que lo eligió ha recobrado un control bastante significativo sobre el consejo (índices cercanos a 0.5), lo cual ayuda a la gobernabilidad de la Unidad Académica.

1. Análisis de la elección de rector en la UNPA

La asamblea de la UNPA es el órgano máximo de dicha Universidad y consta de 58 electores. cada Unidad Académica tiene representantes de los estudiantes, de los profesores y de los no docentes. Las autoridades (el decano y los directores de Departamento) pertenecen a la Asamblea.

También son miembros de ella el último rector y un no docente del rectorado (rec). El siguiente cuadro muestra dicha distribución de electores.

La primera tarea que realiza la Asamblea es elegir un nuevo rector. Siempre es necesario tener una mayoría de votos para esta elección. Así se obtienen los índices de poder que aparecen a continuación.

Es importante subrayar que la UARG y la UACO tienen mayor poder porque si actúan juntas forman coaliciones ganadoras (32 votos). REC, UASJ, UART tienen exactamente el mismo poder entre sí aunque menor que los anteriores porque la suma de sus votos no integra una coalición ganadora (26 votos).

También podemos calcular los índices de poder considerando los diferentes sectores a los que pertenecen los representantes.

1 - Profesores = 24 votos

2 - Estudiantes = 16 votos

3 - Autoridades = 13 votos

4 - No docentes = cinco votos

Así, obtenemos los siguientes índices de poder:

Este último análisis muestra el papel central que desempeñan allí los profesores en la elección del rector, ya que su índice es de 0.5 (la mitad del poder); mientras que si hubiéramos tenido en cuenta la fracción de sus votos, 24/58, ésta resultaba menor pues no tienen mayoría propia.

 

VI. CONCLUSIONES

Hemos analizado aquí la distribución de poder en los consejos Directivos, las Unidades Académicas y la Asamblea Universitaria para elecciones de autoridades en dos universidades argentinas. contar con un sistema de computación facilita los cálculos que deben realizarse; asimismo, pueden analizarse distintas situaciones cuando ciertos grupos son incompatibles. De este modo, es posible confrontar distintos escenarios y distribuciones de poder en elecciones de autoridades.

En varios casos pudo observarse que no es precisamente la cantidad de votos que reúne un determinado sector lo único que cuenta a la hora de saber qué poder tiene realmente dicho grupo, sino su capacidad para formar coaliciones ganadoras.

Una importante conclusión es que, a la hora de medir el poder real de los grupos en un consejo, no es sólo cuestión de contar cuántos votos se obtuvieron, sino averiguar cuáles son las capacidades de asociación de dichos grupos y en definitiva entender para qué sirven dichos votos.

Los sistemas de votación directos eliminan, en parte (para la elección de autoridades), la necesidad de analizar la formación de coaliciones. Los aspectos estratégicos reaparecen durante el funcionamiento de los consejos Universitarios, luego de la elección de las autoridades correspondientes.

Los estudios aquí analizados son comunes a otras universidades argentinas; con algunas modificaciones, podrían adaptarse a otras universidades de la región.

 

Bibliografía

Aguirre, J. F.; R. Guerrero; J. A. Oviedo; y L. G. Quintas. "Computation of Indexes of Power with Incompatibilities". Proceedings CACIC 7, num. 1 (2001): 297-307.         [ Links ]

Banzhaf, J. F. "Weighted Voting Doesn't Work: A Mathematical Analysis". Rutgers Law Review 19 (1965): 317-343.         [ Links ]

----------. "One Man, 3.312 Votes: A Mathematical Analysis of the Electoral College". Villanova Law Review 13 (1968): 304-332.         [ Links ]

Coleman , J. S. "Control of Collectivities and the Power of a Collectivity to Act". En Social Choice, compilado por B. Lieberman. Londres: Gordon and Breach, 1971.         [ Links ]

Dragan, I. "New Mathematical Properties of the Banzhaf Value". European Journal of Operation Research 95 (1996): 451-463.         [ Links ]

Estatuto Universitario. San Luis, Argentina: Universidad Nacional de San Luis, 1990.         [ Links ]

Garrett, G., y G. Tsebelis. "Why Resist the Temptation to Apply Power Indexes to the European Union?". Journal of Theoretical Politics 11 (1999): 291-308.         [ Links ]

Katz, J. N.; A. Gelman; y G. King. "Empirically Evaluating the Electoral College". En Rethinking the Vote: The Politics and Prospects of American Election Reform, compilado por A. N. Crigler, M. R. Just y E. J. McCaffery. Nueva York: Oxford University Press, 2002.         [ Links ]

OWEN, G. "Characterization of the Banzhaf-Coleman Index". SIAM Journal of Applied Mathematics (1978): 35.         [ Links ]

----------. Game Theory. Tercera edición. San Diego, California: Academic Press, 1995.         [ Links ]

SHAPLEY, Lloyd S. Shapley. "A Value for n-person games". Annals 28 (1953).         [ Links ]

STEVENS, David L. Stevens. Internetworking with TCP/IP. Vol. III: ClientServer Programming and Applications. Compilado por Douglas E. Comer y David L. Stevens. New Jersey: Prentice Hall, 1993.         [ Links ]

STROMBERG, D. "Optimal Campaigning in Presidential Elections: The Probability of Being Florida". Technical report, IIES. Estocolmo: Stockholm University, 2002.         [ Links ]

 

Nota

Los autores agradecen las correcciones y sugerencias hechas por tres dictaminadores anónimos, cuyas observaciones mejoraron una versión previa del presente trabajo.

¹ De manera similar se elige al vicedecano de la Facultad.