Introduction
Euclidean geometry allows the quantification of regular objects; however, it presents limitations in the measurement of irregular objects.1 In that order of ideas, Mandelbrot proposed a geometry capable of characterizing irregular objects based on the fractal dimension. Statistical fractals are understood as systems that can be characterized by the distribution of frequencies appearance of certain variables, organized in a hierarchical way. In the mentioned systems, the statistical fractal dimension is measured, calculated by the Zipf-Mandelbrot law. Zipf assigned ranges to frequencies of occurrence of words in a text, evidencing a hyperbolic behavior of the phenomenon.2 Then, Mandelbrot performed a logarithmic linearization of the previously mentioned behavior and calculated the statistical fractal dimension, variable that measures the degree of complexity of a system, as the inverse of the slope of the graph.3
With the statistical fractal dimension it was possible to determine the loss of complexity in the texts of nuns studying with Alzheimer’s.4
Cardiovascular diseases are the leading cause of mortality worldwide. Only in 2012 around 17.5 million people died from these diseases,5 reason why they have a great preponderance in the different health systems. In cardiology, parameters have been sought to establish differences between normality and disease. As part of that search, the analysis of heart rate variability has been used with some frequency,6 whose alterations have been linked to some cardiovascular diseases.7,8 From new perspectives, studies have shown the non-linear behavior of the cardiac system, which can even have chaotic patterns,9,10 whose measurement is possible through fractal geometry, used to evaluate different structures of the human body.11,12
The variability of the heart rate has been analyzed from non-linearity;13 with the called multifractal analysis, it has been possible to evaluate the autonomic regulation of heart rhythm in the context of ischemic episodes.14 Additionally, spectral analyzes have been used and an attempt has been made to establish their relationship with patient mortality, especially after suffering acute myocardial infarction;15 Likewise, the complexity of the dynamics has been associated with the variability of the heart rate16 and two different types of non-linear dynamics have been evidenced in short registration periods.17 However, investigations have shown the imperative need to perform more accurate analysis.
Perspectives based on modern theoretical physics and the theory of dynamic systems, have allowed the advent of new research in fetal cardiac systems,18,19 of adults20,21 and neonatal,22 obtaining objective and reproducible diagnoses. Also, diagnoses have been made in patients with arrhythmias.23,24 An exponential law of chaotic cardiac dynamics was also developed25 and a mathematical method based on the proportions of entropy allowed the establishment of differentiations between normality and pathological states.26,27
It has also allowed established mathematical parameters indicative of evolution towards acute disease, independent of population or statistical analysis. A diagnostic methodology based on the Zipf-Mandelbrot law, allowed to demonstrate the degree of complexity of the normal cardiac systems and in states of exacerbation, this complexity being greater in the case of normal systems, an aspect that can be evidenced by the statistical fractal dimension.28
The objective of this work is to confirm the clinical applicability of a methodology based on the Zipf-Mandelbrot law in the context of a blind study with 50 electrocardiographic tracings of normal and pathological cases.
Material y methods
Definitions:
Statistical fractal dimension: to establish the statistical fractal dimension of Zipf-Mandelbrot, a logarithmic linearization is performed by applying the least squares method, finding the negative multiplicative inverse of the slope, corresponding to the statistical fractal dimension:
being, D: the fractal dimension; σ: the range for each frequency, P: the frequency of appearance of the heart rate. V: is defined by V = 1/(N-1) in which N: is the number of frequencies measured; F: is a secondary cofactor in linearization, obtained from the application of the least squares method.
Procedure
50 ambulatory and continuous electrocardiographic recordings were taken, for at least 21 hours of subjects over 21 years of age, of Insight group databases. These records were for 20 patients with clinical evaluation within normal limits and 30 patients with acute cardiac pathologies, according to the criteria of an expert electrophysiologist, based on conventional medical protocols. Initially, the clinical findings were masked.
From each record, the values of maximum and minimum heart rate were taken in each hour. Then, a count was made of the number of heart rates found in each range of 15 beats/min. The frequency of appearance of the ranges of 15 beats/min was calculated. Subsequently, the Zipf-Mandelbrot law was applied to these values; for this, the frequencies of appearance of the ranges were ordered from highest to lowest, an integer was assigned to each of them, starting with one and increasing by one unit for the following frequencies of appearance, that were ordered in a hierarchical way. The data was graphed to corroborate the hyperbolic behavior and later give rise to the application of the law (see equation #1). A logarithmic linearization using the least squares method was applied to the scatter of points obtained in the graph, and the correlation coefficient (r2) of the line of greatest adjustment of this point dispersion was established. Finally, the statistical fractal dimension of each dynamic was found and, consequently, its degree of complexity.
For the purposes of the statistical analysis, the clinical diagnoses were unmasked. A comparison was made between the mathematical methodology and the conventional diagnosis, taken as gold standard, for which specificity and sensitivity were calculated using a binary classification, where the true positives correspond to the number of patients with diagnosis of abnormality according to the gold standard and the mathematical method, false positives correspond to cases with mathematical values suggestive of abnormality and with a clinical diagnosis of normality, false negatives are cases with mathematical values indicative of normality and clinical diagnosis of abnormality, the true negatives correspond to the records diagnosed both clinically and mathematically as normal.
The agreement between the mathematical diagnosis and the conventional clinician was evaluated, using the kappa coefficient, through the following formula:
Co corresponds to the number of matches observed, that is, the number of patients diagnosed equally by the mathematical method and the conventional diagnosis. To corresponds to the total number of cases. Ca represents the matches attributed to chance, calculated by the formula:
f1 corresponds to the number of patients with mathematical values indicative of normality, C1 corresponds to the number of patients with a clinical diagnosis of normality, f2 corresponds to the number of patients with mathematical values indicative of abnormality, C2 represent cases conventionally diagnosed as abnormal and To represents the total of cases.
Ethical aspects
This study is governed by the ethical principles contemplated in the Declaration of Helsinki of the World Medical Association and adopts Resolution 8430 of 1993 of the Ministry of Health of Colombia. It is declared as a minimum risk investigation, given that mathematical calculations are made based on non-invasive examinations and paraclinics previously prescribed according to conventional medical protocols, protecting the information and integrity of the participants.
Results
In the analysis of the degree of complexity of the dynamics, it was evidenced that the statistical fractal dimensions of the normal cases had values between 0.7123 and 0.9327 and the values for the correlation coefficient of the highest-fit lines (r2) were found between 0.7714 and 0.9742; (Figure 1) whereas for the cases of patients studying with acute pathologies the fractal dimensions were between 0.4253 and 0.6698 and the correlation factor was between 0.6658 and 0.9513 (Table I and Figure 2).
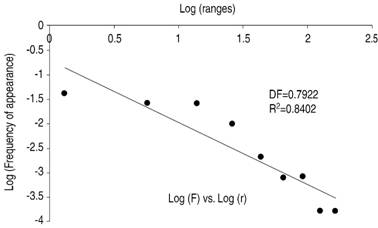
Figure 1: Logarithmic linearization corresponding to case 5 of Table I with normal dynamics. Note the difference with Figure 2, this presents a higher degree of complexity than that of Figure 1.
Table I: Statistical fractal dimension (DF) and correlation coefficient (r2).
| No. | Normal | Acute Myocardial Infarction | ||
|---|---|---|---|---|
| DF | r2 | DF | r2 | |
| 1 | 0.8195 | 0.8422 | 0.5337 | 0.9139 |
| 2 | 0.8253 | 0.9096 | 0.6474 | 0.8794 |
| 3 | 0.7692 | 0.8260 | 0.5895 | 0.6730 |
| 4 | 0.9309 | 0.9696 | 0.6674 | 0.6688 |
| 5 | 0.7922 | 0.8402 | 0.5036 | 0.8781 |
| 6 | 0.7637 | 0.8982 | 0.4738 | 0.8833 |
| 7 | 0.8665 | 0.9038 | 0.4323 | 0.7852 |
| 8 | 0.9109 | 0.8929 | 0.6191 | 0.9398 |
| 9 | 0.8291 | 0.8375 | 0.6234 | 0.8822 |
| 10 | 0.7289 | 0.8172 | 0.4255 | 0.8852 |
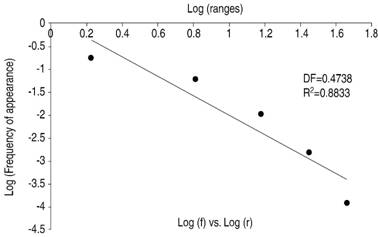
Figure 2: The logarithmic linearization of the frequency distribution in heart rate ranges of case 6 of Table I with acute pathology can be observed. Here on the X axis is the logarithm of the range assigned by the application of Zipf’s law, and on the Y axis is the logarithm of the frequency of appearance of each range. These ranges are ranges of 15 beats/min of heart rates.
In the diagnostic test to confirm the applicability and clinical reproducibility of the methodology with respect to conventional clinical evaluation, had sensitivity and specificity values of 100%, and the Kappa coefficient was 1, which corroborated the ability of the methodology to differentiate with mathematical values the normal cardiac dynamics from acute pathologies.
Discussion
This is the first work in which the clinical applicability and diagnostic capacity of a methodology based on the Zipf-Mandelbrot law is corroborated, through a blind study with 50 normal cardiac and pathological dynamics, from which the degree of complexity of cardiac systems was determined by the statistical fractal dimension, obtaining objective and reproducible results, and reaching the maximum values of sensitivity and specificity. With the analysis of the hierarchical order of the cardiac frequencies it was possible to observe a hyperbolic behavior of the same, evidencing the self-organization of the cardiac system and indicating that the complexity of said system is inversely proportional to the degree of aggravation of the dynamics.
Previously, the greater degree of complexity of the normal versus the pathological dynamics was evidenced and the mathematical values that are associated with exacerbation were established,28 which was confirmed in the present investigation.
From the perspective within which the presented method is framed, other investigations have been developed, giving rise to methodologies capable of differentiating normality, evolution and acute disease; such is the case of proportional entropy, a method that allows to establish high precision diagnoses.27 Also, an exponential mathematical law was developed that allowed the establishment of the totality of chaotic cardiac attractors and the realization of differentiations between normality, disease and evolutive states23,25 with greater precision compared to the methods developed for this purpose.16,17 Rodríguez and cols.29,30 used the theory of probability in order to develop a diagnostic methodology, whose clinical applicability was confirmed. The methodology based on the Zipf-Mandelbrot law, allows the evaluation of the degree of complexity of cardiac systems with clear numerical parameters, independent of causal variables. Its simplicity is highlighted, because by means of a single parameter the degree of complexity of cardiac dynamics is established and subsequently the mathematical diagnosis.
Goldberger et al.10 in the context of dynamic systems allowed the development of a new conception of normality and disease, according to which, the abnormality is associated with very regular or extremely random states, while normality is in the intermediate between these states. Huikuri and cols.,31 performed a characterization of cardiac behavior in patients with acute myocardial infarction and a decreased ejection fraction, establishing predictive mortality rates. However, more studies are required to confirm the applicability of this and other methods based on dynamic systems.32 The presented methodology follows this line of thought and also allows the quantification of cardiac dynamics based on the statistical fractal dimension, which differentiates between disease and normality. In the research carried out, the mathematical order underlying the phenomenon was observed and it was possible to establish mathematical diagnoses of cardiac systems regardless of causal, statistical or other considerations.
The law of Zipf-Mandelbrot has allowed studying biomedical phenomena. The degrees of complexity of the specific T repertoire were differentiated against the P9 allergen in an allergic patient, in the presence and absence of interferon α; likewise, in cell clones Th.33 In gynecology, a diagnostic method of fetal cardiac systems was developed based on the dynamic components of the system (CDS), by the law of Zipf-Mandelbrot,34 establishing clear differentiations between fetal cardiac systems, overcoming some limitations of the methods that are more frequently used in clinical practice.35
From this perspective, predictions of cardiac dynamics of neonates have been possible.23 Also, predictions have been made in infectology,36 immunology,37 in molecular biology,38 public health,39 arterial11 and cellular morphometry.40,41 Predictions of mortality in the ICU have been achieved,42 and diagnoses of cardiac dynamics of the adult have been made based on proportional entropy.26,27
Conclusion
The heart rates obey a hyperbolic mathematical self-organization.
Its evaluation by the Zipf-Mandelbrot law allows to establish differences between normality and acute disease, as confirmed by a blind study with 50 continuous Holter monitoring (20 normal and 30 with acute disease). The results showed that the degree of complexity decreases with the worsening of the cardiac dynamics, achieving objective and reproducible quantifications of cardiac status.











 nueva página del texto (beta)
nueva página del texto (beta)


