Introduction
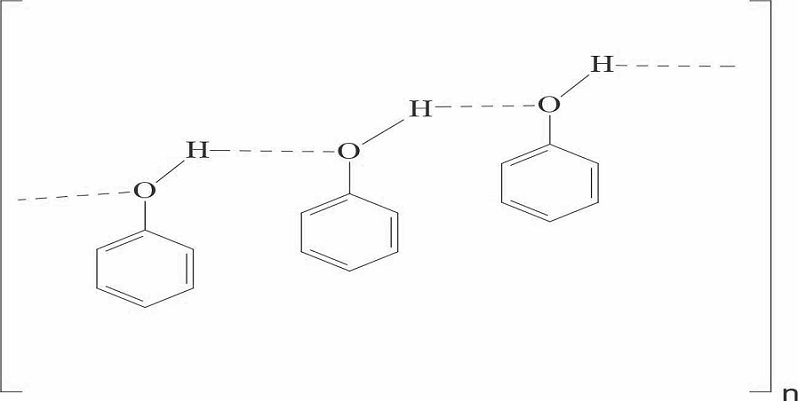
In polar covalent combinations a hydrogen atom tends to become electro-positive by allowing the other atom a greater pull on the shared electron pair. A situation of interest arises if in the surrounding molecules some strong centers of negative charge arise. Such negative charge centers tend to pull the partially positively charged or protonic hydrogen between them. The proton being extremely small, its existence between two other atoms, bring them so close together as if they were at more or less usual bond distance from each other. The distance between the atoms is slightly more than a covalent bond and such a bond is called hydrogen bond. Therefore a hydrogen bond is a kind of attractive interaction between polar molecules, in which hydrogen (H) is bound to a highly electronegative atom, such as nitrogen (N), oxygen (O) or fluorine (F). The name hydrogen bond is a kind of strong dipole-dipole attraction, and should not be mixed with a covalent bond [1]. Phenols, which contain a hydroxyl group, undergo hydrogen bonding in the liquid state, leading to association of molecules, which influences boiling point and surface tension. It is plausible that thiophenols, which do not include a hydroxyl group, would not undergo this association and that molecules would therefore behave as individual molecules in the liquid state. The present article seeks to explain the non-associative behavior of interactions in thiophenols based on surface tension data and the application of Trouton’s rule and linear free energy relationships.
Experimental Data Source
Data on surface tensions, other physical constants and thermo chemical quantities of thiophenols is from reference [2] and references cited therein. The Hammett σ+ and σ values are from the reference [3]. Linear correlations were done using the KaleidaGraph software, Reading, PA, USA.
Discussion
The effect of structure on the benzoic acid dissociative equilibriums (K a) and subsequently on chemical reactivity (k) is well explained by the putative Hammett equation. Based on the concept of this equation several hundreds of papers have emerged in chemical literature in the last century on the effect of structure on reactivity. It relates acid dissociative equilibria (K a) or the chemical reactivity (k) in meta- and para-substituted benzene derivatives in terms of two parameters, the reaction constant (ρ) and the substituent constant (σ). Thus the equation proposed by Hammett for acid dissociative equilibriums (K a) is
where K aX is the dissociation constant of substituted benzoic acid and K aH is that for the unsubstituted benzoic acid in water at 25oC, ρ is the reaction constant and σ is the substituent constant and for chemical reactivity (k), it is:
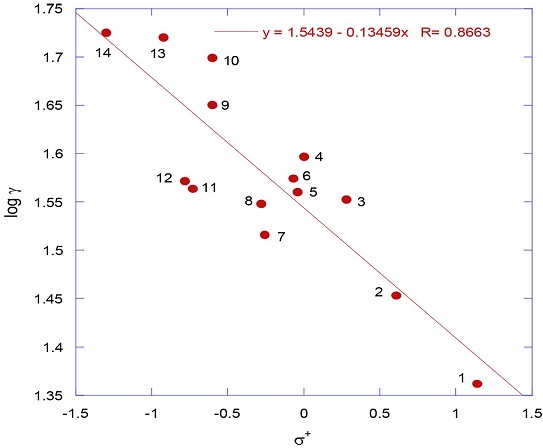
where k X is the rate constant for the substituted benzene derivative and k H is for unsubstituted benzene derivative. Application of Hammett equation to elucidate reaction mechanisms in organic chemistry is a frequently observed phenomenon [4-8]. Even there were Hammett correlations observed on semi-physical properties, for example, quantitative solubilitystructure relationships for several meta- and para- substituted benzoic acids in benzene and in cyclohexane [9] and in 1,4-dioxane and tetrahydrofuran (THF) [10], such kind of application of Hammett equation to pure physical properties like melting points and dipole moments of benzoic acids is a major breakthrough was reported from our laboratory [11]. In continuation of our earlier work on the application of Hammett equation to physical properties like surface tensions of aliphatic amines [12], phenols [13], and carboxylic acids [14] the present study is to search for the non-associative behavior of thiophenols. As a first observation, figure 1 shows the correlation of surface tensions with Hammett σ+ (R = 0.8663). Though the correlation is poor, observation of single straight line plot for all the substituents either electron withdrawing or electron donating unlike in the case of phenols [13] the trend is certainly unmistakable.
The numbers in the figure 1 represent the substituents in the thiophenols (table 1). The linearity in the surface tensions with Hammett σ+ in thiophenols unlike in the case phenols [13] is a clear indication of the non-associative behavior of thiophenols and they exist as individual ideal single molecules either in liquid phase or in gas phase.
Table 1 Physicochemical data of thiophenols (XC6H4SH)a
| Sl. No. | X | σ+ (b) | σ(b) | γ (Dyn/ cm) | Ha | Hd | Had | BPc oC | ∆HV kJ mol-1 | ∆SV J(K. mol)-1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3,5-di-CF3 | 1.14 | 0.92 | 23.0 | 0 | 0 | 0 | 167 (97)d | 38.7 | 88.0 |
| 2 | 4-CF3 | 0.61 | 0.53 | 28.4 | 0 | 0 | 0 | 179 (71)e | 39.8 | 88.1 |
| 3 | 3,4-di-F | 0.28 | 0.49 | 35.7 | 0 | 0 | 0 | 165 (85)f | 38.5 | 87.9 |
| 4 | H | 0.00 | 0.00 | 39.5 (30.7) | 0 | 0 | 0 | 169 (181)c | 39.9 | 90.3 |
| 5 | 4-n-Butyl | -0.04 | -0.16 | 36.3 | 0 | 0 | 0 | 249 (245)g | 46.7 | 89.5 |
| 6 | 4-F | -0.07 | 0.15 | 37.5 | 0 | 0 | 0 | 162 (185)c | 38.2 | 88.1 |
| 7 | 4-t-Bu | -0.256 | -0.15 | 32.8 | 0 | 0 | 0 | 230 (236)c | 44.8 | 93.5 |
| 8 | 4-i-Propyl | -0.28 | -0.15 | 35.3 | 0 | 0 | 0 | 215 (212)c | 43.3 | 88.7 |
| 9 | 4-SMe | -0.60 | 0.00 | 44.7 | 0 | 0 | 0 | 253 (153)c,h | 47.0 | 89.4 |
| 10 | 4-CH3CONH | -0.60 | -0.15 | 50.0 | 2 | 1 | 3 | 367 (388)i | 61.4 | 95.9 |
| 11 | 3,4-di-MeO | -0.73 | -0.18 | 36.6 | 2 | 0 | 2 | 263 (330)g | 48.1 | 89.7 |
| 12 | 3-EtO | -0.78 | -0.24 | 37.3 | 1 | 0 | 1 | 241 (244)j | 45.8 | 89.1 |
| 13 | 4-OH | -0.92 | -0.37 | 53 | 1 | 1 | 2 | 256 (285)g | 51.4 | 97.2 |
| 14 | 4-NH2 | -1.30 | -0.66 | 53.1 | 1 | 2 | 3 | 262 (284)g,k | 50.0 | 87.8 |
bJ. E. Leffler and E. Grunwald, Rates and Equilibriums of Organic Reactions, Wiley, 1963 (Dover reprint)cSource Aldrich Chemical catalog, and the values in the parenthesis are for corresponding phenols. dAt 50mmHg. eAt 8mmHg (source chem. spider). f At 20mmHg, gSource chem. spider. c,hAt 20mmHg. iSource chemicalbook.com. jOf 3-MeO-phenol, from this value one can conclude that the BP of 3-EtO-phenol would be even more. The BP of 3-EtO-phenol is not available in literature. kDecomposes
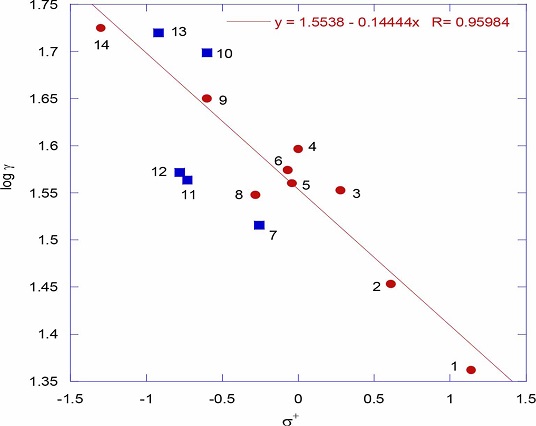
Trouton’s rule: ∆Sv data of thiophenols is presented in table 1. Trouton’s rule is of interest in the context of latent heats of vaporization of liquids. It is an empirical rule based on heats of vaporization of a large number of normal liquids at their boiling points. According to this rule the entropy of vaporization is almost the same value, about 85-88 J K−1 mol−1, for various kinds of liquids at their boiling points [15]. In fact for all the thiophenols the ∆Sv values are in this range indicating that thiophenols exist as normal ideal molecules (table 1). However abnormal values of Troutons’ rule constant suggest abnormal entropy changes during vaporization of concerned liquids. If the Troutons’ rule constant for a liquid is more than the limit of 85-88 J K−1 mol−1 it suggests association of molecules in the liquid form. And if it is less than the limit of 85-88 J K−1 mol−1 it suggests association of molecules in the gaseous form. In fact in the present work the ∆Sv values of two electron donating substituented thiophenols like 4-aceylaminothiophenol and 4-hydroxythiophenol are greater than the limit of 85-88 J K−1 mol−1 suggesting that these two thiophenols may exist in associated form in the liquid state. And less than the limit of 85-88 J K−1 mol−1 for 4-aminothiophenol suggest that this thiophenol can even exist as associated molecule in the gaseous state. These associations are mainly due to intermolecular hydrogen bonding. This is clearly reflected on the total proton acceptor and donor (Had) values of these phenols. However if thiophenols with the substituents having high Had values and with higher ∆Sv values are eliminated from the Hammett plot, the correlation has improved a lot (figure 2, r = 0.9598) which is a strong indication that the remaining thiophenols certainly exist as single ideal molecules.
Eötvös [16] had suggested the following equation (eqn. 3) that explains the effect of temperature on surface tension (γ):
Where ‘M’ is the molecular weight of the liquid, ‘rl’ is the density, ‘tc’ is the critical temperature,‘t’ is temperature and ‘k’ is the Eötvös constant. For most liquids ‘k’ works out to be about 2.12 in the cgs system. Such liquids are considered to be normal liquids and they have identical molecules in all the three states. When smaller values than 2.12 are obtained for ‘k’, as in the case of water and alcohols, it is considered to be due to an association of molecules in the liquid state, generally through hydrogen bonding [17]. If higher values than 2.12 are obtained for ‘k’, as in the case of benzene and its alkyl derivatives, it is considered to be non-association of such kind of liquids [17]. The obvious indication is that benzene and its alkyl derivatives don’t have any hydroxyl groups through which those liquids to be associated via hydrogen bonding [17].
The effect of temperature on surface tension data is available only for thiophenol [17]. Either the effect of temperature on surface tension data for other thiophenols might have not been reported or our attempts might have failed in finding them from the literature. In the present work the value of ‘k’ for thiophenol works out to be 2.64. Using this value which is related to order of association ‘x’ by the following equation (eqn. 4) [13]
and ‘x’ works out to be 0.68. This indicates that 0.68 molecules are associating to form an associated molecule which is not possible. For association at least two molecules are needed. This is yet another indication that thiophenols exist as normal single ideal molecules.
Significance of boiling points: It is noteworthy about the importance of boiling points here. From the table it is clear that the boiling points of thiophenols are less than the corresponding phenols. This certainly indicates that the strong hydrogen bonding exists in phenols and no such type of hydrogen bonding is expected in thiophenols. Therefore thiophenols are considered to be non-associative liquids.
Conclusions
Phenols, which contain a hydroxyl group, undergo hydrogen bonding in the liquid state, leading to association of molecules as shown below in scheme 1:
Whereas thiophenols do not contain a hydroxyl group cannot undergo hydrogen bonding. This is further supported on the basis of the ∆SV values, smaller boiling points of thiophenols than those of phenols, the single line Hammett correlation and successful application of Ramsey-Shields-Eötvös Equation. Therefore thiophenols are assumed to exist as normal liquids.











 text new page (beta)
text new page (beta)