Introducción
Las proteínas son centrales para todos los seres vivos, desde las bacterias hasta las ballenas, pasando por las plantas y los hongos, todos utilizan proteínas. Las proteínas hacen de todo. A estas biomoléculas se les conoce como las máquinas de la vida porque cumplen diversas funciones cruciales para todos los organismos vivos. Muchas de ellas realizan una función enzimática, actuando como biocatalizadores de las reacciones químicas del metabolismo celular; algunos grupos de proteínas tiene funciones de defensa, por ejemplo, los anticuerpos reconocen moléculas ajenas, mientras que la trombina y el fibrinógeno, contribuyen a la formación de coágulos sanguíneos para evitar hemorragias; otras son hormonas, como la insulina y el glucagón, que regulan los niveles de glucosa en la sangre. Las proteínas también pueden tener funciones estructurales, como ciertas glucoproteínas que forman parte de las membranas celulares y actúan como receptores o facilitan la entrada de sustancias a la célula, o la fibroina que las arañas y los gusanos de seda segregan para fabricar sus telas y capullos, respectivamente. Están asimismo las que se dedican al transporte, como la hemoglobina que acarrea el oxígeno y las lipoproteínas que trasladan lípidos, ambas por la sangre. Las hay cuya función es la transducción de señales, como ocurre en el proceso de la visión: la proteína rodopsina que está en la retina, convierte o transduce un fotón luminoso -una señal física- a un impulso nervioso -una señal eléctrica-, el cual gracias a un receptor hormonal se convierte en una señal química que, finalmente, desata los procesos que ocurren en el cerebro para completar el proceso que llamamos “ver”. La proteína más abundante en nuestro planeta es la enzima ribulosa bifosfato carboxilasa, encargada de “fijar” el CO2 atmosférico en las plantas.
Las proteínas son polímeros naturales lineales formados por L-aminoácidos (aa), los cuales contienen un carbono (llamado Cα) unido a tres sustituyentes comunes: un grupo carboxilo, un grupo amino, y un átomo de Hidrógeno. El cuarto sustituyente del Cα es llamado “cadena lateral”. La mayor parte de las proteínas utilizan 20 aminoácidos diferentes, cuya cadena lateral presenta componentes químicos con variedad de formas, volúmenes y propiedades fisicoquímicas. Los L-aminoácidos se encuentran unidos en las proteínas mediante un enlace peptídico, el cual se forma de la condensación del grupo carboxilo de un aminoácido con el grupo amino de otro. Existen cuatro niveles de estructura que describen a las proteínas. El primero es la “estructura primaria”, esto es, la secuencia u orden en el cual están unidos los aminoácidos, también denominados “residuos” una vez incorporados a la cadena polipeptídica. El segundo nivel es la “estructura secundaria”, dada por el arreglo espacial local de la cadena, la cual puede adoptar conformaciones repetitivas como las hélices alfa y las hebras beta; o no repetitivas, como vueltas y giros de conformación definida, que se denominan asas. Los elementos de estructura secundaria se pliegan u organizan espacialmente para formar la “estructura terciaria”, como ilustra la Figura 1. Por último, las proteínas pueden presentar “estructura cuaternaria” cuando su estado nativo requiere de más de una cadena polipeptídica (dímeros, trímeros, etcétera). Todas las proteínas, sin importar cuál sea su papel específico, realizan su función cuando están en su estructura nativa, una disposición espacial de los átomos de la biomolécula que puede conocerse a través de experimentos de difracción de rayos X, de Resonancia Magnética Nuclear o de Criomicroscopía electrónica. Algunas proteínas se encuentran la mayor parte del tiempo en el estado nativo, pero otras lo adquieren únicamente cuando interactúan con otra molécula. En cualquier caso, una condición necesaria para que una proteína lleve a cabo su función es que su estructura nativa sea estable a las condiciones del entorno en las que se encuentre (pH, fuerza iónica, temperatura).
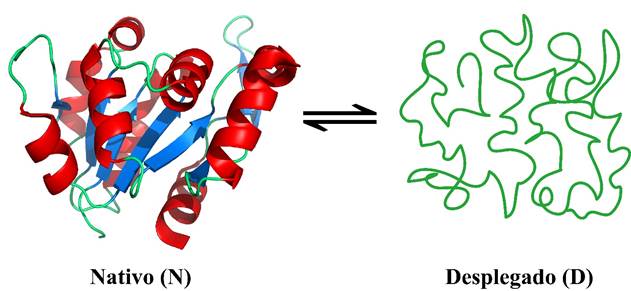
Figura 1 Estructura terciaria de una proteína en el estado nativo (N) donde se muestran las hélices alfa en rojo, las hebras beta en azul y las asas en verde. En el estado desplegado (D) coexisten un gran número de conformaciones inactivas. El proceso de N a D se conoce como desplegamiento o desnaturalización y el proceso de D a N como plegamiento.
El estudio de los determinantes de la estabilidad de las proteínas es de importancia para profundizar en muchos aspectos de las teorías evolutivas, realizar el diseño de novo de proteínas nuevas con propiedades nuevas y útiles, y aumentar nuestro conocimiento de los orígenes moleculares de muchas enfermedades: la pérdida de la estructura nativa de una proteína puede provocar la formación de agregados amorfos y de fibras amiloides, que traen como resultado condiciones patológicas tales como la fibrosis cística, las enfermedades de Alzheimer, de Parkinson y de Huntington, la diabetes tipo 2. En este contexto, en el ámbito biotecnológico resulta crucial entender a fondo la estabilidad de las proteínas, para entonces poder diseñar fármacos que mantengan su estabilidad, inhibiendo o impidiendo su agregación.
La estabilidad de las proteínas tiene tanto aspectos termodinámicos como aspectos cinéticos. La estabilidad cinética es un concepto que está ligado al tiempo promedio en que una proteína mantiene su estructura y su función bajo ciertas condiciones. Cuando una proteína permanece en el estado nativo funcional por un período de tiempo largo que le permite llevar a cabo su función, se dice que es cinéticamente estable. Por otra parte, la estabilidad termodinámica se refiere a las condiciones a las cuales un proceso cumple con el criterio termodinámico de espontaneidad. El proceso por el cual la cadena polipeptídica de una proteína alcanza la estructura nativa se denomina plegamiento, y es uno de los ejemplos más fascinantes y complejos de auto-ensamblaje molecular. Con frecuencia, en los laboratorios de investigación se estudia experimentalmente el proceso inverso al plegamiento, conocido como desplegamiento o desnaturalización (Figura 1). Durante el proceso de desplegamiento pueden aparecer conformaciones intermediarias (I) estables, las cuales presentan características estructurales diferentes a las observadas en los estados nativo y desnaturalizado. El estado desplegado no corresponde a una estructura única sino que está compuesto por un gran número de conformaciones inactivas que colectivamente son llamadas “el estado desnaturalizado”. Los procesos de plegamiento o de desplegamiento de una proteína conllevan la formación o ruptura, respectivamente, de numerosas interacciones débiles (no covalentes), y están caracterizados por un cambio en la energía libre de Gibbs de la proteína al pasar del estado inicial al final. Esta diferencia de energía entre el estado nativo (N) y otras conformaciones intermediarias (I) o desnaturalizadas (D) permite analizar y conocer la estabilidad termodinámica de la proteína.
El objetivo de este trabajo consiste en presentar y discutir los aspectos fundamentales de la estabilidad termodinámica de las proteínas, haciendo énfasis en su caracterización experimental utilizando la calorimetría diferencial de barrido. Se pretende también proporcionar al docente de asignaturas tales como bioquímica, química y termodinámica, la información básica y algunas herramientas prácticas que faciliten ejemplificar varios temas en esas asignaturas. En este contexto, acompañamos este trabajo de una Hoja Didáctica que propone algunas actividades que los docentes pueden emplear con sus estudiantes.
La curva de estabilidad termodinámica
La termodinámica proporciona un criterio claro para determinar si un proceso es o no espontáneo: si el cambio de energía libre de Gibbs es negativo (ΔG < 0), el proceso ocurre de manera espontánea. Una proteína es termodinámicamente estable cuando el cambio de energía libre de Gibbs para el proceso de desnaturalización es positivo y por tanto, desfavorable (cuando el estado incial es el nativo, ΔG = G final - G inicial = G D - G N). Aquí se ha supuesto que la proteína sólo puede estar en dos estados (N y D), sin que existan estados intermediarios significativamente poblados. Cuando para una proteína se cumple que ΔG > 0 a ciertas condiciones de temperatura, presión, concentración y pH se dice que esta proteína es termodinámicamente estable. El andamiaje teórico de la termodinámica clásica proporciona una ecuación para calcular la dependencia del ΔG con la temperatura (ΔG(T)) manteniendo la presión constante (Kumar, Tsai y Nussinov, 2001):
donde ΔH y ΔC p son los cambios de entalpía y de capacidad calorífica a presión constante para el proceso de desnaturalización (N ( D) y T m es la temperatura de referencia, en la cual la concentración de N y D es la misma (por lo tanto, ΔG(T m ) = 0 a la T m ). A la representación gráfica de ΔG v.s. T empleando la Eq. (1), se le conoce como curva de estabilidad termodinámica. La Figura 2 muestra esta curva para dos proteínas diferentes. Para una proteína dada, la curva de estabilidad termodinámica varía en función de las condiciones (pH, solución amortiguadora) del medio en el que se encuentra. Mas importante aun es que la curva de estabilidad en la Figura 2 es diferente para cada proteína, y puede considerarse como una suerte de “huella termodinámica” que la distingue de todas las demás.
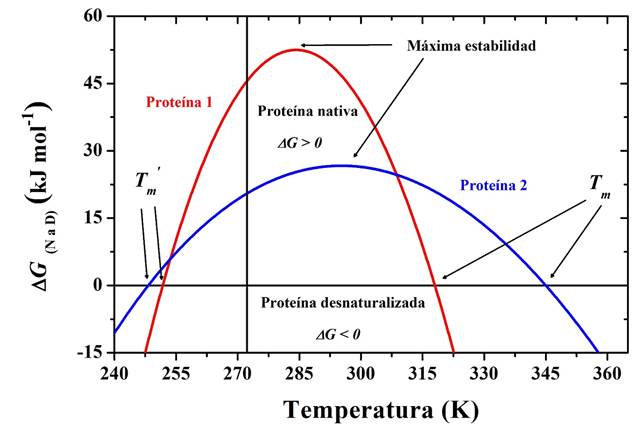
Figura 2 Curvas de estabilidad para dos proteínas. Esta curva se obtiene empleando la Eq. (1) con los valores de (H, (Cp y Tm obtenidos de experimentos de Calorimetría Diferencial de Barrido (ver texto).
La curva de estabilidad en la Figura 2 delimita el rango de temperatura en el cual el estado nativo es estable; esto ocurre a las temperaturas donde ΔG > 0 y por tanto la desnaturalización es no espontánea. La temperatura a la cual el valor de (G es máximo se conoce como la temperatura de máxima estabilidad. Fuera de ese intervalo ΔG < 0, la desnaturalización es espontánea y el estado estable es el desnaturalizado D. La Figura 2 también muestra que hay dos temperaturas (T m y T m ’) a las cuales ΔG = 0. Coloquialmente, la T m se conoce como la temperatura de desnaturalización “por calor”, mientras que T m ’ representa la temperatura de desnaturalización “por frío”. Es importante aclarar que, como se verá más adelante, las proteínas no se desnaturalizan a una sola temperatura sino en un intervalo de temperaturas. Para la mayor parte de las proteínas no es posible medir experimentalmente su T m ’ ya que esta es menor a la temperatura de congelación del medio acuoso (aproximadamente 273.15 K).
La termodinámica nos proporciona una visión global macroscópica del comportamiento de las proteínas en cuanto a su estabilidad (Figura 2). Si, por otro lado, deseamos tener una visión a nivel microscópico de los eventos que ocurren durante el proceso de desnaturalización o de plegamiento es necesario recurrir al empleo de modelos que consideren las interacciones que se rompen o se forman durante dichos procesos. Estos modelos pueden ser empíricos o bien basados en la termodinámica o física estadística. Las interacciones inter-atómicas que mantienen estable al estado na tivo en el medio acuoso son interacciones débiles. Se llaman así para distinguirlas de los enlaces covalentes entre átomos, que son mucho más energéticos. Estas interacciones pueden romperse o establecerse con gran facilidad y son de varios tipos: puentes de hidrógeno, interacciones entre iones, interacciones hidrofóbicas y fuerzas de van der Waals. Es de hacerse notar que el hecho experimental de que una proteína pueda desnaturalizarse calentando o enfriando es un reto importante para el desarrollo de dichos modelos, ya que un modelo exitoso debe ser capaz de explicar ambas, la desnaturalización en caliente y en frío.
Cada conformación que la proteína puede adoptar tiene asociada una energía determinada; al conjunto de las energías correspondientes a todas las conformaciones posibles se le conoce como paisaje energético. Con base en diversos estudios teóricos y experimentales se propone que el paisaje energético de las proteínas tiene forma de embudo, donde el estado desnaturalizado se compone de un gran conjunto de conformaciones de alta energía y entropía. El espacio conformacional se reduce conforme la proteína se acerca al estado de menor energía (nativo) en el fondo del embudo (Figura 3). Como ya se ha señalado, dado que el plegamiento de las proteínas es central para el adecuado funcionamiento de las células, existe una maquinaria celular que “guía” a las proteínas hacia el estado nativo (Dobson, 2003). Sin embargo, en muchos casos el plegamiento ocurre in vitro, sin la ayuda de otro componente en el sistema, lo que ilustra que se trata de un fenómeno fisicoquímico, gobernado por las diferencias en energía y las barreras cinéticas entre los estados conformacionales que adopta la cadena polipeptídica en su ruta hacia el estado nativo, como propone el modelo del embudo multiestado-energético (Figura 3) (Dill, 1990; Dill y Chan, 1997; Goodsell y Olson, 2000).
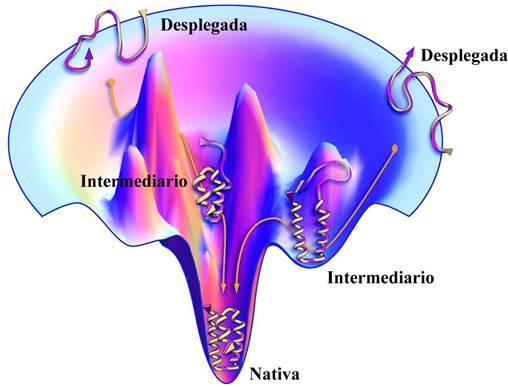
Figura 3 Modelo del embudo para el plegamiento de una proteína. Modificado de Dill y MacCallum, 2012.
La calorimetría diferencial de barrido en el estudio del desplegamiento de proteínas.
Gracias a los avances tecnológicos, las pequeñas cantidades de energía invo lucradas en la formación o ruptura de interacciones débiles que ocurren durante el plegamiento o la desnaturalización pueden medirse empleando la Calorimetría Diferencial de Barrido (CDB o DSC en inglés). A la fecha, estos equipos tienen una precisión a nivel de microjoules (µJ) y emplean cantidades de muestra pequeñas (menos de 100 (g), y siguen desarrollándose para mejorar aun más estas dos características.
La Figura 4 muestra esquemáticamente los elementos fundamentales de un calorímetro diferencial de barrido. Contiene dos celdas idénticas (material, peso, volumen) colocadas dentro de una chaqueta adiabática que las aísla del exterior, evitando así la pér dida o ganancia de energía desde el entorno. En un experimento de CDB, la celda de trabajo contiene la proteína disuelta en un cierto medio (normalmente, una solución amortiguadora) mientras que en la de referencia se coloca ese mismo medio sin proteína; como se explicará más adelante, es necesario también hacer un experimento donde ambas celdas están llenas con esa misma solución amortiguadora. El calorímetro establece una diferencia de temperatura (ΔT) muy pequeña entre las dos celdas. Ambas celdas son entonces simultáneamente calentadas a la misma velocidad (conocida como velocidad de barrido) y, como son idénticas, el ΔT es el mismo a toda temperatura hasta que ocurre algún evento que absorbe o libera energía en la celda de trabajo. Este evento es la desnaturalización de la proteína que, al ocurrir, altera el valor de ΔT. Los circuitos de retroalimentación y los calentadores del calorímetro proporcionan a la celda de trabajo la cantidad de energía necesaria para restablecer el ΔT a su valor original. Esa cantidad de energía, que es registrada por el equipo, es igual a la energía absorbida por la proteína al pasar del estado nativo al desplegado.
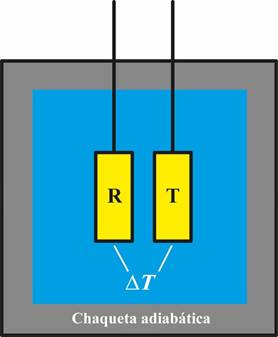
Figura 4 Ilustración esquemática de un Calorímetro Diferencial de Barrido (CDB). Consta de dos celdas idénti cas, la de trabajo T que contiene la muestra de interés y la de referencia R. ΔT es la diferencia de temperatura entre las dos celdas.
La energía que suministra el instrumento a la celda de trabajo para restablecer el ΔT original se realiza aplicando una corriente eléctrica (I) a un voltaje constante (V). Es decir, el equipo aplica una potencia eléctrica (P) que es igual al producto de V e I (P = VI) y cuyas unidades son watts. Dado que 1 watt = 1 Joule/s (energía/tiempo), al dividir P entre la velocidad de calentamiento o barrido empleada en el experimento (dT/dt, donde T = temperatura y t = tiempo) se obtiene que dicho cociente (P/(dT/dt)) tiene unidades de energía/grado. Estas son las unidades (J/K o cal/K) de la propiedad extensiva llamada capacidad calorífica. Al dividir entre el numero de moles de la proteína presente en la celda, se obtiene la capacidad calorífica molar (con unidades de J/K mol o cal/K mol) que es una propiedad intensiva. Dado que el experimento se realiza a presión constante, el experimento de CDB proporciona el C P del sistema, es decir de la proteína disuelta en la solución amortiguadora. En resumen, un equipo de CDB mide el C P como función de la temperatura. Es de hacer notar que los equipos de CDB modernos son capaces de emplear desde veloci dades de barrido muy lentas (10 grados cada hora) hasta muy rápidas (250 grados cada hora), y operan aplicando una presión ligera (entre 3 y 4 atm) a ambas celdas. Esta presurización de los líquidos contenidos en las celdas se logra utilizando un gas (normalmente, nitrógeno), aumentando con ello el punto de ebullición de dichos líquidos. Dado que el contenido de las celdas es básicamente agua, y que el punto de ebullición de esta es de aproximadamente 130 °C a 4 atm de presión, esta presurización permite que la temperatura más elevada a la que puede calentarse la muestra (permaneciendo en el estado líquido) sea de 125 °C. Esta forma de operación ha permitido estudiar proteínas que se desnaturalizan a temperaturas superiores al punto de ebullición normal del agua (100 °C a 1 atm de presión, 92 °C a la presión en la Ciudad de México). Así, en el CDB se determina el C P a una presión ligeramente mayor a la atmosférica. Sin embargo, como la variación del C P con presión es despreciable (dC P /dP ( 0) (Gyftopoulos y Beretta, 2015) los datos obtenidos de un CDB son prácticamente los correspondientes a presión atmosférica. De hecho, la desnaturalización de proteínas puede provocarse aplicando presión a temperatura constante, pero es necesario someterlas a presiones muy elevadas (mayores a 4000 atm) (Gross y Jaenicke, 1994)
Análisis de los datos calorimétricos y obtención de la “huella termodinámica”
La Figura 5A muestra el resultado de un experimento realizado en un CDB para una proteína. A esta representación gráfica de la capacidad calorífica a presión constante C P como función de la temperatura T se le conoce como traza calorimétrica. Como la estruc tura nativa de cada proteína es distinta, la traza calorimétrica de cada una de ellas es diferente. Para una misma proteína, la traza calorimétrica es también diferente de acuerdo a las condiciones experimentales en las que se encuentra la macromolécula (pH, solución amortiguadora). Dado que, como se discutirá a continuación, de la información proporcionada por la traza calorimétrica de una proteína puede construirse su curva de estabilidad termodinámica (Figura 2), la información termodinámica obtenida de la primera y expresada en la segunda son una especie de huella, exclusiva para ella y que la distingue de todas las demás proteínas, de la misma manera que las huellas digitales de cada ser humano son exclusivas.
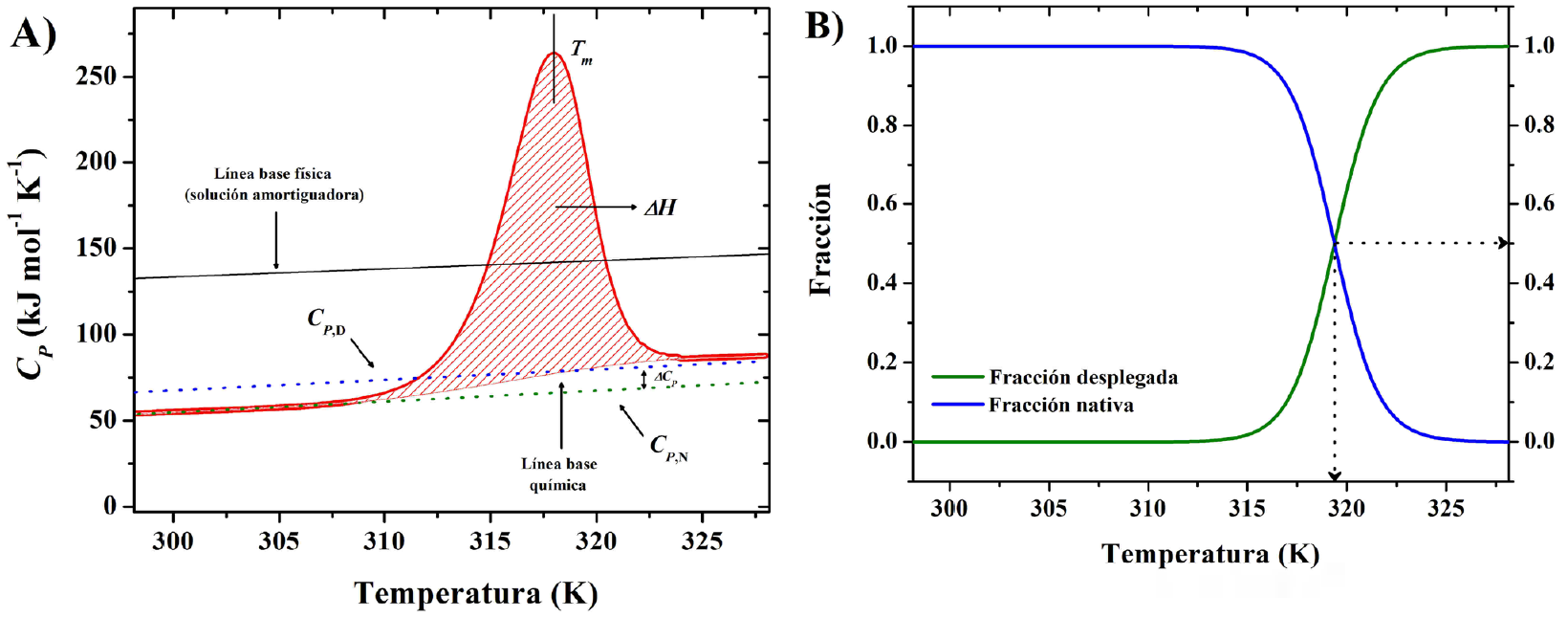
Figura 5 A) Ejemplo de una traza calorimétrica para una proteína en solución. B) Fracciones mol de proteína en los estados nativo y desplegado; a la temperatura Tm, [N] = [D] = 0.5
La traza calorimétrica en la Figura 5A es debida a la cantidad de energía absorbida por la proteína al ocurrir la transición del estado nativo al desplegado o desnaturalizado. La capacidad calorífica de la solución amortiguadora se obtiene en un experimento donde ambas celdas están llenas con esa solución. La Figura 5A muestra esta traza “amortiguador-amortiguador” que es conocida como la línea base física o instrumental que, con el fin de corregir distorsiones instrumentales, debe ser restada de la traza obtenida cuando la celda de trabajo contiene a la proteína. Los valores de C P en la pre-transición y post-transición son las capacidades caloríficas de los estados nativo (C P,N ) y desplegado de la proteína (C P,D ). La diferencia entre estos valores es el cambio en la capacidad calorífica (∆C P = C P,D - C P,N ) para la desnaturalización. Es importante notar que el C P del agua es mayor que la de la proteína en cualquiera de su estados, por lo que la línea base física tiene un valor mayor que C P,D y C P,N. En la Figura 5A se muestra también la llamada línea base química que se obtiene al conectar los estados nativo y desnaturalizado. Dado que d∆H/dT = C P , esta línea delimita el área bajo la curva que es el cambio en la entalpía (∆H) asociado a la desnaturalización proteica. Como ∆H > 0 a la traza calorimétrica también se le conoce como la endoterma. Finalmente, la temperatura a la cual el C p es un máximo se denota como T m . Como se explicó en el contexto de la curva de estabilidad, si la transición ocurre sólo entre dos estados (N y D), es decir sin intermediarios estables significativamente poblados, a esta temperatura la concentración de proteínas en el estado nativo es igual a la concentración de proteínas desplegadas ([N] = [D]). Por esta razón, se nombra como “T m ” a la temperatura media de desnaturalización. Es importante notar que la transición del estado nativo al estado desnaturalizado no ocurre sólo a la temperatura T m sino que acontece en un rango de temperaturas. La Figura 5B muestra que a largo de la endoterma, es decir a cada temperatura, la concentración relativa de N y D es diferente: a T < T m [N] > [D] y cuando T > T m [N] < [D]. La magnitud de este rango está ligado a la cooperatividad de la transición: entre más pequeño sea este intervalo (una endoterma estrecha) la cooperatividad es mayor. La cooperatividad está relacionada con que tan abrupto es el cambio entre los estados nativo y desnaturalizado, sin la presencia de intermediarios.
Los experimentos de CDB como los mostrados en la Figura 5A proporcionan los valores de T m , ∆H y (C P que, empleando la Eq. (1), permiten generar la curva de estabilidad termodinámica de la proteína (Figura 2) a las condiciones de pH y el tipo y concentración de la solución amortiguadora que se hayan empleado. Para lograr esto de manera correcta, en la práctica es necesario tomar ciertas precauciones y también considerar las limitaciones de la Eq. (1). La más importante de las precauciones es no emplear una sola traza calorimétrica para obtener ∆C P . Dado que ∆C P = C P,D - C P,N es una cantidad de magnitud pequeña que se obtiene ajustando líneas rectas en la regiones de la pre- y la post-transición, es susceptible a errores considerables. Por ello, es altamente recomendable realizar experimentos de CDB usando distintas concentraciones de proteína y promediar los valores de (C P obtenidos en cada uno de los experimentos. Otra manera de obtener ∆C P se basa en el hecho de que ∆C P = ((∆H/(T) P . Como se mencionó anteriormente, al alterar las condiciones del solvente se modifica la huella termodinámica, por lo tanto, al obtener endotermas de la proteína en soluciones con diferente pH, es posible graficar los valores de ∆H y T m y obtener el ∆C P como la pendiente de la recta ajustada a los datos (Privalov, 1979). Esta alternativa es válida solamente si la variación en el pH no modifica significativamente las propiedades del estado nativo.
Por otra parte, hay tres limitaciones importantes al uso de la Eq. (1). La primera es que ésta es válida sólo cuando el proceso de desnaturalización es reversible (N ⇌ D), es decir cuando al enfriar la proteína desplegada ésta es capaz de regresar al estado nativo. Experimentalmente, la reversibilidad debe comprobarse en el CDB realizando un segundo barrido a la misma muestra después de haber sido enfriada: si la traza obtenida en el segundo barrido es igual a la obtenida en el primero, la transición es reversible, pero si no lo hace (muy común en proteínas mayores a 100 aminoácidos) la desnaturalización es irreversible. Aunque estrictamente no sea apropiado, típicamente en la literatura se considera que la desnaturalización es reversible si en el segundo barrido el área bajo la endoterma es al menos el 90% del área obtenida en el primer barrido. La irreversibilidad de la transición es debida a que las proteínas desplegadas tienen una gran tendencia a agregarse o aglutinarse formando estructuras donde las cadenas están “enredadas” y, al enfriarse, son incapaces de regresar a la estructura nativa. Otra manera de ver esta limitación es considerar que si la transición es irreversible el ∆H obtenido en el experimento de CDB tiene, al menos, dos contribuciones: la debida a la desnaturalización propiamente dicha y la debida a la formación de los agregados proteicos. Como somos incapaces de evaluar experimentalmente o de calcular esta última contribución, es erróneo emplear ese ∆H en la Eq. (1). La segunda limitación surge del hecho de que la Eq. (1) pertenece al ámbito de la termodinámica clásica, donde se asume que el sistema viaja del estado inicial al final a través de un conjunto de estados en equilibrio; es decir, en la Figura 5 se asume que el estado nativo y el desnaturalizado de la proteína están en equilibrio a toda temperatura. Sin embargo, la desnaturalización puede ser un fenómeno dominado por la cinética del proceso. Esto debe comprobarse en el CDB realizando barridos a diferentes velocidades de calentamiento. Si la traza calorimétrica es la misma a todas las velocidades de barrido los efectos cinéticos son despreciables o no existen, y la Eq. (1) es aplicable. En contraste, si la traza varía, es decir el valor de T m es mayor a mayor velocidad de calentamiento, la desnaturalización está cinéticamente controlada. En este caso, las trazas calorimétricas pueden analizarse con un modelo cinético dando lugar al concepto y la evaluación de la llamada estabilidad cinética de las proteínas (Sanchez-Ruiz, 2010), un tema que está fuera del alcance este trabajo. La tercera limitación de la Eq. (1) es que ésta corresponde a una transición entre sólo dos estados (N y D). La presencia de nuevos estados, esto es, de intermediarios estables; puede generar endotermas no simétricas, con hombros o en las cuales se muestre más de un máximo. También puede ocurrir, que los intermediarios no sean evidentes en la endoterma. Por ello, para verificar el carácter de dos estados de la transición, es recomendable aplicar el “criterio calorimétrico”, el cual consiste en calcular el cociente del ∆H obtenido por CDB (∆H Cal ) y el ∆H calculado mediante la ecuación de van’t Hoff (∆H VH ). (∆H VH ) puede obtenerse aplicando dicha ecuación a los datos obtenidos por CDB o a los datos obtenidos mediante técnicas espectroscópicas como el dicroismo circular o la fluorescencia, que son sensibles a los cambios en la estructura secundaria o terciaria, respectivamente, que acompañan a la transición de N a D (Freire, 1989). Cuando no existen intermediarios estables en el desplegamiento inducido por temperatura ∆H Cal /∆H VH = 1. Cuando estos existen, su estudio detallado proporciona información sobre las características de dominios estables en el desplegamiento. En resumen, las limitaciones en el empleo de la Eq. (1) para obtener la curva de estabilidad de una proteína son que la desnaturalización sea (i) reversible, (ii) independiente de la velocidad de barrido y (iii) de dos estados. Por otra parte, es importante notar que mediante CDB se obtienen directamente los valores de ∆G (T) cercanos a la T m , por lo tanto, para tener una mayor certeza sobre los valores de ∆G en otras regiones de la curva de estabilidad (por ejemplo a temperatura ambiente o a 37 C, la temperatura fisiológica), es altamente recomendable obtener el valor de ∆G mediante experimentos de desnaturalización “química”, en los cuales la temperatura se mantiene constante y se utiliza como perturbante urea o cloruro de guanidina. En estos experimentos el valor de ∆G se determina mediante las técnicas espectroscópicas antes mencionadas (Pace, 1986).
La huella termodinámica de las proteínas se ve afectada por la presencia de las moléculas con las cuales interactuan, lo cual ocasiona en algunos casos rearreglos estructurales importantes. Es por ello que al estudiar el desplegamiento de proteínas en presencia de ligandos, es posible obtener información sobre los componentes entálpicos y entrópicos de dicha interacción y sobre el efecto de dichos ligandos en la estabilidad (Schellman, 1987).
Curvas de estabilidad termodinámica de barriles TIM
A partir del arreglo espacial de las hélices alfa y hebras beta, las proteínas pueden adoptar una gran variedad de conformaciones tridimensionales o topologías. Los primeros estudios de plegamiento se centraron en cinco proteínas estructuralmente muy diferentes que fueron utilizadas como modelo: el citocromo c, la mioglobina (ambas compuestas sólo por hélices alfa), la α-quimiotripsina (compuesta principalmente por hebras beta), la ribonucleasa y la lisozima (compuestas por hélices alfa y hebras beta) (Privalov y Khechinashvili, 1974). Dentro de las diferentes topologías existentes, la superfamilia de proteínas conocida como barriles TIM o barriles (β/α)8 es una de las más abundantes en la naturaleza (aproximadamente el 10% de todas las proteínas conocidas adquieren esta estructura). El plegamiento tipo barril TIM se muestra en la Figura 6. Consiste en un motivo β-asa-α-asa repetido ocho veces, con las ocho hebras beta localizadas al interior del barril, cubiertas por ocho hélices alfa en el exterior (Wierenga, 2001; Höcker, Schmidt y Sterner, 2002; Anantharaman, Aravind y Koonin, 2003). Las proteínas con estructura de barril TIM participan en una gran variedad de funciones celulares y reacciones metabólicas. La mayoría de ellas son enzimas y existen representantes en cinco de las seis clases de enzimas definidas por la comisión internacional de enzimas. (Wierenga, 2001; Nagano, Orengo y Thornton, 2002) Debido a su enorme variedad en funciones, a su origen evolutivo común y a su ubicuidad en distintos tipos de proteínas, el barril TIM es una topología de gran interés para su estudio fisicoquímico. Además, este tipo de estructura representa un andamiaje muy estable para el diseño e ingeniería de proteínas, con numerosas aplicaciones en los campos de la biología sintética, diagnóstico e imagenología (Currin, Swainston, Day y Kell, 2015).
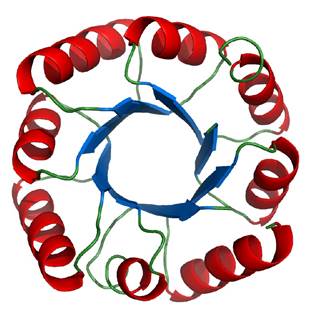
Figura 6 Plegamiento tipo barril TIM. Se muestran las hélices alfa en rojo, las hebras beta en azul y las asas en verde.
Las proteínas con topología de barril TIM han sido ampliamente estudiadas. Sin embargo, debido a la irreversibilidad en el proceso de desplegamiento térmico que sucede en la mayoría de ellas, las curvas de estabilidad sólo han podido determinarse para menos de una decena. Estas curvas para barriles TIM (cuatro triosafosfato isomeras de bacterias y cuatro α-amilasas de diversos organismos) se muestran en la Figura 7B y los valores de T m , ∆H y ∆C P que, empleando la Eq. (1), permiten generar la curva de estabilidad termodinámica, se reportan en la Tabla 1. Estas “huellas termodinámicas” son útiles para entender los cambios en la estabilidad termodinámica de las proteínas. En general, para este fin se siguen tres estrategias: (1) comparar proteínas con diferentes topologías para encontrar los elementos comunes entre éstas que determinan su estabilidad (Figura 7A y Tabla 1), (2) comparar una misma proteína pero proveniente de organismos diferentes; estos estudios se enfocan en comparar los cambios en las proteína que han ocurrido a lo largo de la evolución y bajo la presión de selección distinta que sufre cada organismo (Figura 7B y Tabla 1) y (3) utilizar mutagénesis dirigida en una proteína particular para ver los efectos de los cambios de residuos en posiciones específicas sobre la estabilidad global de la proteína. Todos estos procedimientos exigen determinar las curvas de estabilidad realizando experimentos de desplegamiento con temperatura empleando, como una valiosa primera opción, la calorimetría diferencial de barrido.
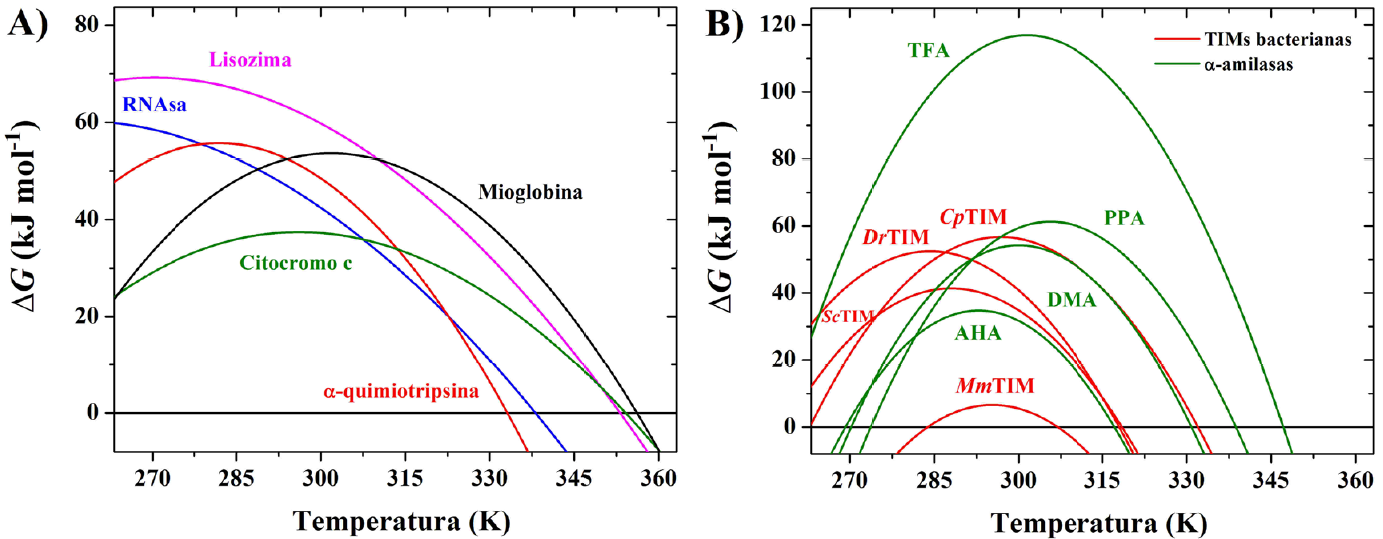
Figura 7 Curvas de estabilidad de diversas proteínas. A) Proteínas con diversas topologías. B) Proteínas con topología de barril TIM. La identidad de cada proteína se proporciona en la Tabla 1.
Tabla 1 Parámetros termodinámicos determinados con CDB para diferentes proteínas.
| Proteína | Topología | Especie | T m (K) | ΔH (kJ mol -1 ) | ∆ C p (kJ mol -1 K -1 ) |
|---|---|---|---|---|---|
| Proteínas con topología variada (figura 7A) | |||||
| Citocromo ca | Sólo hélices α | Bos taurus | 354 | 444 | 7 |
| Mioglobinaa | Sólo hélices α | Physeter macrocephalus | 356 | 684 | 12 |
| α-quimiotripsinaa | Sólo hebras β | Bos taurus | 333 | 705 | 13 |
| RNAsaa | Hélices α con hebras β | Bos taurus | 338 | 478 | 5 |
| Lisozimaa | Hélices α con hebras β | Gallus gallus | 353 | 565 | 6 |
| Proteínas con topología de barril TIM (figura 7B) | |||||
| Cp TIMb | Barril TIM (hélice α con hebra β)8 | Clostridium perfringens | 331 | 895 | 28 |
| DrTIMb | Deinococcus radiodurans | 318 | 812 | 28 | |
| Sc TIMb | Streptomyces coelicolor | 318 | 941 | 27 | |
| Mm TIMc | Moritella marina | 307 | 347 | 29 | |
| AHAd | Pseudoalteromonas haloplanktis | 317 | 895 | 36 | |
| DMAd | Drosophila melanogaster | 331 | 1146 | 36 | |
| PPAd | Sus scrofa | 339 | 1234 | 36 | |
| TFAd | Thermobifida fusca | 347 | 1736 | 36 | |
aPrivalov y Khechinashvili, 1974; bRomero-Romero, Costas, Rodríguez-Romero y Fernández-Velasco, 2015; cRomero-Romero, 2017;dCipolla, Delbrassine, DaLage y Feller, 2012











 nueva página del texto (beta)
nueva página del texto (beta)


