8ª Convención Nacional y 1ª Internacional de Profesores de Ciencias Naturales

 

Coevolución en redes sociales

 

Coevolution in social networks

 

Gerardo Iñiguez and Rafael A. Barrio*

 

* Instituto de Física, Universidad Nacional Autónoma de México, Circuito de la Investigación Científica, Ciudad Universitaria, 04510, México, DF, México. Correo electrónico: barrio@fisica.unam.mx

 

Abstract

Networks are thought to be essential in understanding the emergence and sustainability of collective behaviour in many complex systems often found in fields such as physics, sociology, biology, ecology and economy, to name just a few. The problem is that although they can be represented mathematically as a graph, the characterisation of nodes and links in it is usually quite arbitrary, and therefore basic quantities such as space dimension and metrics are not well defined, which leads to ambiguities in the establishment of dynamical equations to dictate the state of the system.

In this paper we propose and review a general framework to study the dynamical evolution of networks based in the concept of coevolution, which implies a feedback between the state variables defined over the nodes and the structure of the network itself. The usefulness and generality of such a framework is shown by modelling an opinion formation process in human societies, in which the dynamical formation of community structures is predicted and characterised in terms of the parameters of the model.

Keywords: complex systems, coevolution, social networks.

 

Nota introductoria

Este artículo contiene la parte puramente científica de la conferencia invitada "¿Hacia dónde va la Física?" impartida en la VIII Convención Nacional y I Internacional de Profesores de Ciencias Naturales, en Zacatecas, México, el 16 de noviembre de 2008. Allí se abordaron a nivel de divulgación diversos temas relacionados con temas de investigación de actualidad en la Física. Por ejemplo, en Astrofísica se discutió acerca de los nuevos telescopios como el Hubble, y los nuevos descubrimientos de hoyos negros en el centro de las galaxias. En Partículas Elementales se discutió brevemente el Modelo Standard y la construcción del Large Hadron Collider para detectar el bosón de Higgs. En materia condensada se mencionaron la Magnetorresistencia Gigante, la Superconductividad de Alta Temperatura y los Quasicristales. La charla desembocó en el paradigma de las Redes Complejas y los Sistemas No-Lineales. Para ejemplificar las técnicas de investigación en redes complejas se expuso con cierto detalle una línea de investigación que actualmente nuestro grupo está desarrollando, a saber, un modelo sobre la dinámica de formación de opinión en una red social.

En las siguientes secciones expondremos en detalle los ingredientes del modelo desarrollado por nuestro grupo.

 

Introducción

En los últimos años, la comunidad científica ha presenciado la abrumadora producción de trabajos donde el concepto de red se utiliza como elemento básico para describir fenómenos en la Naturaleza, tan variados como las interacciones sociales en una comunidad humana (Wasserman and Faust, 1994), la estructura de la Internet y la WWW (Barabási and Albert, 1999; Faloutsos et al., 1999) y los procesos metabólicos en tejidos biológicos (Jeong et al., 2000), por citar algunos ejemplos. Este enfoque se conoce genéricamente como sistemas complejos en la literatura (Caldarelli, 2007; Newman et al., 2006). Es obvio que los sistemas complejos son inherentemente interdisciplinarios y existen ciertos rasgos universales en todos ellos, como la presencia de propiedades emergentes que provienen de la interacción entre la estructura y la función de tales sistemas. Entonces, el formalismo de sistemas complejos ha sido utilizado para predecir el comportamiento de fenómenos físicos, sociales, biológicos, tecnológicos, económicos y semánticos, entre otros, lo cual se demuestra por la existencia de numerosas revisiones que resumen esta actividad (Albert and Barabási, 2002; Boccaletti et al., 2006; Costa et al., 2007; Dorogovtsev and Mendes, 2002; Newman, 2003).

Desde un punto de vista teórico, gran parte del éxito de este formalismo se debe a la extrema generalidad de sus conceptos básicos. Por un lado la estructura de un sistema complejo se modela con una red, un concepto matemático proveniente de la Teoría de Gráficas (Bollobás, 1979; Diestel, 2000; West, 2001), formada por un conjunto de nodos que representan las partes del sistema y un conjunto de enlaces que unen a los nodos y simulan las interacciones entre ellos. Por otro lado, la función del sistema complejo se modela con un sistema dinámico (Barrio and Varea, 2006; Strogatz, 1994), es decir, con un sistema de ecuaciones diferenciales acopladas de manera no lineal que describe la dinámica de las propiedades de las partes e interacciones del sistema. Así, en principio podemos estudiar las características estáticas o dinámicas de la estructura de una red sin función, o la forma en que la función evoluciona en el tiempo en una estructura de red estática. No obstante, el caso intermedio en el cual la red tiene tanto estructura como función resulta a la vez más interesante y complicado, pues la interacción entre la topología de una red y un sistema dinámico definido sobre ella puede llevar a la generación de propiedades emergentes en el sistema.

En resumen, en un sistema complejo se definen variables dinámicas que describen el estado temporal de cada nodo, es decir la función, la cual hace que la topología de la red, es decir su estructura, cambie en el tiempo adaptándose a la función. Esta mutua influencia ha sido denominada en la literatura coevolución, y se ha estudiado en modelos específicos (Gil and Zanette, 2006; Kozma and Barrat, 2008a,b; Nardini et al., 2008; Zanette and Gil, 2006; Zimmermann et al., 2004).

Sin embargo, hasta donde sabemos, el concepto de coevolución no ha sido aún considerado de manera formal y abstracta, más allá de los detalles característicos de cada fenómeno analizado. En el presente trabajo se propone un marco teórico general que utiliza la coevolución para explicar la existencia de propiedades emergentes en un sistema complejo. Tal marco teórico se ejemplifica en detalle con un modelo específico para describir y caracterizar la presencia de comunidades en un proceso de formación de opinión en una red social.

 

Estructura y función

Como se menciona en la Introducción, el estudio de ciertos fenómenos naturales como sistemas complejos provee de dos análisis extremos: su descripción como estructuras de red sin función, o como funciones sobre redes fijas. En el primer caso en el cual la función del sistema se considera despreciable en la escala de tiempo correspondiente al análisis desarrollado, podemos modelar al fenómeno como una red G formada por un conjunto de nodos {i} y un conjunto de enlaces {(i, j)} que unen a los nodos i y j, la cual puede ser descrita de manera única por una matriz de conectividad A, cuyos elementos A_ij son 1 si el enlace ( i, j ) existe y 0 si no. Dada una matriz A podemos caracterizar de manera local la topología de G alrededor de cierto nodo i con las medidas locales usuales, como:

El grado de cada nodo k_i = (A²)_ii, definido como el número de enlaces o primeros vecinos que tiene i.

El coeficiente de agrupamiento local C_i= (A³)_ii/ [k_i(k_i — 1)], que es la razón entre el número de triángulos que pasan por i y el número máximo posible, que es k_i (k_i — 1) /2.

La longitud característica L_ij, o sea el número mínimo de enlaces necesarios para ir de i a j.

El número de segundos vecinos n₂ (el número de nodos j tales que L_ij = 2) y el tamaño si de un cúmulo que contenga a i, donde un cúmulo en G es un subconjunto de nodos que tienen enlaces entre sí pero que están completamente desconectados del resto de la red.

De esta manera, los promedios de tales medidas locales sobre todos los nodos de G (denotados por los paréntesis 〈•〉) y la distribución de grado P(k) (la probabilidad de que un nodo escogido uniformemente al azar tenga grado k) dan una descripción estadística de la red, que permite definir cuatro estructuras arquetípicas del sistema complejo:

— Las redes ordenadas, donde los enlaces conectan nodos de acuerdo a una condición o algoritmo determinado que no tiene elementos aleatorios, y usualmente se pueden representar gráficamente en un espacio métrico de cierta dimensión. Entre ellas se encuentran las redes cristalinas o redes de Bravais (Kittel, 1996) formadas por la infinita repetición de una unidad estructural de nodos y enlaces (quedan como resultado estructuras típicas como la red cuadrada, y se utilizan con frecuencia en el estudio de cristales en Física del Estado Sólido), los árboles de Cayley o redes de Bethe (Diestel, 2000) que no contienen ciclos o anillos de enlaces y tienen grado único k, y que resultan ser las redes en las cuales la aproximación de campo medio de un sistema magnético es la solución exacta, y las redes exponenciales ordenadas (Rozada and Barrio, 2005) formadas por la unión de dos árboles de Cayley, las cuales han sido usadas como filtros de frecuencias en guías de onda y como un modelo estructural para las interacciones sinápticas entre neuronas.

— Las redes al azar de Erdös y Rényi (1959), donde los enlaces entre nodos se reparten de forma uniformemente aleatoria sobre toda la red a fin de alcanzar un grado promedio 〈k〉 dado. En las redes al azar se cumplen las relaciones asintóticas 〈C〉≃〈k〉 / N, 〈L〉≃ln N/ln〈k〉 y P (k)=〈k〉^k exp^-〈k〉/k! en el límite de un tamaño N de red muy grande y pocos enlaces (Bollobás, 1985). Por sus propiedades analíticas sencillas, las redes al azar generalmente son la primera aproximación a cualquier estructura de red desordenada, como es el caso de las redes de interacción en un proceso de propagación epidémica de enfermedades (Boguñá et al., 2003; Hethcote, 2000).

— Las redes de mundo pequeño de Watts y Strogatz (1998), que presentan a la vez valores pequeños de la longitud característica promedio 〈L〉(como las redes al azar) y valores altos del coeficiente de agrupamiento promedio 〈C〉 (como las redes ordenadas), lo cual da al sistema un efecto "de mundo pequeño" por el que cualquier par de nodos pueden estar separados por una distancia sorprendentemente corta a pesar del gran tamaño de la red. Esta propiedad fue analizada por primera vez a través del estudio de cadenas de conocidos en una red social (Milgram, 1967), y desde entonces su ubicuidad en los sistemas complejos ha sido confirmada con ejemplos tales como las redes neuronales en seres vivos, las redes de energía eléctrica en ciudades, y las redes de colaboración de actores (Boccaletti et al., 2006; Newman, 2003).

— Las redes libres de escala de Barabási y Albert (1999), construidas a partir de dos procesos característicos, el crecimiento (nuevos nodos se añaden a la red de acuerdo a una tasa específica durante todo su proceso de generación) y la conexión preferencial (la probabilidad de que un nuevo nodo se conecte a uno viejo depende de alguna de sus características topológicas locales, como el grado), lo cual lleva la red a un estado final invariante de escala donde la distribución de grado es una ley de potencias de la forma P(k) ∝ k^-γ con un exponente característico γ, de donde estas estructuras toman su nombre. Estos dos procesos se incluyen específicamente para describir el desarrollo relativamente rápido de redes como la Internet y la WWW, donde nuevos routers y páginas web se introducen todo el tiempo, y sus conexiones generalmente se dirigen a routers y páginas web pre-existentes con cierta autoridad en la red debido a su gran número de enlaces. Desde entonces dichas propiedades libres de escala han sido observadas en muchos sistemas complejos, incluyendo redes metabólicas y árboles taxonómicos en biología, procesos de ganancias económicas en una sociedad, sistemas semánticos y redes de colaboración científica (Albert and Barabási, 2002).

En el caso extremo opuesto, donde la escala de tiempo en la que la estructura cambia es tan grande que la red puede considerarse estática, la función del sistema complejo está descrita por un sistema dinámico definido sobre una red fija (ya sea ordenada, al azar, de mundo pequeño o libre de escala, por ejemplo), que no se modifica durante todo el análisis. En este marco de generalidad, un sistema dinámico es descrito por la ecuación , donde el vector contiene las variables de estado s_i(t) definidas sobre los nodos de la red (que codifican las propiedades dinámicas relevantes a estudiar) y las componentes del vector 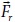son funciones no lineales que dictan la evolución temporal de las variables de estado de forma acoplada y en términos de un conjunto de parámetros {r} que definen las posibles acciones externas sobre el sistema (Barrio and Varea, 2006). Aunque estos sistemas son en general imposibles de resolver analíticamente, gran parte de su comportamiento cualitativo puede ser entendido a través del espacio fase del sistema, un espacio abstracto con un eje por cada variable de estado si donde la evolución temporal de se ve como un "flujo" guiado por el campo de "velocidades" 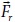. Tal flujo puede ser atraído o repelido por ciertos puntos en el espacio fase (llamados puntos fijos estables o inestables), seguir una trayectoria cerrada (conocida como ciclo límite) que representa una oscilación del sistema sustentada a lo largo del tiempo, o seguir una serie de estados que no se repiten ni acaban (denotados en su conjunto como un atractor extraño), lo cual implica un comportamiento caótico del fenómeno (Strogatz, 1994, 2001).

El conjunto de puntos fijos, ciclos límite y atractores extraños existente para valores dados de los parámetros externos {r} se denomina el retrato fase del sistema. El análisis lineal alrededor de los puntos fijos permite predecir si el sistema presenta patrones en el espacio o comportamientos oscilatorios en el tiempo. Existen ciertos valores críticos de los parámetros externos que llevan al sistema no-lineal a modificar su comportamiento y pasar abruptamente de un estado con ciertas simetrías (operaciones que dejan al sistema invariante) a otro estado en el que algunas simetrías se han perdido. Este tipo de comportamiento se conoce como rompimiento espontáneo de simetría. Ésta es una propiedad universal de los sistemas dinámicos que los hace tan pertinentes en el estudio de los sistemas complejos, y se lleva a cabo por medio de procesos llamados bifurcaciones, en los cuales aparecen nuevos estados que presentan un comportamiento cada vez mas complicado del sistema, es decir, se pasa de la simplicidad a la complejidad (Barrio and Varea, 2006). El rompimiento espontáneo de simetría y las bifurcaciones inherentes a muchos sistemas dinámicos han sido conceptos muy útiles para tratar con gran efectividad problemas tan diversos como la morfogénesis en procesos biológicos y ecológicos (Barrio, 2008), las oscilaciones y sincronizaciones en sistemas químicos, celulares y de grupos de animales (Acebrón et al., 2005; Pérez et al., 1996; Strogatz, 2000), la dispersión y propagación de enfermedades (Boguñá and Pastor-Satorras, 2002; Boguñá et al., 2003; Pastor-Satorras and Vespignani, 2001), el funcionamiento de redes metabólicas, neuronales y de expresión genética (Boccaletti et al., 2006; Newman, 2003), y muchos más.

 

Coevolución en redes complejas

Cuando en una red compleja se encuentra que tanto las variables de estado, que definen el comportamiento dinámico de cada nodo, como las interacciones entre ellos cambian en escalas similares de tiempo, resulta imperativo considerar la evolución temporal de ambos elementos en forma simultánea, es decir, analizar con detenimiento las situaciones en las cuales existe una retroalimentación explícita entre la dinámica de la topología de la red y la de sus variables de estado. Por ejemplo, en el proceso de formación de opinión en una sociedad humana, la forma en que cada individuo desarrolla su opinión respecto a un tema específico (variable de estado, o función) depende en gran medida de las personas con las cuales discute tal tema (es decir, con su red social, o estructura). Esta red de amistades o conocidos cambia todo el tiempo a medida que la opinión de los elementos de la red social cambia, debido a la propia dinámica de la estructura social. Así, esta interacción entre estructura y función, o coevolución, es un ingrediente fundamental para analizar el comportamiento de ciertos sistemas complejos, incluyendo la presencia de propiedades emergentes en ellos como la diferenciación de células en un tejido o la generación de comunidades en una red social.

No obstante, la caracterización del proceso de coevolución en fenómenos particulares y sus consecuencias en los comportamientos de éstos no es suficiente, pues es sabido que la elección de la red compleja, en donde se da la estructura y la función, depende fuertemente de las características o procesos específicos que se desean estudiar, y por tanto un mismo fenómeno natural puede ser asociado con muchas estructuras y funciones acopladas o no entre sí que pueden comportarse de manera abismalmente distinta. Esta particularidad de las redes complejas hace que la elección de cantidades básicas para su descripción general sea complicada o tal vez imposible, a diferencia de lo que pasa en un sistema físico donde existe un espacio que puede ser descrito a través de su métrica y dimensionalidad. Esto lleva a ambigüedades y definiciones informales en la proposición de ecuaciones dinámicas para modelar la estructura y función del sistema. Para intentar resolver tal problema y dar un paso en la formalización abstracta de las redes complejas, proponemos considerar a la coevolución como el elemento fundamental que define a una red compleja, y después derivar el comportamiento y propiedades emergentes de ésta en función de los distintos tipos de interacción que pueden existir entre su estructura y su función. Una breve descripción de este marco teórico se presenta a continuación.

Para un sistema complejo cuya estructura está dada por una red G y cuya función es descrita por el sistema dinámico , la coevolución implica que las funciones F_r actuando sobre cada variable de estado Si dependen de los nodos y enlaces de G, y de la misma forma los nodos y enlaces de la red cambian de acuerdo a los valores de las variables s_i definidas sobre cada elemento de G. En otras palabras, para cada variable de estado podemos escribir la ecuación de coevolución

donde Ô(s_¡,s_j,g) son las componentes de un operador Ô que cambia las entradas y el tamaño de la matriz de conectividad A. En esta ecuación el término ∂s_i/∂t representa la microdinámica del sistema, es decir, la dinámica de Si que sólo depende en forma explícita del conjunto de variables de estado y no de la red, mientras que el término ∑_jÔ(s_i,s_j,g)A_ij se refiere a la macrodinámica del sistema, es decir, a la forma en que s_i cambia explícitamente por la red G y no por el conjunto de variables de estado. Los prefijos micro y macro implican la existencia de dos escalas de tiempo características: una "rápida" dt para la dinámica de las variables de estado (el intercambio de información o transacción en la red), y una "lenta" dT para el cambio de nodos y enlaces en G (la modificación de la topología o generación de la red), las cuales están relacionadas por el parámetro de coevolución g = dT/dt que controla el número de transacciones por generación. De esta forma, el parámetro g delimita tres regiones con comportamientos radicalmente distintos: el caso límite g → 0 en que la dinámica de las variables de estado es irrelevante y por tanto tenemos un sistema complejo descrito tan sólo por su estructura, el otro caso límite g → ∞ en el cual no existe una modificación de la topología de G y por tanto el sistema sólo tiene función, y el caso intermedio en el cual estructura y función interactúan explícitamente a través de la ecuación (1) para definir el comportamiento del sistema complejo en cuestión.

Ahora bien, la ecuación para la microdinámica del sistema puede ser separada en términos que dependen del número de variables de estado que interactúan entre sí en un tiempo dado, ya sean interacciones por pares ("lineales"), por tríos ("cuadráticas"), etcétera, lo cual se puede ver como una expansión en serie de Taylor en términos de la complejidad de la interacción. Así, la microdinámica de la variable si alrededor de un estado estacionario se puede escribir como

donde los coeficientes ƒ₀, ƒ₁, ƒ₂, etc., de la expansión dependen en principio de las variables de estado en toda la red, por lo que es posible tener interacciones de corto alcance (entre primeros o segundos vecinos, por ejemplo) e interacciones de largo alcance que se extiendan a lo largo de G.

Por el otro lado, la macrodinámica del sistema complejo está regida por el operador Ô, el cual actúa en cada generación de forma discreta y sólo puede modificar la red en cuatro formas básicas: agregando/eliminando nodos, o agregando/ eliminando enlaces. Operaciones compuestas llevan a procesos importantes como la reconexión en la red, dada por la eliminación de un enlace seguida de la creación de otro, manteniendo un nodo en común. El operador Ô sólo actúa en los tiempos específicos de generación, lo cual puede representarse matemáticamente por medio de funciones delta de Dirac y reglas lógicas, es decir,

donde (s_i, s_j )A = A' es la matriz de conectividad de G modificada después de cada tiempo de generación por las reglas lógicas , que representan la forma de hacer las reconexiones. A fin de agregar claridad a los términos desarrollados en la presente sección y mostrar un primer ejemplo de la utilidad de este marco teórico, a continuación se analiza un modelo simple de formación de opinión en una red social bajo el concepto de coevolución.

 

Formación de opinión en una red social

Una red social presenta tres características que la distinguen de otras redes, que son: (1) La longitud característica L_ij es muy pequeña (propiedad conocida como "mundo pequeño"), (2) La conectividad es muy baja, es decir, 〈k〉 « N (existe la famosa conjetura de Dunbar que dice que el número promedio de amistades es del orden de 150, sin importar el tipo de interacción social que se trate), y (3) Existen comunidades definidas por una interacción estrecha entre sus miembros, ligadas débilmente al resto de la sociedad. Esta estructura de comunidades aparece en todas las redes sociales por causas aún no identificadas del todo. En el ejemplo que detallaremos a continuación nos centraremos en estudiar estas tres propiedades.

Uno de los problemas fundamentales en el estudio de la sociedad humana y su dinámica se conoce bajo el término de formación de opinión, el cual considera las respuestas conmensurables de los individuos en un grupo social a cierto tema de discusión controversial, como una pregunta política o la aceptación de un elemento de innovación. Con el paso del tiempo tal problema ha atraído bastante atención en la comunidad científica y por tanto existen diversos modelos que han sido introducidos para intentar caracterizarlo y controlarlo. Entre los casos más sencillos se pueden mencionar el modelo de votación (Holley and Liggett, 1975) en el que la opinión de un nodo es una variable con dos estados que se modifica de acuerdo a una elección aleatoria de primeros vecinos, y modelos donde el proceso de elección de una nueva opinión depende de más de dos nodos (Sznajd-Weron, 2005; Sznajd-Weron and Sznajd, 2000; Weidlich, 1991), todos los cuales son reminiscentes de un modelo de Ising para la interacción magnética en un sólido y por tanto generalmente predicen estados finales de consenso de la población (análogos al estado ferromagnètico en su equivalente físico). Sólo hasta hace poco un proceso explícitamente coevolutivo (en el cual la dinámica de las opiniones es mediada por una red de relaciones sociales y a su vez la red es influenciada por tal dinámica) ha sido introducido de forma particular para describir un proceso de formación de opinión (Kozma and Barrat, 2008a,b; Nardini et al., 2008), pero su estudio sigue restringido a caracterizar la generación de consenso en el sistema. Dados estos antecedentes, nuestro objetivo consiste en construir un modelo de formación de opinión basado en el marco teórico de coevolución descrito en la sección anterior que se enfoque en caracterizar dinámicamente la generación de comunidades en la red, una propiedad emergente, sin dar mucha importancia a la existencia o falta de consenso en la población. Para no entrar en detalles innecesarios, a continuación se presenta una breve descripción del modelo y algunos de los resultados cualitativos más importantes.

Dada una red G cuyos nodos representan individuos en una sociedad cerrada, una variable de estado u opinión x_i ∈ [-1;1 ] se asocia con cada nodo i para medir la inclinación instantánea de la persona o agente respecto a una pregunta controversial pero simple, de tal forma que los valores extremos x_i = ±1 se puedan relacionar con las respuestas completamente favorables y desfavorables, y los valores intermedios correspondan a estados de indecisión gradual. Por el otro lado, los elementos A_ij de la matriz de conectividad representan la existencia (1) o ausencia (0) de discusiones entre los agentes i y j acerca del tema propuesto. Como condición inicial se toma una red al azar con grado promedio 〈k₀〉y tamaño N dados, así como una distribución normal de opiniones iniciales sobre todo el intervalo [-1,1].

En cuanto a la microdinámica del sistema, utilizamos la expansión de Taylor de la ecuación (2) hasta el término lineal para escribir

donde la variable aleatoria α_i ∈ [-1,1 ] mide la actitud del agente i respecto a la opinión de la mayoría en términos de su carácter o personalidad, h es un campo externo constante que representa una tendencia global hacia las opiniones extremas x_i = ±1 debido a los medios y la propaganda (radio, TV y periódicos, por ejemplo), y los términos de interacción de corto y largo alcance están dados por

donde las sumas sobre j se restringen a los nodos tales que L_ij = n. El parámetro m define la extensión de la interacción de corto alcance, m_max es el máximo valor de L_ij para nodos j arbitrarios, y C(n) es un factor de normalización para cada "capa" de vecinos n de i. Así, la microdinámica de una opinión x_i está dada por un término completamente independiente de las variables de estado (la propaganda), un término de largo alcance independiente de x_i que mide la opinión promedio de las personas "lejanas" tomando en cuenta su distancia, y un término de corto alcance que promedia las interacciones por pares o discusiones entre el agente y sus vecinos cercanos. Como condición inicial se toma una distribución uniformemente aleatoria para las variables α_i, y los parámetros m y h y el factor C(n) se fijan.

Note que esta forma de modelar las interacciones sociales ya respeta la información adicional que se tiene sobre el sistema. Por ejemplo, la introducción de la variable aleatoria a_i representa la diferente actitud de cada individuo con respecto a la opinión de la mayoría: existen gentes que obstinadamente llevan la contraria (α ≈ -1), y otros que se dejan llevar muy fácil por la opinión ajena (α ≈ 1). También se supone que el resultado de una discusión entre dos personas con inclinaciones similares es reforzar la posición de ambos, y entre dos personas con opiniones diferentes es hacerlos menos seguros de su posición inicial, lo cual se representa con la función signo (sign(x_i)) en el modelo.

La ecuación (4) es altamente no lineal y complicada, y sólo admite solución numérica; por lo tanto, en vez de dar una expresión analítica del operador Ô, la macrodinámica del sistema puede ser descrita con un algoritmo fácilmente incorporable a un programa numérico. Si consideramos que la escala de tiempo del proceso de formación de opinión es suficientemente pequeña como para no tomar en cuenta el nacimiento y muerte de individuos, y que el tiempo que cada agente dedica a las discusiones es limitado y relativamente constante a lo largo del fenómeno, podemos suponer que el tamaño N de la red se mantiene constante y que los individuos no eliminan o crean enlaces de manera excesiva, sino que siguen un proceso de reconexión en el cual dejan de discutir con alguien, por tener diferencias irreconciliables respecto al tema controversial, para empezar a hablar con un agente nuevo que presuntamente los ayudará a alcanzar un valor definitivo de opinión en menos tiempo. De esta forma, en cada generación un agente i tiene como opción cortar su enlace con un cierto primer vecino j si la probabilidad

es suficientemente grande, siempre y cuando después de realizar tal acción escoja un segundo vecino k con el cual pueda crear un nuevo enlace si la probabilidad definida como

también sea suficientemente grande. Aquí el término , identifica los segundos vecinos (L_ik=2). En otras palabras, en cada generación un agente puede terminar discusiones con sus primeros vecinos por la diferencia extrema de opiniones, y puede empezar otras discusiones con los "amigos de sus amigos" (es decir, con sus segundos vecinos) si sus respectivas opiniones son más compatibles entre sí. Este mecanismo para generar nuevas interacciones sociales no es arbitrario, sino que está basado en el proceso general conocido como cerradura cíclica en la literatura (Kossinets and Watts, 2006), y se considera el más importante y fundamental en los estudios sociológicos de las relaciones de amistad. El proceso que estamos considerando es el caso particular de cerradura triádica, o sea el famoso triángulo, o "three-clique".

A fin de esclarecer la forma en que el concepto de coevolución permea todas estas consideraciones, los extremos derechos de las ecuaciones (6) y (7) presentan a las probabilidades de corte y conexión en términos de factores que dependen tanto de la topología de la red (la matriz de conectividad A) como del conjunto de variables de estado (el vector de opiniones x).

Una vez establecida la estructura del modelo, la microdinámica se integra numéricamente en una escala de tiempo rápida dt, mientras que la macrodinámica sigue una escala de tiempo lenta y discreta dT. Nótese que el único parámetro relevante en el modelo es el parámetro de coevolución g = dT/dt, el cual determina el tiempo característico en que las variables de estado evolucionan por sí solas antes de que haya un cambio de generación y la red se modifique. Las opiniones x_i pueden fluctuar caóticamente o acercarse de manera exponencial a los valores de x_i extremos, pero una vez que alcanzan tales límites su microdinámica se detiene a propósito (valores de |x_i| > 1 no tienen sentido), pues se intenta describir un estado de decisión irrevocable en la cual el individuo ya ha tomado su posición respecto al tema controversial. Finalmente, la dinámica acaba cuando la mayoría de los individuos se encuentran en dicho estado de decisión irrevocable, y sólo unos cuantos indecisos permanecen en la red con fluctuaciones mínimas en sus variables de estado. El estado final de la red se caracteriza estadísticamente con una medición de los valores promedio de sus propiedades topológicas locales, y se visualiza para compararlo con la estructura de la red en momentos anteriores de la dinámica.

En la figura 1 se presentan gráficas de las propiedades topológicas de la red consideradas en este artículo como función del parámetro de coevolución. Las líneas verticales dividen tres regiones cualitativamente distintas para el comportamiento del sistema de formación de opinión. Para g → 0 la dinámica de las opiniones es irrelevante pues las reconexiones se hacen demasiado seguido, por lo que la topología de la red se modifica esencialmente de forma aleatoria y el estado final de la red corresponde a dos cúmulos de igual tamaño con opiniones opuestas, completamente conectados en su interior y desconectados entre sí (como se ve en la figura (2a)), lo cual reproduce el resultado de los modelos de formación de opinión basados en sistemas de Ising, que son a fin de cuentas, estructuras de red sin función. En el caso g → ∞ el sistema prácticamente se desarrolla dentro de una sola generación, por lo que no hay reconexiones y las opiniones evolucionan sobre una red fija, lo cual implica que el estado final es una red aleatoria (idéntica a la inicial, como se ve en la figura (2c)) con una distribución no trivial de opiniones sobre ella, que claramente corresponde al estado final de un sistema dinámico definido sobre una estructura de red estática. Este proceso puede generar un patrón espacial que en una red aleatoria no tiene significado. Finalmente, la región de valores intermedios de g produce un resultado revelador: la interacción entre la estructura y la función de la red en escalas de tiempo similares produce una propiedad emergente; la red ya no está completamente conectada ni es aleatoria, sino que posee una estructura heterogénea con subconjuntos de nodos altamente conectados entre sí y poco conectados con el resto de ella, que identificamos como comunidades y se muestran en la figura (2b).

Aunque la definición y caracterización formal del concepto de comunidad en un sistema complejo es un tema de investigación abierto, existen ciertas formas prácticas e intuitivas de describirla que ayudan a clarificar algunas de sus propiedades. Entre los resultados más utilizados en la actualidad se encuentran los algoritmos de detección de comunidades, entre los que destacan aquellos basados en el concepto de modularidad (Lancichinetti et al., 2008; Newman, 2006; Newman and Girvan, 2004), que es una especie de correlación de pares y que es una medida de la eficiencia con la cual un subconjunto de nodos en la red está altamente conectado en su interior y poco conectado con el resto de la red. Con ayuda del algoritmo de Lancichinetti et al. (2008), en la figura (2b) se presenta un ejemplo de cómo un valor intermedio de g genera comunidades en la red identificadas tanto por modularidad como por softwares de visualización, es decir, muestra la forma en que la coevolución en el sistema genera estructuras imposibles de lograr en los casos extremos correspondientes a las figuras (2a) y (2c).

Finalmente, al examinar la razón 〈k〉/[N 〈C〉] como función de g observamos que en los casos extremos g → 0 y g → ∞la relación de redes al azar 〈k〉/[N 〈C〉] = 1 se mantiene, mientras que en la región intermedia de g tal razón disminuye, y conforme N crece se acerca asintóticamente a una constante, 〈k〉/[N 〈C〉] ~ cte. 〈1, lo cual implica que localmente hay subconjuntos de la red con una topología aleatoria que no interactúan entre sí, o en otras palabras, comunidades altamente conectadas dentro de una estructura de red heterogénea. En la figura 3 mostramos que la razón 〈k〉/[N 〈C〉] como función del tamaño de la red N disminuye, lo cual es una demostración de la existencia del número de Dunbar, es decir, el número de individuos en una comunidad es de unas cuantas decenas de personas siempre.

Cabe mencionar que construimos una aproximación de campo medio que permite entender la variación de 〈C〉 como función de 〈k〉 . Asimismo, se puede predecir la manera en que 〈k〉 cambia como función del tiempo en los límites extremos de g, a través de un estudio de la interferencia de las reconexiones entre nodos vecinos. También es posible encontrar una expresión analítica para la evolución temporal del promedio de las opiniones, la cual resulta similar a la magnetización en un sistema ferromagnético clásico. Todos estos estudios caen fuera del alcance de este artículo y serán publicados en el futuro próximo.

 

Conclusiones

Este artículo sirve como una breve revisión de la manera en que el formalismo de sistemas complejos ha sido utilizado últimamente para describir el comportamiento de fenómenos naturales pertenecientes a diversas disciplinas bajo un mismo conjunto de conceptos: una o varias estructuras de red y un conjunto de sistemas dinámicos definidos sobre ellas para describir sus funciones. Al considerar la estructura y función de un sistema complejo, resulta fundamental analizar la retroalimentación entre sus dinámicas, y como se ha reportado en varios casos particulares ya, tal fenómeno de coevolución resulta indispensable para describir la emergencia de propiedades en el sistema. El marco teórico de coevolución presentado en este trabajo, y respaldado por su aplicación en un proceso de formación de opinión, es el intento de un primer paso en el camino de la formalización del estudio abstracto y general de los sistemas complejos, y abre posibles caminos en el futuro. Por un lado es interesante preguntar si somos capaces de seguir un estudio analítico del marco teórico sin entrar en detalles particulares de un fenómeno dado, y por el otro es igualmente importante aplicar tal marco a sistemas fuera del régimen social para descubrir la importancia de la coevolución en diversas áreas del conocimiento científico. Lo único que sabemos con total seguridad hasta el momento es que el campo de sistemas complejos es un reto fascinante, actual y prometedor, que tiene bastantes esperanzas de ampliar la perspectiva del conocimiento humano en un futuro cercano.

 

Agradecimientos

Los autores quisieran agradecer a los profesores Kimmo K. Kaski y Janos Kertész por su fructífera colaboración en este trabajo. Además, se reconoce al Centro de Excelencia en Investigación Computacional de Sistemas Complejos de la Universidad Tecnológica de Helsinki en Finlandia y al Centro de Biología Matemática de la Universidad de Oxford en el Reino Unido por las estancias en que gran parte de este proyecto se desarrolló.

 

Referencias

J. A. Acebrón, L. L. Bonilla, C. J. Pérez Vicente, F. Ritort, and R. Spigler. The Kuramoto model: A simple paradigm for synchronization phenomena, Reviews of Modern Physics, 77(1):137-185, 2005.         [ Links ]

R. Albert and A.-L. Barabási. Statistical mechanics of complex networks, Reviews of Modern Physics, 74(1):47-97, 2002.         [ Links ]

A. -L. Barabási and R. Albert, Emergence of Scaling in Random Networks, Science, 286(5439):509-512, 1999.         [ Links ]

R. A. Barrio. Turing Systems: A General Model for Complex Patterns in Nature. In: I. Licata and A. Sakaji (eds.), Physics of Emergence and Organization, chapter 11, pages 267-296. World Scientific, 2008.         [ Links ]

R. A. Barrio and C. Varea. Non-linear systems, Physica A: Statistical Mechanics and its Applications, 372(2):210-223, 2006.         [ Links ]

S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, and D.-U. Hwang. Complex networks: Structure and dynamics, Physics Reports, 424(4-5):175-308, 2006.         [ Links ]

M. Boguñá and R. Pastor-Satorras. Epidemic spreading in correlated complex networks, Physical Review E, 66(4):047104, 2002.         [ Links ]

M. Boguñá, R. Pastor-Satorras, and A. Vespignani, Epidemic Spreading in Complex Networks with Degree Correlations, volume 625 of Lecture Notes in Physics, chapter 8, pages 127-147. Springer-Verlag, Berlin, 2003.         [ Links ]

B. Bollobás. Graph Theory: An Introductory Course. Springer-Verlag, New York, 1979.         [ Links ]

B. Bollobás. Random Graphs. Academic Press, London, 1985.         [ Links ]

G. Caldarelli. Scale-Free Networks: Complex Webs in Nature and Technology. Oxford University Press, Oxford, 2007.         [ Links ]

L. F. Costa, O. N. Oliveira Jr., G. Travieso, F. A. Rodrigues, P. R. V. Boas, L. Antiqueira, M. P. Viana, and L. E. C. da Rocha. Analyzing and Modeling Real-World Phenomena with Complex Networks: A Survey of Applications. Preprint arXiv:0711.3199, 2007. Available from http://arxiv.org/abs/        [ Links ]

R. Diestel. Graph Theory. Springer-Verlag, New York, 2000.         [ Links ]

S. N. Dorogovtsev and J. F. F. Mendes. Evolution of networks, Advances In Physics, 51(4):1079-1187, 2002.         [ Links ]

P. Erdös and A. Rényi. On random graphs. Publicationes Mathematicae (Debrecen), 6:290-297, 1959.         [ Links ]

M. Faloutsos, P. Faloutsos, and C. Faloutsos. On power-law relationships of the internet topology, Computer Communication Review, 29:251-262, 1999.         [ Links ]

S. Gil and D. H. Zanette. Coevolution of agents and networks: Opinion spreading and community disconnection, Physics Letters A, 356(2):89-94, 2006.         [ Links ]

H. W. Hethcote. The Mathematics of Infectious Diseases. SIAM review, 42(4):599-653, 2000.         [ Links ]

R. A. Holley and T. M. Liggett. Ergodic theorems for weakly interacting infinite systems and the voter model, The Annals of Probability, 3(4):643-663, 1975.         [ Links ]

H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai, and A.-L. Barabási. The large-scale organization of metabolic networks, Nature, 407(6804): 651-654, 2000.         [ Links ]

C. Kittel. Introduction to Solid State Physics. Wiley, New York, 1996.         [ Links ]

G. Kossinets and D. J. Watts. Empirical analysis of an evolving social network, Science, 311(5757):88-90, 2006.         [ Links ]

B. Kozma and A. Barrat. Consensus formation on adaptive networks, Physical Review E, 77:016102, 2008a.         [ Links ]

B. Kozma and A. Barrat. Consensus formation on coevolving networks: groups' formation and structure, Journal of Physics A: Mathematical and Theoretical, 41:224020, 2008b.         [ Links ]

A. Lancichinetti, S. Fortunato, and J. Kertész. Detecting the overlapping and hierarchical community structure of complex networks. Preprint arXiv:0802.1218, 2008. Available from http://arxiv.org/abs/        [ Links ]

S. Milgram. The small world problem, Psychology Today, 2(1):60-67, 1967.         [ Links ]

C. Nardini, B. Kozma, and A. Barrat. Who's Talking First? Consensus or Lack Thereof in Coevolving Opinion Formation Models, Physical Review Letters, 100:158701, 2008.         [ Links ]

M. E. J. Newman. The Structure and Function of Complex Networks, SIAM Review, 45(2):167-256, 2003.         [ Links ]

M. E. J. Newman. Modularity and community structure in networks, Proceedings of the National Academy of Sciences, 103(23):8577-8582, 2006.         [ Links ]

M. E. J. Newman and M. Girvan. Finding and evaluating community structure in networks, Physical Review E, 69: 026113, 2004.         [ Links ]

M. E. J. Newman, A.-L. Barabási, and D. J. Watts. The structure and dynamics of networks. Princeton University Press, 2006.         [ Links ]

R. Pastor-Satorras and A. Vespignani. Epidemic Spreading in Scale-Free Networks, Physical Review Letters, 86(14):3200-3203, 2001.         [ Links ]

C. J. Pérez, A. Corral, A. Díaz-Guilera, K. Christensen, and A. Arenas. On self-organized criticality and synchronization in lattice models of coupled dynamical systems, International Journal of Modern Physics B, 10(10):1111-1151, 1996.         [ Links ]

I. Rozada and R. A. Barrio. Coherent neuron response in ordered exponential networks. In: Statistical Physics and Beyond: 2nd Mexican Meeting on Mathematical and Experimental Physics, volume 757, pages 181-189. AIP, 2005.         [ Links ]

S. H. Strogatz. Nonlinear Dynamics and Chaos. Addison-Wesley, New York, 1994.         [ Links ]

S. H. Strogatz. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators, Physica D: Nonlinear Phenomena, 143(1-4): 1-20, 2000.         [ Links ]

S. H. Strogatz. Exploring complex networks, Nature, 410(6825): 268276, 2001.         [ Links ]

K. Sznajd-Weron. Sznajd Model and Its Applications, Acta Physica Polonica B, 36(8):2537-2547, 2005.         [ Links ]

K. Sznajd-Weron and J. Sznajd. Opinion evolution in closed community, International Journal of Modern Physics C -Physics and Computer, 11(6):1157-1165, 2000.         [ Links ]

S. Wasserman and K. Faust. Social Network Analysis: Methods and Applications. Cambridge University Press, Cambridge, 1994.         [ Links ]

D. J. Watts and S. H. Strogatz. Collective dynamics of 'small-world' networks, Nature, 393(6684):440-442, 1998.         [ Links ]

W. Weidlich. Physics and social science -The approach of synergetics, Physics Reports, 204(1):1-163, 1991.         [ Links ]

D. B. West. Introduction to Graph Theory. Prentice Hall, Upper Saddle River, NJ, 2^nd edition, 2001.         [ Links ]

D. H. Zanette and S. Gil. Opinion spreading and agent segregation on evolving networks, Physica D: Nonlinear Phenomena, 224(1-2):156-165, 2006.         [ Links ]

M. G. Zimmermann, V. M. Eguíluz, and M. San Miguel. Coevolution of dynamical states and interactions in dynamic networks, Physical Review E, 69:065102, 2004.         [ Links ]