Para quitarle el polvo

 

Conservation of Energy. Readings on the Origins of the First Law of Thermodynamics. Part II

 

Jaime Wisniak*

 

* Department of Chemical Engineering, Ben-Gurion University of the Negev, Beer-Sheva, Israel 4105. Correo electrónico: wisniak@bgumail.bgu.ac.il

 

Recibido: 13 de julio de 2007.
Aceptado: 19 de septiembre de 2007.

 

Abstract

In this second part on the history of the development of the first law of thermodynamics, we describe the contributions of the four principal scientists, Colding, Mayer, Joule, and Helmholtz, which provided the statement of the principle of conservation of energy, as we know it today.

In the first part of this paper (Wisniak, 2008) we discussed the general concepts behind the principle of conservation of energy and the impossibility of constructing a perpetuum mobile. We also gave a description of the historical issues that led to the situation that by the end of the first quarter of the nineteenth century the interchangeability between the different forms of mechanical energy, and the equivalence of heat and mechanical work, were already becoming accepted concepts. In the short period between 1840 and 1850 the experimental evidence was ripe enough for the declaration of the general law of conservation of energy. The hypothesis of energy conservation was publicly announced in different forms by four widely scattered European scientists, Ludvig August Colding (1815-1888), Julius Lothar Mayer (1830-1895), James Prescott Joule (1818-1889), and Hermann Ludwig von Helmholtz (1821-1894), all but the last working in complete ignorance of the other (Kuhn, 1959).

We will now continue to study of the ideas that culminated in the statement of the first law of thermodynamics, as we know it today.

Keywords: Heat equivalent, conservation of energy, Colding, Mayer, Joule, Helmholtz.

 

Resumen

En esta segunda parte sobre la historia del desarrollo de la primera ley de la termodinámica, se describe la contribución de cuatro científicos clave, Colding, Mayer, Joule, y Helmholtz, que dieron la expresión del principio de conservación de la energía como lo conocemos hoy.

 

Ludvig August Colding (1815-1888)

Verdet, in his book about the mechanical theory of heat (Verdet, 1862), gave an historical review of the development of the dynamical theory of heat, in which he "attempted to render justice to the principal discoverers". He believed that the initial credit should go to Daniel Bernoulli, who in his book Hydrodynamica (Bernoulli, 1738) gave the first description of the theory of constitution of gases. He then described the contributions of Sadi Carnot (1796-1832), Benoit-Pierre-Emile Clapeyron (1799-1864), Armand Séguin (1767-1835), Mayer, Colding, Joule, Helmholtz, Rudolf Julius Emanuel Clausius (1822-1888), William John Macquorn Rankine (1820-1872), and Benjamin Thomson (1753-1814, Count Rumford), claiming that the priority of order corresponded to Mayer who in his studies on the theory of respiration and comparison of animals to thermal machines had discovered the principle of conservation of energy as known today. According to Verdet, towards the time of the publication of Mayer's first memoir, Colding presented to the Royal Scientific Society of Denmark "a series of memoirs on the power of the steam and gas engines, which contained ideas almost identical with those of Mayer, and an example of the experimental determination of the mechanical equivalent of heat by friction, which does not appear to be very exact. But we ought to remember that the various memoirs of this physicist, written in a language the knowledge of which is but little extended, and first printed several years after their presentation... have exerted scarcely any influence on the subsequent developments of the science."

Helmholtz also credited Colding as one of the first discoverers of the true expression of the law of conservation of energy. He wrote: "The first who saw truly the law here referred to, and expressed it correctly, was a German physician, J. R. Mayer, of Heilbronn, in the year 1842. A little later, in 1843, a Dane named Colding presented a memoir to the Academy of Copenhagen, in which the same law found utterance, and some experiments were described for its further corroboration. In England, Joule began about the same time to make experiments having reference to the same subject. We often find, in the case of questions to the solution of which the development of science points, that several heads, quite independently of each other, generate exactly the same series of reflections" (Guerlac, 1953; Dahl, 1963).

In a paper published in English in 1864 Colding (Colding, 1864) refers to his previous work related to the new principle of conservation of energy, "which in Danish is called The Principle of the Imperishableness or Perpetuity of Energy (Principet for Kræfternes Uforgaengelighead)", and to Verdet's claim that Colding's name should be put next to that of Mayer in relation to the discovery of the new principle touching the forces of nature. Colding then wrote that his first ideas on the relationship between the forces of nature, based on Jean le Rond D'Alembert's (1717-1783) principle of active and lost forces (D'Alembert, 1743), were as follows: "As the forces of nature are something spiritual and immaterial entities... very superior to everything material in the world... it is consequently quite impossible to conceive of these forces as anything naturally mortal or perishable. Surely, therefore, the forces ought to be regarded absolutely imperishable" (Colding, 1864). His belief on these ideas had led Colding, twenty years before, to present to the Royal Society of Science of Copenhagen a treatise in which he exposed his thesis that force was imperishable and immortal; and therefore, when and wherever, force seemed to vanish in performing mechanical, chemical, or other work, it was actually undergoing a transformation and reappearing in a new active form, having the same intensity as the original one (Colding, 1850). On the advise of Hans Christian Ørsted (1777-1851), his former teacher and councilor at the Polytechnic Institute, Colding decided not to present his arguments at the meeting of Natural Philosophers held in Copenhagen in 1840, until he could substantiate them with experimental data. Accordingly, he performed a series of experiments on the heat disengaged in friction phenomena and in 1843 he presented his results to the Royal Society of Copenhagen in the form of a memoir, entitled Theses Concerning Force (Colding, 1856b). In this memoir he stated that "although we cannot know or comprehend what is that constitutes the nature of every force, but we perceive them through their effects, we can draw the following conclusions: (a) When certain moving forces not in equilibrium act on a material point some momentum is imparted, proportional to the acting force. This momentum is imparted to the surrounding parts and propagated from these... so that the originally momentum... is distributed through such a large mass that every perceptible trace of the action as disappeared, (b) one cannot assume that an action may be gradually lost in the material without... giving rise to perceptible action of the same magnitude... the forces must reappear as acting in other ways, (c) when a force seems to disappear it merely undergoes a transformation."

Colding indicated that the results of other scientists were in good agreement with his thesis. For example, Dulong's work on the compression and expansion of gases, of Ørsted on the compression of water and other non-elastic fluids, and of Berthollet, Lagerhjelm, Rumford, Haldat and Morosi on the compression of solids, all indicated that the heat evolved on the compression of gases, liquids, and solids was proportional to the quantity of mechanical energy spent. Colding described then his own experiments for obtaining more precise measurements of the relation between the mechanical work spent and the heat produced by the friction between brass and various solids (brass, zinc, lead, iron, wood, and linen). A total of 200 experiments were made under different pressures and with different velocities and all their results again indicated that the heat released was always proportional to the mechanical energy lost. His conclusions were that "...all earlier well known researches on the evolution of heat upon the loss of moving forces, as well as all my experiments on the proportionality between heat due to friction and the lost force apparently confirm very satisfactorily the above thesis; namely, that when a force seems to disappear it is merely transformed and reappears in other forms... I believe that this thesis holds not only with regard to moving forces; I believe one can assume it as being universally valid for other forces, such that when, for instance, opposing chemical forces annihilate their respective effects, then in reality the form of the force is annihilated, the force appears in other forms but with the original magnitude... for a complete proof of the impossibility of perpetual motion this thesis seems so pressingly necessary that without it every such proof must be regarded as false."

In addition, Colding remarked that an examination of his numerical results showed that "independently of the materials by which the friction and the heat arose, an amount of mechanical work equal to 350 kilogram metre should be able to raise the temperature of 1 kilogram of water 10°C, which is very near the proportion (365 to 1) that M. Mayer in 1842 supposed, but did not prove, to be right."

As told by Dahl (Dahl, 1963), Colding's paper was not printed in the transactions of the Royal Society until thirteen years later (December, 1856), although the Society encouraged him to continue his experiment and granted him a small sum for this purposes.

The new results, described at a meeting of the Society in 1847, indicated that the heat required to increase the temperature of one pound of water by 10°C, was equivalent to the lifting of 1185.4 pounds one foot (3.65 J/cal). Some time afterwards Colding corrected the mechanical equivalent to 1204.3 pounds (3.71 J/cal).

In 1856, Colding published his last memoir on the subject, entitled "A Physical Investigation into the General Relationship Between the Intellectual Powers and the Forces of Nature" (Colding, 1856a) where he tried to show that the "new principle of the perpetuity of the forces of nature had made such progress in all branches of Natural Philosophy that there was scarcely any doubt left that this principle would be found to comprise, a true law for the whole of nature, and perhaps one of the grandest and most successful laws known to us." Here he stated very clearly that as no power is lost in nature, so no power is able to grow in nature, except at the expense of some other power. From here he went on to more philosophical consequences. Acceptance of Immanuel Kant (1724-1804) and Pierre-Simon Laplace's (1749-1827) hypothesis that the world originally given by the Creator was an extremely subtle elastic fluid rotating around an axis, kept together by the mutual gravitation of the particles of the fluid, and assumed to contain all the chemical elements, then the principle of conservation of power allowed assuming that the original material substance had none of the qualities, which characterized the chemical elements, except in so far as it was subjected to the force of gravitation. Then, "without generating a quantity of energy (vis viva) equal to the work done by the force of gravity no condensation of the fluid could take place; and as no loss of energy could take place; and no loss of energy could occur, it had to be admitted that the quantity of energy generated made its appearance in the form of electricity or chemical affinity, different in quality and quantity according to the situation of the matter in the universal globe, which during the conversion, of the quantity of energy thus generated into chemical affinity may be supposed to have divided itself into a great number of smaller globes in a more or less fluid condition."

"As soon as the different chemical substances came into contact with each other, chemical action of course began, and the heat was raised very considerably; but as the pressure and heat were very different in different parts of the earth, for instance, it is possible to understand how the variety of minerals could arise which compose the crust of the earth, and of which it must necessarily be composed in order that organized beings may be able to live upon it. During these great preparations, by which the earth was acquiring its adaptation to the future life upon it, the chemical forces were in a great measure converted into heat, a part of which is preserved in the earth so as to keep the temperature of the surface very nearly constant... At the same... the surface of the earth was passing over from the fluid into the solid state to give a field for a vigorous vegetation, which directly appeared as, soon as the ground was prepared that the plants could meet with the forces proper to the ideal of each individual plant. But remembering the fact that not force is lost, and that no force can grow up out of nothing, it is clear that in the plants a new arena was opened for the action of the several forces, which, from this time were able to take the action on the forms that give origin to each individual plant."

Colding went on to describe the evolution of living things, as the consequence of one factor creating the necessary requirements for the next stage: "After the vegetation had prepared the earth's surface sufficiently for animal life to subsist we find that animal beings living on the plants or at the expense of the energy stored in them were created... By and by new animals, living on the former kinds, were created and after all we find human beings at last created by God... the existence of human life was not possible until the earth was sufficiently prepared and cultivated by the vegetable and animal life which should sustain the life of man; that the intellectual powers of man are but new forms of the powers of nature... by the direct action of the electrical, chemical, mechanical, and magnetic forces, the quantity of energy is constantly increasing at the expense of the quantity of energy intimately connected with matter, but also that the same law holds true whenever we arrange it so that the forces must work in the contrary way... as it is always necessary to employ more power to do the work than we can get stored up by the action, and as the surplus of power is always liberated in the form of vis viva. Consequently the direct action of the forces of nature is to liberate themselves from intimate connection with matter... And as this is a general law of nature for the action of the electrical and chemical, the magnetic and mechanical forces, there is certainly no reason the belief that it should not be a general law for all the forces of nature... Intellectual life commenced with the creation of human beings... I think it must be satisfactory to us to see that according to the principle of perpetuity of energy, we arrive at the conclusion that the intelligent life of man must be an intelligent life forever!"

As stated by Sarton (Sarton, 1929) Colding's memoirs contained not only views very similar to those of Mayer's, but also the account of original experiments. Unfortunately they were published late and in Danish. Moreover it fell short of Mayer and Joule's work for the same reason as Séguin's: it proved the proportionality of heat and work, but failed to calculate the factor of proportionality.

 

Julius Robert Mayer (1814-1878)

Mayer was neither a mathematician, nor an experimental physicist; in the course of his service as a doctor aboard a Dutch ship he discovered the law of conservation of energy by a sudden intuition, by purely abstract means. Although he performed no experimentation he used with considerable cleverness the experimental results of others. He wrote his first paper on the subject (Mayer, 1842) on June 16, 1841 and sent it to Johann Christian Poggendorff's (1796-1877) Annalen der Physik und Chemie, who rejected it and did not return it with an explanation. Fortunately in 1842 Justus von Liebig (1803-1883) accepted a corrected version of it for publication in the Annalen der Chemie und Pharmacie. This was the first paper containing a clear statement of the law of conservation of energy and contained an estimate (very inaccurate) of the value mechanical equivalent of heat. This publication was followed by several others containing elaborations of his views (Mayer, 1848, 1851; Sarton, 1929).

Mayer believed that the creation or annihilation of a force lies without the province of human thought and power. Joule expressed himself to a similar effect: "It is manifestly absurd to suppose that the powers with which God has endowed matter can be destroyed."

In his paper Remarks on the Forces of Nature (Mayer, 1842) Mayer addressed the question what is understood by forces and how different forces are related to each other. To him, forces are causes to which the principle of causa æquat effectum (the cause equals the effect) is applicable. Since in the chain of causes and effects a term can never become zero then causes are indestructible and quantitative objects; since causes can assume various forms they are also qualitatively convertible and imponderable objects. As an example, Mayer writes that the force that causes the fall of objects is related to motion as cause and effect; they are convertible one into the other, two forms of one and the same object. The magnitude of the falling force v is proportional to the magnitude of the mass and the height to which it is raised, that is v = mh and since the measure of the force v is mc² it results that v = mc²; the law of conservation of vis viva is thus found to be based on the general law of indestructibility of causes.

An interesting portion of this paper is Mayer's discussion of the relation between work, motion, and heat. His opening statement: "in numberless cases we see motion cease without having caused another motion or the lifting of a weight, but a force once in existence cannot be annihilated, it can only change its form, and the question arises, what other forms is force... capable of assuming?", leads him to the question whether motion is the cause of heat, whether in the numerous causes in which the expenditure of motion is accompanied by the appearance of heat, the motion has no other effect than the production of heat and the heat some other cause than the motion. "Without the recognition of a causal connection between motion and heat it is just as difficult to explain the production of heat as it is to give any account of the motion that disappears." Mayer described his own experiments in which violent shaking increased had the temperature of water from 12° to 13°C, and then asked the question: "whence now comes this quantity of heat?" His answer was that "if it is now considered that in many cases no other effect of motion can be traced except heat, and that no other cause than motion can be found for the heat that is produced, we prefer the assumption that heat proceeds from motion, to the assumption of a cause without effect and of an effect without a cause... If falling force (today, potential energy) and motion are equivalent to heat, heat must also naturally be equivalent to motion and falling force... A locomotive engine with its train may be compared to a distilling apparatus; the heat applied under the boiler passes off as motion, and this is deposited again as heat at the axles of the wheels."

Mayer closed his paper with a calculation of the mechanical equivalent of heat, "how great is the quantity of heat which corresponds to a given quantity of motion or falling force (how much thermal energy is equivalent to a give amount of kinetic or potential energy)? Using the known experimental value 1.421 for the ratio of the specific heats of air, c_P /c_V, he concluded (without giving the details of his calculations) that the warming of a given weight of water from 0° to 10°C corresponded to the fall of an equal weight from the height of 365 meters (in today's units, 3.59 J/cal). Later Victor Regnault (1810-1878) showed that c_P actually is 0.238 cal/g·°C and c_p/c_V is more nearly 1.40. With these values Mayer's calculations yield a value for the mechanical equivalent of heat in agreement with Joule's measured result.

The details of the calculation of the mechanical equivalent of heat appeared in Mayer's following paper, The Motions of Organisms and Their Relation to Metabolism (Mayer, 1845), which was also rejected and Mayer published it as a monograph (very lengthy, 112 pages). In it he states clearly: "Heat is a force, it may be transformed into mechanical effect" and in reference to a steam engine, "the work done by the machine is inseparably bound to a consumption of heat." Truesdell (Truesdell, 1980) repeats the derivation of the value of the equivalent, as follows: When a gas expands under a piston that exerts a constant pressure P, it gives work at the rate PV, where V(t) is the volume of the gas. At the same time, heat is imparted to the gas at the rate K_Pθ, where is K_P the specific heat at constant pressure and θ the ideal gas temperature. Mayer regards the amount of thermal energy that does work as being (K_P - K_V)θ, where K_V is the specific heat at constant volume. Mayer's general idea of equivalence leads him to assume that the mechanical power generated by this heating will be proportional to it. If the factor of compressibility is J, then the power corresponding to this heating is J(K_P - K_V)θ so

At constant pressure the equation of the state of an ideal gas, PV = Rθ, leads to

All the quantities in the right hand side of eq. 3 can be measured, and substitution of three particular values available to Mayer yields the number he obtained for J. Mayer writes "the same result is obtained if instead of atmospheric air another simple of compound kind of gas is used for the calculation. Heat = mechanical effect is independent of the nature of the elastic fluid, which serves only as a tool for effecting the transformation of the one force into the other." As an example, Mayer carries the numerical calculation for carbon dioxide and for olefiant gas (ethylene), obtaining exactly the same numerical value for J (Truesdell, 1980).

In his following paper about Celestial Mechanics (Mayer, 1863) Mayer discusses the reasons why the sun maintains its power undiminished and continues to send its rays into the universe. Before turning his attention to the subject he considered the means by which heat and light are produced. Here he repeated the arguments he had stated in previous publications: "A general law of nature which knows no exception, is the following: In order to obtain heat, something must be expended; ...this something can be referred to one of two categories, either it consists of some material expended in a chemical process, or some sort of mechanical work... The amount of heat obtained by mechanical means is dependent only on the quantity of power expended and is quite independent of the manner in which this power has been expended. If therefore, the amount of heat which is produced by certain mechanical work is known, the quantity which will be obtained by any other amount of mechanical work can be easily found by calculation." In other words, heat and mechanical work obtained by compression, percussion, or friction, are equivalent entities. Mayer then states that mechanical work may like wise be measured by the velocity obtained by a given weight in passing from a state of rest into that of motion, and that this work is expressed by the product of the weight by the square of its velocity, which he calls vis viva of motion, work done, dynamical effect, or quantity of work. He gives the amount of mechanical work necessary for heating one kilogram of water 1°C as 367 kg·m.

Mayer analyzed the different possibilities for keeping the temperature of the sun constant and arrived at the conclusion that unless we assume the existence of matter with unheard chemical properties as a deus ex machine, no chemical process could maintain the present high radiation of the sun (nuclear processes were not known then). The only reasonable one explanation was the falling of celestial bodies on the sun itself. He calculated that one of such bodies on arriving at the sun is moving at least as quickly as a weight which falls freely towards the sun from a distance as great as the solar radius and thus the conversion of kinetic energy into heat develops from 4600 to 9200 times as much heat as would be generated by the combustion of an equal mass of coal.

The last paper of Mayer on the subject, Remarks on the Mechanical Equivalent of Heat (Mayer, 1851), was published in 1851, again as a private document. Here he repeats the basic arguments raised in previous publications, "if we... measure the quantity of heat developed by mechanical energy, as well as the amount of force used in producing it, and compare these quantities with each other we find that they stand to each other in the simplest conceivable relation... in direct proportion, which holds inversely when mechanical force is again produced by the aid of heat... Heat and motion are transformable one into the other... the law of invariable quantitative relation between motion and heat must be expressed numerically." Mayer then repeats the value of the mechanical equivalent of heat that he had previously reported.

The paper follows with a relation of the events that led Mayer to discovery of the principle of conservation of energy. In 1840 while studying the medical fact that newly arrived Europeans in Java used to bleed, he found that blood taken from veins of the affected had a surprisingly bright red color. His medical background led him to understand that the color change that blood underwent in the capillaries was a result of oxidation processes taking place in the fluid, and that the production of heat and the process of oxidation must be less in the torrid zones than in colder regions. The redness of the venous blood means less oxidation of the food consumed and hence less heat is produced. The person living in the tropics does not need this heat and hence will not oxidize as much food material. A general balance must be stroke in the organism between receipts and expenditure, or between work done and wear and tear; where wear and tear consists in the amount of matter consumed and work done is the evolution of heat. Since the chemical effect of combustible matter must be the same, whether performed within a living organism, or outside it, "it follows that the heat produced mechanically by the organism must bear an invariable quantitative relation to the work expended in producing it" and this is a "postulate of the physiological theory of combustion."

In a paper published in 1849, Joule (Joule, 1849) came against Mayer's claims that he had discovered the equivalence between heat and kinetic energy. Joule justified his right to the paternity of the idea by saying that in 1841 he had already discovered that the heat produced by a galvanic pile was proportional to power, for a given amount of zinc consumed. Not only that, he had also reported that the amount of heat produced by the combustion of the equivalent of a body was proportional to the intensity of its affinity for oxygen, and that heat released by electromagnetic devices was governed by the same laws the regulate the heat produced in a voltaic pile. The overall results of his different experiments proved that "la quantité de calorique capable d'augmenter un gramme d'eau de 1 degré centigrade est égale à, et peut être convertie en une force mécanique capable d'élever 459 grammes a la hauteur d'un métre (the amount of caloric capable of heating one gram of water by 1°C is equal and can be converted into a mechanical force capable of elevating 459 grams to the height of one meter). Joule also indicated that in 1844 he had published his results indicating that the heat developed during the compression of a gas was equivalent to the compression work employed, and that the free expansion of a gas (without mechanical effects) did not change its temperature.

This communication was closed with the statement: "D'aprés ces faits, tout le monde appréciera la sagacité de M. Mayer à prédire les relations numériques qui seraient établies entre la chaleur et la force, mais on ne pas nier, je crois, que j'aie été le premier qui ait démontré l'existence de l'équivalent mécanique de la chaleur, et qui ait fixé sa valeur numérique par des experiences incontestables" (after these facts, everyone will appreciate the sagacity of Mr. Meyer to predict the numerical relations to be established between heat and force, but it cannot be refuted, I believe, that I have been the first to prove the existence of the mechanical equivalent of heat and fixed its numerical value by undisputable experiences).

 

James Prescott Joule (1818-1889)

Mayer's philosophical discovery was confirmed and completed by the experimental investigations made independently at about the same time by Joule, an extremely capable experimentalist. He devised many different methods and built the appropriate equipment by means of which the mechanical equivalent of heat (or the thermal equivalent of work) could be determined with increasing precision. His first paper on the subject was read at the thirteenth annual meeting of the British Association for the Advancement of Science, held on August 21, 1843, at Cork, Ireland, and printed in the Philosophical Magazine (Joule, 1843; Sarton, 1929). In this memoir Joule described his experiments on the "calorific" effects of magneto-electricity and the calculation of the mechanical value of heat. The experimental results led him to state that the heat evolved by a bar of iron revolving between the poles of a magnet was proportional to the square of the inductive force; that the heat evolved by the coil of the magneto-electrical machine was proportional to the square of the current; that the heat evolved by the coil of the magneto-electrical engine was governed by the same laws as those which regulate the heat evolved by the voltaic apparatus, and also existed in the same quantity under comparable circumstance; that the heat evolved by a revolving bar of iron was proportional to the square of the magnetic influence to which it was exposed' and that magneto-electricity was an agent capable of destroying or generating heat.

His final conclusion was that "the quantity of heat capable of increasing the temperature of a pound of water by one degree Fahrenheit's scale is equal to, and may be converted into, a mechanical force capable of raising 838 lbs to the perpendicular height of one foot." He admitted that there was considerable difference between some of his results, but he believed that they were not greater "than may be referred with propriety to mere errors of experiment." He then stated what he believed were "the practical conclusions, which may be drawn from the convertibility of heat and mechanical power into one another" (a) "The combustion of a pound of Welsh coal gives 183° to a cubic foot of water, or otherwise 11.437° to a pound of water... therefore the heat evolved by the combustion of a pound of coal is equivalent to the mechanical force of raising 9,584,206 pounds to the height of one foot, or about 10 times the duty of the best Cornish engines, and (b) one pound of zinc consumed in Daniell's battery produces a current evolving about 1320°; in Grove's battery, about 2200° per pound of water. Therefore the mechanical forces of the chemical affinities, which produce the voltaic currents in these arrangements, are, per pound of zinc, equal respectively to 1,106,160 pounds and 1,843,600 pounds raised to the eight of one foot. But since it will be practically impossible to convert more than about one half of the heat of the voltaic circuit into useful mechanical power, it is evident that the electromagnetic engine, worked by the voltaic batteries at present used, will never supersede steam in an economical point of view."

On April 28, 1847, Joule gave his first and only full and clear exposition of the universality of what now we call the principle of conservation of energy, in a popular lecture at St. Ann's Church reading Room in Manchester on April 28, 1847 (Watson, 1947). As stated by Watson, In order to appreciate it properly it is necessary to remember that the terms potential energy and kinetic energy as used today, had not yet come into existence [the term potential energy was first introduced by William John Macquorn Rankine (1820-1872) in a paper read before the Philosophical Society of Glasgow in 1853, and the term kinetic energy was introduced by William Thomson, Lord Kelvin (1824-1907) in 1879, or a little earlier].

In the opening statements of his lecture On Matter, Living Force and Heat (Watson, 1947) Joule repeated the accepted philosophical and scientific ideas about the properties of matter: impenetrability, extension, weight, attraction and repulsion, and inertia. Inertia he explained was "the inability of any thing to change its own state, a body at rest cannot be set in motion without the application of a force and that once it is moving it will not stop of itself... the force expended in setting a body in motion is carried by the body itself, and exists with it and in it, throughout the whole course of its motion. This force possessed by moving bodies is termed by mechanical philosophers vis viva or living force. The living force of bodies is regulated by their weight and by the velocity of their motion.

"You will...be surprised to hear that until very recently the universal opinion has been that living force could be absolutely and irrevocably destroyed at any one's option. Thus, when a weight falls to the ground, it has been generally supposed that its living force is absolutely annihilated, and that the labour, which may have been expended in raising it... has been entirely thrown away and wasted without the production of any permanent effect whatever. We might reason, a priori, that such absolute destruction of living force cannot possibly take place, because it is manifestly absurd to suppose that the powers with which God has endowed matter can be destroyed any more than that they can be created by man's agency. We have reason to believe that the manifestations of living force on our globe are, at the present time, as extensive as those that have existed at any time since its creation.

What, then, may we inquire, is the cause of this apparent anomaly? How comes it to pass that, though in almost all natural phenomena we witness the arrest of motion and the apparent destruction of living force, we find that no waste or loss of living force has actually occurred? Experiment has enabled us to answer these questions in a satisfactory manner; for it has shown that, wherever living force is apparently destroyed, an equivalent is produced, which in process of time can be reconverted into living force. This equivalent is heat. Experiment has shown that wherever living force is apparently destroyed, whether by percussion, friction, or any similar means, an exact equivalent of heat is restored. The converse of this proposition is also true, namely, that heat cannot be lessened or absorbed without the production of living force, or its equivalent attraction through space.

The most convincing proof of the conversion of heat into living force has been derived from my experiments with the electromagnetic engine. I have proved by actual experiment that, in exact proportion to the force with which this machine works, heat is abstracted from the electrical battery... All three, therefore, namely, heat; living force, and attraction through space (to which I might also add light) are mutually convertible into one another. In these conversions nothing is ever lost... We can therefore express the equivalency as follows: The attraction of 817 lb through the space of one foot is equivalent to, and convertible into the living force possessed by a body of the same weight of 817 lb when moving with the velocity of 8 feet per second, and this living force is again convertible into the quantity of heat which can increase the temperature of 1 pound of water by 1°F.

The earth in its rapid motion round the sun possesses a degree of living force so vast that, if turned into the equivalent of heat, its temperature would be rendered at least 1000 times greater than that of red hot iron, and the globe would in all probability be rendered equal in brightness to the sun itself. And it cannot be doubted that if the course of the Earth were changed so that it might fall into the Sun, that body, so far from being cooled down by the contact of a comparatively cold body, would actually blaze more brightly than before in consequence of the living force with which the Earth struck the Sun being converted into its equivalent of heat. Here we see that our existence depends upon the maintenance of the living force of the Earth.

When we consider our own animal frames, we observe in the motion of our limbs a continual conversion of heat into living force, which may be either converted back again into heat or employed in producing an attraction through space, as when a man ascends a mountain. Indeed the phenomena of nature, whether mechanical, chemical, or vital, consist almost entirely in a continual conversion of attraction through space, living force, and heat into one another. Thus it is that order is maintained in the universe, nothing is deranged, and nothing ever lost, but the entire machinery, complicated as it is, works smoothly and harmoniously."

In another paper published in 1847 Joule (Joule, 1847) described the experiments he had done during the last 40 years to confirm the fact that heat was equivalent to mechanical work and stated that the most interesting of those were the ones related to the friction in liquids. He indicated that agitation of water by a paddle caused an increase in its temperature and that introduction of a mechanical equivalent of elevation of 428.8 grams to a height of one meter was equivalent to raising the temperature of one gram of water by one degree. Notwithstanding that agitation heated liquids in different degrees because of their difference in specific heat, the equivalence between mechanical energy and heat remained the same.

In this particular paper, Joule reported the results of experiments on the thermal effects observed during agitation of mercury initially at room temperature. The experimental system consisted of a vessel containing the liquid and a paddle, which could be rotated by the movement communicated by a mechanism activated by the falling of a weight. The weight and height of fall were used to determine the amount of mechanical energy communicated to the liquid, after taking into account the friction losses. The net heat absorbed by 13269 g of mercury resulted in a temperature increase of 2.2568°C, which again were equivalent to raising the temperature of one gram by one degree, by a mechanical force capable of raising a weight of 432.1 g by one meter.

 

Hermann Ludwig von Helmholtz (1821-1894)

As described by Kahl (Kahl, 1971), Helmholtz approached the problem of conservation of energy with the mentality and techniques of a physicist, trying constantly to analyze them in terms of the principles of physics.

In his most famous lecture on the subject (Helmholtz, 1847), given to the Physical Society of Berlin on July 23, 1847, Helmholtz stated "that the problem of the physical sciences is to trace natural phenomena back to inalterable forces of attraction and repulsion, the intensity of the forces depending upon distance. We shall begin with the assumption that it is impossible, by any combination whatsoever of natural bodies, to create force continuously out of nothing... The purpose of the present memoir is to extend the same principle, in the same manner, to all branches of physics."

The main body of the lecture is then divided into five sections, which will be summarized in what follows.

The first section opens with the assumption "that it is impossible, by any combination of bodies, to create force continuously out of nothing"; that is, the negation of a perpetuum mobile. According to Helmholtz, the principle may be presented as follows: "Let us imagine that a system of bodies, which stand in certain spatial relations to one another, are acted upon by the forces mutually exerted among them so that they are moved until other positions are reached. We can regard the velocities acquired in this way as a specific quantity of mechanical work and can translate them into it. If we wish the same forces to act a second time, so as to produce the same quantity of work again, we must somehow, by means of other forces placed at our disposal, bring the bodies back to their original positions. In doing this, however, a certain quantity of work of these other forces will be consumed. Our principle requires in this case that the quantity of work gained by the passage of the system from the first position to the second, and the quantity lost by the passage of the system from the second back to the first, always be equal, no matter what the form of the movement, the path, or the velocity at which the change is effected... If we inquire into the mathematical expression of this principle, we shall find it in the well-known law of the conservation of vis viva... half of the product mv²... I propose calling mv²/2 also the quantity of work.

After stating that the principle of the conservation of vis viva is not valid for all possible kinds of forces, that in mechanics it is generally related to the principle of virtual velocities, Helmholtz goes on to show mathematically that "the principle is valid only where the forces in action can be resolved into the forces of material points acting in the direction of the lines which unite them (central forces), the intensity of the forces depending only upon the distances between the points."

The second section deals with the principle of conservation of force for cases in which central forces are acting. First, Helmlholtz derives an expression for the vires vivae possessed by one particular mass m at two different distances, assuming that the intensity of the force φ which acts in the direction or r (central) is positive for attraction and negative for repulsion. The final relation is

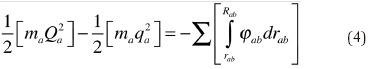
where Q and q are tangential velocities and R and r are distances. The left hand side of this equation represents the difference of the vires vivae possessed by m at two different distances and the right hand side the sum of the tensions between the distance R and r, that is, "The increase of vis viva of a material point during its motion under the influence of a central force is equal to the sum of the tensions which correspond to the alteration of its distance."

Extension of this relation to any number of points leads to

that is, "the sum of the existing tensions and vires vivae is always constant."

Helmholtz concludes this section as follows: "(a) Whenever natural bodies act upon each other by forces of attraction or repulsion, which are independent of time and velocity, the sum of their vires vivae and tensions must be constant; the maximum quantity of work which can be obtained from them is therefore fixed and finite; (b) if, on the contrary, bodies possess forces which depend upon time and velocity, or which act in other directions than the lines which unite each two separate material points, for example, forces of rotation, then combinations of such bodies would be possible in which force might be either lost or gained ad infinitum."

The third section deals with the applications of the principle to the theorems of mechanics, where Helmholtz discusses movements under the influence of gravity, the motion of perfectly elastic solids and fluids, elastic waves, and light phenomena such as reflection, refraction, polarization, and absorption.

In the fourth section Helmholtz deals with the force equivalent of heat, listing the processes in which absolute loss of force had been taken for granted: collision of inelastic bodies and friction, and then problems on heat radiation are examined. Analysis of the available information permits concluding that "the quantity of heat can be increased absolutely by mechanical forces and that thermal phenomena cannot be explained by the simple hypothesis of a substance whose mere presence produces the phenomena; there is need to changes of movements either of a special substance or of the ponderable or imponderable bodies, such as electricity or the ether" (!).

The fifth section deals with the force equivalent of electric processes and the manner in which electric tensions are converted into mechanical action. Many examples are the provided to show the application of the principle. The sixth section discusses the force-equivalent of magnetism and electromagnets and Helmholtz claims that the attractive forces exerted by one magnet on other magnets or soft iron is able to generate kinetic energy. This section is of special interest because it also discusses the case of organic forces: "Of known natural processes those of organic existence are still to be considered, In plants the processes are chiefly chemical, and besides these is a slight development of heat takes place... a vast quantity of chemical tensions is here stored up, the equivalent of which we again obtain as heat by the combustion of the plants. The only vis viva which we know to be absorbed in the accomplishment of this is that of the chemical solar rays... Animals... take up oxygen... and give back the same... as carbonic acid and water... they consume... chemical tensions, and generate in their place heat and mechanical force... By what has been laid in the foregoing pages, I believe I have proved that the law in question does not contradict any known fact in natural science, but in a great number of cases is... corroborated in a striking manner."

The last two sections are devoted the force equivalent of electrical processes and magnetism and electromagnetism. In the first of these, Helmholtz distinguishes between static electricity and metals that follow the law of the galvanic tension series, and those that do not follow this law. His conclusion is that "the increase in vis viva due to any motion whatsoever is equal to the excess of potential at the end of the route over its value at the beginning... the heat θ developed in any circuit whatsoever, where the conduction is effected through any number of branches, is given by θ = J²wt where J is the current intensity, w the resistance, and t the time."

In the analysis of magnetic problems Helmholtz adopts "the two-fluids theory, which attract or repel in the inverse ratio of the square of the distance... it follows without going further that the deduction made at the beginning of this memoir that the principle of conservation of force must hold for the movements of magnetic bodies relative to one another."

Helmholtz's memoir ends with a few remarks regarding organic beings: "In plants the processes are mainly chemical, although...in some a slight development of heat occurs...The only vis viva which we know to be absorbed during the growth of plants is that of chemical rays of sunlight; we are at a total loss, however, for means of comparing the force equivalents which are thereby lost and gained... In animals... the question of conservation of forces reduces to the question whether the combustion and transformation of the substances which serve as food generate a quantity of heat equal to that given out by animals. According to the experiments of Dulong and Despretz (Dulong and Despretz, 1841) this question can, at least approximately, be answered in the affirmative."

Interestingly enough, Poggendorf rejected the publication of this lecture and Helmholtz was forced to publish it privately (Helmholtz, 1847).

Helmholtz addressed the question of application of the law of conservation of force in an address given to the Royal Society on April 12, 1861 (Kahl, 1971): "At last, the general law of conservation of force was discovered... this law shows... no such machine can be constructed to give perpetual motion... We must consider the living bodies under the same point of view... Now if you compare the living body with a steam engine, then you have the complete analogy. The living animals take in food that consists of inflammable materials... and oxygen by respiration. Therefore...you have the substances in the steam engine. The living bodies give out carbonic acid and water and... they give up their nitrogen in the form of urea. Now... take an animal on one day, on any day afterwards. During this time... the animal has taken in food and oxygen and has given out carbonic acid, water and urea... the amount of urea may be changed without any great development of heat into...nitrogen, water and carbonic acid... The conservation of force for chemical processes requires a fixed amount of mechanical work, or its equivalent, to be given out during this process, and the amount is exactly the same in whatever way the process may go out... therefore we must conclude that by the animal as much wok must be done... as by the chemical process of burning... The mechanical work which is spent by an animal to the external world consist... in heat and... real mechanical work. Now we may ask, what follows from this fact as regards the nature of the forces, which act in the living body? The majority of the physiologists... were of opinion that the process in living bodies where determined by one principal agent, which they chose to call the vital principle. The physical forces in the living body... could be suspended or set free again at any moment by the influence of this vital principle and that by this means this agent could produce changes in the interior of the body, so that the health of the body could thereby be preserved or restored. Now the conservation of force can exist only in those systems in which the forces of action have always the same intensity and direction if the circumstances under which they act are the same. If were possible to deprive any body of its gravity, and afterwards restore its gravity, then indeed we would have the perpetual motion; let the weight come down as along as it is heavy; let it rise if its gravity is lost; then you have produced mechanical work from nothing. Therefore, this opinion that the chemical or mechanical power of the elements can be suspended, or changed, or removed from the interior of the living body, must be given up of there is complete conservation of force."

 

Closing remarks

The law of conservation of energy was heralded by Faraday as the most important discovery of the century, as the highest in physical sciences, which our faculties permit us to perceive (Youmans, 1876). Youmans went further in its praise: "this law has a far more extended sway, it might well be proclaimed the highest law of all science, the most far-reaching principle that adventuring reason has discovered in the universe. Its stupendous reach spans all orders of existence. Not only does it govern the movements of the heavenly bodies, but it presides over the genesis of the constellations; not only does it control those radiant floods of power which fill the eternal spaces, bathing, warming, illuminating and vivifying our planet, but it rules the actions and relations of men, and regulates the march of terrestrial affairs. Nor is its dominion limited to physical phenomena; it prevails equally in the world of mind, controlling all the faculties and processes of thought and feeling. The star-suns of the remoter galaxies dart their radiations across the universe; and although the distances are so profound that hundreds of centuries may have been required to traverse them, the impulses of force enter the eye, and impressing an atomic change upon the nerve, give origin to the sense of sight. Star and nerve-tissue are parts of the same system, stellar and nervous forces are correlated" (Youmans, 1876).

Justus von Liebig (1803-1883) commented it as follows (Youmans, 1876): For it two machines possess the same power, it is found that the greater quantity of work will be executed by the one which has to overcome the smaller amount of friction. In mechanics friction is always regarded as acting in direct opposition to motion in every machine. It was believed that the working power of a machine could be absolutely annihilated by it. As the proximate cause of the cessation of motion, friction was a palpable fact, and could as such be taken into account; but a fatal error was committed in giving a theoretical view of its mode of action. For if a power could be annihilated, or in other words, have nothing as its effect, then there would be no contradiction involved in the belief that out of nothing also power could be created. To this erroneous belief we may partly trace the belief, held for centuries by most able men, in the possibility of discovering a machine, which should renew within itself its own power as it was expended, and thus ever continue in motion, without the necessarily for any external motive force. The discovery of such a perpetual motion was, indeed, worthy of every effort. It would be as valuable as the bird that lays the golden eggs; for by its means labour would be performed, and made in abundance without any expenditure... Experience gives the answer by showing that whenever motion is arrested by friction, a blow, or concussion, heat is the result, The motion is the cause of heat." Liebig went one to illustrate the conversion of mechanical power, electricity, magnetic power, and chemical forces (such as in living things) into heat.

Nowadays, we take the law of conservation of energy as obvious and granted. It is very fit to quote Mach on this point (Mach, 1911): "We are accustomed to call concepts metaphysical if we have forgotten how we reached them... Quite analogous difficulties lie in wait for us when we go to school and take more advanced studies, when propositions which have often cost thousand years' labour of thought are represented to us as self-evident."

 

References

Bernoulli, D., Hydrodynamica, sive de viribus et motibus fluidorumcommentarii. Opus academicum ab auctore, dum Petropoli ageret, congestum; J. R. Dulseckeri, 1738. Translated and reprinted as Hydraulics, Dover Publications, New York, 1968.         [ Links ]

Colding, L. A., Undersögelse on de Almindelige Naturkraefter og deres Gjensidige Afhaengighed og Isaerdeleshed om den ved Visse Faste Legemers Gnidning Udviklede Varme, Dansk Vid Selsk Skr., II, 121-146 (1850).         [ Links ]

Colding, L. A., Naturvidenskabelige Betragtninger over Slægtskabet Mellem des Aandelige Livs Virksomheder og de Almindelige Natrukraefter, Oversigt Kgl Dansk Vid Selsk Forhandlinger, 8, 136-168 (May 1856a).         [ Links ]

Colding, L. A., Nogle Saetninger on Kræfterne, Oversigt Kgl Dansk Vid Selsk Forhandlinger, 8, 1-20 (December 1856b).         [ Links ]

Colding, L. A., On the History of the Principle of the Conservation of Energy, London Phil. J., 27, 56-64 (1864).         [ Links ]

Dahl, P. F., Ludvig Colding and the Conservation of Energy, Centaurus, 8, 174-188 (1963).         [ Links ]

D'Alembert, J. L., Traité de Dynamique, David, Paris, 1743.         [ Links ]

Dulong, P. L., Despretz, C. M., De la Chaleur Animale, Ann Chim Phys, [3], 1, 440-455 (1841).         [ Links ]

Guerlac, H., Selected Readings in the History of Science, Cornell, 1953: vol. 2, Part II, chapter XVII.         [ Links ]

Helmholtz, H., Über die Erhaltung der Kräft. Eine Physikalische Abhandlung, G Reimer, Berlin, 1847.         [ Links ]

Joule, J. P., On the Calorific Effects of Magneto-Electricity, and on the Mechanical Value of Heat, Phil Mag, 23, 263-276, 347-355, 435-443 (1843).         [ Links ]

Joule, J. P., Expériences sur l'Identité Entre le Calorique et la Force Mécanique. Détermination de l'Équivalent par la Chaleur Dégagée Pendant la Friction du Mercure, Compt Rendus, 25, 309-311 (1847).         [ Links ]

Joule. J. P., Sur l'Équivalent Mécanique du Calorique, Compt Rendus, 28, 132-135 (1849).         [ Links ]

Kahl, R., Selected Writings of Hermann von Helmholtz, Wesleyan University Press, Middleton, 1971.         [ Links ]

Kuhn, T. S., Energy Conservation as an Example of Simultaneous Discovery, in The Critical Problems in the History of Science, edited by Marshall Clagett, University of Washington Press, Madison, 1959, pp. 321-356.         [ Links ]

Mach, E., History and Root of the Principle of Conservation of Energy, translated by Philip E B Jourdain, The Open Court Publishing Co, Chicago, 1911.         [ Links ]

Mayer, J. R., Bemerkungen Über die Kräfte der Unbelebten Natur, Ann Chem Pharm, 42, 233-240 (1842); an English version appears in Phil Mag, 24, 371-377 (1862).         [ Links ]

Mayer, J. R., Die Organische Bewegung in Ihrem Zusammenhange mit dem Stoffwechsel, Dreschsler, Heilbronn, 1845. A translation appears in the book by R B Lindsay, Julius Robert Mayer. Prophet of Energy, Pergamon Press, 1973, pp. 76-145.         [ Links ]

Mayer, J. R., Beiträge zur Dynamik des Himmels, Heilbronn, 1848; an English version appears in Phil Mag, 25, 241-248, 387-409, 417-428 (1863).         [ Links ]

Mayer, J. R., Bemerkungen Über das Mechanische Aequivalent der Wärme, J U Landherr, Heilbronn, 1851; an English version appears in Phil Mag, [4], 25, 493-522 (1863).         [ Links ]

Sarton, G. The Discovery if the Law of Conservation of Energy, Isis, 13, 18-44 (1929).         [ Links ]

Truesdell, C., The Tragicomical History of Thermodynamics 1822-1854, Springer-Verlag, New York, 1980, pp. 155-158.         [ Links ]

Verdet, É., Exposé de la Théorie Méchanique de la Chaleur, Lahure, Paris, 1862; pp 109-118 [An English summary of these pages appeared in Phil Mag, 25, 467-472 (1864)]         [ Links ].

Watson, E. C., Joule's Only General Exposition of the Principle of Conservation of Energy, Am J Phys, 15, 383-384 (1947).         [ Links ]

Wisniak, J., Conservation of Energy - Readings on the Origin of the First Law of Thermodynamics, Part I, Educ. quím., 19[2], 157-171 (2008).         [ Links ]

Youmans, E. L., The Correlation and Conservation of Forces: A Series of Expositions by Prof. Grove, Prof. Helmholtz, Dr. Mayer. Dr. Faraday, Prof. Liebig, and Dr. Carpenter, Appleton and Co, New York, 1876.         [ Links ]