Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista fitotecnia mexicana
versão impressa ISSN 0187-7380
Rev. fitotec. mex vol.35 no.3 Chapingo Jul./Set. 2012
Artículos científicos
Fórmula para estimar la proporción de plantas genéticamente modificadas mediante pruebas de grupo
Formula for estimating the proportion of genetically modified plants using pooled samples
Osval A. Montesinos López1*, Laura S. Gaytán Lugo1 y Abelardo Montesinos López3
1 Facultad de Telemática, Universidad de Colima. Bernal Díaz del Castillo No.340, Col. de San Sebastián. 28045, Colima, Colima, México. * Autor para correspondencia (oamontes1@yahoo.com.mx)
2 Facultad de Ingeniería Mecánica y Eléctrica, Universidad de Colima. km. 9 Carr. Colima-Coquimatlán. 28400, Coquimatlán, Colima, México.
3 Departamento de Estadística, Centro de Investigación en Matemáticas (CIMAT). Guanajuato, Guanajuato, México.
Recibido: 7 de Julio del 2011
Aceptado: 27 de Julio del 2012
Resumen
La detección y estimación de la prevalencia de plantas genéticamente modificadas (presencia accidental de las plantas transgénicas no deseadas) está atrayendo una gran atención pública debido a las preocupaciones por los posibles riesgos en la salud de los consumidores. El modelo de Dorfman (pruebas de grupo) es útil para la estimación de proporciones pequeñas (≤ 10 %), ya que produce ahorros de hasta 80 % en el número de pruebas de laboratorio requeridas. Aquí se propone una fórmula para calcular el tamaño de muestra requerido para estimar la proporción de plantas genéticamente modificadas, la cual garantiza intervalos de confianza (IC) angostos porque con una alta probabilidad asegura que el intervalo de confianza observado sea menor que el valor especificado. Dicha fórmula se obtiene con los supuestos de homogeneidad en la distribución de plantas transgénicas en la población y con una prueba diagnóstica imperfecta (sensibilidad y especificidad menor que uno, o menor que 100 %). Esta fórmula brinda el número de grupos necesarios para estimar la proporción de plantas transgénicas y garantiza una alta probabilidad de que el IC observado sea menor que el valor deseado. Se presentan cuadros con escenarios prácticos para los investigadores y un programa en R para obtener el tamaño de la muestra de una manera fácil.
Palabras clave: Pruebas de grupo, tamaño de muestra, intervalos de confianza angostos.
Abstract
Detection of the presence of genetically modified (accidental presence of unwanted transgenic plants) plants is attracting a great deal of public attention due to food safety concerns. Group testing under the Dorfman models is useful for estimating small proportions (≤ 10 %) because it produces savings of up to 80 % in the required number of diagnostic tests. We propose a sample size formula that guarantees narrow confidence intervals for estimating the proportion, because a high probability ensures that the observed confidence interval (CI) will be less than the specified value. The proposed sample sizes formula is derived by assuming homogeneity in the distribution of transgenic plants in the population and considering an imperfect diagnostic test (sensitivity and specificity less than 1, or less than 100 %). This formula gives the necessary number of groups to estimate the proportion of transgenic plants and guarantees a high probability that the observed CI will be smaller than the desired value. Tables with practical scenarios for researchers are presented here, as well as an R program for obtaining the required sample size in an easy way.
Key words: Group testing, sample size, narrow confidence intervals.
INTRODUCCIÓN
México es un país megadiverso, que posee una de las mayores riquezas biológicas a nivel mundial; como tal, tiene el reto de aplicar la regulación y normar el uso de organismos genéticamente modificados (OGM) para proteger su patrimonio natural en riesgo. Esta realidad ha creado consternación con respecto al flujo de genes de plantas genéticamente modificadas (GM) a sus parientes silvestres. Esto es especialmente importante en México por ser centro de origen del maíz (Zea mays L.) (Otero-Arnaiz, 2007), y porque los efectos de cruzar maíz GM con el maíz nativo y sus parientes silvestres como tripsacum y teocinte, son desconocidos (Hernández–Suárez et al., 2008).
Hay resultados contrastantes en cuanto a la presencia o ausencia de OGM en los maíces mexicanos. Quist y Chapela (2001, 2002) fueron los primeros en reportar la existencia de genes GM en los maíces nativos recolectados en la región Sierra Juárez en el Estado de Oaxaca. Cuatro años después, Ortiz-García et al. (2005a; 2005b; 2005c) concluyeron que no hay presencia de maíces transgénicos en esa misma región del Estado de Oaxaca. Dos estudios recientes en México muestran la presencia de OGM en las regiones suroeste y centro oeste de México; uno de ellos reporta que 3.1 y 1.8 % de las muestras estudiadas resultaron positivas para presencia de transgénicos (Dyer et al., 2009); el otro muestra evidencia de 1.1 % de transgénicos detectados con base en la reacción en cadena de la polimerasa (PCR, por sus siglas en inglés) y 0.89 % con base en la técnica Southern Blot (Piñeyro-Nelson et al., 2009). Sin embargo, Cleveland et al. (2005) considera que hay que mejorar los métodos de muestreo para mejorar la credibilidad de los estudios.
Puesto que las pruebas de laboratorio son muy costosas y no es factible analizar todas las plantas (o semillas) de manera individual, el método de pruebas de grupo permite juntar el material de k plantas y mezclarlo perfectamente. Así, en lugar de usar pruebas en forma individual se hace una sola prueba de la mezcla resultante de las k plantas (Remund et al., 2001; Hernández–Suárez et al., 2008). Gracias al ahorro significativo de tiempo y dinero por usar pruebas de grupo, en lugar de métodos convencionales, su uso aumenta día a día. Esta técnica se ha utilizado para detectar enfermedades en la sangre (Dodd et al., 2002), para detección de drogas (Remlinger et al., 2006), para estimar la prevalencia de enfermedades en humanos (Verstraeten et al., 2000), en plantas (Tebbs y Bilder, 2004) y en animales (Peck, 2006); también se ha usado para la detección de plantas transgénicas (Hernández-Suárez et al., 2008, Montesinos-López et al., 2010), y para resolver problemas de ciencia ficción (Bilder, 2009). No obstante, se debe tener cuidado con la elección del tamaño del grupo para que la sustancia de interés no se diluya por debajo de la sensibilidad de las pruebas de laboratorio y, por ende, no se aumente la tasa de falsos negativos.
El tamaño de muestra tradicionalmente se ha formulado en términos de potencia (pruebas de hipótesis). Recientemente ha crecido el interés en el uso de intervalos de confianza (IC) en lugar de pruebas de hipótesis para hacer inferencias (Pan y Kupper, 1999). La gran ventaja de los IC es que son relativamente cercanos a los datos y se expresan en la misma escala de medida, mientras que los valores p (probabilidad de obtener un resultado al menos tan extremo como el que realmente se ha obtenido -valor calculado del estadístico de prueba-, al suponer que la hipótesis nula es cierta) son probabilidades abstractas. Además, los IC transmiten información sobre magnitudes y precisión, y mantienen estos dos aspectos de medición cercanamente ligados (Newcombe, 1998; Kelley et al., 2003). El usual intervalo de confianza bilateral se interpreta simplemente como margen de error de una estimación puntual (Newcombe, 1998).
Por lo anterior, se ha dado una creciente atención al diseño de métodos para calcular tamaños de muestra apropiados para IC. Este enfoque en la estimación de tamaños de muestra ha sido denominado aseguramiento de precisión en la estimación de parámetros (APEP), ya que cuando disminuye el ancho del IC con (1 - α) 100 % de confianza, la exactitud esperada en la estimación incrementa (Kelley et al., 2003; Kelley y Maxwell, 2003; Kelley y Rausch, 2006; Montesinos-López et al., 2010). Si bien el enfoque APEP para planificar el tamaño de muestra no es nuevo (Mace, 1964), ha sido examinado más en las ciencias sociales que en ciencias veterinarias y agrícolas (Montesinos-López et al., 2010).
Para estimar los tamaños de muestra es necesario obtener información de algunos parámetros. En la práctica estos parámetros son desconocidos y usualmente son estimados con base en literatura o en estudios piloto. Estas estimaciones son tratadas como parámetros verdaderos, es decir, sin tomar en cuenta la incertidumbre inducida por dichas estimaciones. Como resultado, el tamaño de muestra resultante normalmente da un mayor ancho del IC que el deseado para estimar un parámetro (Wang, 2005). Para dar cuenta de tal incertidumbre inducida por haber usado una estimación del parámetro desconocido, Kelley et al. (2003) y Kupper y Hafner (1989) enfatizan que la naturaleza estocástica del ancho del IC debe ser considerado para evitar subestimaciones grandes de los tamaños de muestra requeridos con la anchura deseada. En particular, estos autores muestran el fenómeno de subestimación en forma numérica al estimar el promedio de una muestra proveniente de una distribución normal y de dos medias provenientes de dos muestras normales bajo el supuesto de igualdad de varianzas. Wang y Kupper (1997) ampliaron esta metodología en muestras aleatorias de dos poblaciones normales con varianzas desiguales.
Los actuales protocolos de muestreo para determinar la presencia de OGM en lotes de grano o en materias primas a granel, a menudo no garantizan precisión en la estimación de parámetros (Hernández-Suárez et al., 2008; Yamamura e Hino, 2007), o requieren una solución computacional (Montesinos-López et al., 2010). Por ello, el objetivo de esta investigación es proponer un método analítico para determinar el tamaño de muestra requerido bajo el marco del modelo de Dorfman (1943), que permita estimar la proporción de plantas transgénicas (p) y garantice un IC angosto y que tome en cuenta la sensibilidad y la especificidad de la prueba de laboratorio.
MATERIALES Y MÉTODOS
Para determinar los tamaños de muestra requeridos bajo pruebas de grupo se necesita contar con la varianza de una proporción a partir de una muestra aleatoria simple (MAS).
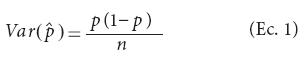
donde Var  denota la varianza del estimador de la proporción, p es la proporción poblacional, y n representa el tamaño de muestra efectivo, porque la varianza [Var
denota la varianza del estimador de la proporción, p es la proporción poblacional, y n representa el tamaño de muestra efectivo, porque la varianza [Var ] se deriva a partir de una distribución binomial bajo la suposición de que hay distribución homogénea de plantas transgénicas en la población, que la prueba de laboratorio es perfecta y que se realizaron pruebas individuales (es decir, a cada planta se le aplicó una prueba de laboratorio). Por prueba perfecta se entiende aquella cuya sensibilidad y especificidad es igual a 100 %. De igual manera, se requiere la varianza del estimador de una proporción bajo una prueba imperfecta (sensibilidad y especificidad menor a 100 %) mediante pruebas de grupo y suponiendo homogeneidad. Esta varianza, de acuerdo con Tu et al. (1994), es igual a
] se deriva a partir de una distribución binomial bajo la suposición de que hay distribución homogénea de plantas transgénicas en la población, que la prueba de laboratorio es perfecta y que se realizaron pruebas individuales (es decir, a cada planta se le aplicó una prueba de laboratorio). Por prueba perfecta se entiende aquella cuya sensibilidad y especificidad es igual a 100 %. De igual manera, se requiere la varianza del estimador de una proporción bajo una prueba imperfecta (sensibilidad y especificidad menor a 100 %) mediante pruebas de grupo y suponiendo homogeneidad. Esta varianza, de acuerdo con Tu et al. (1994), es igual a

donde P*=[1-(1 -p)k ]Se + (1- p)k [1-Sp] (Tu et al., 1994), g = n/k es el número de grupos, k = tamaño de grupo, Se = sensibilidad, y Sp = especificidad de la prueba de laboratorio. La sensibilidad (Se) es la probabilidad de que la prueba de laboratorio resulte positiva porque la planta es transgénica (es decir, la habilidad de la prueba de laboratorio para correctamente clasificar a las plantas transgénicas). La especificidad (Sp) es la probabilidad de que la prueba de laboratorio resulte negativa cuando la planta no es transgénica (es decir, la habilidad de la prueba diagnóstica para identificar correctamente a las plantas no transgénicas).
Por ejemplo, si se analizan 1000 plantas transgénicas y 891 de ellas resultan positivas, esta prueba tiene una sensibilidad de 89.1 %). Por el contrario, si 1000 plantas no transgénicas son analizadas y 985 resultan negativas, la prueba tiene una especificidad de 98.5 %. Por ello es de gran importancia contar con pruebas diagnósticas con alta sensibilidad y especificidad para evitar altas tasas de falsos negativos (FN), que es la probabilidad de que un individuo resulte negativo cuando realmente es positivo (FN = 1 - Se), y de evitar falsos positivos (FP) que es la probabilidad de que un individuo (o planta) sea detectado positivo siendo negativo (FP = 1 - Sp) (Remund et al., 2001). Una buena práctica es ajustar los estimadores de la prevalencia (proporción) por la sensibilidad y especificidad de la prueba diagnóstica. Los valores a usar de sensibilidad y especificidad vienen dados por las pruebas diagnósticas; sin embargo, cuando se utilizan pruebas de grupo en lugar de pruebas individuales existe la necesidad de hacer pruebas preliminares para usar estimaciones de Se y Sp más apropiadas y de esa manera evitar problemas de falsos negativos y positivos.
Estimación de los tamaños de muestra y los efectos de diseño
Sea el caso de estimar el tamaño de muestra mediante pruebas de grupo porque la prueba de laboratorio es imperfecta (sensibilidad y especificidad menor a 1). A continuación se deriva el estimador del tamaño de muestra con el método propuesto por Faes et al. (2009). Al igualar la Ec. 1 con la Ec. 2 y resolver para g, se tiene que

donde n = tamaño de muestra efectivo obtenido bajo la distribución binomial (Ec. 1), al suponer una prueba perfecta y homogeneidad en la distribución de las plantas GM (obtenido en la siguiente sección, que puede ser np sin aseguramiento o nm con aseguramiento);  es el efecto de diseño para una prueba imperfecta bajo homogeneidad mediante pruebas de grupo; g = n/k es el número de grupos requeridos; k = tamaño de grupo, Se = sensibilidad; y Sp = especificidad de la prueba de laboratorio.
es el efecto de diseño para una prueba imperfecta bajo homogeneidad mediante pruebas de grupo; g = n/k es el número de grupos requeridos; k = tamaño de grupo, Se = sensibilidad; y Sp = especificidad de la prueba de laboratorio.
Note en la Ec. 3 que si Se = Sp = 1 y k > 1, el tamaño de muestra se reduce al tamaño de muestra para una prueba perfecta con homogeneidad  ; es decir, se supone una prueba perfecta (Se = Sp = 1) al usar pruebas de grupo para el análisis de laboratorio. Por otro lado, si solamente k = 1 pero Se, Sp < 1, el tamaño de muestra para la prueba imperfecta (Ec. 3) es el tamaño de muestra requerido para una prueba binomial simple con sensibilidad y especificidad menor a 1, y es igual a (n/(Se +Sp -1)2) . Mientras que si Se = Sp = 1 y k = 1, el tamaño de la muestra es igual a n porque se convierte en una prueba binomial simple perfecta.
; es decir, se supone una prueba perfecta (Se = Sp = 1) al usar pruebas de grupo para el análisis de laboratorio. Por otro lado, si solamente k = 1 pero Se, Sp < 1, el tamaño de muestra para la prueba imperfecta (Ec. 3) es el tamaño de muestra requerido para una prueba binomial simple con sensibilidad y especificidad menor a 1, y es igual a (n/(Se +Sp -1)2) . Mientras que si Se = Sp = 1 y k = 1, el tamaño de la muestra es igual a n porque se convierte en una prueba binomial simple perfecta.
La Ec 3 derivada para estimar los tamaños de muestra con pruebas de grupo y suponiendo homogeneidad, muestra claramente que si se usan pruebas de grupo para hacer las pruebas de laboratorio y la estimación del porcentaje de plantas transgénicas, el tamaño de muestra obtenido bajo el método binomial simple debe ajustarse por el incremento de variabilidad debido al uso de pruebas de grupo. Es decir, para obtener el tamaño de muestra con pruebas de grupo el tamaño de muestra binomial simple debe ajustarse por el factor de inflación de varianza (efecto de diseño) ocasionado por realizar las pruebas por grupos de k elementos. Por ello,  donde k es el tamaño del grupo, n el tamaño de muestra efectivo, y DeffPIH es el efecto de diseño para prueba imperfecta en presencia de homogeneidad. La Ec. 3 es válida porque el cálculo del tamaño de muestra es una función lineal de la varianza (Chen y Tipping, 2002). Para poder determinar los tamaños de muestra con la Ec. 3 hace falta determinar el tamaño de muestra efectivo (n) obtenido con la distribución binomial simple, con los supuestos de prueba perfecta y de homogeneidad.
donde k es el tamaño del grupo, n el tamaño de muestra efectivo, y DeffPIH es el efecto de diseño para prueba imperfecta en presencia de homogeneidad. La Ec. 3 es válida porque el cálculo del tamaño de muestra es una función lineal de la varianza (Chen y Tipping, 2002). Para poder determinar los tamaños de muestra con la Ec. 3 hace falta determinar el tamaño de muestra efectivo (n) obtenido con la distribución binomial simple, con los supuestos de prueba perfecta y de homogeneidad.
Derivación del tamaño de muestra efectivo bajo binomial simple
El cálculo del tamaño de muestra efectivo (n) que asegura intervalos de confianza angostos se hará con el enfoque APEP, también bajo el supuesto de una prueba perfecta y homogeneidad en la población. El estimador de máxima verosimilitud (EMV) de una proporción binomial (pruebas individuales) para una prueba perfecta es  , donde y es el número de éxitos observados en la muestra de tamaño n. De acuerdo con Vollset (1993) y Newcombe (1998), su correspondiente IC de Wald es:
, donde y es el número de éxitos observados en la muestra de tamaño n. De acuerdo con Vollset (1993) y Newcombe (1998), su correspondiente IC de Wald es:

donde pI denota el limite inferior del IC, ps denota el limite superior del  es el cuantil de una distribución normal estándar,
es el cuantil de una distribución normal estándar,  es el EMV
es el EMV  de p. Este IC es fácil de calcular y permite derivar fórmulas cerradas de estimadores de tamaño de muestra. Sin embargo, cuando n y p son pequeños este IC a menudo produce límites negativos. Además, la probabilidad de cobertura de este IC algunas veces es menor que 100(1 - α) %.
de p. Este IC es fácil de calcular y permite derivar fórmulas cerradas de estimadores de tamaño de muestra. Sin embargo, cuando n y p son pequeños este IC a menudo produce límites negativos. Además, la probabilidad de cobertura de este IC algunas veces es menor que 100(1 - α) %.
La cantidad añadida y substraída a  en la Ec. 4 se define como W/2. Los límites de confianza superior e inferior son determinados por W/2, la anchura media del intervalo de confianza (W es la anchura total del intervalo de confianza y se calcula como: W = ps - pI ). El grado de precisión del intervalo de confianza, que puede ser conceptualizado como W o W/2, es el valor de mayor interés dentro del marco APEP. Como se verá, el valor de W (o W/2) puede ser establecido a priori por el investigador de acuerdo con la precisión deseada del parámetro a estimar. La anchura total del IC (Ec. 4) es:
en la Ec. 4 se define como W/2. Los límites de confianza superior e inferior son determinados por W/2, la anchura media del intervalo de confianza (W es la anchura total del intervalo de confianza y se calcula como: W = ps - pI ). El grado de precisión del intervalo de confianza, que puede ser conceptualizado como W o W/2, es el valor de mayor interés dentro del marco APEP. Como se verá, el valor de W (o W/2) puede ser establecido a priori por el investigador de acuerdo con la precisión deseada del parámetro a estimar. La anchura total del IC (Ec. 4) es:

Para calcular el tamaño de la muestra necesario para la estimación del que garantice una amplitud IC deseada, n (que aquí se denomina np, tamaño de muestra preliminar) debe ser resuelto de la Ec. 5 haciendo W = ω, que resulta en la siguiente expresión:

La Ec. 6 aparece en la mayoría de los libros de muestreo estadístico (Cochran, 1977) y actualmente es utilizada para obtener el número requerido de individuos para estimar p con MAS. Sin embargo, el mayor inconveniente de esta ecuación es que supone que V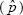 es conocida. Por ello en la Ec. 6, ésta es remplazada por la varianza poblacional. Esta ecuación encuentra el tamaño de muestra necesario para lograr una amplitud del IC (W) que es lo suficientemente estrecha para estimar la proporción de plantas transgénicas; sin embargo, no garantiza que para cualquier IC la amplitud observada (W) será lo suficientemente estrecha porque se utiliza una estimación de V
es conocida. Por ello en la Ec. 6, ésta es remplazada por la varianza poblacional. Esta ecuación encuentra el tamaño de muestra necesario para lograr una amplitud del IC (W) que es lo suficientemente estrecha para estimar la proporción de plantas transgénicas; sin embargo, no garantiza que para cualquier IC la amplitud observada (W) será lo suficientemente estrecha porque se utiliza una estimación de V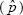 . En realidad, la amplitud del IC, W, es una variable aleatoria que fluctúa de muestra a muestra. Esto implica que alrededor de 50 % de las veces el valor observado de W será menor o igual a ω (Montesinos-López et al., 2010). Por esta razón, en la siguiente sección se propone un método de muestreo que asegura con una alta probabilidad que la amplitud del intervalo de confianza sea corta.
. En realidad, la amplitud del IC, W, es una variable aleatoria que fluctúa de muestra a muestra. Esto implica que alrededor de 50 % de las veces el valor observado de W será menor o igual a ω (Montesinos-López et al., 2010). Por esta razón, en la siguiente sección se propone un método de muestreo que asegura con una alta probabilidad que la amplitud del intervalo de confianza sea corta.
Derivación del tamaño de muestra óptimo que asegura intervalos de confianza cortos
La amplitud del IC para p es  debe ser menor o igual que un valor determinado (ω), con una probabilidad γ. Donde γ es el nivel de aseguramiento deseado (γ ≥ 0.5). Por tanto, el tamaño de muestra óptimo se define como el valor entero más pequeño (nm ) tal que la probabilidad que la anchura observada del IC sea menor que la amplitud especificada, es decir,
debe ser menor o igual que un valor determinado (ω), con una probabilidad γ. Donde γ es el nivel de aseguramiento deseado (γ ≥ 0.5). Por tanto, el tamaño de muestra óptimo se define como el valor entero más pequeño (nm ) tal que la probabilidad que la anchura observada del IC sea menor que la amplitud especificada, es decir,

Dado que la distribución de  es desconocida, no es posible obtener una solución analítica para nm. Una alternativa es utilizar el método delta para obtener la distribución asintótica de
es desconocida, no es posible obtener una solución analítica para nm. Una alternativa es utilizar el método delta para obtener la distribución asintótica de  (los detalles de este método se pueden consultar en Casella y Berger, 2002, capítulo 5 sección 5.4). Se sabe que
(los detalles de este método se pueden consultar en Casella y Berger, 2002, capítulo 5 sección 5.4). Se sabe que  = y / n y
= y / n y  Note que σ2 tiende a cero si nm tiende a infinito,
Note que σ2 tiende a cero si nm tiende a infinito,  es diferenciable con respecto a p ∈ (0 , 1) y la primera derivada de esta función es igual a:
es diferenciable con respecto a p ∈ (0 , 1) y la primera derivada de esta función es igual a:  para
para  . Por tanto, mediante el método delta,
. Por tanto, mediante el método delta,  , se obtiene que:
, se obtiene que:  donde
donde 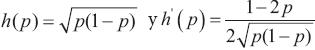
Por tanto, la Ec. 7 puede reescribirse como:

Esto es equivalente a:  y se puede expresar como:
y se puede expresar como:

Note que la Ec. 8 tiene una forma cuadrática: ax2 + bx + c = 0, con  , con dos soluciones dadas por
, con dos soluciones dadas por  . Para
. Para  y un valor fijo de ω, el tamaño de muestra requerido es:
y un valor fijo de ω, el tamaño de muestra requerido es:

donde np es el tamaño de muestra preliminar (reportado en la Ec. 6) sin nivel de aseguramiento (γ = 0.5). γ representa el grado deseado de seguridad (probabilidad requerida) para lograr una amplitud del IC (W) que no supera al valor deseado (ω). Zy es el cuantil γ de la distribución normal estándar. Note que si γ = 0.5, Z = 0 porque corresponde al cuantil 50 % de una distribución normal estándar y esto provoca que la Ec. 9 se reduzca a la Ec. 6 que proporciona el número requerido de individuos, al suponer conocida la varianza V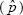 , pero esto implica que la amplitud deseada se logrará solamente alrededor de 50 % de las veces. La Ec. 9 es apropiada para la determinación del tamaño de muestra para pruebas individuales (porque k = 1) y garantiza que W será menor o igual a ω con una probabilidad γ. En otras palabras, sólo (1 - γ) 100 % de las veces W será mayor que la amplitud deseada (ω). Por tanto, al combinar las Ecs. 3 y 9 se obtiene el tamaño de muestra requerido (número de grupos) con el uso de pruebas de grupo bajo homogeneidad y suponiendo una prueba de laboratorio imperfecta, cuya expresión puede reescribirse como:
, pero esto implica que la amplitud deseada se logrará solamente alrededor de 50 % de las veces. La Ec. 9 es apropiada para la determinación del tamaño de muestra para pruebas individuales (porque k = 1) y garantiza que W será menor o igual a ω con una probabilidad γ. En otras palabras, sólo (1 - γ) 100 % de las veces W será mayor que la amplitud deseada (ω). Por tanto, al combinar las Ecs. 3 y 9 se obtiene el tamaño de muestra requerido (número de grupos) con el uso de pruebas de grupo bajo homogeneidad y suponiendo una prueba de laboratorio imperfecta, cuya expresión puede reescribirse como:
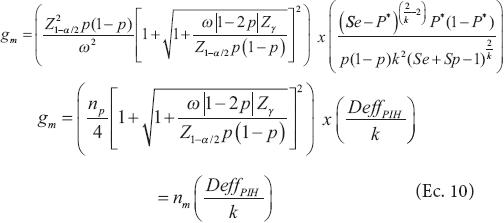
Donde  y
y
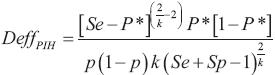
Es importante mencionar que el nivel de aseguramiento debe ser mayor o igual a 50 % (γ ≥ 0.5) y se denominará tamaño de muestra preliminar o número de grupos preliminar gp cuando el nivel de aseguramiento sea igual a 50 % (γ = 0.5) y número de grupos modificado (número de grupos modificados, gm) cuando se utilice un nivel de aseguramiento mayor a 50 % (γ > 0.5). El valor de p a utilizarse en la Ec. 10 normalmente es desconocido, pero puede ser estimado con un estudio piloto o usar el valor de la proporción (p) reportado en estudios similares obtenidos de una revisión de literatura.
RESULTADOS Y DISCUSIÓN
Ilustración del método propuesto para determinar el tamaño de muestra
A continuación se ilustra en detalle la forma de hacer los cálculos para estimar el tamaño de muestra necesario que asegura precisión en la estimación de la proporción (p). Este ejemplo es para estimar la proporción (p) de soya (Glycine max L.) transgénica. Si se postula que p = 0.01 y que la amplitud deseada del IC es 0.05, entonces da un W = [(pS - pI )] ≤ ω = 0.5, y un IC de 95 %  . Además, dado que el investigador no sabe de la existencia del método de Dorfman (pruebas de grupos) entonces realizará una prueba de laboratorio por planta (k = 1); es decir, usará el modelo binomial. También supone que la prueba de laboratorio es perfecta (Se = Sp = 1). Con estos valores y bajo el modelo binomial simple (Ec. 6) se obtiene que el tamaño de muestra requerido es:
. Además, dado que el investigador no sabe de la existencia del método de Dorfman (pruebas de grupos) entonces realizará una prueba de laboratorio por planta (k = 1); es decir, usará el modelo binomial. También supone que la prueba de laboratorio es perfecta (Se = Sp = 1). Con estos valores y bajo el modelo binomial simple (Ec. 6) se obtiene que el tamaño de muestra requerido es:

Sin embargo, note que np = 61 plantas proporciona una amplitud del IC menor que 0.05 solamente la mitad de las veces; es decir, la probabilidad de que se cumpla la amplitud deseada del IC es aproximadamente de 50 %. Por tanto, el investigador incorpora un nivel de aseguramiento de γ = 0.99, lo cual implica que la amplitud absoluta del IC de 95 % será más grande que el ω requerido no más de 1 % de las veces; es decir, la probabilidad de que se cumpla la amplitud absoluta del IC es de 99 %. Dado que γ = 0.99, Zγ = 0.99 = 2.327. Por tanto, el tamaño de muestra modificado (Ec. 9) será:

Con este tamaño de muestra (201 plantas) garantizará con una probabilidad de 99 % que el IC obtenido para p no será más grande que 0.05 unidades. Un problema que el investigador enfrenta ahora es que necesita realizar 201 pruebas de laboratorio, lo cual se sale de su presupuesto. Al buscar alternativas para hacer la estimación de la proporción sin pérdida significativa de la precisión que tendría con las 201 pruebas, el investigador se entera de que el método de Dorfman es una excelente solución. Por tanto, después de una revisión de literatura decide que el tamaño del grupo será igual a k = 10. Sin embargo, ahora la prueba ya no es perfecta, ya que la sensibilidad y especificidad será igual Se = Sp = 0.96. Esto implica que la P* (probabilidad corregida de que un grupo sea positivo; P* = (1 -(1 - p)k ) Se +(1 - Sp)k (1 - Sp)), que al sustituir p, Se y Sp por sus valores da: P* = (1 -(1 - 0.01)10 ) 0.96 +(1 - 0.01)10 (1 - 0.96)=0.12797 y así gm (Ec. 10) será igual a:

Por tanto, el tamaño de muestra requerido (número de grupos) es igual a 33 bajo el marco del modelo de Dorfman.
Dado que sólo se está interesado en estimar la proporción de plantas transgénicas, no es necesario hacer pruebas individuales dentro de los grupos que resulten positivos. Esto implica que sólo se requerirán 33 pruebas de laboratorio en lugar de las 201 requeridas con pruebas individuales, lo que significa un ahorro de 83.58 % en el número de pruebas de laboratorio y garantizan la misma precisión que con las 201 pruebas individuales de laboratorio. Finalmente, suponga que el investigador estima la proporción de plantas transgénicas con las g = 33 pruebas de laboratorio hechas con tamaños de grupo de tamaño k =10, y que tres resultaron positivas (y = 3) para la presencia de un transgen en particular. Como se sabe que Se = Sp = 0.96, la proporción p de plantas GM se estima con;

es decir, se estima que 0.568 % de las plantas de tal población están genéticamente modificadas.
Cuadros para determinar el tamaño de muestra
La fórmula obtenida (Ec. 10) se puede utilizar para obtener el tamaño de muestra necesario que asegura precisión en la estimación de la proporción (p) para cualquier combinación de k, p, ω, α, γ, Se y Sp. También se presentan cuadros para algunos escenarios útiles para los investigadores, los cuales no pretenden incluir todas las condiciones potencialmente interesantes, sino que tienen por objeto proporcionar: 1) Una forma cómoda para planificar el tamaño de la muestra cuando la situación de interés se aproxima por los escenarios contemplados en los cuadros, y 2) Una forma de ilustrar la relación entre k, p, ω, α, γ, Se, Sp y el tamaño de la muestra necesario (gm). Los planes de muestreo más agresivos en la práctica para la detección y estimación de plantas transgénicas han utilizado a lo más 50 000 semillas o plantas. Por tanto, para brindar tamaños de muestra útiles para los investigadores, el ancho de los intervalos de confianza para los escenarios propuestos fueron seleccionados de manera que el número total de plantas a examinar estén por debajo de 50 000. Los investigadores pueden calcular tamaños de muestra para escenarios particulares con esta fórmula propuesta o con el programa en R que se propone (Apéndice).
En este apartado se considera que la prueba es imperfecta, es decir que su sensibilidad y especificidad son menores a 100 %, o 1 en proporción. Los valores de los tamaños de muestra que se exponen en esta sección son para tamaños de grupo (k) de 40 con una confiabilidad de 95 %. Los valores de la proporción (p) son de 0.005, 0.01, 0.015 y 0.020; los valores del error absoluto (ω) van desde 0.006 a 0.014 con incrementos de 0.001. Los valores de sensibilidad (Se) son: 0.92, 0.94 y 0.96 (Cuadro 1); para una especificidad (Sp) de 0.96. De la misma forma, los valores de la especificidad (Sp) son: 0.92, 0.94 y 0.98 (Cuadro 2), para una sensibilidad de 0.96. Los resultados de cada cuadro se presentan en tres subcuadros. Un subcuadro con el número preliminar de grupos (gp) sin nivel de aseguramiento (γ = 0.5), junto con dos subcuadros con el número modificado de grupos (gm) para valores de γ de 0.9 y 0.99. Para todas estas combinaciones se tiene un total de 648 situaciones para planificar un tamaño de muestra adecuado. Además, se aprecia que al aumentar la imperfección de la prueba se incrementa el tamaño de muestra requerido.
Suponga que un investigador necesita estimar la proporción (p) de maíz (Zea mays L.) transgénico. Se plantea hipotéticamente que el IC = 1 - α = 95 %, p = 0.020, Se = 0.96, Sp = 0.96, y k = 40. Además, se asume que la amplitud absoluta deseada del IC es 0.006, W = [(pS - pI)] < ω = 0.0006. Con el uso de estos valores y bajo este método propuesto se obtiene que el número preliminar de grupos requeridos es gp = 378 cada uno de tamaño k = 40. Este tamaño de muestra está contenido en la primera sección del Cuadro 1 (gp sin γ; γ = 0.5, k = 40, p = 0.020, Se = 0.96, Sp = 0.96, y ω = 0.006).
De igual manera, note que gp = 378 proporcionará una amplitud del IC menor que 0.006 con una probabilidad aproximadamente de 50 %. Por tanto, el investigador agregará un nivel de aseguramiento de γ = 0.90, lo cual implica que la amplitud del IC de 95 % será más grande que el ω requerido no más que 10 % de las veces; es decir, la probabilidad de que se cumpla la amplitud absoluta del IC es de 90 %. El tamaño de grupos modificado será 413, cada uno de tamaño k = 40. Con este tamaño de muestra se garantiza, con una probabilidad de 90 %, que el IC obtenido para p no será más grande que 0.006 unidades. Este número de grupos modificados se obtiene en el segundo subcuadro del Cuadro 1 (gm con γ = 0.90, donde k = 40, p = 0.020, Se = 0.96, Sp = 0.96, y ω = 0.006). El Cuadro 2 se usa de la misma manera.
Finalmente, se hace notar que los cuadros que se presentan no cubren todas las posibles combinaciones (ω, k, p, γ, α, Se, Sp), porque el investigador las puede estimar con la Ecuación 10 aquí propuesta. También se desarrolló un programa en R para hacer los cálculos de la formula derivada que facilita al investigador el cálculo del tamaño de muestra requerido, programa que se presenta en el Anexo.
CONCLUSIONES
La ventaja de usar pruebas de grupo es que produce ahorros hasta de 80 % en el número pruebas de laboratorio. Sin embargo, hay que mencionar que el modelo de Dorfman es muy eficiente siempre que la proporción p que se desea estimar sea pequeña (menor a 10 %). Aunque los tamaños de muestra obtenidos no son exactos, son mucho más fáciles de calcular porque se derivan de una fórmula. Además, dado que se derivan bajo el enfoque de aseguramiento de precisión en la estimación de parámetros garantizan precisión en la estimación de la prevalencia. Por tanto, las pruebas de grupo son una excelente opción para los esquemas de muestreo en presencia de homogeneidad que hasta ahora no se han derivado bajo este enfoque en forma analítica.
BIBLIOGRAFĺA
Bilder C R (2009) Human or Cylon? Group Testing on Battlestar Galáctica. Chance 22:46-50. [ Links ]
Casella G, R L Berger (2002) Statistical Inference. Snd ed. Duxbury Press, Florida, USA. 660 p. [ Links ]
Chen C, R W Tipping (2002) Confidence interval for a proportion with over-dispersion. Biometrical J. 44:877-886. [ Links ]
Cleveland D A, D Soleri, F Aragón-Cuevas, J Crossa, P Gepts (2005) Detecting (trans) gene flow to landraces in centers of crop origin: lessons from the case of maize in Mexico. Environ. Biosafety Res. 4:197-208. [ Links ]
Cochran W G (1977) Sampling Techniques. 3rd ed. Wiley, New York, USA. 428 p. [ Links ]
Dyer G A, J A Serratos-Hernández, H R Perales, P Gepts, A Piñeyro-Nelson, A Chavez, N Salinas-Arreortua, A Yúnez-Naude, J E Taylor, E R Alvarez-Buylla (2009) Dispersal of transgenes through maize seed systems in Mexico. PLOS ONE 4:e5734. [ Links ]
Dodd R, E Notari, S Stramer (2002) Current prevalence and incidence of infectious disease markers and estimated window-period risk in the American Red Cross donor population. Transfusion 42:975-979. [ Links ]
Faes C, G Molengerghs, M Aerts, G Verbeke, M G Kenward (2009) The effective sample size and an alternative small-sample degrees-of-freedom method. The Amer. Statist. 63:389-399. [ Links ]
Hernández-Suárez C M, O A Montesinos-López, G McLaren, J Crossa (2008) Probability models for detecting transgenic plants. Seed Sci. Res. 18:77-89. [ Links ]
Kline R L, T A Brothers, R Brookmeyer, S Zeger, T C Quinn (1989) Evaluation of human immunodeficiency virus seroprevalence in population surveys using pooled sera. J. Clinical Microbiol. 27:1449-1452. [ Links ]
Kelley K (2007a) Sample size planning for the coefficient of variation from the accuracy in parameter estimation approach. Behavior Res. Meth. 39:755-766. [ Links ]
Kelley K (2007b) Methods for the Behavioral, Educational, and Social Sciences (MBESS) [Computer software for the Behavioral, Educational, and and manual]. Retrievable from: www.cran.r-project.org/. [ Links ]
Kelley K (2007c) CIs for standardized effect sizes: Theory, application, and implementation. J. Statist. Software 20:1-24. [ Links ]
Kelley K, S E Maxwell (2003) Sample size for multiple regression: Obtaining regression coefficients that are accurate, not simply significant. Psychol. Methods 8:305-321. [ Links ]
Kelley K, S E Maxwell, J R Rausch (2003) Obtaining power or obtaining precision: Delineating methods of sample size planning. Eval. & Health Profes. 26:258-287. [ Links ]
Kelley K, J R Rausch (2006) Sample size planning for the standardized mean difference: Accuracy in parameter estimation via narrow confidence intervals. Psychol. Methods 11:363-385. [ Links ]
Kline R L, T A Brothers, R Brookmayer, S Zeger, T C Quinn (1989) Evaluation of human immunodeficiency virus seroprevalence surveys using pooled sera. J. Clin. Microbiol. 27:1449–1452. [ Links ]
Kupper L L, K B Hafner (1989) How appropriate are popular sample size formulas? The Amer. Statist. 43:101-105. [ Links ]
Mace A E (1964) Sample Size Determination. Reinhold Publishing Group. New York, USA. 226 p. [ Links ]
Montesinos-López O A, A Montesinos-López, J Crossa, K Eskridge, C M Hernández-Suárez (2010) Sample size for detecting and estimating the proportion of transgenic plants with narrow confidence intervals. Seed Sci. Res. 20:1-14. [ Links ]
Newcombe, R. G. (1998) Two-sided CIs for the single proportion: comparison of seven methods. Stat. Med. 17:857-872. [ Links ]
Ortiz-García S, E Ezcurra, B Schoel, F Acevedo, J Soberón, A A Snow (2005a) Absence of detectable transgenes in local landraces of maize in Oaxaca, Mexico (2003-2004). Proc. Natl. Acad. Sci. USA 102:12338-12343. [ Links ]
Ortiz-García S, E Ezcurra, B Schoel, F Acevedo, J Soberón, A A Snow (2005b) Correction. Proc. Natl. Acad. Sci. USA 102:18242. [ Links ]
Ortiz-García S, E Ezcurra, B Schoel, F Acevedo, J Soberón, A A Snow (2005c) Reply to Cleveland et al. "Detecting (trans)gene flow to landraces in centers of crop origin: lessons from the case of maize in Mexico." Environ. Biosafety Res. 4:209-215. [ Links ]
Quist D, I H Chapela (2001) Transgenic DNA introgressed into traditional maize landraces in Oaxaca, Mexico. Nature 414:541-543. [ Links ]
Quist D, I H Chapela (2002) Quist and Chapela reply. Nature 416:602. [ Links ]
Otero-Arnaiz,A (2007) La Importancia de Tener una Red de Monitoreo (ambiental) de OGM en México. Dirección General de Investigación en Ordenamiento Ecológico y Conservación de los Ecosistemas.: Disponible en: http://www2.ine.gob.mx/bioseguridad/descargas/1ertallermonitoreo_adriana_otero.pdf (Enero 2010). [ Links ]
Pan Z, L Kupper (1999) Sample size determination for multiple comparison studies treating confidence interval width as random. Statist. Med. 18:1475-1488. [ Links ]
Peck C (2006) Going after BVD. Beef 42:34-44. [ Links ]
Piñeyro-Nelson A, J van Heerwaarden, H R Perales, J A Serratos-Hernández, A Rangel, M B Hufford, P Guepts, A Garay-Arroyo, R Rivera-Bustamante, E R Álvarez-Buylla (2009) Transgenes in Mexican maize: molecular evidence and methodological considerations for GMO detection in landrace populations. Mol. Ecol. 18:750-761. [ Links ]
Remlinger K, J Hughes-Oliver, S Young, R Lam (2006) Statistical design of pools using optimal coverage and minimal collision. Technometrics 48:133-143. [ Links ]
Remund K M, D A Dixon, D L Wright, L R Holden (2001) Statistical considerations in seed purity testing for transgenic traits. Seed Sci. Res. 11:101–120. [ Links ]
Tebbs J M, C R Bilder (2004) Confidence intervals procedures for probability of disease transmission in multiple-vector-transfer designs. J. Agric. Biol. Environ. Stat. 9:79-90. [ Links ]
Tu X M, E Litvak, M Pagano (1994) Studies of aids and HIV surveillance. Screening tests: Can we get more by doing less. Stat. Med. 13:1905-1919. [ Links ]
Verstraeten T, B Farah, L Duchateau, R Matu (1998) Pooling sera to reduce the cost of HIV surveillance: a feasibility study in a rural Kenyan district. Trop. Med. Internat. Health 3:747-750. [ Links ]
Vollset S E (1993) CIs for a binomial proportion. Stat. Med. 12:809-824. [ Links ]
Wang H, S C Chow, M Chen (2005) A bayesian approach on sample size calculation for comparing means. J. Biopharm. Stat. 15:799-807. [ Links ]
Wang Y, L L Kupper (1997) Optimal sample sizes for estimating the diference in means between two normal populations treating confidence interval length as a random variable. Comm. Stat. – Theory. Meth. 26:727-741. [ Links ]
Yamamura K, A Hino (2007) Estimation of the proportion of defective units by using group testing under the existence of a threshold of detection. Comm. Stat. – Simul. Comput. 36:949-957. [ Links ]














